Lanthanide f7 metalloxenes – a class of intrinsic 2D ferromagnets†
Andrey M.
Tokmachev
,
Dmitry V.
Averyanov
,
Alexander N.
Taldenkov
,
Oleg E.
Parfenov
,
Igor A.
Karateev
,
Ivan S.
Sokolov
 and
Vyacheslav G.
Storchak
and
Vyacheslav G.
Storchak
 *
*
National Research Centre “Kurchatov Institute”, Kurchatov Sq. 1, Moscow 123182, Russia. E-mail: mussr@triumf.ca
First published on 16th April 2019
Abstract
As the thickness of layered compounds approaches the monolayer limit, new electronic states and properties emerge. The sheer range of such properties is astounding but the list did not include intrinsic magnetism. Until recently. At the moment, several compounds do reveal intrinsic ferromagnetism at the 2D limit. However, they seem to be chemically and structurally unrelated, which is not conducive to a systematic search of new 2D magnets. Here, we demonstrate that lanthanide metalloxenes form a class of intrinsic 2D ferromagnets. Their stoichiometric layered structure LnX2 is composed of a triangular lattice of lanthanide ions (Eu or Gd) coupled with a 2D Xene sheet, a honeycomb network formed by Si or Ge. The materials are synthesized by direct reaction between the elements, with varying thickness from the bulk down to 1 monolayer. The common pattern is transformation from 3D antiferromagnetism to 2D ferromagnetism as revealed by magnetization and electron transport measurements. This work sets a path for a rational synthesis of 2D magnets and study of their spin behaviors for spintronic applications.
New conceptsTraditional 2D materials are intrinsically non-magnetic. However, technological demand for robust and controllable magnetic order drives the search for atomically thin materials with intrinsic 2D ferromagnetism (FM). The first reports on intrinsic 2D FM in 3d-magnets whet the appetite for such materials but a coherent approach for their design/engineering is lacking: at the moment, the material landscape of 2D FMs is rather patchy – the compounds are chemically and structurally unrelated. We establish a systematic strategy to the development of an entire class of 2D FMs – lanthanide metalloxenes LnX2. The central concept is LEGO-like design of layered materials by combination of matching building blocks – graphene-like honeycomb networks of silicene and germanene with 2D lanthanide layers. A distinctive feature of this class of materials is 4f-magnetism, thus widening significantly the number of potential 2D FMs. Evolution from 3D antiferromagnetism to 2D ferromagnetism makes the common pattern of LnX2 magnetic behaviour. A remarkable advantage of the discovered materials is their seamless integration with the mature Si and Ge semiconductor technological platforms and compatibility with van der Waals heterostructures. The proposed conceptual approach may open new avenues for design of new 2D FM materials with extended functionality, for applications in spintronics and quantum computing. |
1. Introduction
Recent decades have witnessed momentous progress in spintronics, owing much to extensive research in magnetic thin films and interfaces. Nowadays, however, the demand for ultra-compact spintronics pushes magnetic materials to the 2D limit. Magnetism in 2D systems is suppressed by strong spin fluctuations which, nevertheless, can be sustained by magnetocrystalline anisotropy and/or long-range interactions. The enhanced and tunable fluctuations open a wide range of opportunities for the search of new materials exhibiting quantum and topological phases as well as for their implementation in novel devices.1,2 The traditional 2D materials are non-magnetic; magnetic states can be induced extrinsically by chemical functionalization and defects,3 engineering of edge states in nanoribbons4 or proximity to a ferromagnet (FM).5,6On the other hand, 2D atomic crystals containing regular patterns of magnetic ions provide a wider platform for studies of new phases and fundamental spin behaviors as well as designer van der Waals heterostructures. The intrinsic 2D FM has recently been discovered in atomically thin van der Waals materials Cr2Ge2Te67 and CrI3.8 FM already in the bulk, they acquire new properties: the effective Curie temperature of a few monolayers (MLs) of Cr2Ge2Te6 depends strongly on low magnetic fields,7 CrI3 changes its magnetic state from FM in 1 ML to antiferromagnetic (AFM) in 2 ML and then back to FM in 3 ML samples.8 These discoveries triggered a surge in studies of 2D FM systems. Experimentally, the list of such materials at the ML level has been extended to include VSe2,9 Fe3GeTe2,10 MnSe,11 CrBr3,12 EuSi2 and GdSi2,13 hematene Fe2O3.14 Intrinsic 2D FMs exhibit a remarkable behavior in electron transport, optics, and magnetic state manipulations. Studies of 2D CrI3 are especially prolific: they demonstrate giant tunneling magnetoresistance,15,16 helical luminescence,17 control over magnetism with electric fields and electrostatic doping.18–20 Strong gate-tunability of magnetism has been reported also in 2D Fe3GeTe221 and Cr2Ge2Te6.22
The material landscape of 2D FMs seems to be rather patchy, i.e. largely formed by compounds which are chemically and structurally unrelated. Discoveries of entire classes of 2D FM compounds may provide insights into the role of the chemical composition, leading to coherent strategies for a systematic search/design of new materials. Among the established 2D FMs, CrI38 and CrBr312 are chemically similar and may form a nucleus of a class despite differences in the atomic structure of their parent 3D compounds.23 However, extension of this class is not obvious: 2D CrX3 inherit their FM state from the bulk but FM is lacking among other layered transition metal (TM) halides.23 A promising approach is to derive 2D intrinsic FMs from van der Waals AFMs.24 Indeed, a number of layered AFM systems, such as TM halides, are composed of FM MLs,23 predicted to be a source of 2D FM materials.25 Another proposal to extend the above class is to half-substitute Cr for W.26 MLs of MnNX and CrCX (X = Cl, Br, I; C = S, Se, Te) are predicted to be a family of high-Tc FM semiconductors.27
A nucleus of a class of 2D FM materials can be recognized in lanthanide (Ln) disilicides GdSi2 and EuSi213 – 2D FMs emerging from the AFM bulk. The FM state in LnSi2 is not limited to 1 ML. The magnetic properties of EuSi2 and GdSi2 are quite similar.13 The similarity extends to electron transport which is strongly layer-controlled:28 the temperature dependence of the resistivity R(T) evolves from metallic Kondo-like log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) T for 4 ML to 1/T for 2 ML to semiconducting exp(Δ/T) for 1 ML; 1 ML LnSi2 demonstrate colossal negative magnetoresistance with an exponential dependence R(B).
T for 4 ML to 1/T for 2 ML to semiconducting exp(Δ/T) for 1 ML; 1 ML LnSi2 demonstrate colossal negative magnetoresistance with an exponential dependence R(B).
Potential extensions of the LnSi2 class follow from their structure which is composed of two coupled layers – formed by Ln and Si, respectively. The metal atoms arrange in a 2D triangular net as many other compounds of the same stoichiometry such as TM dihalides.23 Geometrical frustration of this lattice is expected for AFM interactions, a potential reason for the observed FM/AFM interplay.13 On the other hand, Si forms a lattice of silicene,29 the Si analogue of graphene established as a prospective material for electronics.30 Silicene is a member of the class of buckled 2D Xenes;31 buckling being a crucial factor determining their electronic and chemical properties.32,33 One can imagine that lanthanide metalloxenes LnX2 are the type of materials where 2D FM can be searched and found. Variations in the lanthanide ingredient of LnX2 are partially covered by probing Eu(II) and Gd(III);13 however, the study can be extended because silicides of Ln from Gd to Tm are isostructural.34
Here, we replace silicene with germanene,35 another 2D Xene. We synthesize films of EuGe2 and GdGe2, study their atomic structure, magnetic and transport properties. In particular, we track evolution of the magnetic state in LnGe2 with the film thickness; the materials exhibit 2D FM emerging from the AFM bulk. Thus, we establish lanthanide metalloxenes as a versatile class of intrinsic 2D FMs.
2. Results and discussion
2.1. MBE synthesis of LnGe2
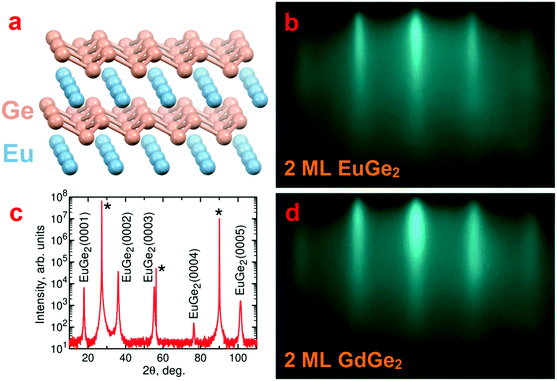
Our aim is to synthesize LnGe2 compounds combining layers of lanthanide Ln and germanene. The use of free-standing germanene is not an option because it requires stabilization by the surface of a substrate.36–39 Different MGe2 compounds with the germanene sublattice are known; it is likely that they host Dirac cone states, in analogy with their silicene counterparts.40 However, their main line of exploration is covalent functionalization via topotactic transformation35,41 producing germanane GeH42 and its derivatives. It has recently been recognized that the simple atomic structure of the Zintl phase 1T-EuGe2 (Fig. 1a) transforms into the GeH polytype with the simplest stacking motif.43For our purposes EuGe2 is an ideal candidate because its magnetism comes from Eu(II) with a half-filled f-shell which ensures a high spin moment and a vanishing orbital moment. The same applies to Gd(III) in GdGe2. Thus, magnetism in Eu- and Gd-based metalloxenes is expected to be more pronounced (in both AFM bulk and FM monolayers) than in other Ln-metalloxenes – a decisive factor for the selection of materials for magnetization measurements at such a featherweight level. Another reason for the use of Eu and Gd compounds is that they cover major differences in lanthanide metalloxenes – divalent vs. trivalent ions; buckled vs. flat 2D-Xene layers. Also, magnetic properties of both LnGe2 can be directly compared with their Si-based counterparts.13
Bulk EuGe2 is extensively studied44 and established as a phase prototype. It is synthesized by heating elemental Eu and Ge in a crucible.43,44 To get nanoscale films we carry out the same reaction
| Eu + 2Ge = EuGe2 |
2.2. Atomic structure of LnGe2 films
The atomic structure of the films is studied with a number of techniques. RHEED is very helpful in control of the surface state of the film in the growth chamber. Fig. 1b demonstrates a typical RHEED image for 2 ML EuGe2 which is characterized by well-developed streaks. The streaks appear in RHEED images of EuGe2 films of different thickness from 1 ML to the bulk (Fig. S1, ESI†) but the distance between them changes. This shift corresponds to a slight increase of the lateral lattice parameter a with the number of MLs, reaching 0.412(3) nm, close to the bulk value 0.41035(1) nm.44 The parameter c in thick EuGe2 films is determined from the θ–2θ XRD scan (Fig. 1c). The extracted c = 0.49804(4) nm agrees well with the bulk value 0.49972(3) nm.44 Only (000n) reflexes from EuGe2 and peaks from the Ge substrate show up certifying the absence of unwanted phases. The synthesis does not result in other Eu–Ge compounds (such as Eu2Ge, Eu5Ge3, EuGe, or Eu3Ge5) because of the presence of virtually unlimited source of Ge (the substrate).A similar picture is observed for GdGe2. Fig. 1d shows the RHEED image for 2 ML GdGe2; the evolution of RHEED from 1 ML to the bulk is illustrated by Fig. S1, ESI.† Ultrathin films are smooth but the roughness increases significantly in thick GdGe2 films. The parameters a = 0.401(3) nm (according to RHEED) and c = 0.4193(2) nm (according to XRD) in thick films of GdGe2 are smaller than those in EuGe2. The most significant difference is in the c parameter which arises from the flat vs. buckled structure of the germanene sublattice in the two compounds.
The structure of the films is further confirmed employing scanning transmission electron microscopy (STEM) in the HAADF mode. Fig. 2a presents a top view of bulk EuGe2 which comprises the triangular sublattice of Eu (brighter dots) and the honeycomb structure of germanene (dimmer dots). The side views on bulk EuGe2 (Fig. 2b) and GdGe2 (Fig. 2c) look different because the Ge layer is buckled in EuGe2 but flat in GdGe2. However, the situation with GdGe2 is more nuanced: the surface Ge layer in 1 ML GdGe2 (Fig. 2d) and 2 ML GdGe2 (Fig. 2e) is buckled as in both Gd silicide34 and a few ML EuGe2 (Fig. S2, ESI†). This buckling is probably a reason for ∼4% larger c parameter in 2 ML GdGe2 than that in the bulk. The termination of the films with a germanene layer may be employed for engineering of van der Waals ferromagnetic heterostructures48 and/or integration of 2D materials with the technological Ge platform. A major type of defects in the LnGe2 films comes from terraces present on the surface of the Ge substrate; they cause atomic steps in the films as illustrated by Fig. S3, ESI.† The lattice parameters in thick films determined by electron microscopy are in agreement with the data of RHEED and XRD. In particular, in EuGe2a = 0.411(4) nm and c = 0.500(4) nm while in GdGe2a = 0.401(3) nm and c = 0.424(3) nm.
2.3. Magnetism of 3D and 2D LnGe2
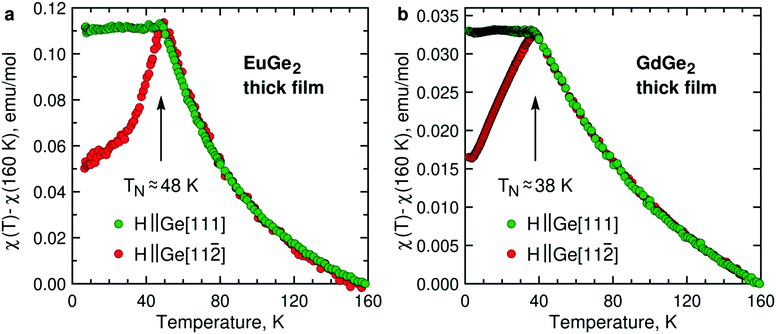
Magnetism is the focal point of this study. To demonstrate that the LnGe2 compounds join LnSi213 in forming a class of 2D FMs, it is sufficient to study a few ML films. However, much insight is gained by tracking changes in the magnetic structure and properties on the way from bulk to 1 ML. Fig. 3 presents temperature dependence of the AFM magnetic susceptibility in bulk films of EuGe2 and GdGe2. The measurements are carried out in two magnetic fields – directed out-of-plane (Ge[111]) and in-plane (Ge[11![[2 with combining macron]](https://www.rsc.org/images/entities/char_0032_0304.gif) ], the choice of in-plane direction is arbitrary because we do not detect any in-plane magnetic anisotropy). The dependences manifest a textbook 3D AFM in both materials. The Néel temperatures TN of EuGe2 and GdGe2 are ∼48 K and ∼38 K, respectively. The pattern observed for different magnetic field directions certifies that the AFM moments prefer the in-plane orientation, as in LnSi2.13 The two LnGe2 compounds seem to be quite similar in terms of magnetism. However, we observe a striking difference between the Curie–Weiss fits of the magnetic susceptibility in the paramagnetic state. While the effective moments in both LnGe2 are consistent with the 4f7 states of the Ln ions, the Curie–Weiss temperatures differ: in GdGe2θCW ≈ −80 K (not far from expectations for such an AFM compound) but in EuGe2θCW ≈ 0 K. This can be a consequence of competing interactions within the geometrically frustrated triangular lattice of Eu ions. Incidentally, bulk EuGe2 demonstrates a positive θCW ≈ 13 K suggesting weak FM coupling between the Eu moments.44 Thus, at least EuGe2 seems to be a promising candidate for the search of 2D FM.
], the choice of in-plane direction is arbitrary because we do not detect any in-plane magnetic anisotropy). The dependences manifest a textbook 3D AFM in both materials. The Néel temperatures TN of EuGe2 and GdGe2 are ∼48 K and ∼38 K, respectively. The pattern observed for different magnetic field directions certifies that the AFM moments prefer the in-plane orientation, as in LnSi2.13 The two LnGe2 compounds seem to be quite similar in terms of magnetism. However, we observe a striking difference between the Curie–Weiss fits of the magnetic susceptibility in the paramagnetic state. While the effective moments in both LnGe2 are consistent with the 4f7 states of the Ln ions, the Curie–Weiss temperatures differ: in GdGe2θCW ≈ −80 K (not far from expectations for such an AFM compound) but in EuGe2θCW ≈ 0 K. This can be a consequence of competing interactions within the geometrically frustrated triangular lattice of Eu ions. Incidentally, bulk EuGe2 demonstrates a positive θCW ≈ 13 K suggesting weak FM coupling between the Eu moments.44 Thus, at least EuGe2 seems to be a promising candidate for the search of 2D FM.
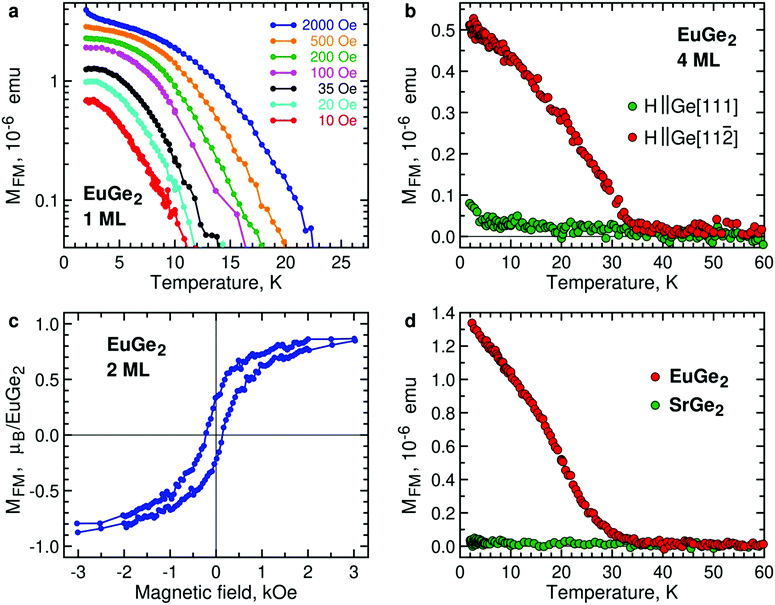
We consider EuGe2 films with a small number of MLs. Temperature dependence of the magnetic moment in 1 ML EuGe2 (Fig. 4a) certifies the emergence of 2D FM: not only the magnetic moment exhibits characteristic evolution but also the effective Curie temperature TC* is controlled by low magnetic fields. The latter property is a hallmark of 2D FM, observed in Cr2Ge2Te67 and LnSi2.13 FM is not limited to 1 ML samples. Fig. S4, ESI† provides data on FM in 2 ML, 4 ML and 9 ML EuGe2. One can notice that the dependence of TC* on low magnetic fields tends to disappear as the number of MLs increases. This fact is best illustrated by normalized temperature dependence curves M(T)/M(2 K) (Fig. S5, ESI†): a set of curves for different magnetic fields (as well as the remnant moment) in 1 ML EuGe2 merges into a single curve in 9 ML thick film.
The direction of the FM moments in 2D EuGe2 is determined from temperature dependence of the magnetic moment in magnetic fields of different orientation: according to Fig. 4b the FM moments are in-plane, as in LnSi2.13 In this case, the 2D FM is likely to be sustained by a combination of high magnetic anisotropy and dipolar interactions, suppressing thermal fluctuations of the local moments.49 The appearance of the FM state is accompanied by divergence of field-cooled (FC) and zero-field-cooled (ZFC) temperature dependences of magnetic moments (Fig. S6a, ESI†). M(H) curves in the FM state of 2 ML EuGe2 have the characteristic form with a sizable hysteresis loop (Fig. 4c). However, hysteresis disappears in 1 ML EuGe2 (Fig. S7, ESI†), probably due to difficulties of forming magnetic domains in the 2D limit. To demonstrate that the magnetism is not an artefact of the substrate or measurement procedure, we synthesized a few ML films of SrGe2 – a compound isomorphous to EuGe2, with close lattice parameters, albeit free of local magnetic moments. The comparison of 2 ML EuGe2 and 2 ML SrGe2 (Fig. 4d) certifies that the observed FM is an intrinsic property of EuGe2.
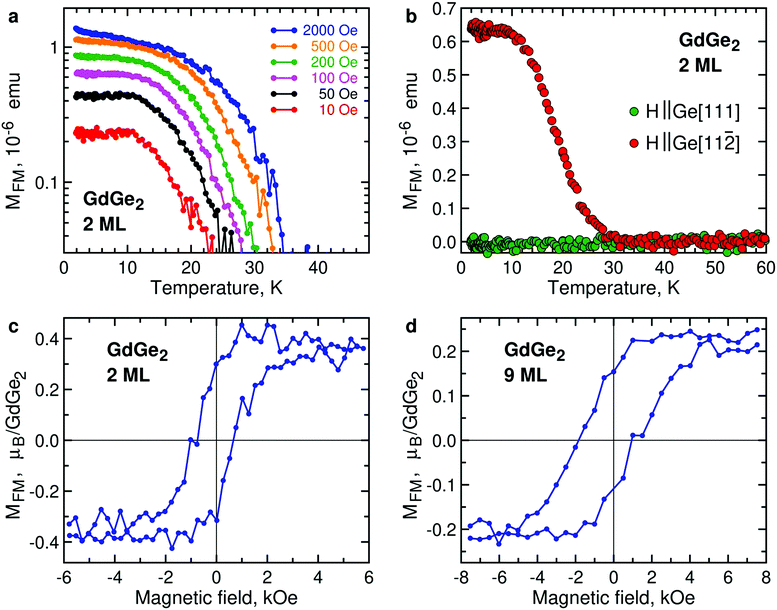
Ultrathin films of GdGe2 also demonstrate FM signals, as illustrated by temperature dependence of the magnetic moment of 2 ML GdGe2 (Fig. 5a). Lower (and therefore noisier) magnetization signals in 1 ML GdGe2 are demonstrated in Fig. S8, ESI.† As in other LnX2, the effective Curie temperature TC* is controlled by low magnetic fields. Another feature common with other 2D LnX2 compounds is that the FM moments prefer the in-plane orientation (Fig. 5b). As expected, the FM state in GdGe2 results in divergence of FC and ZFC curves (Fig. S6b, ESI†) as well as hysteresis in magnetic field dependence of magnetization (Fig. 5c). M(H) measurements for GdGe2 films of intermediate thickness suggest a negative shift of the FM hysteresis loop (Fig. 5d). The exchange bias seems not very much surprising for a system with the thickness-dependent AFM-to-FM transition. The exchange bias field diminishes as the film approaches the 2D limit: ∼470 Oe in 9 ML GdGe2 and ∼300 Oe in 6 ML GdGe2, both at 2 K.
2D EuSi2 and GdSi2 exhibit quantitatively similar magnetic properties, in particular the FM moments are slightly less than 1 μB per formula unit at saturation.13 We expected the same situation for EuGe2 and GdGe2. The saturation moment MS of the film can be normalized either to surface area S or formula unit. Dependence of MS/S on the number of MLs in EuGe2 (Fig. S9a, ESI†) certifies the emerging character of the FM: it increases strongly as the film thins down. On the other hand, in GdGe2 the analogous dependence is not monotonic (Fig. S10a, ESI†): it looks like some mechanism suppressing FM in ultrathin films is still in play. In EuGe2, the saturation moment reaches almost 3 μB per formula unit (for 1 ML, Fig. S9b, ESI†). Such a high value can only be explained by magnetic ordering of Eu ion moments (DFT calculations show that Ge orbitals in EuGe2 are magnetically inactive44). In contrast, the saturation moment in GdGe2 is an order of magnitude smaller than that in EuGe2 (Fig. S10b, ESI†). An explanation of this difference would probably require a detailed theoretical analysis of the electronic and magnetic structures of these strongly correlated materials, which is out of scope of the present experimental study.
2.4. Electron transport in LnGe2 films
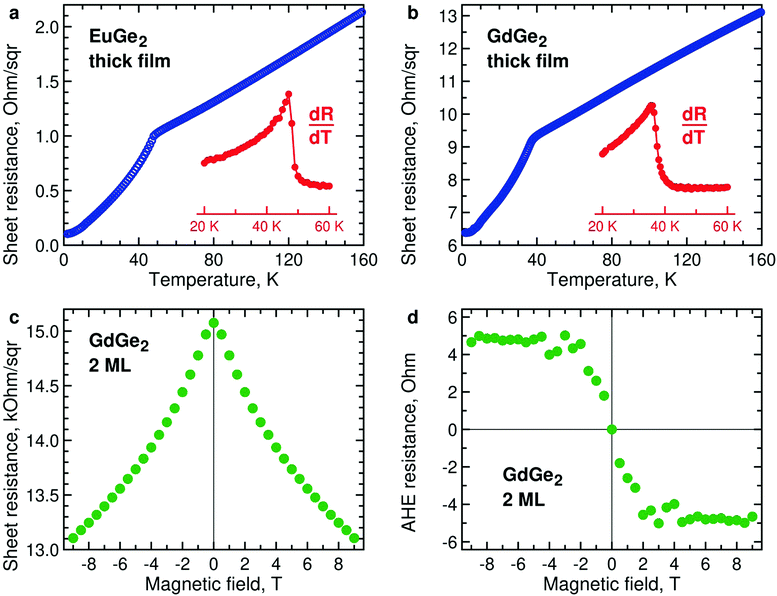
The magnetization measurements are supported by those of lateral electron transport. Temperature dependences of resistance of thick films of EuGe2 (Fig. 6a) and GdGe2 (Fig. 6b) demonstrate pronounced features at the corresponding Néel temperatures – 48 K and 38 K. Below TN, the resistance drops due to suppressed scattering in magnetically ordered systems. Both compounds are metals; thus, they belong to the so-called metallic Zintl phases. The metallic character of EuGe2 is in agreement with electronic structure calculations.44It would be interesting to study temperature dependences of the resistivity in a few ML LnGe2 films, in analogy with LnSi2.28 However, as the film thins down it expectedly becomes progressively insulating. As a result, the Ge substrate shunts current away from the ultrathin LnGe2 film. Nevertheless, the measurements are still possible at the lowest temperatures as the carriers in the substrate essentially freeze out. Fig. 6c demonstrates negative magnetoresistance in 2 ML GdGe2 at 2 K. It may indicate the emerging FM state, especially taking into account the typical positive magnetoresistance in the thick films of GdGe2. Fig. 6d illustrates magnetic field dependence of the anomalous Hall effect in the same film at 2 K – the behavior expected for a ferromagnet. Similar properties – negative magnetoresistance and anomalous Hall effect – are detected in ultrathin EuGe2 films (Fig. S11, ESI†).
3. Conclusions
In this paper, we address the general problem of finding a class of 2D FM materials. More specifically, we would like to establish whether lanthanide metalloxenes form such a class. This problem is still far too general. So, we follow a heuristic proposed by George Pólya in his classic How to Solve It: “If you can't solve a problem, then there is an easier problem you can solve: find it”. Thus, we consider changes in EuX2 and GdX2 brought up by replacement of silicene with germanene. We succeeded in synthesis and characterization of EuGe2 and GdGe2 structures ranging from the bulk down to 1 ML. This study establishes a small but likely to be extendable class of materials LnX2 (Ln = Eu or Gd, X = Si or Ge) which (i) share the same structural motif based on a triangular lattice of magnetic lanthanide ions; (ii) evolve from a paradigmatic 3D AFM to a 2D FM as soon as their thickness goes down. This result provides an excellent occasion to advocate for the use of lanthanide compounds in the rapidly growing field of functional 2D materials. The other intrinsic 2D FMs are based on 3d TMs; suggestions of new such systems do not go beyond “materials with 4d/5d elements”1 thus missing the whole range of opportunities provided by lanthanide magnets, not least in relation to spin–orbit coupling, strong correlations and local character of 4f-electrons. We envisage that the discovery of a class of lanthanide magnets would play an important role in finding new magnetic materials and spintronic applications, studies of fundamental spin systems.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work is supported by NRC “Kurchatov Institute”, the Russian Foundation for Basic Research [grant 19-07-00249] (magnetization measurements), and the Russian Science Foundation [grant 19-19-00009] (transport measurements). The measurements have been carried out using equipment of the resource centers of electrophysical, laboratory X-ray and electron microscopy techniques in NRC “Kurchatov Institute”.Notes and references
- K. S. Burch, D. Mandrus and J.-G. Park, Nature, 2018, 563, 47 CrossRef CAS.
- C. Gong and X. Zhang, Science, 2019, 363, eaav4450 CrossRef.
- H. González-Herrero, J. M. Gómez-Rodríguez, P. Mallet, M. Moaied, J. J. Palacios, C. Salgado, M. M. Ugeda, J.-Y. Veuillen, F. Yndurain and I. Brihuega, Science, 2016, 352, 437 CrossRef.
- M. Slota, A. Keerthi, W. K. Myers, E. Tretyakov, M. Baumgarten, A. Ardavan, H. Sadeghi, C. J. Lambert, A. Narita, K. Müllen and L. Bogani, Nature, 2018, 557, 691 CrossRef CAS.
- F. Katmis, V. Lauter, F. S. Nogueira, B. A. Assaf, M. E. Jamer, P. Wei, B. Satpati, J. W. Freeland, I. Eremin, D. Heiman, P. Jarillo-Herrero and J. S. Moodera, Nature, 2016, 533, 513 CrossRef CAS PubMed.
- D. V. Averyanov, I. S. Sokolov, A. M. Tokmachev, O. E. Parfenov, I. A. Karateev, A. N. Taldenkov and V. G. Storchak, ACS Appl. Mater. Interfaces, 2018, 10, 20767 CrossRef CAS PubMed.
- C. Gong, L. Li, Z. Li, H. Ji, A. Stern, Y. Xia, T. Cao, W. Bao, C. Wang, Y. Wang, Z. Q. Qiu, R. J. Cava, S. G. Louie, J. Xia and X. Zhang, Nature, 2017, 546, 265 CrossRef CAS PubMed.
- B. Huang, G. Clark, E. Navarro-Moratalla, D. R. Klein, R. Cheng, K. L. Seyler, D. Zhong, E. Schmidgall, M. A. McGuire, D. H. Cobden, W. Yao, D. Xiao, P. Jarillo-Herrero and X. Xu, Nature, 2017, 546, 270 CrossRef CAS PubMed.
- M. Bonilla, S. Kolekar, Y. Ma, H. C. Diaz, V. Kalappattil, R. Das, T. Eggers, H. R. Gutierrez, M.-H. Phan and M. Batzill, Nat. Nanotechnol., 2018, 13, 289 CrossRef CAS PubMed.
- Z. Fei, B. Huang, P. Malinowski, W. Wang, T. Song, J. Sanchez, W. Yao, D. Xiao, X. Zhu, A. F. May, W. Wu, D. H. Cobden, J.-H. Chu and X. Xu, Nat. Mater., 2018, 17, 778 CrossRef CAS PubMed.
- D. J. O’Hara, T. Zhu, A. H. Trout, A. S. Ahmed, Y. K. Luo, C. H. Lee, M. R. Brenner, S. Rajan, J. A. Gupta, D. W. McComb and R. K. Kawakami, Nano Lett., 2018, 18, 3125 CrossRef PubMed.
- D. Ghazaryan, M. T. Greenaway, Z. Wang, V. H. Guarochico-Moreira, I. J. Vera-Marun, J. Yin, Y. Liao, S. V. Morozov, O. Kristanovski, A. I. Lichtenstein, M. I. Katsnelson, F. Withers, A. Mishchenko, L. Eaves, A. K. Geim, K. S. Novoselov and A. Misra, Nat. Electron., 2018, 1, 344 CrossRef.
- A. M. Tokmachev, D. V. Averyanov, O. E. Parfenov, A. N. Taldenkov, I. A. Karateev, I. S. Sokolov, O. A. Kondratev and V. G. Storchak, Nat. Commun., 2018, 9, 1672 CrossRef PubMed.
- A. P. Balan, S. Radhakrishnan, C. F. Woellner, S. K. Sinha, L. Deng, C. de los Reyes, B. M. Rao, M. Paulose, R. Neupane, A. Apte, V. Kochat, R. Vajtai, A. R. Harutyunyan, C.-W. Chu, G. Costin, D. S. Galvao, A. A. Martí, P. A. van Aken, O. K. Varghese, C. S. Tiwary, A. M. M. R. Iyer and P. M. Ajayan, Nat. Nanotechnol., 2018, 13, 602 CrossRef PubMed.
- T. Song, X. Cai, M. W.-Y. Tu, X. Zhang, B. Huang, N. P. Wilson, K. L. Seyler, L. Zhu, T. Taniguchi, K. Watanabe, M. A. McGuire, D. H. Cobden, D. Xiao, W. Yao and X. Xu, Science, 2018, 360, 1214 CrossRef CAS PubMed.
- D. R. Klein, D. MacNeill, J. L. Lado, D. Soriano, E. Navarro-Moratalla, K. Watanabe, T. Taniguchi, S. Manni, P. Canfield, J. Fernández-Rossier and P. Jarillo-Herrero, Science, 2018, 360, 1218 CrossRef CAS PubMed.
- K. L. Seyler, D. Zhong, D. R. Klein, S. Gao, X. Zhang, B. Huang, E. Navarro-Moratalla, L. Yang, D. H. Cobden, M. A. McGuire, W. Yao, D. Xiao, P. Jarillo-Herrero and X. Xu, Nat. Phys., 2018, 14, 277 Search PubMed.
- S. Jiang, J. Shan and K. F. Mak, Nat. Mater., 2018, 17, 406 CrossRef CAS PubMed.
- B. Huang, G. Clark, D. R. Klein, D. MacNeill, E. Navarro-Moratalla, K. L. Seyler, N. Wilson, M. A. McGuire, D. H. Cobden, D. Xiao, W. Yao, P. Jarillo-Herrero and X. Xu, Nat. Nanotechnol., 2018, 13, 544 CrossRef CAS PubMed.
- S. Jiang, L. Li, Z. Wang, K. F. Mak and J. Shan, Nat. Nanotechnol., 2018, 13, 549 CrossRef CAS PubMed.
- Y. Deng, Y. Yu, Y. Song, J. Zhang, N. Z. Wang, Z. Sun, Y. Yi, Y. Z. Wu, S. Wu, J. Zhu, J. Wang, X. H. Chen and Y. Zhang, Nature, 2018, 563, 94 CrossRef CAS PubMed.
- Z. Wang, T. Zhang, M. Ding, B. Dong, Y. Li, M. Chen, X. Li, J. Huang, H. Wang, X. Zhao, Y. Li, D. Li, C. Jia, L. Sun, H. Guo, Y. Ye, D. Sun, Y. Chen, T. Yang, J. Zhang, S. Ono, Z. Han and Z. Zhang, Nat. Nanotechnol., 2018, 13, 554 CrossRef CAS PubMed.
- M. A. McGuire, Crystals, 2017, 7, 121 CrossRef.
- N. Miao, B. Xu, L. Zhu, J. Zhou and Z. Sun, J. Am. Chem. Soc., 2018, 140, 2417 CrossRef CAS PubMed.
- V. V. Kulish and W. Huang, J. Mater. Chem. C, 2017, 5, 8734 RSC.
- C. Huang, J. Feng, F. Wu, D. Ahmed, B. Huang, H. Xiang, K. Deng and E. Kan, J. Am. Chem. Soc., 2018, 140, 11519 CrossRef CAS PubMed.
- C. Wang, X. Zhou, L. Zhou, N.-H. Tong, Z.-Y. Lu and W. Ji, Sci. Bull., 2019, 64, 293 CrossRef CAS.
- O. E. Parfenov, A. M. Tokmachev, D. V. Averyanov, I. A. Karateev, I. S. Sokolov, A. N. Taldenkov and V. G. Storchak, Mater. Today, 2019 DOI:10.1016/j.mattod.2019.03.017.
- A. Molle, C. Grazianetti, L. Tao, D. Taneja, Md. H. Alam and D. Akinwande, Chem. Soc. Rev., 2018, 47, 6370 RSC.
- L. Tao, E. Cinquanta, D. Chiappe, C. Grazianetti, M. Fanciulli, M. Dubey, A. Molle and D. Akinwande, Nat. Nanotechnol., 2015, 10, 227 CrossRef CAS.
- A. Molle, J. Goldberger, M. Houssa, Y. Xu, S.-C. Zhang and D. Akinwande, Nat. Mater., 2017, 16, 163 CrossRef CAS PubMed.
- D. Jose and A. Datta, Acc. Chem. Res., 2014, 47, 593 CrossRef CAS.
- A. Nijamudheen, R. Bhattacharjee, S. Choudhury and A. Datta, J. Phys. Chem. C, 2015, 119, 3802 CrossRef CAS.
- S. Sanna, C. Dues, W. G. Schmidt, F. Timmer, J. Wollschläger, M. Franz, S. Appelfeller and M. Dähne, Phys. Rev. B, 2016, 93, 195407 CrossRef.
- N. Liu, G. Bo, Y. Liu, X. Xu, Y. Du and S. X. Dou, Small, 2019, 15, 1805147 CrossRef PubMed.
- M. E. Dávila, L. Xian, S. Cahangirov, A. Rubio and G. Le Lay, New J. Phys., 2014, 16, 095002 CrossRef.
- M. E. Dávila and G. Le Lay, Sci. Rep., 2016, 6, 20714 CrossRef PubMed.
- J. Zhuang, N. Gao, Z. Li, X. Xu, J. Wang, J. Zhao, S. X. Dou and Y. Du, ACS Nano, 2017, 11, 3553 CrossRef CAS PubMed.
- J. Yuhara, H. Shimazu, K. Ito, A. Ohta, M. Araidai, M. Kurosawa, M. Nakatake and G. Le Lay, ACS Nano, 2018, 12, 11632 CrossRef CAS PubMed.
- E. Noguchi, K. Sugawara, R. Yaokawa, T. Hitosugi, H. Nakano and T. Takahashi, Adv. Mater., 2015, 27, 856 CrossRef CAS PubMed.
- W. L. B. Huey and J. E. Goldberger, Chem. Soc. Rev., 2018, 47, 6201 RSC.
- E. Bianco, S. Butler, S. Jiang, O. D. Restrepo, W. Windl and J. E. Goldberger, ACS Nano, 2013, 7, 4414 CrossRef CAS PubMed.
- N. D. Cultrara, Y. Wang, M. Q. Arguilla, M. R. Scudder, S. Jiang, W. Windl, S. Bobev and J. E. Goldberger, Chem. Mater., 2018, 30, 1335 CrossRef CAS.
- S. Bobev, E. D. Bauer, J. D. Thompson, J. L. Sarrao, G. J. Miller, B. Eck and R. Dronskowski, J. Solid State Chem., 2004, 177, 3545 CrossRef CAS.
- A. M. Tokmachev, D. V. Averyanov, I. A. Karateev, O. E. Parfenov, A. L. Vasiliev, S. N. Yakunin and V. G. Storchak, Nanoscale, 2016, 8, 16229 RSC.
- A. M. Tokmachev, D. V. Averyanov, I. A. Karateev, O. E. Parfenov, O. A. Kondratev, A. N. Taldenkov and V. G. Storchak, Adv. Funct. Mater., 2017, 27, 1606603 CrossRef.
- D. V. Averyanov, A. M. Tokmachev, C. G. Karateeva, I. A. Karateev, E. F. Lobanovich, G. V. Prutskov, O. E. Parfenov, A. N. Taldenkov, A. L. Vasiliev and V. G. Storchak, Sci. Rep., 2016, 6, 25980 CrossRef CAS.
- D. Zhong, K. L. Seyler, X. Linpeng, R. Cheng, N. Sivadas, B. Huang, E. Schmidgall, T. Taniguchi, K. Watanabe, M. A. McGuire, W. Yao, D. Xiao, K.-M. Fu and X. Xu, Sci. Adv., 2017, 3, e1603113 CrossRef.
- P. Bruno, Phys. Rev. B: Condens. Matter Mater. Phys., 1991, 43, 6015 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c9mh00444k |
| This journal is © The Royal Society of Chemistry 2019 |

![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0] azimuth of the Ge substrate. (c)
0] azimuth of the Ge substrate. (c)