Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Bright and fast scintillation of organolead perovskite MAPbBr3 at low temperatures
Vitaliy B.
Mykhaylyk
 *a,
Hans
Kraus
b and
Michael
Saliba
*a,
Hans
Kraus
b and
Michael
Saliba
 *cd
*cd
aDiamond Light Source, Harwell Campus, Didcot, OX11 0DE, UK. E-mail: vitaliy.mykhaylyk@diamond.ac.uk
bUniversity of Oxford, Department of Physics, Denys Wilkinson Building, Keble Road, Oxford, OX1 3RH, UK
cAdolphe Merkle Institute, Chemin des Verdiers 4, CH-1700 Fribourg, Switzerland
dInstitute of Materials Science, Technical University of Darmstadt, Alarich-Weiss-Strasse 2, D-64287 Darmstadt, Germany. E-mail: miliba@gmail.com; michael.saliba@opto.tu-darmstadt.de
First published on 29th May 2019
Abstract
We report the excellent scintillation properties of MAPbBr3, an organic–inorganic trihalide perovskite (OTP). The characteristic scintillation time constants were determined using pulsed monochromatic 14 keV X-rays from a synchrotron. We find that between 50 and 130 K the MAPbBr3 crystal exhibits a very fast and intense scintillation response, with the fast (τf) and slow (τs) decay components reaching 0.1 and 1 ns, respectively. The light yield of MAPbBr3 is estimated to be 90![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 ± 18
000 ± 18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 ph MeV−1 at 77 K and 116
000 ph MeV−1 at 77 K and 116![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 ± 23
000 ± 23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 ph MeV−1 at 8 K.
000 ph MeV−1 at 8 K.
Conceptual insightsAt lower cryogenic temperatures, perovskite crystals show excellent scintillation properties in terms of signal output and quick response time. Such materials have been sought after for many decades and could dramatically impact the entire scintillation field. Importantly, the concept of cryogenic scintillation is underexplored and novel because established scintillators do not exhibit dramatically improved performance with decreased temperature. Perovskites, however, do and prove to be among the best scintillation materials measured to date. Remarkably, our work uses yet unoptimized crystals and thus it is possible that further improvements will be achieved over time. Operation at lower temperatures is already common for medical applications. Therefore, this work has the potential to trigger a new generation of cryogenic scintillators, as well as providing a new direction for the perovskite field. In particular, perovskites are promising for the medical sector because of the potential for improved cancer diagnostics through an increased imaging resolution, e.g. for early-stage brain cancer. Importantly, perovskites contain elements with a high atomic number (Z), e.g. Pb, making perovskites highly relevant scintillation materials. |
Scintillators detect ionising radiation by converting energy deposited in them to a proportional number of photons. They are omnipresent in large-scale technical and commercial applications around us. For example, they are found in many branches of physics, security scanners, and medical applications such as nuclear imaging for cancer diagnostics.1,2 An ideal scintillator emits a maximum number of scintillation photons per unit energy deposited, has a high absorption coefficient for gamma quanta, and exhibits a narrow timing profile for its scintillation photons. Brighter and faster scintillators facilitate better timing resolution, which is crucial for measuring the time of the initial particle or radiation interaction with high precision. At present, the dominant limitation of modern scintillators is their timing resolution. The state-of-the-art resolution in coincidence timing has just broken the 100 ps barrier, with the lowest value of 73 ± 2 ps reported for LSO-Ce scintillators3 and 80 ± 4 ps in LGSO-Ce.4 The main limitation towards the ambitious goal of 10 ps resolution is the low light yield and the long decay time of scintillators.5,6 Currently, the best scintillator for this application is deemed to be LaBr3-Ce, exhibiting 16 ns decay time and 70
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 ph MeV−1.7 However, this is still far from ideal. To achieve a timing resolution below 10 ps, a scintillator with a light yield of at least 140
000 ph MeV−1.7 However, this is still far from ideal. To achieve a timing resolution below 10 ps, a scintillator with a light yield of at least 140![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 ph MeV−1 and a decay time of ≤1 ns is required.5,8
000 ph MeV−1 and a decay time of ≤1 ns is required.5,8
Despite the decades of intensive effort, it has been found that meeting all requirements in one material is very difficult; hence nowadays the strategy is to develop and optimize scintillators for specific applications.9 Recently, hybrid metal–halide perovskites have attracted considerable attention. These materials have had a long history, with the first studies of photoconductivity in CsPbX3 (X = Cl, Br or I) carried out in 1958,10 revealing semiconducting behaviour. A shift towards organic–inorganic materials occurred in 1978 when small molecules were included.11 A number of investigations on structure, optical and luminescence properties were published in the following decades, albeit in studies that were not necessarily aimed at application. A drastic change occurred a few years ago with a significant increase in interest due to the rapid evolution of solid-state photovoltaics based on organic–inorganic trihalide perovskites (OTPs) – materials with the general formula MAPbX3, where MA = methylammonium and X = Cl, Br and I.12 It was quickly realised that the remarkable physical properties of OTPs, in particular the exceptional tolerance of their optical and electronic characteristics to structural defects, made them highly attractive for various optoelectronic applications. In particular, the outstanding high photoluminescence quantum yield of OTPs enabled bright light-emitting devices and lasers,13,14 whereas their high current conversion efficiency upon light exposure underpins their application as photodetectors.15 Photovoltaic OTPs have also stimulated solar cell research. However, due to the Shockley–Queisser limit, photovoltaic perovskites are typically tuned to a very narrow band gap range, thus excluding the majority of high-quality perovskites, especially those with larger band gaps.
Less attention was paid to higher-mass elements with a correspondingly high atomic number (Z) used in OTPs, i.e. Pb, Br and I atoms, which make OTPs inherently suitable for applications in which good X-ray absorption capability is required since the cross section increases with ∼Z4. Furthermore, OTPs exhibit a high mobility of charge carriers, which makes them optimal for radiation detection through direct conversion of X-ray photons into current. Detection of soft X-rays (<10 keV), using the photoelectric effect in polycrystalline MAPbI3 films, was first demonstrated by Yakunin et al.16 Improving the detection probability for hard X-rays (>100 keV) called for a decrease in absorption length. This prompted the development of X-ray detectors based on OTP single crystals17–19 or thick films.20 The energy spectra measured with OTP detectors demonstrated energy resolutions of 35% for 59.6 keV of 241Am and 6.5% for 662 keV of 137Cs.17,19
This shows that OTPs are promising materials for the detection of ionising radiation, motivating a systematic exploration for their application in scintillation detectors. An important aim is avoiding limitations that arise from extracting charged particles. This inherent feature of photodetectors with direct photon-to-current conversion imposes two basic constraints. First, it eventually limits the thickness of the absorber and hence the conversion efficiency for high-energy photons. Second, the transit time of charge carriers in the material dictates the relatively slow (∼100 μs) response time of OTP photodetectors.17 The advantage of a scintillation detector is its non-reliance on extracting charged particles from the material. Light can be detected from the bulk of the crystal absorber with a response time governed by the probability of radiative decay of excited particles, and this can be very fast as is the case for exciton emission.
Fully inorganic perovskites have the right properties to be fast scintillators. An intense nanosecond X-ray luminescence of free excitons in CsPbX3 (X = Cl, Br, I) at 77 K was reported by Voloshinovskii et al. already in 1993.21 The light yield at room temperature, however, was too low (<500 ph MeV−1)22 for their application in conventional scintillation detectors. In 2004, interest increased again when sub-nanosecond scintillation decay at room temperature was found in the layered hybrid metal–halide compound (C6H13NH3)2PbI4,23 however, with a light yield of only ∼6000 ph MeV−1. Recently, light yields of 9000 and 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 ph MeV−1 were reported for the layered perovskites (EDBE)PbCl4 (EDBE = 2,2′-ethylenedioxy)-bis(ethylamine)24 and (C6H5C2H4NH3)2PbBr3,25 highlighting the potential of these materials for scintillation detectors. Other researchers compared theoretically the scintillation properties of (EDBE)PbCl4 and MAPbX3 (X = Br and I) at low temperatures and posited, without measurement and assuming no thermal quenching, that the X-ray luminescence yield of MAPbX3 could possibly exceed 150
000 ph MeV−1 were reported for the layered perovskites (EDBE)PbCl4 (EDBE = 2,2′-ethylenedioxy)-bis(ethylamine)24 and (C6H5C2H4NH3)2PbBr3,25 highlighting the potential of these materials for scintillation detectors. Other researchers compared theoretically the scintillation properties of (EDBE)PbCl4 and MAPbX3 (X = Br and I) at low temperatures and posited, without measurement and assuming no thermal quenching, that the X-ray luminescence yield of MAPbX3 could possibly exceed 150![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 ph MeV−1 at T = 10 K.24 Furthermore, the characteristic decay time of luminescence observed at room temperature in OTPs is below 100 ns.24,26 Hence, there is the potential for a representative of the OTP family to outperform modern scintillators due to its higher light yield and faster decay time.
000 ph MeV−1 at T = 10 K.24 Furthermore, the characteristic decay time of luminescence observed at room temperature in OTPs is below 100 ns.24,26 Hence, there is the potential for a representative of the OTP family to outperform modern scintillators due to its higher light yield and faster decay time.
Therefore, in this study we investigated the scintillation light yield and decay time of relatively easy-to-synthesize MAPbBr3 crystals over the temperature range 8–295 K. We found that at cryogenic temperatures the perovskite crystals exhibit exceptionally high light yields (>100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 ph MeV−1) and sub-nanosecond decay times. This finding underpins the potential of OTPs for novel detector applications that rely on the fast timing of scintillation detectors at cryogenic temperatures. In this study, we used synchrotron radiation for measurements of timing characteristics and a multi-photon counting technique for measuring the scintillation light yield at cryogenic temperatures.27 The Materials and methods section contains detailed information on techniques for precisely recording temperature-dependent measurement data and the experimental setup.
000 ph MeV−1) and sub-nanosecond decay times. This finding underpins the potential of OTPs for novel detector applications that rely on the fast timing of scintillation detectors at cryogenic temperatures. In this study, we used synchrotron radiation for measurements of timing characteristics and a multi-photon counting technique for measuring the scintillation light yield at cryogenic temperatures.27 The Materials and methods section contains detailed information on techniques for precisely recording temperature-dependent measurement data and the experimental setup.
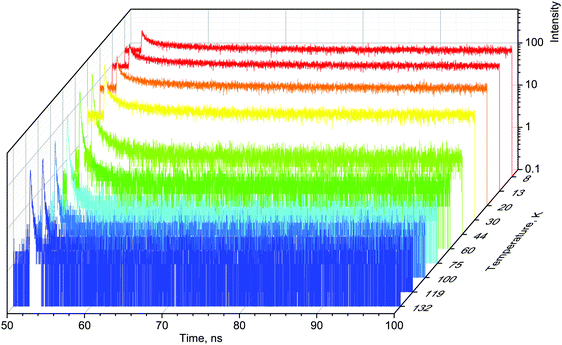
When excited with X-rays, MAPbBr3 exhibits narrow, near-edge emission bands peaking at 560 nm with a very pronounced temperature dependence.24 We studied the scintillation kinetics of MAPbBr3 crystals over a wide temperature range, from 8 to 295 K, using pulsed X-rays. Fig. 1 displays the corresponding scintillation decay curves. The decay curves exhibit very fast, non-exponential kinetics, which is indicative of bimolecular recombination of the charge carriers as reported recently.28
The main feature of the measured scintillation decay curves of the MAPbBr3 crystal, and common for the majority of scintillation materials, is an increase in the decay time constant with a decrease of temperature. We also clearly observe that cooling the crystal results in an increase of the background. Furthermore, the amplitude of the scintillation pulse initially increases with cooling, but when the temperature decreases below 50 K, it starts to decrease. Careful inspection of the plots reveals that the scintillation pulse in MAPbBr3 also undergoes significant changes in shape at low temperatures: the fractional contribution of the background rapidly increases and the long component of the decay curves becomes more pronounced. These features are indicative of a slowing down in the recombination dynamics.
For a more quantitative comparison of these properties and trends, we fitted the measured decay curves with a sum of exponential functions: 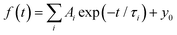 , where Ai is the amplitude, τi the decay time constant and y0 the background. It should be noted that the multi-exponential fit is widely applied to recombination decay in semiconductors.29–31 The quality of the fit was only marginally different between two- and three exponential fits. Two exponentials and a constant background are sufficient for an adequate representation of the measured decay curves. The fitting parameters for MAPbBr3 as functions of temperature are displayed in Fig. 2.
, where Ai is the amplitude, τi the decay time constant and y0 the background. It should be noted that the multi-exponential fit is widely applied to recombination decay in semiconductors.29–31 The quality of the fit was only marginally different between two- and three exponential fits. Two exponentials and a constant background are sufficient for an adequate representation of the measured decay curves. The fitting parameters for MAPbBr3 as functions of temperature are displayed in Fig. 2.
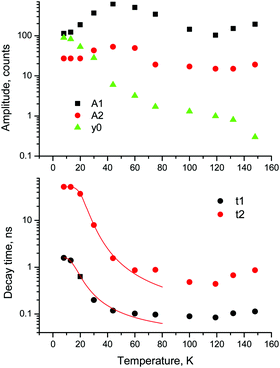 | ||
Fig. 2 Temperature dependent kinetics. Temperature dependence of parameters of decay kinetics in MAPbBr3 crystals obtained from the fitting of the decay curves by the sum of two exponential functions: f(t) = f(t) = A1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−t/τ1) + A2 exp(−t/τ1) + A2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−t/τ2) + y0. Lines show the best fits of the τ = f(T) dependences using eqn (3) with the following parameters τ1 = 1.6 ± 0.5 ns, K1 = 39 ± 11 × 109 s−1 and ΔE1 = 6.4 ± 0.5 meV; and τ2 = 52.4 ± 0.2 ns, K2 = 18 ± 3 × 109 s−1 and ΔE2 = 13.3 ± 0.3 meV. exp(−t/τ2) + y0. Lines show the best fits of the τ = f(T) dependences using eqn (3) with the following parameters τ1 = 1.6 ± 0.5 ns, K1 = 39 ± 11 × 109 s−1 and ΔE1 = 6.4 ± 0.5 meV; and τ2 = 52.4 ± 0.2 ns, K2 = 18 ± 3 × 109 s−1 and ΔE2 = 13.3 ± 0.3 meV. | ||
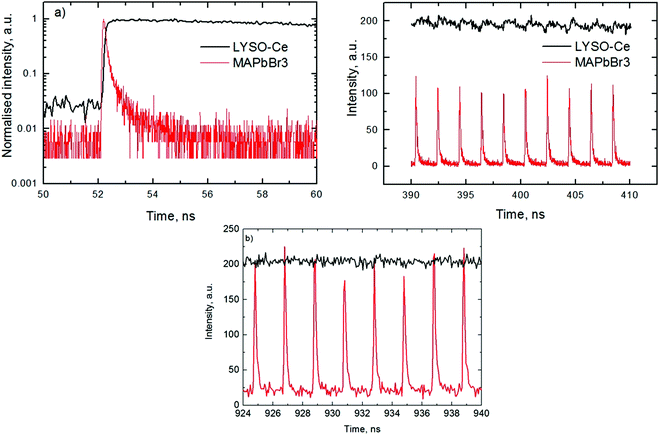
An analysis of the plots reveals further details in the temperature evolution of the luminescence kinetics of the crystal. As can be derived from the decay time versus temperature dependence, the fast and slow decay time constants in the crystal are about 0.1 and 1 ns at T > 50 K. This correlates well with the results from photoluminescence decay studies of MAPbBr3 down to 77 K.32 With cooling to lower temperatures, the decay rate of the luminescence kinetics in MAPbBr3 exhibits steep changes, resulting in a significant increase of the decay time constants, so that at T = 8 K, τf = 2 ns and τs = 50 ns. The amplitudes of the fast and slow components initially increase with cooling, while below 40 K they start to decrease; in particular, the amplitude of the fast component decreases by about a factor of five. At the same time, the amplitude of the background y0 exhibits a steady increase with cooling, becoming comparable to the amplitude of the fast component at T = 8 K. This shows that at this temperature the radiative dynamics is dominated by the slow recombination processes due to trapping and release of charge carriers. This effect causes an afterglow, which has a detrimental impact on the temporal response of the scintillator. Importantly at T > 60 K the fast and slow scintillation components dominate in the radiative decay, while the fractional contribution of the background does not exceed 1%. This implies that at the higher temperature the major fraction of the scintillation response from the crystal is released over a nanosecond time interval, following an excitation pulse. This is further supported through the measurements of the scintillation light yield discussed later. The evidence of the very fast scintillation response of MAPbBr3 is shown in Fig. 3a by comparing it with an LYSO-Ce scintillator. Another example is given in Fig. 3b, which displays the sequence of X-ray pulses from the synchrotron (interval Δt = 2 ns) as detected by MAPbBr3 and LYSO-Ce. It is clear from these figures that the timing performance of the MAPbBr3 crystal, exhibiting a sub-nanosecond decay time, is superior to that of LYSO-Ce. The latter exhibits a decay time constant of 33 ns and offers an example of one of the best results in coincidence timing resolution, which relies on fast timing.5
Numerous studies on the luminescence properties of MAPbX3, X = Br and I, were conducted over a wide temperature range, evidencing that free charge carriers dominate at room temperature, while excitons are stable at low temperature.32–35 Upon high-energy excitation, the thermalized electrons and holes form free excitons, which in turn can interact with defects or impurities. The narrow luminescence bands with a small Stokes shift observed in OTPs at low temperature are attributed to free and bound excitons. The luminescence is very bright at low temperature but exhibits significant thermal quenching. This is due to the exciton binding energies being tens of meV36 and the increase in temperature causing dissociation. Yet the other characteristic features of exciton emission are the fast decay kinetics. The free excitons emit promptly, while the excitons captured at defects or impurity sites recombine more slowly through de-trapping. Consequently, the scintillation mechanism in the crystals at low temperatures is controlled by two main processes that give rise to the fast and slow emission components. The fast decay component corresponds to the radiative decay of free excitons, while the slow component of the emission is attributed to the radiative decay of electrons and holes released from the traps.
The observed temperature dependence of the luminescence decay in both channels can be explained in the framework of a simple quantitative model by considering the dynamics of radiative and non-radiative transitions between the excited and ground states of the emission center. In terms of this model the measured transition rate (the inverse of the luminescence decay constant τ) can be determined as the sum of the radiative (kr) and non-radiative (knr) rates:
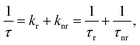 | (1) |
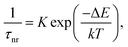 | (2) |
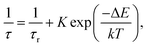 | (3) |
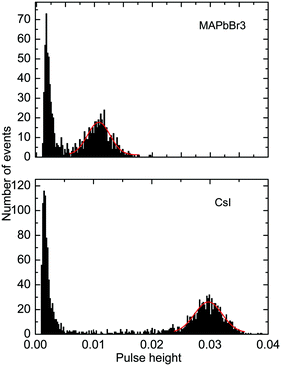
Further to assess the performance of MAPbBr3 as a scintillator, we studied a series of energy spectra induced by α-particles in MAPbBr3 as a function of temperature. Fig. 4 shows the pulse height spectrum measured at 50 K that features a peak with a Gaussian shape attributed to the detection of 5.5 MeV α-particles emitted using an 241Am source by the MAPbBr3 crystal.
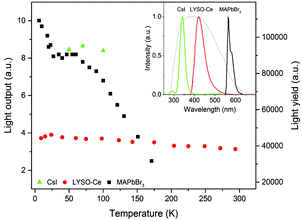
The position of the peak centre is proportional to the amplitude of the scintillation response of the crystal so that it can be used as a measure of scintillation light output at different temperatures. In Fig. 5, we show the variation of the scintillation light output of the MAPbBr3 crystal with temperature (together with CsI and LYSO-Ce). A clearly measurable scintillation response can be detected when the crystal is cooled below 180 K. The scintillation efficiency of MAPbBr3 increases gradually as the temperature is decreased until a plateau is reached at around 70 K. At T > 60 K the individual scintillation event recorded using a data acquisition system exhibits a very short, intense peak that decays within hundred nanoseconds. This peak is caused by the overlap of many scintillation photons arriving over a short initial time interval after excitation by alpha particles. Hence, at these temperatures only the fast emission contributes to the scintillation signal. An increase of the light output by about 20% is observed as the temperature decreases below 30 K. This increase correlates with the rapid increase of the fractional contribution of the afterglow observed at very low temperatures. We also noted that as the temperature decreases below 50 K, a delayed signal appears, distributed over the entire time window of the 1.6 ms used to record the individual scintillation events. This signal is responsible for the additional emission enhancement, observed over this temperature range; it is due to the process of radiative recombination of charge carriers released by shallow traps with activation energies between 10 and 90 meV, as established using thermoluminescence data.24
Having demonstrated that over the 50–150 K temperature range MAPbBr3 crystals exhibit fast scintillations, and taking into consideration the theoretical estimates, we then evaluated the scintillation light yield using as references the commercial scintillators CsI and LYSO-Ce. In such evaluations, it is preferable to use a reference scintillator with characteristics not too dissimilar to the crystals under study. Undoped CsI has a very high light output of ∼100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 ph MeV−1 at 77 K40 and exhibits a strong temperature dependence,41 although the decay time is relatively long (∼1 μs at 77 K). LYSO-Ce is renowned for its high light yield (34
000 ph MeV−1 at 77 K40 and exhibits a strong temperature dependence,41 although the decay time is relatively long (∼1 μs at 77 K). LYSO-Ce is renowned for its high light yield (34![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 ph MeV−1) and fast decay time, both changing only insignificantly with cooling.42,43 The light collection efficiency of the experimental setup used in this study is determined predominantly by the geometrical factors that are constant parameters. Because of their low penetration depth, the energy of the alpha particles is fully absorbed by the thin samples; hence the scintillation light yield can be evaluated by comparing the measured light outputs of the reference scintillator and the perovskite crystals corrected for the difference in the emission-weighted spectral sensitivity, ελ.44 The emission spectra of MAPbBr3, CsI and LYSO-Ce crystals as well as the quantum sensitivity of the photomultiplier used for the calculation of the emission-weighted sensitivity, ελ, are shown in the inset of Fig. 5.
000 ph MeV−1) and fast decay time, both changing only insignificantly with cooling.42,43 The light collection efficiency of the experimental setup used in this study is determined predominantly by the geometrical factors that are constant parameters. Because of their low penetration depth, the energy of the alpha particles is fully absorbed by the thin samples; hence the scintillation light yield can be evaluated by comparing the measured light outputs of the reference scintillator and the perovskite crystals corrected for the difference in the emission-weighted spectral sensitivity, ελ.44 The emission spectra of MAPbBr3, CsI and LYSO-Ce crystals as well as the quantum sensitivity of the photomultiplier used for the calculation of the emission-weighted sensitivity, ελ, are shown in the inset of Fig. 5.
Taking the light yield of CsI as 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 ph MeV−1 at 77 K, we determined that the light yield of MAPbBr3 is equal to 90
000 ph MeV−1 at 77 K, we determined that the light yield of MAPbBr3 is equal to 90![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 ph MeV−1 at 77 K and 116
000 ph MeV−1 at 77 K and 116![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 ph MeV−1 at T = 8 K. On the other hand, measuring LYSO-Ce, we found that the scintillation light yield increases to 40
000 ph MeV−1 at T = 8 K. On the other hand, measuring LYSO-Ce, we found that the scintillation light yield increases to 40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 ph MeV−1 upon cooling to T = 8 K, giving a light yield of MAPbBr3 equal to 110
500 ph MeV−1 upon cooling to T = 8 K, giving a light yield of MAPbBr3 equal to 110![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 ph MeV−1 at this temperature. The estimated values correlate very well despite the relatively large error ±20%, which stems from the uncertainty of ελ and the determination of the centroid in the pulse height spectra. The significance of these values can be appreciated in full when compared with the characteristics of the best modern scintillators (see Table 1).
000 ph MeV−1 at this temperature. The estimated values correlate very well despite the relatively large error ±20%, which stems from the uncertainty of ελ and the determination of the centroid in the pulse height spectra. The significance of these values can be appreciated in full when compared with the characteristics of the best modern scintillators (see Table 1).
| Crystal | Density, g cm−3 | Photoelectric absorption at 511a keV, cm−1 | Emission peak, nm | Decay time, ns | Light yield, ph MeV−1 | Light yield/decay time, ns−1 | Ref. |
|---|---|---|---|---|---|---|---|
| a Calculated using an XCOM web-tool.50 | |||||||
| CsI-Tl | 4.5 | 0.09 | 560 | 1000 | 57![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
57 | 45 |
| SrI2-Eu | 4.6 | 0.07 | 435 | 1200 | 120![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
100 | 46 |
| CsI (77 K) | 4.5 | 0.09 | 340 | 730/3200 | 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
163 | 40 |
| LYSO-Ce | 7.1 | 0.25 | 420 | 33 | 34![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
940 | 43 |
| GGAG-Ce | 6.2 | 0.12 | 540 | 32/156 | 45![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
1400 | 47 |
| BaF2 | 4.9 | 0.08 | 220/310 | 0.8/630 | 1800/10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
2250 | 48 |
| LuI3-Ce | 5.6 | 0.16 | 475;520 | 31/140/1000 | 98![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
3160 | 49 |
| LaBr3-Ce | 5.0 | 0.05 | 355;390 | 16 | 74![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
4630 | 7 |
| MAPbBr3 (77 K) | 3.6 | 0.13 | 560 | 0.1/1 | 90![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
90![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
This work |
A comparison of the MAPbBr3 parameters with commercial scintillators shows that OTPs are very promising scintillation materials. Of particular interest is the excellent initial photon density calculated as the ratio of light yield to decay time – the most important parameter that determines the timing precision of the scintillator detector. The higher density of photons near the peak enables a higher precision in determining the time of interaction. A conservative evaluation shows that this parameter is higher by a factor 20 in MAPbBr3 compared to the best modern scintillator LaBr3-Ce. It should be noted that there are a few other materials with fast scintillations at cryogenic temperatures discussed in the literature (ZnO, PbI2, HgI251) but a low value of the light yield is a major limitation. The stopping power of MAPbBr3, which is defined by the photoelectric fraction of the absorption coefficient, is also very competitive in comparison with other scintillators; only two materials exhibit a higher value. For illustration, the energy dependence of the photoelectric absorption of the three crystals discussed in this study is displayed in Fig. 6.
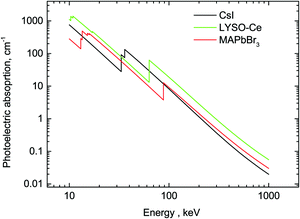 | ||
| Fig. 6 Photoelectric fractions of absorption of gamma-rays in CsI, LYSO-Ce and MAPbBr3. The data are calculated using an XCOM web-tool.50 | ||
In summary, in this study we measured the decay time and light output of MAPbBr3 crystals down to a temperature of 8 K, using X-ray and particle excitation. We found an exceptionally fast and intense scintillation response – the key characteristics for a scintillation detector. At 77 K the fast and slow components of the decay are found to be ∼0.1 ns and 1 ns, respectively. The light yield of MAPbBr3 is estimated as 90![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 ± 18
000 ± 18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 ph MeV−1 at 77 K and 116
000 ph MeV−1 at 77 K and 116![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 ± 23
000 ± 23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 ph MeV−1 at 8 K.
000 ph MeV−1 at 8 K.
The observation of intense sub-nanosecond scintillations in OTPs at low temperatures indicates that they are materials with extremely promising scintillation properties that may offer major advantages over conventional scintillation materials. The potential benefits might outweigh additional effort needed for the development of equipment that provide a low-temperature environment for operation of such scintillation detectors. It should be highlighted that the advanced scintillation characteristics of OTP crystals are attained even upon moderate cooling to a temperature just below 100 K, which can be achieved at relative ease through liquid nitrogen-based refrigeration systems. Modern developments in cryogenics made these temperatures also accessible through using dry cryogenic systems,52 while advances in CMOS silicon photodetectors allow reliable detection of single photons at these temperatures.53 The moderate cooling requirement and the flexibility of the production technology make this approach worth pursuing. There are still challenges in tuning the optical and scintillation parameters, developing the technology to produce crystals with desirable quality and size as well as integration with photodetectors in scintillation arrays. Nonetheless, the compositional flexibility of OTP crystals offers freedom in engineering their optoelectronic properties, whereas solution processing facilitates easy integration with industrial processes.
Methods
The crystals of MAPbBr3 studied in this work were produced by a solution method as described in ref. 54. In this study, commercially available, undoped CsI (Hilger Crystals (UK)) and Ce-doped LYSO (Saint-Gobain (France)) were used as state-of-the-art reference scintillators.The scintillation decay curves of the crystals were measured at beamline B16 of the Diamond Light Source using a 14 keV monochromatic X-ray beam from the synchrotron. The measurements were carried out under special beam conditions by triggering on a single X-ray pulse with an FWHM of Δt = 60 ps, separated from the following pulse by a 300 ns gap. The single crystalline sample with dimensions 4 × 3 × 1 mm3 was glued with silver adhesive to the holder of a continuous-flow, He-cryostat (Oxford Instruments). The temperature in the cryostat was stabilized using a controller using a PID loop with a Si-diode as a temperature sensor and a resistive heater, allowing controlled cooling. The cryostat was attached to an XYZ-translation stage to facilitate swift alignment. One port of the cryostat is equipped with a 0.2 mm thick aluminised Mylar window allowing X-rays to penetrate. Through this window the X-ray beam with a flux of approx. 109 ph (s mm2)−1 irradiated the sample holder placed at 45° to the incoming radiation, while the luminescence was collected in reflection mode at 45° through a quartz window. The emission was detected using an ID100 single photon counting detector sensitive over a 400–900 nm spectral range and a PicoHarp 300 time-correlated single photon counting module.
To measure scintillation light output as a function of temperature, we used the multi-photon counting technique, developed specifically for measurements of the scintillation characteristics of materials at very low temperatures.29 In this method, the sequence of scintillation events is recorded and analyzed. As the measured charge per scintillation event is proportional to the energy released in the crystal, it is used to derive the value of the scintillation light yield. The sample was mounted on the copper sample holder with a 0.9 μCi 241Am source placed just behind the sample. The assembly was then placed inside a He-flow cryostat. The scintillation light emitted by the crystal was detected using a multi-alkali photomultiplier 9124A (Electron Tube Enterprises, Ruislip, UK) connected to the optical window of the cryostat. The photomultiplier detects photons in the 280–650 nm wavelength range, thus allowing measurements of the light yield of the MAPbBr3 crystal. To eliminate the contribution from thermoluminescence due to charge release during heating, the measurements were performed while cooling the crystals.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors thank the Diamond Light Source for the access to beamline B16, where some of the measurements reported here were carried out and the Beam Diagnostic Group for assisting with setting up the time-correlated single photon counting module used in the decay time measurements.References
- S. S. Gambhir, Molecular imaging of cancer with positron emission tomography, Nat. Rev. Cancer, 2002, 2, 683–693 CrossRef CAS PubMed.
- P. Zanzonico, Principles of Nuclear Medicine Imaging: Planar, SPECT, PET, Multi-modality, and Autoradiography Systems, Radiat. Res., 2012, 177, 349–364 CrossRef CAS PubMed.
- S. Gundacker, F. Acerbi and E. Auffray, et al., State of the art timing in TOF-PET detectors with LuAG, GAGG and L(Y)SO scintillators of various sizes coupled to FBK-SiPMs, J. Instrum., 2016, 11, P08008 CrossRef.
- J. W. Cates and C. S. Levin, Advances in coincidence time resolution for PET, Phys. Med. Biol., 2016, 61, 2255–2264 CrossRef CAS PubMed.
- S. Gundacker, E. Auffray, K. Pauwels and P. Lecoq, Measurement of intrinsic rise times for various L(Y)SO and LuAG scintillators with a general study of prompt photons to achieve 10 ps in TOF-PET, Phys. Med. Biol., 2016, 61, 2802–2837 CrossRef CAS PubMed.
- S. Seifert, H. T. van Dam and D. R. Schaart, The lower bound on the timing resolution of scintillation detectors, Phys. Med. Biol., 2012, 57, 1797–1814 CrossRef PubMed.
- G. Bizarri, J. de Haas and P. Dorenbos, et al., Scintillation properties of 1 × 1 inch(3) LaBr3:5% Ce3+ crystal, IEEE Trans. Nucl. Sci., 2006, 53, 615–619 Search PubMed.
- S. E. Derenso, W.-S. Choong and W. W. Moses, et al., Fundamental limits of scintillation detector timing precision, Phys. Med. Biol., 2014, 59, 3261–3286 CrossRef PubMed.
- C. Dujardin, E. Auffray and E. Bourret-Courchesne, et al., Needs, Trends and Advances in Inorganic Scintillators, IEEE Trans. Nucl. Sci., 2018, 65, 1977–1997 CAS.
- C. K. Moller, Crystal structure and photoconductivity of caesium plumbohalides, Nature, 1958, 182, 1436 CrossRef CAS.
- D. Weber, CH3NH3PbX3, a Pb(II)-system with cubic perovskite structure, Z. Naturforsch., B: J. Chem. Sci., 1978, 33, 1443–1445 Search PubMed.
- M. A. Green, A. Ho-Baillie and H. J. Snaith, The emergence of perovskite solar cells, Nat. Photonics, 2014, 8, 505–514 CrossRef.
- Y. Fu, H. Zhu and A. W. Schrader, et al., Nanowire lasers of formamidinium lead halide perovskites and their stabilized alloys with improved stability, Nano Lett., 2016, 16, 1000–1008 CrossRef CAS PubMed.
- S. D. Stranks and H. J. Snaith, Metal–halide perovskites for photovoltaic and light-emitting devices, Nat. Nanotechnol., 2015, 10, 391–402 CrossRef CAS PubMed.
- X. Hu, X. Zhang and L. Liang, et al., High-Performance Flexible Broadband Photodetector Based on Organolead Halide Perovskite, Adv. Funct. Mater., 2014, 24, 7373–7380 CrossRef CAS.
- S. Yakunin, D. N. Dirin and Y. Shynkarenko, et al., Detection of X-ray photons by solution-processed lead halide perovskites, Nat. Photonics, 2015, 9, 444–450 CrossRef CAS PubMed.
- H. Wei, D. DeSantis and W. Wei, et al., Dopant compensation in alloyed H3NH3PbBr3−xClx perovskite single crystals for gamma-ray spectroscopy, Nat. Mater., 2017, 16, 827–833 CrossRef PubMed.
- H. Wei, Y. Fang and P. Mulligan, et al., Sensitive X-ray detectors made of methylammonium lead tribromide perovskite single crystals, Nat. Photonics, 2016, 10, 333–339 CrossRef CAS.
- S. Yakunin, D. N. Dirin and Y. Shynkarenko, et al., Detection of gamma photons using solution-grown single crystals of hybrid lead halide perovskites, Nat. Photonics, 2016, 10, 585–589 CrossRef CAS.
- Y. C. Kim, K. H. Kim and D.-Y. Son, et al., Printable organometallic perovskite enables large-area, low-dose X-ray imaging, Nature, 2017, 550, 87–91 CrossRef CAS PubMed.
- A. S. Voloshinovskii, V. B. Mikhailik and S. V. Myagkota, et al., Exciton luminescence of ionic semiconductors CsPbX3 (X = Cl, Br, I), Ukr. J. Phys., 1993, 38, 1012–1015 CAS.
- M. Kobayashi, K. Omata and S. Sugimoto, et al., Scintillation characteristics of CsPbCl3 single crystals, Nucl. Instrum. Methods Phys. Res., Sect. A, 2008, 592, 369–373 CrossRef CAS.
- K. Shibuya, M. Koshimizu and H. Murakamiet, et al., Development of ultrafast semiconducting scintillators using quantum confinement effect, Jpn. J. Appl. Phys., 2004, 43, L1333–L1336 CrossRef.
- M. D. Birowosuto, D. Cortecchia and W. Drozdowski, et al., X-ray scintillation in lead halide perovskite crystals, Sci. Rep., 2016, 6, 37254–37259 CrossRef CAS PubMed.
- N. Kawano, M. Koshimizu and G. Okada, et al., Scintillating organic–inorganic layered perovskite-type compounds and the gamma-ray detection capabilities, Sci. Rep., 2017, 7, 14754 CrossRef PubMed.
- D. Shi, V. Adinolfi and R. Comin, et al., Low trap-state density and long carrier diffusion in organolead trihalide perovskite single crystals, Science, 2015, 347, 519–522 CrossRef CAS PubMed.
- H. Kraus, V. B. Mikhailik and D. Wahl, Multiple photon counting coincidence (MPCC) technique for scintillator characterisation and its application to studies of CaWO4 and ZnWO4 scintillators, Nucl. Instrum. Methods Phys. Res., Sect. A, 2005, 553, 522–534 CrossRef CAS.
- J. M. Richter, M. Abdi-Jalebi and A. Sadhanala, et al., Enhancing photoluminescence yields in lead halide perovskites by photon recycling and light out-coupling, Nat. Commun., 2016, 7, 13941 CrossRef CAS PubMed.
- S. E. Derenzo, M. J. Weber and M. K. Klintenberg, Temperature dependence of the fast, near-band-edge scintillation from CuI, HgI2, ZnO:Ga and CdS:In, Nucl. Instrum. Methods Phys. Res., Sect. A, 2002, 486, 214–219 CrossRef CAS.
- K. Wakita, K. Nishi, Y. Ohta and N. Nakayama, Time-resolved photoluminescence studies of free excitons in CuInS2 crystals, Appl. Phys. Lett., 2002, 80, 3316–3318 CrossRef CAS.
- Y. X. Zhang, H.-Y. Wang and Z. Y. Zhang, et al., Photoluminescence quenching of inorganic cesium lead halides perovskite quantum dots (CsPbX3) by electron/hole acceptor, Phys. Chem. Chem. Phys., 2017, 19, 1920–1926 RSC.
- Y. Liu, H. Lu and J. Niu, et al., Temperature-dependent photoluminescence spectra and decay dynamics of MAPbBr3 and MAPbI3 thin films, AIP Adv., 2018, 8, 095108 CrossRef.
- M. I. Dar, G. Jacopin and S. Meloni, et al., Origin of unusual bandgap shift and dual emission in organic–inorganic lead halide perovskites, Sci. Adv., 2016, 2, e1601156 CrossRef PubMed.
- Y. Kanemitsu, Luminescent spectroscopy of lead halide perovskites: materials properties and applications, J. Mater. Chem. C, 2017, 5, 3427–3437 RSC.
- H. Diab, G. Trippe-Allard and F. Ledee, et al., Narrow linewidth excitonic emission in organic–inorganic lead iodide perovskite single crystals, J. Phys. Chem. Lett., 2016, 7, 5093–5100 CrossRef CAS PubMed.
- A. Miyata, A. Mitioglu and P. Plochocka, et al., Direct measurement of the exciton binding energy and effective masses for charge carriers in organic–inorganic tri-halide perovskites, Nat. Phys., 2015, 11, 582–594 Search PubMed.
- N. Ahmed, H. Kraus and H. J. Kim, et al., Characterisation of tungstate and molybdate crystals ABO4 (A = Ca, Sr, Zn, Cd; B = W, Mo) for luminescence lifetime cryothermometry, Materialia, 2018, 4, 287–296 Search PubMed.
- M. Isarov, L. Z. Tan and M. I. Bodnarchuk, et al., Rashba effect in a single colloidal CsPbBr3 perovskite nanocrystal detected by magneto-optical measurements, Nano Lett., 2017, 17, 5020–5026 CrossRef CAS PubMed.
- L. Chen, B. Li and C. Zhang, et al., Composition-dependent energy splitting between bright and dark excitons in led halide perovskite nanocrystals, Nano Lett., 2018, 18, 2074–2080 CrossRef CAS PubMed.
- M. Moszynski, M. Balcerzyk and W. Czarnacki, et al., Energy resolution and non-proportionality of the light yield of pure CsI at liquid nitrogen temperatures, Nucl. Instrum. Methods Phys. Res., Sect. A, 2005, 537, 357–362 CrossRef CAS.
- V. B. Mikhailik, V. Kapustyanyk and V. Tsybulskyi, et al., Luminescence and scintillation properties of CsI: a potential cryogenic scintillator, Phys. Status Solidi B, 2015, 252, 804–810 CrossRef CAS.
- D. N. ter Weele, D. R. Schaart and P. Dorenboss, Comparative study of co-doped and non-co-doped LSO:Ce and LYSO:Ce scintillators for TOF-PET, IEEE Trans. Nucl. Sci., 2015, 62, 727–731 CAS.
- S. Blahuta, A. Bessière and B. Viana, et al., Evidence and consequences of Ce in LYSO:Ce,Ca and LYSO:Ce,Mg single crystals for medical imaging applications, IEEE Trans. Nucl. Sci., 2013, 60, 3134–3141 CAS.
- V. B. Mikhailik, S. Henry and H. Kraus, et al., Temperature dependence of CaMoO4 scintillation properties, Nucl. Instrum. Methods Phys. Res., Sect. A, 2007, 583, 350–356 CrossRef CAS.
- J. de Haas and P. Dorenbos, Advances in yield calibration of scintillators, IEEE Trans. Nucl. Sci., 2008, 55, 1086–1092 Search PubMed.
- E. V. van Loef, C. M. Wilson and N. J. Cherepy, et al., Crystal growth and scintillation properties of strontium iodide scintillators, IEEE Trans. Nucl. Sci., 2009, 56, 869–872 CAS.
- M. Tyagi, H. E. Rothfuss and S. B. Donnald, et al., Effect of Co-Doping on the Scintillation Kinetics of Ce Doped Gd3Ga3Al2O12, IEEE Trans. Nucl. Sci., 2014, 61, 297–301 CAS.
- R. Shendrik and E. Radzhabov, Absolute light yield measurements on SrF2 and BaF2 doped with rare earth ions, IEEE Trans. Nucl. Sci., 2014, 61, 406–410 CAS.
- M. D. Birowosuto, P. Dorenbos and C. W. E. van Eijk, et al., High-light-output scintillator for photodiode readout: LuI3:Ce3+, J. Appl. Phys., 2006, 99, 123520 CrossRef.
- https://www.physics.nist.gov/PhysRefData/Xcom/html/xcom1.html .
- S. E. Derenzo, E. Bourret-Courshesne, G. Bizarri and A. Canning, Bright and ultra-fast scintillation from a semiconductor?, Nucl. Instrum. Methods Phys. Res., Sect. A, 2016, 805, 36–40 CrossRef CAS PubMed.
- R. Radebaugh, Cryocoolers: the state of the art and recent developments, J. Phys.: Condens. Matter, 2009, 21, 164219 CrossRef PubMed.
- A. Bondar, A. Buzulutskov and A. Dolgov, et al., MPPC versus MRS APD in two-phase Cryogenic Avalanche Detectors, J. Instrum., 2015, 10, P04013 CrossRef.
- L. C. Schmidt, A. Pertegás and S. González-Carrero, et al., Nontemplate synthesis of CH3NH3PbBr3 perovskite nanoparticles, J. Am. Chem. Soc., 2014, 136, 850–853 CrossRef CAS PubMed.
| This journal is © The Royal Society of Chemistry 2019 |