Open Access Article
Open Access ArticleNegative piezoelectric effect in an organic supramolecular ferroelectric†
Indre
Urbanaviciute
 a,
Xiao
Meng
b,
Michal
Biler
a,
Xiao
Meng
b,
Michal
Biler
 c,
Yingfen
Wei
c,
Yingfen
Wei
 d,
Tim D.
Cornelissen
d,
Tim D.
Cornelissen
 a,
Subham
Bhattacharjee‡
b,
Mathieu
Linares
a,
Subham
Bhattacharjee‡
b,
Mathieu
Linares
 ef and
Martijn
Kemerink
ef and
Martijn
Kemerink
 *a
*a
aComplex Materials and Devices, Department of Physics, Chemistry and Biology (IFM), Linköping University, 58183 Linköping, Sweden. E-mail: martijn.kemerink@liu.se
bLaboratory of Macromolecular and Organic Chemistry, Eindhoven University of Technology, P.O. Box 513, 5600 MB Eindhoven, The Netherlands
cDepartment of Chemistry – BMC, Uppsala University, Box 576, Uppsala S-751 23, Sweden
dZernike Institute for Advanced Materials, University of Groningen, 9747 AG Groningen, The Netherlands
eDepartment of Science and Technology (ITN), Campus Norrköping, Linköping University, SE-60174 Norrköping, Sweden
fSwedish e-Science Research Centre (SeRC), Linköping University, SE-581 83 Linköping, Sweden
First published on 7th May 2019
Abstract
The vast majority of ferroelectric materials demonstrate a positive piezoelectric effect. Theoretically, the negative piezoelectric coefficient d33 could be found in certain classes of ferroelectrics, yet in practice, the number of materials showing linear longitudinal contraction with increasing applied field (d33 < 0) is limited to few ferroelectric polymers. Here, we measure a pronounced negative piezoelectric effect in the family of organic ferroelectric small-molecular BTAs (trialkylbenzene-1,3,5-tricarboxamides), which can be tuned by mesogenic tail substitution and structural disorder. While the large- and small-signal strain in highly-ordered thin-film BTA capacitor devices are dominated by intrinsic contributions and originates from piezostriction, rising disorder introduces additional extrinsic factors that boost the large-signal d33 up to −20 pm V−1 in short-tailed molecules. Interestingly, homologues with longer mesogenic tails show a large-signal electromechanical response that is dominated by the quadratic Maxwell strain with significant mechanical softening upon polarization switching, whereas the small-signal strain remains piezostrictive. Molecular dynamics and DFT calculations both predict a positive d33 for defect-free BTA stacks. Hence, the measured negative macroscopic d33 is attributed to the presence of structural defects that enable the dimensional effect to dominate the piezoelectric response of BTA thin films.
New conceptsMaterials with a negative piezoelectric effect demonstrate atypical, inverse strain-field and polarization-stress characteristics. While the mechanisms driving the conventional – positive – piezoelectricity are transparent and manifest in a plethora of materials, negative piezoelectricity requires special conditions and was only found in two-phased (i.e. coexisting crystalline and amorphous matter) semi-crystalline ferroelectric polymers, with the renowned (and so far only) successfully utilized example of P(VDF–TrFE). Here, we experimentally demonstrate a pronounced negative piezoelectric effect in a whole family of organic small-molecular ferroelectric materials that can be varied with tail-substitution. The well-defined, robust and tunable columnar-hexagonal (liquid)crystalline nanostructure of these self-assembling materials allows precise control of the macroscopic polarization and of the level of structural disorder in the layers. Using this tunability we disclose a counterintuitive, significant growth of the large-signal piezoelectric response with increasing structural disorder, while the small-signal response remains unaffected. Mechanical softening upon polarization switching leads to a unique amplification of the large-signal electromechanical response of longer-substituted compounds. The reported high piezoelectric coefficients, long polarization retention, low fatigue, great temperature and environmental stability accompanied by mechanical softness makes BTA a perspective candidate material for application in flexible transducers and energy harvesters. |
Introduction
Since the discovery of the piezoelectric effect in the last decades of the 19th century, a great number of both natural1,2 and synthetic3,4 materials have been found to demonstrate piezoelectric response. The property of these materials to convert mechanical energy to electrical energy (direct piezoelectric effect) and vice versa (converse piezoelectric effect) has found wide-ranging applications, from energy harvesters to transducers and beyond.5–7 The key materials in the field remain the inorganic ferroelectric perovskites like BTO and PZT. Despite environmental concerns (toxicity, high sintering temperatures, etc.), complex device fabrication procedures and limiting physical properties (e.g. high density, brittleness), these ceramic materials have been used extensively due to their exceptionally high ferroelectric and piezoelectric coefficients. Current advancement in the field of organic ferroelectrics and piezoelectrics has led to materials having comparable parameters, including remnant polarizations of up to 230 mC m−2 in single crystals of DIPAB8 and croconic acid,9 piezoelectric constants reaching 350 pm V−1 in antiferroelectric TFMNI crystals,10 40 pm V−1 in imidazolium perchlorate thin films,11,12 above −60 pm V−1 in P(VDF–TrFE) devices,13–15 and others.16–18 In addition, organic ferro- and piezoelectric materials are typically non-toxic, lightweight, flexible and soft, but most importantly, due to good thin-film forming properties, organic material devices can in many cases be fabricated using cheap and efficient processes. Because of this, organic ferroelectrics may become relevant for a wide variety of applications like conformal and/or flexible sensors, actuators and energy harvesters for which inorganic ferroelectrics are unsuited and can be outperformed.19 Yet, the new materials are rarely characterized in real-device conditions, and their piezoelectric properties are typically studied in bulk single-crystals or using controversial piezoresponse force microscopy (PFM).20 Due to this, with a few notable exceptions, the macroscopic piezoelectric properties of organic ferroelectrics are only sparsely known and far from completely understood.The total longitudinal strain S33 in ferroelectric layers arises from the electrostriction coupled to the electric displacement D and can be expressed as:14
| S33 = Q33D2 = Q33(εrε0E + Pr)2 = Q33(εrε0E)2 + Q33Pr2 + 2Q33εrε0PrE | (1) |
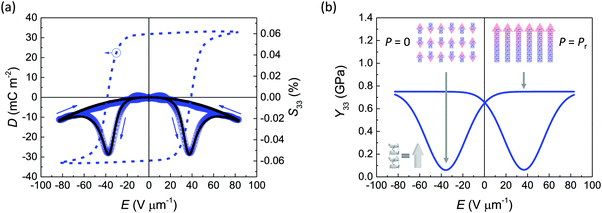
Piezoelectric response in (poly)crystalline materials typically originates from field-induced lattice deformations, as due to the applied electric field the lattice dipoles stretch, resulting in longitudinal expansion, and vice versa.21 For small deformations this gives a linear strain-field (or polarization-stress) dependence with positive longitudinal electrostriction Q33 and piezoelectric d33 coefficients. An inverted response – contraction with increasing field and negative Q33, d33 coefficients – is therefore rare, because it requires different, unconventional mechanisms to be at play. For idealized S–E butterfly loops characteristic to each case see Fig. S1 (ESI†). A recent data-mining study has revealed that the negative piezoelectric coefficient should theoretically be found in a large number of ABC-type inorganic ferroelectrics.22 However, experimentally the negative d33 has been observed principally in organic semi-crystalline ferroelectric polymers, with the renowned example of the P(VDF–TrFE) seen in Fig. 1b, or their composites.23–25 Biopolymers like cellulose or keratin have been shown to have negative piezoelectric constants for shear (d14 < 0) with longitudinal ones being negligible,26 while soft tissues comprising ferroelectric proteins, e.g. aortic walls, have negative electrostriction coefficients yet are likely not piezoelectric.27 The key to the negative longitudinal piezoelectricity in these materials is the coexistence of two phases of different elastic compliance, with a condition that the stiffer of the two is ferroelectric with the polarization in the thickness direction while the softer is anisotropically deformable (with Poisson ratio ν < 0.5). This leads to coupling between the dipole density and the macroscopic dimensions of the sample and has been shown to underly direct as well as converse piezoelectric response (see Dimensional effect in the ESI†).13
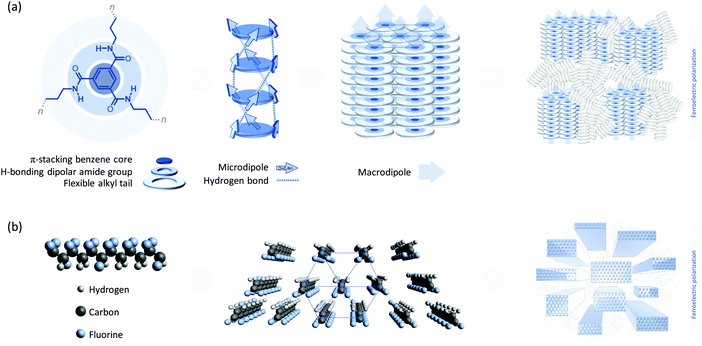
Here, we demonstrate experimentally that the negative longitudinal piezoelectric effect can be found in a small-molecular organic ferroelectric – the trialkylbenzene-1,3,5-tricarboxamide (BTA). BTA is a columnar-hexagonal (liquid)-crystal, see Fig. 1a,28–30 having a remnant polarization of up to ∼60 mC m−2, depending on the tail substituent.31 Differently to the conventional liquid-crystalline materials used for electrooptical applications, BTA maintains its macrodipole orientation at zero external field due to π–π stacking and hydrogen-bonding, which allows it to keep the polarization for up to 10 years at room temperature.31–33 The overall performance of thin-film BTA capacitor devices is comparable to devices based on P(VDF–TrFE), additionally offering some advantages like lower processing temperatures, easy chemical tuning and a wider operational temperature window.31,34,35 In this study we present interferometrically measured converse piezoelectric response in solution-processed thin-film BTA capacitor devices. Using density functional theory (DFT) and molecular dynamics (MD) simulations, we explain the origin of the observed anomalous negative piezoelectric effect in BTA from the microscopic and macroscopic perspective. The observed differences in small-signal and large-signal piezoelectric response further disclose different underlying mechanisms that are strongly influenced by the level of structural disorder in the active layer. The main finding of the study – the negative d33 in small-molecular materials – sheds important new insight on a phenomenon that was previously considered a peculiarity of a specific polymer ferroelectric, P(VDF–TrFE). A new prospective class of organic ferroelectric materials with a negative longitudinal piezoelectric constant is unearthed, that includes but is not limited to the amide-based discotic mesophases.
Results
Typical large-signal and small-signal piezoelectric characteristics of BTA-C6
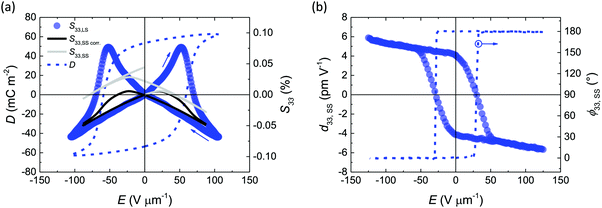
We measured the converse piezoelectric effect in thin-film spin-coated capacitor devices of BTAs using a double-beam laser interferometer system (DBLI),36 coupled with a voltage signal generator, high-voltage amplifier and a multifunctional output analyzer. This allowed for concurrent obtention of the strain and polarization characteristics at large-signal, as well as of the piezoelectric coefficient, phase and capacitance at small-signal measurement conditions. The DBLI system allows to reliably probe the piezoelectric response at real-device conditions (with electrodes) with minimal intervention. For further details see the Methods section and ESI.† All measurements were conducted at 60 °C to allow comparison of different BTA homologues, as will be discussed in detail further in the text. The devices were characterized in 33 mode, i.e. the strain, the polarization and the applied electric field were on the same z axis.Typical large-signal strain-field butterfly loops measured for short-tailed BTA-C6 devices have a close-to-ideal (cf. Fig. S1, ESI†) yet anomalous ‘flipped’ form, see Fig. 2a: the layer expands when the applied field polarity is opposite to the polarization and contracts when electric field and polarization directions match. The reversal occurs around the coercive field. The S–E dependence is linear and has a prominent negative slope, which indicates a negative piezoelectric coefficient, as S33= d33E. From a strain–displacement (S–D) and strain–displacement squared (S–D2) representation of the data (see Fig. S3(a–c), ESI†), based on fits to eqn (1), negative values for the electrostriction coefficient Q33 were obtained, which varied in range −0.55 to −1 m4 C−2 for BTA-C6, depending on the chosen fitting segment. To compare, −0.8 to −1.5 m4 C−2 was found in our P(VDF–TrFE) devices, see Fig. S3(d–f) (ESI†). Based on the description of the piezoelectric constant d33 = 2Q33εrε0Pr, Q33 = −1 m4 C−2 obtained for this typical BTA-C6 device leads to d33 ≈ −7 pm V−1 with εr = 7 (from Fig. S4c, ESI†), which matches the linear slope of −7 pm V−1 and suggests that polarization-induced electrostriction (eqn (1)) is the dominant factor in the piezoelectric behavior. Closely matching values of all piezoelectric coefficients d33, e33, g33 and h33 calculated from independent experimental data of d33, g33 and Q33 (Section II, Table S1 in the ESI†) further prove the fact. Interestingly, we later show that the large-signal d33 can be enhanced to reach values as large as −20 pm V−1, which would correspond to a high Q33 ≈ −3 m4 C−2.
The negative piezoelectric effect was observed at small-signal conditions as well, see Fig. 2b. The small-signal piezoelectric coefficient d33,SS, phase φ33,SS and capacitance were measured on the macroscopic device simultaneously using the DBLI, see Methods section and ESI† for details. The measured textbook-like d33,SS–E hysteresis loop indicates a negative d33 at positive applied voltages, which is opposite to the trends observed in conventional inorganic ferroelectrics with the positive piezoelectric effect.37 Interestingly, the small-signal d33 is lower than the one measured at large-signal conditions: around −4.5 pm V−1 at zero field for BTA-C6 vs. d33,LS = −7 pm V−1 for the same device. A similar mismatch is observed in our P(VDF–TrFE) devices with d33,SS = −25 pm V−1 compared to d33,LS = −38 pm V−1, see Fig. S4(d–f) (ESI†).
To find an explanation for this discrepancy one must consider the differences in switching mechanisms at small- and large-signal conditions. While the large-signal response is considered to be governed by both reversible and irreversible polarization switching processes, the small-signal effects are mostly driven by reversible polarization modulations.37 Irreversible changes are related to extrinsic phenomena as transitions between global energy minima (e.g. +Pr and −Pr) and movement of ferroelectric domain walls; reversible effects rise from the dielectric response and intrinsic phenomena that are coupled to small fluctuations around local minimum potential points, such as ion displacement in perovskite ferroelectrics, or, in the BTA case, columnar macrodipole rotation, as illustrated in the inset of Fig. 3c.
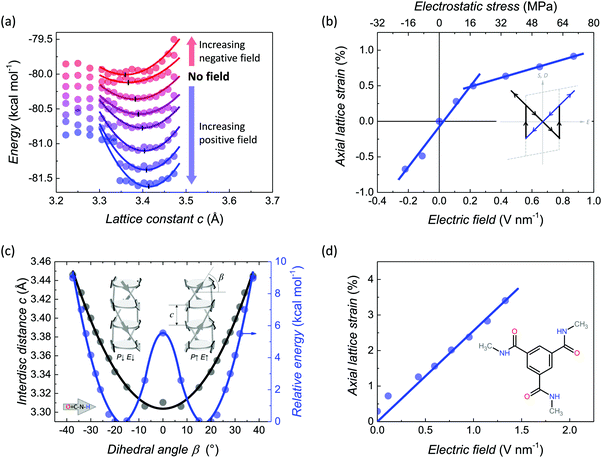
Considering a single self-assembled molecular stack, one would expect a positive piezoelectric response at the nanoscale due to the applied field rotating the amide dipoles further out-of-plane, which does not agree with the measured macroscopic negative piezoelectric constants. To this end, we have simulated the behavior of a single molecular stack consisting of 18 methyl-tailed BTAs using the energy minimization principle in molecular dynamics33 and found that with increasing field, the longitudinal (interdisc) lattice constant c increases, see Fig. 3a. The columnar macrodipole (inset of panel (c)) stretches when placed in an electric field, corresponding to a positive piezoelectric coefficient at the nanoscale. A linear fit of the axial lattice strain versus field trend gives a positive d33,lattice ≈ +28 pm V−1, see panel (b). Mechanical hardening of the lattice is observed at higher fields, which leads to a decreased d33,lattice ≈ +6 pm V−1. The inclination of the calculated stress–strain trend in panel (b), top and left axis, respectively, gives a simulated Young's modulus for a single BTA-C1 molecular stack Y33,lattice of 2.8 GPa and 12.6 GPa for the small and large strain regimes, respectively. The electrostatic stress X here is calculated as the electric force F over the stack area A: X = F/A = E·Q/A = E·P, where E is electric field, Q is total charge and P is ferroelectric polarization. The small-strain elastic modulus matches experimentally measured values on single-crystal nanorods of different short-tailed BTAs.38 For the longer-tailed BTA-C6, due to lower dipole density, the calculated Young's moduli decrease to 1.9 GPa (small-strain) and 8.6 GPa (large-strain). Based on Hooke's law, the notably decreasing width of the parabolic energy landscape in the panel (a) with increasing electric field indicates a growing Young's modulus (through a larger spring constant), as well. The observation of the non-constant Young's modulus will be relevant in our further discussion, see Electromechanical response of other BTA homologues.
We confirmed the positive nanoscopic d33 at a higher level of theory – by quantum-mechanical DFT computations on a self-assembled BTA dimer, see Fig. 3(c and d). BTA columnar macrodipoles (i.e. a helical hydrogen-bonded system of microdipoles) have two preferred orientations UP (P↑, right) or DOWN (P↓, left) with a characteristic dihedral angle ±β between the amide moieties and the benzene plane, and an interdisc distance c, see inset of panel (c). By DFT simulations, the dihedral angle versus interdisc distance relation and the corresponding characteristic potential energy U can be computed. We performed a scan at the QM level to determine this relation for a BTA-C1 (methyl sidechains, see inset of panel (d)) dimer during its macrodipole M flip from “up” to “down” through a planar conformation of the amide moieties (i.e. dihedral angle β = 0°) with respect to the phenyl group, see panel (c). This data can be transformed to the longitudinal lattice strain S33,lattice = Δc/c and the electric field E = U/M, as given in panel (d). A change in magnitude of the macrodipole M with the dihedral angle is taken into account.18 If we fit this trend, its linear slope (solid line) directly gives the nanoscopic piezoelectric constant d33,lattice ≈ +25 pm V−1, which matches the results obtained by molecular dynamics simulations above. Returning to the Young's modulus estimation, DFT calculations using electrostatic stress approach (see Fig. S5a, ESI†) give lower estimates for both BTA homologues at high-field range, being 3.1 GPa and 4.1 GPa for BTA-C6 and BTA-C1, respectively. For BTA-C12 with dodecyl sidechains this coefficient equals 1.7 GPa which will be important for further discussions. Fig. S5b (ESI†) compares the elastic moduli of all three BTA homologues obtained by different approaches. More details on both the MD and DFT simulations can be found in the ESI,† “Simulated BTA strain-field trends at the nanoscale”.
Despite being very close to the experimentally obtained value in magnitude, the piezoelectric constant d33 is of an opposite – positive – sign. In macroscopic devices strictly negative piezoelectric coefficients are observed, which implies that this nanoscopic mechanism is overpowered by other micro- and/or macroscopic phenomena, in particular the dimensional effect as argued throughout the text. Coexistence of nanoscopic positive and macroscopic negative piezoelectric response is very different from the P(VDF–TrFE) case, in which negative strain has been reported to arise at all scales – single polymer chains, crystallites and bulk layers (see ESI,† Dimensional effect for details). However, since the measured real-device macroscopic (large-signal) and microscopic (small-signal) responses in BTA remain negative, we conclude that bulk collective effects, governed by the dimensional effect, preponderate over the nanoscopic single-stack mechanism. In the following we will therefore continue to focus on the different roles of the macroscopic small-signal and large-signal mechanisms.
To evaluate the relative contributions of reversible-microscopic and irreversible-macroscopic processes, the measured large-signal strain was compared to the small-signal one. The latter was calculated by integration of the small-signal d33–E loops of Fig. 2b. The S33,SS–E characteristics obtained in this way (grey lines in Fig. 2a) do not give a closed loop. To fully reproduce the measured curve form, extrinsic contributions to the small-signal strain must be taken into account. Based on ref. 37, the small-signal strain equals 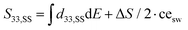 , where ΔS is the mismatch offset of the
, where ΔS is the mismatch offset of the 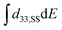 integral and cesw is the fraction of the switched cells. cesw can be approximated by the irreversible polarization loop, normalized from 0 to 1. The irreversible polarization (black solid lines in Fig. S4b, ESI†) can be obtained by subtracting the reversible contribution to the polarization (black dashed line) from the total polarization hysteresis curve (red solid line). For this, the reversible polarization is acquired by integration of the small-signal capacitance C–V butterfly loop (Fig. S4c, ESI†). It is dominated by a linear dielectric response and gives only slight hysteresis with polarization values lower than 0.1 mC m−2 for BTA-C6. Similar procedure was performed on P(VDF–TrFE) and the results are given in Fig. S4(d–f) (ESI†).
integral and cesw is the fraction of the switched cells. cesw can be approximated by the irreversible polarization loop, normalized from 0 to 1. The irreversible polarization (black solid lines in Fig. S4b, ESI†) can be obtained by subtracting the reversible contribution to the polarization (black dashed line) from the total polarization hysteresis curve (red solid line). For this, the reversible polarization is acquired by integration of the small-signal capacitance C–V butterfly loop (Fig. S4c, ESI†). It is dominated by a linear dielectric response and gives only slight hysteresis with polarization values lower than 0.1 mC m−2 for BTA-C6. Similar procedure was performed on P(VDF–TrFE) and the results are given in Fig. S4(d–f) (ESI†).
For BTA-C6 this offset-corrected small-signal strain loop (black solid line in Fig. 2a) reproduces the measured negative large-signal strain quite well, whereas larger deviations are found in the positive strain range. Comparing results for BTA-C6 and P(VDF–TrFE), the large-signal strain appears to be dominated by intrinsic (reversible) effects in the former, while extrinsic (irreversible) effects manifest stronger in the latter. This agrees to the results presented in ref. 14 on P(VDF–TrFE) claiming that its piezoelectric strain, despite being induced by the reversible lattice deformations, as shown by dynamic in situ XRD measurements, is also influenced by macroscopic crystalline–amorphous matter interactions. Below, we will show that in BTA-C6 the proportion of intrinsic and extrinsic contributions can be controllably tuned.
d 33 vs. remnant polarization and disorder
BTA molecules self-assemble to form long supramolecular stacks, see AFM micrographs in Fig. S2 (ESI†). In spin-coated thin-films these molecular columns initially lie in-plane and, to be able to operate in the out-of-plane device structure, molecules are aligned homeotropically by a short field-annealing procedure as discussed in the ESI.†![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 30,31 The possibility to control the molecular alignment allows to tune the macroscopic remnant polarization and the amount of the non-switchable material. Thus, to further study the differences in small- and large-signal piezoelectric response we changed the molecular alignment level of our BTA-C6 devices. First, a d33 dependence on the macroscopic remnant polarization could be established in this way. Second, if the macroscopic piezostriction-dimensional effect (for crystalline matter in an amorphous matrix) is the dominant factor in the electromechanical response of BTA, a larger fraction of (supposedly) softer non-aligned material should lead to an increase in the large-signal strain and d33 through a decrease of the elastic modulus of the bulk Y33, as d33 = 2εrε0Prγ33/Y33. The small-signal response would experience a linear dependence on the fraction of aligned material, i.e. Pr, as, based on the discussion above, it is mostly driven by intrinsic microscopic effects.
30,31 The possibility to control the molecular alignment allows to tune the macroscopic remnant polarization and the amount of the non-switchable material. Thus, to further study the differences in small- and large-signal piezoelectric response we changed the molecular alignment level of our BTA-C6 devices. First, a d33 dependence on the macroscopic remnant polarization could be established in this way. Second, if the macroscopic piezostriction-dimensional effect (for crystalline matter in an amorphous matrix) is the dominant factor in the electromechanical response of BTA, a larger fraction of (supposedly) softer non-aligned material should lead to an increase in the large-signal strain and d33 through a decrease of the elastic modulus of the bulk Y33, as d33 = 2εrε0Prγ33/Y33. The small-signal response would experience a linear dependence on the fraction of aligned material, i.e. Pr, as, based on the discussion above, it is mostly driven by intrinsic microscopic effects.
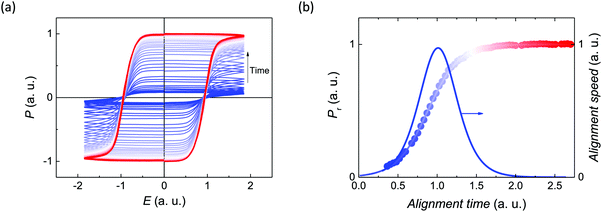
During the homeotropic alignment procedure, the temporal growth of the remnant polarization is of cumulative Gaussian fashion with clear saturation (see Fig. 4) and most likely proceeds via a nucleation-and-growth mechanism. Different levels of remnant polarization can be obtained by stopping the alignment at different stages and cooling to the measurement temperature. The results of the measured dependence show that both the piezoelectric coefficient and the strain decrease in magnitude with lower molecular alignment level, see Fig. S6 (ESI†) for details. A linearly growing d33-polarization dependence is found for both the large- and small-signal response with a slope of around −0.15 pm V−1 and −0.085 pm V−1 per 1 mC m−2 respectively. The disorder parameter (vide infra) was nearly independent of alignment level. To compare, a slope of −0.55 pm V−1 per 1 mC m−2 at large-signal conditions was previously found for P(VDF–TrFE) with Pr controlled by the annealing temperature.14,39 These results clearly show that the piezoelectric response cannot be improved by changing the alignment level. This, and the approximately linear dependence on Pr, point to d33 being dominated by microscopic effects in well-aligned BTA-C6.
We discovered that another way to tune the piezoelectric coefficients is through the layer disorder. Structural disorder of a ferroelectric arises from various defects and manifests itself as a distribution in local coercive fields, as stated by the classical Preisach theory.40 In a recent work we presented an experimental approach to measure this Preisach distribution (PD) and established a direct connection between the material's morphology and the width and shape of the PD.41 However, to evaluate the width of the distribution, a projection of the PD is sufficient, which is straightforwardly obtained as the switching current response to a triangular voltage signal, i.e. the derivative of the macroscopic polarization hysteresis loop.42 Having all the hysteresis loops measured, we fitted the corresponding J–V curves to a Gaussian function, see Fig. S8a (ESI†) for examples. To be able to compare distributions of different devices with different parameters we normalized these to the coercive field value on the abscissa axis and the maximum hysteron (i.e. switching current) density on the ordinate axis. The extracted standard deviation σ was used as a proxy for structural disorder and the amount of amorphous material present in the active layer.41 The obtained σ parameter varied in range 0.1–0.45 for BTA-C6. The measurements were performed at 60 °C to compare the behaviour among the BTA homologues (see below), at which they all are in the columnar-hexagonal liquid-crystalline state and ferroelectrically switchable (see ESI†).31
A surprisingly clear disorder dependency is found among BTA-C6 devices. As seen in Fig. 5a, the small-signal d33 (black open symbols) slightly deteriorates from around −4.7 pm V−1 to −3.5 pm V−1 with disorder. In contrast, the large-signal d33 has a strong growing trend from −5 pm V−1 to −21 pm V−1. This strong d33,LS correlation with the disorder parameter causes the datapoint scattering in the remnant polarization dependence of panel (b) of Fig. 5 as devices with equal Pr can have different disorders. For polarization-dependent data with constant disorder see Fig. S6 (ESI†). Comparing panels (a) and (b), the large-signal response is noticeably disorder-dominated, while the small-signal response is more sensitive to the remnant polarization value. This accords well with the previously discussed macroscopic-extrinsic-irreversible and microscopic-intrinsic-reversible switching processes and suggests that disorder is a macroscopic (bulk) characteristic. The disorder influences the form of the strain-field butterfly loops, similarly to its slanting effect on the polarization hysteresis loops. Fig. 5(c–e) shows that for the least disordered devices close-to-ideal S–E hysteresis loops with small mismatch between the large- and small-signal strain are found, whereas blunt elongated loops, with large mismatch between the large- and small-signal strain, are found for the most disordered ones. Thus, with the help of disorder, the balance between the intrinsic and extrinsic polarization switching contributions is gradually moved towards the extrinsic (irreversible effects) side.
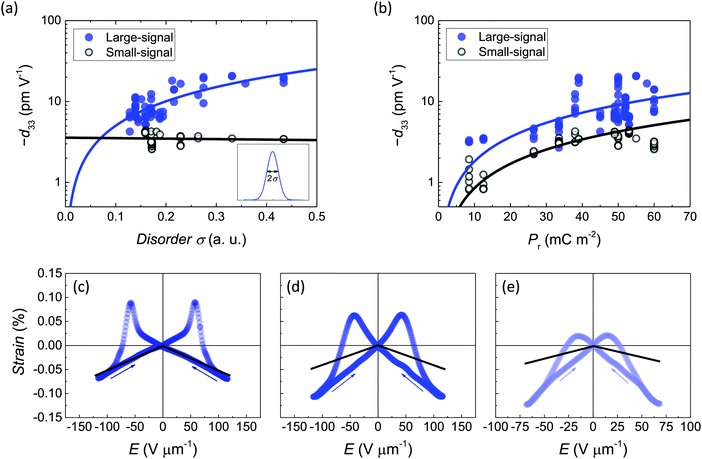 | ||
| Fig. 5 Tuning the piezoelectric coefficients of BTA-C6. Large-signal (blue full symbols) and small-signal (black open symbols) piezoelectric coefficient d33 dependence on (a) the relative energetic disorder σ (for varying Pr) which was obtained from fitting of the normalized switching current transients to a Gaussian function (see inset), and on (b) the remnant polarization (for varying disorder). Polarization and disorder of BTA-C6 devices were controlled as explained in the text. Solid lines are linear fits. Semi-logarithmic scale is used to better represent the small d33 values. (c–e) Examples of large-signal strain-field butterfly loops (blue symbols) for low, medium and large disorder, respectively. Black lines give a slope of corresponding small-signal characteristics (see Fig. S8, ESI†). | ||
To summarize our findings so far, we have shown that BTA-C6 demonstrates a negative longitudinal piezoelectric effect, which can be tuned by the macroscopic remnant polarization and the level of disorder. The piezostriction (polarization-coupled electrostriction) rationalizes the observed linear strain-field dependence, and the dimensional effect determines the negative sign of its slope, d33. For highly-ordered devices both the small- and large-signal piezoelectric responses arise from the intrinsic reversible contributions. For more disordered layers extrinsic irreversible effects begin to dominate the large-signal strain, which boosts the d33 values to −20 pm V−1 and above. This result is roughly twice lower than that of the P(VDF–TrFE), yet it surpasses a large number of organic ferroelectric crystals.18 Despite falling behind the best inorganic piezoelectrics in terms of d33 by an order of magnitude, the material is competitive in terms of the figure of merit for energy harvesting dg due to its relatively high g33 = −0.1 m2 C−1. Based on this combination of the piezoelectric charge and voltage coefficients d33g33 = 2 × 10−12 m3 J−1, BTA-C6 outperforms a number of inorganic and composite piezoelectric materials.6,19 The self-healing quality inherent to liquid-crystals and low electrical fatigue (see Fig. S9, ESI†) are additional advantages. Another important constant – the electromechanical coupling coefficient 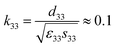 is similar to quartz.6
is similar to quartz.6
Electromechanical response of other BTA homologues
The BTA-C6 molecular core has three short hexyl tails attached to it that determine the relatively short intercolumnar distance ∼1.55 nm. BTA-C6 is in a plastic-crystalline (Fig. S10, ESI†) phase above and crystalline at room temperature and has a geometrically expected dipole density of around 60 mC m−2.31 As piezoelectric coefficients are coupled to the mechanical compliance, easier deformable materials with the same polarization would in principle be preferred. Therefore, we tested different BTA homologues that have longer peripheral chains: C8, C10, C12 and C18, corresponding to a CnH2n+1 alkyl tail. With the molecular core remaining the same, longer flexible alkyl chains bring more intrinsic mobility and thus shift the properties to more liquid-crystalline (see a phase diagram in Fig. S10, ESI†). This also results in higher structural disorder, as previously confirmed by X-ray scattering techniques.43 However, due to the longer side-chains, the dipole density gradually decreases from ∼45 mC m−2 for BTA-C8 to ∼20 mC m−2 for BTA-C18.31Large-signal electromechanical responses for all BTAs are given in Fig. S11 (top row) (ESI†). Interestingly, while BTA-C8 still demonstrates C6-like negative piezoelectric switching with d33 ≈ −8 pm V−1, other homologues have unusual, virtually contraction-only strain-field loops of opposite sense with prominent negative peaks around the coercive field, as shown in Fig. 6a. BTA-C12 is used as an example here and in further analysis. This effect, like the regular negative piezoelectric effect seen in BTA-C6, is not transient and intermediate unsaturated loops fit nicely within the full-saturation curve, see Fig. S12 (ESI†). If operated on the steepest linear branch segment, the device would give an effective strain-field relation coefficient of more than −50 pm V−1. While the electrostriction equation S33 = Q33D2 could reproduce the negative peaks (Fig. S13a, ESI†) when an (atypical) positive Q33 = +0.55 m4 C−2 was used, the fit could not explain the lack of positive strain. In combination with the Maxwell strain (see below), a higher quality fit is obtained (Fig. S13c, ESI†). However, such exceptional behavior does not agree with the negative electrostrictive and piezoelectric coefficients discussed above for BTA-C6. Hence, we propose that the Maxwell strain must be considered as the dominant factor in the electromechanical response of the long-substituted BTAs.
Maxwell stress is a well-known effect, present in parallel-plate capacitors due to attractive electrostatic forces acting on the oppositely charged surfaces. This causes negative strain on dielectric spacers, which is directly proportional to the mechanical compliance (s = 1/Y) of the material. For small deformations (where 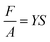 holds) the stress–strain relation is approximately
holds) the stress–strain relation is approximately 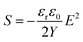 , with Maxwell stress
, with Maxwell stress 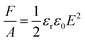 , where F is the compressive force, Y is the Young's modulus, E is the applied field, εrε0 is the dielectric permittivity of the material and A is the contact area. This effect has been extensively studied and successfully applied in the field of elastomer actuators.44,45 The quadratic-to-field Maxwell stress induced strain gave a good fit of the reverse parts of the S–E loops, i.e. after polarization saturation, for a Young's modulus of Y33 = 0.75 GPa for BTA-C12 (Fig. S13b, ESI†). A similar procedure resulted in 0.95 GPa for BTA-C10 and 0.3 GPa for BTA-C18 at 60 °C. This trend leads to extrapolated Y33 values of 1.2 GPa for BTA-C8 and 1.5 GPa for BTA-C6. It was previously found that for single fibers of crystalline compact-tailed BTAs the elastic constant can reach ∼2–3 GPa, depending on the tail substituent (lower Y for longer tails),38 which makes the obtained values in range 0.3–1.5 GPa for our longer-substituted liquid-crystals very reasonable. No direct Y measurements on liquid-crystalline BTAs are known to us. To compare, the elastic constant of P(VDF–TrFE), depending on annealing temperature, varies between 3–4 GPa.46 We suggest that this mechanical softness together with the lower remnant polarization of the longer-substituted BTAs is the reason that the strain-field characteristics are dominated by Maxwell strain rather than piezostriction, which is very different from the BTA-C6 and C8 materials. See Fig. S14 and Supplementary methods (ESI†), Piezostriction vs. Maxwell strain, for a further discussion.
, where F is the compressive force, Y is the Young's modulus, E is the applied field, εrε0 is the dielectric permittivity of the material and A is the contact area. This effect has been extensively studied and successfully applied in the field of elastomer actuators.44,45 The quadratic-to-field Maxwell stress induced strain gave a good fit of the reverse parts of the S–E loops, i.e. after polarization saturation, for a Young's modulus of Y33 = 0.75 GPa for BTA-C12 (Fig. S13b, ESI†). A similar procedure resulted in 0.95 GPa for BTA-C10 and 0.3 GPa for BTA-C18 at 60 °C. This trend leads to extrapolated Y33 values of 1.2 GPa for BTA-C8 and 1.5 GPa for BTA-C6. It was previously found that for single fibers of crystalline compact-tailed BTAs the elastic constant can reach ∼2–3 GPa, depending on the tail substituent (lower Y for longer tails),38 which makes the obtained values in range 0.3–1.5 GPa for our longer-substituted liquid-crystals very reasonable. No direct Y measurements on liquid-crystalline BTAs are known to us. To compare, the elastic constant of P(VDF–TrFE), depending on annealing temperature, varies between 3–4 GPa.46 We suggest that this mechanical softness together with the lower remnant polarization of the longer-substituted BTAs is the reason that the strain-field characteristics are dominated by Maxwell strain rather than piezostriction, which is very different from the BTA-C6 and C8 materials. See Fig. S14 and Supplementary methods (ESI†), Piezostriction vs. Maxwell strain, for a further discussion.
To fit the negative peaks at rising fields, the Maxwell strain equation must be upgraded by including the variation in elastic modulus with field. Alternatively, a similar modulation in εr would have the same effect but would be at odds with the measured near-constant value of εr in e.g. Fig. S4c (ESI†). It is known that P(VDF–TrFE) demonstrates mechanical hardening upon poling – the elastic modulus grows with remnant polarization,39 yet the effect is static. A dynamic Young's modulus variation was observed and measured in inorganic polycrystalline films upon polarization switching and was related to 90°-domain switching.47 A similar dynamic effect is likely to occur in the BTAs upon polarization switching. With a Gaussian distribution of elastic modulus taken into account (Fig. 6b), a very good fit of these odd-shaped S–E loops is obtained, see Fig. 6a (black line). Here, the minimum in elastic modulus at 0.06 GPa would be a consequence of the high density of small domains and domain walls at zero net polarization point that leads to a significant weakening of the hydrogen-bonded supramolecular backbone; in contrast, the fully polarized state consists of large, well-developed axial domains, which leads to mechanical hardening and a steady maximum at 0.75 GPa. This is illustrated in the inset of Fig. 6b. The small positive strain overshoot around the coercive field of highly-ordered BTA-C6 devices (e.g.Fig. 5c and Fig. S6a, ESI†) is likely related to the same material softening in combination with the linear piezostriction. The field-induced mechanical stiffening of the lattice in the axial direction found by DFT/MD simulations that was explained earlier in the text agrees well with the discussed experimental finding. The ratio of the perfect-case simulated elastic modulus of 1.7 GPa for BTA-C12 (Fig. S5, ESI†) and the experimental minimum of 0.06 GPa can be used to roughly estimate the fraction of soft amorphous material in the layer, which approaches ∼5%.
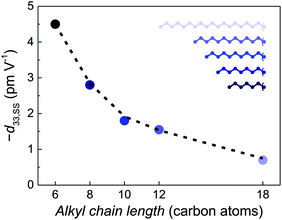
The small-signal response of longer-substituted BTA homologues remains regular with a negative d33, see Fig. S11 bottom row (ESI†). It is typical for liquid-crystalline materials to maintain short-range order while long-range order is absent. This might well explain why close-to-ideal small-signal d33–E loops are possible despite irregular Maxwell stress dominated large-signal strain. Yet, the small-signal d33 decreases significantly with lengthening of the alkyl chains: −4.5, −2.8, −1.8, −1.55, −0.7 pm V−1 for C6, C8, C10, C12 and C18, respectively (Fig. 7). This behavior can be quantitatively reproduced based on the piezostriction formula d33 = 2Q33εrε0Pr with the same Q33 ≈ −0.66 m4 C−2 for all homologues, as shown by the dashed line. Here, we have used typical (measured) remnant polarization Pr and dielectric constant εr values for each homologue.
Discussion
By combination of interferometric small- and large-signal piezoelectric response measurements we demonstrated a negative longitudinal piezoelectric effect in thin films of the small-molecular organic ferroelectric BTA (trialkylbenzene-1,3,5-tricarboxamide). The piezoelectric coefficient d33 was shown to depend strongly on the level of structural disorder in the active layer. While the small-signal d33 declined with increasing disorder (from −4.5 to −3.5 pm V−1), an opposite trend was observed under large-signal conditions – significant growth from around −5 pm V−1 to above −20 pm V−1. A growing mismatch between small- and large-signal strain with increasing disorder indicates that these responses become governed by different mechanisms. For highly ordered devices, both the small- and large-signal strain are dominated by intrinsic microscopic (reversible) effects and can be explained by pure piezostriction (polarization-coupled electrostriction). With growing disorder, the excessive large-signal strain becomes dominated by extrinsic irreversible factors – domain wall motion and consequent macroscopic polarization switching.As piezoelectric coefficients are directly proportional to the mechanical compliance, we tested different BTA homologues with longer mesogenic tails and thus stronger expressed liquid-crystalline properties, i.e. higher disorder and lower Young's modulus. Differently to the textbook-like large-signal strain-field butterfly loops of short-tailed BTA-C6 and C8 devices, the corresponding electromechanical response of other BTA homologues (C10, C12, C18) was mostly caused by the Maxwell strain in combination with a pronounced softening of the bulk upon polarization switching. The small-signal response remained normal, i.e. negative, with gradually decreasing d33 values for longer substituted molecules.
Based on these results, BTA is the first small-molecular organic ferroelectric with an experimentally observed negative piezoelectric effect. Combined with low fatigue (>106 cycles for full polarization switching), long polarization retention (>10 years at room temperature) and a broad operating temperature range, the disorder-tuned piezoelectric response with d33 potentially over −20 pm V−1 and a large figure of merit for energy harvesting d33g33 = 2 × 10−12 m3 J−1 makes BTA a perspective material for flexible and lightweight piezoelectric applications.
Methods
Materials and devices
BTA-C6, C8, C10, C12 and C18 (corresponding to linear alkyl chains CnHn+1) were synthesized following the procedure reported previously.29,31 P(VDF–TrFE) 77%/23% was bought from Solvay and used as received. Thin-film capacitor devices were fabricated from solution by spin-coating on chemically cleaned glass substrates with patterned metal electrodes. P(VDF–TrFE) layers were additionally annealed at 140 °C for 2 hours to increase crystallinity. Top electrodes were thermally evaporated to form cross-bar geometry capacitor devices. Aluminum electrodes were used for BTAs and gold for P(VDF–TrFE). Ferroelectric layers were poled by continuous voltage sweeping prior to further measurements. More Experimental details can be found in the ESI.†Converse piezoelectric effect measurements
Strain-field piezoelectric characteristics were measured using the commercial vibration-damped AixAcct double-beam laser interferometer (DBLI) system with resolution of 10−2 Å and d33 measurement accuracy of 0.2 pm V−1. Large-signal piezoelectric response was measured during a voltage sweep of 10–50 Hz and averaged 50–100 times to avoid secondary effects. Polarization (displacement) hysteresis loops were registered simultaneously. Remnant strain was set to zero. Small-signal piezoelectric response and small-signal capacitance were measured by applying a staircase-like voltage signal with superimposed high-frequency sinusoidal voltage signal (fss = 1–5 kHz, Vss = 1–5 V). As the ferroelectric layer is clamped on a rigid substrate, all piezoelectric characteristics obtained should be considered effective. Measurement temperature was controlled by Linkam heating stage system.Author contributions
I. U. performed experiments, analysed the data and wrote the manuscript draft. X. M. and S. B. synthesized and characterized the BTA materials. Y. W. helped with the piezoelectric measurements. M. B. and M. L. executed the DFT/MD simulations. I. U., T. D. C. and M. K. wrote and edited the paper. M. K. and M. L. supervised the work. All authors discussed the results and reviewed the paper.Data and materials availability
Data and materials are available from the corresponding author upon reasonable request.Conflicts of interest
Authors declare no competing interests.Acknowledgements
We would like to thank Prof. Beatriz Noheda Pinuaga for the opportunity to use the piezoelectric response measurement equipment and for stimulating discussions. We also thank Jacob Baas for the technical support during the piezoelectric measurements. We gratefully acknowledge Rint Sijbesma for guiding the materials synthesis and feedback on the manuscript. I. U. acknowledges funding by Vetenskapsrådet. Y. W. thanks the China Scholarship Council for funding. T. D. C. acknowledges financial support from the Swedish Government Strategic Research Area in Materials Science on Functional Materials at Linköping University (Faculty Grant SFO Mat LiU No. 2009 00971). M. L. thanks the Swedish e-Science Research Center (SERC) for funding and the Swedish National Infrastructure for Computing (SNIC) for providing computer resources.References
- C. Brown, R. Kell, R. Taylor and L. Thomas, Piezoelectric Materials, A Review of Progress, IRE Trans. Compon. Parts, 1962, 9, 193–211 CrossRef.
- W. L. Bond, A Mineral Survey for Piezo-Electric Materials, Bell Syst. Tech. J., 1943, 22, 145–152 CrossRef.
- P. K. Panda, Review: environmental friendly lead-free piezoelectric materials, J. Mater. Sci., 2009, 44, 5049–5062 CrossRef CAS.
- K. S. Ramadan, D. Sameoto and S. Evoy, A review of piezoelectric polymers as functional materials for electromechanical transducers, Smart Mater. Struct., 2014, 23, 33001 CrossRef.
- S. B. Lang and S. Muensit, Review of some lesser-known applications of piezoelectric and pyroelectric polymers, Appl. Phys. A: Mater. Sci. Process., 2006, 85, 125–134 CrossRef CAS.
- J. Rödel, et al., Transferring lead-free piezoelectric ceramics into application, J. Eur. Ceram. Soc., 2015, 35, 1659–1681 CrossRef.
- A. H. Rajabi, M. Jaffe and T. L. Arinzeh, Piezoelectric materials for tissue regeneration: A review, Acta Biomater., 2015, 24, 12–23 CrossRef CAS PubMed.
- D.-W. Fu, et al., Diisopropylammonium Bromide Is a High-Temperature Molecular Ferroelectric Crystal, Science, 2013, 339, 425–428 CrossRef CAS PubMed.
- S. Horiuchi, et al., Above-room-temperature ferroelectricity in a single-component molecular crystal, Nature, 2010, 463, 789–792 CrossRef CAS PubMed.
- K. Kobayashi, S. Horiuchi, S. Ishibashi, Y. Murakami and R. Kumai, Field-Induced Antipolar–Polar Structural Transformation and Giant Electrostriction in Organic Crystal, J. Am. Chem. Soc., 2018, 140, 3842–3845 CrossRef CAS PubMed.
- W. Gao, et al., Flexible organic ferroelectric films with a large piezoelectric response, NPG Asia Mater., 2015, 7, e189 CrossRef CAS.
- Z. Zhang, et al., Tunable electroresistance and electro-optic effects of transparent molecular ferroelectrics, Sci. Adv., 2017, 3, e1701008 CrossRef PubMed.
- T. Furukawa and N. Seo, Electrostriction as the Origin of Piezoelectricity in Ferroelectric Polymers, Jpn. J. Appl. Phys., 1990, 29, 675–680 CrossRef CAS.
- I. Katsouras, et al., The negative piezoelectric effect of the ferroelectric polymer poly(vinylidene fluoride), Nat. Mater., 2016, 15, 78–84 CrossRef CAS PubMed.
- Y. Liu, et al., Ferroelectric polymers exhibiting behaviour reminiscent of a morphotropic phase boundary, Nature, 2018, 562, 96–100 CrossRef CAS PubMed.
- M. Owczarek, et al., Flexible ferroelectric organic crystals, Nat. Commun., 2016, 7, 13108 CrossRef CAS PubMed.
- Y.-M. You, et al., An organic-inorganic perovskite ferroelectric with large piezoelectric response, Science, 2017, 357, 306–309 CrossRef CAS PubMed.
- S. Horiuchi, J. Tsutsumi, K. Kobayashi, R. Kumai and S. Ishibashi, Piezoelectricity of strongly polarized ferroelectrics in prototropic organic crystals, J. Mater. Chem. C, 2018, 6, 4714–4719 RSC.
- D. B. Deutz, et al., Analysis and experimental validation of the figure of merit for piezoelectric energy harvesters, Mater. Horiz., 2018, 5, 444–453 RSC.
- R. K. Vasudevan, N. Balke, P. Maksymovych, S. Jesse and S. V. Kalinin, Ferroelectric or non-ferroelectric: Why so many materials exhibit ‘ferroelectricity’ on the nanoscale, Appl. Phys. Rev., 2017, 4, 21302 Search PubMed.
- B. Noheda, Structure and high-piezoelectricity in lead oxide solid solutions, Curr. Opin. Solid State Mater. Sci., 2002, 6, 27–34 CrossRef CAS.
- S. Liu and R. E. Cohen, Origin of Negative Longitudinal Piezoelectric Effect, Phys. Rev. Lett., 2017, 119, 207601 CrossRef PubMed.
- H. S. Nalwa, Ferroelectric Polymers: Chemistry, Physics, and Applications, CRC Press, Boca Raton, 1995 Search PubMed.
- B. Ploss, B. Ploss, F. G. Shin, H. L. W. Chan and C. L. Choy, Pyroelectric or piezoelectric compensated ferroelectric composites, 2000 Search PubMed.
- I. Graz, et al., Flexible active-matrix cells with selectively poled bifunctional polymer-ceramic nanocomposite for pressure and temperature sensing skin, J. Appl. Phys., 2009, 106, 34503 CrossRef.
- E. Fukada, History and recent progress in piezoelectric polymers, IEEE Trans. Ultrason. Ferroelectr. Freq. Control, 2000, 47, 1277–1290 CAS.
- T. Lenz, et al., Ferroelectricity and piezoelectricity in soft biological tissue: Porcine aortic walls revisited, Appl. Phys. Lett., 2017, 111, 133701 CrossRef.
- C. F. C. Fitié, W. S. C. Roelofs, M. Kemerink and R. P. Sijbesma, Remnant polarization in thin films from a columnar liquid crystal, J. Am. Chem. Soc., 2010, 132, 6892–6893 CrossRef PubMed.
- C. F. C. Fitié, et al., Polar Switching in Trialkylbenzene-1,3,5-tricarboxamides, J. Phys. Chem. B, 2012, 116, 3928–3937 CrossRef PubMed.
- A. V. Gorbunov, et al., True ferroelectric switching in thin films of trialkylbenzene-1,3,5-tricarboxamide (BTA), Phys. Chem. Chem. Phys., 2016, 18, 23663–23672 RSC.
- I. Urbanaviciute, et al., Tuning the Ferroelectric Properties of Trialkylbenzene-1,3,5-tricarboxamide (BTA), Adv. Electron. Mater., 2017, 3, 1600530 CrossRef.
- A. V. Gorbunov, et al., Polarization loss in the organic ferroelectric trialkylbenzene-1,3,5-tricarboxamide (BTA), Phys. Chem. Chem. Phys., 2017, 19, 3192–3200 RSC.
- I. Urbanaviciute, et al., Suppressing depolarization by tail substitution in an organic supramolecular ferroelectric, Phys. Chem. Chem. Phys., 2019, 21, 2069–2079 RSC.
- A. V. Gorbunov, et al., Switchable Charge Injection Barrier in an Organic Supramolecular Semiconductor, ACS Appl. Mater. Interfaces, 2016, 8, 15535–15542 CrossRef CAS PubMed.
- A. V. Gorbunov, et al., Ferroelectric self-assembled molecular materials showing both rectifying and switchable conductivity, Sci. Adv., 2017, 3, e1701017 CrossRef PubMed.
- W. Y. Pan and L. E. Cross, A sensitive double beam laser interferometer for studying high-frequency piezoelectric and electrostrictive strains, Rev. Sci. Instrum., 1989, 60, 2701–2705 CrossRef CAS.
- P. Gerber, C. Kügeler, U. Böttger and R. Waser, Effects of reversible and irreversible ferroelectric switchings on the piezoelectric large-signal response of lead zirconate titanate thin films, J. Appl. Phys., 2005, 98, 124101 CrossRef.
- D. Kluge, et al., Influence of the Molecular Structure and Morphology of Self-Assembled 1,3,5-Benzenetrisamide Nanofibers on their Mechanical Properties, Small, 2012, 8, 2563–2570 CrossRef CAS PubMed.
- T. Furukawa, Piezoelectricity and pyroelectricity in polymers, IEEE Trans. Electr. Insul., 1989, 24, 375–394 CrossRef CAS.
- F. Preisach, Über die magnetische Nachwirkung, Z. Phys., 1935, 94, 277–302 CrossRef.
- I. Urbanavičiūtė, T. D. Cornelissen, X. Meng, R. P. Sijbesma and M. Kemerink, Physical reality of the Preisach model for organic ferroelectrics, Nat. Commun., 2018, 9, 4409 CrossRef PubMed.
- V. Khikhlovskyi, et al., Multi-bit organic ferroelectric memory, Org. Electron., 2013, 14, 3399–3405 CrossRef CAS.
- A. V. Gorbunov, et al., Polarization loss in the organic ferroelectric trialkylbenzene-1,3,5-tricarboxamide (BTA), Phys. Chem. Chem. Phys., 2017, 19, 3192–3200 RSC.
- R. Pelrine, R. Kornbluh, Q. Pei and J. Joseph, High-speed electrically actuated elastomers with strain greater than 100%, Science, 2000, 287, 836–839 CrossRef CAS PubMed.
- A. O’Halloran, F. O’Malley and P. McHugh, A review on dielectric elastomer actuators, technology, applications, and challenges, J. Appl. Phys., 2008, 104, 71101 CrossRef.
- S.-W. Hahm and D.-Y. Khang, Crystallization and microstructure-dependent elastic moduli of ferroelectric P(VDF–TrFE) thin films, Soft Matter, 2010, 6, 5802 RSC.
- C. S. Wojnar, J.-B. le Graverend and D. M. Kochmann, Broadband control of the viscoelasticity of ferroelectrics via domain switching, Appl. Phys. Lett., 2014, 105, 162912 CrossRef.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c9mh00094a |
| ‡ Present address: Department of Chemistry, Kazi Nazrul University, Asansol, Burdwan, 713340, West Bengal, India. |
| This journal is © The Royal Society of Chemistry 2019 |