Design and synthesis of two-dimensional covalent organic frameworks with four-arm cores: prediction of remarkable ambipolar charge-transport properties†
Simil
Thomas‡
a,
Hong
Li‡
a,
Raghunath R.
Dasari‡
 a,
Austin M.
Evans
a,
Austin M.
Evans
 b,
Ioannina
Castano
b,
Taylor G.
Allen
b,
Ioannina
Castano
b,
Taylor G.
Allen
 c,
Obadiah G.
Reid
c,
Obadiah G.
Reid
 cd,
Garry
Rumbles
cd,
Garry
Rumbles
 cd,
William R.
Dichtel
cd,
William R.
Dichtel
 b,
Nathan C.
Gianneschi
b,
Nathan C.
Gianneschi
 bef,
Seth R.
Marder
*a,
Veaceslav
Coropceanu
bef,
Seth R.
Marder
*a,
Veaceslav
Coropceanu
 *a and
Jean-Luc
Brédas
*a and
Jean-Luc
Brédas
 *a
*a
aSchool of Chemistry and Biochemistry, Center for Organic Photonics and Electronics (COPE), Georgia Institute of Technology, Atlanta, Georgia 30332-0400, USA. E-mail: jean-luc.bredas@chemistry.gatech.edu; marder.seth@chemistry.gatech.edu; coropceanu@gatech.edu
bDepartment of Chemistry, Northwestern University, Evanston, Illinois 60208, USA
cNational Renewable Energy Laboratory, 15013 Denver West Parkway, Golden, Colorado 80401, USA
dRenewable and Sustainable Energy Institute, Department of Chemistry, University of Colorado, Boulder, CO 80309, USA
eDepartment of Materials Science and Engineering, Northwestern University, Evanston, IL 60208, USA
fDepartment of Biomedical Engineering, Northwestern University, Evanston, IL 60208, USA
First published on 22nd May 2019
Abstract
We have considered three two-dimensional (2D) π-conjugated polymer network (i.e., covalent organic frameworks, COFs) materials based on pyrene, porphyrin, and zinc-porphyrin cores connected via diacetylenic linkers. Their electronic structures, investigated at the density functional theory global-hybrid level, are indicative of valence and conduction bands that have large widths, ranging between 1 and 2 eV. Using a molecular approach to derive the electronic couplings between adjacent core units and the electron-vibration couplings, the three π-conjugated 2D COFs are predicted to have ambipolar charge-transport characteristics with electron and hole mobilities in the range of 65–95 cm2 V−1 s−1. Such predicted values rank these 2D COFs among the highest-mobility organic semiconductors. In addition, we have synthesized the zinc-porphyrin based 2D COF and carried out structural characterization via powder X-ray diffraction, high-resolution transmission electron microscopy, and surface area analysis, which demonstrates the feasibility of these electroactive networks. Steady-state and flash-photolysis time-resolved microwave conductivity measurements on the zinc-porphyrin COF point to appreciable, broadband photoconductivity while transmission spectral measurements are indicative of extended π-conjugation.
New conceptsTwo-dimensional fully π-conjugated covalent organic frameworks (COFs) represent an emerging class of materials with rich chemistry and physics. Up to now, the charge-carrier mobility within a single, isolated layer of such COFs had not been characterized. Here, we show theoretically that the mobility in these systems can be described on the basis of concepts similar to those applied to organic mixed-valence systems and can potentially reach values higher than in the best organic crystalline semiconductors. We emphasize the importance of considering properly the electron-vibration couplings that play an important role in all π-conjugated organic materials (a feature however overlooked in earlier reports). We also demonstrate the synthetic feasibility of some of these promising materials. Overall, we expect our work to trigger further experimental and theoretical investigations of these fascinating systems. |
1. Introduction
Two-dimensional (2D) materials are garnering a great deal of attention due to their remarkable physical and chemical properties and their high potential for a variety of applications.1–4 While graphene, the prototypical 2D material, displays electron and hole mobilities in excess of 5000 cm2 V−1 s−1 at room temperature,5 its semimetallic nature prevents its use in many electronic applications.6 More recently, other 2D materials based on transition metal dichalcogenides have been developed; these systems have a finite bandgap and charge-carrier mobilities up to 200 cm2 V−1 s−1 have been reported in the case of MoS27 and WSe2.8Covalent organic frameworks (COFs) represent another class of promising materials.9–15 These are porous systems formed by the precise linkage of organic building blocks through covalent bonds in order to generate predetermined assemblies, which can have a three-dimensional (3D)10 or 2D layered structure.9 Promising applications of COFs include gas storage,16,17 gas separation,18 energy storage,19 catalysis,20,21 or optoelectronic devices.14 To date, the measurements of charge-carrier mobilities have been restricted to bulk COF structures.22 Also, pressed pellets of the fully π-conjugated pyrene-based COF synthesized by Jiang and co-workers show conductivities along the stacks on the order of 7 × 10−4 S cm−1 after doping with iodine.15 In such systems, charge transport can be theoretically described with approaches similar to those used for organic molecular crystals.23 Up to now, however, except for a few preliminary studies,24,25 there has been no comprehensive investigation of the charge-transport mechanism within the plane of 2D (isolated) π-conjugated COF sheets. Here, our objective is to develop a theoretical framework to describe charge transport in strictly 2D π-conjugated polymer networks. Our description exploits intra-molecular electron transfer theory,26 which we have extensively applied earlier in the context of organic mixed-valence systems. 2D COF structures are generally designed on the basis of three-arm cores (for instance, benzene or triphenylene) or four-arm cores (for instance, pyrene or porphyrins). Three-arm cores turn out to have the propensity to lead to the formation of highly symmetric (kagome-like) lattices,27 which often result in the appearance of totally flat top valence bands and/or bottom conduction bands; in such cases, the charge-carrier effective masses are extremely large and the related carrier mobilities vanish. Thus, we have chosen to work here with four-arm cores.
Given our earlier experience with quasi-1D polypyrene28 and polyporphyrin29 conjugated chains and the experimental interest in pyrene and porphyrin 2D COFs, we investigate three 2D conjugated polymer networks based on four-arm pyrene (Pyr-COF), porphyrin (Por-COF), and zinc porphyrin (ZnPor-COF) cores; these are connected via diacetylenic linkers, which are selected since they are expected to provide larger electronic couplings between adjacent core units than the typical long, twisted (phenylene-based) linkers.25,30,31 In addition, sp2-carbon-conjugated COFs exhibit a higher degree of conjugation with respect to imine-linked COFs. This comes, however, at the expense of a highly difficult synthesis of crystalline, ordered COFs, due to the irreversible nature of C–C coupling chemistry.15,32–36 The chemical structures of the three 2D COFs under investigation are shown in Fig. 1. We note that the synthesis of Pyr-COF has been recently reported, with powder conductivity measurements giving an electrical conductivity on the order of 10−5 S cm−1.33
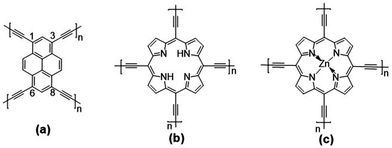 | ||
| Fig. 1 Chemical structures of the: (a) pyrene (Pyr-COF); (b) porphyrin (Por-COF); and (c) zinc porphyrin (ZnPor-COF) 2D COFs. | ||
In this work, we first combined density functional theory (DFT) calculations with an oligomer approach to estimate the charge-transport parameters. In view of the strength of the connection between the electronic structure and geometric structure in π-conjugated systems,37 we then evaluated the charge-carrier mobilities by taking explicit account of electron-vibration couplings. We synthesized the Zn-Por COF and, with the insight from the theoretical calculations, carried out: (i) its structural characterization via IR, transmission spectral measurements, solid-state 13C NMR, powder X-ray diffraction (PXRD), high-resolution transmission electron microscopy (HR-TEM), and Brunauer–Emmett–Teller (BET) surface area analysis; and (ii) its charge-transport characterization via steady-state and flash-photolysis time-resolved microwave conductivity (fp-TRMC) measurements.
2. Computational methodology
The geometry optimizations of the 2D periodic structures were performed at the density functional theory (DFT) level with the global-hybrid PBE0 functional and the POB-TZVP basis set (optimized for periodic solid-state calculations),38 using a 5 × 5 k-point mesh. During the optimizations, both the atomic positions and the unit-cell parameters were fully relaxed. The electronic band structures were calculated at the same level of theory. The effective masses were evaluated by diagonalizing the inverse of the effective mass tensor (1/mij); the latter was obtained from the valence band maximum or conduction band minimum using a finite-difference method with a 0.01 1/Bohr step. All these calculations were performed with the CRYSTAL17 package.39,40 The electronic couplings and electron-vibration (phonon) couplings were evaluated from the energies of the ground and excited states of molecular fragments, as discussed below. All molecular electronic-structure calculations were performed with the PBE0 functional and the 6-31G(d,p) basis set, using the Gaussian 09 package.413. Results and discussion
3.1. Geometric and electronic structure
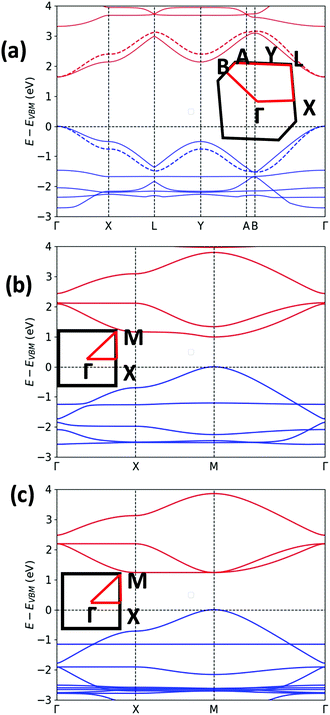
The unit cell of Pyr-COF contains four ethynylene linkers that are connected to the 1, 3, 6, and 8 positions of a pyrene core, as illustrated in Fig. 1(a). The optimized Pyr-COF lattice symmetry belongs to the p2gg plane group (characterized by glide reflection symmetry), with unit-cell parameters a1 = a2 = 12.08 Å and γ = 96°. In both Por-COF and ZnPor-COF, the four ethynylene linkers are connected to the meso positions of the porphyrin or zinc porphyrin cores, see Fig. 1(b) and (c). The optimized unit-cell parameters of the Por-COF and ZnPor-COF are a1 = a2 = 13.44 Å and γ ≈ 90°, and a1 = a2 = 13.43 Å and γ ≈ 90°, respectively. Assuming that in Pyr-COF the two hydrogens effectively delocalize among the four inner N atoms, both systems belong to the p4mm plane group (characterized by reflection symmetry with mirrors at 45°). The band structures of the three COFs are shown in Fig. 2. They are direct-gap semiconductors with calculated bandgaps of 1.63 eV (at the Γ-point) for Pyr-COF, 0.99 eV (at the K-point) in Por-COF, and 1.23 eV (at the K-point) in ZnPor-COF. These systems can thus be classified as low bandgap COF materials, which are of current great interest.42 Importantly, the conduction and valence bands exhibit large widths in all three COFs: 1.5 eV [1.5 eV] for the valence band [conduction band] in Pyr-COF; 1.7 eV [1.1 eV] in Por-COF, and 1.8 eV [1.0 eV] in ZnPor-COF. As a direct result of the strong dispersion of the frontier electronic bands, the effective masses for both holes and electrons are small. Given that the Pyr-COF unit cell is oblique and thus deviates from a square unit cell, the charge-transport properties are expected to be anisotropic; we find indeed effective masses in Pyr-COF of 0.13 m0 and 0.24 m0 for holes and 0.12 m0 and 0.26 m0 for electrons. In the porphyrin COFs, the hole effective masses are calculated to be even smaller and more isotropic (in view of the quasi-square lattice symmetry): 0.07 m0 and 0.09 m0 in Por-COF and 0.08 m0 and 0.10 m0 in ZnPor-COF. In the case of electrons, the situation in the porphyrin systems turns out to be more complex due to (quasi-)degeneracy of the LUMO and LUMO+1 orbitals (see ESI†), which results in a strong mixing of the electronic states around the conduction band minimum; this feature is particularly evident in the case of ZnPor-COF where the two corresponding sub-bands are degenerate at the M point. In this instance, in analogy with the case of the valence band in GaAs, it would be necessary to introduce effective masses for each sub-band;43 since a full account of this issue is beyond the scope of the present work, we simply mention that, based on a fitting of the lowest conduction sub-bands in Por-COF and ZnPor-COF, the electron effective masses are estimated to be as small as ca. 0.1 m0. It is important to emphasize that, overall, such small effective masses are among the lowest calculated for organic-based semiconductors and can be expected to give rise to high charge-carrier mobilities.3.2. Electronic couplings
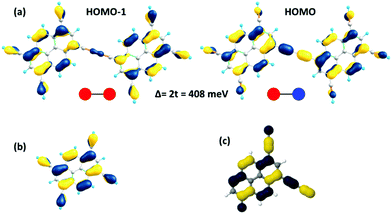
As a useful step towards determining the strength of the electronic couplings between adjacent core units, we take Pyr-COF as an example and show next that its electronic structure can be rationalized in the framework of a simple tight-binding, Hückel-like model. Inspection of the 2D-periodic wave functions indicates that the charge transport for both electron and holes can be viewed as originating in electron/hole transfer between adjacent pyrene units, which play the role of charge-carrying moieties. This is more clearly seen when considering the frontier orbitals (see Fig. 3) of a molecular model consisting of two diacetylene-linked pyrene units (to which we refer below as a dimer; see also Fig. S1, ESI†). As illustrated by Fig. 3, the HOMO (highest occupied molecular orbital) and HOMO−1 represent symmetric and anti-symmetric linear combinations of the HOMOs of the pyrene units. The same holds true for the LUMO (lowest unoccupied molecular orbital) and LUMO+1, see Fig. S2 (ESI†). It is also useful to note the similarity between the dimer HOMO and the wavefunction of the 2D Pyr-COF at the valence band maximum (Γ-point). Importantly, this picture is strongly reminiscent of that typically found in the case of intra-molecular electron transfer in organic mixed-valence systems.26 Indeed, since there is no direct overlap between the frontier orbitals of the pyrene cores, the electron transfer between two localized (diabatic) pyrene states is in fact mediated by the linker units, as is usually the case for mixed-valence systems. Thus, the electronic couplings between the (charge-carrying) pyrene moieties has a super-exchange nature and come from the mixing of the pyrene frontier with the diacetylenic linker orbitals. This feature clearly underlines that the choice of both the charge-carrying units and the linkers is critical to secure good charge-transport properties. Taking advantage of the similarity with mixed-valence systems, we can use the energies of the frontier orbitals of the pyrene dimer to estimate the effective electronic couplings, teff, between adjacent core units by means of the dimer energy-splitting approach:23,26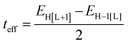 | (1) |
3.3. Electronic-vibration couplings
In addition to the electronic couplings, the characterization of the charge-transport properties also requires the knowledge of the electron-vibration (phonon) couplings. As was shown in the case of organic molecular crystals,23 there exist two electron-vibration mechanisms that affect charge transport. The first mechanism comes from the vibration-induced modulations of the site energies and is usually referred to as the local electron-vibration coupling; the local coupling is the key interaction accounted for in Holstein-type polaron models45,46 and Marcus electron-theory;47 its strength is expressed in terms of the polaron binding energy, Epol, or the reorganization energy, λ (whose value is twice Epol). The local electron-vibration contributions can be evaluated from the energies of the neutral and anion or cation states of the charge-carrying moieties, as discussed in detail elsewhere.23 The DFT calculations yield Epol values for holes [electrons] of 67 [96] meV, 27 [85] meV, and 28 [47] meV in Pyr-COF, Por-COF, and ZnPor-COF, respectively. Since these Epol values are significantly smaller than the relevant electronic bandwidths, the local electron-vibration interactions are not strong enough to lead to charge-carrier localization and the formation of small (molecular) polarons. The second electron-vibration coupling mechanism is referred to as non-local or Peierls coupling;23,48 it stems from the modulation of the transfer integrals by vibrational (phonon) modes:| teff = t(0)eff + ∑vjQj | (2) |
3.4. Charge-carrier mobilities
In order to estimate the carrier mobilities, the local electron-vibration coupling, being mainly due to high-frequency vibration modes, can be taken to contribute only to a renormalization of the transfer integrals and non-local electron-vibration couplings. Following Zhu et al.,49 the renormalization parameter α corresponds to:α = exp{−Epol![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) coth(ℏω/2kBT)/ℏω} coth(ℏω/2kBT)/ℏω} | (3) |
The mobilities along the [10] and [01] directions can then be calculated by means of eqn (4), which has originally been derived for a one-dimensional case in the limit where the bandwidth is much larger than kBT, which is the case here:50,51
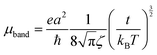 | (4) |
Finally, we note that we also calculated the mobilities by treating the electron-vibration couplings in the framework of the deformation potential (DP)53 model (see ESI,† for details). The reason is that this model has been recently used to estimate the mobilities in single-layer Hittorf's phosphorus,54 graphene,55 graphdiyne sheets,56 and triangulene-based COF.57 The DP-based mobilities (see Table S4, ESI†) are calculated to reach nearly 8 × 103 cm2 V−1 s−1 for both holes and electrons in Pyr-COF and are even one order of magnitude larger in Por-COF. These results underline that the charge-carrier scattering due to the DP mechanism plays only a minor role on the charge-transport properties of the 2D COFs investigated here; thus, given the propensity of the DP model to hugely overestimate the mobilities of π-conjugated 2D COFs, its application to such systems should be made with much caution.57
3.5. Synthesis and characterization of ZnPor-COF
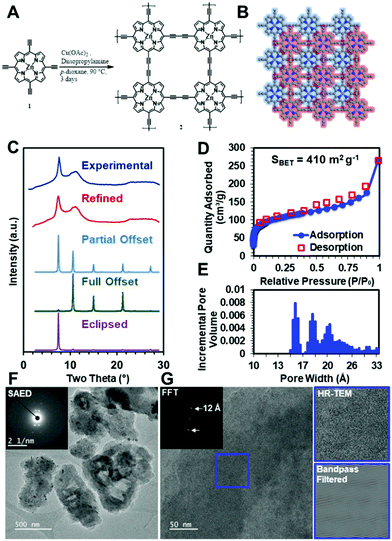
To demonstrate that these diacetylene-linked porphyrin COF materials can be realized, the zinc-metallated porphyrin 2D COF, ZnPor-COF, 2, was synthesized by copper-catalyzed Eglinton coupling of the 5,10,15,20-tetrakis(ethynyl)porphyrin-zinc(II) monomer, 1, ZnTEP, which was itself synthesized according to literature procedures,58,59 see Fig. 4A and the ESI,† for more details. We note that the metal-free porphyrin COF, Por-COF, could not be synthesized due to the insolubility of the ZnTEP monomer in common organic solvents.To evaluate whether the ZnPor-COF synthesis conditions created a crystalline network, we collected powder X-ray diffraction (PXRD) patterns of the resultant materials. The optimized reaction conditions yielded 2 as a micro-crystalline solid, as indicated by its PXRD pattern (Fig. 4C). A diffraction feature was observed at approximately two theta = 7.5°, which we assigned to the approximate spacing between Zn atoms and the 100 Bragg peak. This, combined with the geometric constraints of the monomers, indicated to us that the 2D structure was that shown in Fig. 4B. We thus modelled the structure using a primitive P4 unit cell. However, we were also interested in assigning the stacking structure of the 2D sheets. We first modelled the stacking of a completely eclipsed (AA stacking) and completely offset structure (AB stacking), which we then used to predict their respective XRD patterns (Fig. 4C). The relative intensities of the 100 and 110 features indicated that the stacking was between fully eclipsed and fully offset. Using this information, we conducted a Pawley refinement to more appropriately determine the correct structure. This produced a partially offset structure with a predicted diffraction pattern in good agreement with the experimentally obtained patterns (Fig. 4C). We then allowed the predicted pattern to broaden due to finite-grain effects (details available in the ESI†). This analysis indicates that the crystallites have an average in-plane dimension of 30 nm, which is consistent with previously reported COFs.60 To assess the extent of functional group conversion, we collected the attenuated total reflectance-infrared spectrum of 2, and compared with the tetraethynylzinc-porphyrin monomer 1 spectrum in Fig. S9a, see ESI.† The characteristic terminal alkyne C–H stretch at 3269 cm−1 of monomer 1 is absent in 2, indicating consumption of terminal acetylene of 1. The alkyne CC vibration at 2087 cm−1 of 1 was observed at 2150 cm−1 in 2. Similar shifts in alkyne CC vibration peaks were observed for the diphenylbutadiyne61 model compound, which was synthesized using the same synthesis conditions as for the COF, see Fig. S9b in ESI.† Solid-state CP/MAS 13C NMR of 2 show three resonances related to the porphyrin ring, and two weak resonances are attributed to the acetylene moiety at 85.4 and 74.3 ppm (Fig. S9c, ESI†). However, the appearance of resonances at 49.1 and 20.7 ppm suggest that trace amounts of diisopropylamine, which was used as a base in the COF synthesis, might present in COF 2 sample pores. To more fully characterize the structure of the COF material, we performed N2 isotherm experiments and a Brunauer–Emmett–Teller (BET) analysis to determine the surface area and pore size distribution of this COF (Fig. 4D and E). This measurement shows that the COF has a high surface area of >400 m2 g−1, to be compared with a theoretical surface area of 900 m2 g−1, see ESI,† for details; this deviation in surface area from the theoretical value is typical for microcrystalline COF powders. Moreover, the contaminants in the COF sample, as confirmed by solid-state 13C NMR, may have contributed to the observed lower surface area values. Additionally, the pore size distribution shows a maximum at approximately 1 nm, which is consistent with expected pore size of the offset structure. However, the broad XRD features, lower than ideal surface area, and broad pore size distributions indicate that defects are present within the material. To investigate the Zn-porphyrin material structure further, we imaged the COF using high-resolution transmission electron microscopy (HR-TEM). The low-resolution images in Fig. 4F show that the crystallites are unfaceted sheet-like particles of approximately one-micron length. Selected-area electron diffraction (SAED) (Fig. 4F inset) of the particles resulted in a four-fold diffraction pattern consistent with the spacing observed by bulk XRD. High-resolution images (Fig. 4G) of the same crystallites showed lattice fringes of approximately 1.2 nm, which were more easily seen when the image was bandpass filtered, further substantiating the structural assignment of the offset layers. Additional TEM images of ZnPor-COF are presented Fig. S10 and S11 (ESI†).
fp-TRMC measurements62,63 were performed on ZnPor-COF and monomer-like ([5,10,15,20-tetraphenylporphyrinato]zinc(II), ZnTPP) films to obtain an estimate of the mobilities for both materials. In doing so, we seek to deduce empirically the extent of delocalization in ZnPor-COF relative to ZnTPP. To facilitate measurements, the insoluble ZnPor-COF powder was embedded in inert polymer hosts (poly(methyl methacrylate), PMMA) or polystyrene (PS), (see ESI† for film processing details) to afford films with complete surface coverage of the substrate. Analysis of the AC mobilities obtained by fp-TRMC for crystalline particles is usually done with the Kubo relation,64,65 which requires as input the crystallite size. Taking for ZnPor-COF the crystallite size (30 nm) measured by PXRD and assuming the intrinsic (large-scale) mobility predicted theoretically (90 cm2 V−1 s−1), the Kubo relation gives 3.5 × 10−2 cm2 V−1 s−1 as the maximum AC mobility that could be measured at 9 GHz for such particle sizes (Fig. S12, ESI†). Upon photoexcitation at 700 nm of the ZnPor-COF–polymer films, the fp-TRMC measurements provide a yield-mobility product (ϕΣμ) of ca. 3 × 10−5 cm2 V−1 s−1. This experimental value of the yield-mobility product combined with the theoretical estimate of the maximum AC mobility allows us to place limits on both the actual charge carrier yield and the AC mobility. The former may range from 100–0.1%, and the latter from 3 × 10−5–3.5 × 10−2 cm2 V−1 s−1 (see Fig. 5 and Fig. S13–S15, ESI†). There is no reasonable expectation that every photon would generate a pair of charges (100% yield); thus, the AC mobility is likely in the upper end of the estimated range. Since neat conjugated polymers rarely exhibit charge yields above 10%,66–68 this suggests that the AC mobility within ZnPor-COF 30 nm crystallites should be over 10−4 cm2 V−1 s−1.
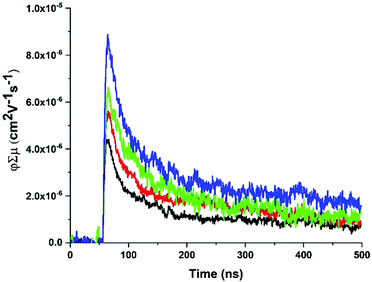 | ||
| Fig. 5 Representative fp-TRMC transients with increasing fluence (1 × 1014–4 × 1015 photons per cm2) for a ZnPor-COF-PS film at 700 nm photoexcitation with 7 ns pulse width. | ||
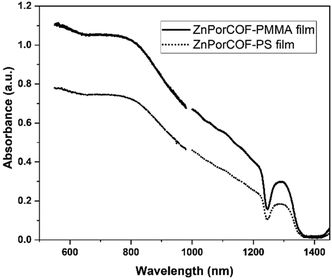
fp-TRMC measurements on a neat film of the monomer-like ZnTPP upon excitations at 430, 550, and 700 nm – i.e., on resonance with the Soret (430 nm) and Q-band (550 nm) transitions, and off-resonance at 700 nm – did not result in measurable yield-mobility products, see Fig. S16 (ESI†). The generation of photocarriers at 700 nm in ZnPorCOF–polymer films, far from typical Zn-porphyrin monomer resonances, is thus indicative of delocalized excitations due to electronic couplings among Zn porphyrin units in the COF. This is corroborated by the absorption spectra (acquired via transmission measurements) of ZnPor-COF–polymer films that show considerable optical density over the range of 300–1800 nm relative to the more discrete spectrum of ZnTPP (Fig. S17, ESI†). We note that, to rule out scattering contributions, absorption spectra of ZnPorCOF–polymer films were collected using an integrating sphere; these spectra also show extended absorption over the visible-to-NIR range, see Fig. 6.
In support of these data, photoconductivity action spectra were acquired by a steady-state microwave conductivity experiment (see ESI,† for details). Like the absorption spectra of ZnPor-COF–polymer films, the action spectra showed broadband photoconductivity over the range of 600–1100 nm (Fig. S18 and S19, ESI†), which is consistent with the band structures calculated in Section 3.1. Akin to fp-TRMC measurements, neat ZnTPP did not afford measurable steady-state photoconductivity over a wavelength range of 400–750 nm.
4. Conclusions
We have investigated at the DFT-PBE0 level the electronic structure of 2D π-conjugated polymer networks based on four-arm pyrene, porphyrin, and zinc porphyrin cores connected via diacetylenic linkers. The three 2D COFs are characterized by large widths of both valence and conduction bands, on the order of 1.5 to 2 eV, which leads to small hole and electron effective masses. Our work demonstrates that the charge-transport properties of these 2D polymer networks, based on fully π-conjugated core and linker building blocks, can be described by models akin to those used to characterize electron transfer in organic mixed-valence systems. Thus, calculations on fragments extracted from 2D COF structures can provide simple (and quick) estimates of the electronic and electron-vibration couplings. Our approach can therefore be used for screening the potential mobility values in new materials, even though more extended first-principles calculations of the electron-vibration (phonon) couplings could provide a more comprehensive description of the charge-transport properties in π-conjugated COFs. Considering the impact of (local and nonlocal) electron-vibration couplings, remarkable charge-carrier mobility values in the 65–95 cm2 V−1 s−1 range are predicted for both electrons and holes in the 2D COFs investigated here. These rank among the largest values, predicted and measured, in organic (macro-) molecular semiconductors.A COF network consisting of four-arm zinc porphyrin cores was synthesized. We obtained a micro-crystalline structure, which based on the correlation between the experimental and simulated PXRD patterns, nitrogen isotherms, and electron microscopy, shows the expected tessellated structure. Steady-state and time-resolved microwave conductivity measurements reveal appreciable, broadband photoconductivity for ZnPor-COF whereas monomer-like ZnTPP shows no measurable mobilities. The next, challenging steps are to develop experimental protocols that will both enable the formation of COF with larger grain sizes and allow for exfoliation of the 2D sheets and direct characterization of their intrinsic charge-transport properties. Our joint theoretical and experimental study points to important new directions for the development of COFs with exceptional electronic properties.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
J. L. B., S. R. M. and W. R. D. acknowledge the United States Army Research Office for a Multidisciplinary University Research Initiative (MURI) award under grant number W911NF-15-1-0447. A. M. E. is supported by the National Science Foundation Graduate Research Fellowship under Grant No. (DGE-1324585). I. C. is supported by the Ryan Fellowship and the Northwestern University International Institute for Nanotechnology. V. C. acknowledges support by the National Science Foundation (DMR-1708147). We thank Vamsi Krishna Narra, Cameron Feriante, Johannes E. Leisen, and Ruhui Chen for help with synthesis, PXRD, solid-state NMR, and ICP-MS measurements, respectively. We are grateful to Timothy C. Parker for helpful discussions. This work has also made use of the EPIC facility of NUANCE Center at Northwestern University, which has received support from the Soft and Hybrid Nanotechnology Experimental (SHyNE) Resource (NSF ECCS-1542205), the MRSEC program (NSF DMR-1720139) at the Materials Research Center, the Keck Foundation, the State of Illinois and International Institute for Nanotechnology (IIN). This work was authored by the National Renewable Energy Laboratory, operated by Alliance for Sustainable Energy, LLC, for the U.S. Department of Energy (DOE) under Contract No. DE-AC36-08GO28308. Funding for microwave measurements provided by Department of Energy, Office of Basic Energy Sciences, Division of Chemical Sciences, Biosciences, and Geosciences. The views expressed in the article do not necessarily represent the views of the DOE or the U.S. Government. The U.S. Government retains and the publisher, by accepting the article for publication, acknowledges that the U.S. Government retains a nonexclusive, paid-up, irrevocable, worldwide license to publish or reproduce the published form of this work, or allow others to do so, for U.S. Government purposes.Notes and references
- M. C. Lemme, L.-J. Li, T. Palacios and F. Schwierz, MRS Bull., 2014, 39, 711–718 CrossRef CAS.
- K. I. Bolotin, K. J. Sikes, Z. Jiang, M. Klima, G. Fudenberg, J. Hone, P. Kim and H. L. Stormer, Solid State Commun., 2008, 146, 351–355 CrossRef CAS.
- Z. Yin, H. Li, H. Li, L. Jiang, Y. Shi, Y. Sun, G. Lu, Q. Zhang, X. Chen and H. Zhang, ACS Nano, 2012, 6, 74–80 CrossRef CAS PubMed.
- G. R. Bhimanapati, Z. Lin, V. Meunier, Y. Jung, J. Cha, S. Das, D. Xiao, Y. Son, M. S. Strano, V. R. Cooper, L. Liang, S. G. Louie, E. Ringe, W. Zhou, S. S. Kim, R. R. Naik, B. G. Sumpter, H. Terrones, F. Xia, Y. Wang, J. Zhu, D. Akinwande, N. Alem, J. A. Schuller, R. E. Schaak, M. Terrones and J. A. Robinson, ACS Nano, 2015, 9, 11509–11539 CrossRef CAS PubMed.
- A. S. Mayorov, R. V. Gorbachev, S. V. Morozov, L. Britnell, R. Jalil, L. A. Ponomarenko, P. Blake, K. S. Novoselov, K. Watanabe, T. Taniguchi and A. K. Geim, Nano Lett., 2011, 11, 2396–2399 CrossRef CAS PubMed.
- F. Xia, D. B. Farmer, Y.-m. Lin and P. Avouris, Nano Lett., 2010, 10, 715–718 CrossRef CAS PubMed.
- B. Radisavljevic, A. Radenovic, J. Brivio, V. Giacometti and A. Kis, Nat. Nanotechnol., 2011, 6, 147 CrossRef CAS PubMed.
- Q. H. Wang, K. Kalantar-Zadeh, A. Kis, J. N. Coleman and M. S. Strano, Nat. Nanotechnol., 2012, 7, 699 CrossRef CAS PubMed.
- A. P. Côté, A. I. Benin, N. W. Ockwig, M. O'Keeffe, A. J. Matzger and O. M. Yaghi, Science, 2005, 310, 1166–1170 CrossRef PubMed.
- H. M. El-Kaderi, J. R. Hunt, J. L. Mendoza-Cortés, A. P. Côté, R. E. Taylor, M. O'Keeffe and O. M. Yaghi, Science, 2007, 316, 268–272 CrossRef CAS PubMed.
- F. J. Uribe-Romo, J. R. Hunt, H. Furukawa, C. Klöck, M. O’Keeffe and O. M. Yaghi, J. Am. Chem. Soc., 2009, 131, 4570–4571 CrossRef CAS PubMed.
- X. Feng, X. Ding and D. Jiang, Chem. Soc. Rev., 2012, 41, 6010–6022 RSC.
- J. W. Colson and W. R. Dichtel, Nat. Chem., 2013, 5, 453 CrossRef CAS PubMed.
- M. Dogru and T. Bein, Chem. Commun., 2014, 50, 5531–5546 RSC.
- E. Jin, M. Asada, Q. Xu, S. Dalapati, M. A. Addicoat, M. A. Brady, H. Xu, T. Nakamura, T. Heine, Q. Chen and D. Jiang, Science, 2017, 357, 673–676 CrossRef CAS PubMed.
- H. Furukawa and O. M. Yaghi, J. Am. Chem. Soc., 2009, 131, 8875–8883 CrossRef CAS PubMed.
- Z. Yongfei, Z. Ruqiang and Z. Yanli, Adv. Mater., 2016, 28, 2855–2873 CrossRef PubMed.
- S. Kandambeth, B. P. Biswal, H. D. Chaudhari, K. C. Rout, S. K. H, S. Mitra, S. Karak, A. Das, R. Mukherjee, U. K. Kharul and R. Banerjee, Adv. Mater., 2017, 29, 1603945 CrossRef PubMed.
- D. Ya, Y. Haishen, W. J. Michael, W. Shun, J. Yinghua, L. Se-Hee and Z. Wei, Angew. Chem., Int. Ed., 2016, 55, 1737–1741 CrossRef PubMed.
- S.-Y. Ding, J. Gao, Q. Wang, Y. Zhang, W.-G. Song, C.-Y. Su and W. Wang, J. Am. Chem. Soc., 2011, 133, 19816–19822 CrossRef CAS PubMed.
- H. Li, Q. Pan, Y. Ma, X. Guan, M. Xue, Q. Fang, Y. Yan, V. Valtchev and S. Qiu, J. Am. Chem. Soc., 2016, 138, 14783–14788 CrossRef CAS PubMed.
- D. Xuesong, G. Jia, F. Xiao, H. Yoshihito, G. Jingdong, S. Shu, M. Phornphimon, S. Akinori, N. Shigeru and J. Donglin, Angew. Chem., Int. Ed., 2011, 50, 1289–1293 CrossRef PubMed.
- V. Coropceanu, J. Cornil, D. A. da Silva Filho, Y. Olivier, R. Silbey and J.-L. Brédas, Chem. Rev., 2007, 107, 926–952 CrossRef CAS PubMed.
- V. Laszlo and T. Kowalczyk, J. Mater. Chem. A, 2016, 4, 10500–10507 RSC.
- V. Posligua, A. Aziz, R. Haver, M. D. Peeks, H. L. Anderson and R. Grau-Crespo, J. Phys. Chem. C, 2018, 122, 23790–23798 CrossRef CAS.
- V. Coropceanu, M. Malagoli, J. M. André and J. L. Brédas, J. Am. Chem. Soc., 2002, 124, 10519–10530 CrossRef CAS PubMed.
- S. Thomas, H. Li, C. Zhong, M. Matsumoto, W. R. Dichtel and J.-L. Bredas, Chem. Mater., 2019, 31, 3051–3065 CrossRef CAS.
- J. M. Toussaint, F. Wudl and J. L. Brédas, J. Chem. Phys., 1989, 91, 1783–1788 CrossRef CAS.
- D. Beljonne, G. E. O’Keefe, P. J. Hamer, R. H. Friend, H. L. Anderson and J. L. Brédas, J. Chem. Phys., 1997, 106, 9439–9460 CrossRef CAS.
- B. Sun, C.-H. Zhu, Y. Liu, C. Wang, L.-J. Wan and D. Wang, Chem. Mater., 2017, 29, 4367–4374 CrossRef CAS.
- H. Liao, H. Wang, H. Ding, X. Meng, H. Xu, B. Wang, X. Ai and C. Wang, J. Mater. Chem. A, 2016, 4, 7416–7421 RSC.
- X. Zhuang, W. Zhao, F. Zhang, Y. Cao, F. Liu, S. Bi and X. Feng, Polym. Chem., 2016, 7, 4176–4181 RSC.
- P. Prabakaran, S. Satapathy, E. Prasad and S. Sankararaman, J. Mater. Chem. C, 2018, 6, 380–387 RSC.
- E. Jin, J. Li, K. Geng, Q. Jiang, H. Xu, Q. Xu and D. Jiang, Nat. Commun., 2018, 9, 4143 CrossRef PubMed.
- S. Wu, M. Li, H. Phan, D. Wang, T. S. Herng, J. Ding, Z. Lu and J. Wu, Angew. Chem., Int. Ed., 2018, 57, 8007–8011 CrossRef CAS PubMed.
- Y. Zhao, H. Liu, C. Wu, Z. Zhang, Q. Pan, F. Hu, R. Wang, P. Li, X. Huang and Z. Li, Angew. Chem., Int. Ed., 2019, 58, 5376–5381 CrossRef CAS PubMed.
- J. L. Bredas and G. B. Street, Acc. Chem. Res., 1985, 18, 309–315 CrossRef CAS.
- M. F. Peintinger, D. V. Oliveira and T. Bredow, J. Comput. Chem., 2013, 34, 451–459 CrossRef CAS PubMed.
- R. Dovesi, V. R. Saunders, C. Roetti, R. Orlando, C. M. Zicovich-Wilson, F. Pascale, B. Civalleri, K. Doll, N. M. Harrison, I. J. Bush, P. D’Arco, M. Llunell, M. Causà, Y. Noël, L. Maschio, A. Erba, M. Rerat and S. Casassa, CRYSTAL17 User's Manual, University of Torino: Torino, 2017 Search PubMed.
- R. Dovesi, A. Erba, R. Orlando, C. M. Zicovich-Wilson, B. Civalleri, L. Maschio, M. Rérat, S. Casassa, J. Baima, S. Salustro and B. Kirtman, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, 8, e1360 Search PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, Revision B.01, Wallingford, CT, 2016 Search PubMed.
- N. Keller, D. Bessinger, S. Reuter, M. Calik, L. Ascherl, F. C. Hanusch, F. Auras and T. Bein, J. Am. Chem. Soc., 2017, 139, 8194–8199 CrossRef CAS.
- Y.-S. Kim, M. Marsman, G. Kresse, F. Tran and P. Blaha, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 205212 CrossRef.
- D. P. Arnold, R. D. Hartnell, G. A. Heath, L. Newby and R. D. Webster, Chem. Commun., 2002, 754–755, 10.1039/b200803n.
- T. Holstein, Ann. Phys., 1959, 8, 325–342 CAS.
- T. Holstein, Ann. Phys., 1959, 8, 343–389 CAS.
- R. A. Marcus, Rev. Mod. Phys., 1993, 65, 599–610 CrossRef CAS.
- R. E. Peierls, Quantum theory of solids, Oxford University Press, 1955 Search PubMed.
- L. Zhu, Y. Yi, Y. Li, E.-G. Kim, V. Coropceanu and J.-L. Brédas, J. Am. Chem. Soc., 2012, 134, 2340–2347 CrossRef CAS PubMed.
- F. Simone, M. Didier and C. Sergio, Adv. Funct. Mater., 2016, 26, 2292–2315 CrossRef.
- Y. Li, Y. Yi, V. Coropceanu and J.-L. Brédas, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 245201 CrossRef.
- X. Qian, H. Liu, C. Huang, S. Chen, L. Zhang, Y. Li, J. Wang and Y. Li, Sci. Rep., 2015, 5, 7756 CrossRef PubMed.
- J. Bardeen and W. Shockley, Phys. Rev., 1950, 80, 72–80 CrossRef CAS.
- G. Schusteritsch, M. Uhrin and C. J. Pickard, Nano Lett., 2016, 16, 2975–2980 CrossRef CAS PubMed.
- L. Chen, L. Wang, Z. Shuai and D. Beljonne, J. Phys. Chem. Lett., 2013, 4, 2158–2165 CrossRef CAS.
- M. Long, L. Tang, D. Wang, Y. Li and Z. Shuai, ACS Nano, 2011, 5, 2593–2600 CrossRef CAS PubMed.
- Y. Jing and T. Heine, J. Am. Chem. Soc., 2019, 141, 743–747 CrossRef CAS PubMed.
- H. L. Anderson, Tetrahedron Lett., 1992, 33, 1101–1104 CrossRef CAS.
- W.-N. Yen, S.-S. Lo, M.-C. Kuo, C.-L. Mai, G.-H. Lee, S.-M. Peng and C.-Y. Yeh, Org. Lett., 2006, 8, 4239–4242 CrossRef CAS PubMed.
- A. M. Evans, L. R. Parent, N. C. Flanders, R. P. Bisbey, E. Vitaku, M. S. Kirschner, R. D. Schaller, L. X. Chen, N. C. Gianneschi and W. R. Dichtel, Science, 2018, 361, 52–57 CrossRef CAS.
- G. Baranović, L. Colombo, K. Furić, J. R. Durig, J. F. Sullivan and J. Mink, J. Mol. Struct., 1986, 144, 53–69 CrossRef.
- O. G. Reid, D. T. Moore, Z. Li, D. Zhao, Y. Yan, K. Zhu and G. Rumbles, J. Phys. D: Appl. Phys., 2017, 50, 493002 CrossRef.
- T. J. Savenije, A. J. Ferguson, N. Kopidakis and G. Rumbles, J. Phys. Chem. C, 2013, 117, 24085–24103 CrossRef CAS.
- M. J. Bird, O. G. Reid, A. R. Cook, S. Asaoka, Y. Shibano, H. Imahori, G. Rumbles and J. R. Miller, J. Phys. Chem. C, 2014, 118, 6100–6109 CrossRef CAS.
- P. Prins, F. C. Grozema, J. M. Schins and L. D. A. Siebbeles, Phys. Status Solidi B, 2006, 243, 382–386 CrossRef CAS.
- O. G. Reid and G. Rumbles, J. Phys. Chem. Lett., 2013, 4, 2348–2355 CrossRef CAS.
- O. G. Reid, J. A. N. Malik, G. Latini, S. Dayal, N. Kopidakis, C. Silva, N. Stingelin and G. Rumbles, J. Polym. Sci., Part B: Polym. Phys., 2012, 50, 27–37 CrossRef CAS.
- O. G. Reid, R. D. Pensack, Y. Song, G. D. Scholes and G. Rumbles, Chem. Mater., 2014, 26, 561–575 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c9mh00035f |
| ‡ These authors contributed equally. |
| This journal is © The Royal Society of Chemistry 2019 |