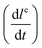Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Continuous focusing, fractionation and extraction of anionic analytes in a microfluidic chip†
Vasileios A.
Papadimitriou
 *,
Loes I.
Segerink
*,
Loes I.
Segerink
 and
Jan C. T.
Eijkel
and
Jan C. T.
Eijkel
BIOS Lab on a Chip group, MESA+ Institute for Nanotechnology, Max Planck Centre for Complex Fluid Dynamics and Technical Medical Centre, University of Twente, The Netherlands. E-mail: v.papadimitriou@utwente.nl
First published on 2nd September 2019
Abstract
Electrokinetic focusing and separation methods, specifically ion concentration polarization focusing (ICPF), provide a very powerful and easy to use analytical tool for several scientific fields. Nevertheless, the concentrated and separated analytes are effectively trapped inside the chip in picoliter volumes. In this article we propose an ICPF device that allows continuous and selective extraction of the focused analytes. A theoretical background is presented to understand the dynamics of the system and a 1D model was developed that describes the general behavior of the system. We demonstrate the selective extraction of three fluorescent model anionic analytes and we report selective extraction of the analytes at a 300-fold increased concentration.
Introduction
Electrokinetic separation methods are powerful tools that have found application in a wide range of fields, from biological/chemical research to food industry and forensics. Since the early days of microfluidics many electrokinetic separation methods have been translated to lab-on-chip systems. A special class of electrokinetic techniques combines separation and focusing such as isoelectric focusing (IEF), electric field gradient focusing (EFGF) and isotachophoresis (ITP). These techniques require an application-specific electrolyte preparation which can be a tedious process and significantly reduce their usability for point-of-care systems. For example, ITP requires a leading and trailing electrolyte with electrophoretic mobilities higher and lower than the target analyte. In recent years ion concentration polarization focusing (ICPF) was introduced, which is capable of concentrating and separating analytes without the use of specific electrolytes. ICPF focuses analytes in the electric field gradient created by the phenomenon of ion concentration polarization (ICP).ICPF was introduced by Wang et al.1 more than a decade ago and it was capable of concentration factors of proteins and peptides in the order of millions. Since its introduction vast amount of research has been performed with this technique, where Quist et al.2 demonstrated that apart from concentration also separation occurred.3–7,34 Though the technique offers a very powerful and simple analytical tool, a disadvantage is that the focused and separated analytes are “trapped” inside the chip in picoliter volumes. Further analysis, for example by mass spectrometry, thus is impossible. Attempts to extract the preconcentrated analytes have been reported, but they require the use of Quake valves8 or magnetically actuated valves.9 Continuous extraction of the concentrated biomolecules and cells in non-selective fashion has been demonstrated by Kwak et al.10 In this article we propose an ICPF device modified to selectively and continuously extract the fractionated and concentrated analytes from their complex background, allowing further downstream analysis.
Theory
Concentration polarization and establishment of a depletion zone
In order to understand the dynamics of the device we will first briefly describe the process of ICPF. For a more extensive theoretical description of ICPF the reader is referred to the recent report by Ouyang et al.11 In addition the feasibility of extraction of concentrated (cationic) analytes via ICPF was reported via numerical simulations of similar systems.12,13 ICPF is based on differential ionic migration in an electric field gradient. The electrical field gradient is created by applying a steady potential difference over a microchannel which contains a region in the axial direction with a salt concentration gradient. As the current density must be equal in the entire system, an electric field gradient results, which can be formulated as| E(x) = J·ρ(x) | (1) |
 | ||
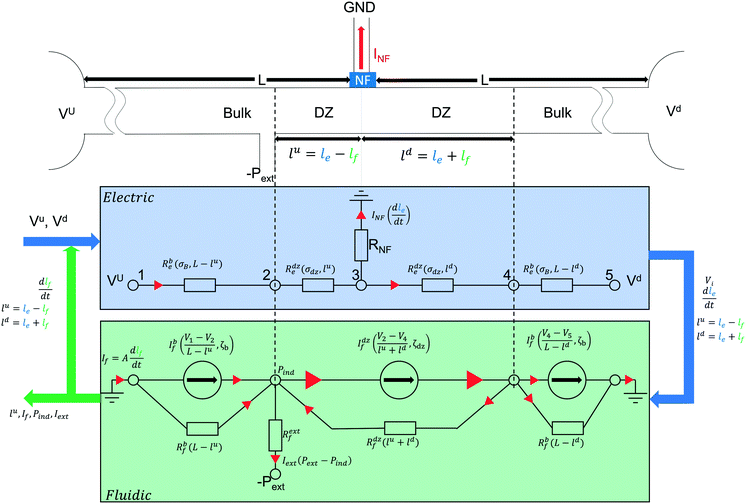
| Fig. 1 Device outline (a) and concept of our ICPF device for extraction (b). (a) A potential is applied in the upstream (Vu) and downstream (Vd) reservoir with Vu > Vd. A low negative pressure is applied in the extraction channels marked with green. The side channels are filled with a buffer and they are grounded. A depletion zone (shown in white (b)) is formed due to ICP when an E-field is applied across an exclusion zone (Nafion) (b and c). At the interface between dz and the bulk (shown in orange) the concentration gradient (c) creates an E-field gradient zone when a second E-field is applied across it. All ions move towards the dz with a constant net flow (vconv) but due to their difference in electrophoretic mobility (μeph) they experience different electrophoretic velocity (veph) in the E-field gradient zone resulting in separation. The analytes will start focusing at the position in the E-field that electrophoretic (veph) and bulk flow velocity (vconv) are equal and opposite (d). Due to non-uniformities of the electro-osmotic flow (EOF) an induced pressure (Pind) is created at the focusing location (e). 1D area averaged flow velocities. The focused analytes can be placed at the extraction channel and will be extracted under low negative pressure, which needs to be lower than the induced pressure (Pext < Pind) note: on figure (e) the EOF arrow accounts for both the primary and secondary EOF due to the extended space charge close to the Nafion membrane.11 | ||
Fig. 1a shows the separation channel connected to two buffer channels via a Nafion membrane, which was patterned by capillarity15 in a manner previously reported.5 The buffer channels are grounded while two different potentials are applied at the ends of the separation channel (Vu at upstream and Vd at downstream reservoir with Vu > Vd). This configuration will create a depletion zone in the separation channel and simultaneously apply an axial electrical field. At the interface between the depletion zone and the bulk solution an E-field gradient is generated, where anionic analytes will be focused (see below).
The novelty of our device is, that to perform continuous extraction, we added two extraction channels to this configuration, intersecting the separation channel perpendicularly (Fig. 1b). The focused analytes are extracted by applying a small negative pressure (Pext) in these extraction channels. The system variables relevant for the extraction process are the analyte position, analyte extraction rate and analyte concentration rate. The two reservoir potentials (Vu and Vd) and the extraction pressure (Pext) all influence these variables and their effects are coupled. To describe this complex system an approximative one-dimensional (1D) model was created. It consists of two coupled parts: a model for the electrical currents (Fig. 2, blue) and a model for the hydrodynamic fluxes in the system (Fig. 2, green). The model is limited in its scope as it does not provide a description of the formation of the different analyte zones in the E-field gradient zone. However, it serves as a model to understand the coupling of the electrical and hydrodynamic phenomena of the device.
Electric model (Fig. 2)
As mentioned above, the cation-permselective Nafion membrane creates a local gradient of the cation and anion fluxes, creating the depletion zone in the separation channel. For simplicity of the model we assume that the current is carried exclusively by the background electrolyte (not by the analytes) and that the cation and anion transport numbers in the bulk solution are equal. We also assume that the membrane is perfectly cation selective. We denote the salt concentration in the depletion zone as Cdz. Under these conditions, the growth rate of the depletion zone length in the channel, dle/dt [m s−1], depends on the current running through the Nafion membrane as | (2) |
The conductivity in the depletion zone is generally measured to be several orders of magnitude lower than in the bulk,4 and hence the total resistance of the system increases when the depletion zone grows and occupies an increasing part of the channel. Since constant potentials are applied to the reservoirs, the current through the channel and the Nafion membrane decreases as the depletion zone grows, resulting in a reduced growth rate of this zone as time proceeds. The electric model shown in Fig. 2 was created to calculate at any moment in time the size of each zone (bulk, depletion zone) both upstream and downstream from the Nafion membrane, as well as the various currents and the potentials at each interface between the zones.
Fluidic model (Fig. 2)
The fluxes of the analyte ions i, Ji [mol m−2 s−1] are given by the Nernst–Planck equation. We formulate the fluxes as a function of axial position x as:| Ji(x) = Ji,diff(x) + Ji,conv(x) + Ji,eph(x) | (3) |
Here Ji,diff, Ji,conv and Ji,eph are the flux contributions of diffusion, convection and electrophoresis of analyte ions i, respectively. In our initial analysis we neglect diffusion for reasons of simplicity (Ji,diff(x) = 0).
We will now discuss the separate contributions to the flux of analyte i in eqn (3) in more detail.
The contribution by convection is
| Ji,conv(x) = vconvCi(x) | (4) |
Here Ci [mol m−3] is the concentration of the species i and vconv [m s−1] the linear convective liquid velocity assuming constant channel cross section. It has been demonstrated that the area-averaged bulk flow velocity in a channel can be obtained by a linear combination of pressure-driven (vPDF [m s−1]) and electroosmotic flow (vEOF [m s−1]).16 In our channel a pressure distribution is created by the suction that is applied at the extraction channels, as well as by the axial variation of EOF stemming from the conductivity gradient, that by the requirement of mass conservation locally generates a restoring pressure-driven flow. Below we will briefly treat both contributions.
 | (5) |
In addition, close to the membrane a space charge region exists due to ICP.18–22 The space charge region has a large net positive charge, so the action of the electrical field in the bulk is to move it to the cathodic reservoir (same direction as the main EOF). Because this EOF (usually named electroosmosis of the second kind11) is so much larger than anywhere else in the channel, we get the PDF back-flow vortices. A small part of the extra ‘push’ on the solution is translated to a PDF towards the cathode. Summarizing, the space charge region at the Nafion acts as a small and strong pump.
The device is operated in the over-limiting current regime19 where these EOF induced vortices have a strong contribution to the local 2D flow velocity profile. The 2D flow velocity profile that will result from the combination of all PDF and EOF contributions is a rich scientific topic,4,11,23,24,30 which for simplicity we here reduce to an area-averaged 1D flow velocity (Fig. 1e).
Adding both contributions to the bulk flow velocity (vconv = vEOF(x) + vPDF(x)), we can write the convectional flux as:
| Ji,conv(x) = vEOF(x)Ci(x) + vPDF(x)Ci(x) | (6) |
| vi,eph(x) = μi,ephE(x) | (7) |
Here μi,eph [m2 s−1 V−1] is the electrophoretic mobility. At the interface between the depletion zone and the bulk a region exists with a concentration and thus E-field gradient. The further the analytes move up the electric field in this zone, the higher their electrophoretic velocity. Within a certain mobility window, each ionic species will have a specific point in the gradient where its electrophoretic velocity is equal and opposite to the convective flow velocity, at which point it will be focused (Fig. 1d).2 The analytes will thus be separated and create focused bands, sorting themselves out based on their electrophoretic mobilities with the lowest mobility ion closest to the depletion zone, where the E-field is highest.
The basic principle of the model is shown in Fig. 2. An in-depth analysis is presented in the ESI† along with a description of the effect of the down-stream and up-stream potential on the size of the depletion zone (i.e. focusing location), on the concentration rate and on the maximum induced negative pressure. In the ESI† the model results are compared and explained based on previous theoretical and experimental works.16–21 The fitting parameters of the model are the zeta potential in the bulk and in the depletion zone, and the salt concentration in the depletion zone.32,33 For the latter we used the parameter “depletion factor” which describes how many times the average concentration in the depletion zone is lower than the bulk. An estimate for the depletion factor was taken from literature.24
Separation and extraction resolution
To determine the separation resolution of the system, we need to distinguish between two operational modes, namely peak mode and plateau mode, as can be found also in other focusing techniques such as ITP.2,35 A schematic of the two modes is shown in Fig. 3. . This approach results in the concentration profile:
. This approach results in the concentration profile:

| (8) |
 | (9) |
 | (10) |
The derivation of eqn (8) and (9) is presented in the ESI.† The focusing location of species i is given by eqn (9). In peak mode we then obtain the resolution Rs
 | (11) |
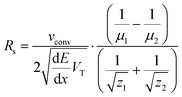 | (12) |
In eqn (12) the first term is device- and actuation potential-dependent while the second term depends on analyte properties. As shown in eqn (9) the focusing location is inversely proportional to the mobility. Analytes with low electrophoretic mobility will thus focus closer to the depletion zone where the E-field is high. It follows from eqn (12) that the resolution of such slower analytes, for constant Δμ = μ1 − μ2, will be better than for the faster analytes that focus at a location with lower E-field.
If the analytes are in peak mode, the mobilities of the analytes that are extracted from their focusing position by an extraction channel of determined width lie in a mobility window that can be calculated by equating Δx to the extraction channel width. If the mobility difference between two analytes in peak mode is smaller than that mobility window for a specific extraction channel width, then the extraction of a single analyte is impossible, and adjacent analyte(s) will be extracted along at varying concentration.
Finally, only analytes within a specific mobility window will focus in the device, which window is given by the maximum and minimum electric field and the convective flow velocity. As the analytes require an electrophoretic velocity equal and opposite to the convective flow hence this mobility window (assuming that the analyte i is peak mode and does not contribute to the local conductivity and electric field) is given by
 | (13) |
 | (14) |
A conservation law can be derived that requires that the KRF value remains constant across all zones in a capillary (i.e. the bulk zone and any plateau formed from an analyte) on application of an electrical field. The E-field gradient is not affected on either side of the plateau hence other less abundant analytes will still be focusing there in peak mode. A known substance can be added to the solution with an electrophoretic mobility intermediate to the two analytes to push them apart (Fig. 3c). Such a compound is usually named electrophoretic spacer which has been previously reported in ICPF.3,40
Experimental
In order to test the proposed system and procedure, polydimethyl siloxane (PDMS, DOWSIL™ 184 silicone elastomer kit)(1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10 crosslinker to polymer ratio) chips were fabricated. A silicon wafer was spin coated with 35 μm of MicroChem® SU-82050 negative photoresist and patterned with photolithography mask of the pattern of Fig. 1a. The supplier's instructions for exposure and development were followed to create the SU-8 soft lithography mould. The mould was used for standard soft lithography of PDMS chips41 which were bonded after O2 plasma treatment to microscopy glass slides.
10 crosslinker to polymer ratio) chips were fabricated. A silicon wafer was spin coated with 35 μm of MicroChem® SU-82050 negative photoresist and patterned with photolithography mask of the pattern of Fig. 1a. The supplier's instructions for exposure and development were followed to create the SU-8 soft lithography mould. The mould was used for standard soft lithography of PDMS chips41 which were bonded after O2 plasma treatment to microscopy glass slides.
A droplet of Nafion® perfluorinated resin solution (20 wt% – Sigma-Aldrich) was introduced in the two reservoirs marked with blue in Fig. 1a. The Nafion solution filled and pinned in the channel via capillary forces. The Nafion solution was dried at 60 °C for 30 minutes to create the solid cation selective Nafion membrane. During the drying process Nafion experiences a significant shrinkage. Because of the shrinkage occasionally Nafion detaches from the PDMS and gaps are formed that allow undesired flow from the separation to the buffer channels. To eliminate this flow, the buffer channels were filled with 2% wt UltraPure™ Agarose (Invitrogen) in 1× phosphate buffered saline (PBS) (Sigma-Aldrich).
For the fluorescent microscopy an Olympus IX51 was used and images/videos were captured with FLIR Grasshopper® 3 color camera. As model cation analytes BODIPY™ 492/515 disulfonate (BDP) (Invitrogen), Alexa Fluor™ 647 carboxylic acid, tris(triethylammonium) (AF647) (Invitrogen) salt, and Cascade Blue™ hydrazide trisodium salt (CB) (Invitrogen) were chosen and diluted in 1× PBS or 0.1× PBS which served as a background electrolyte buffered at pH 7.4. A calibration curve between fluorescent analyte concentration and fluorescent intensity for each analyte was prepared for the specific microscope and camera settings used in the experiments. The concentration factors were then calculated using this curve.
The electric potentials were applied by two Keithley 2410 sourcemeter power supplies and the extraction pressure via a Fluigent MFCS-EZ.
Results and discussion
Analyte position control
As described in the model, the analyte focusing position is regulated by regulating the size of the depletion zone, which scales with the ratio of the upstream over downstream potential. An example of the analyte position control is shown in Fig. 4 where the potential control is used to locate the focused analyte band at the intersection with the two extraction channels. The device could subsequently successfully be used for prolonged extraction of a single fluorescent concentrated analyte. In our devices we achieved reproducible and stable extraction for up to 20 minutes with the limit being only posed by the small size of our reservoirs. Longer extractions require larger reservoirs in order to avoid hydrostatic pressure changes and pH changes due to electrolysis.In Fig. 5 the focusing position is plotted against the ratio of upstream (Vu) and downstream (Vd) potential. The upstream potential was kept steady at 110 V and the downstream potential was varied from 110 V to 10 V and back to 110 V with steps of 10 V over a period of 35 minutes. The blue points denote the measured position of the analyte over time, while the red line connects the average values for each potential ratio (red bars: standard deviation of the focusing location over time). The instabilities in the position mainly stem from electroconvective vortices and instabilities in the depletion zone.24,31 The higher the flow rate (higher Vu![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Vd) the smaller the deviation from the mean focusing value (standard deviation of 9 μm at Vu
Vd) the smaller the deviation from the mean focusing value (standard deviation of 9 μm at Vu![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Vd of 11), while for lower flow rates the standard deviation increases (19 μm for Vu
Vd of 11), while for lower flow rates the standard deviation increases (19 μm for Vu![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Vd of 1.22).
Vd of 1.22).
Analyte selection control
We also investigated the use of the analyte positioning control for the selection of focused analyte to be extracted. In Fig. 6 the selection between two negatively charged analytes, namely BDP and AF647 is shown. The electrophoretic mobilities of the two analytes as determined by on-chip electrophoresis were μBDP = 2.11 × 10−8 m2 V−1 s−1 (a mobility of 1.76 × 10−8 m2 V−1 s−1 is reported in the literature42) and μAF647 = 1.58 × 10−8 m2 V−1 s−1. The slower analyte (i.e. the red AF647) is expected to focus closer to the depletion zone at the right of the figure where the E-field is higher, while the green BDP will focus closer to the bulk solution on the left of the figure, at the lower E-field. By tuning the actuation potentials (Vu, Vd) we could select which of the focused analytes positionally overlaps with the extraction channel and will be extracted.As shown in experiment A of Fig. 6, in the extraction channels only the fluorescence of the targeted analyte (BDP) is present, while the fluorescence of the “interfering” analyte (AF647) remains below the limit of detection of our microscope (ESI† video). A similar result is shown for experiment B but now with AF647 as target analyte and BDP as “interfering” analyte. The lack of fluorescence of the interfering species in the extraction channel demonstrates that our method in this case could be used for selective extraction.
As shown in Fig. 6 there is a clear difference in the resolution between experiments A and B before the extraction. This difference is caused by the difference in potential difference applied in the two experiments (30 V in A and 5 V in B). As described by eqn (12) the resolution improves with a lower electric field gradient (i.e. lower potential difference) at the cost of the concentration rate. The poor resolution results in the substantial overlap between the concentrated analytes seen in Fig. 6A. A selective extraction of analyte in that case is still possible but requires a small width of the extraction channel relative to the width of the desired concentrated analyte band.
The extraction of fluorescent analytes is a straightforward, reproducible and robust process, since we can monitor our analyte of interest until its position overlaps with the extraction channel. Extraction of non-fluorescent analytes would be a more cumbersome process, since the electrophoretic mobility of the analyte of interest must be known with respect to the electrophoretic mobilities to the other species in the solution. A possible experimental solution is to use a fluorescent substance with a mobility close to analyte of interest as a marker, placing it adjacent to the extraction channel.
Higher concentration factors
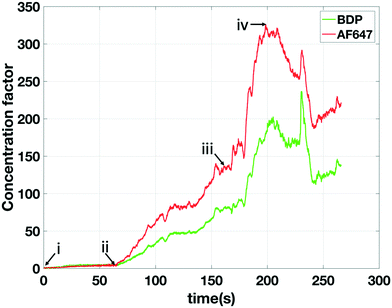
The factor with which the extracted analyte can be concentrated is tuneable. A steady extracted concentration factor is achieved when the extracted analyte flux matches the arriving analyte flux through the main channel towards the extraction location. A typical operational scheme for this purpose is the following: i) the process is initiated with actuation potentials such that the focusing location of the analyte is not overlapping the extraction channel; ii) a sufficient waiting time (typically a concentration rate is 1 times the bulk concentration per second) ensures that the desired concentration factor is achieved; iii) the potentials are adjusted to move the focused analyte band to the extraction channel; iv) a negative pressure is applied at the extraction channel to create an extraction flux that approximately matches the incoming analyte flux. An example of an extraction attempting to follow this scheme is shown in Fig. 7. We obtained an average concentration factor of about 200 in the continuously extracted analyte over several minutes. During the experiments (as also can be seen in Fig. 7) a slow response time of the pressure-driven flow was noticed varying between 5 to 40 seconds. We attribute this to instabilities of the pressure controller which was operated at its resolution limit. In addition, as can be seen in Fig. 7, the change of only 2 mBar in extraction pressure introduced at moment iii has a strong influence on the extraction rate. We conclude that a better controllability of the extraction process is needed In future devices, which can be implemented e.g. by increasing the hydraulic resistance of the extraction channel.Despite the high concentration factor of AF647 as seen in Fig. 7, in this experiment we obtained low selectivity since also BDP was extracted (at a concentration factor approximately 2/3 of AF647). Similar to Fig. 6A this was due to the poor separation resolution caused by the high potential difference.
As described in the theory section the separation resolution can be improved using an electrophoretic spacer. In Fig. 8 an example of the use of a spacer is shown. A third fluorescent marker (CB) was added with a mobility higher than BDP and the added phosphate of the buffer, causing the phosphate (H2PO4−) to reach its plateau concentration and act as a spacer, while AF647 and BDP remained in peak mode and at their initial position.
Comparison to the theoretical model
In the experiments characterizing the analyte positioning (Fig. 4) a single fluorescent analyte was used and the focusing position (i.e. depletion zone length) was found to scale, as predicted by our model, with the ratio of upstream over downstream potential. We found experimentally that the baseline width (4σ) of the focused analyte varied between 57 μm (for Vu = 60 V, Vd = 0 V) and 141 μm (for Vu = 60 V, Vd = 55 V). Eqn (10) allows us to derive the local E-field gradients from these measured peak widths. As the model provides us with the electric field in the bulk section of the channel and in the depletion zone at the applied potentials, the length of the E-field gradient zone can now be estimated assuming a constant electric field gradient. With this approach we derived an E-field gradient zone length of approximately 500 μm. Since the extraction channels have a width of 20 μm, this allows us safe overlap and a steady extraction of an analyte even in the case of a slight variation in the position of the focused analyte over time (standard deviation 19 μm in the focusing position as calculated from Fig. 5).The σ of the Gaussian (green and red) peaks in the experiments at higher concentration factors (Fig. 8b) is approximately 26 μm indicating an electric field gradient of 1.849 × 106 V m−2 (based on eqn (10)). At this field gradient our model predicts a spacing between the peaks of BDP and AF647 of 23 μm comparing well to the experimentally observed spacing of 19 μm. Interestingly it was found that the σ of the blue peak (CB) increased from 19 μm (Fig. 8a) to 31 μm (Fig. 8b) during the experiment indicating that the electric field gradient is less steep further away from the depletion zone. Fig. 9 shows the maximum concentration factor of the three analytes over time in the separation channel (Fig. 9a) and in the extraction channel (9b). Our model predicts a concentration rate of 2.7 times the bulk concentration per second while an average concentration rate of 2.1 can be seen in Fig. 9a. Before the extraction pressure was applied (t < 150 s) all three analytes focussed with approximately the same concentration rate. Once the extraction pressure was applied, AF647 was extracted together with a lower concentration of BDP, similarly to Fig. 7. However, no detectable amount of the CB was extracted as it was pushed away from the extraction channel by the electrophoretic spacer.
In Fig. 7 and 9b a strong variation can be seen in the maximum concentration of the extracted analytes. This can be attributed to hydrodynamic instabilities in the focusing location at high potentials (ESI† video) in ICPF, causing variations in the spatial overlap between the focused analyte band and the extraction channel.
Summarizing, the high electric field gradients that result in narrowly focused and highly concentrated bands, also drastically reduce the resolution of the method as can be seen from the denominator in eqn (12). The resolution of the system will thus be superior for lower potential differences between upstream and downstream reservoirs. This is further theoretically described in the ESI† and can also be seen in Fig. 6B. There thus exists a trade-off between high resolution and high concentration rate. This conundrum can be solved by increasing increase the value of the numerator in eqn (12) by a method independent of EOF. This can be done e.g. by additional PDF. The addition of a PDF will also shift the mobility window of analytes that will be focused in the device.
We can thus envision two potential future uses of this method. If the main interest is to obtain extracted analytes at enhanced concentration in continuous flow, the default operation (i.e. without the addition of spacers and/or added convective flow) of the device can be used, if needed in combination with pressure-driven flow. If the main interest is the purity of the extract, electrophoretic spacers can be used (if the mobility of the analyte is known) or an external pressure driven flow can be added for improved separation resolution.
Conclusion
We demonstrated a device capable of selective extraction and concentration of anionic analytes out of a complex background solution. The maximum concentration factor of the extracted analytes found was above 300, as measured by an increased fluorescence intensity. In order to investigate the dynamics of the system and deepen our understanding of the phenomena at play, a simple two-part one-dimensional model (i.e. an electric and a fluidic) was developed that describes the input–output relations of the system (applied potentials, extraction pressure – focusing position, concentration rate, extraction rate) to a level that allowed prediction of the system behaviour. Different future modes of operation are described based on the model and the experiments.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported and funded by Horizon 2020 Framework Programme of the European Union under the project H2020-PHC-634013 (PHOCNOSIS).References
- Y. C. Wang, A. L. Stevens and J. Han, Anal. Chem., 2005, 77(14), 4293–4299 CrossRef CAS PubMed.
- J. Quist, K. G. H. Janssen, P. Vulto, T. Hankemeier and H. J. Van Der Linden, Anal. Chem., 2011, 83, 7910–7915 CrossRef CAS PubMed.
- J. Quist, P. Vulto, H. Van Der Linden and T. Hankemeier, Anal. Chem., 2012, 84, 9065–9071 CrossRef CAS PubMed.
- S. J. Kim, L. D. Li and J. Han, Langmuir, 2009, 25, 7759–7765 CrossRef CAS PubMed.
- V. Liu, Y.-A. Song and J. Han, Lab Chip, 2010, 10, 1485 RSC.
- J. Khandurina, S. C. Jacobson, L. C. Waters, R. S. Foote and J. M. Ramsey, Anal. Chem., 1999, 71, 1815–1819 CrossRef CAS PubMed.
- S. H. Ko, Y.-A. Song, S. J. Kim, M. Kim, J. Han and K. H. Kang, Lab Chip, 2012, 12, 4472 RSC.
- J. Choi, K. Huh, D. J. Moon, H. Lee, S. Y. Son, K. Kim, H. C. Kim, J. H. Chae, G. Y. Sung, H. Y. Kim, J. W. Hong and S. J. Kim, RSC Adv., 2015, 5, 66178–66184 RSC.
- Y. Y. Chen, P. H. Chiu, C. H. Weng and R. J. Yang, Biomicrofluidics, 2016, 10(1), 014119 CrossRef PubMed.
- R. Kwak, S. J. Kim and J. Han, Anal. Chem., 2011, 83(19), 7348–7355 CrossRef CAS PubMed.
- W. Ouyang, X. Ye, Z. Li and J. Han, Nanoscale, 2018, 10(32), 15119–15412 RSC.
- L. Gong, W. Ouyang, Z. Li and J. Han, J. Membr. Sci., 2018, 556, 34–41 CrossRef CAS PubMed.
- L. Gong, Z. Li and J. Han, Sep. Purif. Technol., 2019, 217, 174–182 CrossRef CAS.
- Q. Pu, J. Yun, H. Temkin and S. Liu, Nano Lett., 2004, 4, 1099–1103 CrossRef CAS.
- V. A. Papadimitriou, L. I. Segerink, A. van den Berg and J. C. T. Eijkel, Anal. Chim. Acta, 2018, 1000, 232–238 CrossRef CAS PubMed.
- A. E. Herr, J. I. Molho, J. G. Santiago, M. G. Mungal, T. W. Kenny and M. G. Garguilo, Anal. Chem., 2000, 72(5), 1053–1057 CrossRef CAS PubMed.
- K. Mogi, Micromachines, 2018, 9(4), 167 CrossRef PubMed.
- S. S. Dukhin, Adv. Colloid Interface Sci., 1991, 35, 173–196 CrossRef CAS.
- S. M. Rubinstein, G. Manukyan, A. Staicu, I. Rubinstein, B. Zaltzman, R. G. H. Lammertink, F. Mugele and M. Wessling, Phys. Rev. Lett., 2008, 101, 236101 CrossRef CAS PubMed.
- I. Rubinstein, B. Zaltzman and I. Lerman, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2005, 72, 011505 CrossRef PubMed.
- I. Rubinstein and B. Zaltzman, Math. Models Methods Appl. Sci., 2001, 11(02), 263–300 CrossRef CAS.
- I. Rubinstein and B. Zaltzman, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top, 2000, 62, 2238 CrossRef CAS PubMed.
- F. C. Leinweber and U. Tallarek, Langmuir, 2004, 20(26), 11637–11648 CrossRef CAS PubMed.
- S. J. Kim, Y. C. Wang, J. H. Lee, H. Jang and J. Han, Phys. Rev. Lett., 2007, 99, 044501 CrossRef PubMed.
- A. Plecis and Y. Chen, Anal. Chem., 2000, 72(18), 4317–4321 CrossRef PubMed.
- X. Xuan and D. Li, J. Micromech. Microeng., 2003, 14(2), 290 CrossRef.
- A. Ajdari, C. R. Phys., 2004, 5(5), 539–546 CrossRef CAS.
- T. Glawdel, C. Elbuken, L. E. J. Lee and C. L. Ren, Lab Chip, 2009, 9, 3243–3250 RSC.
- K. W. Oh, K. Lee, B. Ahn and E. P. Furlani, Lab Chip, 2012, 12(3), 515–545 RSC.
- T. A. Zangle, A. Mani and J. G. Santiago, Anal. Chem., 2010, 82, 3114–3117 CrossRef CAS PubMed.
- J. C. De Valença, R. M. Wagterveld, R. G. H. Lammertink and P. A. Tsai, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2015, 92, 031003 CrossRef PubMed.
- B. J. Kirby and E. F. Hasselbrink, Electrophoresis, 2004, 25, 187–202 CrossRef CAS PubMed.
- B. J. Kirby and E. F. Hasselbrink, Electrophoresis, 2004, 25, 203–213 CrossRef CAS PubMed.
- J. K. Sung and J. Han, Anal. Chem., 2008, 80, 3507–3511 CrossRef PubMed.
- S. Rubin, O. Schwartz and M. Bercovici, Phys. Fluids, 2013, 26, 012001 CrossRef.
- D. A. MacInnes and L. G. Longsworth, Chem. Rev., 1932, 11, 171–230 CrossRef CAS.
- A. Tiselius, Trans. Faraday Soc., 1937, 33, 524–531 RSC.
- J. C. Giddings, Unified Separation Science, John Wiley & Sons, 1991 Search PubMed.
- R. Kohlrausch, Ann. Phys., 1854, 167, 179–214 CrossRef.
- L. F. Cheow, A. Sarkar, S. Kolitz, D. Lauffenburger and J. Han, Anal. Chem., 2014, 86(15), 7455–7462 CrossRef CAS PubMed.
- D. B. Weibel, W. R. DiLuzio and G. M. Whitesides, Nat. Rev. Microbiol., 2007, 5, 209–218 CrossRef CAS PubMed.
- B. G. Splawn and F. E. Lytle, Anal. Bioanal. Chem., 2002, 373(7), 519–525 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c9lc00434c |
| This journal is © The Royal Society of Chemistry 2019 |