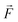Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Rational design of a high-throughput droplet sorter†
Simon S.
Schütz
a,
Thomas
Beneyton
 b,
Jean-Christophe
Baret
b,
Jean-Christophe
Baret
 *bc and
Tobias M.
Schneider
*bc and
Tobias M.
Schneider
 *a
*a
aEmergent Complexity in Physical Systems Laboratory (ECPS), École Polytechnique Fédérale de Lausanne (EPFL), Station 9, 1015 Lausanne, Switzerland. E-mail: tobias.schneider@epfl.ch
bCNRS, Univ. Bordeaux, CRPP, UMR 5031, 115 Avenue du Dr. Albert Schweitzer, 33600 Pessac, France. E-mail: jean-christophe.baret@u-bordeaux.fr
cInstitut Universitaire de France, France
First published on 3rd June 2019
Abstract
The high-throughput selection of individual droplets is an essential function in droplet-based microfluidics. Fluorescence-activated droplet sorting is achieved using electric fields triggered at rates up to 30 kHz, providing the ultra-high throughput relevant in applications where large libraries of compounds or cells must be analyzed. To achieve such sorting frequencies, electrodes have to create an electric field distribution that generates maximal actuating forces on the droplet while limiting the induced droplet deformation and avoid disintegration. We propose a metric characterizing the performance of an electrode design relative to the theoretical optimum and analyze existing devices using full 3D simulations of the electric fields. By combining parameter optimization with numerical simulation we derive rational design guidelines and propose optimized electrode configurations. When tested experimentally, the optimized design show significantly better performance than the standard designs.
Introduction
Sorting and selection are universal operations in technology. The ability to process, identify and select rare hits or targets among large populations is of relevance for biotechnological applications, pharmaceutical screening and molecular diagnostics.1 Finding interesting hits is more likely in large libraries and therefore requires high-throughput capabilities. Droplet-based microfluidics is a groundbreaking technology for the miniaturization and automation of biochemical assays at a ultra-high throughput.2 The technology is key in a wide range of applications, for example for protein engineering,3–5 cell and microorganism screening,6–8 sequencing9,10 or molecular diagnostics.11The fastest sorting speeds to date are achieved by actuating droplets using electric fields.5,12,13 Individual droplets are interrogated and actuated into different microchannels depending on their individual properties.3,5,13,14 The principle of sorting is based on dielectrophoresis (DEP): For droplets that have a dielectric contrast with the continuous phase, a non-uniform electric field leads to a net force on the droplet. This force then allows steering droplets across the streamlines of the background flow and into the desired outlet channel. Two effects control the performance of a droplet sorting device: first, the electrical actuation moves droplets across streamlines of the flow. The deflection of the droplet is a function of the magnitude of the field and of duration the droplet is exposed to the field while being advected downstream. Second, the geometry of the microchannel ensures that the droplets deflected to different streamlines are actuated into the right outlet. Based on these simple considerations, many different electrode shapes have been designed for droplet sorters,3,4,12,13,15–18 reaching sorting throughputs of up to 30 kHz.15 A part of the rich genealogy of sorter designs is presented in Fig. 1. Over the past years, these devices were adapted and used to match the constraints of the biological assays performed in the droplet format. The throughputs achieved depend on the droplet size, larger droplet being usually sorted at lower throughput. In addition the reported throughputs usually account for the need to have systems reliably functioning over several hours and do not represent the maximum throughput of the device. To the best of our knowledge, these devices were optimized by experimental trial and error and none of the existing sorting devices are based on rationally optimizing the electric field distribution. We therefore need impartial and universal metrics for the analysis of sorting systems.
 | ||
| Fig. 1 Following the seminal designs by Ahn12 and Baret,13 different sorters3,4,12,13,15–17,20,26,29–35 have been developed over the past decade. Electrode geometries have been guided by experimental trial and error, but none is based on rationally optimizing the field distribution in order to avoid droplet disintegration at high-throughput while maximizing the actuating force. We analyze the highlighted sorter designs for their field distribution to unravel design guidelines based on the optimisation of dielectrophoretic force acting on the droplets at the sorting junction. | ||
Considering optimisation of sorting, a seemingly straightforward solution to optimize sorting systems is to increase the strength of the electric fields, inducing a larger net force on the droplet. Thereby, the necessary deflection is achieved in shorter time and higher sorting frequencies become accessible. Yet, this solution is not reliable: while in dielectrophoresis the net force is given by the gradients of the field, the field itself contributes to the deformation of the droplet without displacing the center of mass. The electric field cannot be arbitrarily large and droplets disintegrate when the field gets too strong.19 Thus the achievable actuation depends on the shape of electrodes controlling the field distribution to avoid droplet disintegration at high throughput while maintaining a decent net force to move the droplets across streamlines.
Here, we focus on the actuation of droplets in electric fields. For the sake of clarity, we want to point out that our goal is not to optimize the overall throughput in the design – which depends on electric actuation but also on the channel design and emulsion formulations – but to focus on the optimization of the electric actuation. We first propose a universal metric to characterize quantitatively the sorting efficiency of microsystems and highlight the role of the electrode geometry on the performance of droplet actuation. Then, we use fully resolved 3D simulations of the electric field coupled to parameter optimization to rationally design optimized electrode designs that reduce the Maxwell stress on droplets during sorting. We finally test these predictions in experimental conditions, showing the better performance of the optimized systems. The new electrode design allows to reliably actuate droplets while significantly reducing droplet deformation so that higher sorting frequencies can be reached before the electric forces lead to droplet disintegration. The proposed electrodes can easily be integrated and do not complicate the device fabrication compared to alternative inferior designs. Because the deformation of droplets in electric fields is counteracted by interfacial tension, optimized electrode designs that generate more gentle actuation forces are especially important for applications that require the sorting of droplets with low surface tension.4,5,20–22
Results and discussion
Principle of droplet sorting
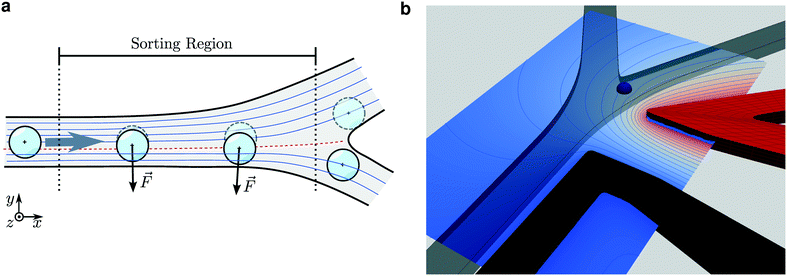
The functioning principle of DEP droplet sorting is illustrated in Fig. 2: in a flow region upstream from a microchannel junction, a dielectrophoretic force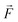 is applied to a droplet when the electric field is activated.
is applied to a droplet when the electric field is activated.
This force causes the droplet to drift across stream lines, and be guided into one outlet channel. The asymmetric design of the channel ensures that without an electric field the droplet is guided into the other channel. Selectively applying a voltage between the active and the ground electrode thereby allows to sort droplets.
The dielectric force emerges from the interaction of the electric field with dipoles induced in the droplet phase. The force 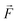 thus grows with the gradient
thus grows with the gradient 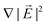 of the square of the electric field
of the square of the electric field 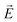 , and is independent of the field direction. For small, spherical droplets, the force is given by23
, and is independent of the field direction. For small, spherical droplets, the force is given by23
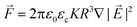 | (1) |
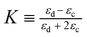 . Here, ε0, εc, εd and R are the vacuum permittivity, the relative permittivity of the continuous and droplet phase, and the droplet radius, respectively. This relationship holds for droplets smaller than the typical length scale over which the field gradient varies. Corrections to this small-droplet approximation are discussed in the ESI.†
. Here, ε0, εc, εd and R are the vacuum permittivity, the relative permittivity of the continuous and droplet phase, and the droplet radius, respectively. This relationship holds for droplets smaller than the typical length scale over which the field gradient varies. Corrections to this small-droplet approximation are discussed in the ESI.†
In response to the force, the droplet drifts across the stream lines. At near-unity viscosity ratio between droplet and continuous phase, the drift velocity is Udrift ≈ F/(5πμR),‡ with F the cross-stream component of the dielectric force, and μ the viscosity of the outer fluid.24 For reliable sorting, the droplet needs to be displaced by approximately one droplet diameter, which takes a time T = 2R/Udrift. This typical displacement represents a sufficient displacement of the droplet center of mass accross the streamlines for efficient sorting. The maximum sorting frequency therefore scales as
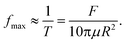 | (2) |
The sorting frequency is proportional to the dielectrophoretic force on the droplet, and inversely proportional to the viscosity of the continuous phase. If the actuation force varies along the path of the droplet, the time-averaged force determines the sorting frequency.
Upper limit for the electric field.
The force on the droplet may be increased by increasing the field gradient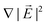 . However, there is a critical upper limit for the field strength: The dielectric force moving the droplet is caused by electric Maxwell stresses at the interface. In a field gradient the Maxwell stress varies over the droplet surface, resulting in the dielectrophoretic net force. The stress everywhere points outward of the droplet and deforms the initially round droplet. Surface tension counteracts the deforming Maxwell stresses, but when the field strength surpasses a critical value Ecrit, surface tension becomes insufficient to maintain the round droplet shape, so that the droplet deforms and eventually disintegrates in the surrounding shear flow.25
. However, there is a critical upper limit for the field strength: The dielectric force moving the droplet is caused by electric Maxwell stresses at the interface. In a field gradient the Maxwell stress varies over the droplet surface, resulting in the dielectrophoretic net force. The stress everywhere points outward of the droplet and deforms the initially round droplet. Surface tension counteracts the deforming Maxwell stresses, but when the field strength surpasses a critical value Ecrit, surface tension becomes insufficient to maintain the round droplet shape, so that the droplet deforms and eventually disintegrates in the surrounding shear flow.25
Quantitatively, the relative strength of the Maxwell stress compared to surface tension is given by the electrical Bond number 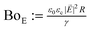 , with γ the surface tension coefficient. The Maxwell stress surpasses the surface tension at a BoE near unity, so that the critical field strength scales with
, with γ the surface tension coefficient. The Maxwell stress surpasses the surface tension at a BoE near unity, so that the critical field strength scales with 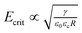 . Consequently, the critical field strength is particularly small for low surface tensions and large droplet radii.
. Consequently, the critical field strength is particularly small for low surface tensions and large droplet radii.
The largest possible field gradient is achieved for a field increasing from zero to the critical strength Ecrit across the droplet diameter 2R. With eqn (1) this yields an upper bound Fmax = πε0εcKR2Ecrit2 for the force on a droplet. If one could generate arbitrary electric fields, droplets could be actuated with this maximum force. However, the field distribution is not arbitrary as the field has to satisfy Maxwell's equations and is generated by electrodes of fixed geometry. Consequently, the aim is to design electrodes such that the actuating force given by the gradient 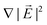 is maximized along the path of the droplet while the field strength remains below a maximum value Emax.
is maximized along the path of the droplet while the field strength remains below a maximum value Emax.
To quantify the efficiency of an electrode design, we normalize the spanwise force component |Fy| acting on the droplet at each location by the maximum force Fmax to define the non-dimensional DEP force
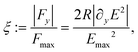 | (3) |
An efficient sorter will apply the maximum possible force over the entire length of the sorting segment to move the droplet across the stream lines. Outside this segment, forces should be minimized, so that subsequent droplets and other parts of the setup are not affected and droplets can be addressed individually. To quantify the overall performance of the sorter, we thus define the DEP efficiency
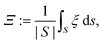 | (4) |
Sorter comparison
To determine the DEP force and efficiency for a given system, we perform a 3D boundary-element simulation of the electric field around the sorting electrodes. The boundary-element method solves the electrostatic Laplace equation by finding the electric potential and flux on the surface of the sorting electrodes, and then extends the field into the volume. Details of the method are given in the Materials and Methods section. As we will discuss later, 3D features of the electric field play a vital role in the sorting process, so that a fully resolved 3D computation is indispensable. From the 3D simulation, we calculate the electric field and its gradients in a 2D plane at half-height in the channel (Fig. 2b). We analyze the efficiency of several electrode designs3,4,12,13,15–17,26 that were developed in the past years (Fig. 3).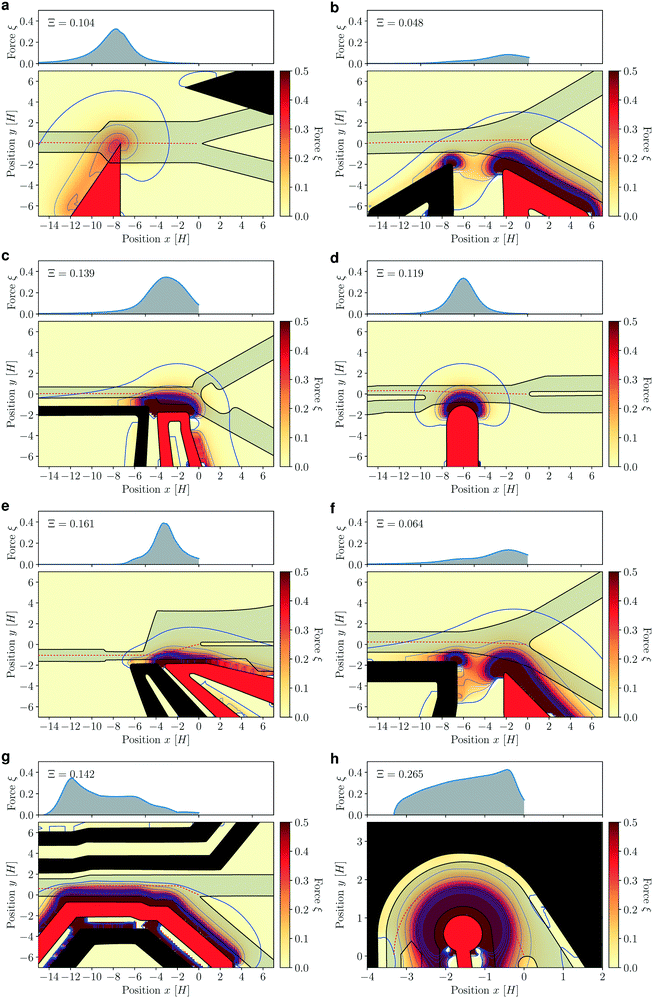 | ||
| Fig. 3 Relative DEP force ξ around the electrode designs of (a) Ahn et al.,12 (b) Baret et al.,13 (c) Agresti et al.,3 (d) Sciambi and Abate,15 (e) Gielen et al.,16 (f) Obexer et al.,4 (g) Frenzel and Merten17 and (h) Clark et al.26 The thick contour line is ξ = 10−2. The dashed line in the channel center estimates the dividing streamline between the outlets, along which we average the DEP force ξ to get the total DEP efficiency Ξ. The top panel shows the DEP force ξ along the droplet path and the total DEP efficiency Ξ. The electrodes in Ahn's design (a) are coated on a plane below the microchannel; all other designs have electrodes next to the channel and of equal height H. In the design of Clark (h), the definition of the DEP force ξ was adapted to a polar coordinate system around the electrode. The channel height is (a) H = 25 μm, (b) H = 21 μm, (c) H = 25μm, (d) H = 30 μm, (e) H = 80 μm, (f) H = 21 μm, (g) H = 75 μm, (h) H = 95μm. | ||
The 3D simulation of the field shows the localisation of the field gradients for the different designs. The channels are presented in gray and the electrodes in black (ground electrode) and red (active electrode). To obtain quantitative measurements, we compute the normalized DEP force ξ in the channel midplane along the approximate path of a droplet (red dashed line). The force distribution along the path of the droplet is shown in the upper panel together with the integrated performance metric Ξ. The design by Ahn et al.12 (a) was the first design to demonstrate DEP droplet sorting, and uses two different layers in the design for the microchannels and the electrodes. The subsequent sorters have electrodes on the same level as the microchannels. The sorters by Baret et al. and Agresti et al.3,13 (b and c) place an active electrode parallel to the sorting segment. In Agresti et al. the sorting is improved with droplets slowing down during sorting by widening the channel. Sciambi and Abate15 (d) focus on reducing the shear on droplets, which allows them to increase the flow rate. Their electrode is close to the microchannel, but rounded, which is less efficient. The recent designs used by Gielen et al.16 (e), Obexer et al.4 (f) and Frenzel and Merten17 (g) have long active electrodes, which are very effective. The efficiencies of the design by Baret et al. and Obexer et al. are low because a strong and constant actuation force on droplets is reached only after the sorting junction. Clark et al. deviate from the traditional design of a straight sorting channel with a concentric design (h). In doing so, they make full use of the in-plane gradient in the field strength, which maximizes the DEP force along the entire sorting segment. These sorter designs have been developed over a time period of 12 years (2006–2018), and show a trend of increasing efficiency, with Gielen et al. reaching the highest efficiency for a straight-channel design of Ξ = 0.161, and Clark et al. reaching an efficiency of Ξ = 0.265 with a curved channel.
Improving designs
The performance metric allows to quantitatively compare the efficiency of different electrode geometries and design better electrodes that substantially outperform previous sorter designs. Well performing existing sorters include an extended flat electrode parallel to the channel as well as shielding electrodes. We will first consider the optimal shape of a single active electrode and then discuss further benefits of increasing the device complexity by additional shielding electrodes. This rational design procedure yields efficiency improvements of almost 100% over the latest design by Gielen et al. and optimized electrodes significantly outperform classical designs in experimental tests.For a straight, rectangular microchannel of constant cross-section and aspect ratio 2, we consider one active electrode parallel to the channel with grounded counter-electrodes at infinity, as shown in Fig. 4a. The straight electrode causes a strong deflection force along its whole length (Fig. 4b), with an efficiency Ξ = 0.212 that is 32% higher than what existing designs achieve.
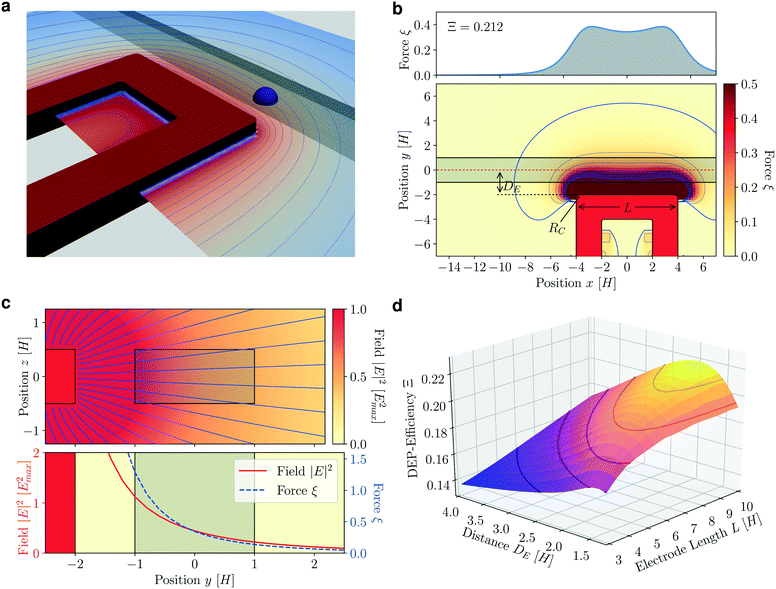 | ||
| Fig. 4 Sorting with a simple bar electrode. (a) 3D geometry of an electrode of height H and length L = 8H, next to a microchannel of height H and width 2H. The droplet radius is R = H/2. (b) Deflection force ξ on a droplet traveling through the microchannel shown in (a). Contours and DEP force ξ as in Fig. 3. (c) Side view of electrode and microchannel. Field lines spread in z-direction, causing a strong field gradient (top). This 3D effect leads to a high deflection force. With the distance from the main electrode, the force ξ decays faster than the field |E|2 (bottom). (d) The sorting efficiency changes with the electrode length L and distance DE between electrode and channel center. Longer electrodes are more efficient, and DE ≈ 2H gives the highest sorting efficiency for long electrodes. | ||
The side view on the electrode (Fig. 4c) reveals the reason for the large force along the whole electrode: the field lines spread in the out-of-plane direction, which leads to the high field gradients that attract droplets. When designing a sorting device in a 2D top view, one easily overlooks this 3D effect of the electric field, which cannot be captured by any 2D analysis of the device. Free parameters in the design of this simple bar electrode are the electrode length L, and its distance DE from the channel center line. We optimize the two geometric parameters L and DE to maximize the efficiency Ξ (Fig. 4d). The distance between electrode and channel center has a clear optimum at DE ≈ 2H: the field decays with the distance from the electrode, so that the actuation force is stronger when the droplet is close to the electrode. However, in very close proximity to the electrode, the field geometry is set by the electrode height, which weakens field gradient and thereby the actuation force. The optimum distance DE is thus on the scale of the electrode height. Long electrodes perform better because they offer a longer region of strong droplet actuation, relative to regions of stray field where droplet actuation is suboptimal. In practice, to maintain a high sorting frequency, a sorter with a long electrode must be operated at a high flow rate that poses other challenges. We therefore limit the electrode length to 8H, where further efficiency gains due to longer electrodes become marginal.
An appropriately dimensioned active electrode with ground at infinity provides a 32% performance increase. However, far reaching stray fields are created, that may have unwanted side-effects on parts of the microfluidic chip not associated with the droplet sorter. To integrate many sorters in a chip and address individual sorters while minimizing crosstalk, shielding electrodes are necessary. Such additional electrodes at ground potential not only help isolate the sorter from the remainder of the microchip, but can also further increase the sorting efficiency.
For a main electrode of length L = 8H, ground electrodes as shown in Fig. 5a reduce the length of the sorting segment by 30% and increase efficiency by roughly the same amount, to Ξ = 0.270. This correponds a 68% improvement over the reference design by Gielen et al., where half of the improvement is due to the added shielding electrodes. By reducing stray fields, the shielding causes the desired step-like transition from zero to the full actuation force of the straight electrode. This effect is enhanced by sharp corners of the electrodes (Fig. 5b).
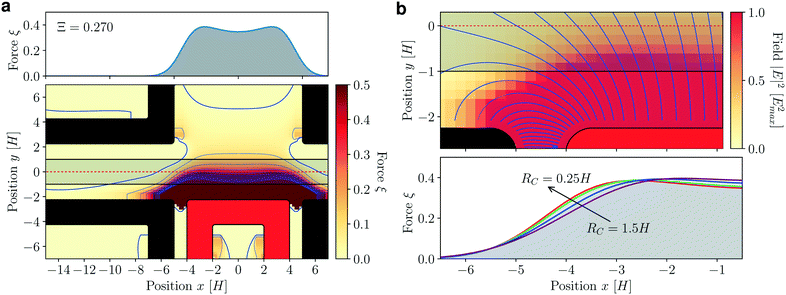 | ||
| Fig. 5 Sorting with a shielded electrode. (a) Deflection force ξ of a simple electrode of height H and L = 8H, DE = 2.25H. Contours and DEP force ξ as in Fig. 3. (b) The field is particularly strong at the corners of the electrode. Sharp corners with small radius of curvature RC increase the force on the droplet locally, and lead to an overall higher efficiency. | ||
In the design of the shielding, it is critical to not place any shielding electrode directly across the active electrode. Otherwise both electrodes form a typical capacitor geometry and field lines emanating from the active electrode no longer freely spread in the out-of-plane direction but become parallel, creating a homogenous field across the microchannel (Fig. 6c). A shielding electrode directly across the active electrode thus reduces the field gradient and should be avoided.
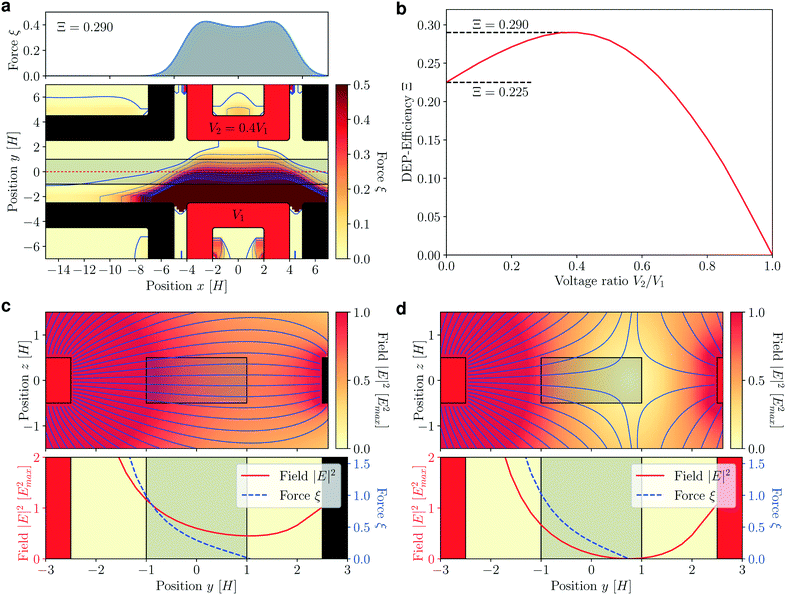 | ||
| Fig. 6 Sorting with two active electrodes. (a) Deflection force of a pair of two active electrodes at a voltage ratio V2/V1 = 0.4, at L = 8H, DE = 2.5H. Contours and DEP force ξ as in Fig. 3. (b) The overall efficiency depends on the voltage ratio. The highest efficiency is reached at V2/V1 ≈ 0.4; for higher or lower voltages on the second electrode, the efficiency decays quickly and is often lower than in the complete absence of the second active electrode. (c) Side view of electrode and microchannel at V2 = 0. When the second electrode is present, but not active, the field gradient is weaker, so that the efficiency of the sorter decreases. (d) Side view of electrode and microchannel at V2/V1 = 0.7. The field lines spread in the vertical z-direction, creating a region where the field almost vanishes (top). The field gradient remains high, so that a high deflection force can be reached (bottom). | ||
In the design of Fig. 5a, adding a second active electrode in the gap leads to a symmetrical device (Fig. 6a). By varying the voltage ratio of the secondary electrode relative to the primary one, we can maximize the sorting efficiency. The DEP efficiency as a function of the voltage ratio V2/V1 between secondary and primary electrode is shown in Fig. 6b. When the secondary electrode is at zero potential and acts like a shielding electrode (Fig. 6c), the sorting efficiency is lower than for a device without the secondary electrode (Ξ = 0.225 vs. Ξ = 0.270). Field lines emanating from the primary electrode converge onto the secondary electrode. This leads to approximately parallel field lines, reduces the gradient and thereby lowers efficiency. When the voltage on the secondary electrode is increased, the fields of the electrodes partially cancel each other, forming a region of very low field strength in the space between the electrodes (Fig. 6d). Consequently, both electrodes can be operated at a higher absolute voltage without their combined field reaching the critical limit. While the field gradient vanishes at the minimum of the field strength, close to the minimum the gradient remains high. In this region, the local DEP force ξ increases. Strikingly, the highest sorting efficiency (Ξ = 0.290) is reached when the voltage of the secondary electrode is ∼40% of the voltage of the primary electrode. For even higher voltages on the secondary electrode, the region of high gradient and low field is no longer located within the microchannel. Consequently, the efficiency decreases again. For a voltage ratio approaching unity, the field is symmetric with vanishing gradient in the microchannel center, causing zero actuation force.
Choosing the optimal voltage for a second active electrode further improves the sorter efficiency, but the increase is less dramatic than the increase due to suitably optimizing a single active electrode or introducing shielding electrodes. Furthermore, a second electrode at a different potential increases the complexity of the device so that a single active electrode might be the best choice in most applications. However, a second active electrode may be very beneficial if not only the electrodes but also the channel design is adapted and the operation of the sorter is modified. If the electrodes and the channel are chosen to be symmetric, droplets in the channel center only need to be moved by half the distance for reliable sorting (switching the field on the opposite electrode would then lead to a similar displacement in the other direction) This actuation can be achieved by always activating one of the two electrodes. Such a symmetric design strategy effectively doubles the sorting frequency and is used for example in the multiplexed sorter discussed by Girault et al.18 In summary, the combination of one active electrode and appropriately designed shielding electrodes allows for significant sorting efficiency improvements: The field strength in the channel is minimized, whereas the field gradient remains strong. Increasing the complexity of the design by adding a second independently controllable active electrode is a further option with an additional minor gain in efficiency.
Based on performance metrics for the efficiency of dielectrophoretic sorters, we have optimized electrode designs and shown that efficiency improvements of 32% relative to the best existing designs can be achieved by a single active electrode, and that the improvement increases to 68% when appropriate shielding is added. Even 77% can be achieved using a second active electrode, which however complicates the device significantly. Relative to the common electrode design by Obexer et al., multifold efficiency improvements are achieved. We experimentally compare the performance of the two devices providing most significant performance improvements, the single active electrode with and without shielding, to the common setup. Table 1 presents parameters of the tested electrodes including efficiency, sorting segment length and required electrode voltage.
Experimental validation
To characterize the performance of the electrode shape independent of flow related parameters, we perform experiments for fixed microchannel geometry, flow rates, droplet volume and sorting frequency. In this experiment, we focus on the optimisation of the droplet deformation rather than improving throughput in order to maintain the flow parameters similar between the devices tested. Electrode and microchannel designs are taken from Obexer et al.4 (Fig. 3e) and compared to the bar electrode of length L = 8H = 196 μm without and with local shielding (Fig. 4a and 5a). Width and height of the microchannel and droplet diameter are 50 μm, 24 μm, and 25 μm, respectively (Fig. S2†). We apply a 20 kHz AC field at a voltage between 0 and 1 kV. By varying the voltage applied to the sorting electrode, we determine the voltage at which all droplets are correctly sorted into the sorting outlet. The existing sorter requires a voltage of 450 V for reliable sorting, whereas the new designs without and with shielding perform the same task at the much lower voltage of 350 V and 200 V, respectively (Fig. 7).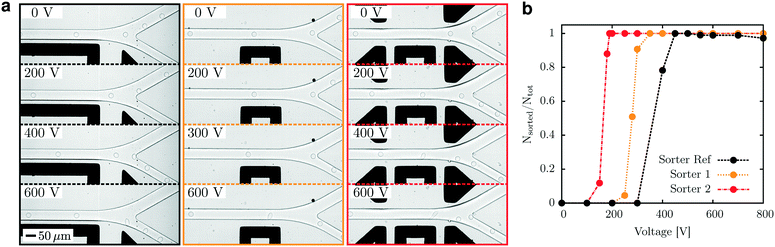 | ||
| Fig. 7 Droplet sorting at different electrode voltages, for the reference sorter by Obexer et al.4 (sorter ref), and our new designs without (sorter 1) and with (sorter 2) local shielding. (a) Typical droplet trajectories at the different electrode voltages. (b) Success rate of sorting for the different designs. The new designs sort droplets at a low voltage, making them easy to integrate and to operate at high throughput. | ||
A lower sorting voltage reduces stray fields and thus simplifies the integration of a sorter with complex microchannel designs. Reduction of the sorting voltage alone does however not imply an increase of the highest achievable sorting frequencies. The limitation is the induced deformation of droplets which will eventually lead to droplet disintegration and limit the sorting frequency. Improved electrode designs will thus induce much less droplet deformation while still reliably actuating droplets. At the minimum voltage where reliable sorting is possible, we compare the deformation of droplets between the existing and the (shielded) new design (Fig. 8). In the reference design, droplets significantly deform. With the new design, fields are weaker, and thus move droplets gently across the stream lines. To achieve higher sorting frequencies the actuating force and thus voltage needs to be increased. We experimentally confirm that the actuating force controlling the drift speed across stream lines as well as the maximum droplet deformation show the expected dependence on voltage (Fig. S4†). Critical droplet deformations are reached much later for the optimized electrode design so that higher frequencies are possible.
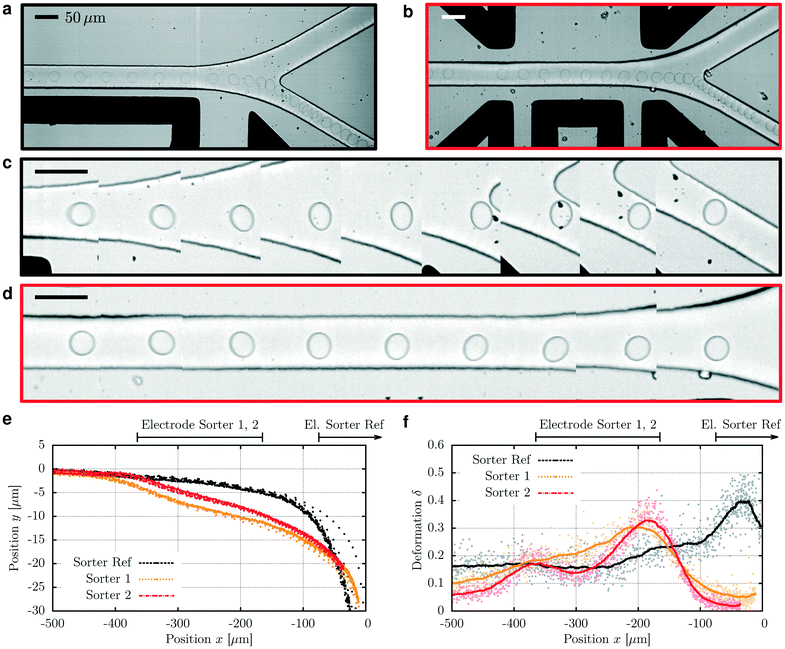 | ||
Fig. 8 Droplet trajectories and deformations in identical microchannel designs and flow conditions, but with different sorting electrodes. (a) Droplet trajectory in the reference geometry by Obexer et al.4 at an electrode voltage of 450 V. (b) Droplet trajectory with the optimized electrode design at an electrode voltage of 200 V. The chosen electrode voltages are the respective thresholds for reliable sorting. (c) and (d) show the droplet shape in detail. (e) Trajectory of the droplet centers in sorter ref at 500 V, sorter 1 at 450 V and sorter 2 at 250 V. x is the downstream and y the cross stream coordinate with y = 0 the centerline. The tip of the divider at the sorting junction is located at coordinate x = 0. Despite the different voltages, droplets reach the same y-deflection just before the junction. In the optimized design, droplets are moved away from the channel centerline (y = 0) earlier and are actuated more gently. (f) Deformation 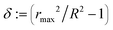 ) of droplets for the droplet trajectories from (e). In the optimized electrode design, droplets show a smaller maximum deformation. In addition, the actuation takes place before droplets reach the junction (x = 0). As a consequence, the electric droplet deformation does not interfere with any potential hydrodynamically induced deformation at the junction. Consequently, higher sorting frequencies can be achieved before the droplet disintegrates. ) of droplets for the droplet trajectories from (e). In the optimized electrode design, droplets show a smaller maximum deformation. In addition, the actuation takes place before droplets reach the junction (x = 0). As a consequence, the electric droplet deformation does not interfere with any potential hydrodynamically induced deformation at the junction. Consequently, higher sorting frequencies can be achieved before the droplet disintegrates. | ||
Conclusion
We investigate physical limits of the throughput that can be achieved in electrically activated droplet sorting. Based on those physical limits we propose a metric characterizing the performance of electrode designs relative to the theoretical optimum. Using fully resolved 3D boundary-element simulations together with the performance metric, we analyze the efficiency of electrode shape for common sorting devices developed over the past decade. We demonstrate that 3-dimensional effects are of prime importance in the actuation force and that they must be accounted for in a correct description of the force acting on the droplet. In practice, our analysis revealed that 3D effects render long, straight electrodes along the microchannel much more effective than the 2D picture would suggest, and that well-placed ground electrodes increase the sorting efficiency further.Based on the quantitative performance analysis of existing devices we propose a rational design approach for optimizing electrode designs. By combining parameter optimization with numerical simulation we derive rational design guidelines and suggest technically feasible designs significantly improving the sorting performance compared to existing standard designs. We demonstrate experimentally the superior performance of these optimised devices, by showing that under identical conditions, droplets are sorted at much smaller deformations in the new designs. Moreover, significantly lower voltages need to be applied.
One practical consequence of our results is that the sorting rate can be pushed much higher before droplets start to disintegrate. The gentle actuation of droplets limiting their deformation is especially relevant for low surface tension applications and systems with large droplets, which are particularly susceptible to breaking up in strong fields. The improved electrode designs do not increase the complexity of microfluidic chips and should thus be easily integrated into existing devices. We believe the proposed sorter design will help improve the performance of many microsystems for critical selection operation.
Our work yields sorter designs that in practice outperform previous designs. In addition we demonstrate that rational design approaches involving numerical simulation, performance metrics and optimization can and should complement intuition guided design and experimental tests. Rational design starting from physical principles setting fundamental physical limitations will help to provide optimized high-throughput analysis tools that allow targeting important challenges in molecular diagnostics, pharmaceutical screening and other biotechnological applications.
Materials and methods
Numerical simulation
The electric field around the electrodes was calculated using a boundary element method (BEM) numerical code written in C++, which is based on the finite-element framework deal.ii.27 We solved the Laplace equation for the electrostatic potential φ (with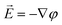 ),
),| Δφ = 0, | (5) |
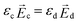 . Depending on the mesh complexity, the electrode surfaces were represented by 103–104 bilinear quadrangular elements. Numerical solution of the discretized boundary integral equation with the GMRES method yielded the field strength on the electrode surfaces, from which we constructed (via integration with appropriate Green's functions) the field and field gradient at discrete points in the volume. The simulation code is parallelized with MPI. Each simulation took 3 minutes on a standard desktop computer. We analyzed 8 existing sorter geometries and performed 800 simulations with different parameter combinations (electrode length, spacing between electrode and channel center, corner radius, voltage of the secondary electrode) for the new electrode designs.
. Depending on the mesh complexity, the electrode surfaces were represented by 103–104 bilinear quadrangular elements. Numerical solution of the discretized boundary integral equation with the GMRES method yielded the field strength on the electrode surfaces, from which we constructed (via integration with appropriate Green's functions) the field and field gradient at discrete points in the volume. The simulation code is parallelized with MPI. Each simulation took 3 minutes on a standard desktop computer. We analyzed 8 existing sorter geometries and performed 800 simulations with different parameter combinations (electrode length, spacing between electrode and channel center, corner radius, voltage of the secondary electrode) for the new electrode designs.
Sorting experiments
Poly-(dimethylsiloxane) (PDMS, Sylgard 184) microfluidic devices were fabricated from SU-83025 negative photoresists molds as described in28 (Fig. S2†). Aquapel (PPG Industries) was used to hydrophobize the channels. Nemesys syringe pumps (Cetoni) were used to control the flows in the microfluidic channels and syringes were connected to the devices with PTFE tubing (ID 0.3 mm, OD 0.76 mm; Fisher Scientific). 8 pL w/o droplets were produced (3500 Hz) using a 20 × 15 μm nozzle dropmaking device (Fig. S3†) in fluorinated oil (Novec7500, 3M) and were stabilized against coalescence by a perfluoropolyether–polyethyleneglycol block-copolymer surfactant (3% w/w).8 Droplets were collected off-chip and stored in a glass vial. Droplets were then co-flown with fluorinated oil in sorting devices with a 50 μm (width) × 24 μm (height) main channel. Sorting efficiency was investigated with constant hydrodynamics conditions (Femulsion = 20 μL h−1 and Foil = 700 μL h−1) by applying a 20 kHz AC field from 0 to 1 kV (Agilent 33210A function generator connected to a Trek 623B high voltage amplifier). Droplets were imaged at 13000 fps using a high-speed camera (Phantom v210) and movies were analyzed using the Phantom Camera Control software (PCC 2.1.4). Details of the image processing and data analysis are given in the ESI.†Conflicts of interest
There are no conflicts to declare.Acknowledgements
J.-C. B. acknowledges the support from the ERC (FP7/2007-2013/ERC Starting Grant 306385-SofI), from the French state in the frame of the “Investments for the future”, Programme IdEx Bordeaux, ANR-10-IDEX-03-02, from the “Région Aquitaine” and from the Institut Universitaire de France. We would like to thank Dr. Ouriel Caen and Dr. Valérie Taly (Univ. Paris Descartes) for fruitful discussions.References
- R. Turk-MacLeod, A. Henson, M. Rodriguez-Garcia, G. M. Gibson, G. Aragon Camarasa and D. Caramelli, et al. Approach to classify, separate, and enrich objects in groups using ensemble sorting, Proc. Natl. Acad. Sci. U. S. A., 2018, 115(22), 5681–5685 CrossRef CAS PubMed , Available from: http://www.ncbi.nlm.nih.gov/pubmed/29760051,%20http, http://www.pubmedcentral.nih.gov/articlerender.fcgi?artid=PMC5984510.
- A. B. Theberge, F. Courtois, Y. Schaerli, M. Fischlechner, C. Abell and F. Hollfelder, et al. Microdroplets in microfluidics: An evolving platform for discoveries in chemistry and biology, Angew. Chem., Int. Ed., 2010, 49(34), 5846–5868 CrossRef CAS PubMed , Available from: http://dx.doi.org/10.1002/anie.200906653.
- J. J. Agresti, E. Antipov, A. R. Abate, K. Ahn, A. C. Rowat and J. C. Baret, et al. Ultrahigh-throughput screening in drop-based microfluidics for directed evolution, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 4004–4009 CrossRef CAS PubMed.
- R. Obexer, M. Pott, C. Zeymer, A. D. Griffiths and D. Hilvert, Efficient laboratory evolution of computationally designed enzymes with low starting activities using fluorescence-activated droplet sorting, Protein Eng., Des. Sel., 2016, 29(9), 355–366 CrossRef CAS PubMed.
- P. A. Romero, T. M. Tran and A. R. Abate, Dissecting enzyme function with microfluidic-based deep mutational scanning, Proc. Natl. Acad. Sci. U. S. A., 2015, 112(23), 7159–7164 CrossRef CAS PubMed , Available from: http://www.pnas.org/lookup/doi/10.1073/pnas.1422285112.
- E. Brouzes, M. Medkova, N. Savenelli, D. Marran, M. Twardowski and J. B. Hutchison, et al. Droplet microfluidic technology for single-cell high-throughput screening, Proc. Natl. Acad. Sci. U. S. A., 2009, 106(34), 14195–14200 CrossRef CAS PubMed , Available from: http://www.pnas.org/content/106/34/14195.abstract.
- K. Eyer, R. C. L. Doineau, C. E. Castrillon, L. Briseño-Roa, V. Menrath and G. Mottet, et al. Single-cell deep phenotyping of IgGsecreting cells for high-resolution immune monitoring, Nat. Biotechnol., 2017, 35(10), 977–982 CrossRef CAS PubMed.
- T. Beneyton, I. P. M. Wijaya, P. Postros, M. Najah, P. Leblond and A. Couvent, et al. High-throughput screening of filamentous fungi using nanoliter-range droplet-based microfluidics, Sci. Rep., 2016, 6, 27223 CrossRef CAS PubMed , Available from: http://www.ncbi.nlm.nih.gov/pubmed/27270141.
- A. M. Klein, L. Mazutis, I. Akartuna, N. Tallapragada, A. Veres and V. Li, et al. Droplet barcoding for single-cell transcriptomics applied to embryonic stem cells, Cell, 2015, 161(5), 1187–1201 CrossRef CAS PubMed , Available from: http://dx.doi.org/10.1016/j.cell.2015.04.044.
- R. Zilionis, J. Nainys, A. Veres, V. Savova, D. Zemmour and A. M. Klein, et al. Single-cell barcoding and sequencing using droplet microfluidics, Nat. Protoc., 2017, 12(1), 44–73 CrossRef CAS PubMed , Available from: http://dx.doi.org/10.1038/nprot.2016.154.
- D. Pekin, Y. Skhiri, J. C. Baret, D. Le Corre, L. Mazutis and C. B. Salem, et al. Quantitative and sensitive detection of rare mutations using droplet-based microfluidics, Lab Chip, 2011, 11(13), 2156 RSC.
- K. Ahn, C. Kerbage, T. P. Hunt, R. M. Westervelt, D. R. Link and D. A. Weitz, Dielectrophoretic manipulation of drops for high-speed microfluidic sorting devices, Appl. Phys. Lett., 2006, 88(2), 024104 CrossRef , Available from: http://scitation.aip.org/content/aip/journal/apl/88/2/10.1063/1.2164911.
- J. C. Baret, O. J. Miller, V. Taly, M. Ryckelynck, A. El-Harrak and L. Frenz, et al. Fluorescence-activated droplet sorting (FADS): efficient microfluidic cell sorting based on enzymatic activity, Lab Chip, 2009, 9(13), 1850–1858 RSC , Available from: http://xlink.rsc.org/?DOI=b902504a.
- H. Xi, H. Zheng, W. Guo, A. M. Ganan-Calvo, Y. Ai and C. W. Tsao, et al. Active droplet sorting in microfluidics: a review, Lab Chip, 2017, 751–771 RSC , Available from: http://pubs.rsc.org/en/Content/ArticleLanding/2017/LC/C6LC01435F.
- A. Sciambi and A. R. Abate, Accurate microfluidic sorting of droplets at 30 kHz, Lab Chip, 2015, 15(1), 47–51 RSC , Available from: http://xlink.rsc.org/?DOI=C4LC01194E.
- F. Gielen, R. Hours, S. Emond, M. Fischlechner, U. Schell and F. Hollfelder, Ultrahigh-throughput-directed enzyme evolution by absorbance-activated droplet sorting (AADS), Proc. Natl. Acad. Sci. U. S. A., 2016, 113(47), E7383–E7389 CrossRef CAS PubMed , Available from: http://www.ncbi.nlm.nih.gov/pubmed/27821774.
- D. Frenzel and C. A. Merten, Microfluidic train station: highly robust and multiplexable sorting of droplets on electric rails, Lab Chip, 2017, 17(6), 1024–1030 RSC , Available from: http://xlink.rsc.org/?DOI=C6LC01544A.
- M. Girault, H. Kim, H. Arakawa, K. Matsuura, M. Odaka and A. Hattori, et al. An on-chip imaging droplet-sorting system: a real-time shape recognition method to screen target cells in droplets with single cell resolution, Sci. Rep., 2017, 7, 40072 CrossRef CAS PubMed , Available from: http://www.nature.
- G. Taylor, Disintegration of Water Drops in an Electric Field, Proc. R. Soc. London, Ser. A, 1964, 280(1382), 383–397 Search PubMed.
- B. Kintses, C. Hein, M. F. Mohamed, M. Fischlechner, F. Courtois and C. Lainé, et al. Picoliter cell lysate assays in microfluidic droplet compartments for directed enzyme evolution, Chem. Biol., 2012, 19(8), 1001–1009 CrossRef CAS PubMed , Available from: http://rspa.royalsocietypublishing.org/cgi/doi/10.1098/rspa.1964.0151.
- D. J. Eastburn, A. Sciambi and A. R. Abate, Identification and genetic analysis of cancer cells with PCR-activated cell sorting, Nucleic Acids Res., 2014, 42(16), 1–10 CrossRef PubMed.
- P. Y. Colin, B. Kintses, F. Gielen, C. M. Miton, G. Fischer and M. F. Mohamed, et al. Ultrahigh-throughput discovery of promiscuous enzymes by picodroplet functional metagenomics, Nat. Commun., 2015, 6, 10008 CrossRef CAS PubMed.
- H. A. Pohl, Some effects of nonuniform fields on dielectrics, J. Appl. Phys., 1958, 29(8), 1182–1188 CrossRef.
- E. Guyon, J. P. Hulin, L. Petit, C. Mitescu and D. Jankowski, Physical Hydrodynamics, Oxford, Oxford University Press, 2001 Search PubMed.
- J. D. Sherwood, Breakup of fluid droplets in electric and magnetic fields, J. Fluid Mech., 1988, 188(1), 133 CrossRef CAS.
- I. C. Clark, R. Thakur and A. R. Abate, Concentric electrodes improve microfluidic droplet sorting, Lab Chip, 2018, 18(5), 710–713 RSC , Available from: http://xlink.rsc.org/?DOI=C7LC01242J.
- W. Bangerth, R. Hartmann and G. Kanschat, deal.II—A generalpurpose object-oriented finite element library, ACM Trans. Math. Softw., 2007, 33(4), 24 CrossRef , Available from: http://portal.acm.org/citation.cfm?doid=1268776.1268779.
- T. Beneyton, F. Coldren, J. C. Baret, A. D. Griffiths and V. Taly, CotA laccase: high-throughput manipulation and analysis of recombinant enzyme libraries expressed in E. coli using droplet-based microfluidics, Analyst, 2014, 139(13), 3314–3323 RSC , Available from: http://xlink.rsc.org/?DOI=C4AN00228H.
- L. M. Fidalgo, G. Whyte, D. Bratton, C. F. Kaminski, C. Abell and W. T. S. Huck, From microdroplets to microfluidics: Selective emulsion separation in microfluidic devices, Angew. Chem., Int. Ed., 2008, 47(11), 2042–2045 CrossRef CAS PubMed.
- A. Fallah-Araghi, J. C. Baret, M Ryckelynck and A. D. Griffiths, A completely in vitro ultrahigh-throughput droplet-based microfluidic screening system for protein engineering and directed evolution, Lab Chip, 2012, 12(5), 882 RSC , Available from: http://xlink.rsc.org/?DOI=c2lc21035e.
- B. E. Debs, R. Utharala, I. V. Balyasnikova, A. D. Griffiths and C. A. Merten, Functional single-cell hybridoma screening using droplet-based microfluidics, Proc. Natl. Acad. Sci. U. S. A., 2012, 109(29), 11570–11575 CrossRef PubMed , Available from: http://www.pnas.org/cgi/doi/10.1073/pnas.1204514109.
- S. L. Sjostrom, Y. Bai, M. Huang, Z. Liu, J. Nielsen and H. N. Joensson, et al. High-throughput screening for industrial enzyme production hosts by droplet microfluidics, Lab Chip, 2014, 14(4), 806–813 RSC , Available from: http://xlink.rsc.org/?DOI=C3LC51202A.
- L. Mazutis and A. D. Griffiths, Selective droplet coalescence using microfluidic systems, Lab Chip, 2012, 12(10), 1800–1806 RSC , Available from: http://xlink.rsc.org/?DOI=c2lc40121e.
- E. Zang, S. Brandes, M. Tovar, K. Martin, F. Mech and P. Horbert, et al. Real-time image processing for label-free enrichment of Actinobacteria cultivated in picolitre droplets, Lab Chip, 2013, 13(18), 3707 RSC , Available from: http://xlink.rsc.org/?DOI=c3lc50572c.
- B. L. Wang, A. Ghaderi, H. Zhou, J. Agresti, D. A. Weitz and G. R. Fink, et al. Microfluidic high-throughput culturing of single cells for selection based on extracellular metabolite production or consumption, Nat. Biotechnol., 2014, 32(5), 473–478 CrossRef CAS PubMed , Available from: http://dx.doi.org/10.1038/nbt.2857.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c9lc00149b |
| ‡ Here we use a factor 5 as an intermediate between the drift for a no-slip boundary condition and a full-slip boundary condition. |
| This journal is © The Royal Society of Chemistry 2019 |