Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Temperature dependence of the vibrational spectrum of porphycene: a qualitative failure of classical-nuclei molecular dynamics†
Yair
Litman
a,
Jörg
Behler
 b and
Mariana
Rossi
b and
Mariana
Rossi
 *a
*a
aFritz Haber Institute of the Max Planck Society, Faradayweg 4-6, 14195 Berlin, Germany. E-mail: rossi@fhi-berlin.mpg.de
bUniversität Göttingen, Institut für Physikalische Chemie, Theoretische Chemie, Tammannstr. 6, 37077 Göttingen, Germany
First published on 20th June 2019
Abstract
The temperature dependence of vibrational spectra can provide information about structural changes of a system and also serve as a probe to identify different vibrational mode couplings. Fully anharmonic temperature-dependent calculations of these quantities are challenging due to the cost associated with statistically converging trajectory-based methods, especially when accounting for nuclear quantum effects. Here, we train a high-dimensional neural network potential energy surface for the porphycene molecule based on data generated with DFT-B3LYP, including pairwise van der Waals interactions. In addition, we fit a kernel ridge regression model for the molecular dipole moment surface. The combination of this machinery with thermostatted path integral molecular dynamics (TRPMD) allows us to obtain well-converged, full-dimensional, fully-anharmonic vibrational spectra including nuclear quantum effects, without sacrificing the first-principles quality of the potential-energy surface or the dipole surface. Within this framework, we investigate the temperature and isotopologue dependence of the high-frequency vibrational fingerprints of porphycene. While classical-nuclei dynamics predicts a red shift of the vibrations encompassing the NH and CH stretches, TRPMD predicts a strong blue shift in the NH-stretch region and a smaller one in the CH-stretch region. We explain this behavior by analyzing the modulation of the effective potential with temperature, which arises from vibrational coupling between quasi-classical thermally activated modes and high-frequency quantized modes.
1 Introduction
Porphycene, a structural isomer of free-base porphyrin, provides a unique example of double hydrogen transfer (DHT) in a multidimensional anharmonic potential-energy surface (PES).1 In the gas-phase, the most stable isomer at the PES corresponds to a trans state, where the hydrogen atoms within the cage are located on opposite sides, as shown in Fig. 1. The strong in-cage hydrogen bonds give rise to pronounced vibrational couplings which are evidenced, for example, by the extreme broadening and complex structure of the NH vibrational band.2,3 The ability to enhance, deactivate or trigger hydrogen transfer events in this family of molecules has a potential impact on the fabrication of molecular machines and nanodevices.4–6 Different strategies can be followed to achieve this control, for example modifying the electronic structure by addition of different substituents, altering the thermodynamic conditions, or using external stimuli.7–10Addressing this system using computer simulations requires a reliable description of the PES beyond the harmonic approximation, a full-dimensional representation of the system, and the inclusion of nuclear quantum effects (NQEs). Neglecting any of these aspects may lead to results that are qualitatively incorrect, as we have shown for the room-temperature IR spectrum of porphycene and the double hydrogen transfer reaction rates in the deep tunneling regime in ref. 2. In this work, we investigate whether certain approximations, like classical nuclei or dimensionality reduction, can grasp the essential physical aspects that modulate the vibrational fingerprints of porphycene and its isotopologues at different temperature regimes. Due to the high dimensionality of this system, density-functional theory (DFT) allied to path-integral based approximations to quantum dynamics are the state-of-the-art methodologies that can be applied with a tractable computational cost.
Temperature-dependent changes in vibrational fingerprints often include quite subtle changes in peak shapes and positions.11–15 Within trajectory-based methods, it is therefore necessary to ensure statistical convergence in order to achieve predictive results from simulation. The computational cost of the hundreds of thousands of force evaluations with a hybrid exchange–correlation functional for the hundreds of path-integral replicas necessary to bridge different temperature regimes presents a considerable challenge. Recent developments of different types of machine-learning potentials in the realm of atomistic simulations16–22 can be used to overcome this computational cost.
In this paper, we report the training of a high-dimensional neural network potential23,24 (HDNNP) based on data from density-functional theory (DFT) with a hybrid exchange–correlation functional (B3LYP25–28) and including pairwise van der Waals interactions.29 We complement this potential by a Kernel Ridge Regression (KRR) model trained on the same ab initio calculations to reproduce the dipole moment of this molecule. This setup allows the classical-nuclei and path-integral-based molecular dynamics simulations to effortlessly reach the nanosecond time scale with ab initio accuracy. We address standard porphycene (Pc-d0), the isotopologue where the inner-cage hydrogens have been substituted by deuterium (Pc-d2), and the isotopologue where only the outer-cage hydrogens have been substituted by deuterium (Pc-d12) (see Fig. 1). These isotopologues have been the subject of previous experimental and theoretical work.3,30–33 Based on the linear response time-correlation formalism, we compute the vibrational density of states and infrared spectra in a wide temperature range for the different isotopologues. We analyze their similarities and differences and address the relevance of including anharmonic contributions and nuclear-quantum effects in their full-dimensional nature, especially focusing on the NH-stretch signal which is the most puzzling feature of the vibrational spectrum of this molecule.
This manuscript is organized as follows: in Section 2.1 we present the details of the DFT calculations used to generate the data on which the HDNNP and the KRR are based. In Section 2.2, we provide a short theoretical background on the observables that we are going to compute. The training of the HDNNP potential and the KRR model, with the respective data set description and the validation tests are described in Sections 2.3 and 2.4 followed by the simulations protocol in Section 2.5. Having established a reliable description of our system we discuss our results for the temperature dependence of the vibrational spectra and the physical origins of the observed behaviors in Section 3. Finally, in Section 4, we close the manuscript summarizing our most important findings.
2 Methods
2.1 Electronic structure
The density-functional theory calculations were performed with the FHI-aims all-electron code.34 According to previous benchmarks performed in ref. 2, the B3LYP functional including pairwise van der Waals (vdW) corrections yields a good agreement to benchmark-quality CCSD(T) reference data for stationary points on the PES, barrier heights and geometrical properties. In this manuscript, we used most of the data generated from the ab initio molecular dynamics trajectories in ref. 2 and augmented it by a few points, as detailed below, to train the HDNNP. We have therefore consistently used the light settings of the FHI-aims code package for all new calculations. For stationary points on the potential energy surface, we observed that light settings yield differences below 5 meV in relative energies and 0.005 Å in atomic distances (see ref. 2) with respect to tight settings. An assessment of the impact of different numerical grids and basis sets settings on the vibrational spectrum of porphycene is shown in Fig. S1 in the ESI.† We observe differences in peak positions of at most 20 cm−1 and minimal differences in the harmonic peak intensities.2.2 IR spectrum and vibrational density of states
The IR spectrum and vibrational density of states presented in this paper were calculated within the linear-response time-correlation formalism. Within this formalism, based on Fermi’s golden rule,35 the IR adsorption cross section σ(ω) is proportional toσ(ω) ∝ ω2![[C with combining tilde]](https://www.rsc.org/images/entities/i_char_0043_0303.gif) μμ(ω), μμ(ω), | (1) |
![[C with combining tilde]](https://www.rsc.org/images/entities/i_char_0043_0303.gif) μμ(ω) is the Fourier transform of the Kubo-transformed dipole–dipole time-correlation function.
μμ(ω) is the Fourier transform of the Kubo-transformed dipole–dipole time-correlation function.
The vibrational density of states is given by36,37
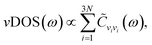 | (2) |
The time evolution of the dipole moment and the positions (and their derivatives) have been computed within the Born–Oppenheimer approximation with classical nuclei molecular dynamics (MD) and thermostatted ring-polymer molecular dynamics (TRPMD).40 TRPMD is an approximation to nuclear quantum dynamics based on classical dynamics in the extended phase space of the ring polymer.40,41 The methodology is very similar to ring-polymer molecular dynamics,41 with the difference that the internal modes of the ring polymer are attached to thermostats, while the centroid follows Hamiltonian dynamics. Its connection to quantum dynamics has been shown as the short-time approximation to Matsubara dynamics.42–44 There is a freedom in the choice of the thermostatting procedure,40 and it has been recently shown that generalized Langevin equation (GLE) thermostats can be tailored to yield optimal spectra.45 Here, we used the parameters proposed in ref. 45 for the GLE thermostats, which mitigate the spurious broadening of the TRPMD vibrational lineshape. The estimator for the dipole was computed as 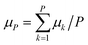 , where k runs over the P ring-polymer beads and μk is the dipole moment of the k-th replica. The estimator entering the vibrational density of states, due to the linearity of the velocity operator, is simply the velocity of the ring-polymer centroid. TRPMD is known to yield a good approximation to quantum time correlation functions that involve operators with a linear or almost linear dependence on positions. It does not capture nuclear quantum-mechanical coherence, and that can become more relevant at lower temperatures. We do not expect these effects to play a determinant role in the temperature range considered in the present study.
, where k runs over the P ring-polymer beads and μk is the dipole moment of the k-th replica. The estimator entering the vibrational density of states, due to the linearity of the velocity operator, is simply the velocity of the ring-polymer centroid. TRPMD is known to yield a good approximation to quantum time correlation functions that involve operators with a linear or almost linear dependence on positions. It does not capture nuclear quantum-mechanical coherence, and that can become more relevant at lower temperatures. We do not expect these effects to play a determinant role in the temperature range considered in the present study.
2.3 Potential energy surface from high-dimensional neural networks
High-dimensional neural network potentials as proposed by Behler and Parrinello23 allow complex potential energy surfaces of very large systems containing thousands of atoms and all their associated degrees of freedom to be represented. In this approach the total energy E of the system is constructed as a sum of atomic energies Ei,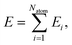 | (3) |
| Set # | Description | Structures |
|---|---|---|
| 1 | Stationary points set | 244 |
| 2 | Classical MD set | 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 033 033 |
| 3 | Path integral MD set | 80![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 665 665 |
| 4 | High temperature set | 7795 |
| 5 | Umbrella sampling set | 2000 |
We trained seven different HDNNPs with different architectures, data sets and numbers of symmetry functions (SM) (see Table 2). Their overall accuracy is commonly evaluated in terms of the energy and force root mean square error (RMSE) for both training and test sets. Overall, we have been able to reach the typical RMSEs of less than ∼1 meV per atom for the energy and less than ∼100 meV per Bohr for the force,47 which are known to yield very good results. We show in Fig. S2 in the ESI† scatter plots comparing DFT energies and HDNNP predictions for points spanning up to 1 eV from the global minimum and append to the ESI† the numerical parameters for all symmetry functions of all NNs.
| HDNNP | A | B | C | D | E | F | G |
|---|---|---|---|---|---|---|---|
| Data set | 1, 2, 3, 4 | 1, 2, 3, 4 | 1, 2 | 1, 2, 5 | 1, 2, 5 | 1, 2, 3, 4 | 1, 2, 3, 4, 5 |
| Hydrogen SM | 50 | 50 | 50 | 50 | 72 | 72 | 72 |
| Carbon SM | 44 | 44 | 55 | 55 | 72 | 72 | 72 |
| Nitrogen SM | 40 | 40 | 40 | 40 | 72 | 72 | 72 |
| Architecture | G-22-22-1 | G-15-15-1 | G-15-15-1 | G-15-15-1 | G-22-22-1 | G-22-22-1 | G-22-22-1 |
| Training energy RMSE | 1.2 | 1.5 | 0.7 | 0.8 | 0.6 | 0.8 | 1.1 |
| Test energy RMSE | 1.5 | 1.7 | 0.8 | 1.0 | 0.7 | 1.0 | 1.2 |
| Training force RMSE | 88 | 99 | 82 | 83 | 72 | 63 | 75 |
| Test force RMSE | 86 | 98 | 83 | 87 | 70 | 62 | 73 |
We start our validation tests looking at the stationary points generated by the HDNNP. For this purpose, instead of using the geometries given by DFT, which are not necessarily stationary points on the new generated PES, we performed new geometry optimizations for each HDNNP. The results are shown in Table 3 and show an overall overestimation of the energies of ∼5% with respect to the reference values even though the optimized geometries with the HDNNPs are almost identical (see Table SII in ESI†). More interesting are the NH stretch frequencies at those stationary points reported in Table 4. The degree of accuracy observed is remarkable, given that we have not explicitly included any Hessian information during the training procedure.
| DFT | NN | |
|---|---|---|
| cis | 93 | 101 (5) |
| SD1 | 189 | 199 (5) |
| SD2 | 290 | 308 (9) |
| DFT | NN | |
|---|---|---|
| Neg. freq. SD1 | 1228 | 1268 (27) |
| Neg. freq. SD2 (1) | 1263 | 1283 (21) |
| Neg. freq. SD2 (2) | 1126 | 1153 (33) |
| N–H trans | 2903 | 2917 (15) |
| N–H trans | 2907 | 2929 (14) |
| N–H cis | 2678 | 2644 (40) |
| N–H cis | 2640 | 2673 (64) |
A considerably more challenging task is the evaluation of the accuracy of the HDNNP on finite-temperature properties of interest. We were in the favorable situation where we had many pre-computed DFT molecular dynamics trajectories at our disposal so we could compare the predictions of the HDNNP and DFT for such properties directly. In Sections II.C and II.D of the ESI† we show these validation tests for quantum-nuclear potential-energy probability densities, VDOS and IR spectra. We find in general that the HDNNP is very accurate for all of these quantities. Small discrepancies appear between ∼600 cm−1 and ∼1250 cm−1 in the vibrational spectra, and we can connect them to inaccuracies either in the HDNNP potential or in the KRR model for the dipole (described below). Because in this work we will not be focusing in detail on this frequency region, we consider the current setup to be accurate enough for our purposes.
2.4 Dipole surface from kernel ridge regression
Although it is possible to incorporate an approximation to the dipole moment within the HDNN,49 we here chose to use a KRR model50 with Gaussian kernels in order to compute the molecular dipole moment of a particular molecular structure. This is a non-linear regression where an l2-norm regularization is considered in the loss-function, which is then minimized. This method is formally equivalent to a Gaussian Process Regression,51 but the hyperparameter optimization procedure can differ.Here we do not make any assumption on the analytical form of the dipole moment, and model each Cartesian component μi separately by
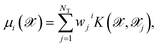 | (4) |
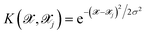 is the kernel with σ being an hyper-parameter which controls the degree of correlation between training points.
is the kernel with σ being an hyper-parameter which controls the degree of correlation between training points. 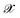 is a vector containing the representation of a particular molecular structure.
is a vector containing the representation of a particular molecular structure.
By equating the derivative of the loss function to zero, the weights for each dipole component are straightforwardly determined by
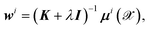 | (5) |
The efficiency of most KRR models depends on the representation 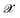 that enters the model. Many groups have proposed strategies to find optimal representation of molecular geometries that can greatly reduce the size of the training set necessary to reach acceptable accuracy.18,52,53 Symmetry considerations that allow the extension of this model to the prediction of full tensorial quantities of different ranks have also been recently addressed.54 However, for this work, a very large quantity of data was already available from previous simulations and the system considered here is a relatively rigid molecule. Therefore, we could simply align all geometries and dipole moments to a reference frame and use the Cartesian components as a representation (i.e. no representation) to predict each component of the dipole moment separately. The alignment was performed using the following expression
that enters the model. Many groups have proposed strategies to find optimal representation of molecular geometries that can greatly reduce the size of the training set necessary to reach acceptable accuracy.18,52,53 Symmetry considerations that allow the extension of this model to the prediction of full tensorial quantities of different ranks have also been recently addressed.54 However, for this work, a very large quantity of data was already available from previous simulations and the system considered here is a relatively rigid molecule. Therefore, we could simply align all geometries and dipole moments to a reference frame and use the Cartesian components as a representation (i.e. no representation) to predict each component of the dipole moment separately. The alignment was performed using the following expression
| y′ = R(y)y | (6) |
| μ′(y′) = R(y)μ(y) | (7) |
We used a total of ∼9500 data points of which 90% were selected as part of training and the remaining 10% were assigned to the test set. We performed a random selection 5 times in order to obtain statistically meaningful results for the performance of our model. For each division of the data, the hyperparameters σ and λ were determined using the QML package56 by a grid search minimization of the root mean square error (RMSE) on the test set (see Table 5). As shown in Table 5, the parameters are very similar for all three components, and using the same values for all would result in a minimal difference in the errors.
| Hyperparameters | Training set | Test set | ||||
|---|---|---|---|---|---|---|
| σ (Å) | λ | ε (%) | r 2 | ε (%) | r 2 | |
| μ x | 3.0 | −20 | 3.74 ± 0.03 | 0.999 ± 0.001 | 20.67 ± 0.65 | 0.957 ± 0.003 |
| μ y | 2.5 | −20 | 1.87 ± 1.19 | 0.999 ± 0.001 | 19.14 ± 0.93 | 0.962 ± 0.004 |
| μ z | 2.5 | −19 | 0.52 ± 0.16 | 0.999 ± 0.001 | 3.44 ± 0.12 | 0.999 ± 0.001 |
In order to describe the accuracy of the dipole moment fit, we report in Table 5 the coefficient of determination, r2, and the RMSE normalized by the standard deviation (STD) ε = 100 × RMSE/STD. ε has the advantage of being more sensitive to outliers, in comparison to the mean absolute error, and also allows quantities of different natures to be compared to one another.
Although the errors on the test set are somewhat large (in percentage), they are of a comparable magnitude to what was reported in previous work, that nevertheless could reach the same accuracy with a lesser amount of data and more sophisticated approaches.54,57 We observe that the models above (with such errors), actually lead to a very good prediction (with smaller errors) of the IR intensities, as shown in Fig. S6 in the ESI.† This effect has also been observed and discussed in ref. 58 for Raman intensities.
2.5 Simulation protocol
All trajectories were computed with HDNNP B using the LAMMPS software59 and its interface with the RuNNer code.60 We then used the socket interface between LAMMPS and the i-PI code61,62 in order to communicate energy and forces to perform classical-nuclei and path-integral molecular dynamics. In order to obtain the TRPMD VDOS, we ran 10 different imaginary path-integral trajectories of 110 ps per temperature, with a time-step of 0.25 fs. The first 10 ps of these runs were discarded as equilibration. We launched a 10 ps long TRPMD trajectory each 10 ps after that. This represents a total amount of 1 ns of statistical sampling per temperature and per isotopologue. In Table 6 we report the number of replicas used for the TRPMD simulations at each temperature.| T | 50 | 100 | 200 | 300 | 400 |
| P | 256 | 128 | 48 | 32 | 32 |
For classical nuclei simulations, we followed a similar strategy, with the following few differences: (i) since within classical mechanics any time independent equilibrium property is mass independent, we could use the same classical-nuclei NVT trajectories for different isotopologues; (ii) we employed a time step of 0.5 fs and (iii) started NVE trajectories from the thermalization run.
In all cases the dipole-moments were obtained a posteriori with the KRR model described above, and were calculated at an interval of 2.5 fs.
3 Results and discussion
3.1 Temperature dependent geometrical properties
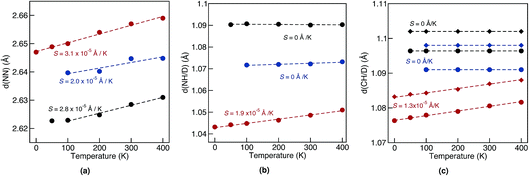
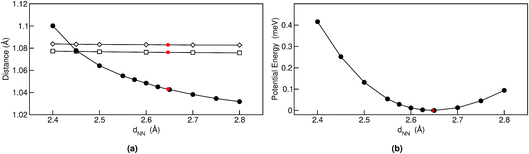
Geometrical equilibrium properties often have a decisive impact on time dependent properties. In porphycene, a particular geometrical property of interest is the equilibrium N–N distance d(NN) at a given temperature. This is because the dynamics of the hydrogens within the cage are strongly coupled to low frequency modes which modulate the cage size and therefore also d(NN).63,64In Fig. 2(a) we show the average d(NN) as a function of temperature, for the Pc-d0 and Pc-d2 isotopologues, considering quantum and classical nuclei. For classical nuclei simulations, both isotopologues (must) yield the same equilibrium geometrical properties. In all cases, the cage size, reflected by d(NN), increases linearly with temperature. In the temperature range studied, d(NN) of Pc-d0 is smaller than that of Pc-d2 and both are smaller than the classical nuclei d(NN). This geometrical isotope effect (GIE) is the so-called secondary-GIE or the Ubbelohde effect.65–67 We obtain an almost temperature-independent value of this secondary GIE of 0.016 Å, which compares very well with the experimental inferred one of 0.02 Å.32 As pointed out by Ubbelohde more than 60 years ago, the “structures may generally be expected to be closer for H than for D-bonds, because of differences in zero-point vibrations”,65 even though inverse Ubbelohde effects are possible for weak H-bonds, and have been observed.67,68 In porphycene, where strong directional H-bonds are present, the nuclear-quantum fluctuations along the anharmonic N–H bond increase the N–H bond length d(NH). As shown in Fig. 2(b) this effect is greater for Pc-d0 than for Pc-d2, which is the so-called primary isotope effect. In both cases, this bond elongation strengthens the H-bond and consequently reduces d(NN), inducing also a correlation between d(NN) and d(NH/D), shown in Fig. 3(a). The similarity of the values of the linear slope S of d(NN) for Pc-d0 and Pc-d2 above 100 K mean that the cage expansion can be treated classically in this temperature range. At 50 K we observe a deviation from the linear slope for Pc-d0, which is consistent with the observation that the lowest cage vibration mode lies at 65 cm−1 (≈90 K).
The positive sign of S can also be rationalized by analyzing the 1-D PES cut along the d(NN) coordinate shown in Fig. 3(b). The cage modulation is quite anharmonic and the potential is softer towards larger d(NN), such that when more thermal energy is available the average d(NN) will increase. The fact that the cage is much smaller in the quantum case than in the classical case also promotes the population of quasi-cis structures that present a permanent dipole, as has been discussed in ref. 2. For the situations above we found that the analysis for Pc-d12 is the same as for Pc-d0, such that we do not show this data.
For d(CH/D) and d(NH/D) in Fig. 2(b) and (c) we observe no temperature dependence when treating the nuclei quantum mechanically. This is expected, since the frequencies of the corresponding vibrational modes (>1900 cm−1, 2730 K) mean that more than 99.9% of the population stays in the vibrational ground state. In contrast, for classical nuclei the bond elongation increases with temperature even though the coupling between d(CH/D)/d(NH/D) and d(NN) is rather small, as shown in Fig. 3(a). The bond length increase is thus due to the temperature-dependent increase in population of this mode when treated classically and its anharmonic profile. The (quantum) temperature dependence of these geometrical properties for the deuterated isotopologues follows closely the ones for standard porphycene, but the deuterated bonds are always smaller than their hydrogenated counterparts.
3.2 Temperature-dependent vibrational spectra
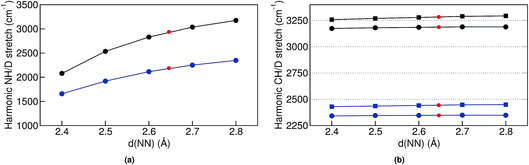
Having analyzed the geometrical properties of porphycene and its isotopologues, we turn our attention to vibrational spectra. In Fig. 4 we show the TRPMD VDOS for the three isotopologues in the NH (upper panels) and CH (bottom panels) stretch regions. The full frequency range is reported in the ESI, Fig. S10.† For Pc-d0 and Pc-d12 (panels a and c), the position and temperature dependence of the NH stretch peak around 2600 cm−1 is similar. Importantly, the broadening increases with temperature and it presents an unexpected blue shift of 150 cm −1 when the temperature is increased from 50 to 400 K. For Pc-d2 (panel b), the ND stretch peak appears at around 2050 cm−1. This value is 200 cm−1 above the trivial harmonic mass-scaled frequency, which highlights the anharmonic nature of this vibration. In this case the peak is narrower, and while both the blue shift and the broadening with increasing temperature are still present, their magnitude is smaller if compared to Pc-d0.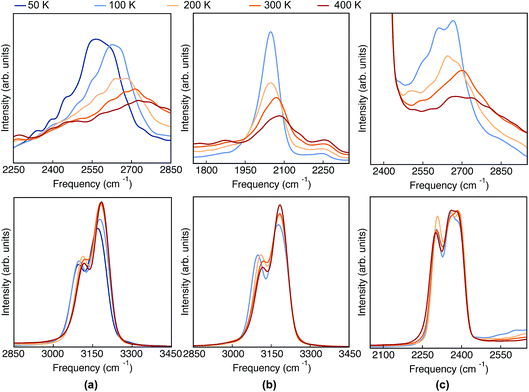 | ||
| Fig. 4 VDOS obtained from TRPMD simulations at 50 K, 100 K, 200 K, 300 K and 400 K, color coded going from blue (cold) to red (hot) for (a) Pc-d0, (b) Pc-d2 and (c) Pc-d12. | ||
The CH/D stretch peaks present, for all temperatures and isotopologues, a bimodal distribution emerging from the two types of CH bonds in this molecule: the ones belonging to the pyrrole rings and the ones which are connected to the ‘bridge’ positions. For the Pc-d0 and Pc-d2 cases (panels a and b), the CH peaks show a modest blue shift of ∼20 cm−1 and 10 cm−1 when the temperature is increased. On the contrary, the blue shift is not observed for Pc-d12 (panel c).
The classical-nuclei VDOS at the same vibrational regions and temperatures are shown in Fig. 5 for Pc-d0 (panel a) and Pc-d2 (panel b). The full frequency range is reported in the ESI, Fig. S11.† It is clear that, contrary to the TRPMD spectra, the NH and ND-stretch peaks slightly red-shift (20 cm−1) with increasing temperature. Additionally, these vibrations are situated much closer to the values predicted by the harmonic approximation in this case: 2950 and 2180 cm−1 for Pc-d0 and Pc-d2, respectively. The CH-stretch peaks also consistently red-shift with increasing temperature, and are also situated very close to the harmonic-approximation values of about 3175 and 3250 cm−1.
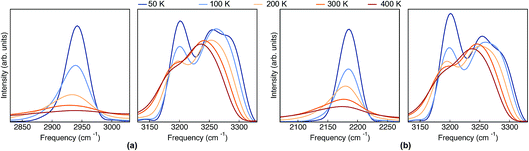 | ||
| Fig. 5 VDOS obtained from (classical-nuclei) MD simulations at 50 K, 100 K, 200 K, 300 K and 400 K color coded going from blue (cold) to red (hot) for (a) Pc-d0 and (b) Pc-d2. Note that in this figure the frequency axis spans a range of 200 cm−1 while in Fig. 4 it spans a range of 600 cm−1. | ||
Clearly, the nature of the high frequency vibrational peaks is strongly affected by nuclear quantum fluctuations, altering both the peak positions and their temperature dependence. In the next section, we explore the physical origins of these effects.
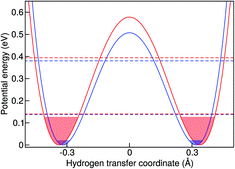
The simplest model to understand the physics of the NH-stretch potential energy, where exact quantum dynamics can be solved numerically, is a 1D double-well potential that changes with temperature, as shown in Fig. 7. The potential energy surfaces shown there were obtained by calculating the minimum-energy pathway (MEP) projected on the hydrogen-transfer coordinate (see caption of Fig. 7 for a definition of this coordinate). We calculated the MEP for two constrained d(NN) that are representative of the lowest and highest temperatures in this study. The MEP between these two constrained minima was obtained with the nudged elastic band method69 and it was extended by a harmonic potential at low and high d(NN), consistent with the corresponding NH frequency, in order to model the repulsive parts of the well.
In the classical-nuclei picture, temperature has two important effects. On the one hand, it induces a cage expansion with increasing temperature, and on the other hand, it also increases the thermal population of the NH vibrational well, as pictorially shown in Fig. 7. The first effect makes the walls of the potential increase more steeply with increasing temperature, thus increasing the curvature of the well (blue-shift), as evidenced in Fig. 6(a). The second effect causes the nuclei to explore more anharmonic parts of the well at higher energies, thus causing a red-shift. The final result is a competition between both effects and, for the classical case, the full-dimensional VDOS (Fig. 5) shows that the second one wins at certain temperatures, giving a net red-shift that becomes smaller (and eventually could turn into a blue shift) as the temperature is increased.
In quantum mechanics, however, the situation is quite different. The cage modulation with increasing temperature is similar to the classical-nuclei case. This can be easily understood since the energies of these modes lie at around 200 cm−1 (287 K) such that the thermal energy is comparable to the energy level spacing. On the other hand, the NH mode is still completely quantized up to 400 K and its thermal activation is negligible. The ZPE connected to this mode ensures that at all temperatures studied here, the anharmonic parts of the potential are assessed beyond what could be assessed by the classical nuclei simulations, thus explaining the overall red-shift when comparing quantum simulations to the classical ones. However, the insignificant thermal activation in this temperature interval makes this vibration solely sensitive to the modulation of the cage-mode with temperature, such that there is no competition between two effects and the result can only be a blue shift. This effect is also exemplified in Fig. 7. We have calculated the exact quantum mechanical first and second vibrational states connected to the 1D double well potentials presented in the figure, following the algorithm of ref. 70, where the MEP was fitted by a fourth order polynomial in the [−0.5 Å, +0.5 Å] interval in order to obtain an analytical form of the potential. We show an average of the tunneling-split levels, since these cannot be captured by TRPMD and would be smaller than the temperature broadening at the temperatures studied here. The less-pronounced effect for ND can also be understood within this model, in that the differences between the first vibrational excited state in the two potentials would be smaller.
The 1D potentials shown in Fig. 7 are useful to understand the physics of this problem and the differences between classical and quantum treatment of vibrational degrees of freedom when vibrational coupling between low and high energy modes is present. It also shows that the classical dynamics in the extended phase space of the ring polymer of TRPMD are successful in capturing the main quantum effect that would dictate the temperature dependence of this vibrational peak in full quantum dynamics. However, we find that it is not possible to obtain quantitative results for the observed temperature-dependence of the vibrational frequencies with this simple model. This once more highlights the inherently multi-dimensional nature of this problem.
Finally, for the CH vibrations we observed a much less pronounced blue-shift with increasing temperature. In this case, the CH potential is better described by a Morse potential and perturbative treatments could give reasonable results. We have thus performed second order vibrational perturbation calculations71,72 (VPT2). They show important couplings between the CH stretch and the CH bending modes. The results reproduce the average peak positions (see Table S4 in the ESI†) that we observe in the TRPMD simulations, and these are all red-shifted with respect to the harmonic estimation. However, also this coupling does not immediately explain the blue-shift with increasing temperature, since the bending modes have frequencies starting at 800 cm−1, which correspond only to a 5% thermal population at the highest temperature. We could not find any clear direct coupling between cage modes and the CH stretch, so it is less clear why and how the expansion of the cage modifies the CH-stretch potential. Nevertheless, since the blue shift with increasing d(NN) is very tenuous as shown in Fig. 6(b), for classical nuclei, increasing the thermal population of this mode results in a very pronounced net red shift. For quantum nuclei, again, there is no competition and we only observe a very small blue shift, which is ∼20 times smaller than in the NH case.
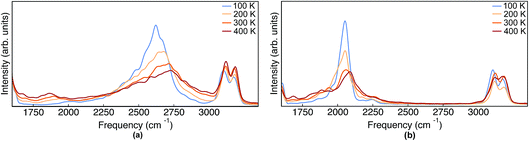 | ||
| Fig. 8 IR spectra obtained from TRPMD simulations of (a) Pc-d0 and (b) Pc-d2 at 100 K, 200 K, 300 K and 400 K. | ||
As mentioned above, in contrast to the VDOS, the IR spectra contain cross terms involving different nuclei and dipole selection rules. Therefore, lineshapes between VDOS and IR spectra are different and it is not obligatory that trends observed in the VDOS are exactly reflected in the IR spectra. Indeed, the lineshapes in Fig. 8 are different to the VDOS, but the observed temperature dependence of the vibrational peaks in this region is very similar to what was discussed for the VDOS. Specifically, Pc-d0 presents a blue shift of 100 cm−1 and 20 cm−1 for NH and CH stretch peak maxima respectively. For Pc-d2 the CH blue shift remains comparable (15 cm−1) and the NH one is only 40 cm−1. Both the peak positions and the blue-shifts are larger than what would be predicted by the trivial harmonic isotope 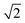 scaling factor, highlighting once more the anharmonic nature of this problem.
scaling factor, highlighting once more the anharmonic nature of this problem.
Finally, we comment on the region of the IR spectrum situated between 1750 and 2000 cm−1 of Pc-d0. The modes in this region are absent in the harmonic spectrum and they are thermally activated in a similar manner (red-shift with increasing temperature) for quantum and classical nuclei. One can thus infer that this band is a combination or overtone of lower-frequency vibrations, as was previously discussed by Gawinkowski and coworkers in ref. 3. The red-shift of 100 cm−1 we observe in the TRPMD spectrum is the largest in the whole spectrum (including lower frequencies) and we find the red-shifts of the bands situated between 800 and 1000 cm−1 to be more consistent with the combined shift, thus pointing to overtones. We could not further analyze our results at this point in order confirm this interpretation.
4 Concluding remarks
In this work we have studied the temperature dependence of structural and vibrational properties of the gas-phase porphycene molecule and its isotopologues, namely Pc-d0, Pc-d2 and Pc-d12, in temperatures ranging from 50 to 400 K. We employed high-dimensional neural-network potentials trained on B3LYP + vdW data to calculate energy and forces, augmented by a kernel ridge regression model for the dipole surface. We took nuclear quantum effects into account through imaginary-time path integral and thermostatted ring polymer molecular dynamics.We could explain the primary and secondary geometric isotope effects related to the N–N and N–H/D distances, and found good agreement with experiment. The strong hydrogen bonds within the cage are strengthened by nuclear quantum effects, such that the N–N distances are larger for Pc-d2 than for Pc-d0, while the N–H/D distances are smaller for Pc-d2 than for Pc-d0. In all cases the cage of porphycene expands with increasing temperature.
Regarding vibrational properties of Pc-d0, we find that anharmonic vibrational spectra derived from classical-nuclei molecular dynamics show a red-shift of both NH and CH stretch regions with increasing temperature. Approximate quantum dynamics (TRPMD) instead predicts a pronounced blue-shift (150 cm−1) in the NH stretch region with increasing temperature and a small blue-shift in the CH stretch region. For Pc-d2, the ND stretch shows a less pronounced blue-shift and for Pc-d12 the CD stretch region remains unchanged throughout this temperature range.
The temperature behavior of the NH(ND) stretch regions is a consequence of vibrational coupling between quasi-classical thermally activated cage expansion/contraction modes and high-frequency quantized modes. We could understand the underlying physics of the problem by analyzing a 1D double-well model where the distance (and the barrier height) between the two wells increases with temperature. In classical mechanics there is a competition between the increasing thermal population of the well and the increasing curvature of the potential as the temperature increases. The first causes a red-shift due to the anharmonicity of the potential, while the second causes a blue-shift due to the effective decrease of anharmonicity at the bottom of the well. In quantum mechanics, at all temperatures studied here, the thermal population of excited vibrational states is completely negligible, such that only the modulation of the potential with temperature plays a role and the result is a pronounced blue shift. The approximate quantum dynamics of TRPMD are able to grasp this effect, because ZPE is correctly described at the different temperatures and the linear-response transition probabilities are only sensitive to the stiffening in the effective curvature of the potential with increasing temperature. Even though the 1D model in this case is useful to understand the underlying physics, no quantitative predictions could be achieved with it, highlighting the inherent high-dimensionality of the problem.
For the CH/D stretch regions the direct coupling between low and high frequency modes is less clear, but we observe the that the cage expansion is correlated to a blue shift with increasing temperature. We note that the (quantum) blue-shift with increasing temperature observed for this isolated gas-phase molecule seems not to have the same origin as the ones observed in condensed phase systems,11,13,73 where it is understood that the shifts are due to the weakening of intermolecular H-bonds with increasing temperature.
In summary, we have shown that the porphycene molecule is a clear example where considering nuclei as classical particles makes the theory inaccurate and completely removes its predictive power for a range of geometrical and vibrational properties. On the other hand, path-integral based approximations to quantum dynamics, which conserve the quantum Boltzmann distribution and therefore are free from ZPE leakage, are able to grasp the correct underlying physics in this system. In fact, even though we treated an isolated molecule here, the large amount of (anharmonic) degrees of freedom and the temperature range considered washes out most dynamical quantum coherence effects, which presents an ideal ground for such methods. We have also demonstrated that when a large amount of data from ab initio simulations is available, the effort to train high dimensional neural network potentials and kernel ridge regression models that accurately reproduce energy, forces and dipoles can be minimal. This makes it possible to address new physical problems that would be too cost-intensive with accurate DFT potentials – in particular, problems that take the quantum nature of nuclei into account. Open access data repositories that can handle, specifically, data related to ab initio molecular dynamics trajectories will be paramount to make this approach more common in the near future.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
MR thanks David Manolopoulos for an early version of the code that calculates exact quantum solutions for 1D-potentials that we used for preliminary interpretation of the data in this manuscript. YL thanks Nathaniel Raimbault, Marcel Langer and Matthias Rupp for helpful discussion regarding the application of the KRR model for dipole moment prediction. MR and YL thank the Max Planck Society for funding. JB thanks the DFG for a Heisenberg professorship (BE3264/11-2, project number 329898176). Open Access funding was provided by the Max Planck Society.References
- J. Waluk, Chem. Rev., 2017, 117, 2447–2480 CrossRef CAS.
- Y. Litman, J. O. Richardson, T. Kumagai and M. Rossi, J. Am. Chem. Soc., 2019, 141, 2526–2534 CrossRef CAS.
- S. Gawinkowski, L. Walewski, A. Vdovin, A. Slenczka, S. Rols, M. R. Johnson, B. Lesyng and J. Waluk, Phys. Chem. Chem. Phys., 2012, 14, 5489–5503 RSC.
- P. Fita, L. Grill, A. Listkowski, H. Piwonski, S. Gawinkowski, M. Pszona, J. Sepiol, E. Mengesha, T. Kumagai and J. Waluk, Phys. Chem. Chem. Phys., 2017, 19, 4921–4937 RSC.
- J. Kügel, M. Leisegang and M. Bode, ACS Nano, 2018, 12, 8733–8738 CrossRef.
- J. Kügel, M. Leisegang, M. Böhme, A. Krönlein, A. Sixta and M. Bode, Nano Lett., 2017, 17, 5106–5112 CrossRef.
- H. Böckmann, S. Liu, J. Mielke, S. Gawinkowski, J. Waluk, L. Grill, M. Wolf and T. Kumagai, Nano Lett., 2016, 16, 1034–1041 CrossRef.
- T. Kumagai, F. Hanke, S. Gawinkowski, J. Sharp, K. Kotsis, J. Waluk, M. Persson and L. Grill, Phys. Rev. Lett., 2013, 111, 246101 CrossRef.
- J. N. Ladenthin, T. Frederiksen, M. Persson, J. C. Sharp, S. Gawinkowski, J. Waluk and T. Kumagai, Nat. Chem., 2016, 8, 935–940 CrossRef CAS.
- T. Kumagai, J. N. Ladenthin, Y. Litman, M. Rossi, L. Grill, S. Gawinkowski, J. Waluk and M. Persson, J. Chem. Phys., 2018, 148, 102330 CrossRef.
- F. Paesani, J. Phys. Chem. A, 2011, 115, 6861–6871 CrossRef CAS PubMed.
- S. K. Reddy, D. R. Moberg, S. C. Straight and F. Paesani, J. Chem. Phys., 2017, 147, 244504 CrossRef PubMed.
- T. Morawietz, O. Marsalek, S. R. Pattenaude, L. M. Streacker, D. Ben-Amotz and T. E. Markland, J. Phys. Chem. Lett., 2018, 9, 851–857 CrossRef CAS PubMed.
- Y. C. Shen, P. C. Upadhya, E. H. Linfield and A. G. Davies, Appl. Phys. Lett., 2003, 82, 2350–2352 CrossRef CAS.
- E. Garrone and C. Otero Areán, Chem. Soc. Rev., 2005, 34, 846–857 RSC.
- J. Behler, Phys. Chem. Chem. Phys., 2011, 13, 17930–17955 RSC.
- J. Behler, J. Chem. Phys., 2016, 145, 170901 CrossRef PubMed.
- A. P. Bartók and G. Csányi, Int. J. Quantum Chem., 2015, 115, 1051–1057 CrossRef.
- V. Botu, R. Batra, J. Chapman and R. Ramprasad, J. Phys. Chem. C, 2017, 121, 511–522 CrossRef CAS.
- S. Chmiela, A. Tkatchenko, H. E. Sauceda, I. Poltavsky, K. T. Schütt and K. R. Müller, Sci. Adv., 2017, 3, 1–6 Search PubMed.
- M. Ceriotti, J. Chem. Phys., 2019, 150, 150901 CrossRef.
- M. Rupp, Int. J. Quantum Chem., 2015, 115, 1058–1073 CrossRef CAS.
- J. Behler and M. Parrinello, Phys. Rev. Lett., 2007, 98, 146401 CrossRef.
- J. Behler, J. Chem. Phys., 2011, 134, 074106 CrossRef.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789 CrossRef CAS PubMed.
- S. H. Vosko, L. Wilk and M. Nusair, Can. J. Phys., 1980, 58, 1200–1211 CrossRef CAS.
- P. J. Stephens, F. J. Devlin, C. F. Chabalowski and M. J. Frisch, J. Phys. Chem., 1994, 98, 11623–11627 CrossRef CAS.
- A. Tkatchenko and M. Scheffler, Phys. Rev. Lett., 2009, 102, 073005 CrossRef.
- P. Ciacka, P. Fita, A. Listkowski, C. Radzewicz and J. Waluk, J. Phys. Chem. Lett., 2016, 7, 283–288 CrossRef CAS.
- E. T. Mengesha, A. Zehnacker-Rentien, J. Sepioł, M. Kijak and J. Waluk, J. Phys. Chem. B, 2015, 119, 2193–2203 CrossRef CAS PubMed.
- M. F. Shibl, M. Pietrzak, H. H. Limbach and O. Kühn, ChemPhysChem, 2007, 8, 315–321 CrossRef CAS.
- T. Yoshikawa, S. Sugawara, T. Takayanagi, M. Shiga and M. Tachikawa, Chem. Phys., 2012, 394, 46–51 CrossRef CAS.
- V. Blum, R. Gehrke, F. Hanke, P. Havu, V. Havu, X. Ren, K. Reuter and M. Scheffler, Comput. Phys. Commun., 2009, 180, 2175–2196 CrossRef CAS.
- D. A. McQuarrie, Statistical mechanics, University Science Books, 2000 Search PubMed.
- C. James, Structural Chemistry of Glasses, Elsevier Science Ltd, Oxford, 2002, pp. 137–183 Search PubMed.
- R. Zwanzig, Phys. Rev., 1964, 133, A50–A51 CrossRef.
- B. J. Braams, T. F. Miller III and D. E. Manolopoulos, Chem. Phys. Lett., 2006, 418, 179–184 CrossRef CAS.
- S. Habershon, B. J. Braams and D. E. Manolopoulos, J. Chem. Phys., 2007, 127, 174108 CrossRef.
- M. Rossi, M. Ceriotti and D. E. Manolopoulos, J. Chem. Phys., 2014, 140, 234116 CrossRef PubMed.
- I. R. Craig and D. E. Manolopoulos, J. Chem. Phys., 2004, 121, 3368–3373 CrossRef CAS.
- T. J. H. Hele, M. J. Willatt, A. Muolo and S. C. Althorpe, J. Chem. Phys., 2015, 142, 134103 CrossRef.
- T. J. H. Hele, M. J. Willatt, A. Muolo and S. C. Althorpe, J. Chem. Phys., 2015, 142, 191101 CrossRef.
- T. J. H. Hele, Mol. Phys., 2016, 114, 1461–1471 CrossRef CAS.
- M. Rossi, V. Kapil and M. Ceriotti, J. Chem. Phys., 2018, 148, 102301 CrossRef.
- J. Behler, Int. J. Quantum Chem., 2015, 115, 1032–1050 CrossRef CAS.
- J. Behler, Angew. Chem., Int. Ed., 2017, 56, 12828 CrossRef CAS PubMed.
- J. Behler, RuNNer - A Neural Network Code for High-Dimensional Potential-Energy Surfaces, Universität Göttingen, 2018, http://www.uni-goettingen.de/de/560580.html Search PubMed.
- M. Gastegger, J. Behler and P. Marquetand, Chem. Sci., 2017, 8, 6924 RSC.
- T. Hastie, R. Tibshirani and J. Friedman, The Elements of Statistical Learning, 2nd edn, Springer, New York, 2009 Search PubMed.
- C. E. Rasmussen and C. K. I. Williams, Gaussian Processes for Machine Learning, MIT Press, 2006 Search PubMed.
- H. Huo and M. Rupp, arXiv:1704.06439, 2017.
- M. Rupp, A. Tkatchenko, K. R. Müller and O. A. von Lilienfeld, Phys. Rev. Lett., 2012, 108, 058301 CrossRef PubMed.
- A. Grisafi, D. M. Wilkins, G. Csányi and M. Ceriotti, Phys. Rev. Lett., 2018, 120, 036002 CrossRef CAS PubMed.
- W. Kabsch, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr., 1978, 34, 827–828 CrossRef.
- A. S. Christensen, F. A. Faber, B. Huang, L. Bratholm, A. Tkatchenko, K. R. Muller and O. A. von Lilienfeld, QML: A Python Toolkit for Quantum Machine Learning, https://github.com/qmlcode/qml Search PubMed.
- M. J. Willatt, F. Musil and M. Ceriotti, J. Chem. Phys., 2019, 150, 154110 CrossRef.
- N. Raimbault, A. Grisafi, M. Ceriotti and M. Rossi, New J. Phys., 2019 DOI:10.1088/1367-2630/ab4509.
- S. Plimpton, J. Comput. Phys., 1995, 117, 1 CrossRef CAS.
- A. Singraber, J. Behler and C. Dellago, J. Chem. Theory Comput., 2019, 15, 1827–1840 CrossRef CAS PubMed.
- V. Kapil, M. Rossi, O. Marsalek, R. Petraglia, Y. Litman, T. Spura, B. Cheng, A. Cuzzocrea, R. H. Meißner, D. M. Wilkins, B. A. Helfrecht, P. Juda, S. P. Bienvenue, W. Fang, J. Kessler, I. Poltavsky, S. Vandenbrande, J. Wieme, C. Corminboeuf, T. D. Kühne, D. E. Manolopoulos, T. E. Markland, J. O. Richardson, A. Tkatchenko, G. A. Tribello, V. V. Speybroeck and M. Ceriotti, Comput. Phys. Commun., 2019, 236, 214–223 CrossRef CAS.
- M. Ceriotti, J. More and D. E. Manolopoulos, Comput. Phys. Commun., 2014, 185, 1019–1026 CrossRef CAS.
- M. F. Shibl, M. Tachikawa and O. Kühn, Phys. Chem. Chem. Phys., 2005, 7, 1368–1373 RSC.
- M. Gil and J. Waluk, J. Am. Chem. Soc., 2007, 129, 1335–1341 CrossRef CAS PubMed.
- A. R. Ubbelohde and K. J. Gallagher, Acta Crystallogr., 1955, 8, 71–83 CrossRef CAS.
- H. Benedict, H. H. Limbach, M. Wehlan, W.-P. Fehlhammer, N. S. Golubev and R. Janoschek, J. Am. Chem. Soc., 1998, 120, 2939–2950 CrossRef CAS.
- X. Z. Li, B. Walker and A. Michaelides, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 6369–6373 CrossRef CAS.
- H.-H. L. A. Kohen, Isotope Effects In Chemistry and Biology, CRC Press, 2005 Search PubMed.
- G. Henkelman and H. Jónsson, J. Chem. Phys., 2000, 113, 9978–9985 CrossRef CAS.
- D. T. Colbert and W. H. Miller, J. Chem. Phys., 1992, 96, 1982–1991 CrossRef CAS.
- S. Califano, Vibrational States, John Wiley & Sons, 1976, pp. 266–302 Search PubMed.
- V. Barone, J. Chem. Phys., 2005, 122, 014108 CrossRef PubMed.
- Y. Katsumoto, H. Komatsu and K. Ohno, J. Am. Chem. Soc., 2006, 128, 9278–9279 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c9fd00056a |
| ‡ This is easy to see if one would assume the dipole to be a linear function of the coordinates. |
| This journal is © The Royal Society of Chemistry 2020 |