Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Towards measuring reactivity on micro-to-millisecond timescales with laser pump, NMR probe spectroscopy†
Meghan E.
Halse
 *a,
Barbara
Procacci
*a,
Barbara
Procacci
 b,
Robin N.
Perutz
b,
Robin N.
Perutz
 a and
Simon B.
Duckett
a and
Simon B.
Duckett
 b
b
aDepartment of Chemistry, University of York, Heslington, York, YO10 5DD, UK. E-mail: meghan.halse@york.ac.uk
bCentre for Hyperpolarisation in Magnetic Resonance, Department of Chemistry, University of York, Heslington, York, YO10 5NY, UK
First published on 11th June 2019
Abstract
We present a quantitative analysis of the timescales of reactivity that are accessible to a laser pump, NMR probe spectroscopy method using para-hydrogen induced polarisation (PHIP) and identify three kinetic regimes: fast, intermediate and slow. These regimes are defined by the relative rate of reaction, k, compared to δω, the frequency of the NMR signal oscillations associated with the coherent evolution of the hyperpolarised 1H NMR signals created after para-hydrogen (p-H2) addition during the pump-probe delay. The kinetic regimes are quantitatively defined by a NMR dephasing parameter, ε = δω/k. For the fast regime, where k ≫ δω and ε tends to zero, the observed NMR signals are not affected by the chemical evolution of the system and so only an upper bound on k can be determined. In the slow regime, where k ≪ δω and ε tends to infinity, destructive interference leads to the complete dephasing of the coherent NMR signal intensity oscillations. As a result, the observed NMR signal evolution during the pump-probe delay reflects only the chemical change of the system and NMR relaxation. Finally, in the intermediate regime, where k ∼ δω, characteristic partial dephasing of the NMR signal oscillations is predicted. In the limit where the dephasing parameter is small but non-zero, chemical evolution manifests itself as a phase shift in the NMR signal oscillation that is equal to the dephasing parameter. As this phase shift is predicted to persist for pump-probe delays much longer than the timescale of the formation of the product molecules, it provides a route to measure reactivity on micro-to-millisecond timescales through NMR detection. We predict that the most significant fundamental limitations of the accessible reaction timescales are the duration of the NMR excitation pulse (∼1 μs) and the chemical shift difference (in Hz) between the p-H2-derived protons in the product molecule.
Introduction
NMR spectroscopy is a well-established technique for the study of chemical reactivity and chemical exchange on timescales ranging from microseconds to days. Exchange interactions can be probed in the steady-state via line-shape analysis, where the accessible timescales are determined by the chemical shift difference between the exchanging resonances.1 Alternatively, exchange spectroscopy (EXSY) methods allow for the quantitation of exchange processes on longer timescales, where the limiting factor is the NMR relaxation properties of the system.2 Outside of the steady-state regime, chemical reactivity can be monitored in real time over periods of seconds to days. NMR flow methods, which access faster reaction timescales in a manner similar to flow UV, have also been demonstrated for applications such as rapid-injection protein unfolding3–7 and metabolomics studies.8Recently, we demonstrated a new method for monitoring reactivity by NMR spectroscopy using a pump-probe approach,9–11 which has also been implemented by Yurkovskaya and co-workers.12 This method is analogous to that used with optical detection methods such as UV/vis,13,14 IR15 and Raman spectroscopy,16–18 and shares many features with time-resolved EPR spectroscopy, which is used to probe photoexcited paramagnetic species at nanosecond and longer timescales.19–21 In a time-resolved NMR experiment, the sample is pumped photochemically using a laser synchronised to the NMR spectrometer to initiate the reaction of interest. Specifically, a single laser pulse is applied to the sample in situ, followed, after a well-defined pump-probe delay, by a radio-frequency (rf) probe pulse and subsequent NMR signal detection. The success of this methodology rests on the synchronisation of the laser pump pulse with the NMR probe pulse, and the use of hyperpolarisation to overcome the inherent insensitivity of NMR spectroscopy. Para-hydrogen induced polarisation (PHIP) is used to provide the necessary boost in NMR sensitivity. A related approach, laser-initiated chemically induced dynamic nuclear polarisation (photo-CIDNP), in which a spin-correlated radical pair is used to generate NMR signal enhancements on the order of 102, has been used to observe short-lived radicals and to monitor reactivity on millisecond to second timescales.22–25
PHIP is a well-established technique for signal amplification in NMR. It was first predicted by Bowers and Weitekamp in 1986 (ref. 26) and subsequently observed experimentally.27–29 PHIP has found wide-spread use for the study of reactivity in inorganic and organic chemistry.30,31 This method takes advantage of the pure nuclear spin state of para-hydrogen (p-H2), which is the thermally preferred spin isomer of molecular hydrogen. The pair of spin-1/2 1H nuclei in p-H2 exist in a singlet state, which has no net magnetic moment and is NMR silent. If the symmetry of the chemical and/or the magnetic environments of the 1H nuclei in p-H2 is broken, for example by means of oxidative addition to a metal centre, the singlet state will evolve into NMR observable triplet states in the product molecule. The resultant NMR signals will be enhanced, often by several orders of magnitude over the standard levels. In the traditional PHIP methodology, thermally-activated reactions are used to build up the population of product molecules containing a pair of p-H2-derived 1H nuclei over a period of seconds.30 The asynchronous nature of this approach means that the p-H2 hyperpolarisation of the product is detected through a time-averaged response. In the photochemical pump, NMR probe experiment, we observe the initially created p-H2-derived hyperpolarisation after a delay as short as 10 μs, using photochemistry to initiate the reaction with p-H2 in a coherent and synchronised way.9,10 Therefore this time-resolved method provides a route to measuring reactivity outside of the steady-state regime on a much faster timescale than is available through using non-hyperpolarised NMR spectroscopy methods.
In this paper we explore the rates of reactivity that can be followed using this photochemical pump, NMR probe technique. We identify three kinetic regimes: fast, intermediate and slow, which are defined by the relative rate of reaction compared to the rate of the magnetic evolution of the p-H2-derived hyperpolarisation. We focus in particular on the intermediate regime where the kinetic and magnetic evolution of the system occur on the same timescale. We present a first-principles analysis to predict how quantitative information on the reaction rate can be obtained in this regime, even at pump-probe times longer than the reaction time-scale. In addition, we explore the experimental considerations that constrain the upper limit on reaction rates that are accessible to the laser pump, NMR probe technique.
Theory
(A) Laser pump, NMR probe spectroscopy
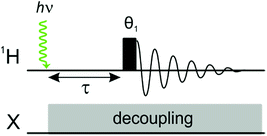
Laser pump, NMR probe spectroscopy is a time resolved experiment in which a single laser pulse is applied in situ to initiate a photochemical reaction involving the pairwise addition of p-H2 to a transition metal complex or to an unsaturated substrate.9,10 The hyperpolarised product molecule containing a pair of protons from p-H2 is then detected following a well-defined pump-probe delay using a standard NMR detection sequence (Fig. 1). The evolution of the system is monitored by acquiring a series of time-resolved NMR experiments with different pump probe delays. This method can be used to provide insights into the mechanism and kinetics of the underlying chemical reactivity.A unique feature of the laser-pump, NMR probe experiment, when compared to other time-resolved spectroscopies, is that the NMR response can contain information about the product identity and both the kinetics of the photochemical reaction and the coherent magnetic evolution of the initial p-H2-derived singlet state into observable magnetisation. The details of the coherent magnetic evolution will depend on the specific NMR parameters of the nuclei in the product molecule. For a detailed description of this phenomenon for a range of different types of spin system, we direct the interested reader to ref. 9.
In the following section, we provide a brief introduction to the theory of p-H2 hyperpolarisation and a description of the magnetic evolution of the pair of p-H2-derived protons for the case where they form a simple AX spin system in the product molecule.
Para-hydrogen is the spin isomer of H2 that exists in a nuclear singlet state. The theory of p-H2 hyperpolarisation has been described extensively, for example in the reviews of Natterer and Bargon32 and Green et al.31 In the product operator basis, the p-H2 singlet state can be described by the density matrix, ρp-H2:
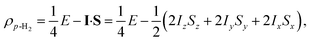 | (1) |
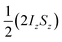 and the transverse term, zero-quantum-x (ZQx, eqn (2)).
and the transverse term, zero-quantum-x (ZQx, eqn (2)).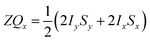 | (2) |
In the case where the 1H nuclei are magnetically equivalent, as in molecular hydrogen, this state is NMR silent. It is only by breaking the symmetry of the 1H environments that we can observe magnetisation originating from this state. In PHIP, we routinely break the symmetry through the spin-conserved pair-wise addition of p-H2 to a metal complex or through the subsequent relay of these protons into the hydrogenation of an unsaturated substrate. It has been shown that the p-H2 singlet state can be conserved upon the oxidative addition of p-H2 at a metal centre.33 If we assume this is the case and that the former p-H2 nuclei are placed into magnetically different environments in the product, the p-H2-derived singlet state will evolve into observable states under the influence of the internal spin Hamiltonian, H, according to the Liouville–von-Neumann equation (eqn (3)), where the density matrix at t = 0 is equal to the parahydrogen singlet state, ρ(0) = ρp-H2.
| dρ(t)/dt = −i[H,ρ(t)] | (3) |
(B) Magnetic evolution: AX spin system
Consider a situation where the p-H2-derived protons are placed into two chemically distinct environments on a timescale much faster than the magnetic evolution of the system. This high-field AX system has been solved previously by Bowers and Weitekamp.26 We summarise here the results for the high-field (weakly-coupled) case. The time-independent internal spin Hamiltonian for an AX spin system is given by eqn (4), where ωA and ωX are the Larmor frequencies of the two spins, respectively, and JAX is the scalar coupling between them.| HAX = −ωAIz − ωXSz + 2πJAXIzSz | (4) |
The AX Hamiltonian in eqn (4) can be divided into a part that commutes with the density matrix at all points in time, HAX0, and a part that does not commute, HAX1, where the difference in chemical shift between the two spins (in rad s−1) is defined as: δω = ωA − ωX.
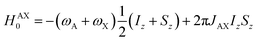 | (5) |
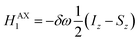 | (6) |
Only the non-commuting part of the Hamiltonian, HAX1, results in the coherent evolution of the density matrix. The longitudinal term, 2IzSz in eqn (1), commutes with both HAX0 and HAX1 at all points in time and so this part of the initial density matrix is invariant during the pump-probe delay. The ZQx term evolves during the pump-probe delay (τ) according to eqn (7), where the zero-quantum coherence, ZQy, is defined in eqn (8).
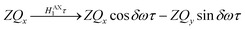 | (7) |
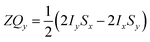 | (8) |
The time-dependent density matrix during the pump-probe delay can therefore be written as a combination of the longitudinal term and the zero-quantum-coherence terms (eqn (9a)–(9d)). The time dependent amplitudes of these terms will vary according to the coherent magnetic evolution of the system, as described above, and NMR relaxation. Here we have included relaxation effects using the Bloch approach through the introduction of effective zero-quantum relaxation rates, R1,ZQ and R2,ZQ, which describe the average NMR relaxation behaviour of the longitudinal two-spin order term and the zero-quantum coherences, respectively. The density matrix as a function of the pump-probe delay, τ, is therefore:
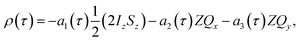 | (9a) |
| a1(τ) = exp(−R1,ZQτ), | (9b) |
a2(τ) = cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δωτ δωτ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−R2,ZQτ), exp(−R2,ZQτ), | (9c) |
a3(τ) = −sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δωτ δωτ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−R2,ZQτ). exp(−R2,ZQτ). | (9d) |
To probe the evolution of the density matrix during the pump-probe delay, we can apply any appropriately adapted NMR pulse sequence at a fixed time, τ, following a single laser pulse. The simplest detection pulse sequence consists of a single broadband (non-selective) 1H rf pulse of tip angle θ1, applied at a time τ after the laser shot (Fig. 1).
The single-quantum density matrix for an AX spin system, derived from p-H2 addition following the application of a non-selective 1H rf pulse of tip angle θ1, is presented in eqn (10a)–(10c), where the amplitudes: a1,a2, and a3 are defined in eqn (9a)–(9d).9 This density matrix contains all of the directly observable terms following the application of the rf pulse.
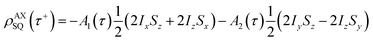 | (10a) |
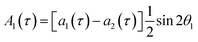 | (10b) |
A2(τ) = a3(τ)sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ1 θ1 | (10c) |
The amplitude of the first term in eqn (10a)–(10c) (A1) is proportional to the difference in amplitude between the longitudinal two-spin-order and ZQx terms immediately prior to the rf pulse. The amplitude of the second term in eqn (10a)–(10c) (A2) is proportional to the amplitude of the ZQy coherence prior to the rf pulse. We can exploit the differences in relative phase between these terms to isolate the contribution of each to the observed NMR signal through selective integration as described in ref. 9.
Results and discussion
(A) Magnetic and chemical evolution: AX spin system
The introductory theory outlined in the previous section focuses exclusively on the magnetic evolution of the system and neglects the effects of the chemical reaction. The kinetics of the chemical reaction determines the rate of the formation of the p-H2-labelled product. If this rate is comparable to the frequency of the magnetic oscillations in the product, then destructive interference between the oscillations for molecules formed at different points in time will occur, leading to a net decoherence or dephasing of the oscillating signals. In this work, we derive analytical expressions for the effect of the relative rates of magnetic and chemical evolution on observed NMR signal changes during the pump-probe delay. In particular, we explore how the dephasing effect can be used to obtain quantitative information about the kinetics of the p-H2 addition, even at pump-probe times that are long compared to the inverse of the addition rate, k−1. We note that in this work we exemplify our results by considering the case of oxidative addition of p-H2 to a metal centre; however, the same conclusions also apply to the hydrogenation of an unsaturated substrate with p-H2.In a laser pump, NMR probe experiment, chemical initiation is provided by a short (∼10 ns) laser pulse, which causes the reductive elimination of the hydride ligands from the metal complex on a picosecond to nanosecond timescale.34–37 Due to the large excess of p-H2 in solution, we treat the subsequent oxidative addition of p-H2 to the unsaturated intermediate using a pseudo-first-order kinetic model. Accordingly, we write down the following differential equation (eqn (11)) to describe the time-dependence of the concentration of the unsaturated intermediate, f(τ), where τ = 0 is the time at which the laser pulse is applied and k is the pseudo-first-order rate constant for the oxidative addition of H2 under the given experimental conditions.
| df(τ)/dτ = −kf(τ) | (11) |
Using the boundary condition f(0) = f0, the solution for the concentration of the intermediate as a function of time is an exponential decay (eqn (12)).
f(τ) = f0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−kτ) exp(−kτ) | (12) |
Consider the effect that the kinetics of the formation of the product molecule will have on the amplitudes of the three terms in the density matrix for an AX spin system defined in eqn (9a). In all of the p-H2-enhanced experiments described here, which are assumed to occur in the high magnetic field regime, the longitudinal two-spin-order term does not evolve under the influence of the internal Hamiltonian. Therefore the amplitude of this term, a1(τ), during the pump probe delay will build up according to the chemical evolution of the system and decay due to NMR relaxation. If we assume that the magnetically-labelled dihydride is the only product formed and we introduce the NMR relaxation rate R1,ZQ, the amplitude of the longitudinal term as a function of time, a1(τ), can be described by the differential equation in eqn (13), where the concentration of the intermediate, f(τ), is normalised by the concentration at τ = 0, f0.
da1(τ)/dτ = kf(τ)/f0 − R1,ZQa1(τ) = k![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−kτ) − R1,ZQa1(τ) exp(−kτ) − R1,ZQa1(τ) | (13) |
The solution to eqn (13) for the initial condition a1(τ) = 0 is given in eqn (14), where we define an effective rate constant that includes both the rate of formation of the product, k, and the rate of relaxation of the p-H2 hyperpolarisation,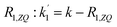 .
.
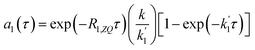 | (14) |
If the relaxation rate is much faster than the rate constant (R1,ZQ ≫ k), this term will tend to zero and no hyperpolarised signal will be observed. However, if we assume that hyperpolarisation is observable, i.e. that the relaxation rate is slower than or comparable to the rate constant (R1,ZQ ≲ k), the amplitude a1 will exhibit an initial exponential growth, with a characteristic rate of 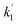 , and an overall exponential decay with a characteristic rate equal to R1,ZQ.
, and an overall exponential decay with a characteristic rate equal to R1,ZQ.
The amplitude of the longitudinal term (a1) should not be considered independently of the zero-quantum coherences, because in the NMR experiment we observe the difference between the amplitude of 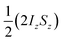 , a1, and a2, the amplitude of ZQx. That is, we observe A1(τ) ∝ [a1(τ) − a2(τ)] and A2(τ) ∝ a3(τ) (as defined in eqn (10a)–(10c)). For the AX spin system, we can write down the following set of coupled differential equations for the amplitudes of the zero-quantum coherences, ZQx(a2) and ZQy(a3), where R2,ZQ is the effective NMR relaxation rate for these coherences. Here we have used the same pseudo-first order kinetic model with rate constant k to describe the formation of the magnetically-labelled dihydride.
, a1, and a2, the amplitude of ZQx. That is, we observe A1(τ) ∝ [a1(τ) − a2(τ)] and A2(τ) ∝ a3(τ) (as defined in eqn (10a)–(10c)). For the AX spin system, we can write down the following set of coupled differential equations for the amplitudes of the zero-quantum coherences, ZQx(a2) and ZQy(a3), where R2,ZQ is the effective NMR relaxation rate for these coherences. Here we have used the same pseudo-first order kinetic model with rate constant k to describe the formation of the magnetically-labelled dihydride.
da2(τ)/dτ = k![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−kτ) − R2,ZQa2(τ) + δωa3(τ) exp(−kτ) − R2,ZQa2(τ) + δωa3(τ) | (15a) |
| da3(τ)/dτ = −δωa2(τ) − R2,ZQa3(τ) | (15b) |
Applying the boundary conditions a2(0) = 0 and a3(0) = 0, and solving for the amplitudes, we obtain the expressions in eqn (16a) and (16b). We have introduced an effective rate constant: 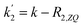 , which mimics that of
, which mimics that of 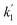 for the longitudinal terms, and a dephasing parameter,
for the longitudinal terms, and a dephasing parameter, 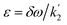 , to simplify the result and aid in the analysis. This dephasing parameter quantifies the extent of interference between the chemical and magnetic evolution and has units of radians. If the chemical evolution is very fast compared to the magnetic evolution (k ≫ δω), the dephasing parameter will be negligible and no interference will occur. However, if the chemical and magnetic evolution proceeds on the same timescale, the dephasing parameter will play a significant role in the observed evolution of the NMR signals.
, to simplify the result and aid in the analysis. This dephasing parameter quantifies the extent of interference between the chemical and magnetic evolution and has units of radians. If the chemical evolution is very fast compared to the magnetic evolution (k ≫ δω), the dephasing parameter will be negligible and no interference will occur. However, if the chemical and magnetic evolution proceeds on the same timescale, the dephasing parameter will play a significant role in the observed evolution of the NMR signals.
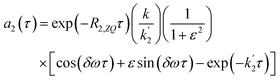 | (16a) |
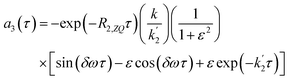 | (16b) |
As was the case with the longitudinal term, both amplitudes, a2 and a3, will tend to zero if the effective relaxation rate, R2,ZQ, is much faster than the rate constant, k. If the relaxation rate is less than, or comparable to, the rate constant (R2,ZQ ≲ k), the maximum amplitude of the zero-quantum coherences (a2 and a3) will depend on the ratio of the chemical shift difference and the rate constant (i.e. the dephasing parameter, ε). In the following discussion we will assume that both the longitudinal and transverse ZQ relaxation rates, R1,ZQ and R2,ZQ, are sufficiently slow for hyperpolarisation to be observed 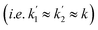 .
.
(B) Identification of kinetic regimes: fast, intermediate, and slow
In order to understand the physical meaning of the amplitudes defined in eqn (14) and eqn (16a) and (16b), we need to consider the relative rate of formation of the hyperpolarised product molecules with respect to the frequency for the magnetic oscillations. This is defined quantitatively by the dephasing parameter, ε = δω/k. Fig. 2 presents a plot of the extent of the dephasing (destructive interference) of the zero-quantum coherences, ZQx and ZQy, as a function of the dephasing parameter, ε. The dephasing is calculated as the normalised root-mean-square-difference between the amplitude of the ZQy coherence (a3) calculated with and without the inclusion of the chemical evolution, i.e. from eqn (9c) and eqn (16b), respectively.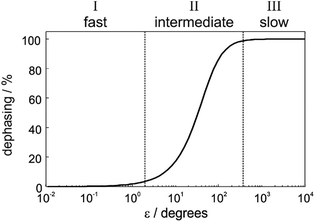 | ||
| Fig. 2 Definition of three kinetic regimes based on the extent of the dephasing of the zero-quantum coherences due to interference between the formation of the product molecules and the oscillations associated with the coherent magnetic evolution of the system. Dephasing is calculated as the root-mean-squared-difference between the amplitude a3 calculated from eqn (16b) (including chemical and magnetic evolution) and from eqn (9d) (including magnetic evolution only). | ||
In Fig. 2, we identify three distinct kinetic regimes based on the extent of the dephasing. These are: the fast regime (k ≫ δω, ε < 1°), where there is no significant dephasing, the slow regime (k ≪ δω, ε > 360°), where there is complete dephasing and the intermediate regime, where k and δω are of a similar order of magnitude (k ∼ δω, 1° < ε < 360°) and there is partial but incomplete dephasing. The behaviour of the observed NMR signals as a function of the pump-probe delay within these three regimes is exemplified by the curves in Fig. 3. The top plots present the amplitude A1 (defined in eqn (10a)), which is proportional to the difference between the amplitudes of the longitudinal two-spin-order term, a1, and the ZQx coherence, a2. The bottom plots present the amplitude A2 (defined in eqn (10b)), which is proportional to the amplitude of the ZQy coherence, a3. The green curves reflect both the chemical and magnetic evolution of the system and are calculated from eqn (10a)–(10c), (14) and (16a) and (16b), with ε = 1°, ε = 20°, ε = 90°, and ε = 720°. The black reference curves correspond to the pure magnetic evolution case for the fast and intermediate regimes (calculated from eqn (9a)–(9d)) and the pure chemical evolution case in the slow regime (calculated from eqn (14) with the assumption of complete dephasing such that a2 = a3 = 0).
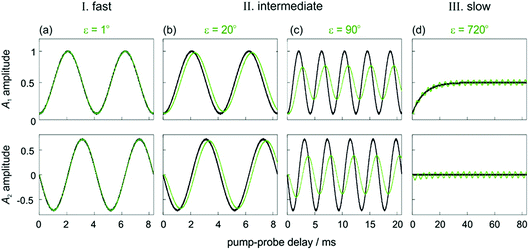 | ||
| Fig. 3 Amplitudes of the two observable components of the density matrix, A1 (top) and A2 (bottom), as defined in eqn (10a)–(10c) for an AX spin system with δω = 2π* 240 Hz and θ1 = 45°. Green curves are calculated from eqn (10a)–(10c), (14) and (16a) and (16b) for different values of ε that exemplify the three kinetic regimes: (a) ε = 1° (fast), (b) ε = 20° and (c) ε = 90° (intermediate) and (d) ε = 720° (slow). The black curves correspond to pure magnetic evolution (fast and intermediate cases, calculated from eqn (10a)–(10c) and (9a)–(9d) and pure chemical evolution (slow regime, calculated from eqn (10a)–(10c) and (14), assuming complete ZQ dephasing such that a2 = a3 = 0). Relaxation was neglected in all cases (R1,ZQ = R2,ZQ = 0). | ||
In the fast regime, the rate of formation of the product molecules is much faster than the frequency of the magnetic oscillations (k ≫ δω, ε → 0) and eqn (16a) and (16b) reduces to the expressions for coherent magnetic evolution from eqn (9a)–(9d). Therefore, for very small values of the dephasing parameter (ε < 1°), the dephasing percentage in Fig. 2 tends to zero and the evolution of the NMR signal amplitudes during the pump-probe delay (ε = 1°, green in Fig. 3a) is virtually indistinguishable from the case of no chemical evolution (black in Fig. 3a). In this limit, no kinetic information is directly available. Only a lower bound on the value of k can be obtained.
In the slow regime, the rate of formation of the product molecules is much slower than the frequency of the magnetic oscillations and the dephasing parameter tends to infinity (k ≪ δω, ε → ∞). As a consequence, significant dephasing of the zero-quantum coherences occurs and their amplitudes tend to zero. This is demonstrated in Fig. 3d for a dephasing parameter of ε = 720°. In this case, the A1 term (green curve) tends to the limit where the magnetic evolution can be neglected and only the longitudinal two-spin-order term is observed (black curve). In this regime, the rate constant can be extracted from a series of 1D pump-probe 1H NMR spectra, acquired with a single rf pulse of θ1 = 45°, and where the hydride amplitudes as a function of the pump-probe delay are fitted to eqn (14).
(C) Intermediate kinetic regime
In the intermediate regime, where k and δω are of a similar order of magnitude, 1° < ε < 360°, there will be partial dephasing of the zero-quantum coherences, which can be analysed to determine k. Interestingly, even at times that are long compared to the time taken to consume 95% of the intermediate, τ ≫ 3/k, the evolution of the amplitudes of the zero-quantum coherences will contain information about the rate constant via the dephasing parameter, ε. Consider the two cases in the intermediate regime illustrated in Fig. 3b and c. In Fig. 3b, where ε = 20°, the evolution of the amplitudes during the pump-probe delay (green) is very similar to the limiting case of pure magnetic evolution (black). The difference between the two appears to be a small phase shift. By contrast, for a larger value of the dephasing parameter (ε = 90°, Fig. 3c) the amplitudes (green) deviate much more significantly from the limiting case of pure magnetic evolution (black). Not only is there a significant phase shift of the oscillations but the envelope of the oscillations is also significantly perturbed from the reference case.To understand the limiting case where ε is very small but non-zero (0 < ε ≪ 90°) we make the following approximations (neglecting all terms of order ≥ ε2):
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ε ≈ ε, ε ≈ ε, | (17a) |
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ε ≈ 1, ε ≈ 1, | (17b) |
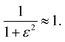 | (17c) |
Substituting these approximations into eqn (16a) and (16b) we obtain the following:
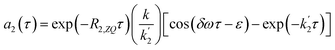 | (18a) |
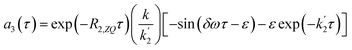 | (18b) |
According to eqn (18a) and (18b), at very short times 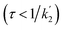 the form of the curves will deviate from pure sine and cosine oscillations due to the exponential decay terms. However, even at times that are long compared to the inverse of the effective rate constant
the form of the curves will deviate from pure sine and cosine oscillations due to the exponential decay terms. However, even at times that are long compared to the inverse of the effective rate constant 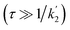 , the evolution of the amplitudes will still contain information about the rate of formation of the product via an apparent phase shift by ε in the sine and cosine oscillations, the observation of which is limited experimentally only by NMR relaxation. This is in agreement with the apparent phase shift observed in the oscillations in Fig. 3b. Therefore, the dephasing parameter can be directly obtained from the oscillations by fitting them to phase-shifted sine and cosine functions (eqn (18a) and (18b)). The dephasing parameter can then be used to calculate k, as the difference in chemical shift is easily determined with a high degree of accuracy from a 1D NMR spectrum. It is important to note that this straight-forward analysis can only be applied in the limit where ε ≪ 90°. For larger dephasing parameters, as illustrated in Fig. 3c for ε = 90°, the signal amplitude curves will need to be fit to the full expressions in eqn (14) and (16a), (16b) in order to determine k.
, the evolution of the amplitudes will still contain information about the rate of formation of the product via an apparent phase shift by ε in the sine and cosine oscillations, the observation of which is limited experimentally only by NMR relaxation. This is in agreement with the apparent phase shift observed in the oscillations in Fig. 3b. Therefore, the dephasing parameter can be directly obtained from the oscillations by fitting them to phase-shifted sine and cosine functions (eqn (18a) and (18b)). The dephasing parameter can then be used to calculate k, as the difference in chemical shift is easily determined with a high degree of accuracy from a 1D NMR spectrum. It is important to note that this straight-forward analysis can only be applied in the limit where ε ≪ 90°. For larger dephasing parameters, as illustrated in Fig. 3c for ε = 90°, the signal amplitude curves will need to be fit to the full expressions in eqn (14) and (16a), (16b) in order to determine k.
In the intermediate regime, our ability to extract quantitative information about the rate of reaction will depend on the size of the phase shift (i.e. the value of ε) and the accuracy with which it can be measured experimentally. The measurement accuracy will depend on several factors including: (a) how well we can define the delay between the 10 ns laser pulse and the μs rf pulse, (b) the duration of the rf pulse, (c) the signal-to-noise (SNR) of the NMR spectra, (d) the reproducibility of the experiment, and (e) the lifetime of the ZQ coherences.
The photochemical pump, NMR probe experiment has been shown previously to be highly reproducible9–11 and the use of p-H2 hyperpolarisation provides high SNR values. Furthermore, while single-shot experiments are desirable, signal averaging could be used to boost SNR in the usual way, if necessary. Therefore, the fundamental limit on the maximum reaction rates that can be quantified using this approach arises from the size of the difference in chemical shift (δω) between the p-H2-derived protons in the product molecule, the accuracy with which the pump-probe delay can be defined, and the duration of the rf pulse. The time between sending the instruction for the application of the laser pulse and the actual firing of the laser is controlled by a digital delay generator. Since this delay is incorporated into the NMR pulse sequence, the accuracy of the timing of the laser shot is determined by the digital clock of the spectrometer, which has a period of 200 ns in our instrument. Thus the largest source of uncertainty in τ arises from the duration of the rf pulse, which is 13.5 μs for θ1 = 90° using our experimental set-up. This value can be decreased through the use of a higher-power rf probe and tip angles of θ1 < 90°. However, the minimum achievable rf pulse length is likely to be on the order of 1 μs. Therefore, the reaction rates accessible to this approach are k < 106, where the precise limit will also depend on the size of δω. The difference in chemical shift is dependent on the identity of the product molecule, but also on experimental conditions such as solvent, temperature and magnetic field strength. Of these, magnetic field strength is the most significant as the difference in chemical shift in Hz scales linearly with field.
(D) Examples: iridium and ruthenium dihydride complexes
Consider the three ruthenium dihydride complexes in Scheme 1: RuH2(CO)2(dpae) 1, RuH2(CO)(PPh3)(dppp) 2, and cis-RuH2(dppe)2(H)23 (dpae = Ph2AsCH2CH2AsPh2, dppe = Ph2PCH2CH2PPh2, and dppp = Ph2PCH2CH2CH2PPh2). These complexes were used to exemplify the laser-pump, NMR probe method in a previous publication.9 In 1, the hydrides form an AX spin system, while in 2 they form an AXY system with the 31P ligated trans to one of the hydrides. Note, we can neglect the effect of the mutually-trans31P nuclei in this case because they couple similarly to each of the hydrides and so do not contribute significantly to NMR signal evolution during the pump-probe delay.9 By applying broadband 31P decoupling during the pump-probe delay and acquisition, the hydrides in 2 can be reduced to a simple AX spin system. Therefore the 1H pump-probe NMR spectra of 1 and 2 can be analysed using the procedures presented above. By contrast, the hydrides in 3 are chemically equivalent but magnetically inequivalent, forming an AA′XX′ spin system38,39 with the pair of 31P nuclei coordinated to the metal trans to the hydrides. In this case, it is the difference in coupling between the trans and cis2J(1H,31P) couplings, ΔJ = Jtrans − Jcis = JAX − JA′X = JA′X′ − JAX′, that breaks the symmetry of the hydrides and allows for hyperpolarisation to be observed.10 Equations describing the evolution of the amplitudes of the four possible magnetic states during the pump-probe delay for an AA′XX′ system with JXX′ ≪ 1 Hz are derived in the ESI.† These expressions build on the analytical solutions for the magnetic evolution of this spin system derived in ref. 9. Interestingly, the effect of the chemical evolution is comparable to that for the AX spin case, where for values of ε that are small but non-zero (0 < ε ≪ 90°), the effect of the chemical evolution is to introduce a phase shift into the sine and cosine oscillations of the ZQ coherences (eqn (S4)†). All of the same measurement considerations apply as detailed above for the AX case; however, for chemically equivalent hydrides the dephasing parameter is defined as: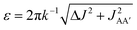 , where the difference in frequency is provided by the J coupling network and is dominated by ΔJ.
, where the difference in frequency is provided by the J coupling network and is dominated by ΔJ.
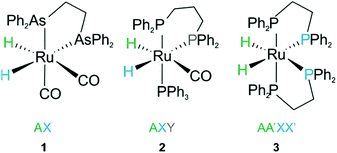 | ||
| Scheme 1 Ruthenium dihydride complexes investigated by laser-pump, NMR probe spectroscopy in ref. 9 | ||
In the experiments presented in ref. 9, the three complexes in Scheme 1 were assumed to undergo photochemical loss of H2 on a picosecond to nanosecond timescale (i.e. during the 10 ns laser pulse), before being reformed by reaction with hydrogen. This assumption was based on time-resolved studies of 3 and other analogous Ru dihydride complexes in the literature,34–37 as well as the time-resolved UV measurements of 2 reported in the ESI of ref. 9. The kinetics of the reaction of 2 and 3 with H2, following photochemical loss of H2, have been determined using time-resolved absorption spectroscopy; the rates for recombination under 3 atm H2 at 295 K are 6.2 × 105 s−1 (ref. 9) and 2.1 × 105 s−1 (ref. 35), respectively. Within the context of the analysis presented here, these rates correspond to dephasing parameters of ε = δω/k = 0.0029 (0.2°) and 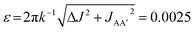 (0.1°) (in C6D6, at 3 atm p-H2, 295 K and 14 T) for 2 and 3, respectively. Both of these values for the dephasing parameter are well below the expected detection limit of this method. This is consistent with the fact that no phase shift was observed in the oscillations of the measured signal amplitudes for 2 and 3 during the pump-probe delay.9
(0.1°) (in C6D6, at 3 atm p-H2, 295 K and 14 T) for 2 and 3, respectively. Both of these values for the dephasing parameter are well below the expected detection limit of this method. This is consistent with the fact that no phase shift was observed in the oscillations of the measured signal amplitudes for 2 and 3 during the pump-probe delay.9
No kinetic measurements of the rate of H2 addition for 1 are available. However, we can use the pump-probe data presented in Fig. 4 (taken from ref. 9) to determine a rough lower bound for the rate of H2 addition for this complex at 3 atm p-H2 and 295 K. In these experiments no phase shift is observed.
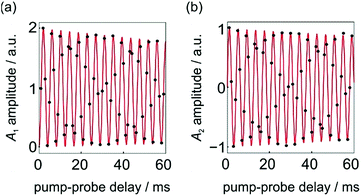 | ||
| Fig. 4 Integrated hydride signal intensities from a series of 1D 1H NMR pump-probe spectra with 0 ≤ τ ≤ 60 ms and θ1 = 45°. (a) A1 and (b) A2 amplitudes were calculated according to the method reported in ref. 9. The black dots are experimental points and the red lines are the lines of best fit to the expressions for A1 and A2 in eqn (10a)–(10c), where a1, a2 and a3 are defined by eqn (9a)–(9d) and δω = 2π* 241 Hz. All data was originally published in ref. 9. | ||
The fit of the experimental data (black points) to sine and cosine curves without any phase shift (red lines) is excellent. This implies that the dephasing parameter, ε, is below the detection limit in this case. If we assume a detection limit of ε > 5° (0.09 rad), we would expect rates of k < δω/ε = (2π* 241 Hz)/0.09 rad = 2 × 104 s−1 to give rise to a detectable phase shift, where δω/2π = 241 Hz is the chemical shift difference for the hydrides of 1 in C6D6 at 14 T. Note, here we neglect the relaxation rate, R2,ZQ = 3.8 s−1, because it is much slower than both the frequency of the oscillations and the rate of oxidative addition.9 Therefore, the absence of an observed phase shift in the data presented in Fig. 4 suggests that the rate of oxidative addition of p-H2 to form 1 following the photochemical loss of H2 (at 295 K and under 3 atm p-H2) is bound by k > 2 × 104 s−1.
Laser-pump, NMR probe spectroscopy has also been used previously to measure the rate of reaction of IrI(CO)(PPh3)2 with p-H2 to form Ir(H)2I(CO)(PPh3)2.11 The difference in chemical shift between the hydrides in Ir(H)2I(CO)(PPh3)2 is 3840 Hz (6.4 ppm) at 14 T and 295 K. By contrast, the rate of H2 addition is on the order of 2–5 s−1 over the range of H2 pressures studied. These rates correspond to a dephasing parameter of ε ∼ 3 × 105 degrees. Therefore this is within the slow regime, as defined in Fig. 2, and we expect complete dephasing of the ZQ coherences to occur for this system. Indeed, no oscillations associated with the ZQ coherences were observed in these experiments.11
In summary, ruthenium complexes examined by pump-probe NMR spectroscopy in the literature have rates of hydrogen addition that fall into the fast regime, while the rate of addition of H2 to the iridium complex reported in ref. 11 is within the slow regime. We anticipate that the most promising route to observing the predicted phase-shift behaviour in the intermediate regime will be to explore ruthenium complexes which add H2 on a slower timescale (k < 104) and where the difference in chemical shift between the hydrides is very large (>5 ppm).
Conclusions
In this work, we explored the potential for photochemical pump, NMR probe spectroscopy with para-hydrogen hyperpolarisation to be used for the quantitative measurements of reaction kinetics for a range of rates extending down to micro and millisecond timescales. We developed a first-principles analysis that combines the coherent magnetic evolution of the NMR signals for an AX spin system with the chemical evolution of the system during the pump-probe delay. Assuming a pseudo-first-order reaction with p-H2 to form the hyperpolarised product molecules, we have derived expressions for the time-dependent evolution of the two components of the hyperpolarised 1H NMR response during the pump-probe delay. Based on these results, we identify three distinct kinetic regimes that can be explored by our time-resolved NMR method: fast, intermediate and slow. These regimes are defined by the relative rate of reaction compared to the rate of the magnetic evolution of the p-H2-derived NMR signals. This relationship is quantified through a NMR dephasing parameter, ε, that is defined as the ratio of the oscillation frequency that characterises the magnetic evolution, δω, to the rate of formation of the product molecule, k. For an AX spin system δω is the difference in chemical shift between the pair of p-H2 derived protons in the product molecule. For an AA′XX′ spin system,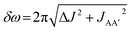 , where ΔJ = JAX − JA′X = JA′X′ − JAX′.
, where ΔJ = JAX − JA′X = JA′X′ − JAX′.
In the fast regime the rate of formation of the product is much faster than the rate of magnetic evolution during the pump-probe delay (k ≫ δω). Therefore the dephasing parameter tends to zero and the rate of reaction, k, cannot be determined quantitatively from the evolution of the NMR signals. Only an upper bound for this rate can be established in this regime.
In the slow regime, the rate of formation of the product is much slower than the magnetic evolution during the pump-probe delay (k ≪ δω). As a result, the dephasing parameter tends to infinity and the NMR signal intensity oscillations associated with the evolution of zero-quantum coherences originating from p-H2 destructively interfere and are not observed. In this regime, the evolution of the observed 1H NMR signals during the pump-probe delay reflects the chemical evolution of the system as well as NMR relaxation. The evolution of the NMR signals in this regime are analogous to the traditional asynchronous PHIP approach, where thermally-activated reactions are used to build-up the population of product molecules containing a pair of p-H2-derived protons over a period of seconds.
In the intermediate regime, the rate of formation of the product is similar to the frequency of oscillation of the magnetic states during the pump probe delay (k ∼ δω). In this case, we predict that a characteristic partial dephasing of the NMR signal oscillations will be observed. In the limit where the dephasing parameter is small but non-zero, this dephasing is expected to lead to an apparent phase shift in the magnetic oscillations that can be used to obtain quantitative information about the rate of hydrogen addition. Importantly, this kinetic information can be obtained even at pump-probe times that are long compared to the inverse of the reaction rate, τ ≫ k−1. The persistence of this phase shift is only limited by the relaxation time of the associated zero-quantum coherences and the lifetime of the product species. For a cascading series of reactions involving p-H2-derived protons, which leads to the formation of an alkene as an example, these effects would be relayed through intermediate stages to the product. In this case, more advanced kinetic modelling would be required to predict and analyse the observed NMR signals for the p-H2-derived protons in the product and any long-lived intermediates in order to extract quantitative mechanistic information.
We have identified the size of the NMR dephasing parameter, which is determined by the size of the difference in frequency between the p-H2-derived protons in the product molecule, and the duration of the rf excitation pulse to be the current limiting factors on the reaction timescales accessible to this technique. Assuming a minimum rf duration of 1 μs and a sufficiently large dephasing parameter (e.g. ε ≥ 5°), the maximum observable rate is on the order of k = 106 s−1. This means that we expect pump-probe NMR spectroscopy with para-hydrogen hyperpolarisation to be a complementary method to time-resolved UV or IR spectroscopy for the study of chemical evolutions on this timescale, while simultaneously offering significant information on the chemical identity of the product. We also note that a range of NMR methods have been developed to create molecules that are characterised by a hyperpolarised singlet state similar to p-H2.40–45 Therefore we expect this pump-probe NMR method to be applicable in the future to a much wider range of chemical systems than might initially be anticipated.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
We are grateful to the EPSRC for support (grant EP/K022792/1).References
- B. E. Mann, in Encyclopedia of Nuclear Magnetic Resonance, ed. D. M. Grant and R. K. Harris, Wiley, Chichester, UK, 1996, p. 3400 Search PubMed.
- C. L. Perrin and T. J. Dwyer, Chem. Rev., 1990, 90, 935–967 CrossRef CAS.
- G. E. Wagner, P. Sakhaii, W. Bermel and K. Zangger, Chem. Commun., 2013, 49, 3155–3157 RSC.
- J. Balbach, V. Forge, W. S. Lau, N. A. J. vanNuland, K. Brew and C. M. Dobson, Science, 1996, 274, 1161–1163 CrossRef CAS.
- E. Rennella, T. Cutuil, P. Schanda, I. Ayala, V. Forge and B. Brutscher, J. Am. Chem. Soc., 2012, 134, 8066–8069 CrossRef CAS.
- M. Adler and H. A. Scheraga, Biochemistry, 1988, 27, 2471–2480 CrossRef CAS.
- K. Yamasaki, Y. Ohara, M. Hasegawa, H. Tanaka, T. Yamasaki, T. Wakuda, M. Okada and T. Kohzuma, Anal. Chem., 2013, 85, 9439–9443 CrossRef CAS.
- J. Bart, A. J. Kolkman, A. J. Oosthoek-de Vries, K. Koch, P. J. Nieuwland, H. Janssen, P. J. M. van Bentum, K. A. M. Ampt, F. P. J. T. Rutjes, S. S. Wijmenga, H. Gardeniers and A. P. M. Kentgens, J. Am. Chem. Soc., 2009, 131, 5014–5015 CrossRef CAS.
- M. E. Halse, B. Procacci, S. L. Henshaw, R. N. Perutz and S. B. Duckett, J. Magn. Reson., 2017, 278, 25–38 CrossRef CAS.
- O. Torres, B. Procacci, M. E. Halse, R. W. Adams, D. Blazina, S. B. Duckett, B. Eguillor, R. A. Green, R. N. Perutz and D. C. Williamson, J. Am. Chem. Soc., 2014, 136, 10124–10131 CrossRef CAS.
- B. Procacci, P. M. Aguiar, M. E. Halse, R. N. Perutz and S. B. Duckett, Chem. Sci., 2016, 7, 7087–7093 RSC.
- A. N. Pravdivtsev, A. V. Yurkovskaya, P. A. Petrov and H. M. Vieth, Phys. Chem. Chem. Phys., 2017, 19, 25961–25969 RSC.
- A. H. Zewail, Angew. Chem., Int. Ed., 2000, 39, 2587–2631 Search PubMed.
- R. Zhang and M. Newcomb, Acc. Chem. Res., 2008, 41, 468–477 CrossRef CAS.
- J. M. Butler, M. W. George, J. R. Schoonover, D. M. Dattelbaum and T. J. Meyer, Coord. Chem. Rev., 2007, 251, 492–514 CrossRef CAS.
- P. Kukura, D. W. McCamant and R. A. Mathies, in Annu. Rev. Phys. Chem., 2007, vol. 58, pp. 461–488 Search PubMed.
- E. T. J. Nibbering, H. Fidder and E. Pines, in Annu. Rev. Phys. Chem., 2005, vol. 56, pp. 337–367 Search PubMed.
- W. R. Browne and J. J. McGarvey, Coord. Chem. Rev., 2007, 251, 454–473 CrossRef CAS.
- S. Weber, eMagRes, 2017, 6, 255–269 CAS.
- M. D. E. Forbes, L. E. Jarocha, S. Sim and V. F. Tarasov, in Adv. Phys. Org. Chem., ed. I. H. Williams and N. H. Williams, 2013, vol. 47, pp. 1–83 Search PubMed.
- R. Bittl, A. Vanderest, A. Kamlowski, W. Lubitz and D. Stehlik, Chem. Phys. Lett., 1994, 226, 349–358 CrossRef CAS.
- S. M. Harper, L. C. Neil, I. J. Day, P. J. Hore and K. H. Gardner, J. Am. Chem. Soc., 2004, 126, 3390–3391 CrossRef CAS PubMed.
- A. S. Kiryutin, O. B. Morozova, L. T. Kuhn, A. V. Yurkovskaya and P. J. Hore, J. Phys. Chem. B, 2007, 111, 11221–11227 CrossRef CAS.
- K. H. Mok, T. Nagashima, I. J. Day, J. A. Jones, C. J. V. Jones, C. M. Dobson and P. J. Hore, J. Am. Chem. Soc., 2003, 125, 12484–12492 CrossRef CAS.
- S. Perrier, E. Mugeniwabagara, A. Kirsch-De Mesmaeker, P. J. Hore and M. Luhmer, J. Am. Chem. Soc., 2009, 131, 12458–12465 CrossRef CAS.
- C. R. Bowers and D. P. Weitekamp, Phys. Rev. Lett., 1986, 57, 2645–2648 CrossRef CAS.
- C. R. Bowers and D. P. Weitekamp, J. Am. Chem. Soc., 1987, 109, 5541–5542 CrossRef CAS.
- T. C. Eisenschmid, R. U. Kirss, P. P. Deutsch, S. I. Hommeltoft, R. Eisenberg, J. Bargon, R. G. Lawler and A. L. Balch, J. Am. Chem. Soc., 1987, 109, 8089–8091 CrossRef CAS.
- M. G. Pravica and D. P. Weitekamp, Chem. Phys. Lett., 1988, 145, 255–258 CrossRef CAS.
- S. B. Duckett and R. E. Mewis, Acc. Chem. Res., 2012, 45, 1247–1257 CrossRef CAS.
- R. A. Green, R. W. Adams, S.B. Duckett, R. E. Mewis, D. C. Williamson and G. G. R. Green, Prog. Nucl. Magn. Reson. Spectrosc., 2012, 67, 1–48 CrossRef CAS.
- J. Natterer and J. Bargon, Prog. Nucl. Magn. Reson. Spectrosc., 1997, 31, 293–315 CrossRef.
- D. Blazina, S. B. Duckett, T. K. Halstead, C. M. Kozak, R. J. K. Taylor, M. S. Anwar, J. A. Jones and H. A. Carteret, Magn. Reson. Chem., 2005, 43, 200–208 CrossRef CAS.
- R. Osman, R. N. Perutz, A. D. Rooney and A. J. Langley, J. Phys. Chem., 1994, 98, 3562–3563 CrossRef CAS.
- L. Cronin, M. C. Nicasio, R. N. Perutz, R. G. Peters, D. M. Roddick and M. K. Whittlesey, J. Am. Chem. Soc., 1995, 117, 10047–10054 CrossRef CAS.
- M. Colombo, M. W. George, J. N. Moore, D. I. Pattison, R. N. Perutz, I. G. Virrels and T. Q. Ye, J. Chem. Soc., Dalton Trans., 1997, 2857–2859, 10.1039/a704484d.
- M. V. Campian, R. N. Perutz, B. Procacci, R. J. Thatcher, O. Torres and A. C. Whitwood, J. Am. Chem. Soc., 2012, 134, 3480–3497 CrossRef CAS.
- J. A. Pople, W. G. Schneider and H. J. Bernstein, Can. J. Chem., 1957, 35, 1060–1072 CrossRef CAS.
- H. Gunther, Angew. Chem., Int. Ed., 1972, 11, 861–874 CrossRef.
- P. Ahuja, R. Sarkar, S. Jannin, P. R. Vasos and G. Bodenhausen, Chem. Commun., 2010, 46, 8192–8194 RSC.
- P. R. Vasos, A. Comment, R. Sarkar, P. Ahuja, S. Jannin, J. P. Ansermet, J. A. Konter, P. Hautle, B. van den Brandt and G. Bodenhausen, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 18469–18473 CrossRef CAS.
- M. H. Levitt, Annu. Rev. Phys. Chem., 2012, 63, 89–105 CrossRef CAS.
- Y. Feng, T. Theis, T.-L. Wu, K. Claytor and W. S. Warren, J. Chem. Phys., 2014, 141, 134307 CrossRef.
- W. S. Warren, E. Jenista, R. T. Branca and X. Chen, Science, 2009, 323, 1711–1714 CrossRef CAS.
- S. S. Roy, P. J. Rayner, P. Norcott, G. G. R. Green and S. B. Duckett, Phys. Chem. Chem. Phys., 2016, 18, 24905–24911 RSC.
Footnote |
| † Electronic supplementary information (ESI) available: Analytical solutions for an AA′XX′ spin system. See DOI: 10.1039/c9fd00039a |
| This journal is © The Royal Society of Chemistry 2019 |