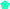Open Access Article
Open Access ArticleMicrophysics of the aqueous bulk counters the water activity driven rate acceleration of bromide oxidation by ozone from 289–245 K†
Jacinta
Edebeli
ab,
Markus
Ammann
 a and
Thorsten
Bartels-Rausch
a and
Thorsten
Bartels-Rausch
 *a
*a
aLaboratory of Environmental Chemistry, Paul Scherrer Institut, Villigen PSI, Switzerland. E-mail: thorsten.bartels-rausch@psi.ch
bSwiss Federal Institute of Technology, ETH Zurich, Zurich, Switzerland
First published on 10th December 2018
Abstract
The reaction of ozone with bromide is an initiation process in bromine activation resulting in the formation of reactive bromine species with impacts on the fate of compounds in the lower atmosphere. Environmental halide sources often contain organics, which are known to influence aqueous bulk reactivity. Here, we present a study investigating the temperature dependence of bromide oxidation by ozone using a coated wall flow tube reactor coated with an aqueous mixture of citric acid, as a proxy for oxidized secondary organic matter, and sodium bromide. Using the resistor model formulation, we quantify changes in the properties of the aqueous bulk relevant for the observed reactivity. The reactive uptake coefficient decreased from 2 × 10−6 at 289 K to 0.5 × 10−6 at 245 K. Our analysis indicates that the humidity-driven increase in concentration with a corresponding increase in the pseudo-first order reaction rate was countered by the colligative change in ozone solubility and the effect of the organic fraction via increased viscosity and decreased diffusivity of ozone as the temperature decreased. From our parameterization, we provide an extension of the temperature dependence of the reaction rate coefficients driving the oxidation of bromide, and assess the temperature-dependent salting effects of citric acid on ozone solubility. This study shows the effects of the organic species at relatively mild temperatures, between the freezing point and eutectic temperature of sea as is typical for the Earth's cryosphere. Thus, this study may be relevant for atmospheric models at different scales describing halogen activation in the marine boundary layer or free troposphere including matrices such as sea-spray aerosol and brine in sea ice, snow, and around mid-latitude salt lakes.
Environmental significanceTropospheric halide oxidation by ozone is a prevalent process in regions of the world containing halide sources such as polar regions and around salt lakes. This process has significant implications on the tropospheric ozone budget and on the fate of compounds such as elemental mercury in the marine boundary layer. This study investigated the oxidation of bromide by ozone in a medium containing an organic species representative of secondary organic matter from 16 °C to −25 °C. Our results indicate that the presence of the organic species counters the rate acceleration associated with decreasing water activity with decreasing temperature due to effects on the viscosity of the medium and solubility of ozone in the medium. |
Introduction
The reaction of ozone (O3) with halides producing reactive halogen species (RHS) in the troposphere is an important chemical process with implications for the oxidation capacity of the atmosphere and the fate of compounds in the atmosphere.1–3 Of importance is the reaction between RHS and gas phase mercury resulting in increased mercury deposition, which has implications on human and ecosystem health.1,2,4 While all halides may be involved, with respect to sea ice and sea spray aerosols, bromide may dominate due to its relative abundance and high reactivity compared to other halides.1,3,5Studies show that aerosols containing halides such as sea spray aerosols significantly contribute to global halogen chemistry via multiphase chemistry on and within aerosol particles.6–9 Sea-spray aerosol is also partly responsible for the salinity of surface snow3,10 resulting from scavenging and deposition along with snow fall onto polar and alpine snow packs. Field and satellite measurements have identified local, regional, and global scale effects of atmospheric halogen chemistry on O3 and on the mercury cycle.8,9 However, there are still uncertainties in the mechanism of halide oxidation by ozone especially in less understood complex sources such as aerosols or snow containing mixtures of organics and salts.6,7
While the microphysics of aqueous aerosol particles is reasonably well understood, in complex environments such as snow and sea-ice, the structural arrangement of the non-frozen aqueous phase is less obvious. It may be expected that the water activity is controlled by the presence of ice.3,5,11 The concentration of aqueous solutes in equilibrium with ice depends on temperature and follows the phase diagram of the aqueous mixtures.5,12 Below the freezing point of ice, as the temperature decreases, the water activity in solution decreases until the eutectic point is reached (Fig. 1). The activity of the solutes increases similarly to the so-called “freeze concentration effect” described by Takenaka and Watson.13 When the concentration of the solutes in the unfrozen aqueous phase exceeds the solubility limit of a solute, precipitation of that solute may occur.3 In sea-ice formation, sodium chloride (NaCl) precipitates out at a warmer temperature than bromide leading to an enrichment of bromide relative to NaCl.3Fig. 1 gives an example and shows how the equilibrium mass fraction of sodium bromide (NaBr) in aqueous solution increases during freezing.14 The environmental impact of this increase in the concentration of solutes with decreasing temperature has been discussed5 and may include the formation of products not typically formed at lower concentrations.15
 | ||
| Fig. 1 Representation of the phase diagram of a NaBr–water binary solution (lines) and of the water activity in the film of study (Purple ‘*’) as a function of water activity and temperature. The blue line denotes the solid–liquid equilibrium curve of ice; the red dot line is the weight fraction of NaBr in solution in equilibrium with ice; the grey line indicates the eutectic temperature, where NaBr crystallises.14 Water activity = relative humidity with respect to liquid water (%)/100. | ||
Investigations of the composition of sea-spray aerosol show a significant organic component, which may be up to 50% of the aerosol mass.16 The organic fraction plays a role in the properties of the aerosol, such as hygroscopic properties and viscosity.17–19 Indeed, investigations of halide oxidation in organic acid–halide mixtures indicate the effects of the organic fraction on the uptake of O3.20 These studies show that in addition to providing acidity (which catalyses the reaction), the acids may affect the prevalence of the surface reaction20 and the propensity of halide ions for the interface.21,22 Regarding the physical properties of organic containing solutions, studies show that the viscosity of organic solutions may reduce bulk reactivity by decreasing the diffusivity of the reactive solute (in this case, O3).23–25
Thus, the organic fraction of sea-spray aerosols, though not considered in atmospheric chemistry models, may impact the observed multiphase halogen activation, both during long range transport of sea spray aerosol in the troposphere and in snow or on sea-ice after deposition. Environmental ice compartments, such as sea ice and snow also contain halides and can partake in halide oxidation.26–29 Just like inorganic salts, organics may also be excluded to the brine pockets during freezing and may similarly affect the properties of the unfrozen aqueous phase in snow and environmental ice.30 These effects, in particular the influence of viscosity on reactivity, usually require rather low relative humidity as is typically found in the free troposphere. Here we focus on these effects of an organic acid on the chemical reactivity at moderate humidity as is typical for the snow covered boundary layer and the interstitial air in snow.
The reaction between O3 in the gas phase and bromide in the condensed phase of aerosols, sea ice, and snow is one initiation process for the formation of reactive bromine species. This is a multiphase reaction, which can occur in the dark, leading to the production of photo-labile bromine (Br2; R1–R5) with R2 and R3 as the rate limiting steps.31–34 Br2 produced during the night or during the polar winter may serve as a reservoir for daytime or polar spring photolytic halogen activation.4,35 Reactions R4 and R5 may also involve chloride and/or iodide leading to the production of reactive inter-halogen species (e.g. IBr, BrCl).36,37 Production of inter-halogen species, especially BrCl, may also depend on the relative abundance of the respective halides.38
Here, we focus on the reaction of bromide with ozone in the dark. Kinetic studies on bromide (Br−) oxidation by O3 indicate a multiphase process with a significant interfacial component.39–41 Aqueous bulk bromide oxidation by ozone is relatively slow with a rate coefficient of ∼258 M−1 s−1 at 298 K.32 Hunt et al. showed that the observed Br2 production resulting from this reaction system exceeded that expected from bulk aqueous production alone, and suggested a contribution from interfacial processes.39 Other studies probing possibilities of additional interfacial processes corroborate this suggestion by Hunt et al.40–43 Oldridge and Abbatt, while monitoring Br2 production, showed that the interfacial processes become significant at atmospherically relevant low ozone concentrations.40
Studies on the interfacial process indicate that this process proceeds via the formation of an adsorbed intermediate species on the surface of the observed system.39 Artiglia et al. recently observed this intermediate, the bromide ozonide, BrOOO−, and showed that it is surface active and stabilized by water molecules on the surface.41 The mechanism of formation and the role of this intermediate has also been studied by theoretical calculations.44 Gladich et al., in their theoretical study of this reaction, showed that via intersystem crossing of BrOOO− from the singlet state to triplet state, this Br− oxidation process can proceed successfully in the dark.44
Often, studies investigate halide oxidation in salt solutions only. In addition, though research has concentrated mostly on halogen chemistry with O3 in polar regions, similar halogen activation has been observed in warmer environments.40,45 Temperature influences properties such as solubility, viscosity, and reaction rates with implications on the observed reactive loss of O3.
 | (R1) |
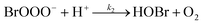 | (R2) |
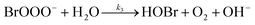 | (R3) |
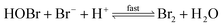 | (R4) |
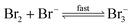 | (R5) |
Therefore, there are two objectives for the study presented herein. The first objective is to measure the uptake of O3via reaction with bromide in a mixture containing citric acid (CA) and NaBr in water, over a wide temperature (T) range (−25 °C to 16 °C). CA was chosen to be a proxy for oxidised organic material representative of aged primary or secondary organic material abundant in marine environments. Experiments were conducted using thin films (equilibrated to experimental conditions) of the mixture in a temperature-regulated coated wall flow tube setup. An essential requirement of the experimental design was to avoid freezing while staying close to the ice-liquidus line in the NaBr–water–organic ternary solution at temperatures below 0 °C (Fig. 1). This was achieved by maintaining a relative humidity of about 96% with respect to water vapour pressure over ice (RHice) in the setup at temperatures below 0 °C and a relative humidity of 96% above 0 °C (RHwater).46,47 This means that the relative humidity with respect to liquid water (RHwater) ranged from 96% at 16 °C to 75% at −25 °C.46,47 Thus, the RHwater − T space covered in this study is directly relevant for atmospheric aerosol trajectories, but also remains close, in terms of water activity, to the conditions of liquid phases in equilibrium with ice, such as within snow or sea ice. As such, it allows for covering a significant temperature range without the complications related to ice formation.
The second objective is to extensively assess the influence of temperature-induced changes in the system on the observed uptake coefficients of O3via temperature-dependent variables controlling the microphysics and kinetics.5,23,48 Using the resistor model formulation,50,51 we attempt to describe the changes in reactant concentration, diffusivity, and pH to provide information on how these potentially opposing effects influence the observed temperature-dependent O3 uptake. Development of the parameterization used in this study focuses on the properties and reactivity in the aqueous bulk.
Experimental
Materials and methods
The experimental work in this study was conducted using a temperature-regulated coated wall flow tube setup at atmospheric pressure (ESI Fig. S1†). The setup is fitted with a temperature-regulated injector for dosing humidified O3 (and other gases) into the coated flow tube. This study was conducted using sodium bromide (NaBr, Sigma Aldrich, >99.0%), citric acid monohydrate (CA, Sigma Aldrich >99.0%), and ultrapure water (18 MΩ cm).Experiments were conducted from −25 °C to 16 °C. At each temperature, a cycle between the bypass and the flow tube was repeated at least three times with an exposure length of 25 cm (exposed surface area of 94.3 cm2). Ozone concentrations were also measured at 0 cm (just outside the tube) to account for losses that were not from the coated part of the flow tube (<1%). The ozone concentration was also measured as a function of injector position, and thus length of the coated flow tube, exposed at 5 °C and −5 °C to confirm the first order kinetics for our analyses (ESI Fig. S2†). At least one independent repeat was conducted on a different day for each temperature. O3 loss was also measured at different O3 concentrations at some temperatures (0 °C, −10 °C, −20 °C, and −25 °C).
Data analyses
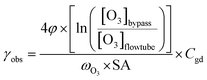 | (1) |
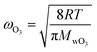 | (2) |
In this study, we assume that accommodation on the surface (preceding the surface reaction described by Γsurf and also preceding the surface to bulk transfer) is not rate limiting. We also assume that the surface to bulk transfer of O3 is not rate limiting, as justified further below. Thus, within these assumptions, the surface reaction operates independently of and parallel to diffusion and reaction in the bulk. Hence, the total uptake can be represented by the sum of the inverse resistances for diffusion and reaction in the bulk (Γbulk) and for the surface reaction (Γsurf) (eqn (3)). By themselves, Γbulk and Γsurf are reaction rates normalized to the gas kinetic collision if they would be the only limiting processes.
| γcalc = Γsurf + Γbulk, | (3) |
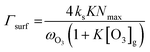 | (4) |
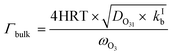 | (5) |
The reactive surface uptake (Γsurf) calculated using eqn (4)50 represents a “Langmuir–Hinshelwood-type” surface reaction mechanism,40 in which “Langmuir-type” adsorption precedes reaction. Partitioning of the reactive gas to the surface from the gas phase is described by the equilibrium constant, K, such that K × [O3]g/(1 + K × [O3]g) is the fractional surface coverage.40 Artiglia et al. have recently shown that the Langmuir equilibrium constant, K, and the maximum surface coverage, Nmax, in eqn (4) are linked to the equilibrium and maximum coverage of the reaction intermediate, a bromide ozonide, at the surface, when describing the oxidation of bromide. Here, we used the same approach and set Nmax to 1012 molecules per cm2, the saturation surface concentration of the bromide ozonide intermediate as reported by Artiglia et al. The apparent equilibrium partitioning coefficient K represents a lumped parameter describing the equilibrium between gas-phase ozone and the surface concentration of the ozonide and was set to (K = 6 × 10−13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(686/T−1)) cm3 per molecule. The surface reaction rate coefficient is denoted as ks and was set to
exp(686/T−1)) cm3 per molecule. The surface reaction rate coefficient is denoted as ks and was set to 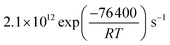 .41 We note that the transfer of O3 into the bulk aqueous phase also first involves the adsorption of O3 to the surface, in parallel to and independently of the formation of the bromide ozonide. Given the fairly low bromide concentrations, the surface is still largely dominated by water molecules. The adsorption equilibrium constant and the value of Nmax for this process (presumably driven by the dimensions of the molecule and thus likely to be in the range of 1014 molecules per cm2) are both not known. As is obvious from the present data set and also from others discussed further below, there are no indications so far that the adsorption saturation of O3 on water affects surface to bulk transfer.
.41 We note that the transfer of O3 into the bulk aqueous phase also first involves the adsorption of O3 to the surface, in parallel to and independently of the formation of the bromide ozonide. Given the fairly low bromide concentrations, the surface is still largely dominated by water molecules. The adsorption equilibrium constant and the value of Nmax for this process (presumably driven by the dimensions of the molecule and thus likely to be in the range of 1014 molecules per cm2) are both not known. As is obvious from the present data set and also from others discussed further below, there are no indications so far that the adsorption saturation of O3 on water affects surface to bulk transfer.
The parameterization for Γbulk (eqn (5)) contains temperature-dependent parameters (Henry's law constant (H), diffusivity (DO3l), the mean thermal velocity of O3 (ωO3), and the pseudo-first order bulk aqueous phase rate coefficient (kIb = kIIb × a[Br−] (a[Br−] is bromide activity)). R is the ideal gas constant. There is limited information on the aforementioned parameters and their temperature dependences. In cases where there are measurement data, these are often conducted for single solute solutions not below 0 °C. Therefore, we have parameterized these factors for ternary mixtures and lower temperatures as described below.
Results and discussion
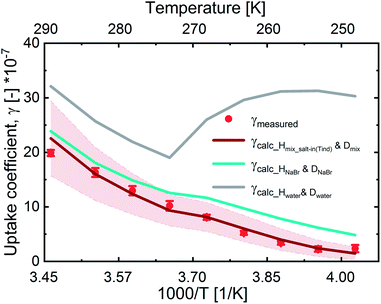
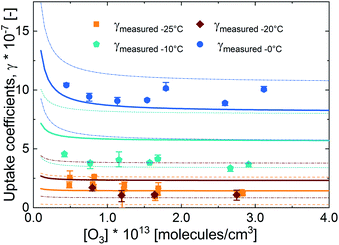
In Fig. 3, we present the measured uptake coefficients (γobs) corrected for the gas phase diffusion limitation of O3 in the in the mixed citric acid/NaBr solutions as a function of temperature from −25 °C to 16 °C. The observed temperature dependence shows that uptake coefficients of ozone decrease with decreasing temperature. This decrease slows down and plateaus below −10 °C. The observed uptake coefficients at −20 °C and −25 °C are invariant. The uptake coefficients observed in our study were about 1 × 10−7 at −20 °C with 3 × 1013 molecules per cm3 ozone concentration which compares well with that of Oldridge and Abbatt's study on acidic ternary mixtures of NaCl, NaBr, and water.40 The concentration of the condensed phase reactant in both studies is determined by the freezing point depression at temperatures below 0 °C (Fig. 1). Thus the agreement of the observed uptake coefficients for this particular run with similar experimental conditions supports the finding of the earlier study. The comparison is, however, hampered by the presence of citric acid in our study. In this study, we have extended the temperature range and in particular increased the sampling interval to investigate the multiphase reactivity in more detail. As described below, there are distinct differences in observed uptake coefficients as a function of ozone concentrations between the studies.In Fig. 3, we also present three predictions of the uptake coefficients (γcalc, lines) as a function of temperature. The runs differ in the parameterization of the diffusivity of ozone and the ozone solubility in the film. The grey line denotes a run where the diffusivity and the solubility of ozone in the reactive medium are parameterized without considering the effect of solutes on either. Such a parameterization based on the diffusivity of ozone54 and ozone solubility in water55 does not capture the observations. In particular, the marked increase in the uptake coefficient at 273 K, when water activity decreases leading to an increase in bromide activity (Fig. 1), is not evident in the experimental data. The agreement between the parameterization output and the observations is drastically improved, when accounting for the impact of bromide on the solution's properties. Finally, incorporating the effect of the organic solute as well further optimizes the parameterization result showing the importance of accurately describing the physical properties of organic–inorganic mixtures. The relevant film properties and parameters such as the viscosity and diffusivity of ozone, solubility of ozone in the film, pH of the film, and rate of the reaction in the aqueous bulk are developed further below and summarized in Table 1 and ESI Tables S1–S3.†
Aqueous bulk reaction rate coefficients
One parameter of Γbulk is the pseudo-first order rate coefficient for the reaction of ozone with bromide (kIb, eqn (5)) which is the product of the activity of bromide (aBr−) and the second-order rate coefficient (kIIb). The activities and concentrations of the bromide and citric acid solutes were calculated using the AIOMFAC model, web version 2.18.49 The mass fractions calculated using the AIOMFAC model for the binary water–bromide and water–citric acid systems, respectively, compare well with that obtained using freezing point depression data for NaBr14 and growth factors for citric acid.56 To convert the AIOMFAC output to activities based on molarity as required for the kinetics description, the density of the film was estimated using the mass fraction (of dry solute) mixing rule of the individual solutes and their solutions. The density of the citric acid solution was determined using the parameterization proposed by Lienhard et al.17 The density of the NaBr solution was estimated by extrapolating measurements of Isono.57The second order rate coefficient for the reaction of Br− with O3 (eqn (6)) is based on the mechanism presented in R1–R5, and is pH dependent.32
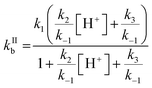 | (6) |
Estimation of the pH of the film was based on citric acid dissociation constants and activity in the film.58 The estimated pH ranged from ∼2 at 16 °C to ∼1.7 at −25 °C (Table 1). The temperature dependence of kIIb was a free tuning parameter benchmarked against the pH independent rate coefficient involving R3 but not R2 (kH2O = k1/((k−1/k3) + 1)) proposed by Liu et al., 258 M−1 s−1 at 25 °C.32 This study's parameterized kIIb at 16 °C was 388 M−1 s−1. The calculated kIIb with our own fit at 25 °C and 1 M H+ is 1.7 × 103 M−1 s−1, which is much smaller than that calculated by Liu et al. at 25 °C, 3.64 × 103 M−1 s−1.32 The pH independent rate coefficient, which was used as a benchmark, from our parameterization is 257 M−1 s−1 at 25 °C and, like that of Liu et al., is larger than that of Haruta and Takeyama (211 M−1 s−1 at 27 °C33) and Haag and Hoigné (206 M−1 s−1 at 25 °C at pH 2).59
| T [°C] | a [Br−] [M] | a [CA] [M] | pH | k IIb [M−1 s−1] | D O3l_mix [cm2 s−1] | H mix_salt-in(T-ind) [mol (L atm)−1] | O3 [#/cm−3] | k s I [s−1] | K cm3 per molecule |
|---|---|---|---|---|---|---|---|---|---|
| a T is temperature; a[Br−] is Bromide activity and a[CA] is citric acid activity (AIOMFAC calculations); kIIb is second order bulk rate coefficient; DO3l is O3 diffusivity; Hmix is ozone solubility, kIs is the surface rate coefficient, K is the surface adsorption coefficient. | |||||||||
| 16 | 0.6 | 0.09 | 2.1 | 388 | 1.20 × 10−5 | 9.94 × 10−3 | 4.31 × 1012 | 3.31 × 10−2 | 6.43 × 10−12 |
| 0 | 0.6 | 0.08 | 2.1 | 123 | 6.80 × 10−6 | 1.40 × 10−2 | 4.57 × 1012 | 5.15 × 10−3 | 7.38 × 10−12 |
| −20 | 3.8 | 0.5 | 1.7 | 25 | 5.70 × 10−7 | 1.20 × 10−2 | 4.93 × 1012 | 3.61 × 10−4 | 9.00 × 10−12 |
This comparison illustrates the uncertainty in the present second order rate coefficients and their temperature dependence, which is directly reflected in the uncertainty of kIb. Further uncertainty in the pseudo-first order rate coefficients arises from the uncertainties in the activity coefficients as derived from the AIOMFAC model, the density estimates for the film, and the pH of the film (ESI Table S4†). We have assigned about 20% (35%) uncertainty to this parameter at temperatures above 0 °C (at −20 °C) taking the aforementioned sources of errors into consideration. A 22% change in the pseudo-first order rate coefficient at 0 °C results in a 9% change in the γcalc and a 34% change in the rate coefficient at −20 °C results in a 16% change in the γcalc (Table 2).
| H O3Mix | D O3l_mix | k Ib | |||||||
|---|---|---|---|---|---|---|---|---|---|
| T [°C] | 16 | 0 | −20 | 16 | 0 | −20 | 16 | 0 | −20 |
| % Uncertainty applied | 20 | 20 | 35 | 5 | 5 | 9 | 22 | 22 | 34 |
| % Change in Γbulk | 19 | 20 | 34 | 3 | 2 | 4 | 11 | 11 | 17 |
| % Change in γcalc | 12 | 17 | 32 | 2 | 2 | 4 | 7 | 9 | 16 |
Overall, the increase in γcalc_Hwater_Dwater following the trend in bromide activity with temperature is in line with a concentration driven acceleration of apparent reaction rates observed in other bimolecular (or higher-order) reactions.5Fig. 3 shows that other factors reduce the apparent reactivity in this multiphase system, which we will discuss in the following.
Ozone solubility in the aqueous bulk
Fig. 3 shows the profound influence of composition driven equilibrium partitioning of ozone between the gas phase and the aqueous bulk on Γbulk (eqn (5)). This is a well-known effect;60,61 however, there are no data quantifying these effects at the high molarities and at the low temperatures typical for atmospheric chemistry. Here, we present and test approaches to overcome this limitation.The effect of solutes on solubility is referred to as “Salting,” which may be salting-out or salting-in and is described with the so-called “Sechenov relationship” (eqn (7)).60–64
| log(Hsolution/Hwater) = Ksas | (7) |
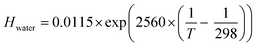 | (8) |
In the presence of NaBr the ozone gas-aqueous bulk partitioning coefficient decreases significantly by ∼30% above 0 °C with a stronger salting-out as NaBr concentrations increase with decreasing temperatures below 0 °C (Fig. 3). This is in agreement with the general trend for gases less polar than water, where inorganic salts tend to decrease gas solubility (a salting-out effect).63,65 The solubility was derived using parameterizations of the Sechenov constants for NaBr solutions as described by Weisenberger and Schumpe.65 These parameterizations were done using data obtained above 0 °C.64,65 Due to low confidence on the temperature dependence as expressed by the authors,65 we fixed it to that at 25 °C.64
Additional incorporation the effect of the organic co-solute on Γbulk leads to a perfect agreement with the experimental data (Fig. 3). To achieve this, two scenarios estimating the solubility of O3 in the aqueous citric acid solution were developed as part of this study. On the one hand, we described the salting effect of citric acid as that typical for organic species, for which a salting-in effect with increasing concentration of the organic species is generally observed.61 For this, we used measurements of O3 solubility in propionic acid–water mixtures at room temperature between 0 weight percent and 100 weight percent propionic acid.60 On the other hand, measurements of oxygen solubility in citric acid solutions at 25 °C indicate a salting-out effect with increasing citric acid concentrations (between 0.13 and 1.04 M citric acid).66,67 Since O3 solubility often follows similar dependences as that of O2,61 we consider this salting-out scenario as likely as the salting-in.
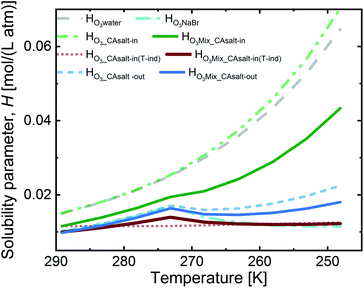
Fig. 4 presents the solubility for the aforementioned two scenarios. The salting-in scenario, HO3_CAsalt-in, shows a strong increase of ozone solubility with decreasing temperature. This trend is driven by the temperature dependence of Hsolution that we set to that of Hwater. Since we are uncertain about the temperature dependence of ozone solubility in this solution, we considered a second alternative to this salting-in scenario, where the solubility has no temperature dependence and the small trend in Fig. 4 is only caused by the change in citric acid concentration.
The salting-out scenario, HO3_CAsalt-out, shows a similar temperature dependence to HO3NaBr with an increase in solubility with decreasing temperature, a decrease at 0 °C as concentrations increase and a further increase as the temperature effect dominates again. HO3CA_salt-out is significantly lower than Hwater. The solubility of O3 in the film mixture (HO3Mix) was calculated by applying the volume mixing rule to the three scenarios for the citric acid fraction and the solubility in the NaBr fraction, HO3NaBr (eqn (9)).
In summary, the solubility in the different fractions shows an increase with decreasing temperature up to 0 °C. Below 0 °C, there is a discontinuity (except in HO3_CAsalt-in and HO3_CAsalt-in(T-ind)) due to the effect of increasing solute concentrations with decreasing water activity as temperatures decrease. All mixture scenarios (HO3Mix) show an overall salting-out effect; that is, HO3Mix is less than Hwater. The discontinuity at 0 °C in the fractions is also reflected in the HO3Mix.
| HO3Mix = VolfracNaBr·HO3NaBr + VolfracCA·HO3CA | (9) |
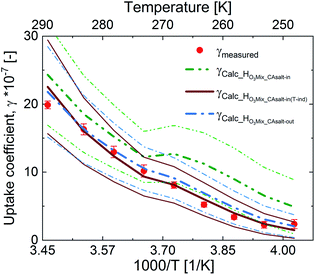
Fig. 5 shows an assessment of the impact of the different solubility scenarios on the uptake coefficients, with all other factors remaining the same. The γcalc for the salting-in scenario with HO3_CAsalt-in, γHO3Mix_salt-in, does not concur with the observed uptake coefficients below 0 °C. This indicates that the rather strong temperature dependence described by the temperature dependence of HO3water poorly represents the temperature dependence of O3 solubility with the salting-in effect. This observation is in agreement with the small general temperature dependence found in the salting effect of the organic co-solute.68 Decoupling the temperature dependence of the solubility effect of the organic fraction from that of water gives better results (γHO3Mix_CAsalt-in(T-ind) and γHO3Mix_CAsalt-out).
The difference between these two scenarios calls for further studies on gas solubility in organic mixtures at low temperatures. In general, due to the absence of measurements of ozone solubility in organic–inorganic mixtures at temperatures below 0 °C, there are large uncertainties. We have estimated this uncertainty based on the difference between the different scenarios (ESI Table S4†). A 20% change in the solubility parameter at 0 °C resulted in a 12% change in the γcalc and a 35% change in the solubility parameter resulted in a 32% change in γcalc at −20 °C (Table 2).
In summary, both HO3Mix_CAsalt-in(Tind) and HO3Mix_CAsalt-out give good results and can be used to assess ozone solubility in mixed systems at temperatures below the freezing point of water.
Viscosity and aqueous bulk diffusivity of ozone
The excellent agreement between γcalc and γobs in Fig. 3 was also achieved by parameterizing the diffusivity in the film. The viscosity of the film influences the diffusivity of ozone and the products within the film. The diffusivity of ozone in the film was estimated using the Stokes–Einstein relationship (eqn (10)), in which diffusivity is inversely related to viscosity. The Stokes–Einstein relationship is valid for small molecules and viscosities lower than 10 Pa s.69 The viscosity of the film was obtained by measuring the viscosity of the solutions at the equilibrium concentrations, as calculated by AIOMFAC, at each experimental temperature. The viscosity of the film increased from 1.4 mPa s at 16 °C to 43.9 mPa s at −24 °C, which leads to almost a 40 times decrease in diffusivity. The measured viscosity of the mixture is similar to that measured in citric acid solutions.70 Therefore, this increase in viscosity with decreasing T and increasing concentration is predominantly driven by citric acid (ESI Fig. S3†).14,71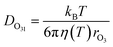 | (10) |
Γ bulk as presented in eqn (5) above is applicable if the reacto-diffusive length (lrd) is smaller than the thickness of the film (tfilm). In this case, the uptake in the aqueous bulk is limited by both reaction and diffusion in the aqueous bulk. The lrd is defined as the characteristic distance over which the reactant (O3) is lost due to reaction in the film (eqn (11)).51
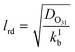 | (11) |
If the lrd is almost equal to or larger than the tfilm, the reaction occurs almost throughout the depth or thickness of the film; Γbulk will be proportional to the volume of the film (or thickness). The thickness of the film was obtained by dividing the estimated volume of the film by the internal surface area of the tube (188.5 cm2). The film thickness ranged from ∼2 μm at −25 °C to ∼13 μm at 16 °C while the lrd ranged from 0.7 μm at −25 °C to 2.3 μm at 16 °C. Hence, we assumed that eqn (5) is a good representation of Γbulk.
We have assigned a low uncertainty to the diffusivity parameter due to the viscosity measurements for the equilibrium concentrations of solutes in the film, which were conducted as part of this study. The equilibrium concentrations calculated using the AIOMFAC model may also be a source of uncertainty for this parameter. A 5% change in the diffusivity parameter at 0 °C results in a 2% change in γcalc and a 10% change in the diffusivity at −20 °C results in a 4% change in γcalc (Table 2).
Uncertainty in aqueous bulk properties and impact on γcalc
Although we are able to predict the measured uptake coefficients in this system, there are uncertainties in the parameters. The uncertainties arise from the lack of measurements of the parameters for the organic component and mixture in particular below 0 °C. Therefore, extrapolation to lower temperatures comes with large uncertainties. Fig. 5 shows the γcalc with error bands (thinner lines). The error bands were determined via error propagation with increasing percentage error as temperatures decreased below 0 °C for all surface and bulk parameters.Table 2 presents a summary of the uncertainties in the bulk parameters and their implications on the bulk uptake coefficients and total uptake coefficients at 16 °C, 0 °C, and −20 °C. Uncertainties in all parameters increase as temperatures decrease below 0 °C due to the absence of measurements and parameterizations at colder temperatures and high concentrations. ESI Table S4† contains information on uncertainties assigned to each parameter and at different temperatures. In summary, the bulk uptake coefficients and the total uptake coefficients are most sensitive to the solubility parameter. The solubility parameter is also the largest source of uncertainty.
Fig. 6 presents the measured uptake coefficients as a function of ozone concentration at 0 °C, −10 °C, −20 °C and −25 °C, also corrected for the gas phase diffusion limitation. The uptake coefficients were independence of ozone concentration at 0 ° and −10 °C. At temperatures less than −10 °C, this independence occurs only at high ozone concentrations. That the uptake coefficient is invariant with increasing ozone concentration shows that Γbulk is not limited by the uptake of ozone from the gas phase. Only at higher ozone concentrations, the surface to bulk transfer rate may be limited by saturation in surface coverage.40,52 There is some evidence of negative O3 concentration dependence at −20 °C and −25 °C, but not at higher temperatures. At −20 and −25 °C, the uptake coefficients decrease with increasing ozone concentration and then plateau to a constant value at high O3 concentrations. This negative O3 concentration dependence of the uptake coefficient is the result of the saturation of the surface coverage of the bromide ozonide occurring at ozone concentrations below those employed here. This observation is different from that of Oldridge and Abbatt with 8.6 mM NaBr concentration at 0 °C,40 and Artiglia et al. with 0.12 M and 0.24 M NaBr concentration at 1 °C41 where a negative O3 concentration dependence was observed. Considering that bromide was 0.7 M at 0 °C in the study presented here, the absence of O3 concentration dependence is not linked to the bromide concentration.
The uptake coefficients at −20 °C and −25 °C are essentially the same. This observation is similar to the levelling off with temperature observed by Oldridge and Abbatt below −30 °C in their system without organics.40 This plateauing in temperature dependence at a warmer temperature in our study may be due to the presence of the organic component. Due to the increase in viscosity with temperature (and concentration of the organic species), the decrease in the diffusivity may lower the contribution of the aqueous bulk to the total O3 uptake; hence similar total uptake coefficients are observed. These conditions may also increase the potential for surface uptake.
The parameterization output, also presented in Fig. 6, was able to predict the O3 concentration dependence of the uptake coefficients reasonably well. At −20 °C, the parameterization is not able to capture the observed similarity in the uptake coefficients between −20 °C and −25 °C. This may be due to uncertainties in the solubility parameter at low temperatures and higher viscosity as well as uncertainties in the surface uptake parameters.
The surface uptake parameterization used in this study was that developed by Artiglia et al. for a system without organics.41 This may not be ideal for the mixed matrix in this study, where the partitioning of the solutes to the surface may not be the same as in a single solute solution.20–22 In particular, recent X-ray photoelectron spectroscopy data of Lee et al. have demonstrated that the presence of citric acid led to a reduction of the bromide abundance at the solution–air interface.22 In addition, the temperature dependence of the surface rate coefficient, ks, may be different in this study due to the presence of organics. The ks from Artiglia et al. applied in this study was based on the energy difference between the water stabilized surface intermediate, BrOOO−·4H2O and the transition state species after intersystem crossing in the reaction scheme on the surface.41 The organics present on the surface may influence the stabilization of this intermediate, as citric acid is a good ligand, with impacts on the ks.
The γcalc is quite sensitive to the magnitude of Nmax and ks in eqn (4). An increase in ks by a factor of 10 increases γcalc by a factor of 4.3 at 16 °C and 1.25 at −25 °C. An increase in Nmax by a factor of 10 increases γcalc by a factor of 2.2 at 16 °C and 1.1 at −25 °C. γcalc is partly sensitive to K with a maximum of about 2% increase with an increase by a factor of 10. Increasing K increases surface coverage of the intermediate ozonide. Since the parameterization of the surface uptake coefficients is already close to the maximum surface coverage, there is no significant change with an increase in K. A decrease in K by a factor of 10 decreases γcalc at warmer temperatures by about 8% due to a significant decrease in surface coverage at warmer temperatures. At temperatures below 0 °C, the change (increase) is about 1% due to a much weaker effect on the surface coverage. This is due to the temperature dependence of K.
In summary, the data indicate a surface process at low temperatures (−20 °C and −25 °C) and low ozone concentrations. The lower surface adsorption equilibrium constant and lower coverage at warmer temperatures result in lower contributions from the surface reaction. At colder temperatures, the coverage is higher, but the surface reaction rate coefficients are lower. The parameterization indicates a significant surface process at ozone concentrations lower than the experimental range. We attribute this difference to uncertainties in ks and K, and their temperature dependence.
Conclusions and implications
In this study, we measured the temperature dependence of the dark reaction of O3 with bromide in a proxy for sea-spray aerosols and brine on sea-ice and in snow. This proxy contained a mixture of an organic species and an inorganic salt (citric acid and sodium bromide). A decrease in temperature resulted in a significant increase in the concentration of solutes below 0 °C as the water vapour pressure decreased. This further resulted in an increase in the pseudo-first order rate coefficients.For this mixed system with organics, a combination of increased viscosity and a strong decrease in the solubility of ozone due to increase in the concentrations of the solutes countered the reaction acceleration. Increased viscosity due to the increased concentration of citric acid with decreasing temperature led to a significant decrease in diffusivity. Sea-spray aerosols and brine on environmental ice surfaces such as snow and sea ice contain a significant organic component, which may strongly influence their viscosity.16,19 This effect of citric acid on the viscosity and on the uptake of O3 in this study is in agreement with that in other studies, which have shown similar reduced reactivity due to the impact of high viscosity on heterogeneous reactions.23,24 We note, though, that the viscosity effect seen here becomes relevant even at high relative humidity, as it is common for environmental compartments where brine is in equilibrium with ice. This effect has implications for the reaction of halides with O3 in snow covered Arctic sea-ice where a significant source of salinity on surface snow is sea-spray aerosols,3 and where aged organic species (represented by citric acid in this study) are likely co-located with halide ions.3,30
There is limited information on the solubility of O3 and other oxidants in organic solutions and in organic/inorganic mixtures although O3 is one of the important oxidants in the atmosphere. The heterogeneous reactions of O3 in aerosols or brine pockets, which contain complex mixtures of solutes, may not be properly assessed without properly accounting for the concentration of O3 in the condensed phase. From our solubility calculations, the composition of the mixture resulted in a significant salting-out effect on O3 relative to O3 solubility in water; using the solubility of O3 in water overestimates the uptake coefficients. Based on our results, atmospheric models may simply be able to use a general representation of the salting effect of solutes on the solubility of the reacting gas.
Halogen activation via reaction between O3 and halides in sea-spray aerosols has recently been updated in global atmospheric chemistry models.7 The addition of the multiphase chemistry contribution from sea-spray aerosols has been shown to improve model predictions. These models may be further improved by including some information about the average viscosity of sea-spray aerosols and the composition effect on solubility. This implies that there is a need for measurements of solubility of O3 in mixtures which is presently lacking. Recently, there have been more studies measuring the viscosity of sea-spray aerosol.19
In addition, we did not focus on the surface uptake of ozone in the mixture as part of this study. There is increasing knowledge of significant surface contributions to the uptake of O3 in aerosols at lower, atmospherically relevant O3 concentrations. Organics have been shown to influence the partitioning of the halides to the surface21,22 and the reactivity on the surface.20 Further studies at low ozone concentrations on the influence of organics and mixtures on the surface uptake of ozone is needed for information on the surface uptake parameters such as the surface rate coefficients, the surface adsorption coefficients, and the maximum coverage of the reactants on the surface (Nmax). The total uptake coefficients are particularly sensitive to the Nmax and the surface rate coefficients.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors would like to thank Mario Birrer for assistance in building the experimental set-up. This project was funded by the Swiss National Foundation (grant number 155999).Notes and references
- W. R. Simpson, R. von Glasow, K. Riedel, P. Anderson, P. Ariya, J. Bottenheim, J. Burrows, L. J. Carpenter, U. Friess, M. E. Goodsite, D. Heard, M. Hutterli, H. W. Jacobi, L. Kaleschke, B. Neff, J. Plane, U. Platt, A. Richter, H. Roscoe, R. Sander, P. B. Shepson, J. Sodeau, A. Steffen, T. Wanger and E. Wollf, Atmos. Chem. Phys., 2007, 7, 4375–4418 CrossRef CAS.
- W. R. Simpson, S. S. Brown, A. Saiz-Lopez, J. A. Thornton and R. Glasow, Chem. Rev., 2015, 115, 4035–4062 CrossRef CAS PubMed.
- J. P. D. Abbatt, J. L. Thomas, K. Abrahamsson, C. Boxe, A. Granfors, A. E. Jones, M. D. King, A. Saiz-Lopez, P. B. Shepson, J. Sodeau, D. W. Toohey, C. Toubin, R. von Glasow, S. N. Wren and X. Yang, Atmos. Chem. Phys., 2012, 12, 6237–6271 CrossRef CAS.
- M. Nerentorp Mastromonaco, K. Gårdfeldt, B. Jourdain, K. Abrahamsson, A. Granfors, M. Ahnoff, A. Dommergue, G. Méjean and H. W. Jacobi, Atmos. Environ., 2016, 129, 125–132 CrossRef CAS.
- T. Bartels-Rausch, H. W. Jacobi, T. F. Kahan, J. L. Thomas, E. S. Thomson, J. P. D. Abbatt, M. Ammann, J. R. Blackford, H. Bluhm, C. Boxe, F. Domine, M. M. Frey, I. Gladich, M. I. Guzmán, D. Heger, T. Huthwelker, P. Klán, W. F. Kuhs, M. H. Kuo, S. Maus, S. G. Moussa, V. F. McNeill, J. T. Newberg, J. B. C. Pettersson, M. Roeselová and J. R. Sodeau, Atmos. Chem. Phys., 2014, 14, 1587–1633 CrossRef.
- M. S. Long, W. C. Keene, R. C. Easter, R. Sander, X. Liu, A. Kerkweg and D. Erickson, Atmos. Chem. Phys., 2014, 14, 3397–3425 CrossRef.
- J. A. Schmidt, D. J. Jacob, H. M. Horowitz, L. Hu, T. Sherwen, M. J. Evans, Q. Liang, R. M. Suleiman, D. E. Oram, M. Le Breton, C. J. Percival, S. Wang, B. Dix and R. Volkamer, J. Geophys. Res.: Atmos., 2016, 121, 11819–11835 CAS.
- S. Wang, J. A. Schmidt, S. Baidar, S. Coburn, B. Dix, T. K. Koenig, E. Apel, D. Bowdalo, T. L. Campos, E. Eloranta, M. J. Evans, J. P. DiGangi, M. A. Zondlo, R. S. Gao, J. A. Haggerty, S. R. Hall, R. S. Hornbrook, D. Jacob, B. Morley, B. Pierce, M. Reeves, P. Romashkin, A. Ter Schure and R. Volkamer, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 9281–9286 CrossRef CAS PubMed.
- P. K. Peterson, D. Pöhler, H. Sihler, J. Zielcke, S. General, U. Frieß, U. Platt, W. R. Simpson, S. V. Nghiem, P. B. Shepson, B. H. Stirm, S. Dhaniyala, T. Wagner, D. R. Caulton, J. D. Fuentes and K. A. Pratt, Atmos. Chem. Phys., 2017, 17, 7567–7579 CrossRef CAS.
- F. Dominé, R. Sparapni, A. Ianniello and H. J. Beine, Atmos. Chem. Phys., 2004, 4, 2259–2271 CrossRef.
- T. Koop, A. Kapilashrami, L. T. Molina and M. J. Molina, J. Geophys. Res., 2000, 105, 26393–26402 CrossRef CAS.
- H. Cho, P. B. Shepson, L. A. Barrie, J. P. Cowin and R. Zaveri, J. Phys. Chem. B, 2002, 106, 11226–11232 CrossRef CAS.
- N. Takenaka, U. Akihiro and M. Yasuaki, Nature, 1992, 358, 736–738 CrossRef CAS.
- Concentrative properties of aqueous solutions: density, refractive index, freezing point depression, and viscosity, in CRC Handbook of Chemistry and Physics, ed. J. R. Rumble, CRC Press/Taylor & Francis, Boca Raton, FL, 2018 Search PubMed.
- R. O'Concubhair and J. R. Sodeau, Environ. Sci. Technol., 2012, 46, 10589–10596 CrossRef PubMed.
- C. D. O'Dowd, M. C. Facchini, F. Cavalli, D. Cebrunis, M. Mircea, S. Decesari, S. Fuzzi, Y. J. Yoon and J.-P. Putaud, Nature, 2004, 431, 672–676 CrossRef PubMed.
- D. M. Lienhard, D. L. Bones, A. Zuend, U. K. Krieger, J. P. Reid and T. Peter, J. Phys. Chem. A, 2012, 116, 9954–9968 CrossRef CAS PubMed.
- J. P. Reid, B. J. Dennis-Smither, N. O. Kwamena, R. E. Miles, K. L. Hanford and C. J. Homer, Phys. Chem. Chem. Phys., 2011, 13, 15559–15572 RSC.
- J. P. Reid, A. K. Bertram, D. O. Topping, A. Laskin, S. T. Martin, M. D. Petters, F. D. Pope and G. Rovelli, Nat. Commun., 2018, 9, 956 CrossRef PubMed.
- S. Hayase, A. Yabushita, M. Kawasaki, S. Enami, M. R. Hoffmann and A. J. Colussi, J. Phys. Chem. A, 2011, 115, 4935–4940 CrossRef CAS PubMed.
- J. Werner, M. Dalirian, M. M. Walz, V. Ekholm, U. Wideqvist, S. J. Lowe, G. Ohrwall, I. Persson, I. Riipinen and O. Bjorneholm, Environ. Sci. Technol., 2016, 50, 7434–7442 CrossRef CAS PubMed.
- M. T. Lee, M. A. Brown, S. Kato, A. Kleibert, A. Turler and M. Ammann, J. Phys. Chem. A, 2015, 119, 4600–4608 CrossRef CAS PubMed.
- S. S. Steimer, M. Lampimäki, E. Coz, G. Grzinic and M. Ammann, Atmos. Chem. Phys., 2014, 14, 10761–10772 CrossRef.
- F. H. Marshall, R. E. H. Miles, Y. C. Song, P. B. Ohm, R. M. Power, J. P. Reid and C. S. Dutcher, Chem. Sci., 2016, 7, 1298–1308 RSC.
- L. Renbaum-Wolff, J. W. Grayson, A. P. Bateman, M. Kuwata, M. Sellier, B. J. Murray, J. E. Shilling, S. T. Martin and A. K. Bertram, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 8014–8019 CrossRef CAS PubMed.
- D. Toom-Sauntry and L. A. Barrie, Atmos. Environ., 2002, 36, 2683–2693 CrossRef CAS.
- D. L. Mitchell and D. Lamb, J. Geophys. Res., 1989, 94, 14831–14840 CrossRef CAS.
- V. F. McNeill, A. M. Grannas, J. P. D. Abbatt, M. Ammann, P. Ariya, T. Bartels-Rausch, F. Domine, D. J. Donaldson, M. I. Guzman, D. Heger, T. F. Kahan, P. Klán, S. Masclin, C. Toubin and D. Voisin, Atmos. Chem. Phys., 2012, 12, 9653–9678 CrossRef CAS.
- A. M. Grannas, W. C. Hockaday, P. G. Hatcher, L. G. Thompson and E. Mosley-Thompson, J. Geophys. Res., 2006, 111 Search PubMed.
- A. M. Grannas, A. R. Bausch and K. M. Mahanna, J. Phys. Chem. A, 2007, 111, 11043–11049 CrossRef CAS PubMed.
- K. W. Oum, M. J. Lakin and B. J. Finlayson-Pitts, Geophys. Res. Lett., 1998, 25, 3923–3926 CrossRef CAS.
- Q. Liu, L. M. Schurter, C. E. Muller, S. Aloiso, J. S. Francisco and D. W. Margerum, Inorg. Chem., 2001, 40, 4436–4442 CrossRef CAS PubMed.
- K. Haruta and T. Takeyama, J. Phys. Chem., 1981, 85, 2383–2388 CrossRef CAS.
- Y. Sakamoto, M. Goda and J. Hirokawa, J. Phys. Chem. A, 2018, 122, 2723–2731 CrossRef CAS PubMed.
- J. Liao, L. G. Huey, D. J. Tanner, F. M. Flocke, J. J. Orlando, J. A. Neuman, J. B. Nowak, A. J. Weinheimer, S. R. Hall, J. N. Smith, A. Fried, R. M. Staebler, Y. Wang, J. H. Koo, C. A. Cantrell, P. Weibring, J. Walega, D. J. Knapp, P. B. Shepson and C. R. Stephens, J. Geophys. Res.: Atmos., 2012, 117, 1–11 Search PubMed.
- J. P. Abbatt, Geophys. Res. Lett., 1994, 21, 665–668 CrossRef CAS.
- S. Fickert, J. W. Adams and J. N. Crowley, J. Geophys. Res., 1999, 104, 23719 CrossRef CAS.
- E. K. Frinak and J. P. Abbatt, J. Phys. Chem., 2006, 110, 10456–10464 CrossRef CAS PubMed.
- S. W. Hunt, M. Roeselová, W. Wang, L. M. Wingen, E. M. Knipping, D. J. Tobias, D. Dabdub and B. J. Finlayson-Pitts, J. Phys. Chem. A, 2004, 108, 11559–11572 CrossRef CAS.
- N. W. Oldridge and J. P. Abbatt, J. Phys. Chem. A, 2011, 115, 2590–2598 CrossRef CAS PubMed.
- L. Artiglia, J. Edebeli, F. Orlando, S. Chen, M.-T. Lee, P. Corral Arroyo, A. Gilgen, T. Bartels-Rausch, A. Kleibert, M. Vazdar, M. Andres Carignano, J. S. Francisco, P. B. Shepson, I. Gladich and M. Ammann, Nat. Commun., 2017, 8, 700 CrossRef PubMed.
- S. N. Wren, T. F. Kahan, K. B. Jumaa and D. J. Donaldson, J. Geophys. Res., 2010, 115 Search PubMed.
- A. Clifford and D. J. Donaldson, J. Phys. Chem. A, 2007, 111, 9809–9814 CrossRef PubMed.
- I. Gladich, J. S. Francisco, R. J. Buszek, M. Vazdar, M. A. Carignano and P. B. Shepson, J. Phys. Chem. A, 2015, 119, 4482–4488 CrossRef CAS PubMed.
- K. Hebestreit, J. Stutz, D. Rosen, V. Matveiv, M. Peleg, M. Luria and U. Platt, Science, 1999, 283, 55–57 CrossRef CAS PubMed.
- J. Marti and K. Mauersberger, Geophys. Res. Lett., 1993, 20, 363–366 CrossRef.
- D. M. Murphy and T. Koop, Q. J. R. Metereol. Soc., 2005, 131, 1539–1565 CrossRef.
- N. Takenaka and H. Bandow, J. Phys. Chem. A, 2007, 111, 8780–8786 CrossRef CAS PubMed.
- A. Zuend, C. Marcolli, B. P. Luo and T. Peter, Atmos. Chem. Phys., 2008, 8, 4559–4593 CrossRef CAS.
- M. Ammann, R. A. Cox, J. N. Crowley, M. E. Jenkin, A. Mellouki, M. J. Rossi, J. Troe and T. J. Wallington, Atmos. Chem. Phys., 2013, 13, 8045–8228 CrossRef.
- B. J. Finlayson-Pitts and J. N. J. Pitts, Chemistry of the Upper and Lower Atmosphere, Academic Press, San Diego California, USA, 2000 Search PubMed.
- U. Poschl, Y. Rudich and M. Ammann, Atmos. Chem. Phys., 2007, 7, 5989–6023 CrossRef.
- M. Shiraiwa, C. Pfrang, T. Koop and U. Pöschl, Atmos. Chem. Phys., 2012, 12, 2777–2794 CrossRef CAS.
- P. N. Johnson and R. A. Davis, J. Chem. Eng. Data, 1996, 41, 1485–1487 CrossRef CAS.
- W. L. Chaimedes and A. W. Stelson, J. Geophys. Res., 1992, 97, 20565–20580 CrossRef.
- A. A. Zardini, S. Sjogren, C. Marcolli, U. K. Krieger, E. Weingartner, U. Baltensperger and T. Peter, Atmos. Chem. Phys., 2008, 8, 5589–5601 CrossRef CAS.
- T. Isono, J. Chem. Eng. Data, 1984, 29, 45–52 CrossRef CAS.
- A. B. Hastings and D. D. V. Slyke, J. Biol. Chem., 1922, 53, 269–276 CAS.
- R. W. Haag and J. Hoigné, Environ. Sci. Technol., 1983, 17, 261–267 CrossRef.
- R. Battino, Ozone Solubilities, Pergamon Press Ltd, Oxford UK, 1981 Search PubMed.
- A. K. Biń, Ozone: Sci. Eng., 2006, 28, 67–75 CrossRef.
- M. Sechenov, Z. Phys. Chem., 1889, 4, 117–125 Search PubMed.
- A. Schumpe, Chem. Eng. Sci., 1993, 48, 153–1158 CrossRef CAS.
- E. Rischbieter, H. Stein and A. Schumpe, J. Chem. Eng. Data, 2000, 45, 338–340 CrossRef CAS.
- S. Weisenberger and A. Schumpe, AIChE J., 1996, 42, 298–300 CrossRef CAS.
- R. Battino, Oxygen and Ozone - Solubility Data Series, International Union of Pure and Applied Chemistry, 1981 Search PubMed.
- M. Popovic, H. Niebelschuetz and M. Reuss, Eur. J. Appl. Microbiol. Biotechnol., 1979, 8, 1–15 CrossRef CAS.
- D. D. Eley, Trans. Faraday Soc., 1939, 35, 1421–1432 RSC.
- R. M. Power, S. H. Simpson, J. P. Reid and A. J. Hudson, Chem. Sci., 2013, 4, 2597 RSC.
- D. M. Lienhard, A. J. Huisman, D. L. Bones, Y. F. Te, B. P. Luo, U. K. Krieger and J. P. Reid, Phys. Chem. Chem. Phys., 2014, 16, 16677–16683 RSC.
- A. Apelblat, Properties of citric acid and its solutions, in Citric Acid, Springer, Cham, 2014, ch. 2, pp. 13–141, DOI:10.1007/978-3-319-11233-6_2.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c8em00417j |
| This journal is © The Royal Society of Chemistry 2019 |