Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Quantifying and elucidating the effect of CO2 on the thermodynamics, kinetics and charge transport of AEMFCs†
Yiwei
Zheng
a,
Travis J.
Omasta
 a,
Xiong
Peng
a,
Lianqin
Wang
a,
Xiong
Peng
a,
Lianqin
Wang
 b,
John R.
Varcoe
b,
John R.
Varcoe
 b,
Bryan S.
Pivovar
c and
William E.
Mustain
b,
Bryan S.
Pivovar
c and
William E.
Mustain
 *a
*a
aDepartment of Chemical Engineering, University of South Carolina, Columbia, South Carolina 29208, USA. E-mail: mustainw@mailbox.sc.edu
bNational Renewable Energy Laboratory, Golden, Colorado 80401, USA
cDepartment of Chemistry, University of Surrey, Guildford, GU2 7XH, UK
First published on 22nd July 2019
Abstract
It has been long-recognized that carbonation of anion exchange membrane fuel cells (AEMFCs) would be an important practical barrier for their implementation in applications that use ambient air containing atmospheric CO2. Most literature discussion around AEMFC carbonation has hypothesized: (1) that the effect of carbonation is limited to an increase in the Ohmic resistance because carbonate has lower mobility than hydroxide; and/or (2) that the so-called “self-purging” mechanism could effectively decarbonate the cell and eliminate CO2-related voltage losses during operation at a reasonable operating current density (>1 A cm−2). However, this study definitively shows that neither of these assertions are correct. This work, the first experimental examination of its kind, studies the dynamics of cell carbonation and its effect on AEMFC performance over a wide range of operating currents (0.2–2.0 A cm−2), operating temperatures (60–80 °C) and CO2 concentrations in the reactant gases (5–3200 ppm). The resulting data provide for new fundamental relationships to be developed and for the root causes of increased polarization in the presence of CO2 to be quantitatively probed and deconvoluted into Ohmic, Nernstian and charge transfer components, with the Nernstian and charge transfer components controlling the cell behavior under conditions of practical interest.
Broader contextAnion exchange membrane fuel cells (AEMFCs) have shown significant promise to provide clean, sustainable energy for grid and transportation applications – and at a lower theoretical cost than more established proton exchange membrane fuel cells (PEMFCs). Adding to the excitement around AEMFCs is the extremely high peak power that can now be obtained (>3 W cm−2) and continuously improving durability (1000+ h), which has made the future deployment of AEMFCs in real-world applications a serious consideration. For some applications (e.g. automotive), the most critical remaining practical issue with AEMFCs is understanding and mitigating the effects of atmospheric CO2 (in the air supply) on cell behavior and performance. This study is the first comprehensive experimental investigation into the effects of CO2 on operating AEMFCs. It is also the first study to be able to quantitatively determine the root causes for performance decline when CO2 is added to the system, where cell behavior is directly linked to cell chemistry and reaction dynamics. In addition to the demonstrated technology, the lessons learned in this work can also provide transformational insights to other air breathing and/or AEM-based electrochemical systems such as metal–air batteries, regenerative fuel cells, electrochemical CO2 capture, CO2 reduction reactors and dialyzers. |
Introduction
For decades, the proton exchange membrane fuel cell (PEMFC) has dominated the research space for low temperature polymer electrolyte fuel cells. Though significant advances have been made regarding the performance and stability of PEMFCs over the years, one of the factors that has limited its wide deployment is cost.1 It has been broadly suggested in recent years that a change of electrolyte to a solid alkaline polymer electrolyte might be able to significantly reduce the cost of polymer-based fuel cell systems2 because the alkaline environment would allow for the deployment of a broader range of noble metal free catalysts as well as less expensive materials to be used for other cell components such as the membrane and bipolar plates.Early development of these so-called anion exchange membrane fuel cells (AEMFCs) was hindered by anion exchange membranes (AEMs) with very poor alkaline stability3 and very poor performance, with typical peak power densities well below 0.5 W cm−2. The combination of low achievable power and limited durability4,5 made AEMFCs uncompetitive with PEMFCs for years. However, over the past two years, a significant increase in the peak power density has been observed,5–9 with state-of-the-art AEMFCs having the ability to achieve values over 3 W cm−2 operating on H2/O2 gas feeds.10 Also, the performance stability of AEMFCs has improved dramatically during this time, with multiple groups reporting 500+ hour stability at low degradation rates (5–10%).11–14
Now that AEMFC performance and stability has been enhanced to the point where their future deployment in real applications can be seriously contemplated, it is now an important time in AEMFC development to begin to answer some of the other lingering issues that have to date been mostly put aside in the literature. It can be argued that one of the most important of these issues is understanding and mitigating the effects of atmospheric CO2 on AEMFC performance. It is widely known that when CO2-containing air is fed to the AEMFC cathode, the OH− anions that are produced from the oxygen reduction reaction (ORR), eqn (1), react with CO2 to produce carbonate and/or bicarbonate anions, eqn (2) and (3).
| O2 + 2H2O + 4e− → 4OH− | (1) |
| CO2 + OH− ⇌ HCO3− | (2) |
| HCO3− + OH− ⇌ CO32− + H2O | (3) |
Therefore, the purpose of this study is to establish a resolute understanding of the influence of CO2 on the performance of AEMFCs. Herein, the CO2 concentration in both the cathode and anode are parametrically changed over a wide range of conditions (current density and temperature) that represent reasonable ranges for their practical operation. Finally, this work explores the lower limits of CO2 exposure to determine whether or not there is a baseline CO2 tolerance in AEMFCs, which informs the field to what degree oxidant gas scrubbing might be needed.
Experimental
Electrode preparation
The electrodes in this work were prepared using a method that has been detailed in our previous publications.8,9 Briefly, the anode and cathode catalysts were 60 wt% PtRu supported on Vulcan XC-72R (Alfa Aesar HiSPEC 10000, 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio of Pt
1 ratio of Pt![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ru by mass – Pt nominally 40 wt%, and Ru, nominally 20 wt%) and 40 wt% Pt supported on Vulcan XC-72R (Alfa Aesar HiSPEC 4000, Pt nominally 40 wt%), respectively. Electrode preparation was initiated by placing an ethylene tetrafluoroethylene (ETFE) benzyltrimethylammonium (BTMA) solid powder anion exchange ionomer (AEI) with an ion-exchange capacity (IEC) of 1.24 mmol g−1
Ru by mass – Pt nominally 40 wt%, and Ru, nominally 20 wt%) and 40 wt% Pt supported on Vulcan XC-72R (Alfa Aesar HiSPEC 4000, Pt nominally 40 wt%), respectively. Electrode preparation was initiated by placing an ethylene tetrafluoroethylene (ETFE) benzyltrimethylammonium (BTMA) solid powder anion exchange ionomer (AEI) with an ion-exchange capacity (IEC) of 1.24 mmol g−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 18 into a mortar and manually grinding it with a pestle for 10 min. The catalyst powder, additional Vulcan carbon (XC-72R, Cabot), and 1 mL of Millipore deionized (DI) water (18.2 MΩ cm resistivity) were added to the mortar and ground for 10 min. The mass fraction of AEI in the catalyst layer was always 0.20 and the total mass fraction of carbon was maintained at 0.48 for both electrodes. Next, the catalyst-AEI slurry was transferred to a polypropylene vial. Isopropyl alcohol was added, and the mixture was sonicated (Fisher Scientific FS30H) for 60 min. The water in the ultrasonic bath was maintained below 5 °C to avoid degrading the supported catalyst and the AEI and to maximize the electrochemically active area by avoiding agglomeration. The ink dispersions were sprayed onto Toray TGP-H-0600 gas diffusion layers with 5% PTFE wetproofing with an Iwata Eclipse HP-CS (feed gas was 15 psig Ultra High Purity N2) to create gas diffusion electrodes (GDEs). The target GDE catalyst loading was 0.6 ± 0.1 mgPt cm−2.
18 into a mortar and manually grinding it with a pestle for 10 min. The catalyst powder, additional Vulcan carbon (XC-72R, Cabot), and 1 mL of Millipore deionized (DI) water (18.2 MΩ cm resistivity) were added to the mortar and ground for 10 min. The mass fraction of AEI in the catalyst layer was always 0.20 and the total mass fraction of carbon was maintained at 0.48 for both electrodes. Next, the catalyst-AEI slurry was transferred to a polypropylene vial. Isopropyl alcohol was added, and the mixture was sonicated (Fisher Scientific FS30H) for 60 min. The water in the ultrasonic bath was maintained below 5 °C to avoid degrading the supported catalyst and the AEI and to maximize the electrochemically active area by avoiding agglomeration. The ink dispersions were sprayed onto Toray TGP-H-0600 gas diffusion layers with 5% PTFE wetproofing with an Iwata Eclipse HP-CS (feed gas was 15 psig Ultra High Purity N2) to create gas diffusion electrodes (GDEs). The target GDE catalyst loading was 0.6 ± 0.1 mgPt cm−2.
Anion exchange membrane fuel cell (AEMFC) assembly and break-in procedure
Before cell assembly, the GDEs were soaked in 1 M aqueous KOH solutions (prepared from Fisher Chemical pellets/certified ACS and DI water) for 60 min, exchanging the solution twice during this time. At the same time, the AEM was also soaked in an identical solution. Two different AEMs were used in this work. The first was a 50 μm thickness (fully swollen in water) ETFE–BTMA radiation-grafted AEM,19 which was used for the CO2 dosing experiments at 60 °C. The second AEM was a 25 μm thickness (fully swollen in water) LDPE (low density polyethylene)–BTMA radiation-grafted AEM.7 The LDPE–BTMA AEM is more chemically and mechanically stable at elevated temperatures than its ETFE–BTMA counterpart and was used when investigating the influence of elevated temperature on CO2-related overpotential losses.After soaking for 1 h, excess KOH was removed from the GDEs and AEMs before cell assembly. The GDEs and AEMs were pressed together in the cell to form the membrane electrode assembly (MEA) with no prior hot pressing. The MEAs were loaded into 5 cm2 Scribner hardware between two single pass serpentine graphite flow plates. An 850e Scribner Fuel Cell Test Station was used to control the gas stream dew points, cell temperature, gas flowrates and the operating current density.
Before CO2 measurements were made, all cells underwent a break in procedure. First, the cell was brought to its operating temperature under N2 flow on both sides of the cell at 100% relative humidity. Next, the feed gases were switched to ultra high purity H2 and O2 (Airgas) at the anode and cathode, respectively. Then, the cell was operated galvanostatically stepwise from 0.7 V to 0.3 V (0.1 V steps, held for a minimum of 30 min at each step) as the reacting gas dew points were optimized per our standard procedure.8 The optimized reacting gas dew points were very repeatable from cell-to-cell; the dew points were typically 52 °C at the anode and 54 °C at the cathode for an AEMFC operating at 60 °C. Following the optimization of the reacting gas dew points, the cells were operated galvanostatically at the current density of interest (0.2, 0.5, 1.0 or 2.0 A cm−2) and allowed to equilibrate for at least 30 min before CO2 exposure was initiated. Multiple cells (no less than three) were constructed and tested for each measurement.
AEMFC carbon dioxide measurements
Following the break-in procedure and 30 min equilibration, the cell current was maintained and CO2 was parametrically added to the ultra high purity O2 cathode stream. We chose to add CO2 to O2 instead of air in order to simplify observations and isolate the effects of CO2 on performance, since air has additional O2 mass transport impact (e.g. N2 dilution) during cell operation, which is largely eliminated by utilizing O2 as the reacting gas. The flowrate for O2 and H2 in all experiments was 1 L min−1. CO2 cathode concentrations as low as 2 ppm and as high as 3200 ppm were tested. Typically, after CO2 addition, the cell was operated for 30 min, which was much longer than the time required to reach quasi-steady-state operation (typically <5 min, though lower CO2 concentrations took longer). After 30 min operation at constant current, CO2 was removed from the gas stream and the cell was allowed to decarbonate for an initial 30 min. After this, the cell was further decarbonated through self-purging by one of two approaches: (i) the cell was allowed to operate at the same current density until the voltage reached its pre-CO2 level and no CO2 emission was measured at the anode (shown in Fig. S1 in the ESI†); or (ii) more typically, to reduce the time between CO2 trials, the cell potential was pulsed down to 0.1 V for 1 min (Fig. S2 in the ESI†), after which no CO2 emission was measured in the anode stream. When CO2 was fed to the cathode, the concentration of CO2 being emitted from the anode and cathode were both constantly monitored in real time using a PP Systems WMA-5 non-dispersive infrared CO2 gas analyzer (a water trap was placed in-line before the WMA-5 in order to preserve the unit and its calibration).A second set of experiments were done where CO2 at concentrations between 2 and 400 ppm were added to the anode instead of the cathode. This was meant to simulate two possible scenarios: (i) CO2 accumulation in the anode; and (ii) CO2 exposure at the anode from the oxidation of carbonaceous fuels (through reforming or direct alcohol oxidation). When CO2 was fed to the anode, the concentration of CO2 being emitted from the anode and cathode was constantly monitored in real time using the WMA-5. The cathode data will not be shown since the CO2 concentration there was always below the detection limit during operation (though a very small amount of CO2 was observed in the cathode exhaust when the cell current was turned off due to diffusion across the AEM, which is shown).
The final set of experiments investigated the effects of temperature on CO2-related voltage losses. CO2 was fed separately to both the cathode and anode at 400 ppm. The cell setup and operation were identical to the previous description with one exception: the AEM used for these temperature studies was LDPE–BTMA (IEC = 2.5 mmol g−1), and not ETFE–BTMA (IEC = 2.05 ± 0.05 mmol g−1), because of its superior thermomechanical stability.
Results and discussion
In a typical analysis of fuel cell performance, it is often assumed that the cell voltage (Vcell) can be represented by eqn (4):| Vcell = VOCV − i(RΩ + Rct + Rmt) | (4) |
The electrochemical production of hydroxide anions in the presence of CO2 and their subsequent equilibrium reactions were summarized in eqn (1)–(3). It should be noted here that OH−/CO32−/HCO3− equilibrium constants exist such that OH− and HCO3− can never exist together in large quantities. However, CO32− can exist in high concentrations with either OH− or HCO3−. During cell operation at practical current densities, a significant amount of OH− is produced and CO2 is purged from the cell. Therefore, the two ions that dominate under operating conditions are OH− and CO32−, which has been confirmed through theoretical modeling.16 For this reason, the remainder of the discussion in this work will only consider the presence of “carbonate” as CO32−, although it is recognized that bicarbonate is often present in highly carbonated AEMs and AEMFCs before significant levels of electrochemical ORR have occurred at the cathode. It is also possible for there to be at least some bicarbonate accumulated in the anode if the degree of carbonation in the AEMFC is high.
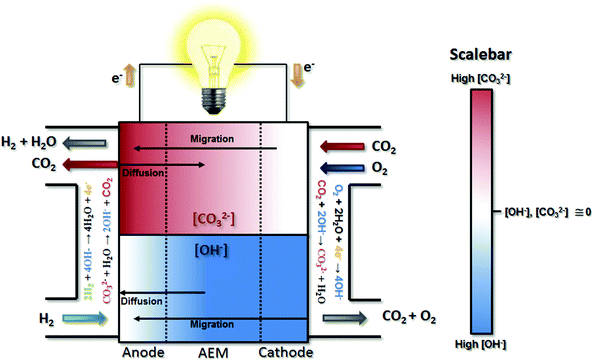
After their formation at the cathode, the CO32− anions are transported through the AEM to the anode by migration, resulting in the “carbonation” of the AEM and the catalyst layer ionomers (Fig. 1). This carbonation reduces the AEM conductivity since CO32− has a lower intrinsic mobility than OH−,21–23 which increases the area-specific resistance (ASR, estimated as the product of the measured high frequency resistance and the cell active area) relative to OH−-only operation (ΔASR). However, this effect should not be overstated as it is only able to account for a small fraction of the performance loss when CO2 is added to the cathode stream. Definitive experimental evidence will be presented below to support this. Less discussed, though thoughtfully pointed out and modeled by a few studies in the literature,16,24,25 migration is not the only mass transport event that influences the location and distribution of CO32−; diffusion also plays a role. The interplay between migration and diffusion results in carbonate concentration profiles that impact performance in two primary ways beyond Ohmic considerations, one pH-based (Nernstian) and the other electrocatalytic.26
Nernstian performance loss in the presence of CO2 in operating AEMFCs is due to concentration gradients that develop across the cell. Under typical operating currents, net migration of ions across the AEM is very fast (on the order of 1 s at relevant current densities and AEM thicknesses). This ionic flux towards the anode leads to lower concentrations of CO32− in the AEM and cathode compared to the anode (though the extent will depend on factors including membrane thickness, current density and the CO2 concentration in the cathode stream). The resulting CO32− concentration gradient provides a driving force for back-diffusion of CO32− anions from the anode towards the cathode – setting up a steady-state concentration gradient where there is significant carbonate accumulation within the anode,16,24,26 although the absolute and variation of the carbonate level within the anode has yet to be determined directly. The presence of carbonate in the anode decreases the local pH, leading to an increase in the anode potential (ΔVNernst) according to the Nernst equation during operation, which has been theoretically estimated to be as high as 180–350 mV.16,27
Electrocatalytically-driven CO2-related voltage losses arise from the reduced migrational supply and reduced local concentration of reacting OH− anions as CO32− carries charge from the cathode to the anode and accumulates there. Previous work (and the data in Fig. S2 in the ESI† for a cell pulsing to 0.1 V) has shown evidence that at high anode overpotentials CO2 is quickly removed from operating AEMFCs – suggesting that carbonate may directly react with H2 at those overpotentials to produce water and CO2, thereby significantly accelerating decarbonization (also supported by data on slide 17 in ref. 28). However, the long timescales needed to completely decarbonate AEMFCs at typical operating current and higher cell voltages (lower anode overpotentials), such as Fig. S1 in the ESI,† strongly suggests that such direct reaction does not appreciably occur at conditions of practical interest. Hence, it can be assumed in this work that essentially the entirety of the steady-state electrochemical current is generated through OH−-based ORR and HOR reactions (eqn (1) and (5), respectively). Therefore, when CO32 anions carry charge through the AEM, the balance of reacting OH− that is no longer supplied by migration (due to CO32− conduction) must be compensated for by diffusion, which is an intrinsically slower process.
| H2 + 2OH− = H2O + 2e− | (5) |
These new resistances lead to a more complex equation for the operating cell voltage, though one that is insightful for the analysis of AEMFCs that have been carbonated:
| Vcell = VOCV − i(RΩ,OH + RctORR + RmtORR + RctHOR) − ΔVNernst − i(ΔASR + ΔRctHOR) | (6) |
The above-discussed behavior of carbonated AEMFCs is very similar to cation-contaminated PEMFCs,31–34 though some critical differences do exist. Most importantly, in this case the “contaminant”, CO32−, is continuously created at the cathode, moved to the anode, and removed from the anode gas stream. Similar processes do not exist for cation-contaminated PEMFCs with the exception of the NH3/NH4+ couple.35 For CO2 containing AEMFCs, CO32− can be removed during operation by introducing a CO2-free oxidant, activating a “self-purging” mechanism, which has been discussed elsewhere.15 For reasons discussed above, under normal operating conditions this self-purging is not a result of direct electrochemical reaction of carbonates, but rather thermodynamic equilibrium. Under pseudo steady-state conditions, the CO2 uptake rates at the cathode equal the release rates at the anode and a static concentration polarization exists across the anode, AEM, and cathode – based on balancing between migration and diffusion of OH− and CO32−, as illustrated in Fig. 1.
In order to minimize the effect of CO2 and carbonation on operating AEMFCs, it is important for the field to better understand how CO2 uptake, membrane carbonation, and CO2 release occur. There are both transient and steady-state concerns with little experimental data to provide insight or validate existing models. The results presented here quantify the uptake and release rates of CO2, quantify the amount of CO2 within the MEA under different steady-state conditions, and provide data as to the performance and resistance of AEMFCs under specific CO2 conditions. This first of its kind data provides significant insight into the performance losses and ultimate potential of AEMFCs when exposed to CO2. This work provides direct evidence regarding the extent to which the CO2 fed to the cathode becomes integrated into the AEMFC, directly correlates carbonation with AEMFC performance, and provides critical data needed to validate modeling efforts that try to quantify rates of CO2 uptake and release, as well as the negative effects of CO2 on performance.
Dynamic observation of CO2 uptake and transport in operating AEMFCs
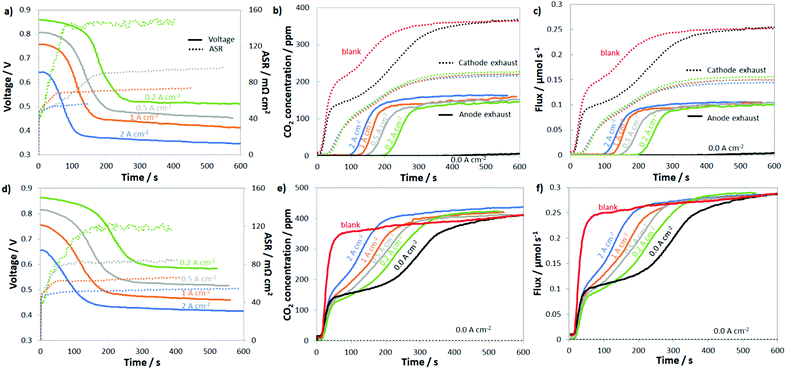
To probe the uptake and release of CO2 in AEMFCs, CO2 (100, 200, 400, 800, 1600 and 3200 ppm) was added to the cathode of cells under open circuit conditions as well as cells operated at 0.2, 0.5, 1.0 and 2.0 A cm−2. For the entire data set, the concentration of CO2 leaving both the anode and cathode was measured in real time. The results for 400 ppm CO2 in O2 are shown in Fig. 2a and b, and the results for all of the other CO2 concentrations are shown in the ESI,† Fig. S3–S7. The first condition assessed was steady-state at the open-circuit voltage (OCV, labeled as 0.0 A cm−2), which allows the diffusional dynamics of ionomer and membrane carbonation to be observed since there is no current driving the movement of CO32− from the cathode to the anode. Though the OCV did not change, in agreement with the work by Inaba et al.,36 it was clear during the experiment that the AEM and AEI were being converted to the carbonate form since the amount of CO2 leaving the cathode was far below the 400 ppm feed, Fig. 2b, especially over the first 300 s.After the CO2 was added to the cathode at OCV, the concentration initially rose from zero to ca. 130 ppm as two things were occurring: absorption of CO2 into the AEM and ionomer and the increase in the CO2 partial pressure in the gas stream (the humidifier and cell lag in the CO2 concentration is denoted as “blank” in Fig. 2b – determined in a cell containing a Teflon membrane, which does not uptake CO2 and form CO32− anions). Comparing the “blank” and 0.0 A cm−2 (black dotted line) plots in Fig. 2b, it was clear that there was rapid CO2 uptake into the AEM because the concentration of CO2 leaving the AEM-containing cell was always lower than the “blank”. By 600 s, the concentration of CO2 in the cathode rose to the inlet concentration, suggesting that the AEM was extensively carbonated after 10 min, which is in good agreement with previous studies on AEM carbonation in the presence of gas-phase CO2.15,37,38 Also from the difference in the response of the AEM and “blank”, it was possible to calculate that essentially all of the charge carrying groups in the AEM and AEI were carbonated during this time (and at steady-state contained a mixture of HCO3− and CO32−, details in the ESI,† Fig. S8 and accompanying discussion).
When CO2 was added to the cathode of a fully broken-in cell operating at a constant current density, the cell response was very different. In all cases (from 0.2 A cm−2 to 2.0 A cm−2), after a brief time lag, the cell operating voltage precipitously declined, the ASR increased, and CO2 was emitted at the anode; this is shown in Fig. 2a and b. What changed with current density were the magnitude and timing of these phenomena. At the highest current density that was tested, 2.0 A cm−2, it took approximately 31 s for CO2 to be measured in the anode stream (from the time that the reacting gas CO2 concentration increased). It took another 96 s after CO2 was initially measured in the anode gas before a quasi-steady-state was achieved. When the current was halved to 1.0 A cm−2, the time for CO2 break-through to the anode was approximately doubled (65 vs. 31 s), though the time to reach equilibration was very similar (90 vs. 96 s). This trend continued for 0.5 A cm−2 and 0.2 A cm−2.
The CO2 breakthrough time increasing with decreasing current density is intuitive as the rate of ion movement through the AEM is slower at lower current density. The timescale for CO2 breakthrough was much longer than the amount of time it would take for an ion to travel between the cathode and anode. At current densities of 2.0 A cm−2, 1.0 A cm−2, 0.5 A cm−2, and 0.2 A cm−2, the average time for a net single-charged anion to travel through the AEM is 410 ms, 820 ms, 1.6 s and 4.1 s, respectively (the ETFE–BTMA AEM had an IEC of 2.05 ± 0.05 mmol g−1 with ca. 43 μmol of charge-carrying, covalently-bound positively-charged groups in the 5 cm2 membrane active area). The fact that the breakthrough time for CO2 was much longer than the average time it takes for an anion to move from the cathode to the anode directly supports the idea that CO2 is not emitted as part of a direct electrochemical process during normal operation and needs time to reach a critical concentration in the anode that allows it to be released into the anode exhaust (through the equilibrium reactions of eqn (2) and (3)). This explains the lag in the CO2 release as well as provides an explanation as to why breakthrough occurs earlier at higher currents since CO32− back-diffusion is less effective – resulting in critical anode concentrations being reached sooner. At steady-state, the rate of CO32− formation at the cathode will equal the rate of carbonate release (CO2 emission) at the anode; the transient and steady-state fluxes for CO32− reaction and CO2 emission at several current densities and CO2 concentrations to the cathode are given in Fig. 2c.
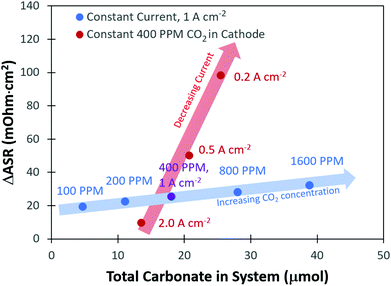
From the transient flux data, the amount of carbonate in the system at steady-state, as well as the degree of carbonation, could be calculated (Table S1 and subsequent discussion in the ESI†). As expected, there was a greater amount of CO32− present in the system with higher concentrations of CO2 in the cathode stream. It was also found that the total amount of CO32− in the system decreased with increasing current density. The change in the total number of CO32− anions in the system with current density and cathode CO2 concentration clearly explains the trends in the ASR. However, one interesting observation was that a plot of the total carbonate in the system vs. the change in the ASR, Fig. 3, did not yield a single straight line for all conditions, but there were trends as a function of current density and CO2 concentration. To understand this, it should be noted that the high frequency resistance measurement by the fuel cell test station is only measuring the two closest points separated by the ionomer; in other words, it is essentially a measurement of the membrane resistance. Therefore, the fact that the ASR is lower at a higher current density, even under conditions where the total amount of CO32− in the cell is nearly identical to a lower current density, suggests that there is less carbonate in the AEM and more carbonate in the anode electrode as the current density is increased.
In summary, there were seven interesting observations when CO2 was fed to the AEMFC cathode: (1) the CO2 concentration leaving the cathode was only very modestly affected by the current density (Fig. 2b), at least at the high flowrates investigated in this work; (2) the decrease in the cell voltage (Fig. 2a) started to occur before CO2 was measured in the anode exhaust; (3) the ASR increased immediately when CO2 was added to the cell (Fig. 2a); (4) the steady-state ASR was realized before the steady-state voltage was achieved and CO2 was measured in the anode effluent (Fig. 2a and b); (5) the steady-state ASR increased with decreasing current density (Fig. 2a); (6) increasing current density decreased the amount of CO32− present in the system at steady-state (Table S1, ESI†); and (7) even at the highest current density and lowest CO2 concentration (2.0 A cm−2 and 100 ppm, respectively) the CO2-related overpotential was significant (167 mV), and the CO2-related overpotential at 2.0 A cm−2 and pseudo-air conditions (400 ppm CO2) was even higher (259 mV). Combined, these observations suggest that: (i) CO32− formation at the cathode is very rapid (likely in quasi-equilibrium, which will be discussed more later); (ii) initially CO32− accumulates in the membrane and anode electrode and CO2 release in slow until a critical concentration is reached; and (iii) higher current densities increase the amount of CO32− in the anode electrode.
To further study the dynamics of CO2 uptake and CO32− formation in the AEMFC system, as well as to simulate CO2 that would build up in the anode or could be formed as an oxidative product of an alcohol fuel, CO2 was also directly fed to the anode. For comparison sake, the CO2 concentration in the anode H2 reacting gas was also 400 ppm. The results of these experiments are shown in Fig. 2d–f. The first thing that should be noted is that while current was flowing, no measurable CO2 was ever found leaving the cathode, which can be attributed to the high net anionic flux relative to typical diffusion rates. Simply, CO32− cannot diffuse and accumulate to a critical concentration at the cathode faster than migration pushes it to the anode under the conditions tested. Therefore, Fig. 2e only shows the CO2 concentration of the anode effluent and Fig. 2f only shows the anode CO2 flux. Like the cathode, there was approximately a 45 s lag between the time that CO2 was turned on and its measurement (Fig. S3, ESI†). In this set of experiments, the dynamic CO2 concentration in the effluent (before steady-state) increased with increasing current density, suggesting lower CO2 uptake and CO32− formation at higher currents. Also, the overall voltage decrease and ASR increase were both lower (but only slightly so) when CO2 was fed to the anode vs. the cathode, most likely because of reduced carbonation stemming from the direction of ion transport.
Relationship between anode-evolved CO2 and the CO2 concentration in the cathode
At practical fuel cell current densities, the vast majority of the charge is carried by OH−, not CO32−, even at very high levels of carbonation. Therefore, a metric relating the amount of charge carried by CO32− (measured by the flux of CO2 leaving the anode at steady state) at various current densities and CO2 levels in the cathode (e−/CO2) would be useful – not only for fuel cells, but also for potential applications such as AEM-based electrochemical CO2 capture.39 Relating this ratio to the partial pressure of CO2 in the cathode starts by defining the metric: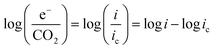 | (7) |
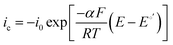 | (8) |
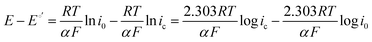 | (9) |
It has been noted in the literature,15 and suggested by the data in Fig. 2, that carbonation during the ORR is very fast, and, therefore, it can be assumed that the CO2 in the cathode gas stream is always in quasi-equilibrium with the generated anions. This Nernstian process can be represented by the Nernst equation, combining the reactions in eqn (1) and (2), where the equilibrium potential is replaced by the actual electrode potential:
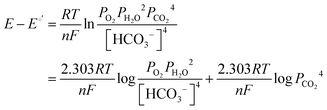 | (10) |
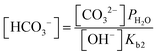 | (11) |
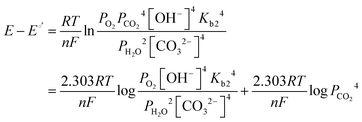 | (12) |
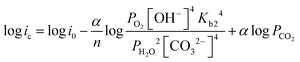 | (13) |
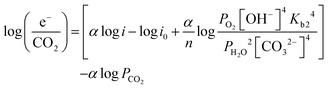 | (14) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) e−/CO2 and log
e−/CO2 and log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) PCO2 with a negative slope equal to the effective ORR transfer coefficient. The slope in Fig. 4 is approximately −1, which is consistent with measurements of the effective transfer coefficient for the ORR in operating fuel cells.40,41 Second, this equation predicts that lines at other current densities should be parallel as long as the mechanism is unchanged, and that higher current densities will yield a lower portion of CO32− carrying the charge (increasing log
PCO2 with a negative slope equal to the effective ORR transfer coefficient. The slope in Fig. 4 is approximately −1, which is consistent with measurements of the effective transfer coefficient for the ORR in operating fuel cells.40,41 Second, this equation predicts that lines at other current densities should be parallel as long as the mechanism is unchanged, and that higher current densities will yield a lower portion of CO32− carrying the charge (increasing log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) e−/CO2). In fact, Fig. 4 shows that charge is overwhelmingly carried by OH− in these systems – even when the degree of carbonation at steady-state (Table S1 in the ESI†) is high. Only at very high CO2 concentrations (3200 ppm) and low operating current densities (0.2 A cm−2) is the portion of the charge carried by the CO32− ion significant (ca. 10%), though these are not realistic operating conditions for AEMFCs (whereas 400 ppm is). However, the fact that carbonate does carry charge through the system when CO2 is present has significant impacts on the operating voltage, which will be discussed later.
e−/CO2). In fact, Fig. 4 shows that charge is overwhelmingly carried by OH− in these systems – even when the degree of carbonation at steady-state (Table S1 in the ESI†) is high. Only at very high CO2 concentrations (3200 ppm) and low operating current densities (0.2 A cm−2) is the portion of the charge carried by the CO32− ion significant (ca. 10%), though these are not realistic operating conditions for AEMFCs (whereas 400 ppm is). However, the fact that carbonate does carry charge through the system when CO2 is present has significant impacts on the operating voltage, which will be discussed later.
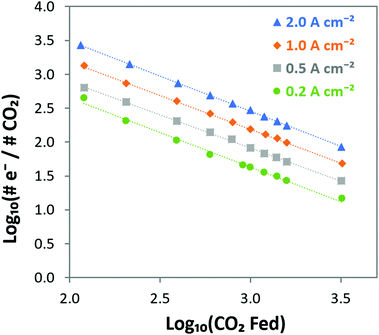 | ||
| Fig. 4 Visualizing the steady-state transport of CO2/CO32− from the cathode to the anode in AEMFCs operating at 0.2, 0.5, 1 and 2 A cm−2 at 60 °C over a wide range of CO2 concentrations. The linear relationship with a slope of −1 verifies the relationship predicted in eqn (14) between the cathode CO2 feed concentration and the portion of the charge that is carried by CO32−, showing that CO2 uptake and CO32− incorporation is a Nernstian process and driven by the ORR. | ||
The results from Fig. 2, 4 and Table S1 (ESI†) show that the large overpotentials experienced by AEMFCs when CO2 is added to the inlet streams are caused by a relatively small overall CO32− population. What is missing from the literature, and the discussion thus far, is a conclusive determination of which of the fundamental drivers (Ohmic, Nernstian or anode HOR kinetics) primarily control the carbonate-related losses. Such insight would be invaluable in understanding the behavior (and design) of ambient air-utilizing AEMFC systems.
Deconvolution of carbonate-related losses in operating AEMFCs
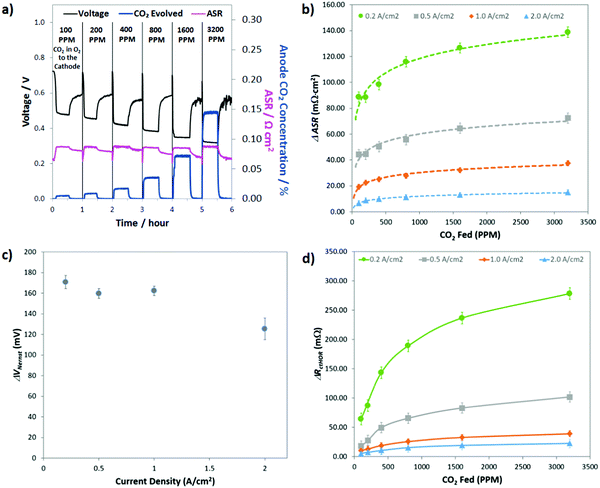
Though the previous two sections have established some basic parameters for the behavior of CO32− in operating AEMFCs (e.g. it induces polarization losses, is formed in quasi-steady-state with the ORR and its concentration gradient changes with feed concentration and current density), what would be the most helpful from a design and operation perspective is a quantitative deconvolution of the polarization losses. Identifying which of the carbonate-related processes is performance-limiting would allow for solutions to be proposed and evaluated systematically.The first step in quantifying the carbonate-related losses in operating AEMFCs was to track the performance decline for cells operating at steady-state at several current densities over a wide range of cathode CO2 concentrations. The response of a steady-state AEMFC operating at 1 A cm−2 to the introduction of 100, 200, 400, 800, 1600, and 3200 ppm CO2 to the cathode reacting gas is shown in Fig. 5a, and equivalent data for AEMFCs operating at 0.2, 0.5 and 2.0 A cm−2 are provided in Fig. S9a–c in the ESI.† Between each tested CO2 concentration, the cell was rapidly decarbonated as described in the Experimental section. The data shown in Fig. 5a and Fig. S9a–c (ESI†) show one hour of AEMFC behavior at each CO2 concentration – the first 30 min segment shows the carbonation event and the re-establishment of a new steady-state. The second 30 min segment shows the initial response following CO2 removal (where pure O2 is again fed).
As discussed earlier, the introduction of CO2 to operating AEMFCs initiates an interesting series of dynamic events that, in concert, lead to reduced steady-state performance through three mechanisms: increasing the Ohmic resistance (ΔASR), increasing the anode charge transfer resistance (ΔRctHOR) and increasing the thermodynamic anode potential (ΔVNernst). The challenge here is to find a systematic way to use the CO2 exposure and removal data in Fig. 5a (and Fig. S9 in the ESI†) to quantify the contribution of each of these resistances to the total CO2-related overpotential. The general approach to extracting these three losses from the data was consistent regardless of the experiment. A representative description for 400 ppm CO2 at 1.0 A cm−2 is given here for illustrative purposes, and then the summary of all of the calculated parameters is shown in Fig. 5b–d.
Before adding any CO2 to the AEMFC operating at 1.0 A cm−2, steady-state performance was established. The steady-state operating voltage at this condition was 0.72 V. The operating voltage for this cell is given by eqn (4). What this means is that the CO2-free steady-state operating voltage already contains RΩ,OH, RctORR and RmtORR; hence, the deviation of the operating voltage after adding CO2 will only come from ΔVNernst, ΔASR and ΔRctHOR, as shown in eqn (6). After adding 400 ppm CO2 to the cell, the new steady-state voltage that was reached was 0.44 V – meaning that the total CO2-related overpotential was ca. 280 mV. While the stoichiometries used in these experiments were high, leading to high CO2 dosages, the observed performance losses (in combination with the total CO2-related overpotential of ∼260 mV for a cell operating at 2.0 A cm−2 with 400 ppm CO2) suggest that the “self-purging” mechanism has a relatively modest effect in decarbonating the cell, and reducing CO2-related voltage losses to an acceptable level during operation on direct ambient air will be a significant challenge, and may not be possible at all.
The first CO2-related loss that was calculated was ΔASR. The ASR as a function of time is shown in Fig. 5a, and under this operating condition, ΔASR was 25 mΩ cm2. Assuming this ΔASR resulted in proportional Ohmic losses, at 1 A cm−2 this would result in an Ohmic loss of 25 mV. For completeness, we acknowledge that the measured ASR values do not yield the exact potential drop related to ion movement through the AEM due to the influence of diffusion.31,32 However, the value measured here does give an accurate measure of average anion mobility and is presented here as an overestimation of the maximum Ohmic resistance that could be attributed to carbonation. Perhaps what is most important is that this observation clearly shows that the ASR change caused by the emergence and transport of CO32− through the AEM represents a very small portion of the overall CO2-related overpotential (<10%).
For the AEMFC operating at 1.0 A cm−2 with 400 ppm CO2 in the cathode, at minimum, 255 mV of the CO2-related loss remains to be accounted for. The next stage of the deconvolution comes when CO2 is removed from the cathode stream. Experimentally, a rapid increase in the cell potential was observed, to ca. 0.54 V, though the potential never exactly levels off to reach a new steady-state. That is because the only way that a true steady-state can be reestablished is for all of the CO32− to be removed, either by waiting for many hours (Fig. S1, ESI†), or by accelerated decarbonation at 0.1 V (Fig. S2, ESI†). However, it is important to consider what is happening phenomenologically in the AEMFC when the cathode gas is switched from CO2-containing O2 to pure O2. When CO2 is removed from the cathode, no new CO32− anions are generated there and the concentration of CO32− at that electrode drops towards zero. As OH− is produced, the CO32− that was in the cathode and the AEM is progressively pushed toward the anode by migration (recall that the migrational residence time through the AEM at this current is 820 ms). This suggests that there will be a brief transient period to establish a new quasi steady-state (on the order of ∼10 min according to Fig. 5a) after which essentially all of the migrational charge that is carried from the cathode to the anode is carried by OH−. If this is the case, at the new quasi steady-state, no OH− will need to be provided by diffusion in the anode for the HOR to occur. Therefore, the voltage increase during this 10 min establishment of the new quasi steady-state after CO2 is removed can be mostly attributed to the relaxation of the kinetic limitations described by ΔRctHOR (though the new ASR acting on charge transport needs to be corrected for as well). At the condition above, 1.0 A cm−2 with 400 ppm CO2 fed to the cathode, ΔRctHOR was calculated by eqn (15) and (16).
| ΔVctHOR (mV) = [0.544 V − 0.443 V] × 1000 − (1.0 A cm−2)(83.5 mΩ cm2 − 75.3 mΩ cm2) = 93.7 mV | (15) |
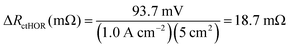 | (16) |
Because not all of the reacting catalyst in the anode can be assumed to be completely void of carbonation effects (because of the balance of carbonate migration and diffusion), the calculations made from eqn (15) and (16) are likely a lower limit for ΔRctHOR, though the real value should be close since the rate of carbonate removal after the initial voltage increase is slow.
From here, the Nernst-related loss can be calculated for this case: 162 mV (281 mV − 25 mV − 94 mV = 162 mV). Because the estimate for ΔRctHOR is a lower bound, 162 mV is an upper bound for the for ΔVNernst, though it should be close to the true value for the reasons discussed above. Interestingly, the Nernstian and charge-transport losses had a similar effect on the cell performance, and both were far more important in dictating the performance decline than the Ohmic loss.
Conducting the same analysis over the entire range of current densities and CO2 concentrations can yield values for the total CO2-related overpotential, ΔASR, ΔRctHOR, and ΔVNernst as well as the Ohmic voltage loss (ΔVOhmic) and the CO2-related kinetic polarization (ΔVctHOR) at every condition. All of these values are given in Table S2 of the ESI.† Performing the data deconvolution over such a wide range of current densities and cathode CO2 concentrations yielded some very revealing trends and important insight into the behavior of carbonated AEMFCs. Not too surprisingly, the total CO2-related overpotential was increased with decreasing current density and increasing CO2 concentration in the cathode (Table S2 in the ESI†). However, understanding why this happened requires digging into the trends in ΔASR, ΔRctHOR, and ΔVNernst more extensively.
Fig. 5b presents the ΔASR values at all conditions. As the concentration of CO2 in the cathode reacting gas was decreased, there was less of a negative impact on the ASR. This makes sense from the transient and steady-state experimental results (Table S1, ESI†), which showed that the total amount of CO32− in the AEMFC was lower at lower cathode CO2 concentration and increased current density. As discussed earlier, the overall trends in the ASR with current density and cathode CO2 concentration (Fig. 3) led to the conclusion that increasing the current density shifts the CO32− concentration gradient toward the anode electrode. Hence, with increasing current density, relatively less and less CO32− is present in the AEM (though the total CO32− flux is higher, Fig. 2c), resulting in a lower ASR.
The fact that the concentration gradient shifts toward the anode with current density might lead to the assumption that ΔVNernst (Fig. 5c) should also increase with current density. However, there are two counter points that require discussion. First, the total quantity of carbonate in the cell is decreasing with increasing current density, which alone might limit the achievable value for ΔVNernst, particularly at high currents. Second, the anode potential is measured at the outermost portion of the anode at the gas diffusion layer, which is likely the point of the highest CO32− concentration, as illustrated in Fig. 1, and it is possible for that one specific location to be close to saturation over a wide range of conditions. We observed that ΔVNernst appeared to decrease with increasing current density, though the values at current densities ≤1.0 A cm−2 were very similar.
The assertion that the outermost portion of the anode can be close to saturation was supported by the magnitude of ΔVNernst at the lower current densities, ∼165 mV. The effective alkalinity of an AEMFC cathode is between pH 13–14. It is also known that CO32− is overwhelmingly the dominant carbon-based charge carrier and this can only happen in water at pH values >11. Therefore, the maximum pH shift that could be expected at the anode in an operating cell would be 3, resulting in a ΔVNernst,max of ca. 180 mV. The only data point in Fig. 5c where ΔVNernst is markedly lower is at very high current, 2.0 A cm−2, where ΔVNernst is ∼125 mV. This lower value can be explained by either the lower overall carbonate concentration in the cell and anode at higher currents, and/or the development of a mixed potential throughout the anode because at high current density there is a significant number of OH− ions being released throughout the anode as CO2 is evolved through the reverse of eqn (2) and (3), though the root cause for this behavior will likely need to be teased out through computational modeling. It is also noteworthy that ΔVNernst was essentially unaffected by the cathode CO2 concentration, which gives additional support to the arguments above. One area where the higher carbonate concentration in the anode did have a major impact on the AEMFC behavior is ΔRctHOR, Fig. 5d. At higher overall carbonate content (increased cathode CO2 concentration and/or lower current density) ΔRctHOR was also higher, and the current density had a particularly profound influence on the effect of the cathode CO2 concentration. This observation yields important insight into the location of carbonate in electrodes, suggesting that higher current densities compress the volume occupied by carbonates to the outermost portion of the anode, which effectively allows more catalyst sites to have easy access to reacting OH−.
AEMFC response at low CO2 concentrations
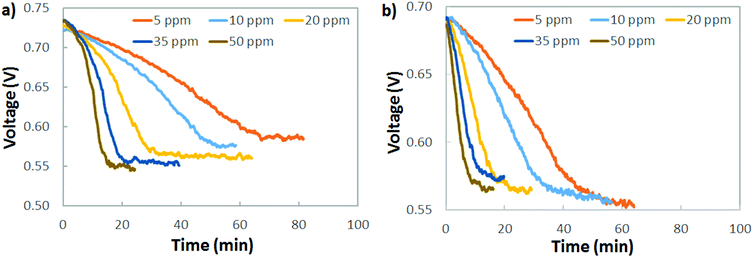
A practical interpretation of the experiments shown in Fig. 5 is that the polarization losses from AEMFC carbonation are significant at all current densities and near-ambient CO2 concentrations, and that AEMFCs will likely require pre-scrubbing of CO2 from the operating air. Additionally, the dynamics of CO2 uptake (fast) and release (slow) mean that even if CO2 could be quickly removed from the anode stream to avoid significant accumulation, losses would still be high. One sensible approach to reducing CO2-related overpotential is to lower the cathode inlet concentration, which is particularly intriguing for stationary implementations of AEMFCs where the volume and weight of a CO2 scrubber is less of a concern than it is for mobile or transportation applications. Fig. 6a explores the response of an AEMFC operating at 1 A cm−2 with 5–50 ppm CO2 in the cathode reacting gas. Though the voltage loss was less than at higher concentrations, even down to 5–10 ppm CO2 in the cathode, the CO2-related polarization was significant, approximately 140 mV.Fig. 6b shows the response of an AEMFC operating at 1 A cm−2 with 5–50 ppm CO2 added to the anode H2 reacting gas. The behavior of low-level CO2 in the anode is very similar to the cathode. At 10 ppm, the total CO2-related voltage loss was 136 mV. For CO2 present in both the cathode and anode, Fig. 6 suggests that if there is a lower threshold below which an operating AEMFC is immune to carbonation, it is very low – below 5 ppm (although it should be noted that dosage is also important and decreasing flow rates could also have a beneficial impact).
Influence of temperature on CO2-related polarization losses at 400 ppm
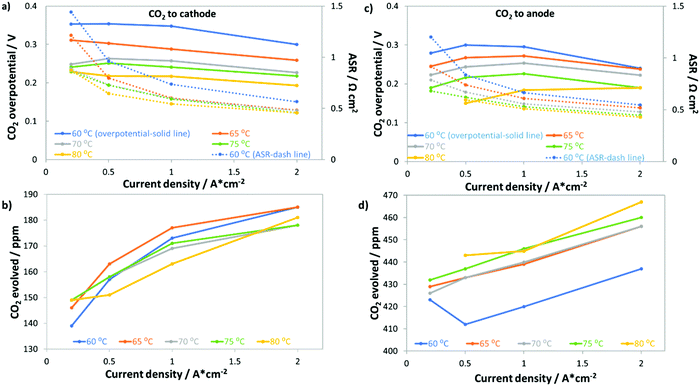
Fig. 6 shows that removing even a large portion of the CO2 in ambient air will not be sufficient to eliminate the CO2-related losses in operating AEMFCs. In fact, we demonstrated that even at 5 ppm CO2 significant performance losses occurred. Therefore, it is important for researchers to identify some fundamental and operational properties of the system that can be manipulated to reduce the AEMFC sensitivity to CO2. One pathway to reducing the amount of carbonate accumulated in the system is to increase the cell operating temperature. Increasing temperature could possibly impact cell carbonation because: (i) CO2 has lower solubility in water as the temperature is increased;42 (ii) the kinetics for CO2 release (reverse of eqn (2) and (3)) at the anode will improve; (iii) the mass transport rate of evolved gaseous CO2 from the anode will increase; and (iv) the intrinsic kinetics for the ORR and HOR will improve.Fig. 7 summarizes the response of AEMFCs with a LDPE–BTMA membrane operating at 0.2, 0.5, 1.0 and 2.0 A cm−2 and several temperatures (60, 65, 70, 75, and 80 °C) following the introduction of 400 ppm CO2 to the cathode or anode. Regardless of where the CO2 was introduced, increasing the temperature simultaneously decreased the total CO2 overpotential and the ASR (Fig. 7a and c). This experimental result is in stark contrast to recent modeling results that suggested increasing the cell temperature would not have a beneficial effect on AEMFC operation with CO2 in the feed gas.16Fig. 7b shows that as the temperature was increased, the concentration of CO2 being emitted from the anode side of the cell (when it is fed to the cathode) decreased. The most likely explanation for this trend, and coupled performance increase, is that less CO2 was taken up into the system. Fig. 7d shows that when CO2 was fed to the anode, increasing the temperature resulted in lower CO2 uptake at that electrode as well, which is shown by the increasing concentration of CO2 in the anode effluent. It should also be noted in Fig. 7b and d that the values trend upward with increasing current density due to the consumption of the fuel and oxidant gases. Positively, the improved performance at elevated temperatures suggests that increasing temperature is indeed one possible mechanism to improve the CO2 tolerance of operating AEMFCs; however, the CO2-related overpotential is still too high for many practical applications. A combination of lower CO2 concentration, more modest air stoichiometry, and elevated temperature can further reduce the total CO2 overpotential. For instance, we observed that an AEMFC operating at 1 A cm−2 and 80 °C with 10 ppm CO2 fed to the cathode (the same LDPE–BTMA membrane) had a total CO2 overpotential of only 90 mV.
Deconvoluted data for AEMFCs operating at different temperatures but at a constant current of 1 A cm−2 and constant cathode CO2 concentration of 400 ppm (showing the ΔASR, ΔVNernst and ΔRctHOR) can be found in Table S3 in the ESI.† As expected, the ASR generally decreased with increasing temperature due to the lower quantity of carbonates that were taken up into the membrane. However, the ASR value only varied slightly with increasing temperature, which meant that a similar portion of CO32− anions were carrying the charge through the AEM (supported by the results of accelerated decarbonation experiments at 0.1 V, Table S4 in the ESI†), which led ΔRctHOR to be fairly constant with temperature as well. Therefore, the primary impact of an overall reduced number of CO32− anions in the AEM was that the carbonate accumulation in the anode (and hence the concentration gradient across the cell) was less severe with increased temperature. As a result, ΔVNernst was the most dependent on temperature, decreasing by nearly 50% from 60–80 °C.
It is possible that even higher temperatures (>90 °C) may help. Though no AEMs are currently readily available with stability above 80 °C in highly alkaline media that also have acceptable conductivity and water transport properties,3 there is promising work ongoing in this area. Recent reports by Yan and coworkers3,43 have shown that it is possible to create AEMs that are conductive and stable to at least 95 °C. Another important consideration for AEM and AEMFC researchers is that the membrane chemistry (both backbone and headgroup) and morphology are likely to influence the uptake, transport and release of CO2. What this really points to is that improving the CO2 tolerance of AEMFCs will likely require a combination of approaches to achieve success, at least some of which are not known today and will be particularly challenging for dynamic operation.
Conclusions
Even in highly performing AEMFCs, the addition of CO2 has a severe negative impact, where the cell operating voltage is generally decreased by 200–400 mV depending on the reaction conditions. Lower CO2 concentration in the reacting gas, higher current density and higher operating temperature all reduce the voltage penalty, but none have been shown be able to sufficiently minimize the CO2 impact. One of the primary reasons for this is that decarbonation of the cell does not occur through direct electrochemical reaction. This means that decarbonation during operation by the so-called “self-purging” mechanism is slow, taking several hours even after only transient exposure to CO2. Hence, “self-purging” cannot be relied upon to decarbonate AEMFCs efficiently.The dominating loss in operating AEMFCs in the presence of CO2 is not due to an increase in the Ohmic resistance from electrolyte carbonation. The dominating mechanism for voltage loss is accumulation of carbonate anions in the anode, which results in two performance-robbing mechanisms: (1) a Nernstian thermodynamic shift in the anode potential from a decrease in the anode pH with carbonates; and (2) an increase in charge transfer resistance due to a lack of availability of reacting OH− anions. The CO2 concentration in the cathode and the current density are both determining factors for the quantity of CO32− in the system, and the current density appears to play a primary role in dictating the CO32− location and distribution. The HOR charge transfer resistance increases markedly with both increased CO2 concentration and lower current density. Increasing the cell operating temperature appears to have almost no effect on the charge transfer resistance, but a significant effect on the Nernstian loss, meaning that the total CO2-related overpotential can be reduced by increasing the temperature – or better yet, through a combination of higher current density, lower CO2 concentration and higher operating temperature.
These new insights can help both modeling groups and experimental researchers to better understand operating AEMFCs, as well as allow them to pose and assess new solutions.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
USC gratefully acknowledges the financial support of the U.S. National Science Foundation (Award Number: 1803189) for the effort expended by Y. Z., T. J. O. and W. E. M. to perform the AEMFC experiments, analyze data and prepare the manuscript. The AEM and AEI materials were synthesized using resources funded by the UK's Engineering and Physical Sciences Research Council (grant EP/M014371/1). Funding for B. S. P. was provided by the U.S. Department of Energy Office of Energy Efficiency and Renewable Energy Fuel Cell Technologies Office. The views and opinions of the authors expressed herein do not necessarily state or reflect those of the United States Government or any agency thereof. Neither the United States Government nor any agency thereof, nor any of their employees, makes any warranty, expressed or implied, or assumes any legal liability or responsibility for the accuracy, completeness, or usefulness of any information, apparatus, product, or process disclosed, or represents that its use would not infringe privately owned rights. The U.S. Government retains and the publisher, by accepting the article for publication, acknowledges that the U.S. Government retains a nonexclusive, paid-up, irrevocable, worldwide license to publish or reproduce the published form of this work, or allow others to do so, for U.S. Government purposes.References
- B. P. Setzler, Z. Zhuang, J. A. Wittkopf and Y. Yan, Nat. Nanotechnol., 2016, 11, 1020–1025 CrossRef CAS PubMed.
- J. R. Varcoe, P. Atanassov, D. R. Dekel, A. M. Herring, M. A. Hickner, P. A. Kohl, A. R. Kucernak, W. E. Mustain, K. Nijmeijer, K. Scott, T. Xu and L. Zhuang, Energy Environ. Sci., 2014, 7, 3135–3191 RSC.
- J. Wang, Y. Zhao, B. P. Setzler, S. Rojas-carbonell, C. Ben Yehuda, A. Amel, M. Page, L. Wang, K. Hu, L. Shi, S. Gottesfeld, B. Xu and Y. Yan, Nat. Energy, 2019, 4, 392–398 CrossRef CAS.
- S. Gottesfeld, D. R. Dekel, M. Page, C. Bae, Y. Yan, P. Zelenay and Y. S. Kim, J. Power Sources, 2018, 375, 170–184 CrossRef CAS.
- W. E. Mustain, Curr. Opin. Electrochem., 2018, 12, 233–239 CrossRef CAS.
- S. Maurya, S. Noh, I. Matanovic, E. J. Park, C. N. Villarrubia, U. Martinez, J. Han, C. Bae and Y. S. Kim, Energy Environ. Sci., 2018, 11, 3283–3291 RSC.
- L. Wang, J. J. Brink, Y. Liu, A. M. Herring, J. Ponce-González, D. K. Whelligan and J. R. Varcoe, Energy Environ. Sci., 2017, 10, 2154–2167 RSC.
- T. J. Omasta, L. Wang, X. Peng, C. A. Lewis, J. R. Varcoe and W. E. Mustain, J. Power Sources, 2018, 375, 205–213 CrossRef CAS.
- T. J. Omasta, A. M. Park, J. M. Lamanna, Y. Zhang, X. Peng, L. Wang, D. L. Jacobson, J. R. Varcoe, D. S. Hussey, B. S. Pivovar and W. E. Mustain, Energy Environ. Sci., 2018, 11, 551–558 RSC.
- G. Huang, M. Mandal, X. Peng, A. C. Yang-Neyerlin, B. S. Pivovar, W. E. Mustain and P. A. Kohl, J. Electrochem. Soc., 2019, 166, F637–F644 CrossRef.
- S. M. Alia, K. Neyerlin, K. Hurst, J. W. Zack, S. A. Mauger, W. W. McNeary, A. Weimer, W. Medlin, S. Zaccarine, C. Ngo, S. Pylypenko, K. Buechler and B. S. Pivovar, The Electrochemical Society Meeting Abstracts, 2018, vol. 44, p. 1505.
- S. M. Alia, S. Stariha, R. L. Borup and B. S. Pivovar, The Electrochemical Society Meeting Abstracts, 2018, vol. 46, p. 1604.
- W. E. Mustain, The Electrochemical Society Meeting Abstracts, 2018, vol. 47, p. 1637.
- T. J. Omasta, X. Peng and W. E. Mustain, The Electrochemical Society Meeting Abstracts, 2018, vol. 30, p. 1754.
- N. Ziv, W. E. Mustain and D. R. Dekel, ChemSusChem, 2018, 11, 1136–1150 CrossRef CAS PubMed.
- U. Krewer, C. Weinzierl, N. Ziv and D. R. Dekel, Electrochim. Acta, 2018, 263, 433–446 CrossRef CAS.
- M. R. Gerhardt, L. M. Pant, H.-S. Shiau and A. Z. Weber, ECS Trans., 2018, 86, 15–24 CrossRef CAS.
- S. D. Poynton, R. C. T. Slade, T. J. Omasta, W. E. Mustain, R. Escudero-Cid, P. Ocón and J. R. Varcoe, J. Mater. Chem. A, 2014, 2, 5124–5130 RSC.
- J. Ponce-Gonzalez, D. K. Whelligan, L. Wang, R. Bance-Soualhi, Y. Wang, Y. Peng, H. Peng, D. C. Apperley, H. N. Sarode, T. P. Pandey, A. G. Divekar, S. Seifert, A. M. Herring, L. Zhuang and J. R. Varcoe, Energy Environ. Sci., 2016, 9, 3724–3735 RSC.
- R. Zeng, S. D. Poynton, J. P. Kizewski, R. C. T. Slade and J. R. Varcoe, Electrochem. Commun., 2010, 12, 823–825 CrossRef CAS.
- A. Amel, N. Gavish, L. Zhu, D. R. Dekel, M. A. Hickner and Y. Ein-Eli, J. Membr. Sci., 2016, 514, 125–134 CrossRef CAS.
- T. P. Pandey, A. M. Maes, H. N. Sarode, B. D. Peters, S. Lavina, K. Vezzù, Y. Yang, S. D. Poynton, J. R. Varcoe, S. Seifert, M. W. Liberatore, V. Di Noto and A. M. Herring, Phys. Chem. Chem. Phys., 2015, 17, 4367–4378 RSC.
- M. L. Disabb-Miller, Y. Zha, A. J. DeCarlo, M. Pawar, G. N. Tew and M. A. Hickner, Macromolecules, 2013, 46, 9279–9287 CrossRef CAS.
- Z. Siroma, S. Watanabe, K. Yasuda, K. Fukuta and H. Yanagi, ECS Trans., 2010, 33, 1935–1943 CAS.
- J. A. Wrubel, A. A. Peracchio, B. N. Cassenti, T. D. Myles, K. N. Grew and W. K. S. Chiu, J. Electrochem. Soc., 2017, 164, F1063–F1073 CrossRef CAS.
- M. R. Gerhardt, L. M. Pant and A. Z. Weber, J. Electrochem. Soc., 2019, 166, F3180–F3192 CrossRef CAS.
- Y. Wang, L. Li, L. Hu, L. Zhuang, J. Lu and B. Xu, Electrochem. Commun., 2003, 5, 662–666 CrossRef CAS.
- K. Fukuta, in AMFC Workshop, 2011.
- J. A. Vega, S. Smith and W. E. Mustain, J. Electrochem. Soc., 2011, 158, B349–B354 CrossRef CAS.
- Y. Matsui, M. Saito, A. Tasaka and M. Inaba, ECS Trans., 2010, 25, 105–110 CAS.
- T. A. Greszler, T. E. Moylan and H. A. Gasteiger, Handbook of Fuel Cells-Fundamentals, Technology and Applications, 2009, vol. 6, pp. 729–748 Search PubMed.
- T. Greszler, T. Moylan and H. Gasteiger, The Electrochemical Society Meeting Abstracts, 2008, vol. 11, p. 955.
- B. Kienitz, B. Pivovar, T. Zawodzinski and F. H. Garzon, J. Electrochem. Soc., 2011, 158, B1175–B1183 CrossRef CAS.
- B. Kienitz, The effects of cationic contamination on polymer electrolyte membrane fuel cells, PhD thesis, Case Western Reserve University, 2009 Search PubMed.
- Y. A. Gomez, A. Oyarce, G. Lindbergh and C. Lagergren, J. Electrochem. Soc., 2018, 165, F189–F197 CrossRef CAS.
- M. Inaba, Y. Matsui, M. Saito, A. Tasaka, K. Fukuta, S. Watanabe and H. Yanagi, Electrochemistry, 2011, 5, 322–325 CrossRef.
- H. Yanagi and K. Fukuta, ECS Trans., 2008, 16, 257–262 CAS.
- A. G. Divekar, B. S. Pivovar and A. M. Herring, ECS Trans., 2018, 86, 643–648 CrossRef CAS.
- W. A. Rigdon, T. J. Omasta, C. Lewis, M. A. Hickner, J. R. Varcoe, J. N. Renner, K. E. Ayers and W. E. Mustain, J. Electrochem. Energy Convers. Storage, 2017, 14, 1–8 Search PubMed.
- J. X. Wang, F. A. Uribe, T. E. Springer, J. Zhangc and R. R. Adzic, Faraday Discuss., 2008, 140, 347–362 RSC.
- H. Xu, Y. Song, H. R. Kunz and J. M. Fenton, J. Electrochem. Soc., 2005, 152, A1828 CrossRef CAS.
- B. Pivovar, D. Ruddy, M. Sturgeon and H. Long, FY 2013 Annu. Prog. Rep. DOE Hydrog. Fuel Cells Progr., 2013, v235–v237.
- T. Wang, L. Shi, J. Wang, Y. Zhao, B. P. Setzler, S. Rojas-carbonell and Y. Yan, J. Electrochem. Soc., 2019, 166, F3305–F3310 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Fig. S1–S9, Tables S1–S4, experimental details and additional analysis. See DOI: 10.1039/c9ee01334b |
| This journal is © The Royal Society of Chemistry 2019 |