Open Access Article
Open Access ArticleCity-scale decarbonization experiments with integrated energy systems†
Jacques A.
de Chalendar
 *a,
Peter W.
Glynn
b and
Sally M.
Benson
*a,
Peter W.
Glynn
b and
Sally M.
Benson
 a
a
aDepartment of Energy Resources Engineering, Stanford University, Stanford, CA, USA. E-mail: jdechalendar@stanford.edu
bDepartment of Management Sciences and Engineering, Stanford University, Stanford, CA, USA
First published on 29th April 2019
Abstract
Decarbonization of electricity generation together with electrification of energy-and-carbon-intensive services such as heating and cooling is needed to address ambitious climate goals. Here we show that city-scale electrification of heat with large-scale thermal storage also cost-effectively unlocks significant additional operational benefits for the power sector. We build an optimization model of fully electrified district heating and cooling networks integrated with other electric loads. We leverage real-world consumption and operational data from a first-of-a-kind facility that meets heating, cooling and electrical energy requirements equivalent to a city of 30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 people. Using our model, we compute optimal operational strategies for the controllable loads and thermal storage in this system under different economic hypotheses. In our example, electrifying the previously gas-based heating and cooling infrastructure has led to a 65% reduction in the overall campus carbon footprint. Through least-cost scheduling, the load shape of the aggregate energy system can be flattened and annual peak power demand can be reduced by 15%. Through carbon-aware scheduling that takes advantage of variations in grid power carbon intensity, heating and cooling emissions could further decrease by over 40% in 2025 compared to the 2016 baseline, assuming a policy-compliant electricity mix for California. However, rethinking electricity rates based on peak power usage will be needed to make carbon-aware scheduling economically attractive.
000 people. Using our model, we compute optimal operational strategies for the controllable loads and thermal storage in this system under different economic hypotheses. In our example, electrifying the previously gas-based heating and cooling infrastructure has led to a 65% reduction in the overall campus carbon footprint. Through least-cost scheduling, the load shape of the aggregate energy system can be flattened and annual peak power demand can be reduced by 15%. Through carbon-aware scheduling that takes advantage of variations in grid power carbon intensity, heating and cooling emissions could further decrease by over 40% in 2025 compared to the 2016 baseline, assuming a policy-compliant electricity mix for California. However, rethinking electricity rates based on peak power usage will be needed to make carbon-aware scheduling economically attractive.
Broader contextIt was estimated in 2017 that two-thirds of global carbon emissions from fuel combustion were attributable to electricity, heat and transportation. Such statistics are strong arguments for massively electrifying transportation and heat while decarbonizing electricity: the power sector will play a pivotal role in a low-carbon future, and successfully integrating different energy networks will be a key component of that future. Cross-sectoral energy flexibility will have special value, both to face structural uncertainty about the future and to ease the integration of non-dispatchable renewable generation. Urban centers are large and growing. Meeting their heating, cooling and electrical energy demands is both a challenge and an opportunity. By considering consumption data from a first-of-a-kind facility that meets energy requirements equivalent to a city of 30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 people, this work provides a prime example of how to reduce challenging heating and cooling related emissions. Thermal-storage-backed, electrified district energy systems open the door to least-cost or carbon-aware scheduling and represent a very real option for introducing low-cost flexibility in future power grids while decarbonizing the energy sector. This option should be considered alongside electrochemical storage as it will often represent a cheaper alternative to provide the same energy services. 000 people, this work provides a prime example of how to reduce challenging heating and cooling related emissions. Thermal-storage-backed, electrified district energy systems open the door to least-cost or carbon-aware scheduling and represent a very real option for introducing low-cost flexibility in future power grids while decarbonizing the energy sector. This option should be considered alongside electrochemical storage as it will often represent a cheaper alternative to provide the same energy services.
|
Driven by the need to curb global emissions,1,2 large-scale penetration of renewables is occurring around the world.3 While adding carbon-free and zero-marginal cost renewable electricity has many advantages, it creates a challenge for power grid operators both at the transmission and distribution system levels and entails a necessary paradigm shift in overall system design and operation to accommodate these new sources of variability.4–9 Electric loads can offer energy services and flexibility, in the form of demand-side management,10–13 to maintain the balance of supply and demand that is so critical to reliable grid operations. In this work, we explore a deeper integration between the heat and power sectors in an urban setting through the grid-friendly management of electrified district heating and cooling networks with thermal storage. The discussion is of special relevance in the context of rapid urbanization, grid decarbonization, and the interaction between the urban environment and energy systems.
Alongside electricity and transportation, heat is one of the three main pillars of our energy systems, but also one of the major contributors to carbon dioxide (CO2) emissions: the International Energy Agency estimates that two thirds of global CO2 emissions from fuel combustion are attributable to two sectors: the generation of electricity and heat (42%) and transport (24%) in 2015.14 Heating buildings alone corresponds to about 13% of global energy demand.15 While the word heat will be used throughout this paper, most of the discussion applies to both heating and cooling systems.
If heat and transportation are electrified in an uncontrolled fashion, they become a threat to the stability of the power system because of the sheer energy volumes involved. On the other hand, there are numerous opportunities for virtual storage that arise from the fact that physical processes, and therefore characteristic operational times, are typically much slower in the heat sector compared to the electrical energy sector. This potentially significant source of flexibility will only appear through a deeper integration of our energy systems across energy pathways and scales.16,17 Given that forecasting our long-term energy needs is so difficult,18 such cross-sectoral and structural flexibility will have special value. There is a wealth of previous work on managing demand-side resources to prove that exploiting their flexibility is a cost-effective way of integrating renewable energy. At the residential and commercial levels, Thermostatically Controlled Loads (TCLs) are a popular target19–28 because they represent such a high share of home energy consumption (80% in Europe and 60% in the United States), but several other controllable loads show potential.29–34 Industrial demand response has also been studied extensively35–38 since the famous Alcoa aluminum smelting plant experiment.39
District heating systems originated in the 1880s and supplied 11.5 EJ of heat in 2014, 85% of which were for China, Russia, and the European Union (to be compared with a total heat demand from buildings of 74 EJ in 2014).15 District cooling systems originated much more recently, in the 1960s, and supply around 300 PJ of cooling each year (200 PJ for the Middle East, 80 PJ for the US, and 10 PJ for Europe).15 In most of the European Union, China and Japan, district cooling capacity represents less than a percent of district heating capacity (except France, Italy, Norway and Sweden where it represents less than 4%), to be compared to 30% in the United States, where the vast majority of district cooling systems use chilled water supplied by steam-driven absorption chillers.40,41
Large-scale, fully electric, district energy systems integrating hot water and chilled water delivery such as the one that provides the data for this study remain first-of-a-kind experiments. Only 1% of the energy used by district energy in the U.S. was electrical energy (all for electric chillers). The bulk of the academic literature on integrating heat and electricity at the district level has originated from and focused on European and, in particular, Scandinavian countries.15,42–45 In the case of Sweden, the country consumed 200 PJ of heat in 2014, 55% of which were met by district heating and 28% by local heat pumps.46 Notable recent work has focused on optimizing design and operations, stochastic control for district heating networks, as well as how the industry can adapt to heat demand reductions and future energy prices.47–52 A recent example of renewed interest in district heating in the context of decarbonization and grid integration of large-scale renewable power is in northern China, where Combined Heat and Power (CHP) plants constrain the flexibility of the regional grid there.53–55 In the winter, the (mostly coal-based) CHP units are used to supply district heating networks, but also produce electrical energy, thereby leading to high curtailment rates for wind energy (15% in 2015).56 In the majority of the literature related to district energy, CHP is the main heat producer, and the (more recent) cooling networks receive much less attention.
However, recent efforts have highlighted the value of large-scale heat pumps, electric boilers and thermal storage for decarbonizing the energy system.57–60 Calls for 100% renewable energy systems emphasize the need for a holistic, cross-sector approach.61,62 City63 and country-scale64,65 road maps highlight that electrification of heat (and transport) will likely be required to achieve climate goals and is possible without compromising grid reliability and at low cost,66 although other low-carbon heat supply options have been explored, such as hydrogen-based pathways for micro-CHP.67
Here we expand on the benefits of electrified heating and cooling by showing that, when achieved at the district scale, it also opens the door to inexpensive flexibility for the power grid, whether in the form of demand charge management, demand response or carbon-aware scheduling. In this paper, we critically assess the financial, grid and carbon benefits of thermal-storage-backed electrified district energy systems, in an operational context. We leverage a unique source of real-world data to assess these operational and decarbonization benefits for the power grid. A data-driven optimization model is built to study the operations schedules for such systems under different pricing schemes and used to show how they can provide flexibility, both to the local energy ecosystem they serve and to the larger grid they draw power from, by consuming or shedding load at different times of the day.
By applying our modeling framework to a real-life case study, we are able to provide insights into the opportunities from the coupling of heat and electricity in solar-dominated power grids. In this work, we assume that the heating and cooling infrastructure is fixed to our case study and study operational behavior under different economic hypotheses. However, the insights we derive are widely applicable to other district heat electrification designs incorporating thermal storage at scale.
Storage-backed heat recovery to meet concurrent heating and cooling needs
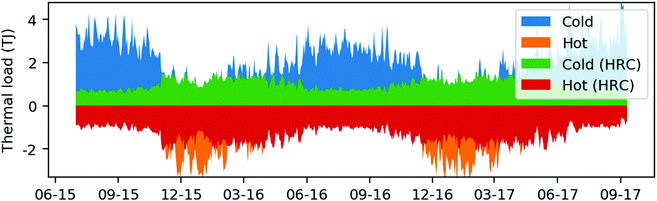
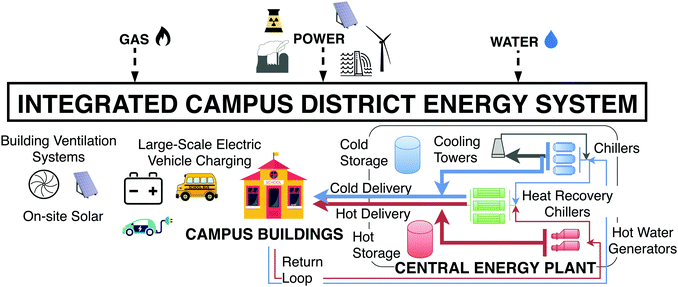
As the main supplier of heating and cooling to over 150 buildings on campus, the California-based Stanford Energy System Innovations (SESI) project provides an ideal case study for this work.68 In a $485 million overhaul completed in 2015, the campus district energy system switched from a gas-fired co-generation-based system with steam distribution to the current electrified, integrated heating and cooling system with hot and cold water distribution, meeting the bulk of its heating and cooling loads with large heat recovery chillers. These are electric heat pumps that use the return heating and cooling streams from the buildings as a heat sink and source, respectively, and that simultaneously produce usable heating and cooling streams. The energy system redesign led to an estimated reduction of 65% in the annual carbon emissions that can be associated with campus energy operations, from 200 to 70 thousand tonnes of CO2 (see Note 1; metric tonnes will be used throughout this paper, ESI†).From 0.6 to 2.9 TJ of hot water and 0.5 to 5.7 TJ of chilled water is produced daily with electric heat pumps and stored in large tanks before it is sent to the campus buildings. These also consume from 1.9 to 2.4 TJ of electrical energy daily. Annually, the campus uses 0.81 PJ of cooling, 0.57 PJ of heating and 0.75 PJ of electricity. This represents the annual energy consumption of 33![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 households in California (more detailed energy consumption data can be found in the ESI†). Typical for a university campus, thermal loads are seasonal, whereas electrical loads are mostly driven by occupancy. Although the demand for hot water is dominant in the winter and chilled water dominant in the summer, a significant daily overlap for heating and cooling demand can be observed. Fig. 1 shows this daily overlap in 2016 and how up to 51% of cooling and 90% of heating loads could potentially be met by electric Heat Recovery Chillers (HRCs) simultaneously producing heating and cooling. When there are greater energy needs for heating in the winter or cooling in the summer, the HRCs are complemented by chillers and gas-fired boilers, respectively. The maximum cooling output of the chillers is 1.6 times that of the HRCs, and the maximum heating output of the boilers is 1.5 times more that of the HRCs.
000 households in California (more detailed energy consumption data can be found in the ESI†). Typical for a university campus, thermal loads are seasonal, whereas electrical loads are mostly driven by occupancy. Although the demand for hot water is dominant in the winter and chilled water dominant in the summer, a significant daily overlap for heating and cooling demand can be observed. Fig. 1 shows this daily overlap in 2016 and how up to 51% of cooling and 90% of heating loads could potentially be met by electric Heat Recovery Chillers (HRCs) simultaneously producing heating and cooling. When there are greater energy needs for heating in the winter or cooling in the summer, the HRCs are complemented by chillers and gas-fired boilers, respectively. The maximum cooling output of the chillers is 1.6 times that of the HRCs, and the maximum heating output of the boilers is 1.5 times more that of the HRCs.
Nine different designs were considered: steam was compared to hot water as a carrier for heat, co-generation was compared to buying power from a utility and the value of heat recovery was assessed.68 The selected design was the lowest cost option, with a net present cost of $1.3 billion from 2015–2050, to be compared with $1.6 billion for the business-as-usual option. In the remainder of this paper, the discussion is focused on operational considerations. We assume the infrastructure design is fixed to the one shown in Fig. 2, and assess the additional financial, carbon and grid benefits from operating this integrated system under different regimes.
Optimal operations scheduling for district energy systems
To study the rational behavior of a district energy system under different pricing signals, an optimization model is built to minimize the campus energy bill over the course of a year. Like many large energy consumers, Stanford pays a monthly price for gas and both a time-varying price for electrical energy and a capacity-based price for its maximum electrical demand (called a demand charge). The problem solved here is that faced by the manager of the CEP: (i) decide how much power and gas to buy from the grid at each hour, and (ii) set the hourly schedule of the different machines in the CEP in order to meet demand from the campus buildings for electricity, heating, and cooling. The yearly scheduling problem is formulated in the Methods section as a Quadratic Program with around 150k variables and 240k constraints. This formulation is implemented using the Julia JuMP package69 and solved using the Gurobi software.70 Since our aim is to assess the operational value of thermal storage, we solve a planning problem based on historical data. It should be noted that our formulation could be used almost as is to implement a control strategy however, e.g., using a classic look-ahead algorithm like Model Predictive Control.71We use a modular approach to describe the different components of the campus district energy system, where the different terms in the objective function are additive and tied together by global import variables for quantities such as electricity and gas. A program was built to describe the rational behavior of the Stanford energy system, but the framework that is used could easily be extended to describe a district energy system with other components, such as CHP for heat generation.
Real energy data are used, measured on campus during the year of 2016 for the heating, cooling and electricity demand from the campus buildings, as well as the publicly available Locational Marginal Price (LMP) paid by the university. The possibility for the campus management to self-impose a carbon tax is also modeled. In that case, the price for electricity is augmented by an hourly price that is calculated from the carbon tax and hourly Average Emissions Factors (AEFs) for the California Independent System Operator's (CAISO) balancing area. These AEFs are estimated from the Intergovernmental Panel on Climate Change's Life-Cycle Analysis estimates for generation sources and CAISO historical generation data, as described in detail in the Methods section.
Power and energy scheduling
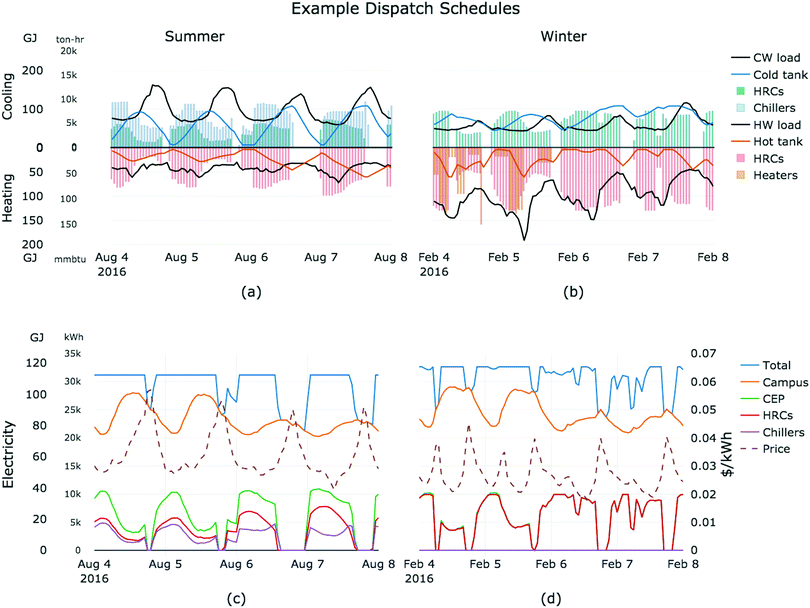
Fig. 3 shows the thermal dispatch schedules and corresponding power injections that are computed by the optimization model for four days in the summer and winter of 2016. Both in the summer and winter, the bulk of the heating and cooling loads is met by the heat recovery chillers; these are supplemented by chillers in the summer, and gas-fired heaters in the winter. The hot and cold thermal storage tanks are used to create hot and chilled water buffers and shift the electrical energy consumption of the CEP throughout the day. They can store five hours to a day's worth of both heating and cooling loads. As operated today, the HRCs produce most heavily at night and when both the electricity price and the campus electricity load are low. During peak price periods, they are typically turned off.These figures illustrate how systems that couple heating and cooling streams can adapt to a range of operating conditions. The utilization patterns of the thermal storage highlight very different operating regimes: whereas they are fully charged and discharged in a fairly simple, repetitive daily pattern during the summer, the trajectories that are chosen by the optimization model are more complex in the winter. For 2016, 50% of cooling and 89% of heating loads are met by the HRCs, within two percent of the values calculated in Fig. 1. The remainder is met by the chillers and heaters, so that electricity is the main energy input to the system, and yearly gas consumption is kept low.
The hot and cold storage provide a buffer to decouple the output hot and cold water streams from the HRCs and shift loads in time. By using this buffer, the CEP is scheduled so as to avoid high price periods and minimize peak demand. The flat electrical profile that is presented by the aggregate campus to the utility is typical of demand-side resources under a schedule that includes a demand charge. Here, the annual peak demand is reduced from 40 to 34 MW (15%) through the introduction of thermal storage. Meeting loads with the same number of HRCs and boilers but without thermal energy storage would also require almost twice as many chillers, which represents significant capital costs (see Economic case section below).
The CEP consumes only 25% of the annual electrical campus energy, but its maximum power draw represents 45% of the campus peak load, so the energy impacts of shifting loads are necessarily less significant than the power impacts. Typical electricity distribution systems are sized for the worst-case load, in this case 48 MW, or 29% above the 2016 annual peak load with thermal storage.
Carbon-aware scheduling
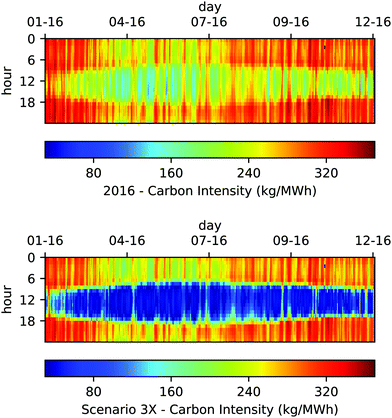
We now turn to carbon-aware operations scheduling for district energy systems. Since we are considering a hypothetical future with some form of carbon pricing, a decision needs to be made on how to account for carbon. In order for carbon considerations to guide scheduling decisions, we choose to attribute a carbon intensity to electrical energy flowing through the power system in units of kgCO2 per MW h. Carbon-aware scheduling will have value in grids where the carbon intensity varies over the course of the day depending on the mix of generating sources. In the extreme case with a zero-emission grid, carbon-aware scheduling becomes irrelevant.Two scenarios for the AEFs of the CAISO balancing area are shown in Fig. 4 and correspond to (top) AEFs that are estimated using 2016 generation data, when gas-fired generation was dominant, and (bottom) AEFs for a 2025 scenario where solar generation is increased to three times (scenario 3×) the 2016 capacity of utility-scale solar installations and provides 27% of the annual produced energy, up from 9% in 2016, and significantly reduces the carbon intensity of the grid in the middle of the day. This scenario does not attempt to accurately represent the future grid mix for California but represents one possible future in order to evaluate to what extent thermal storage can be used to shape electricity consumption patterns.
Optimal CEP operating schedules are computed for these scenarios in three different operating modes: (i) a business-as-usual mode that uses the current tariff as its objective function; (ii) a mode where a $100 per tonne carbon tax is assumed and the hourly carbon intensities shown in Fig. 4 are used to modify the objective function; and (iii) a carbon-optimal mode that uses a very high price on carbon, so that the carbon intensity of the grid now plays a predominant role in making scheduling decisions. The resulting changes in demand charges, attributable emissions and annual peak load are reported in Table 1, where operating costs are calculated according to the current tariff, i.e., excluding carbon payments.
| Operating mode | 2016 AEFs | Scenario 3X AEFs | ||||||
|---|---|---|---|---|---|---|---|---|
| Total op. emissions (ktonnes) | CEP op. emissions (ktonnes) | Demand charge increase (%) | Total peak load (MW) | Total op. emissions (ktonnes) | CEP op. emissions (ktonnes) | Demand charge increase (%) | Total peak load (MW) | |
| Business-as-usual | 73.5 | 17.6 | 0.0 | 33.9 | 54.3 | 14.2 | 0.0 | 33.9 |
| $100 per tonne tax | 73.3 | 17.4 | 0.8 | 33.9 | 53.0 | 12.9 | 3.4 | 35.5 |
| CO2-Optimal | 72.2 | 16.3 | 30.7 | 44.5 | 49.9 | 9.8 | 33.0 | 44.7 |
Under the 2016 carbon intensity data, carbon policies have practically no impact on the electrical consumption schedule of the campus, due to the small daily variations in carbon intensity (μ = 265, σ = 47 kg MW h−1), as can be seen in Fig. 4. In contrast, scenario 3× (μ = 195, σ = 105 kg MW h−1) illustrates the double benefit for an electrified district energy system in a power grid with increased solar generation: (i) a reduction in carbon emissions in the business-as-usual mode that comes from the fact that most of the campus energy needs are now met through electricity; and (ii) the even greater reductions that can be achieved by following the carbon intensity fluctuations of a highly renewable grid and switching to carbon-aware scheduling policies.
A $100 per tonne carbon tax corresponds to a volumetric price for energy of 4.7 cents per kW h for natural gas-powered generation, which is comparable to current wholesale electricity prices paid by Direct Access customers (ignoring transmission and distribution costs). While 2025 emissions are reduced by 20% compared to the 2016 business-as-usual baseline for the $100 per tonne case, the increased cost paid for peak load (demand charge) remains severe and continues to guide scheduling. The solution from the optimization model avoids high carbon intensity periods to reduce emissions but also avoids the increase in peak load and therefore cannot fully respond to the solar power injections. In the 2025 carbon-optimal mode, heating-and-cooling-related CEP emissions are reduced by over 40% compared to the 2016 business-as-usual baseline (17.6 to 9.8 ktonnes). This reduction in the heating and cooling system operational footprint is an added benefit to the 65% reduction in the overall carbon footprint that was already achieved by switching the primary fuel from gas to electricity.
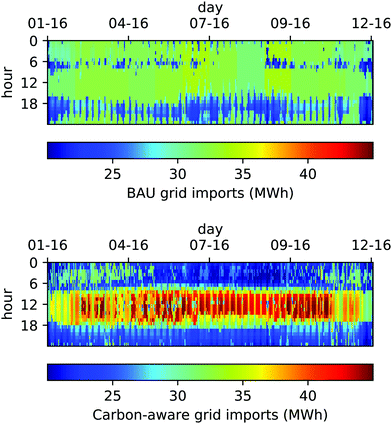
Fig. 5 compares the aggregate campus electricity imports for a Business-as-Usual (BAU) schedule (top) to those for a carbon-optimal schedule where the scenario 3× grid carbon intensity guides operations (bottom). This figure illustrates how operations are shifted from a mode that minimizes peak load and avoids the high prices that recurrently occur in the early evening to one that increases load in the middle of the day and avoids nighttime emissions. The annual grid imports are the same in both schedules, but consumption patterns are very different. The HRCs are used at full capacity during the daylight hours to fill the hot and chilled water storage tanks, regardless of energy costs and demand charges, as shown in Fig. S4 (ESI†). The compressed operating schedule of the HRCs result in the higher demand charges reported in Table 1. The major portion of the operating cost changes are due to the demand charge, which suggests that this would be the major constraint to switching to carbon-aware scheduling.
The peak-to-trough change in energy consumption that is highlighted by Fig. 5(bottom) directly relates to the solar generation capacity that can be accommodated in this case: here estimated to be roughly 15–20 MW from Fig. S5 (ESI†), corresponding to 66–88% of heating sector-related electricity consumption (but only 13–18% of the total campus electricity consumption).
Carbon abatement cost curves
For any given table of hourly prices, the optimal scheduling model can produce a schedule of corresponding hourly power draws. We now use that capability to build carbon abatement cost curves for a range of scenarios, shown in Fig. 6. The baseline scenario corresponds to the 2016 hourly carbon intensity of the grid; also shown are results for 2018, and cases with two, three and five times the 2016 solar generation. Fig. 6 also considers reducing the demand charges to 50% and 10% of 2016 values. These are redistributed as a fixed cost so that the total bill does not change. These curves show the cost per tonne of reducing heating-and-cooling-related emissions from 2016 BAU levels. Under a policy-compliant 2025 energy mix for California (scenario 3×), Fig. 6 shows that heat sector emissions could be reduced by above 40% from 2016 levels but that the cost for this would be just above $200 per tonne. If the demand charge is reduced to 10% of the current rate, costs are reduced to below $40 per tonne.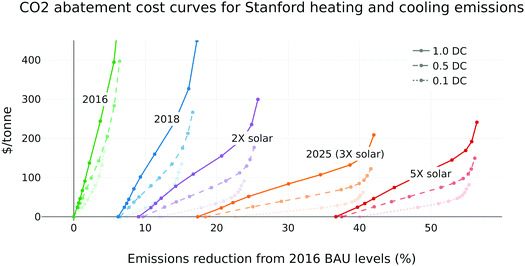 | ||
| Fig. 6 Carbon abatement cost curves in different scenarios for the increase of solar penetration (1× to 5×) on the California grid relative to 2016, and in 2018. For a range of different prices on carbon, optimal hourly operating schedules are computed. We report the change in annual operating costs as a function of heating and cooling emissions reductions from 2016 BAU levels. Costs are normalized by emissions reductions to calculate an effective carbon cost. For the full lines, costs are calculated according to the current rate structure, while for the paler lines, demand charges are reduced by first 50% and then 90%. In each scenario, the effective cost per tonne is zero for the BAU operating mode. In the 3× scenario, there is a small amount of overgeneration (see Table S2, ESI†). In the 5× scenario, it is assumed that overgeneration is evenly redistributed throughout the day (through some form of storage), lowering the carbon intensity of all hours (see Fig. S3, ESI†). As the daily variability of carbon intensity reduces, so does the value of loads that shift consumption in time. | ||
In each scenario, emissions are lowered first through reductions in the overall carbon intensity of the grid and further through carbon-aware scheduling, that is shown here to be an effective mechanism to deal with challenging heat sector emissions. The value of thermal storage is directly tied to the daily variability of the grid carbon intensity: reducing emissions becomes cheaper as we move from the 2016 California energy mix to one where solar generation capacity doubles and then triples. In scenario 5×, overgeneration is assumed to be redistributed evenly on all hours of the day by storage, which reduces the daily variability of grid carbon intensity and consequently the need for load-shifting.
The economic case for thermal storage
Fig. 7 shows the summary results from an analysis of the annual operating cost savings attributable to thermal storage, and of an economic comparison of thermal storage to electrochemical storage. The peak load reductions shown in Fig. 7a represent direct savings in the form of operating cost reductions that can be estimated to be $0.77 million (3.5% savings) of the $22 million annual operating costs from Fig. 7b. These direct savings are mostly tied to reduced demand charges, that typically represent $5–20 kW−1 in California.72 Peak load reductions also translate to substantial economic benefits for the grid, as they allow for distribution system upgrade deferrals in the short-term and smaller distribution system sizes in the longer term. Increasing the size of the hot storage does not reduce peak load but reduces the need for gas heaters and thus decreases capital costs (as well as emissions).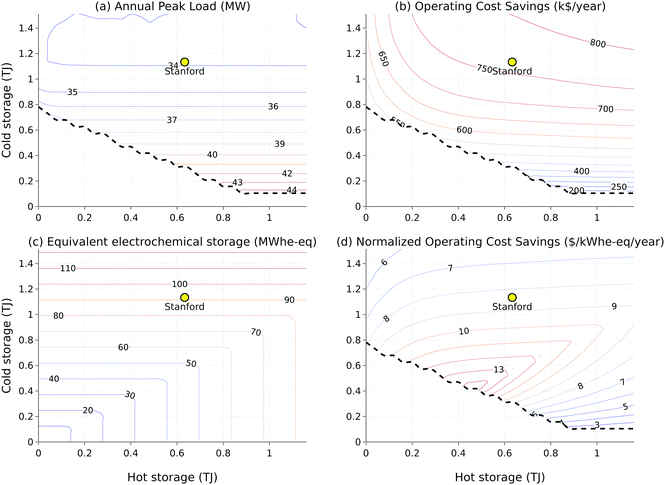 | ||
| Fig. 7 Estimating the operating value of thermal storage: (a) annual electrical peak load, (b) operating cost savings, (c) equivalent electrochemical storage size and (d) normalized operating cost savings as a function of thermal storage capacity. Figure (c) answers the question of how much electrochemical storage would be needed to replace a given hot and chilled storage design. The minimal amount of thermal storage needed for the 2016 dataset that is used here can be computed by reducing the capacity of the thermal storage tanks until the optimization program no longer finds a feasible hourly operations schedule to meet hot and chilled loads throughout the year with the existing HRCs, chillers, and boilers. The corresponding frontier is shown as a dashed black line in Fig. 6a, b and d. Below that threshold, additional chillers are needed, which results in significant increases in capital costs. In the extreme case with no thermal storage, seven chillers are needed (up from four in the present-day design). Cost savings are reported on an annual basis. Calculations are discussed in the Methods section and Note 2 (ESI†). | ||
Large-scale battery technologies are increasingly proposed as a means to integrate ever larger shares of renewable power. For comparison, we compute the electrical energy required to fully recharge hot and chilled water tanks of a given size in Fig. 7c, assuming the electricity is first stored in a battery with a round trip efficiency of 85%. According to this calculation, detailed in the Methods section and Note 2 (ESI†), the thermal storage tanks in the Stanford design are equivalent to 85–95 MW h of electrochemical storage.
The equivalent electrochemical storage capacity in Fig. 7c is then used to normalize the operating cost savings from Fig. 7b and generate Fig. 7d. These normalized operating cost savings can directly be used to generate the payback periods of storage for different capital costs. At Stanford, thermal storage saves $8.3 kWhe-eq−1 year−1, which corresponds to a ten-year payback period for thermal storage tanks that are expected to have a lifetime of 35 years and cost $7.4 million. Finally, while capital costs for commercial battery storage are estimated to be $280 kW h−1 in 201873 they would have to drop beyond current expectations74,75 to below $45 kW h−1 to become a more financially attractive option than thermal storage (assuming a ten-year lifetime for electrochemical storage;76 see Note 2, ESI†).
We note that the comparison in Fig. 7c is only an energetic equivalence however, since it would not be technically possible to directly replace the thermal storages with electrochemical storage. The HRCs produce heating and cooling streams at a fixed ratio. When cooling demand is high and heating demand is low, the excess heating that is produced by the HRCs is sent to the hot storage, and the opposite is true when cooling demand is low and heating demand is high. A battery cannot play this decoupling role.
Conclusions
This study demonstrates the operation and value of an electrified heating and cooling system with large-scale thermal storage, using data from a real-world city-scale experiment. Benefits from electrification are provided in three ways: (1) shifting electrical loads to reduce operating costs; (2) decreasing CO2 emissions now and in the future as the carbon intensity of the electrical grid decreases; and (3) a cost-effective alternative to battery storage for providing operational flexibility and price arbitrage.We leverage real-world consumption and operational data from a first-of-a-kind facility that meets heating, cooling and electrical energy requirements equivalent to a city of 30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 people. Heat-recovery chillers provide the backbone of the heating and cooling system. Thermal storage enables them to be turned off when electricity prices are high and to avoid large demand charges. Based on actual operating conditions, the campus heating and cooling system provides a 15 MW dispatchable load corresponding to 25% of annual campus electrical energy and 45% of peak power.
000 people. Heat-recovery chillers provide the backbone of the heating and cooling system. Thermal storage enables them to be turned off when electricity prices are high and to avoid large demand charges. Based on actual operating conditions, the campus heating and cooling system provides a 15 MW dispatchable load corresponding to 25% of annual campus electrical energy and 45% of peak power.
Compared to the case where no thermal storage is available, peak demand is reduced from 40 to 34 MW, annual operating cost savings represent $770![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 (3.5% of the entire campus energy bill), and the number of electrical chillers required to meet cooling loads drops from 7 to 3.
000 (3.5% of the entire campus energy bill), and the number of electrical chillers required to meet cooling loads drops from 7 to 3.
On top of the 65% reduction in the overall campus carbon footprint that was achieved by electrifying the heating and cooling infrastructure, thermal storage can also drive a reduction of over 40% in heating sector carbon emissions from 2016 to 2025 under a policy-compliant solar generation scenario, and the combined district energy system can absorb the output from a 15 to 20 MW solar farm.
The flexibility provided by thermal storage is very inexpensive: achieving comparable flexibility with battery storage would require costs of $45 kW h−1, to be compared with 2018 estimated prices for batteries ($280 kW h−1).73
Today, the main economic value proposition for thermal storage lies in the mitigation of demand charges by decreasing peak load. In the future, if carbon-aware scheduling becomes the norm, thermal storage can and should be used to increase load in the middle of the day when solar power is abundant. However, capabilities to increase load in times of excess generation or low carbon intensity are not valued by utility signals today. Current rate structures encourage consumers to present a high load factor to the utility (ratio of average load to maximum load). Even with time-varying prices, the optimal operations schedule for a rational consumer that is subject to a tariff with a demand charge maintains an aggregate load that is as flat as possible. The carbon abatement curves that we build quantify the potential to reduce heating sector emissions. Under today's demand charges, unlocking that potential is prohibitively expensive.
The work presented here draws on data and experience from a real-world case study, but the statements that are made are, in fact, quite general. While they were derived in the context of a specific location, we believe the main conclusions to be robust, in particular concerning the capability of thermal storage to provide peak-load management and to unlock the potential for carbon-aware scheduling in electrified district energy systems, at a low cost. Demand charges, also called capacity charges, are very common in the power sector, and are usually linked to either monthly or annual peak usage. Given the typical weight of such charges,72 thermal storage will remain attractive to provide peak shaving under a rate structure that includes a flat, time-of-day-dependent, or dynamic volumetric price in addition to a demand charge. As for the carbon-aware scheduling mode that was explored, our modeling efforts make two generic assumptions: (i) some price is put on carbon (this applies equally to a carbon tax or a cap-and-trade system), and (ii) the carbon accounting metric that is used captures hourly fluctuations in the carbon intensity of the grid. Under the carbon-optimal mode where the price on carbon is dominant in scheduling operating decisions, the carbon intensity of the grid plays the role of a dynamic electricity price, which highlights that thermal storage would also provide significant benefits under a rate structure that does not include a demand charge, but only includes a dynamic electricity price. The hourly carbon intensities that are used in this paper are specific to solar-rich California, and so our quantitative results on decarbonization benefits are also specific to the California grid mix. However, similar decarbonization benefits are to be expected in other locations where the availability in clean power varies throughout the day.
The type of energy system we describe is directly applicable to universities, hospitals and industrial campuses that typically operate shared infrastructure. It is also more broadly applicable to cities, towns municipalities and communities in urban areas. District heating and cooling networks already play a key role in many developed countries and are expected to be economically competitive in urban areas in the future,50,77 but their energy supply is currently dominated by fossil fuels.15 In the design that was described here, a central authority manages the district heating and cooling networks but does not control the electrical consumption of the other components of the energy system, which greatly simplifies implementation, but limits the potential for complete decarbonization of the campus energy system. However, the framework we consider is flexible enough that other energy assets controlled by a central authority could be incorporated. A notable example would be the charging infrastructure for an electrified transportation network. This study outlines a viable path forward to electrify preexisting systems and provides further arguments to expand their utilization.
As was noted by previous authors,42,44,63 the main barriers to adoption of such renewable district energy systems are more political and social than technological or economic. For example, in the case we describe here, retrofit of the existing systems using electrification and heat recovery for the heating and cooling system had the lowest cost of all the options considered. For campuses and large commercial/industrial facilities, investment planning is centralized thus making cost-effective investments in such systems easier. Similarly, for newly built communities, installation at the time of construction can also be easily accomplished if the appropriate regulations or incentives are in place. However, for cities with many property owners in communities that are not centrally planned, retrofit of district heating and cooling systems will require a high degree of cooperation in urbanized areas, as well as strong commitments to support the high upfront capital costs that are typical of such systems. The experiment we considered in this paper was driven by financial and social responsibility decisions on the part of a university, and there were no policies in place to incentivize the electrification of heat at a district scale. The other condition necessary for such systems to have large carbon reduction benefits is access to an electric power supply with low carbon intensity. California does provide a strong and stable framework for decarbonization of the electricity grid through its Renewable Portfolio Standard.78 Any set of policy measures to decarbonize the electricity grid will benefit the decarbonization of electrified heating and cooling. Even at a modest price of $50 per metric tonne, electrifying the heating and cooling system would have resulted in net present savings of $106 million over 35 years for the Stanford campus, to be compared with a net present cost that was estimated at $1.3 billion (assuming a 5% annual discount rate). This paper explored the further benefits that would be achieved by a carbon price from carbon-aware scheduling, which will have strong value in energy grids with high shares of solar and wind power.
Thermal-storage-backed electrification is a prime example of how to reduce emissions in the challenging heat sector. This work provides new options for regulators and policymakers and highlights that district scale thermal storage represents a very real option to provide low-cost flexibility for future power grids and decarbonization of the heating sector.
Methods
Summary
This paper models the rational behavior of a district energy system. Hourly thermal and electrical energy consumption and emissions factors data are compiled from different sources. These data are entered into an optimization model that determines the optimal operating schedule for the different energy assets in the district energy system. The program we build minimizes operating costs subject to a set of technological constraints and such that thermal and electrical campus loads are met. The objective function can include components to reflect costs from the monthly peak power draw (demand charges), hourly energy usage, or carbon dioxide emissions. The weights that are chosen for these different components determine what mode the system is operating in. The equivalent electrochemical storage system to a given thermal storage design is also computed, to compare the economic values of thermal and electrochemical storage in the context of district energy networks.Energy consumption data
Electrical, cooling and heating loads are provided by the Stanford Energy Systems Innovations Project68 (SESI). These hourly time series data are measured at the Central Energy Plant (CEP) and provide an estimate of the aggregate campus consumption served by the CEP. The electrical load measurements are taken from the master meter at the substation, which is the point of entry for electrical energy on campus. Thermal loads reported here correspond to measurements of energy leaving the CEP, so they include both the consumption of the buildings and losses in the ten-mile distribution networks for hot and chilled water. Missing data points are filled by taking the average of the surrounding values. Heat maps for the three energy streams are presented in the ESI.† To produce Fig. 1, the daily loads for heating and cooling are computed by summing the corresponding hourly loads. The maximum daily heating and cooling load that could be met by heat recovery chillers is then computed, assuming that they produce 1.37 GJ of heating per GJ of cooling (or 0.016 mmbtu per ton-hour).Emissions factors
Average Emissions Factors (AEFs) measure the average carbon intensity of the electrical energy flowing through the power grid, calculated in units of kgCO2-eq per MW h from the generation sources that are producing at a given instant. Generation data for the CAISO balancing area can be publicly accessed79 and are used together with Life-Cycle Assessment carbon intensities from the IPCC80 to estimate hourly AEFs for the considered time frame (also see Tables S1, S2 and Fig. S2, ESI†). AEFs should not be confused with Marginal Emissions Factors (MEFs), that measure the short-term avoided emissions impact of an intervention on the power grid, by calculating the carbon intensity of generators that are dispatched last in a marginal-cost-based system. These would also be the first to be shut down if demand is reduced or zero-marginal cost renewable generation increases. In the context for this work, we are considering the carbon payments that should be made for actual attributable emissions, so we choose to use AEFs. We emphasize that changing from one metric to another or using more granular grid data does not affect the methodology presented in this work – as long as we use some form of hourly price that reflects the environmental impact associated with the electrons flowing through the power system – although it could change the results and their interpretation.Optimal scheduling of the different energy assets in a district energy system
We model a district energy system in which scheduling decisions are made centrally to minimize aggregate system operating costs. The decision epoch is hourly, and we consider a program with T timesteps. In the infrastructure design we consider, three types of machines are used to produce heat: gas boilers, heat recovery chillers (HRCs) and conventional chillers. Both types of chillers are heat pumps, that extract heat from the environment. The decision variables associated with the heat pumps are their hourly electrical power input pHRC,t and pCh,t. They are characterized by their efficiency (hot and chilled water efficiency for the HRCs, and chilled water efficiency for the chiller):| ∀t = 1…T − 1, qC,HRC,t = ηC,HRCpHRC,t, | (1) |
| ∀t = 1…T − 1, qH,HRC,t = ηH,C,HRCqC,HRC,t, | (2) |
| ∀t = 1…T − 1, qCh,t = ηChpCh,t. | (3) |
In eqn (1)–(3), the letter η denotes an efficiency (typical values are given in Table S3, ESI†) and q denotes a water flow rate. The output of the machines is constrained:
∀t = 1…T − 1, qC,HRC,t ∈ [0,![[q with combining macron]](https://www.rsc.org/images/entities/i_char_0071_0304.gif) HRC], HRC], | (4) |
∀t = 1…T − 1, qCh,t ∈ [0,![[q with combining macron]](https://www.rsc.org/images/entities/i_char_0071_0304.gif) Ch]. Ch]. | (5) |
| ∀t = 1…T − 1, qBo,t = ηBogBo,t. | (6) |
| ∀t = 1…T − 1, pBo,t = ηG,E,BogBo,t. | (7) |
![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) , t = 1…T − 2 and the 2(T − 2) constraints:
, t = 1…T − 2 and the 2(T − 2) constraints:| ∀t = 1…T − 2, zj,t ≥ pj,t − pj,t+1, | (8) |
| ∀t = 1…T − 2, zj,t ≥ pj,t+1 − pj,t. | (9) |
| ∀t = 1…T − 2, zj,t ≥ |pj,t+1 − pj,t|. | (10) |
| ∀t = 1…T − 1, sH,t+1 = sH,t + qH,HRC,t + qBo,t − dH,t + duH,t, | (11) |
| ∀t = 1…T − 1, sC,t+1 = sC,t + qC,HRC,t + qCh,t − dC,t + duC,t. | (12) |
∀t = 1…T, sH,t ∈ [0,![[s with combining macron]](https://www.rsc.org/images/entities/i_char_0073_0304.gif) H], H], | (13) |
∀t = 1…T, sC,t ∈ [0,![[s with combining macron]](https://www.rsc.org/images/entities/i_char_0073_0304.gif) C]. C]. | (14) |
| sH,1 = sH,i, sH,T = sH,f, | (15) |
| sC,1 = sC,i, sC,T = sC,f. | (16) |
| ∀t = 1…T − 1, pt = pHRC,t + pCh,t + pBo,t + dE,t, | (17) |
| ∀t = 1…T − 1, gt = gBo,t. | (18) |
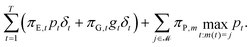 | (19) |
![[scr M, script letter M]](https://www.rsc.org/images/entities/char_e145.gif) , where
, where ![[scr M, script letter M]](https://www.rsc.org/images/entities/char_e145.gif) is the set of months, and enforcing the constraints:
is the set of months, and enforcing the constraints:| ∀t = 1…T − 1, ym(t) ≥ pt. | (20) |
![[scr M, script letter M]](https://www.rsc.org/images/entities/char_e145.gif) . We note that eqn (19) is general enough to account for an hourly carbon price. This can be done simply by replacing the hourly prices for electricity πE,t and gas πG,t by prices
. We note that eqn (19) is general enough to account for an hourly carbon price. This can be done simply by replacing the hourly prices for electricity πE,t and gas πG,t by prices ![[small pi, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e1de.gif) E,t and
E,t and ![[small pi, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e1de.gif) G,t that factor the carbon externality:
G,t that factor the carbon externality:![[small pi, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e1de.gif) E,t = πE,t + πE,CO2,t, E,t = πE,t + πE,CO2,t, ![[small pi, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e1de.gif) G,t = πG,t + πG,CO2,t. G,t = πG,t + πG,CO2,t. | (21) |
Equivalency between thermal storage and electrochemical storage
We calculate the electrical storage size that would be required to generate as much chilled and hot water as what is in the thermal tanks. We call r the proportion of the cooling loads that are met by heat recovery chillers, the remainder being met by the conventional chillers. Since heat recovery chillers and chillers are each used to meet half of the cooling loads in our 2016 cost-minimization solution to the scheduling problem, we use that as an assumption here. We further assume that heat recovery chillers consume ηHRC,c = 1.32 kW h of electricity to produce 1 ton-hour of cooling and ηHRC,h = 0.02 mmbtu of heating; that the chillers consume ηCh,c = 0.45 kW h per ton of cooling; and that the round-trip a.c.–a.c efficiency of electrochemical storage is ηe = 85%.82 We calculate the equivalent electrochemical storage size to (Sc, Sh) of chilled and hot thermal storage as: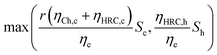 | (22) |
The main assumption behind eqn (22) is that there must be at least enough electrochemical storage to generate enough hot or chilled water as specified by (Sc, Sh). We note that the energetic equivalence described by eqn (22) only relates to the ability of thermal storage to shift electrical load, not to the ability of the hot and cold water storage to align non-concurrent heating and cooling loads. Technically, electrochemical storage could therefore not directly replace thermal storage in this system. Some amount of thermal storage would still be needed to fully enable the use of the HRCs by allowing machines that must output heating and cooling streams with a constant ratio to meet thermal loads that do not have a constant ratio. Also see the discussion in Note 2 (ESI†).
Data availability
The code and data that were used for this study are available on GitHub.83Conflicts of interest
There are no conflicts to declare.Acknowledgements
Funding for this research was supported by Stanford's Global Climate & Energy Project and a State Grid Graduate Student Fellowship through Stanford's Bits & Watts initiative. The authors thank Joe Stagner, executive director of Stanford's Sustainability & Energy Management Department, for providing energy load data for this study.References
- S. Chu and A. Majumdar, Nature, 2012, 488, 294 CrossRef CAS PubMed.
- IPCC, in Global warming of 1.5 degrees C. – Summary for Policymakers, ed. V. Masson-Delmotte, P. Zhai, H. O. Pörtner, D. Roberts, J. Skea, P. Shukla, A. Pirani, W. Moufouma-Okia, C. Péan, R. Pidcock, S. Connors, J. Matthews, Y. Chen, X. Zhou, M. Gomis, E. Lonnoy, T. Maycock, M. Tignor and T. Waterfield, World Meteorological Organization, Geneva, Switzerland, 2018, book section SPM, pp. 1–32 Search PubMed.
- M. Milligan, B. Frew, B. Kirby, M. Schuerger, K. Clark, D. Lew, P. Denholm, B. Zavadil, M. O'Malley and B. Tsuchida, IEEE Power and Energy Mag., 2015, 13, 78–87 Search PubMed.
- US Department of Energy (DOE), Grid Modernization Multi-Year Program Plan, 2015 Search PubMed.
- M. Ahlstrom, E. Ela, J. Riesz, J. O'Sullivan, B. F. Hobbs, M. O'Malley, M. Milligan, P. Sotkiewicz and J. Caldwell, IEEE Power and Energy Mag., 2015, 13, 60–66 Search PubMed.
- R. N. Anderson, A. Boulanger, W. B. Powell and W. Scott, Proc. IEEE, 2011, 99, 1098–1115 Search PubMed.
- E. Lannoye, D. Flynn and M. O'Malley, IEEE Trans. Power Syst., 2012, 27, 922–931 Search PubMed.
- P. L. Joskow, J. Econ. Perspect., 2012, 26, 29–48 CrossRef.
- J. Olauson, M. N. Ayob, M. Bergkvist, N. Carpman, V. Castellucci, A. Goude, D. Lingfors, R. Waters and J. Widén, Nat. Energy, 2016, 1, 16175 CrossRef.
- G. Strbac, Energy Policy, 2008, 36, 4419–4426 CrossRef.
- P. Palensky and D. Dietrich, IEEE Trans. Ind. Inform., 2011, 7, 381–388 Search PubMed.
- D. S. Callaway and I. A. Hiskens, Proc. IEEE, 2011, 99, 184–199 Search PubMed.
- J. L. Mathieu, PhD thesis, UC Berkeley, 2012.
- IEA, CO2 emissions from fuel combustion 2017 – highlights, 2017 Search PubMed.
- S. Werner, Energy, 2017, 137, 617–631 CrossRef.
- J. Kiviluoma, S. Heinen, H. Qazi, H. Madsen, G. Strbac, C. Kang, N. Zhang, D. Patteeuw and T. Naegler, IEEE Power and Energy Mag., 2017, 15, 25–33 Search PubMed.
- M. O'Malley, B. Kroposki, B. Hannegan, H. Madsen, M. Andersson, W. D'haeseleer, M. F. McGranaghan, C. Dent, G. Strbac, S. Baskaranet al., Energy systems integration: defining and describing the value proposition, National renewable energy lab.(nrel), golden, co (united states) technical report, 2016.
- V. Smil, Technol. Forecast Soc., 2000, 65, 251–264 CrossRef.
- J. L. Mathieu, S. Koch and D. S. Callaway, IEEE Trans. Power Syst., 2013, 28, 430–440 Search PubMed.
- Z. Yu, L. Jia, M. C. Murphy-Hoye, A. Pratt and L. Tong, IEEE Trans. Smart Grid, 2013, 4, 2244–2255 Search PubMed.
- N. Lu, D. P. Chassin and S. E. Widergren, IEEE Trans. Power Syst., 2005, 20, 725–733 CrossRef.
- S. H. Tindemans, V. Trovato and G. Strbac, et al. , IEEE Trans. Control Systems Technol., 2015, 23, 1685–1700 Search PubMed.
- E. C. Kara, M. Bergés and G. Hug, IEEE Trans. Smart Grid, 2015, 6, 2560–2568 Search PubMed.
- M. Kintner-Meyer and A. F. Emery, Energy Build., 1995, 23, 19–31 CrossRef.
- J. L. Mathieu, M. Kamgarpour, J. Lygeros, G. Andersson and D. S. Callaway, IEEE Trans. Power Syst., 2015, 30, 763–772 Search PubMed.
- J. L. Mathieu, P. N. Price, S. Kiliccote and M. A. Piette, IEEE Trans. Smart Grid, 2011, 2, 507–518 Search PubMed.
- E. Vrettos, E. C. Kara, J. MacDonald, G. Andersson and D. S. Callaway, IEEE Trans. Smart Grid, 2018, 9, 3213–3223 Search PubMed.
- D. Patteeuw, K. Bruninx, A. Arteconi, E. Delarue, W. D'haeseleer and L. Helsen, Appl. Energy, 2015, 151, 306–319 CrossRef.
- W. Kempton and J. Tomić, J. Power Sources, 2005, 144, 280–294 CrossRef CAS.
- S. Chen, Y. Ji and L. Tong, Comput. Eng., 2015, 389–395 Search PubMed.
- S. P. Meyn, P. Barooah, A. Busic, Y. Chen and J. Ehren, IEEE Trans. Automatic Control, 2015, 60, 2847–2862 Search PubMed.
- D. J. Hammerstrom, R. Ambrosio, T. A. Carlon, J. G. DeSteese, G. R. Horst, R. Kajfasz, L. L. Kiesling, P. Michie, R. G. Pratt, M. Yaoet al., Pacific Northwest GridWise™ Testbed Demonstration Projects; Part I. Olympic Peninsula Project, Pacific northwest national laboratory (pnnl), richland, wa (us) technical report, 2008.
- W. Ma, S. Fang, G. Liu and R. Zhou, Appl. Energy, 2017, 204, 181–205 CrossRef.
- Y. Xu, S. Çolak, E. C. Kara, S. J. Moura and M. C. González, Nat. Energy, 2018, 3, 484–493 CrossRef.
- S. Ashok, Appl. Energy, 2006, 83, 413–424 CrossRef.
- P. M. Castro, I. Harjunkoski and I. E. Grossmann, Ind. Eng. Chem. Res., 2009, 48, 6701–6714 CrossRef CAS.
- S. Mitra, I. E. Grossmann, J. M. Pinto and N. Arora, Comput. Chem. Eng., 2012, 38, 171–184 CrossRef CAS.
- Q. Zhang, I. E. Grossmann, C. F. Heuberger, A. Sundaramoorthy and J. M. Pinto, AIChE J., 2015, 61, 1547–1558 CrossRef CAS.
- D. Todd, M. Caufield, B. Helms, A. P. Generating, I. M. Starke, B. Kirby and J. Kueck, ORNL/TM, 2008, vol. 233.
- EuroHeat & Power, District Heating and Cooling – Country by country 2015 survey, 2015, https://www.euroheat.org/wp-content/uploads/2016/03/2015-Country-by-country-Statistics-Overview.pdf.
- International District Energy Association, U.S. District Energy Services Market Characterization – an EIA report, 2018.
- H. Lund, S. Werner, R. Wiltshire, S. Svendsen, J. E. Thorsen, F. Hvelplund and B. V. Mathiesen, Energy, 2014, 68, 1–11 CrossRef.
- G. Chicco and P. Mancarella, Renewable Sustainable Energy Rev., 2009, 13, 535–551 CrossRef.
- B. Rezaie and M. A. Rosen, Appl. Energy, 2012, 93, 2–10 CrossRef.
- J. Allegrini, K. Orehounig, G. Mavromatidis, F. Ruesch, V. Dorer and R. Evins, Renewable Sustainable Energy Rev., 2015, 52, 1391–1404 CrossRef.
- S. Werner, Energy, 2017, 126, 419–429 CrossRef.
- M. Sameti and F. Haghighat, Energy Build., 2017, 121–130 CrossRef.
- T. Nuytten, B. Claessens, K. Paredis, J. Van Bael and D. Six, Appl. Energy, 2013, 104, 583–591 CrossRef.
- E. Dotzauer, Appl. Energy, 2002, 73, 277–284 CrossRef.
- U. Persson and S. Werner, Appl. Energy, 2011, 88, 568–576 CrossRef.
- M. Åberg, J. Widén and D. Henning, Energy, 2012, 41, 525–540 CrossRef.
- E. A. M. Ceseña and P. Mancarella, IEEE Trans. Smart Grid, 2019, 10, 1122–1131 Search PubMed.
- X. Chen, C. Kang, M. O'Malley, Q. Xia, J. Bai, C. Liu, R. Sun, W. Wang and H. Li, IEEE Trans. Power Syst., 2015, 30, 1848–1857 Search PubMed.
- M. R. Davidson, D. Zhang, W. Xiong, X. Zhang and V. J. Karplus, Nat. Energy, 2016, 1, 16086 CrossRef.
- N. Zhang, X. Lu, M. B. McElroy, C. P. Nielsen, X. Chen, Y. Deng and C. Kang, Appl. Energy, 2016, 184, 987–994 CrossRef.
- National Energy Administration, Wind Industry Development Statistics 2015, 2016, http://www.nea.gov.cn/2016-02/04/c_135073627.htm.
- B. Bach, J. Werling, T. Ommen, M. Münster, J. M. Morales and B. Elmegaard, Energy, 2016, 107, 321–334 CrossRef.
- M. G. Nielsen, J. M. Morales, M. Zugno, T. E. Pedersen and H. Madsen, Appl. Energy, 2016, 167, 189–200 CrossRef.
- R. Lund, D. D. Ilic and L. Trygg, J. Cleaner Prod., 2016, 139, 219–229 CrossRef.
- R. Lund and U. Persson, Energy, 2016, 110, 129–138 CrossRef.
- H. Lund, P. A. Østergaard, D. Connolly, I. Ridjan, B. V. Mathiesen, F. Hvelplund, J. Z. Thellufsen and P. Sorknæs, Int. J. Sustainable Energy Planning Management, 2016, 11, 3–14 Search PubMed.
- B. V. Mathiesen, H. Lund, D. Connolly, H. Wenzel, P. A. Østergaard, B. Möller, S. Nielsen, I. Ridjan, P. Karnøe and K. Sperling, et al. , Appl. Energy, 2015, 145, 139–154 CrossRef.
- M. Z. Jacobson, M. A. Cameron, E. M. Hennessy, I. Petkov, C. B. Meyer, T. K. Gambhir, A. T. Maki, K. Pfleeger, H. Clonts and A. L. McEvoy, et al. , Sustainable Cities Soc., 2018, 42, 22–37 CrossRef.
- H. Lund and B. V. Mathiesen, Energy, 2009, 34, 524–531 CrossRef.
- M. Z. Jacobson, M. A. Delucchi, M. A. Cameron and B. V. Mathiesen, Renewable Energy, 2018, 123, 236–248 CrossRef.
- M. Z. Jacobson, M. A. Delucchi, M. A. Cameron and B. A. Frew, Proc. Natl. Acad. Sci.U. S. A., 2015, 112, 15060–15065 CrossRef CAS PubMed.
- P. E. Dodds, I. Staffell, A. D. Hawkes, F. Li, P. Grünewald, W. McDowall and P. Ekins, Int. J. Hydrogen Energy, 2015, 40, 2065–2083 CrossRef CAS.
- Sustainable Stanford, Stanford Energy Systems Innovations, http://sustainable.stanford.edu/sesi/.
- I. Dunning, J. Huchette and M. Lubin, SIAM Rev., 2017, 59, 295–320 CrossRef.
- Gurobi Optimization Incorporated, Gurobi Optimizer Version 7.5, 2018.
- S. J. Qin and T. A. Badgwell, Contr. Eng. Pract., 2003, 11, 733–764 CrossRef.
- Pacific Gas & Electric, Gas and electric rate schedules, https://www.pge.com/tariffs/.
- Lazard, Lazard's levelized cost of storage – version 3.0, 2017, pp. 1–21 Search PubMed.
- O. Schmidt, A. Hawkes, A. Gambhir and I. Staffell, Nat. Energy, 2017, 6, 17110 CrossRef.
- N. Kittner, F. Lill and D. M. Kammen, Nat. Energy, 2017, 2, 17125 CrossRef.
- X. Luo, J. Wang, M. Dooner and J. Clarke, Appl. Energy, 2015, 137, 511–536 CrossRef.
- D. Connolly, H. Lund, B. V. Mathiesen, S. Werner, B. Möller, U. Persson, T. Boermans, D. Trier, P. A. Østergaard and S. Nielsen, Energy Policy, 2014, 65, 475–489 CrossRef.
- California Energy Comission, Renewables Portfolio Standard, 2019, https://www.energy.ca.gov/portfolio/.
- CAISO, Daily Renewables Watch, http://content.caiso.com/green/renewrpt/20180318_DailyRenewablesWatch.txt.
- Annex II: Methodology, ed. W. Moomaw, P. Burgherr, G. Heath, M. Lenzen, J. Nyboer and A. Verbruggen, 2011, vol. 16 Search PubMed.
- J. Bisschop, AIMMS Modeling Guide – Optimization Modeling, 2012 Search PubMed.
- R. L. Fares and M. E. Webber, Nat. Energy, 2017, 2, 17001 CrossRef CAS.
- J. A. de Chalendar, P. W. Glynn and S. M. Benson, Supplemental code and data repository, 2016, https://github.com/jdechalendar/city-scale-suppl/.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c8ee03706j |
| This journal is © The Royal Society of Chemistry 2019 |