Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
CO2 reduction on gas-diffusion electrodes and why catalytic performance must be assessed at commercially-relevant conditions†
Thomas
Burdyny
 * and
Wilson A.
Smith
* and
Wilson A.
Smith
 *
*
Materials for Energy Conversion and Storage, Department of Chemical Engineering, Delft University of Technology, 2629 HZ Delft, The Netherlands. E-mail: t.e.burdyny@tudelft.nl; W.smith@tudelft.nl
First published on 10th January 2019
Abstract
Electrocatalytic CO2 reduction has the dual-promise of neutralizing carbon emissions in the near future, while providing a long-term pathway to create energy-dense chemicals and fuels from atmospheric CO2. The field has advanced immensely in recent years, taking significant strides towards commercial realization. Catalyst innovations have played a pivotal role in these advances, with a steady stream of new catalysts providing gains in CO2 conversion efficiencies and selectivities of both C1 and C2 products. Comparatively few of these catalysts have been tested at commercially-relevant current densities (∼200 mA cm−2) due to transport limitations in traditional testing configurations and a research focus on fundamental catalyst kinetics, which are measured at substantially lower current densities. A catalyst's selectivity and activity, however, have been shown to be highly sensitive to the local reaction environment, which changes drastically as a function of reaction rate. As a consequence of this, the surface properties of many CO2 reduction catalysts risk being optimized for the wrong operating conditions. The goal of this perspective is to communicate the substantial impact of reaction rate on catalytic behaviour and the operation of gas-diffusion layers for the CO2 reduction reaction. In brief, this work motivates high current density catalyst testing as a necessary step to properly evaluate materials for electrochemical CO2 reduction, and to accelerate the technology toward its envisioned application of neutralizing CO2 emissions on a global scale.
Broader contextIn addition to improving existing technologies and adapting behaviour, new energy technologies are needed to accelerate an energy transition away from fossil-fuels. A CO2 electrolyzer, which can electrochemically reduce CO2 into base chemicals and fuels, is one technology that has the potential to be less carbon-intensive than current production routes. To be a viable option which can measurably impact society and the environment, however, CO2 electrolyzers must be technically and economically feasible at globally-relevant scales (>1 GW). This requires advancements in catalyst development, process intensification and system design which have largely been investigated independently, despite their interconnected nature. Here in this perspective the interactions between reduction catalysts and the surrounding system are discussed in-depth, with the results motivating future research efforts to consider a shift towards a more applied end goal. In particular, reaction-driven changes in the local environment require catalysts to be tested at elevated current densities. Further, process intensification requires catalysts to be deposited onto a gas-diffusion layer or membrane electrode assembly. Finally, we consider that the unavoidable interactions between an acidic reagent and commonly-used electrolytes may result in inherently unstable CO2 reduction systems, suggesting that greater research focus is needed in system design to avoid this outcome. |
Under an applied potential and in the presence of an appropriate catalyst, carbon-dioxide (CO2) and water can be electrocatalytically converted into syngas (CO + H2), ethylene (C2H4), methane (CH4), ethanol (C2H5OH) and formate (HCOOH) among other products. The collective market size of these reduction products is >500 Mton per year, indicating the potential scale of a commercially competitive CO2 electrolyzer;1 in the process, and of utmost importance and urgency, this process may aid in reducing fossil fuels by supplanting current production routes. Excitingly, CO2 electroreduction catalysts have shown enough promise that we are beginning to see the first steps towards commercial application of the technology, including more and more start-ups (see OPUS12, CERT, Dioxide Materials) and established companies (Siemens) focusing on system design and engineering. As a result, researchers are now targeting lower overall cell potentials by improving other parts of the conversion unit,2–5 while looking to more efficiently integrate electrochemical CO2 conversion units with upstream and downstream processes.6 Future devices will also need to demonstrate stable long-term operation (>20
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 hours) at substantial current densities (>200 mA cm−2) to minimize the capital-expenditure of a conversion unit to economically-compelling levels.1,7,8 Due to the low solubility of CO2 in aqueous-fed systems that limits CO2 conversion to current densities of ∼35 mA cm−2,9–11 researchers have turned to pressurized electrolytes and gas-diffusion layer-based systems to supply enough CO2 to the catalyst layer to sustain higher current densities. Despite these capabilities, an overwhelming percentage (>95%)12,13 of fundamental studies and catalytic materials are still developed, tested and characterized in classical H-cell configurations, where current densities are limited. The local catalytic environment, and subsequently the energetics of the reactions occurring on a catalyst's surface, are known however to be highly sensitive to changes in reaction rate. Therefore a fundamental question remains: How representative are the conclusions from aqueous-fed systems that are constrained to ∼35 mA cm−2 when the goal is to achieve >200 mA cm−2?
000 hours) at substantial current densities (>200 mA cm−2) to minimize the capital-expenditure of a conversion unit to economically-compelling levels.1,7,8 Due to the low solubility of CO2 in aqueous-fed systems that limits CO2 conversion to current densities of ∼35 mA cm−2,9–11 researchers have turned to pressurized electrolytes and gas-diffusion layer-based systems to supply enough CO2 to the catalyst layer to sustain higher current densities. Despite these capabilities, an overwhelming percentage (>95%)12,13 of fundamental studies and catalytic materials are still developed, tested and characterized in classical H-cell configurations, where current densities are limited. The local catalytic environment, and subsequently the energetics of the reactions occurring on a catalyst's surface, are known however to be highly sensitive to changes in reaction rate. Therefore a fundamental question remains: How representative are the conclusions from aqueous-fed systems that are constrained to ∼35 mA cm−2 when the goal is to achieve >200 mA cm−2?
This perspective seeks to shed light on this question by summarizing how the local reaction environment is known to vary as a function of current density, and how these changes may impact reactions occurring on a catalyst's surface when pushed to commercial current densities. To aid in the analysis we draw upon recent literature findings from electrochemical experiments, transport phenomena and Density-Functional Theory (DFT) modelling.
Due to the promise of electrochemical CO2 reduction technology, and a lack of selective and efficient cathode materials, a large fraction of the field has undergone a global, multidisciplinary effort over the last decade to find new and better catalysts. The search is complicated by the large number of surface factors impacting activity including intermediate binding energy,14,15 (via coordination16,17 and site availability18–20), packing,21,22 kinetic supply of reactants,23 desorption of products,24 adsorbate–adsorbate interactions,25etc. The urgency of these efforts is illustrated by the large number of material-centric review papers published in the last year alone on catalyst development/optimization.10,26–30 Here, we define the catalyst as the surface on which CO2 is reduced. As with any catalytic process, however, the local and system reaction environments play equally important roles in efficiently driving specific reactions, while suppressing unwanted competing ones. Many researchers have reported the extreme sensitivity of the reaction to changes in local pH,31–35 electrolytes36,37 and cations38–41 (easily illustrated by replacing K+ with Na+). The ‘catalyst’ that notably reduces the energy barrier for CO2 reduction processes is then very much a combined material and environmental effect, rather than that of the catalyst's surface (composition, coordination, nano/mesostructure) alone.
The above distinction, while central to any catalytic process, warrants particular attention here due to the unique peculiarities of electrocatalytic CO2 reduction in aqueous solvents. Specifically, while the local environment directly influences reaction pathways and kinetics, the reduction reaction itself greatly disturbs the local environment. At the root of this reaction-driven sensitivity is the requirement for both CO2 and protons (H+) to participate in the CO2 reduction process. The ever-present, and in many cases more thermodynamically favourable, hydrogen evolution reaction (HER) then simultaneously competes with CO2 reduction for protons and electrons. At extremely low current densities (<1 mA cm−2), these protons can be supplied to either reaction directly by hydronium contained within the local electrolyte (Fig. 1a).42 As hydronium is depleted, water reduction fills the role as a hydrogen source while the unused hydroxide molecule generated as a by-product, rapidly increases the local electrolyte pH (Fig. 1c).43,44 At slightly more moderate CO2 reduction current densities in aqueous-fed systems (∼35 mA cm−2 for C1 products, ∼100 mA cm−2 for C2 products32,36), CO2 ultimately becomes depleted by a combination of diffusion limitations from the bulk electrolyte, and the now unfavourable bicarbonate-equilibrium conditions as a result of the increased local pH.45,46 Thus, as the reaction proceeds from 0 mA cm−2 to CO2-depletion (Fig. 1b), the surface coverage and binding energies of key intermediates on a catalyst's surface are ultimately impacted through these changes in the local environment;44,47,48 not dissimilar from the surface effects incurred by varying material composition, structure or morphology. The activity of a catalyst is then identified by the environment around it, as much as its physical make-up.
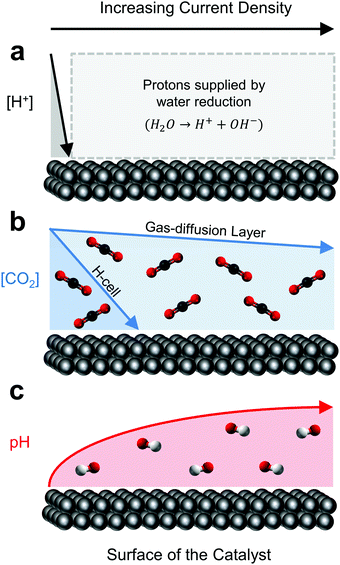 | ||
| Fig. 1 The relative effect of current density on the reaction (a) proton source, (b) concentration of CO2 and (c) pH at the surface of a CO2 reduction catalyst. | ||
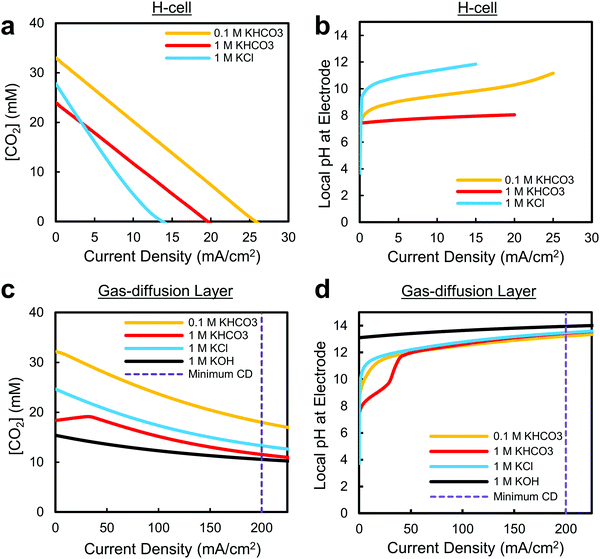
The inherent sensitivity of the reaction to changing local conditions is seen in literature to directly and indirectly drive many of the experimental choices in electrolyte type and concentration. Unsurprisingly, a catalyst can perform exceptionally well or poorly depending on the medium in which it is tested. The importance of the electrolyte medium on catalytic behaviour is most clearly displayed through the near ubiquitous use of low KHCO3 concentrations in reports of high selectivity C2 production on nanostructured49–51 and oxide-derived Cu52–55 in H-cells. Here the poor buffering capacity of the electrolyte causes the pH close to the electrode to quickly increase at low current densities (<20 mA cm−2), helping to promote C2 products and suppress the competing CH4 and H2 reactions.31,56 The morphology of the catalyst can be used to provide similar cumulative effects,52 which ultimately makes properly separating the direct contributions of intrinsic catalytic activity and the local environment even more difficult. To this point, the field has collectively learned to manipulate both catalysts and local electrochemical conditions as needed to optimize CO2 reduction performance metrics at primarily indiscriminate current densities. Given this widely-implemented knowledge that the environment is critical to catalytic behaviour, and that these conditions change as a function of current density, it is our perspective that the environment at commercially-relevant current densities (>200 mA cm−2) should be used as the criterion for assessing catalytic performance and suitability.
Effect of cell configuration and reaction rate on CO2 reduction environments
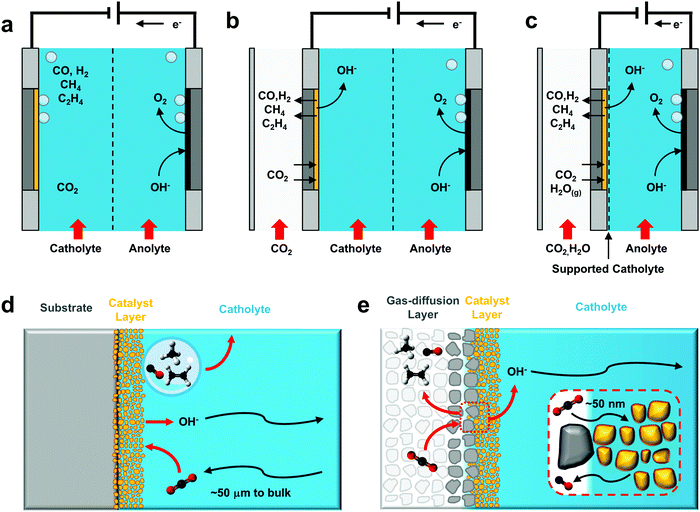
The number of CO2 electroreduction experiments reported at elevated current densities is rapidly increasing, owed in part to the maturity of the field as well as the observed performance benefits. Recent work has reviewed various electrochemical architectures capable of delivering enough CO2 to the catalyst to reach current densities >200 mA cm−2,12,13 summarizing in detail the impacts of different components and configurations on system performance. While we refer the reader to these publications for specific technical advances in the field, we will briefly summarize several commonly-used architectures (Fig. 2) and aspects of their operation to illustrate how the reaction environment around the catalyst layer is influenced by elevated current densities.In each of the described configurations CO2 is supplied to a catalyst layer that is fully or partially immersed in a conductive electrolyte. This CO2 can diffuse through the hydrodynamic boundary layer of a saturated bulk electrolyte as in a standard H-cell configuration (Fig. 2a and d),45,46,57 or from a nearby gas-phase with a much shorter diffusion pathway (Fig. 2b, c and e).58–61 Configurations where CO2 is provided from the gas-phase use a gas-diffusion layer to form a gas–liquid interface adjacent to the catalyst layer. Electrochemical CO2 reactors using gas-diffusion layers have historically been used in diverse configurations,13,62–64 but range primarily from a Kenis-type reactor with a flowing catholyte58,65–73 (Fig. 2b), to membrane electrode assemblies2,5,12,74,75 which directly combine a gas-diffusion layer, catalyst and ion exchange membrane into one unit (Fig. 2c). These latter configurations are occasionally denoted as ‘catholyte-free’ or gas-phase electrolysis due to the lack of a flowing electrolyte between the catalyst layer and ion-exchange membrane. Liquid water, however, is reported to be present in the porous catalyst layer in the majority of cases. Further, research has shown that without the direct presence of a solid-supported electrolyte, CO2 reduction selectivity can be heavily penalized.2,5,64 The two cathode variations shown in Fig. 2b and c then similarly involve the diffusion of CO2 across a gas–liquid interface and through a thin electrolyte to a porous catalyst layer (Fig. 2e), where evidence suggests that the reaction occurs primarily in the aqueous phase via dissolved CO2 rather than at a three-phase solid–liquid–gas interface. Water management is essential to maintain a stable gas–liquid equilibrium as both flooding of the gas-diffusion layer and evaporation of the catholyte will impact CO2 transport to the catalyst layer.5,70,76 A catalyst can be applied to the gas-diffusion layer via drop-casting, airbrushing, electrodeposition, compression, or incorporation into the porous layer itself.
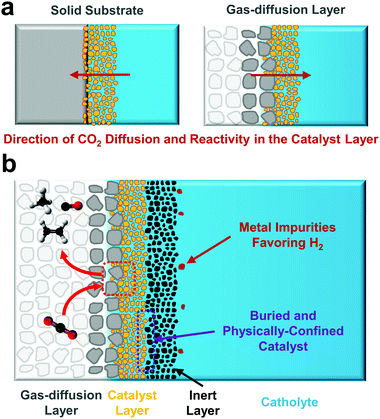
The primary difference between these architectures is a roughly 3-order of magnitude reduction in the CO2 diffusion pathway to the surface of the catalyst: from ∼50 μm in an H-cell to ∼50 nm using a gas-diffusion layer (Fig. 2b and c), which allows for the increased maximum current densities reported in literature. Using a simple 1D reaction–diffusion model developed previously,45,46,57–59 we can also approximate the similarities and differences in the local catalytic environments as a function of reaction rate for both cases.
The first observation from these curves is that the CO2 concentration and pH in the electrolyte at low current densities is relatively similar for both configurations (Fig. 3). This is to be expected as the decreased CO2 diffusion pathway does not affect the maximum availability of CO2 in an electrolyte, and OH− diffusion is moderated by the catholyte. In each case a sudden increase in local pH is observed for the weakly-buffered electrolytes (1 M KCl, 0.1 M KHCO3) as the hydroxide generated as a by-product of water-splitting cannot diffuse away fast enough or be immediately buffered by the solution (Fig. 3b and d). Shown here, and in recent experimental work by the Koper group,42 the electrode pH can in fact shift by as much as 6 units within the first 1–2 mA cm−2. Not only could the reaction itself be altered by this shift, but large pH differences between the reference and working electrodes in this current density range complicate determination of the equilibrium potential, and subsequently, product onset potentials and potential-dependent Tafel slopes.77 Furthermore, for slightly acidic CO2-saturated electrolytes, the solvent itself can also act as the sole proton source (via H3O+) at current densities <1 mA cm−2 until becoming depleted and replaced by water reduction (Fig. 1a). The change in the source of protons for the reaction from hydronium to water-splitting may then result in altered energetics or reaction pathways for CO2 reduction and hydrogen evolution as a function of current density. Within this low current density region, where the most important electrochemical characterizations of a material take place, the reaction environment is then extremely sensitive, complicating analysis of intrinsic catalyst behaviour and the reaction mechanisms at play.
In our reaction–diffusion model, the maximum predicted CO2 reduction current densities in the aqueous-fed system are again <35 mA cm−2 for two-electron reduction processes (Fig. 3a). As shown here in Fig. 3c, and in previous gas-diffusion layer modelling work, we can see however that the maximum current densities are much higher in the case of a gas-diffusion layer as a result of the reduced CO2 diffusion distance; here all electrolytes are capable of sustaining current densities over the proposed 200 mA cm−2 minimum. This agrees well with experimental literature where current densities substantially higher than 200 mA cm−2 have been reported, including the first report using gas-diffusion layers for CO2 reduction from Cook et al. in 1990.62 In recent work by Dinh et al., for example, current densities of 1 A cm−2 were reached in 1 M KOH at 1 atm with an overall CO2 reduction selectivity over 90%.70 While these current densities might not be desired economically due to the corresponding increase in cell potential required,1,7 it indicates that substantial CO2 reduction reaction rates are possible even if the CO2 partial pressure is reduced. This is extremely important for future large-scale devices (>100 cm2 catalyst areas) where the desire to achieve sufficiently-high single-pass conversion efficiencies (CO2 utilization) will require that the partial pressure of CO2 decreases throughout the device. A real system must then be capable of reaching much higher current densities under 100% CO2 conditions (e.g. 1 A cm−2), even if the actual operation occurs at lower current densities (e.g. 200 mA cm−2). If the catalyst near the inlet of the reactor were to instead operate closer to the limiting current density, there would not be enough CO2 to maintain the reaction further into the reactor as the partial pressure decreases. It is also worth noting that the proposed 200 mA cm−2 minimum current density is defined primarily for two-electron reduction products. For multi-carbon products requiring more electrons per CO2 molecule converted, this current density limit must be higher to have the same molecular yield per unit area.
A final extremely important takeaway from Fig. 3 is that the pH near the electrode will be inevitably high at commercially-viable current densities (>200 mA cm−2) in all of the most commonly-used electrolytes, regardless of the choice of catalyst or electrolyte (Fig. 3d). Due to the extremely large quantity of hydroxide generated as a by-product of water reduction and limitations in transporting hydroxide away from the electrode, we predict the pH within the catalyst layer will greater than 12, even for a 1 M KHCO3 buffered electrolyte. While the use of a 0.1 M KHCO3 electrolyte can, and has, been used in an H-cell to approach the local pH values reached at high current densities (Fig. 2b), these conditions are reached only when CO2 is largely depleted and over a small current density/potential range. It is worth noting that the locally alkaline conditions could potentially be avoided by using a sufficiently acidic electrolyte (pH ∼ 1.5 depending on mass transport), but the reaction kinetics for CO2 would have to outweigh the heavily-favoured hydrogen evolution rate in acidic media. In any of these cases all changes in local pH will also ultimately have to be paid for in the overall cell potential, regardless of the locally corrected cathode potential. In brief, the results presented in Fig. 3d show a convergence towards local conditions that have far-reaching implications for not only catalytic activity, but the stability and maximum efficiency of an entire CO2 reduction system, as discussed in later sections.
From existing knowledge about CO2 reduction, we can infer that the thermodynamics and kinetics of reactions on a catalytic surface will be impacted by testing under these elevated reaction conditions. Further modelling and direct-measurement experimental studies of the local electrolyte environment are of course warranted, however, to even better understand how various factors may influence the reaction (e.g. 2D/3D effects, morphology, partial pressure of CO2 in the gas-diffusion layer, etc.). A more detailed representation of CO2 diffusion through a porous electrode structure, for instance, may provide further insight but requires consideration of pore sizes, structures and additives.78 These however are catalyst-specific and beyond the scope of this perspective. These studies are particularly needed for zero-gap membrane electrode assemblies where the extremely-low catholyte volume is expected to make the local reaction conditions more sensitive to the specific device configuration and the properties of the ion-exchange membrane. Finally, additional work integrating reaction–diffusion and microkinetic modelling is needed to see how the predicted cation concentration, which can influence the reaction,79 changes as a result of high current density operation.
Impact of high current densities on CO2 reduction catalyst testing
In the previous section we discussed the impact that both hydrogen evolution and CO2 reduction have on the local environment up to commercially-relevant current densities. This section discusses the important opposite side of the equation: how does access to surplus CO2 and the predicted local environment at higher current densities impact the reactions occurring on the surface of the catalyst. More importantly, can we use this understanding to design even better catalysts or conditions that may advance CO2 electroreduction performance further.In catalyst design the surface of a material is altered as a means of modifying catalytic behaviour. By changing a surface's composition, nanostructure or even substrate, the binding energies of molecules to the surface and the reaction rate of different pathways can be tuned to promote certain reactions, and hopefully, suppress unwanted ones. In electrochemical CO2 reduction, the local environment can provide a similar function. Numerous experimental studies have particularly noted the tendency for higher local pH conditions to favour CO and multi-carbon products while suppressing H2 and CH4 on metals such as Ag and Cu.32,36 As shown in Fig. 3d, when operating at higher current densities the local pH is pushed to highly alkaline levels, even in highly buffered solutions. An important place to start is then to discuss the effect of pH on the selectivity of both CO2 reduction products and hydrogen evolution.
Due to its role as the primary competing reaction to CO2 reduction, H2 evolution is one of the most important products to consider. Under basic conditions the H2 evolution reaction proceeds through direct water reduction and the Volmer–Tafel or Volmer–Heyrovsky steps (see ESI,† Fig. S2). For commonly-used metals such as Cu, Au and Ag, the Volmer step is particularly sluggish in basic conditions due to both poor water dissociation properties and weak *H binding energies, which is pushed even further to the right and away from the peak of the classical volcano plot under higher pH conditions.80,81 Simultaneous CO2 reduction occurring on a catalyst's surface also tends to further suppress H2 activity by weakening hydrogen binding, occupying surface sites and consuming protons.25,82 For catalysts on the left side of the hydrogen binding energy volcano curve, however, hydrogen evolution under locally basic conditions may increase for the same fundamental reasons.
For the most commonly-used set of materials, access to >200 mA cm−2 current densities can then provide a secondary means of suppressing hydrogen evolution by weakening hydrogen binding energies under higher local pH conditions. A secondary, non-material approach for suppressing hydrogen is particularly important for multi-carbon product formation where, despite achieving 100-fold C2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C1 ratios, many of the best catalysts when operated in an H-cell are constantly dogged by a persistent 20–30% H2 selectivity.51,52,83,84 When these same catalysts are operated under elevated current densities in the configurations and electrolytes described here (Fig. 2 and 3), the selectivity towards target products could be increased purely by penalizing hydrogen evolution, rather than necessarily promoting CO2 reduction activity. From Fig. 3 one can expect that any pH-dependent suppression of H2 would be a function of current density and buffering strength, with the simultaneous requirement that the overpotentials needed for CO2 reduction are also competitive with H2 evolution.
C1 ratios, many of the best catalysts when operated in an H-cell are constantly dogged by a persistent 20–30% H2 selectivity.51,52,83,84 When these same catalysts are operated under elevated current densities in the configurations and electrolytes described here (Fig. 2 and 3), the selectivity towards target products could be increased purely by penalizing hydrogen evolution, rather than necessarily promoting CO2 reduction activity. From Fig. 3 one can expect that any pH-dependent suppression of H2 would be a function of current density and buffering strength, with the simultaneous requirement that the overpotentials needed for CO2 reduction are also competitive with H2 evolution.
The local pH environment can also separately influence the energetics of different CO2 reduction products. For catalysts capable of producing only CO and H2, the suppression of H2 can lead directly to high CO selectivities. On a Ag catalyst CO formation under alkaline conditions has been also been observed to be produced almost immediately following the equilibrium potential of −0.11 V vs. RHE, indicating that the reaction itself is improved as compared to lower pH experiments where CO formation on polycrystalline Ag may not begin until −0.5 V vs. RHE.58,67 The behaviour of CO formation on Cu also differs from that of a more neutral H-cell environment. In H-cell tests CO selectivities of >20% are observed on Cu and Cu-derivatives only at very low current densities (<5 mA cm−2) before being supplanted by CO2 reduction to methane, ethylene and ethanol. Under alkaline conditions performed in a gas-diffusion layer, high CO selectivities appear over a much broader range (0–200 mA cm−2).70,73 This suggests that the binding energy of CO on Cu may be weakened under alkaline conditions, promoting faster desorption of the formed *CO intermediate more than under neutral conditions.70 The selectivity towards CO does eventually decrease in favour of higher order products similar to what is observed in an H-cell, but at much higher overall current densities.
Similar to H2 evolution, methane formation on Cu has been shown to be suppressed by increased local pH on oxide-derived samples. If locally alkaline (pH > 12) conditions are indeed unavoidable with the currently-used electrolytes, then these results suggest that an alternate reaction mechanism or catalyst may be needed to realize selective methane formation at elevated current densities. An interesting fundamental result would then be the demonstration of a catalyst capable of selective methane formation under alkaline or locally alkaline conditions. Inversely, for multi-carbon product formation on Cu, higher local pH conditions have been experimentally demonstrated31,73,85 to be an important factor for promoting carbon–carbon coupling. The higher observed activity toward multi-carbon species at lower potentials could be due to the improved CO onset potentials, changes to the binding energy of *CO, a direct effect of the local conditions on the energetics of the coupling step itself, or a cumulative effect of multiple factors. There does not appear to be any strong correlations between pH and product distribution after C–C coupling, however, as most studies report similar alkane to alkene ratios as in lower current density H-cell experiments.
While several studies have operated at elevated current densities using membrane electrode assemblies or neutral-pH catholytes such as KCl and bicarbonate-based salts,2,5,12,13,73,86 a larger number of gas-diffusion layer experiments have used KOH directly as a bulk catholyte,58,65–68,70,71,87 with much of the original CO2 reduction research pioneered by the Kenis Group. By using an alkaline catholyte directly, the impact of a higher pH environment on catalyst performance can be probed across both low and high current densities.65–68,87 In a 1 M KOH environment, CO2 reduction products have been observed on Cu, Au and Ag catalysts at earlier overall onset potentials than in neutral conditions, with current densities of >100 mA cm−2 having been reached for CO, C2H4 and ethanol at more anodic potentials than −0.6 V vs. RHE and with <10% H2 selectivities.61,65,67,70,88 These experiments, however, do not pay the same overpotential price associated with the large local pH swing from neutral to alkaline conditions, which are not taken into account when cathode potential are reported versus a reversible hydrogen electrode (RHE). Additionally, the interaction between unreacted CO2 and hydroxide is problematic for overall stability, as described in the following section. Using an alkaline electrolyte for testing and characterizing catalyst performance is however a promising means of mimicking the local environment of high current densities while being able to measure catalytic activity even at lower current densities.
A final consideration for our prediction that many electrolytes will be forced towards high local pH conditions pertains to catalyst stability. Depending on the properties and composition of a given catalyst, such conditions may result in the dissolution of metals into solution or the removal of some species from the surface. While this has not been observed for many of the Cu and Ag catalysts tested in gas-diffusion layer configurations to date, it should be a consideration in the design of new catalysts.
A second important property of the local reaction environment at commercial-relevant current densities is access to excess CO2. While we have imposed a current density of 200 mA cm−2 as a threshold to reach, from Fig. 3c we can see that additional unreacted CO2 surrounding the catalyst provides the capacity for even higher current densities. An increased CO2 concentration, even at elevated current densities, helps to kinetically ensure that CO2 rather than protons are able to populate the reaction surface. More importantly, the reaction will not be hindered by a deficit of CO2, even at higher local pH conditions. While single-carbon CO2 reduction products such as CO,89 HCOOH90,91 and CH492 can reach relatively high selectivities even at lower current densities in an H-cell configuration, the highest Faradaic efficiencies reported for multi-carbon products typically appear at current densities where CO2 is almost depleted. This is in part due to the necessity for multi-carbon products to follow from *CO (Fig. S2, ESI†) and C–C coupling which requires both sufficient potentials and current densities.48,88,93 Testing novel catalysts at elevated current densities with less CO2 limitations would allow the surface coverage of the *CO reaction intermediate to be maximized over a wider current and potential range without being kinetically-limited by CO2 availability. This is in contrast to current H-cell environments where peak C2 selectivities are often observed only at singular operating conditions (i.e. at a specific potential, current density and pH). Access to a larger operating window then allows more attention to be placed on modifying catalysts to specifically alter CO2 reduction product selectivity between higher-order products such as alkenes vs. alcohols and C2 vs. C3 products. Finally, operating under an excess CO2 environment reduces the overpotential losses associated with transport limitations (sometimes called concentration polarizations). As a result, plots of voltage versus log(j) have been observed to remain linear even up to 300 mA cm−2, helping to remove one of the barriers to gauging intrinsic catalyst activity.58
While the exact implications of high current density catalyst testing will vary slightly with materials, we can assert that the local environment will differ greatly from the bulk electrolyte with a substantial chance of changing important surface kinetics and the observed catalytic activity. Tuning catalysts to optimize morphology or surface binding energies for low current density characterization may then risk optimizing the catalyst for the wrong environment unless higher current conditions can be appropriately mimicked. Performing such experiments adds an additional degree of complexity due to the need for researchers to adopt either a pressurized system or a gas-diffusion layer to supply additional CO2 (Fig. 2), in addition to developing new catalysts. We believe, however, that this is an essential step to make the best (highest activity, selectivity and stability) CO2 reduction catalyst possible. Fortunately, the range of experimental reports already performed at higher current densities indicate that CO2 reduction is typically improved versus operating in the same electrolyte at lower current densities, at least in part due to increased CO2 availability and suppression of pH-independent products.
Impact of high current densities on system design
Up to this point we have discussed the impacts of configuration and reaction conditions on the CO2 reduction reaction, and vice versa. While understanding the CO2 reduction reaction and catalyst behaviour over a range of conditions is important, our preferred choice of catalyst and catholyte will have implications and constraints for the system as a whole. Further catalyst testing in a more commercial-type reactor will help to bring operational issues to the forefront of the field and may result in new ingenious scientific and engineering solutions to these issues.One topic that has large implications for system and catalyst design using gas-diffusion layers is the concept of whether the CO2 reduction reaction occurs at a three-phase reaction interface (gaseous CO2–liquid water–catalyst) or a two-phase aqueous reaction with dissolved CO2 (Fig. 2e). The concept of a three-phase reaction interface for CO2 reduction was described in the original reports using gas-diffusion layers62 without explicit proof, and has since been used to describe operation of these devices. Here we briefly discuss this controversy and present evidence arguing in favour of a two-phase reaction interface with dissolved CO2 as the reagent. We hope this will open a discussion on this extremely important aspect of gas-diffusion layer operation which has implications in the design of devices, catalysts and their subsequent integration.
A first indication that dissolved CO2 is the primary reagent comes from the tendency for the most metals to be hydrophilic when under a negatively applied potential, meaning that water will readily wet the reaction surface. A thin film of water (even on the order of nm's) then likely surrounds the catalyst at all times, even near the gas–liquid interface. Additionally, the nano and micropores within the porous catalyst layer result in strong capillary forces that encourage immediate wetting of all metal surfaces and pores, rather than a partially-wetted catalyst layer scenario. An important experimental observation can also be made when a gas-diffusion layer itself floods, indicating that a gas–liquid–catalyst interface is not maintained. Even under these flooding conditions, however, stable CO2 reduction has been shown to be maintained76 which would not be possible if the primary mechanism required a three-phase interface. These separate reasons then indicate to us that the catalyst layer itself is fully-wetted and that CO2 reaches the catalyst surface only by diffusing through the aqueous solvent, and the reaction takes place explicitly in the liquid phase.
If we then move forward assuming that the reaction then happens only at a two-phase interface, we can better design our systems to improve performance. This was illustrated in the work by Dinh et al.70 where changing the concentration of KOH as well as the thickness of the catalyst layer (e.g. 50 nm vs. 1000 nm) resulted in different CO2 limiting current densities. The reduction reaction then takes place throughout the porous catalyst layer and factors such as porosity, salting out effects, tortuosity and equilibrium reactions are then important considerations for designing an optimal catalyst and system. While these considerations are on average secondary to the design of new catalysts with specific facet orientations or alloy compositions, they have important implications for both performance and scaling-up these devices.
Finally, if a purely two-phase reaction for CO2 reduction is occurring as we suggest, this has large implications for membrane electrode assemblies where liquid water can only be provided through condensation of the humidified CO2 stream and transport through the ion exchange membrane. While we believe CO2 reduction proceeds through the dissolution of CO2 into this water layer, one route for H2 evolution can be achieved by direct proton transfer from the ion exchange membrane directly to the metal surface, without water present. The membrane in this case could then function similar to an ionomer in a PEM electrolyzer if a Nafion membrane was used. These considerations then emphasize the importance of encouraging water in membrane electrode assemblies to promote CO2 reduction rather than hydrogen evolution, either through humidifying the CO2 stream, adding a fixed water layer or improving water transport through the polymer membrane.2,5
Following on this point that the reaction proceeds through the dissolution of CO2 through the electrolyte, another issue that arises pertains to the twist of fate that the most efficient CO2 reduction conditions appear to occur when a highly-alkaline electrolyte is used as a catholyte. While an alkaline catholyte may provide optimal cathode performance, it comes at the cost of system stability due to the interaction between unreacted CO2 and hydroxide in the electrolyte. This is particularly an issue for scale-up as we have indicated previously. Having a high single-pass conversion efficiency will require excess CO2 to be present at the beginning of the cell such that a sufficient current density can be maintained at the end of the cell, where the CO2 partial pressure is lower. The capacity to reach higher limiting current densities near the beginning of the cell then also means that excess CO2 is capable of dissolving into the electrolyte. For 1 M KOH our reaction–diffusion model shows that this interaction can decrease the pH within the porous catalyst layer by 1–2 units at lower current densities depending on the replenishment rate from a bulk liquid phase (Fig. 3d). While this pH change can be accounted for when trying to ascertain the intrinsic activity of the catalyst, a portion of the CO2 crossing the gas–liquid interface will be converted to bicarbonate upon interacting with hydroxide, and then subsequently into carbonate.61 Not only does this decrease CO2 utilization, but over a long enough operating time it will destroy the expensive KOH catholyte, itself energy-intensively produced through electrochemical reactions. At the moment there is no engineering solution to completely mitigate this effect even at small scales, let alone a more complex >100 cm2 reactor design. We may then be resigned to the use of neutral-pH catholytes which to date would represent an increase in expected cathode overpotentials. Further, overall cell potentials will be higher due to the need for the oxygen evolution reaction to occur in a similar pH electrolyte, or by using a bipolar membrane to maintain an alkaline anolyte. While CO2–hydroxide interactions are typically only considered as a critical issue for alkaline catholytes such as KOH, systems using neutral electrolytes should also aim to balance the generated hydroxide ions with protons generated by the anode reaction.94 Even in a neutral-pH medium the system's electrolyte balance would similarly be steadily shifted away from the initial condition due our CO2 reagent that can influence pH; in this case, however, the electrolyte could be externally regenerated without additional energy input.
Another cell design issue with using alkaline electrolytes is the need for anion exchange membranes, which have comparatively slower ion transport than proton exchange membranes and overall limited mobility for both bicarbonate and carbonate anions.12,95 For these reasons a large amount of research is being undertaken to improve OH−, HCO3− and CO32− transport through anion exchange membranes, with a fair amount of work done by Dioxide Materials’ and their Sustainion© membrane which has shown 1000's of hours of stability, albeit under specific operating conditions.74,96 Without sufficient bicarbonate/carbonate transport through the membrane, the concentration of buffering ions will increase over time, forcing co-ion transport through the membrane and resulting in electrolyte precipitation, destroying the membrane and/or the gas-diffusion layer. Without solutions to these issues it will be difficult for either membrane electrode assemblies or alkaline catholytes to be paired with anion exchange membranes in a practical CO2 reduction device.
An additional reaction constraint brought on by the need for >200 mA cm−2 operation pertains to the practical choice of electrolytes, independent of their impact on catalytic activity. Using this minimum current density as a target threshold we can approximate the expected ohmic losses of commonly-used electrolytes at 25 °C, regardless of the catalyst or substrate used. Assuming a combined catholyte and anolyte thickness of 3 mm, for example, it is clear that certain electrolytes will cause prohibitive ohmic losses (Fig. 4). The 0.1 M KHCO3 electrolyte used in the majority of the highest selectivity C2H4 studies, for instance, results in heating losses of 6 V at 200 mA cm−2, five-fold larger than the thermodynamic cell potential when using an oxygen-evolving anode (Fig. S3, ESI†). Such a low conductivity electrolyte can then never be used in a functioning system unless the electrolyte pathway between the anode and cathode is eliminated or greatly reduced, as in the case of membrane electrode assemblies (Fig. 2c).2,5 These ohmic drops also put into perspective how other cell losses may be more influential than further decreases to cathode overpotentials. It is worth noting that the result in Fig. 4 becomes even more pronounced when the presumed even higher current densities needed for multi-carbon products such as C2H4 are considered. Finally, separate from our discussion motivating the testing of catalysts at elevated current densities, this result highlights the need to test catalysts in higher conductivity electrolytes to see the effect that a higher concentration of supporting ions may or may not impact a catalyst's activity.
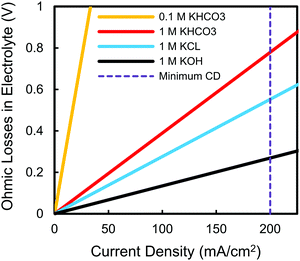 | ||
| Fig. 4 Expected ohmic losses as a function of current density for commonly-used electrolytes in an electrochemical cell with a combined 3 mm catholyte and anolyte thickness at 25 °C. | ||
A final notable difference to performing CO2 electroreduction in an H-cell versus a gas-diffusion layer configuration is subtler. As has been recently demonstrated, under high current density operation the CO2 reduction reaction is confined to a relatively small portion of a porous catalyst layer and takes place on the backside of the material (Fig. 5a).70 This is in contrast to an H-cell where CO2 diffuses to the catalyst layer from the front-side bulk electrolyte (Fig. 5a). Much like the effects of varying morphology and porosity in H-cell catalyst studies allowed for performance to be improved and varied, the reversed flow direction of CO2 transport allows for unique gas-diffusion and catalyst layer engineering to take place. One recent example is placing an inactive material on top of the catalyst layer (Fig. 5b) to provide an additionally conductive layer. While this layer is used as a current collector, it may also help to prevent both catalyst restructuring that can change catalytic behaviour as well as the deposition of contaminants on the active catalyst surface. Contaminants are a problem largely unique to CO2 reduction due to the tendency for most electrolytes to contain minute concentrations of Ni, Fe or Co, metals capable of preferentially promoting hydrogen evolution even at low potentials and are a primary source of catalyst deactivation.2,97,98 One could further imagine layering catalyst structures on gas-diffusion layers for either unique catalyst designs or supportive layers that provide new functionalities. While many possibilities have yet to be explored for CO2 reduction, a gas-diffusion layer provides a porous electrode structure which fundamentally changes both reagent and product transport pathways compared to the impermeable supports traditionally used in fully-aqueous reactors. As adoption increases substantial opportunity then exists for further innovative catalyst-support integrations to improve either stability or performance. The subtle operational difference also means the traditionally described benefits of catalyst nanostructuring (for increased surface area, mass transport, facet exposure, etc.) have to be somewhat reassessed, which may be difficult as the primary active surface is no longer easily accessible to surface characterization techniques.
Conclusion
In summary, in this perspective we have shown that the minimum current density requirements for future commercial systems will ultimately drive CO2 reduction away from the operating conditions where much of the cutting-edge catalyst research has been performed. Acknowledging these realities and testing state-of-the-art catalysts under these more realistic operating conditions will be important not only for further improving performance metrics such as selectivity, activity and stability, but to accelerate research towards commercial applications that are exceedingly needed sooner rather than later. It is encouraging that there has been a recent noticeable shift in literature towards more system-integrated testing platforms for electrochemical CO2 reduction, and we hope that this new perspective further motivates adoption and helps incite new discoveries.Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
This project has received funding from the European Research Council (ERC) under the European Union's Horizon 2020 research and innovation programme (grant agreement no. 759743 – WUTANG). The authors greatly acknowledge the stimulating research conversations with Dr Cao-Thang Dinh, Dr Ali Seifitokaldani, Dr Md Kibria, Dr Recep Kas, Dr Christine Gabardo, Dr Nathan Nesbitt, Jonathan Edwards and Divya Bohra, as well as Dr David Sinton and Dr Edward Sargent, that over time have allowed this article to come to fruition.References
- M. Jouny, W. Luc and F. Jiao, Ind. Eng. Chem. Res., 2018, 57, 2165–2177 CrossRef CAS.
- Y. C. Li, D. Zhou, Z. Yan, R. H. Gonçalves, D. A. Salvatore, C. P. Berlinguette and T. E. Mallouk, ACS Energy Lett., 2016, 1, 1149–1153 CrossRef CAS.
- H.-R. “Molly” Jhong, F. R. Brushett and P. J. A. Kenis, Adv. Energy Mater., 2013, 3, 589–599 CrossRef.
- T. Li, Y. Cao, J. He and C. P. Berlinguette, ACS Cent. Sci., 2017, 3, 778–783 CrossRef CAS PubMed.
- D. A. Salvatore, D. M. Weekes, J. He, K. E. Dettelbach, Y. C. Li, T. E. Mallouk and C. P. Berlinguette, ACS Energy Lett., 2018, 3, 149–154 CrossRef CAS.
- T. Haas, R. Krause, R. Weber, M. Demler and G. Schmid, Nat. Catal., 2018, 1, 32–39 CrossRef.
- S. Verma, B. Kim, H.-R. “Molly” Jhong, S. Ma and P. J. A. Kenis, ChemSusChem, 2016, 9, 1972–1979 CrossRef CAS PubMed.
- J. M. Spurgeon and B. Kumar, Energy Environ. Sci., 2018, 11, 1536–1551 RSC.
- K. Jiang, S. Siahrostami, T. Zheng, Y. Hu, S. Hwang, E. Stavitski, Y. Peng, J. Dynes, M. Gangisetty, D. Su, K. Attenkofer and H. Wang, Energy Environ. Sci., 2018, 11, 893–903 RSC.
- W. Zhang, Y. Hu, L. Ma, G. Zhu, Y. Wang, X. Xue, R. Chen, S. Yang and Z. Jin, Adv. Sci., 2018, 5, 1700275 CrossRef PubMed.
- F. Li, L. Chen, G. P. Knowles, D. R. MacFarlane and J. Zhang, Angew. Chem., Int. Ed., 2017, 56, 505–509 CrossRef CAS PubMed.
- D. M. Weekes, D. A. Salvatore, A. Reyes, A. Huang and C. P. Berlinguette, Acc. Chem. Res., 2018, 51, 910–918 CrossRef CAS PubMed.
- B. Endrődi, G. Bencsik, F. Darvas, R. Jones, K. Rajeshwar and C. Janáky, Prog. Energy Combust. Sci., 2017, 62, 133–154 CrossRef.
- D. Kim, J. Resasco, Y. Yu, A. M. Asiri and P. Yang, Nat. Commun., 2014, 5, 4948 CrossRef CAS PubMed.
- X. Liu, J. Xiao, H. Peng, X. Hong, K. Chan and J. K. Nørskov, Nat. Commun., 2017, 8, 15438 CrossRef CAS PubMed.
- H. Mistry, R. Reske, Z. Zeng, Z.-J. Zhao, J. Greeley, P. Strasser and B. R. Cuenya, J. Am. Chem. Soc., 2014, 136, 16473–16476 CrossRef CAS PubMed.
- R. Reske, H. Mistry, F. Behafarid, B. Roldan Cuenya and P. Strasser, J. Am. Chem. Soc., 2014, 136, 6978–6986 CrossRef CAS PubMed.
- W. Zhu, Y.-J. Zhang, H. Zhang, H. Lv, Q. Li, R. Michalsky, A. A. Peterson and S. Sun, J. Am. Chem. Soc., 2014, 136, 16132–16135 CrossRef CAS PubMed.
- W. Zhu, R. Michalsky, Ö. Metin, H. Lv, S. Guo, C. J. Wright, X. Sun, A. A. Peterson and S. Sun, J. Am. Chem. Soc., 2013, 135, 16833–16836 CrossRef CAS PubMed.
- S. Liu, X.-Z. Wang, H. Tao, T. Li, Q. Liu, Z. Xu, X.-Z. Fu and J.-L. Luo, Nano Energy, 2018, 45, 456–462 CrossRef CAS.
- S. Sen, D. Liu and G. T. R. Palmore, ACS Catal., 2014, 4, 3091–3095 CrossRef CAS.
- A. Loiudice, P. Lobaccaro, A. Kamali Esmail, T. Thao, H. Huang Brandon, W. Ager Joel and R. Buonsanti, Angew. Chem., Int. Ed., 2016, 55, 5789–5792 CrossRef CAS PubMed.
- A. S. Hall, Y. Yoon, A. Wuttig and Y. Surendranath, J. Am. Chem. Soc., 2015, 137, 14834–14837 CrossRef CAS PubMed.
- X. Min and M. W. Kanan, J. Am. Chem. Soc., 2015, 137, 4701–4708 CrossRef CAS PubMed.
- E. R. Cave, C. Shi, K. P. Kuhl, T. Hatsukade, D. N. Abram, C. Hahn, K. Chan and T. F. Jaramillo, ACS Catal., 2018, 3035–3040 CrossRef CAS.
- B. Khezri, A. C. Fisher and M. Pumera, J. Mater. Chem. A, 2017, 5, 8230–8246 RSC.
- X. Duan, J. Xu, Z. Wei, J. Ma, S. Guo, S. Wang, H. Liu and S. Dou, Adv. Mater., 2017, 29, 1701784 CrossRef PubMed.
- J. Wu, Y. Huang, W. Ye and Y. Li, Adv. Sci., 2017, 4, 1700194 CrossRef PubMed.
- J. He, N. J. J. Johnson, A. Huang and P. Berlinguette Curtis, ChemSusChem, 2017, 11, 48–57 CrossRef PubMed.
- F. Li, D. R. MacFarlane and J. Zhang, Nanoscale, 2018, 10, 6235–6260 RSC.
- K. J. P. Schouten, E. Pérez Gallent and M. T. M. Koper, J. Electroanal. Chem., 2014, 716, 53–57 CrossRef CAS.
- Y. Pang, T. Burdyny, C.-T. Dinh, M. G. Kibria, J. Z. Fan, M. Liu, E. H. Sargent and D. Sinton, Green Chem., 2017, 19, 4023–4030 RSC.
- J. E. Pander, D. Ren, Y. Huang, W. X. Loo Nicholas, H. L. Hong Samantha and B. S. Yeo, ChemElectroChem, 2017, 5, 219–237 CrossRef.
- Y. Zhang, X. Zhang, A. M. Bond and J. Zhang, Phys. Chem. Chem. Phys., 2018, 20, 5936–5941 RSC.
- C. F. C. Lim, D. A. Harrington and A. T. Marshall, Electrochim. Acta, 2017, 238, 56–63 CrossRef CAS.
- R. Kas, R. Kortlever, H. Yılmaz, M. T. M. Koper and G. Mul, ChemElectroChem, 2015, 2, 354–358 CrossRef CAS.
- A. S. Varela, M. Kroschel, T. Reier and P. Strasser, Catal. Today, 2016, 260, 8–13 CrossRef CAS.
- J. Resasco, L. D. Chen, E. Clark, C. Tsai, C. Hahn, T. F. Jaramillo, K. Chan and A. T. Bell, J. Am. Chem. Soc., 2017, 139, 11277–11287 CrossRef CAS PubMed.
- O. Ayemoba and A. Cuesta, ACS Appl. Mater. Interfaces, 2017, 9, 27377–27382 CrossRef CAS PubMed.
- E. Pérez-Gallent, G. Marcandalli, M. C. Figueiredo, F. Calle-Vallejo and M. T. M. Koper, J. Am. Chem. Soc., 2017, 139, 16412–16419 CrossRef PubMed.
- M. R. Singh, Y. Kwon, Y. Lum, J. W. Ager and A. T. Bell, J. Am. Chem. Soc., 2016, 138, 13006–13012 CrossRef CAS PubMed.
- H. Ooka, M. C. Figueiredo and M. T. M. Koper, Langmuir, 2017, 33, 9307–9313 CrossRef CAS PubMed.
- J. D. Goodpaster, A. T. Bell and M. Head-Gordon, J. Phys. Chem. Lett., 2016, 7, 1471–1477 CrossRef CAS PubMed.
- M. R. Singh, J. D. Goodpaster, A. Z. Weber, M. Head-Gordon and A. T. Bell, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, E8812–E8821 CrossRef CAS PubMed.
- N. Gupta, M. Gattrell and B. MacDougall, J. Appl. Electrochem., 2006, 36, 161–172 CrossRef CAS.
- M. R. Singh, E. L. Clark and A. T. Bell, Phys. Chem. Chem. Phys., 2015, 17, 18924–18936 RSC.
- T. Cheng, H. Xiao and W. A. Goddard, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, 1795–1800 CrossRef CAS PubMed.
- J. H. Montoya, C. Shi, K. Chan and J. K. Nørskov, J. Phys. Chem. Lett., 2015, 6, 2032–2037 CrossRef CAS PubMed.
- M. Ma, B. J. Trześniewski, J. Xie and W. A. Smith, Angew. Chem., Int. Ed., 2016, 55, 9748–9752 CrossRef CAS PubMed.
- D. Kim, C. S. Kley, Y. Li and P. Yang, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, 10560–10565 CrossRef CAS PubMed.
- P. D. Luna, R. Quintero-Bermudez, C.-T. Dinh, M. B. Ross, O. S. Bushuyev, P. Todorović, T. Regier, S. O. Kelley, P. Yang and E. H. Sargent, Nat. Catal., 2018, 1, 103–110 CrossRef.
- H. Mistry, A. S. Varela, C. S. Bonifacio, I. Zegkinoglou, I. Sinev, Y.-W. Choi, K. Kisslinger, E. A. Stach, J. C. Yang, P. Strasser and B. R. Cuenya, Nat. Commun., 2016, 7, 12123 CrossRef PubMed.
- A. D. Handoko, C. W. Ong, Y. Huang, Z. G. Lee, L. Lin, G. B. Panetti and B. S. Yeo, J. Phys. Chem. C, 2016, 120, 20058–20067 CrossRef CAS.
- D. Ren, Y. Deng, A. D. Handoko, C. S. Chen, S. Malkhandi and B. S. Yeo, ACS Catal., 2015, 5, 2814–2821 CrossRef CAS.
- Y. Lum, B. Yue, P. Lobaccaro, A. T. Bell and J. W. Ager, J. Phys. Chem. C, 2017, 121, 14191–14203 CrossRef CAS.
- R. Kortlever, J. Shen, K. J. P. Schouten, F. Calle-Vallejo and M. T. M. Koper, J. Phys. Chem. Lett., 2015, 6, 4073–4082 CrossRef CAS PubMed.
- T. Burdyny, P. J. Graham, Y. Pang, C.-T. Dinh, M. Liu, E. H. Sargent and D. Sinton, ACS Sustainable Chem. Eng., 2017, 5, 4031–4040 CrossRef CAS.
- C. M. Gabardo, A. Seifitokaldani, J. P. Edwards, C.-T. Dinh, T. Burdyny, M. G. Kibria, C. P. O’Brien, E. H. Sargent and D. Sinton, Energy Environ. Sci., 2018, 11, 2531–2539 RSC.
- A. Seifitokaldani, C. M. Gabardo, T. Burdyny, C.-T. Dinh, J. P. Edwards, M. G. Kibria, O. S. Bushuyev, S. O. Kelley, D. Sinton and E. H. Sargent, J. Am. Chem. Soc., 2018, 140, 3833–3837 CrossRef CAS PubMed.
- L.-C. Weng, A. T. Bell and A. Z. Weber, Phys. Chem. Chem. Phys., 2018, 20, 16973–16984 RSC.
- C.-T. Dinh, F. P. Garcia de Arquer, D. Sinton and E. H. Sargent, ACS Energy Lett., 2018, 3, 2835–2840 CrossRef CAS.
- R. L. Cook, R. C. MacDuff and A. F. Sammells, J. Electrochem. Soc., 1990, 137, 607–608 CrossRef CAS.
- H. Yano, F. Shirai, M. Nakayama and K. Ogura, J. Electroanal. Chem., 2002, 519, 93–100 CrossRef CAS.
- C. Delacourt, P. L. Ridgway, J. B. Kerr and J. Newman, J. Electrochem. Soc., 2008, 155, B42–B49 CrossRef CAS.
- S. Ma, R. Luo, J. I. Gold, A. Z. Yu, B. Kim and P. J. A. Kenis, J. Mater. Chem. A, 2016, 4, 8573–8578 RSC.
- B. Kim, F. Hillman, M. Ariyoshi, S. Fujikawa and P. J. A. Kenis, J. Power Sources, 2016, 312, 192–198 CrossRef CAS.
- S. Verma, X. Lu, S. Ma, R. I. Masel and P. J. A. Kenis, Phys. Chem. Chem. Phys., 2016, 18, 7075–7084 RSC.
- E. J. Dufek, T. E. Lister and M. E. McIlwain, Electrochem. Solid-State Lett., 2012, 15, B48–B50 CrossRef CAS.
- T. T. H. Hoang, S. Ma, J. I. Gold, P. J. A. Kenis and A. A. Gewirth, ACS Catal., 2017, 7, 3313–3321 CrossRef CAS.
- C.-T. Dinh, T. Burdyny, M. G. Kibria, A. Seifitokaldani, C. M. Gabardo, F. P. G. de Arquer, A. Kiani, J. P. Edwards, P. D. Luna, O. S. Bushuyev, C. Zou, R. Quintero-Bermudez, Y. Pang, D. Sinton and E. H. Sargent, Science, 2018, 360, 783–787 CrossRef CAS PubMed.
- T.-T. Zhuang, Z.-Q. Liang, A. Seifitokaldani, Y. Li, P. D. Luna, T. Burdyny, F. Che, F. Meng, Y. Min, R. Quintero-Bermudez, C. T. Dinh, Y. Pang, M. Zhong, B. Zhang, J. Li, P.-N. Chen, X.-L. Zheng, H. Liang, W.-N. Ge, B.-J. Ye, D. Sinton, S.-H. Yu and E. H. Sargent, Nat. Catal., 2018, 1, 421–428 CrossRef.
- E. Irtem, T. Andreu, A. Parra, M. D. Hernández-Alonso, S. García-Rodríguez, J. M. Riesco-García, G. Penelas-Pérez and J. R. Morante, J. Mater. Chem. A, 2016, 4, 13582–13588 RSC.
- J.-J. Lv, M. Jouny, W. Luc, W. Zhu, J.-J. Zhu and F. Jiao, Adv. Mater., 2018, 30, 1803111 CrossRef PubMed.
- Z. Liu, R. I. Masel, Q. Chen, R. Kutz, H. Yang, K. Lewinski, M. Kaplun, S. Luopa and D. R. Lutz, J. CO2 Util., 2016, 15, 50–56 CrossRef CAS.
- W. Lee, Y. E. Kim, M. H. Youn, S. K. Jeong and K. T. Park, Angew. Chem., Int. Ed., 2018, 57, 6883–6887 CrossRef CAS.
- P. Jeanty, C. Scherer, E. Magori, K. Wiesner-Fleischer, O. Hinrichsen and M. Fleischer, J. CO2 Util., 2018, 24, 454–462 CrossRef CAS.
- M. Dunwell, W. Luc, Y. Yan, F. Jiao and B. Xu, ACS Catal., 2018, 8, 8121–8129 CrossRef CAS.
- N. Nonoyama, S. Okazaki, A. Z. Weber, Y. Ikogi and T. Yoshida, J. Electrochem. Soc., 2011, 158, B416–B423 CrossRef CAS.
- M. Liu, Y. Pang, B. Zhang, P. De Luna, O. Voznyy, J. Xu, X. Zheng, C. T. Dinh, F. Fan, C. Cao, F. P. G. de Arquer, T. S. Safaei, A. Mepham, A. Klinkova, E. Kumacheva, T. Filleter, D. Sinton, S. O. Kelley and E. H. Sargent, Nature, 2016, 537, 382–386 CrossRef CAS PubMed.
- W. Sheng, M. Myint, J. G. Chen and Y. Yan, Energy Environ. Sci., 2013, 6, 1509–1512 RSC.
- J. K. Nørskov, T. Bligaard, A. Logadottir, J. R. Kitchin, J. G. Chen, S. Pandelov and U. Stimming, J. Electrochem. Soc., 2005, 152, J23–J26 CrossRef.
- Y.-J. Zhang, V. Sethuraman, R. Michalsky and A. A. Peterson, ACS Catal., 2014, 4, 3742–3748 CrossRef CAS.
- K. Jiang, R. B. Sandberg, A. J. Akey, X. Liu, D. C. Bell, J. K. Nørskov, K. Chan and H. Wang, Nat. Catal., 2018, 1, 111–119 CrossRef.
- D. Ren, J. Fong and B. S. Yeo, Nat. Commun., 2018, 9, 925 CrossRef PubMed.
- M. G. Kibria, C.-T. Dinh, A. Seifitokaldani, P. D. Luna, T. Burdyny, R. Quintero-Bermudez, M. B. Ross, O. S. Bushuyev, F. P. G. de Arquer, P. Yang, D. Sinton and E. H. Sargent, Adv. Mater., 2018, 30, 1804867 CrossRef PubMed.
- A. D. Castillo, M. Alvarez-Guerra and A. Irabien, AIChE J., 2014, 60, 3557–3564 CrossRef.
- S. Ma, R. Luo, S. Moniri, Y. Lan and P. J. A. Kenis, J. Electrochem. Soc., 2014, 161, F1124–F1131 CrossRef CAS.
- S. Ma, M. Sadakiyo, R. Luo, M. Heima, M. Yamauchi and P. J. A. Kenis, J. Power Sources, 2016, 301, 219–228 CrossRef CAS.
- Q. Li, J. Fu, W. Zhu, Z. Chen, B. Shen, L. Wu, Z. Xi, T. Wang, G. Lu, J. Zhu and S. Sun, J. Am. Chem. Soc., 2017, 139, 4290–4293 CrossRef CAS PubMed.
- X. Zheng, P. De Luna, F. P. García de Arquer, B. Zhang, N. Becknell, M. B. Ross, Y. Li, M. N. Banis, Y. Li, M. Liu, O. Voznyy, C. T. Dinh, T. Zhuang, P. Stadler, Y. Cui, X. Du, P. Yang and E. H. Sargent, Joule, 2017, 1, 794–805 CrossRef CAS.
- A. Klinkova, P. De Luna, C.-T. Dinh, O. Voznyy, E. M. Larin, E. Kumacheva and E. H. Sargent, ACS Catal., 2016, 6, 8115–8120 CrossRef CAS.
- H. Hashiba, H. K. Sato, S. Yotsuhashi, K. Fujii, M. Sugiyama and Y. Nakano, Sustainable Energy Fuels, 2017, 1, 1734–1739 RSC.
- Y. Huang, A. D. Handoko, P. Hirunsit and B. S. Yeo, ACS Catal., 2017, 7, 1749–1756 CrossRef CAS.
- S. Hernández, M. A. Farkhondehfal, F. Sastre, M. Makkee, G. Saracco and N. Russo, Green Chem., 2017, 19, 2326–2346 RSC.
- J. R. Varcoe, P. Atanassov, D. R. Dekel, A. M. Herring, M. A. Hickner, P. A. Kohl, A. R. Kucernak, W. E. Mustain, K. Nijmeijer, K. Scott, T. Xu and L. Zhuang, Energy Environ. Sci., 2014, 7, 3135–3191 RSC.
- J. J. Kaczur, H. Yang, Z. Liu, S. D. Sajjad and R. I. Masel, Front. Chem., 2018, 6, 263 CrossRef PubMed.
- Y. Hori, H. Konishi, T. Futamura, A. Murata, O. Koga, H. Sakurai and K. Oguma, Electrochim. Acta, 2005, 50, 5354–5369 CrossRef CAS.
- A. Wuttig and Y. Surendranath, ACS Catal., 2015, 5, 4479–4484 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c8ee03134g |
| This journal is © The Royal Society of Chemistry 2019 |