Mixed phononic and non-phononic transport in hybrid lead halide perovskites: glass-crystal duality, dynamical disorder, and anharmonicity†
Taishan
Zhu
 and
Elif
Ertekin
and
Elif
Ertekin
 *
*
Department of Mechanical Science & Engineering and Materials Research Laboratory, University of Illinois at Urbana-Champaign, Urbana, IL 61801, USA. E-mail: ertekin@illinois.edu
First published on 10th December 2018
Abstract
In hybrid materials, a high-symmetry lattice is decorated by low-symmetry building blocks. The result is an aperiodic solid that hosts many nearly-degenerate disordered configurations. Using the perovskite methylammonium lead iodide (MAPbI3) as a prototype hybrid material, we show that the inherent disorder renders the conventional phonon picture of transport insufficient. Ab initio molecular dynamics and analysis of the spectral energy density reveal that vibrational carriers simultaneously exhibit features of both classical phonons and of carriers typically found in glasses. The low frequency modes retain elements of acoustic waves but exhibit extremely short lifetimes of only a few tens of picoseconds. For higher frequency modes, strong scattering due to rapid motion and reconfiguration of the organic cation molecules induces a loss of definition of the wave vector. Lattice dynamics shows that these carriers are more akin to diffusons – the nonwave carriers in vitreous materials – and are the dominant contributors to thermal conduction near room temperature. To unify the framework of glassy diffusons with that of phonons scattered at the ultimate limit, three-phonon interactions resolved from first-principles expose anharmonic effects two orders of magnitude higher than in silicon. The dominant anharmonic interactions occur within modes of the PbI6 octahedral framework itself, as well as between modes of the octahedral framework and modes localized to the MA molecules. The former arises from long-range interactions due to resonant bonding, and the latter from polar rotor scattering of the MA molecules. This establishes a clear microscopic connection between symmetry-breaking, dynamical disorder, anharmonicity, and the loss of wave nature in MAPbI3.
Broader contextVibrational energy transport in complex hybrid materials underlies performance and stability in scenarios ranging from thermoelectrics to batteries, and from photochemical catalysis to biological tissues. Hybrid materials – in which low-symmetry building blocks decorate a higher symmetry lattice – exhibit an intermediate nature that is neither crystalline nor glassy. As such, in this work we demonstrate that the vibrational modes in the lead halide pervoskites, a classic hybrid material, exhibit a mixed nature in between those of phonons found in crystalline materials and propagons, diffusons, and locons found in glasses. In the lead halide perovskites, the dynamical motions of the methylammonium molecules strongly couple to and scatter the phonon-like modes of the underlying inorganic PbI6 framework, resulting in phonon lifetimes on the order of their vibrational period. The scattering due to rapid motion and reconfiguration of the molecules is sufficient to induce a loss of wave character, especially to the optical modes. We link the strong scattering to long-range interactions due to resonant bonding and molecular polar rotor scattering. Our present theory brings together existing pictures of transport in the crystalline and amorphous limit and should be generally applicable to a broad spectrum of complex crystals with hierarchical chemical bonding. |
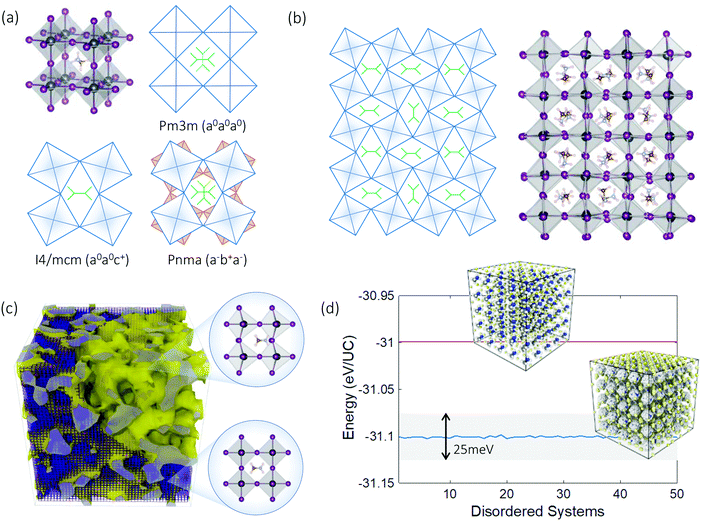
Hybrid materials – composed of two or more constituents at the molecular or nano scale – have become an emerging avenue for materials design, with applications ranging from optoelectronics to energy harvesting to biomedicine.1–6 The halide perovskite methylammonium lead iodide (MAPbI3), a prominent example, has shown a sharp rise in photovoltaic conversion efficiency from 3% to 22% in the last ten years.7,8 Other examples of hybrid materials include molecular motors,9–11 van der Waals heterostructures,12 hierarchically organized hybrid materials,13 and other organic–inorganic halide perovskites.1,4 In terms of symmetry, hybrid materials emerge as procrystals,14,15 featuring mixed chemical bonds and low-symmetry groups sitting on higher-symmetry lattices,11,16 which gives rise to multiple forms of disorder. Fig. 1(a) illustrates this for MAPbI3, in which covalently bonded methylammonium (MA) molecules (C3v) have lower symmetry than and interact with the octahedral PbI6 lattice (Oh). The chemistry of such hybrid materials capitalizes on the disparate structures and motifs present and their interactions. Naturally such hybrid stereochemistry leads to vibrational atomic dynamics at distinct spatiotemporal scales.17
For these materials, knowledge of vibrational properties at atomic scales gives direct insights on phase transitions, thermal stability, and lattice conduction, among other structure–property relations.17–20 In lead halide perovskites, vibrational dynamics is important not only for characterizing energy transport and phase transformations,21 but also for resolving their thermal instability, a key barrier hindering large-scale adoption.22 The picture of vibrational transport in these materials remains incomplete. So far the mechanisms responsible for their ultralow thermal conductivities (∼0.5 W m−1 K−1 at room temperature) have been ascribed to either low group velocity,23,24 strong anharmonicity,25 or both.26 Related mechanisms, such as polar rotor scattering27 and cluster rattling,28 have been suggested. These explanations all rely on conventional phonon descriptions of transport, and a direct link between these factors and disorder is missing. For hybrid organic–inorganic perovskites, it is only recently that the dynamics of the organic molecules have been characterized, showing rapid reorientations about their average lattice position.19,29,30 It is unclear how the MA dynamics and the induced structural disorder affects vibrational, and thus thermal, electro-magnetic, and other, properties.
Further complexity arises because the disorder exhibited by MAPbI3 is present at several distinct spatial and temporal scales. Fig. 1(a–c) shows three types of disorder inherent to hybrid perovskites that are correlated and dynamical in nature: (i) phase coexistence, (ii) random orientations of the A-site MA molecules, and (iii) incommensurate tilings of the PbI6 framework. The coexistence of different types of octahedral tilts and of molecular orientations has been experimentally demonstrated.19,31 With both phase coexistence and MA orientational degrees of freedom, the PbI6 octahedra could in principle preserve their shape despite the disorder. In contrast, the snapshots shown in Fig. 1(b) from ab initio molecular dynamics (AIMD) simulations (Methods section) also show large shape changes and incommensurate octahedral tilings. The isosurface in Fig. 1(c) separates octahedra with maximum angle change >10° from those <10° for one snapshot from the simulations. Fig. 1(d) compares the lattice energy of 50 representative disordered systems, obtained via slow cooling of independent configurations taken from AIMD. These represent distinct local minima in the MAPbI3 configuration space, all energetically lower than that of the cubic prototype. The energy differences amongst the configurations are an order of magnitude lower than room temperature thermal energy, so although each is an independent microstate of the ensemble, the configurations are thermodynamically equivalent at room temperature. With disorder present in multiple forms and scales, characterizing vibrational transport in hybrid perovskites and other hybrid materials is theoretically challenging.32,33 For crystalline and amorphous materials, phonon transport and diffusive hopping theories are, respectively, well established.34,35 However, the general transport theory for intermediate disordered heterogeneous materials is still under development. For example, in partially-ordered-partially-disordered heterogeneous systems such as glass-in-crystal silicon metamaterials, the extended phonon-like modes on the higher symmetry lattice interact with the localized modes of the less symmetrical groups in intriguing ways that dominate the transport physics.36
Here we demonstrate that hybrid perovskites are intrinsically glass-crystal dual materials, featuring both phononic and non-phononic elements to vibrational transport. Our analysis is divided into two principal themes. First, we establish the nature of the vibrational carriers explicitly accounting for disorder. Using first principles, the population of vibrational carriers is characterized by the spectral energy density (SED), which remains valid even when wave vectors are ill-defined. The SED, modal mean free paths, and modal relaxation times all indicate that most vibrational modes cannot be described as typical phonons exhibited by crystalline materials. Instead, many elements of the framework of propagons and diffusons, originally developed to describe vibrational energy transport in amorphous media,37 are shown to be well-suited, and we find the diffuson-like contribution to the thermal conductivity to be dominant at room temperature. In the second theme, we reconcile the picture of diffuson-like carriers with that of highly scattered phonons. Third order interatomic force constants obtained from first principles are used to determine the three-phonon scattering rates in MAPbI3, and compared to those of CsPbI3 (a lead halide perovskite without A-site symmetry breaking) and silicon (a conventional semiconductor). For MAPbI3 and CsPbI3, scattering rates are two orders of magnitude larger than in silicon, both between modes on the inorganic PbI6 octahedral framework as well as between the perovskite A-site species and the framework. The former is shown to arise from resonant bonding, i.e., the long-range nature of p-orbital interactions on the inorganic framework. The latter are the A-site local rattling phenomena in CsPbI3 and polar rotor scattering in MAPbI3. Altogether our analysis shows that the hybrid perovskites represent a unique middle ground where the carriers may be described as highly scattered phonons, or as propagon and diffuson – like. In practice, MAPbI3 is a member of a broad family of hybrid materials, so this understanding may provide a formalism for thinking about the nature of vibrational transport in such systems. It also serves to directly link the ultralow thermal conductivity to the underlying microscopic mechanisms of disorder, anharmonicity, and resonant bonding, which may be of value to the design of hybrid materials.
Spectral energy density and non-phononic vibrational transport
To characterize the carriers present, using AIMD we first trace the vibrations that occur in MAPbI3. Modal wave vectors may not be well defined if the disorder is sufficient. However the SED ϕ (Methods section), which extracts the wave vector and frequency (k,ω) content of the atomic dynamical trajectories, remains well-defined in the presence of significant disorder. In Fig. 2(a–c), the SED clearly shows the loss of definition of wave vectors as T increases and the disorder grows. At ultralow temperature (T = 1 K, Fig. 2(a)), both the organic MA molecules and inorganic PbI6 octahedral framework only vibrate around their equilibrium positions. Rotations of the MA molecules are hindered by the PbI6 framework, and only MA librations are active. The dispersion is well-resolved and the material can, to a large extent, be viewed as crystalline and exhibiting phonon vibrations with well-defined wave vector and frequency.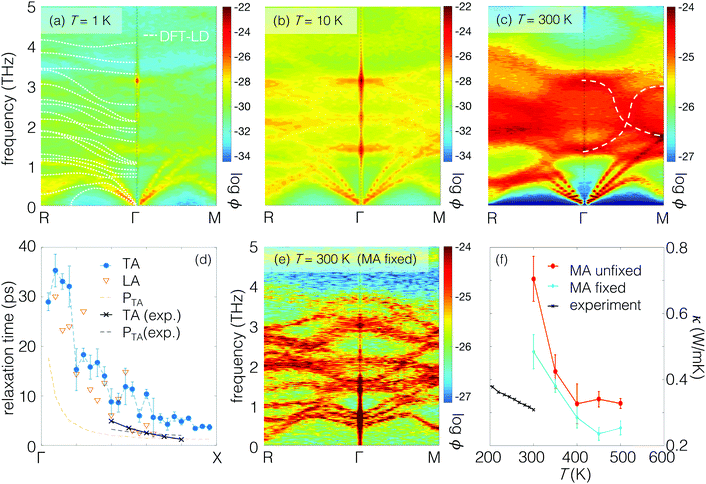 | ||
| Fig. 2 (a–c) Spectral energy density of dynamical modes in MAPbI3 at different temperatures from ab initio molecular dynamics. The dotted white line for T = 1 K shows the lattice dynamics result for comparison. The band line-widths broaden as temperature increases. At T = 300 K, the vibrational modes between 3–4 THz that are well-defined at low temperatures are now heavily blurred. (d) The modal relaxation time extracted from SED compared to recent experimental measurements.24 The relaxation time is close to the wave period for each thermal carrier, suggesting the conventional phonon picture is not an adequate description of the carriers (see also Fig. S1, ESI†). (e) Freezing the rotations of the MA molecules recovers the well-defined lattice dynamical modes, which suggests that interactions between the inorganic framework and sublattice MA orientational disorder are responsible for the loss of wave nature in (c). (f) Thermal conductivity calculated via Green–Kubo formalism using classical molecular dynamics, with MA fixed and unfixed, compared with experiments.25 | ||
As the temperature increases, Fig. 2(b and c) show the loss of definition of the phonon wave vector for the higher frequency modes between ∼1–4 THz, while the lowest acoustic modes retain their wave nature. The lowest acoustic bands broaden as temperature increases to T = 10 K and T = 300 K, but remain resolvable. Compared to the acoustic branches, the optical bands in the SED in Fig. 2(b and c) are more inter-mixed and blurry. At T = 10 K, although blurred the optical modes are somewhat resolvable. At T = 300 K (Fig. 2(c)), they are heavily blurred out and the SED intensity is more uniform throughout (k,ω), and the emergent trend denoted by the white dashed lines is reminiscent of “waterfall” phonons observed earlier in relaxor perovskites.15,38,39 The waterfall phonons were previously ascribed to the presence of polar nanoregions38 and later to acoustic-optical coupling.39
Although resolvable, the broadening of the acoustic mode linewidth with increasing temperature signals a reduction in relaxation time in Fig. 2(b). By fitting the SED linewidths to Lorentzian functions (Methods section), it is possible to extract the relaxation time. Fig. 2(d) shows the relaxation times for LA and TA modes along Γ → X at T = 300 K, which vary from ∼40 ps at Γ to ∼5 ps at X, two orders of magnitude shorter than acoustic mode relaxation in silicon.40Fig. 2(d) also shows recently reported experimental TA mode relaxation times24 showing satisfactory agreement. From both experiment and computation, almost all the acoustic modes exhibit relaxation times close to their vibrational period indicated by the orange line. Considered as oscillators these modes are highly damped. In the spatial domain, the mean free paths of the acoustic modes can be estimated (see ESI† Section S1) as the product of the group velocity and scattering time obtained from the SED. For the Γ → X TA modes the mean free paths lie between 7 nm and 0.5 nm at room temperature, also in decent agreement with experiment24 and small in comparison to silicon (∼1 μm at room temperature41). So although a wave-like nature to the acoustic modes is present in the SED, the mean free paths are close to or even lower than the corresponding modal wavelengths and the concept of a phonon can only be weakly defined. For the higher-frequency modes (∼1–4 THz), which exhibit even lower group velocity and higher scattering rate, the mean free paths should be even smaller. As described below, such carriers in many ways resemble the localized modes described by the Einstein and Cahill models for amorphous materials.35,42 Therefore, it is clear that energy transport in hybrid perovskites possesses mixed phononic and non-phononic characteristics.
The strong optical mode blurring at T = 300 K in Fig. 2(c) occurs upon activation of the rotational vibrations of the MA molecules in the AIMD simulations. In Fig. 2(e) we consider a fictitious version of MAPbI3 in which the rotational degrees of freedom of all MA molecules are artificially fixed. Remarkably the optical modes are recovered and now resolvable in the SED. (The lowest modes also start from non-zero energies in Fig. 2(e) due to the artificial constraints imposed.) The reemergence of the optical bands indicates that dynamical disorder due to the rapid reorientations of the MA molecules and their coupling to the optical modes is the mechanism that induces the blurring, highlighting the effect of A-site symmetry breaking. Returning to Fig. 1(d), the time evolution of MAPbI3 can then be viewed as a trajectory of stochastic jumps between disordered, nearly degenerate microstates sampled by the system in time, as exhibited by procrystalline materials.14,15 Structurally, these disordered microstates average to the experimentally measured cubic phase. The blurring results from sampling over the microstates, and the waterfall-like effect in Fig. 2(c) is an emergent behavior connecting the microstates' statistically dominant vibrational modes.
The effect of molecular rotations on the thermal conductivity can be determined using molecular dynamics and the Green–Kubo formalism, which also remains valid for disordered systems. For this we used classical rather than ab initio molecular dynamics (Methods section), but the physical insights are still relevant. Fig. 2(f) compares the thermal conductivity of MAPbI3 and of fictitious MAPbI3 with previous experimental measurements.25 The overall temperature dependence in Fig. 2(f) follows a crystal-like decay, to be discussed below. The calculated thermal conductivity is as small as 0.4 W m−1 K−1 at room temperature, which compares reasonably with experiment. Also surprising is that the constrained system has only a slightly lower thermal conductivity than the unconstrained one, despite that the optical bands are well-defined for the former. The trend is consistent with a prior result that the overall thermal conductivity is reduced slightly when rotational constraints are introduced to the MA cations.43 In another molecular dynamics study, the thermal conductivity is shown to increase slightly when the MA cations are replaced by spherical cations,44 slightly distinct from the situation here where the MA cations are frozen in place. The scattering by MA molecular reorientations inducing the loss of definition of the optical modes in the SED seems contradictory to the observed marginal effect on the thermal conductivity.
Diffusons, propagons, and locons – Allen/Feldman theory
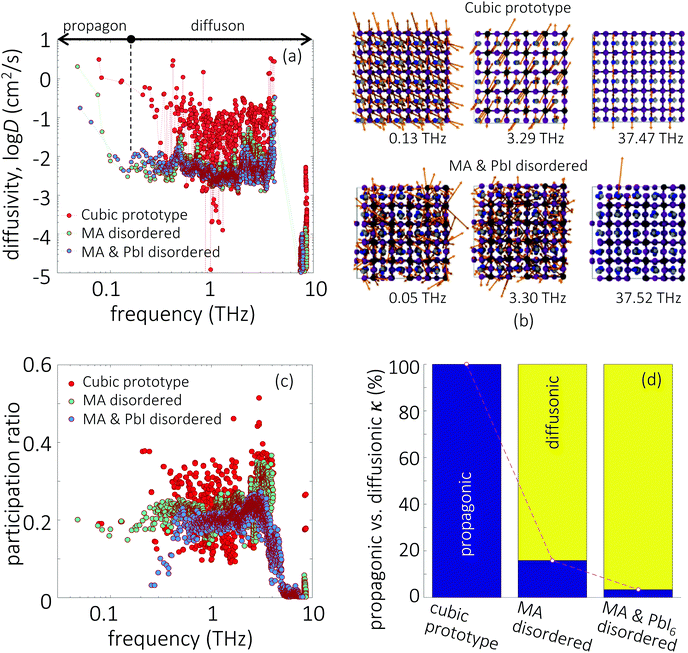
Given the evidence of a non-phononic character to the transport, to better analyze these observations a different framework may be useful to describe the carriers present in MAPbI3. In 1993, Allen and Feldman37 introduced a schema to describe vibrational carriers in disordered media. According to their framework, vibrational modes can be classified as propagons, diffusons, and locons. Propagons are the lowest frequency modes that most resemble typical phonons: wavelike and spatially delocalized. Diffusons are intermediate frequency modes that remain spatially delocalized but, due to the disorder, have lost their wave nature. These carriers transport energy in a diffusive, random-walk manner. In amorphous 3D materials such as vitreous silica diffusons are the dominant contributors to the thermal conductivity at temperatures T > 10 K.45,46 Meanwhile locons, the highest frequency carriers, are highly localized in space and contribute negligibly to thermal conductivity in all cases.We consider the taxonomy suggested by Allen and Feldman as a framework for the vibrational carriers in MAPbI3. To elucidate how different types of disorder affect the nature of the carriers, three representative systems exhibiting different degrees of crystallinity/disorder in Fig. 3(a) are used and their features are compared. The three systems, in order of increasing disorder, are: (i) the ideal cubic prototype with fixed, aligned MA molecules, (ii) the cubic prototype with MA molecules randomly oriented, and (iii) a system with both MA molecules randomly oriented and PbI6 octahedra randomly tilted. For each, the lattice dynamical equations are solved to obtain the modes and the modal diffusivities, which can be used to characterize the modes as propagons, diffusons, or locons. It is expected that as the disorder grows, the nature of the modes becomes less wavelike and more random and localized. The diffusivity Di of mode i, defined in the Methods section, eqn (8), measures the energy-carrying capability of each thermal carrier, and the total thermal conductivity is given as a sum over contributions from all carriers 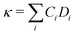 where Ci is the modal heat capacity.
where Ci is the modal heat capacity.
Fig. 3(a) shows the modal diffusivity distribution for all real modes calculated using Allen–Feldman theory. Since the cubic prototype is (artificially) perfectly ordered, all modes have well-defined wave vectors and are periodic and spatially spanning, so all modes are rigorously propagons. Real space representations of some propagons are illustrated in the top row in Fig. 3(b). Even the highest frequency mode at ω = 37.47 THz consists of internal vibrations of the MA molecules, and represents a regular periodic distortion of the perfect system. This mode corresponds to in-phase oscillations of the MA molecules (essentially a periodic sum of isolated delta-function vibrations oscillating in phase). Despite that these modes are all propagons, they are not necessarily effective heat carriers: most of the modes still exhibit low diffusivities, and the diffusivity distribution for the cubic prototype in Fig. 3(a) exhibits large fluctuations. The large fluctuations can also be seen in the modal participation ratios shown in Fig. 3(c).
For the two disordered systems, the diffusivity distribution in Fig. 3(a) exhibits a different nature than the cubic prototype. The diffusivity initially decreases and then plateaus to a steady value beyond a transition frequency. This is the typical scaling behavior exhibited by many disordered materials, for which the transition frequency corresponds to the boundary between propagons and diffusons. The transition frequencies for the two disordered systems are rather similar to each other, ∼0.15 THz. In the real space representation (Fig. 3(b), bottom row), the propagon (ω = 0.05 THz) and diffuson (ω = 3.30 THz) modes remain globally spanning, with inorganic and organic atoms all participating. The difference between these two types, according to Allen/Feldman, is their itinerant nature. The former exhibits patterns, albeit vague, but an effective wave vector could be defined based on homogenized elastic constants. In contrast, the latter does not exhibit wave nature and transport occurs in a diffusive, hopping manner. Additionally, the in-phase oscillations of the MA molecules observed for the cubic prototype are now broken, and instead isolated MA molecular vibrations, such as for ω = 37.52 THz, are present as locons.
Comparing all three systems exhibiting different degrees of disorder, several observations are noteable. Compared to the cubic prototype, the diffusivities of both propagons and diffusons for the two disordered systems are reduced on average by several orders of magnitude. Yet, the fluctuations in the modal diffusivities exhibited by the cubic prototype are not present in the disordered ones. Interestingly, the diffusons for both disordered systems show a similar distribution, indicating that once the disorder of the MA molecules is activated, the introduction of disorder to the octahedral network does not appreciably change the diffusivities. We observe the same effect if the octahedral distortions are first introduced, followed by the disorder associated with MA molecules. The histogram in Fig. 3(d) tallies the contribution to the total thermal conductivity from diffusons versus propagons in all three systems based on the 0.15 THz turnover frequency for the latter two. As structural disorder is progressively introduced, the diffuson contribution becomes increasingly dominant. The acoustic mode-like propagons, by contrast, contribute little to the thermal conductivity, in contrast to conventional crystalline semiconductors where acoustic modes are often dominant. In fact, in parallel to 3D disordered materials at room temperature, the MA and PbI6 disordered system shows dominant contributions from diffusons, with a negligible contribution from propagons. So the dominant source of thermal conductivity in MAPbI3 are less like classic phonons and more like the carriers in disordered/glassy media. This further explains why the Green–Kubo thermal conductivities in Fig. 2(f) are so similar for MAPbI3 and fictitious MAPbI3 – although MA rotations suppress the optical modes, they also activate a large density of diffusons and thus helping maintain the thermal conductivity.
Interestingly the thermal conductivity in Fig. 2(f) decays with temperature. This is more reminiscent of crystals than glasses, which instead show increasing thermal conductivity with temperature due to activation of diffusons. In amorphous silica, the classic example, the thermal conductivity increases up to T = 1000 K, whereas for α-quartz it peaks around T = 10 K.35 The crystalline trend shown in Fig. 2(f) is consistent with experiments,21,25 which also have not revealed an amorphous dependence. Therefore, although the carriers in MAPbI3 exhibit many features of diffusons in classical amorphous materials, the analogy is not complete. The measured temperature dependence reflects the cumulative effect of several competing factors, and we do not expect that an amorphous trend can be observed in MAPbI3, which is different from glassy silica in a few ways. Rather than being a static amorphous material, it is more crystalline at low temperature and becomes dynamically disordered at higher temperature. As temperature increases the optical phonon modes lose their wave nature and become more diffusonic (and thus, less effective heat carriers) while also more and more diffusons become activated. Here a more crystalline temperature dependence is observed, so it appears that the former effect dominates the temperature dependence. Also, in contrast to amorphous silica which has a melting temperature >1000 K, in MAPbI3 as the temperature exceeds 300 K and approaches the melting temperature (<500 K), thermal instabilities due to the loss of MA to the gaseous phase and decomposition reactions are activated.47
The observed crystalline trend corresponds to both a recent analysis of the ultralow thermal conductivity in crystalline Tl3VSe4,48 where a two-channel model including phononic and non-phononic carriers was shown to give rise to a similar temperature dependence as well as to a generalized physical picture formulated previously.46 For comparison, in more crystalline Tl3VSe4, the contribution from non-phononic carriers was estimated to be around 50%.48 For the halide perovskites considered here, although we estimate a larger ∼95% contribution from the diffusonic carriers at room temperature, the decreasing trend persists. Note that our assessment that an amorphous trend is not present in MAPbI3 is complicated by the fact that, even if it did exist, classical MD simulations would not necessarily capture the trend due to the reliance on classical (rather than quantum) occupation statistics. For this reason, classical MD also incorrectly predicts a decreasing trend even in amorphous silica.49
Harmonics & anharmonics
In lieu of the conventional phononic picture, the vibrational modes in MAPbI3 at room temperature show a character reminiscent of those in glassy materials. As with bulk amorphous solids, diffusons dominate room-temperature energy transport in MAPbI3. At the same time, the SED profiles show that the lowest energy modes still retain elements of traditional phonon character and, additionally, most investigations to date have been able to capture several aspects of the thermal transport physics in MAPbI3 relying on conventional phonon pictures. It is insightful to use the hybrid perovskites as a case study to establish microscopically how the diffuson picture emerges from the disorder present within this system. According to Anderson's description of localization,50 as disorder is slowly introduced into a crystalline material, scattering of the modes intensifies. If the disorder is strong enough that scattering events are no longer independent but coupled, then the multiple interferences that take place upon scattering result in a loss of wave nature and the onset of localization. Starting from the phonon picture, we will establish from first-principles lattice dynamics the link between the low thermal conductivities, disorder, the soft lattice modes, anharmonicity, and the nature of the electronic structure. This brings together the picture of the carriers as conventional phonons with extreme anharmonicity and the propagon/diffuson picture described above.Fig. 4(a–c) shows the phonon dispersion for MAPbI3, compared to that of CsPbI3 and crystalline silicon obtained using density functional theory (Methods section). CsPbI3, a lead iodide perovskite without A-site symmetry breaking, and crystalline silicon, an sp3-bybridized covalent semiconductor, serve as reference cases for comparison. Cubic unit cells are used for all three materials; for MAPbI3 the methylammonium molecules are all oriented in the same direction. In this hypothetical perfectly ordered, crystalline cubic model, the conventional phonon picture is nominally valid. The first observable trend is the well-known presence of the imaginary modes for both perovskites centered at M and R, indicating structural distortions to the low symmetry, low temperature phases. A second difference is that the dispersion curves for both perovskites at Γ are noticeably more flat than those for silicon, which indicate the lower group velocities, as shown in Fig. 4(d–f). We use the thermally averaged group velocity
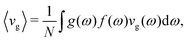 | (1) |
 | ||
| Fig. 4 Dispersion relationships of (a) MAPbI3, (b) CsPbI3 and (c) silicon, colored by the localization function ζ. All modes in silicon are delocalized (ζ ≈ 1/8), whereas localized modes are found between 0.5–1 THz for CsPbI3 and 3–4 THz for MAPbI3. The localized modes are the A-site rattling and polar rotor scattering modes respectively. (d–f) Anharmonic scattering rate (upper) and group velocities (lower). The scattering rates are a factor of ∼100 higher in the perovskites compared to silicon. (g–i) The lattice conductivity and atomic configurations of the three materials calculated ab initio and compared to experimental values from ref. 51 for silicon, and ref. 25 for the perovskites. | ||
Beyond the group velocities, details about the nature of the modes shown in Fig. 4(a–c) are indicated by the mode localization factor, defined here as
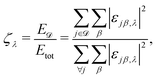 | (2) |
![[scr D, script letter D]](https://www.rsc.org/images/entities/char_e523.gif) is the domain under investigation. The vibration localization on one MA cation, one Cs cation, and one silicon atom is color-mapped on the dispersion curves in Fig. 4(a–c) respectively. For silicon, all the modes exhibit localization factors around the theoretical value 1/8 (8 is the number of atoms in the conventional fcc unit cell). In contrast, the red colored lines indicate localization on A-sites, effectively the rattling behavior of Cs cations and the polar rotor scattering of the MA molecules for CsPbI3 and MAPbI3. These interactions in CsPbI3 appear at lower frequencies ∼0.5 THz than in MAPbI3 around ∼3–4 THz.
is the domain under investigation. The vibration localization on one MA cation, one Cs cation, and one silicon atom is color-mapped on the dispersion curves in Fig. 4(a–c) respectively. For silicon, all the modes exhibit localization factors around the theoretical value 1/8 (8 is the number of atoms in the conventional fcc unit cell). In contrast, the red colored lines indicate localization on A-sites, effectively the rattling behavior of Cs cations and the polar rotor scattering of the MA molecules for CsPbI3 and MAPbI3. These interactions in CsPbI3 appear at lower frequencies ∼0.5 THz than in MAPbI3 around ∼3–4 THz.
Fig. 4(d–f) also shows the calculated mode-resolved scattering rates for the two perovskites and silicon, obtained from direct calculations of three phonon scattering processes. Phonon lifetimes depend upon the three-phonon scattering phase space that satisfy the constraints of energy and momentum conservation, and are obtained from direct calculation of the third order interatomic force constants (Methods section). Due to their ill-defined energy, scattering due to the imaginary modes around M and R are not included; previous studies have also neglected these modes in first-principles scattering rate calculations for the cubic phase.52 In any case, the imaginary modes are associated with acoustic mode like propagons which contribute negligibly to the thermal conductivity, so the effect is expected to be small. All in all the scattering rate in the perovskites is two orders of magnitude higher than in silicon (note the difference in the scale of the y-axis). Such large scattering rates and short lifetimes have strong ramifications for device applications, related to electron–phonon coupling, thermal carrier relaxation rates, and carrier recombination. Within the two perovskites, the largest scattering rates appear in the range of 3–4 THz for MAPbI3 and around 0.5 THz for CsPbI3. This corresponds to the localized modes identified in Fig. 4(a–c), highlighting that the short lifetimes arise from strong three-phonon interactions associated with the degrees of freedom of the A-site, for both perovskites.
Fig. 4(g–i) show directly how the slow group velocities and strong scattering rates combine to realize the ultralow thermal conductivity in the perovskites. These were obtained with the relaxation time approximation (Methods section). The ab initio thermal conductivity is compared to experimental measurements.21,25,51 As expected the relaxation time approximation underestimates lattice conductivity compared to experiment,53 but remains within a factor of four for all materials.
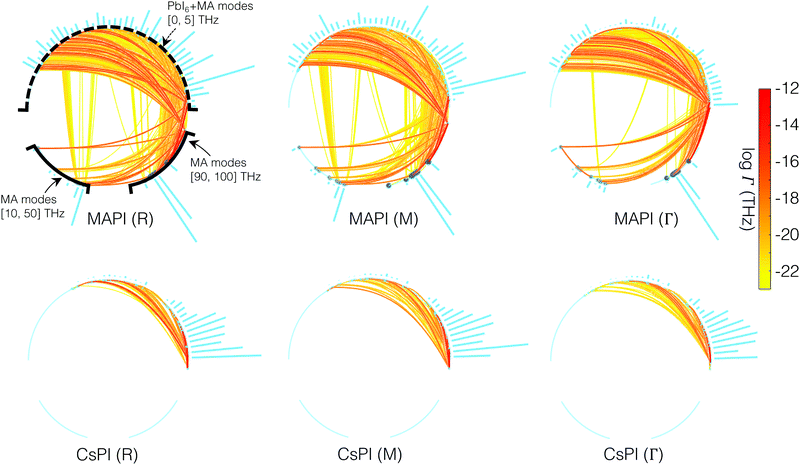
To reveal the scattering nature in detail, the scattering network plots in Fig. 5 pictorially show the mode-resolved three-phonon scattering channels. We present the scattering networks involving three high-symmetry reciprocal points (R,M,Γ) for the two perovskites, meaning that each three-phonon process indicated involves at least one (R,M,Γ) mode respectively. Along the circumference of each circle in Fig. 5 different frequency ranges are indicated. The upper arc of each circle indicates modes in the 0–5 THz range, which consist of both the modes of the octahedral framework and collective vibrations in which an MA molecule vibrates together with the framework. The lower arc of the circles indicate higher frequency modes that are the internal vibrations of the MA molecule. Since these high frequency vibrations are not present for CsPbI3, the lower arc of those circles are empty. Every pair of segments within the circle connects three modes, and the color denotes the associated interaction strength for the three phonon process. For MAPbI3 two types of scattering channels are observed to be strong: (i) interactions entirely within the lower frequency (0–5 THz) modes, and (ii) interactions between lower frequency and higher frequency intra-vibrational modes of the MA molecules. The first indicates that the motions of the A-site cation couples strongly to the PbI6 octahedral framework for both the inorganic and the hybrid organic/inorganic perovskite. The second indicates strong coupling between the phonon modes of the octahedral network and the isolated vibrations of the methylammonium molecules, unique to the hybrid perovskite with broken A-site symmetry. These molecular vibrations increase greatly the number of scattering channels available.
Origins of anharmonicity in lead halide perovskites
To understand microscopically what gives rise to these anharmonic interactions, we turn to stereochemistry and electronic structure. Recently, resonant bonding – a “resonance” taking place between different possible degenerate or near-degenerate electron configurations of available orbitals – has been suggested to be closely connected to the strong anharmonicity and low thermal conductivities exhibited by several thermoelectric materials such as IV–VI semiconductors,54,55 V2–VI3 materials,56 phosphorene,57 and SnSe.58 Such resonance bonding usually gives rise to high electronic polarizability, dielectric constants and Born effective charges. Here we will demonstrate that an effect akin to resonant bonding plays a large role in the observed anharmonicity, but that the effect manifests differently for MAPbI3 compared to CsPbI3 due to the broken symmetry of the A-site. Typically, materials exhibiting resonant bonding are those for which the atomic species exhibit a coordination number of six as in the rock salt structure. They exhibit a weak sp-hybridization, with the s-derived orbitals lower in energy and distinct from the p-derived orbitals. If the number of valence p electrons is fewer than six, the number of available covalent bonds between an atom and its neighbors, then the choice of bond occupation is not unique. The degeneracy in how the valence p electrons occupy the available bonds results in long-ranged interactions and anharmonicity: a slight displacement of one atom induces changes to the occupation of the available bonds that extend and penetrate throughout the ‘resonant’ network. It has theoretically been shown using a one-dimensional chain model that such long-range interactions result in soft optical modes.59 Using the diatomic-chain model, we show further in the ESI,† Section S5 that the softening depends solely on the long-range interactions between atoms of the same type.The band structures for MAPbI3 and CsPbI3 are shown in Fig. S3 and S4 (ESI†). The Pb and I s-derived bands are low in energy, well-separated from the valence band, as are all of the MA or Cs-derived states. The valence bands are primarily composed of I 5p orbitals while the conduction bands primarily of Pb 6p orbitals. Importantly there is a small degree of Pb 6p character present in the valence states, and correspondingly of I 5p orbitals present in the conduction bands. This orbital mixing is more prevalent in lead halide, compared to transition metal oxide, perovskites due to their more covalent and less ionic nature. This mixing enables a resonance-like effect to take place in the lead halide perovskites. Were the materials completely ionic, with a fully I 5p valence band and Pb 6p conduction band, all three I 5p states would be completely filled and all three Pb 6p states would be completely empty, with no degeneracy in the selection of the occupation of available states. Instead, the small presence of Pb 6p states in the valence band introduces occupation degeneracy (the 6p states are partially, not completely, filled). This leads to long-ranged interactions and anharmonicity that is present for both CsPbI3 and MAPbI3.
To illustrate, in Fig. 6(a and b) we consider the disturbance of the electron density due to two possible structural perturbations: the displacement of one Pb atom and the rotation of one PbI6 octahedron. For Pb atom displacement, one lead atom in a 5 × 5 × 2 supercell is shifted in the (100) direction by 5% of the cubic lattice constant. Here long-ranged interactions in both lead halide perovskites are readily observed, with the disturbance in electron distribution persisting to the third neighboring cell due to the bonding resonance. The I 5p and Pb 6p orbitals states are most perturbed. The displacement of one atom affects the p orbitals of the neighboring atoms and their occupation, which in turn affects the p orbitals and occupation of the neighbor's neighbors, and so on. This is the origin of the softness of the PbI octahedral framework, and gives rise to the strong three-phonon interactions occurring within 0–5 THz lower frequency modes for both perovskites in Fig. 5. For MAPbI3 the perturbation is also present on the MA p states, which is surprising because the MA p states are not hybridized and much lower in energy than the Pb p states. For sake of comparison, the charge density perturbation arising from the displacement of one atom in silicon is shown in Fig. S2 (ESI†): the perturbation is localized to within a single bond length. We note that the strong interactions arising from the long-ranged electric fields are common to all heteropolar materials, and not unique to the halide perovskites. However, they are particularly strong in the halide perovskites. For instance the Born effective charges tabulated in Table S2 of the ESI† are comparable to those of PbTe, indicating the strength of the interactions and a similar chemistry of resonance bonding.
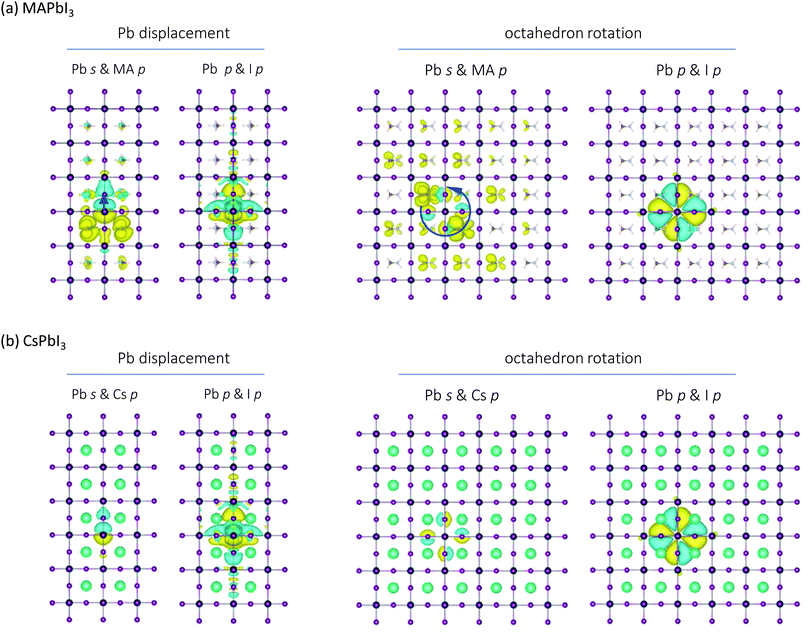 | ||
| Fig. 6 Perturbation of electron density due to octahedron rotation and displacement of one lead atom in (a) MAPbI3 and (b) CsPbI3. In comparison to silicon (see Fig. S2, ESI†), the long-range interactions can be observed in the hybrid perovskites. While the charge density perturbation due to octahedron rotation is localized in CsPbI3, it is long-ranged in MAPbI3 and extends throughout the network via interactions of the MA molecules. On the other hand, both lead halide perovskites exhibit long range interactions due to the displacement of one Pb atom, particularly on the Pb and I p orbitals. | ||
For the case of octahedron rotation, the center octahedron is rotated counter-clockwise in the same supercell by 1° in Fig. 6(a and b). For the case of CsPbI3, the rotation induced charge difference is localized within one unit cell; the perturbation does not extend throughout the system. For MAPbI3, it is long-ranged and delocalized, and extends throughout the system via only on the MA cations. The perturbations to the MA cations for Pb atom displacement and octahedron rotation cannot be due to resonant bonding, since the electronic states of the MA molecules are very low in energy and not hybridized with those of the PbI6 framework. We ascribe them instead to the polarizability and large dipole moment of the MA molecules: simply, electrostatic interactions that perturb the electronic charge density of the polarizable molecules around as a result of the octahedron rotation. This now directly links the A-site symmetry breaking, the molecular polarizability, and the anharmonicity. It provides an underlying mechanism for the strong three-phonon processes observed in Fig. 5 between the intra-molecular vibrations of the molecules and the vibrations of the inorganic network.
Beyond resonant bonding, a second mechanism that can induce strong anharmonicity is the lone pair instability.60,61 Stable s2 lone-pair orbitals are responsible for many phenomena including strong bond anharmonicity in I–V–VI2 rock-salts (I = Ag/Cu/alkali metals; V = Sb/Bi; and VI = chalcogens)62,63 and IV–VI chalcogenides,64 and the off-centering of the Sn atoms that occurs in CsSnBr3 upon increased temperature.65 The resonant bonding mechanism discussed here does not exclude the possibility that the lone pair instability plays a role in the large anharmonicity present in MAPbI3. But the effect is believed to be larger in CsSnBr3 than CsPbBr365 and in GeTe than PbTe,66 due to greater relativistic stabilization of the lone pair for Pb compared to Sn,Ge respectively. The strong cation-s-anion-p interaction induces a rhombohedral distortion in GeTe (second-order Jahn–Teller effect) to stabilize the Ge-4s2 orbitals. However, due to relativistic effects, the 6s2 lone pair becomes increasingly stable if the group IV element is Pb rather than Ge, thus PbTe favors the rock salt structure. In contrast to the delocalized lone-pair s2 electrons for the lone-pair active I–V–VI2 class of materials, the Pb-s electrons are rather localized in our case (Fig. S3 and S4, ESI†). Therefore, we surmise the lone pair effect to be more mild in MAPbI3 compared to some other compounds.
Bringing together our key findings the following picture of thermal transport in MAPbI3 emerges, showing how diffuson-like carriers arise from the conventional phonon picture. For the hybrid perovskite, analysis of the phonon dispersion in Fig. 4, mode localization, and scattering rates illustrate the soft, anharmonic nature of the optical modes throughout the Brillouin zone. As a result of resonant bonding, these soft optical modes are dominant scattering channels in both CsPbI3 and MAPbI3, as shown from the scattering networks presented in Fig. 5. For MAPbI3, the bonding resonance is augmented by the intra-molecular vibrations and polarizability of the MA molecules, which provides additional scattering channels in the system. Ultimately, in these perovskites the strength of the scattering is sufficient that frequent optical mode scattering and associated wave interferences result in the loss of the wave vector, and the emergence of diffusonic carriers. This is borne out in the SED in Fig. 2 and in the real space representation of the modes of the disordered systems in Fig. 3. Even for the acoustic modes the lifetimes are on the order of the carrier periods, and in many cases the mean free paths are similar to or even shorter than the carrier wavelengths. Remarkably hybrid perovskites appear to present a unique middle ground where carriers can be described as ultra highly scattered phonons, or as propagons/diffusons. This parallels the crystal structure of the material itself, which represents a middle ground between an ordered and a disordered system. In fact, there are insights to be gained from both perspectives and from their relationship to each other.
Conclusion
In conclusion, we have shown the mixed phononic and non-phononic characteristics of the vibrational transport in MAPbI3, an example hybrid material. Analysis of the spectral energy density from ab initio molecular dynamics shows that at room temperature, the lifetimes of the acoustic phonon modes are on the order of their periods, and that the optical modes are not well-defined. Accounting for the sub-lattice symmetry breaking and the disorder present in these systems, we consider Allen-Feldman theory and demonstrate that these modes exhibit features reminiscent of diffusons – diffusive modes that are the dominant contributors to thermal conduction in glassy materials. Meanwhile, propagons resembling typical phonons, and locons highly localized on A-sites, coexist with diffusons, but contribute negligibly to the overall conductivity. To see how the diffusonic nature arises in this system as a result of intense scattering and anharmonicity, we use a hypothetical perfectly ordered, crystalline cubic model of MAPbI3, for which he conventional phonon picture is valid. We establish from first-principles lattice dynamics the link between the low thermal conductivities, disorder, the soft lattice modes, anharmonicity, and the nature of the electronic structure for the perovskites. Scattering rates for the optical modes are two orders of magnitude larger than in silicon, particularly for scattering processes involving modes localized to the perovskite A site. The origin of the strong anharmonicity is resonant bonding in both MAPbI3 and CsPbI3, augmented by the polarizability, dipole moment, and symmetry breaking of the MA molecules in MAPbI3. Ultimately, in these perovskites the strength of the scattering is sufficient that frequent optical mode scattering and associated wave interferences result in the loss of the wave vector, and the diffusonic picture of carrier transport emerges. Although we focused on the hybrid perovskites, the findings in this work may be useful for better understanding the vibrational characteristics of a large family of hybrid materials, such as metal–organic frameworks and hierarchically organized hybrid materials.Methods
Density functional theory
All DFT calculations employed the generalized gradient approximation (GGA) and projector augmented-wave (PAW) pseudopotentials67,68 as implemented in the Vienna Ab Initio Simulation Package (VASP).69,70 For unit-cells, a 10 × 10 × 10 Monkhorst–Pack k-point mesh centered at Γ point for perovskites, and 20 × 20 × 20 for silicon was used. We kept the density of k-mesh approximately constant for supercell calculations. We used a 600 eV plane-wave cutoff energy, the tetrahedron method for Brillouin zone integration, a Gaussian broadening of 0.01 eV, and (v) 0.01 eV Å−1 force threshold criterion for geometry optimization. For different elements, the corresponding outermost valence electrons were treated explicitly: 14 for Pb (5d106s26p2), 7 for I (5s25p5), 9 for Cs (5s25p66s1), 4 for C (2s22p2), 5 for N (2s22p3), and 1 for H (1s1).Second- and third-order interatomic force constants
For the second-order and third-order interatomic force constants (IFCs), denoted by Φλ,λ′ and Φλ,λ′,λ′′, we applied the finite displacement technique implemented in Phonopy71 and Phono3py72 respectively. For the second-order IFC calculations, to construct the dynamical matrices, we displaced each atom by 0.01 Å in 4 × 4 × 4 supercells (768 atoms for MAPbI3 and 320 atoms for CsPbI3). A Γ-centered 3 × 3 × 3 k-mesh was used for Brillouin zone sampling. For the third-order IFC calculations, we used a 2 × 2 × 2 supercell, atomic displacements of 0.03 Å, and a 6 × 6 × 6 k-grid. For both second-order and third-order IFCs, we used density functional theory as described above for total energy calculations. Due to the symmetry of the cubic unit cells, the number of energy calculations is reduced to 72 (MAPbI3) and 3 (CsPbI3) for second-order and 41![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 544 (MAPbI3) and 220 (CsPbI3) for third-order force constants, respectively.
544 (MAPbI3) and 220 (CsPbI3) for third-order force constants, respectively.
Given the third-order IFCs, the three-phonon scattering rate 1/τ(i,q) can be formulated based on the Fermi's golden rule,
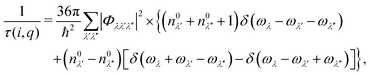 | (3) |
The above formalism of Fermi's golden rule is consistent with the single-mode relaxation time approximation of the Boltzmann equation. Both of these assumes the single-particle transport picture. In the RTA, the lattice thermal conductivity can be defined as
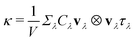 | (4) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(x)/(exp(x) − 1)2 is modal heat capacity, x = ħωλ/kBT, and vλ and τλ are group velocity and relaxation time for mode λ.
exp(x)/(exp(x) − 1)2 is modal heat capacity, x = ħωλ/kBT, and vλ and τλ are group velocity and relaxation time for mode λ.
Classical lattice dynamics & Allen–Feldman theory
For the disordered MAPbI3 systems, we employed large supercells and determined the individual vibrational modes by solving the classical lattice dynamical equations59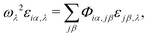 | (5) |
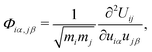 | (6) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 atoms.
000 atoms.
The Allen–Feldman thermal conductivity is obtained as a sum over modes i37 as
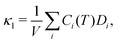 | (7) |
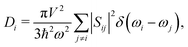 | (8) |
![[capital Delta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e135.gif) ) in the vibrational spectra. Our results were obtained by setting the broadening factor to be 5
) in the vibrational spectra. Our results were obtained by setting the broadening factor to be 5![[capital Delta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e135.gif) , which corresponds to 0.03 THz for the 10 × 10 × 10 supercell.
, which corresponds to 0.03 THz for the 10 × 10 × 10 supercell.
Ab initio molecular dynamics & spectral energy density analysis
For the ab initio molecular dynamics simulations, we employed VASP as described above, and simulated the atomic dynamics with a 5 × 5 × 2 supercell and a time step of 0.1 fs. The temperature was first established via a Nosé–Hoover thermostat. Since the MA rotations occur on the order of tens of picoseconds, simulations were carried out for ∼500 picoseconds. The atomics dynamics are used for subsequent analysis of spectral energy density (SED). For a vibrational mode (k,ω), its SED is defined by73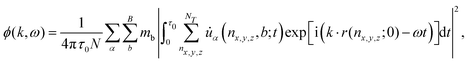 | (9) |
![[u with combining dot above]](https://www.rsc.org/images/entities/i_char_0075_0307.gif) α is obtained from our molecular dynamics simulations, N = nxnynz is the total number of cells, B is total number of atoms in each conventional unit cell, mb the atomic mass, and τ0 the total sampling time. This expression captures the energy density of modes with wave vector k and frequency ω contained in the vibrations of the system. If there were no interactions between modes and the system were purely harmonic, then evaluation of the SED would reproduce precisely the harmonic phonon dispersion; anharmonic effects manifest as a broadening of the SED profiles. Phonon lifetimes can be extracted from the spectra as τ = 1/2γ, where γ is the half-width at the half-maximum of the best fit Lorentzian to SED profiles ϕ(k,ω) = ϕ0(1 + [(ω − ω0)/γ]2)−1, and ϕ0 is the peak SED centered at ω0.
α is obtained from our molecular dynamics simulations, N = nxnynz is the total number of cells, B is total number of atoms in each conventional unit cell, mb the atomic mass, and τ0 the total sampling time. This expression captures the energy density of modes with wave vector k and frequency ω contained in the vibrations of the system. If there were no interactions between modes and the system were purely harmonic, then evaluation of the SED would reproduce precisely the harmonic phonon dispersion; anharmonic effects manifest as a broadening of the SED profiles. Phonon lifetimes can be extracted from the spectra as τ = 1/2γ, where γ is the half-width at the half-maximum of the best fit Lorentzian to SED profiles ϕ(k,ω) = ϕ0(1 + [(ω − ω0)/γ]2)−1, and ϕ0 is the peak SED centered at ω0.
Classical MD & Green–Kubo formalism
The classical molecular dynamics (MD) simulations utilize an interatomic potential derived from first principles.30 This model consists of three parts: (i) the organic interactions, which includes both intramolecular and intermolecular interactions described by the AMBER force field; (ii) the interactions between MA molecules and PbI3 framework described as the sum of Buckingham, electrostatic, and Lennard-Jones potentials, and (iii) the inorganic Pb–I framework described by Buckingham potential. More details are available in ref. 30. These MD simulations were carried out on 20 × 20 × 10 supercells (48![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 atoms) via LAMMPS.74 All MD simulations were performed with a time step of 0.5 fs. The temperature was set at 300 K and pressure at 0 Pa using the Nosé–Hoover thermostat and the Parrinello–Rahman barostat. The system was first equilibrated to the desired temperature for 20 ps, and then sampled in the microcanonical ensemble (NVE) for an additional 20 ps. The heat current was then recorded for a simulation time of ∼10 ns. Due to the weak ergodicity of the system, 5 independent micro-states were simulated for each temperature starting from different initial configurations.
000 atoms) via LAMMPS.74 All MD simulations were performed with a time step of 0.5 fs. The temperature was set at 300 K and pressure at 0 Pa using the Nosé–Hoover thermostat and the Parrinello–Rahman barostat. The system was first equilibrated to the desired temperature for 20 ps, and then sampled in the microcanonical ensemble (NVE) for an additional 20 ps. The heat current was then recorded for a simulation time of ∼10 ns. Due to the weak ergodicity of the system, 5 independent micro-states were simulated for each temperature starting from different initial configurations.
The Green–Kubo formalism75 is used to estimate the lattice thermal conductivity from the fluctuations in the heat current
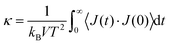 | (10) |
Conflicts of interest
There are no conflicts to declare.Acknowledgements
We are grateful to Dallas R. Trinkle from Illinois and Michael Toney from Stanford for helpful discussions. We acknowledge financial support from the National Science Foundation DMREF program under Grant No. DMR 1729149. Computational resources were provided by both (i) the Blue Waters sustained petascale computing facilities, and (ii) the Illinois Campus Computing Cluster.References
- W. Li, Z. Wang, F. Deschler, S. Gao, R. H. Friend and A. K. Cheetham, Nat. Rev. Mater., 2017, 2, 16099 CrossRef.
- X. Cao, C. Tan, M. Sindoro and H. Zhang, Chem. Soc. Rev., 2017, 46, 2660–2677 RSC.
- X. Li, J. Zhu and B. Wei, Chem. Soc. Rev., 2016, 45, 3145–3187 RSC.
- T. M. Brenner, D. A. Egger, L. Kronik, G. Hodes and D. Cahen, Nat. Rev. Mater., 2016, 1, 15007 CrossRef CAS.
- Y. Cui, B. Li, H. He, W. Zhou, B. Chen and G. Qian, Acc. Chem. Res., 2016, 49, 483–493 CrossRef CAS.
- A. Sutton, T. Shirman, J. V. Timonen, G. T. England, P. Kim, M. Kolle, T. Ferrante, L. D. Zarzar, E. Strong and J. Aizenberg, Nat. Commun., 2017, 8, 14700 CrossRef PubMed.
- A. Kojima, K. Teshima, Y. Shirai and T. Miyasaka, J. Am. Chem. Soc., 2009, 131, 6050–6051 CrossRef CAS PubMed.
- N.-G. Park, J. Phys. Lett., 2013, 4, 2423–2429 CAS.
- A. Comotti, S. Bracco and P. Sozzani, Acc. Chem. Res., 2016, 49, 1701–1710 CrossRef CAS PubMed.
- J. Dong, K. Zhang, X. Li, Y. Qian, H. Zhu, D. Yuan, Q.-H. Xu, J. Jiang and D. Zhao, Nat. Commun., 2017, 8, 1142 CrossRef PubMed.
- C. S. Vogelsberg, F. J. Uribe-Romo, A. S. Lipton, S. Yang, K. Houk, S. Brown and M. A. Garcia-Garibay, Proc. Natl. Acad. Sci. U. S. A., 2017, 201708817 Search PubMed.
- K. Novoselov, A. Mishchenko, A. Carvalho and A. C. Neto, Science, 2016, 353, aac9439 CrossRef CAS PubMed.
- H.-B. Yao, H.-Y. Fang, X.-H. Wang and S.-H. Yu, Chem. Soc. Rev., 2011, 40, 3764–3785 RSC.
- D. A. Keen and A. L. Goodwin, Nature, 2015, 521, 303 CrossRef CAS PubMed.
- A. R. Overy, A. B. Cairns, M. J. Cliffe, A. Simonov, M. G. Tucker and A. L. Goodwin, Nat. Commun., 2016, 7, 10445 CrossRef CAS PubMed.
- J. M. Frost and A. Walsh, Acc. Chem. Res., 2016, 49, 528–535 CrossRef CAS PubMed.
- M. R. Ryder, B. Van de Voorde, B. Civalleri, T. D. Bennett, S. Mukhopadhyay, G. Cinque, F. Fernandez-Alonso, D. De Vos, S. Rudić and J.-C. Tan, Phys. Rev. Lett., 2017, 118, 255502 CrossRef PubMed.
- M. T. Ruggiero, W. Zhang, A. D. Bond, D. M. Mittleman and J. A. Zeitler, Phys. Rev. Lett., 2018, 120, 196002 CrossRef PubMed.
- A. M. Leguy, J. M. Frost, A. P. McMahon, V. G. Sakai, W. Kockelmann, C. Law, X. Li, F. Foglia, A. Walsh and B. C. O'regan, et al. , Nat. Commun., 2015, 6, 7124 CrossRef PubMed.
- V. Martelli, J. L. Jiménez, M. Continentino, E. Baggio-Saitovitch and K. Behnia, Phys. Rev. Lett., 2018, 120, 125901 CrossRef PubMed.
- A. Pisoni, J. Jacimovic, O. S. Barisic, M. Spina, R. Gaál, L. Forró and E. Horváth, J. Phys. Lett., 2014, 5, 2488–2492 CAS.
- N.-G. Park, M. Grätzel, T. Miyasaka, K. Zhu and K. Emery, Nat. Energy, 2016, 1, 16152 CrossRef CAS.
- G. A. Elbaz, W.-L. Ong, E. A. Doud, P. Kim, D. W. Paley, X. Roy and J. A. Malen, Nano Lett., 2017, 17, 5734–5739 CrossRef CAS PubMed.
- A. Gold-Parker, P. M. Gehring, J. M. Skelton, I. C. Smith, D. Parshall, J. M. Frost, H. I. Karunadasa, A. Walsh and M. F. Toney, arXiv preprint arXiv:1807.06679, 2018.
- A. Kovalsky, L. Wang, G. T. Marek, C. Burda and J. S. Dyck, J. Phys. Chem. C, 2017, 121, 3228–3233 CrossRef CAS.
- X. Qian, X. Gu and R. Yang, Appl. Phys. Lett., 2016, 108, 063902 CrossRef.
- B. Li, Y. Kawakita, Y. Liu, M. Wang, M. Matsuura, K. Shibata, S. Ohira-Kawamura, T. Yamada, S. Lin and K. Nakajima, et al. , Nat. Commun., 2017, 8, 16086 CrossRef CAS.
- W. Lee, H. Li, A. B. Wong, D. Zhang, M. Lai, Y. Yu, Q. Kong, E. Lin, J. J. Urban and J. C. Grossman, et al. , Proc. Natl. Acad. Sci. U. S. A., 2017, 201711744 Search PubMed.
- A. Mattoni, A. Filippetti and C. Caddeo, J. Phys.: Condens. Matter, 2016, 29, 043001 CrossRef PubMed.
- A. Mattoni, A. Filippetti, M. Saba and P. Delugas, J. Phys. Chem. C, 2015, 119, 17421–17428 CrossRef CAS.
- P. Whitfield, N. Herron, W. Guise, K. Page, Y. Cheng, I. Milas and M. Crawford, Sci. Rep., 2016, 6, 35685 CrossRef CAS.
- P. B. Allen and J. L. Feldman, Phys. Rev. Lett., 1989, 62, 645 CrossRef CAS.
- T. Zhu and E. Ertekin, Nano Lett., 2016, 16, 4763–4772 CrossRef CAS PubMed.
- R. E. Peierls and R. S. Peierls, Quantum theory of solids, Oxford University Press, 1955 Search PubMed.
- D. G. Cahill and R. O. Pohl, Phys. Rev. B: Condens. Matter Mater. Phys., 1987, 35, 4067 CrossRef CAS.
- T. Zhu, K. Swaminathan-Gopalan, K. J. Cruse, K. Stephani and E. Ertekin, Adv. Funct. Mater., 2018, 28, 1706268 CrossRef.
- P. B. Allen and J. L. Feldman, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 48, 12581 CrossRef CAS.
- P. Gehring, S.-E. Park and G. Shirane, Phys. Rev. Lett., 2000, 84, 5216 CrossRef CAS PubMed.
- J. Hlinka, S. Kamba, J. Petzelt, J. Kulda, C. Randall and S. Zhang, Phys. Rev. Lett., 2003, 91, 107602 CrossRef CAS.
- B. Liao, B. Qiu, J. Zhou, S. Huberman, K. Esfarjani and G. Chen, Phys. Rev. Lett., 2015, 114, 115901 CrossRef PubMed.
- J. Cuffe, J. K. Eliason, A. A. Maznev, K. C. Collins, J. A. Johnson, A. Shchepetov, M. Prunnila, J. Ahopelto, C. M. S. Torres and G. Chen, et al. , Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 245423 CrossRef.
- A. Einstein, Ann. Phys., 1911, 340, 679–694 CrossRef.
- T. Hata, G. Giorgi and K. Yamashita, Nano Lett., 2016, 16, 2749–2753 CrossRef CAS PubMed.
- T. Hata, G. Giorgi and K. Yamashita, Nano Lett., 2016, 16, 2749–2753 CrossRef CAS PubMed.
- J. M. Larkin and A. J. McGaughey, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 144303 CrossRef.
- T. Zhu and E. Ertekin, Phys. Rev. B, 2016, 93, 155414 CrossRef.
- B. Brunetti, C. Cavallo, A. Ciccioli, G. Gigli and A. Latini, Sci. Rep., 2016, 6, 31896 CrossRef CAS PubMed.
- S. Mukhopadhyay, D. S. Parker, B. C. Sales, A. A. Puretzky, M. A. McGuire and L. Lindsay, Science, 2018, 360, 1455–1458 CrossRef CAS PubMed.
- W. Lv and H. Asegun, Sci. Rep., 2016, 6, 35720 CrossRef CAS PubMed.
- P. W. Anderson, Phys. Rev., 1958, 109, 1492 CrossRef CAS.
- C. Glassbrenner and G. A. Slack, Phys. Rev., 1964, 134, A1058 CrossRef.
- L. D. Whalley, J. M. Skelton, J. M. Frost and A. Walsh, Phys. Rev. B, 2016, 94, 220301 CrossRef.
- G. Fugallo, A. Cepellotti, L. Paulatto, M. Lazzeri, N. Marzari and F. Mauri, Nano Lett., 2014, 14, 6109–6114 CrossRef CAS PubMed.
- J. Phillips, Phys. Rev. Lett., 1967, 19, 415 CrossRef CAS.
- G. Lucovsky and R. White, Phys. Rev. B: Solid State, 1973, 8, 660 CrossRef CAS.
- S. Lee, K. Esfarjani, T. Luo, J. Zhou, Z. Tian and G. Chen, Nat. Commun., 2014, 5, 3525 CrossRef PubMed.
- G. Qin, X. Zhang, S.-Y. Yue, Z. Qin, H. Wang, Y. Han and M. Hu, Phys. Rev. B, 2016, 94, 165445 CrossRef.
- C. W. Li, J. Hong, A. F. May, D. Bansal, S. Chi, T. Hong, G. Ehlers and O. Delaire, Nat. Phys., 2015, 11, 1063 Search PubMed.
- A. A. Maradudin, Theory of Lattice Dynamics in the Harmonic Approximation, London, Academic Press, 1971 Search PubMed.
- E. S. Božin, C. D. Malliakas, P. Souvatzis, T. Proffen, N. A. Spaldin, M. G. Kanatzidis and S. J. Billinge, Science, 2010, 330, 1660–1663 CrossRef.
- A. Walsh, D. J. Payne, R. G. Egdell and G. W. Watson, Chem. Soc. Rev., 2011, 40, 4455–4463 RSC.
- D. Morelli, V. Jovovic and J. Heremans, Phys. Rev. Lett., 2008, 101, 035901 CrossRef CAS PubMed.
- M. D. Nielsen, V. Ozolins and J. P. Heremans, Energy Environ. Sci., 2013, 6, 570–578 RSC.
- L.-D. Zhao, S.-H. Lo, Y. Zhang, H. Sun, G. Tan, C. Uher, C. Wolverton, V. P. Dravid and M. G. Kanatzidis, Nature, 2014, 508, 373 CrossRef CAS.
- D. H. Fabini, G. Laurita, J. S. Bechtel, C. C. Stoumpos, H. A. Evans, A. G. Kontos, Y. S. Raptis, P. Falaras, A. Van der Ven, M. G. Kanatzidis and R. Seshadri, J. Am. Chem. Soc., 2016, 138, 11820–11832 CrossRef CAS PubMed.
- U. Waghmare, N. Spaldin, H. Kandpal and R. Seshadri, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 67, 125111 CrossRef.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953 CrossRef.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758 CrossRef CAS.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169 CrossRef CAS.
- G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS.
- A. Togo and I. Tanaka, Scr. Mater., 2015, 108, 1–5 CrossRef CAS.
- A. Togo, L. Chaput and I. Tanaka, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 094306 CrossRef.
- J. A. Thomas, J. E. Turney, R. M. Iutzi, C. H. Amon and A. J. McGaughey, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 081411 CrossRef.
- S. Plimpton, J. Comput. Phys., 1995, 117, 1–19 CrossRef CAS.
- D. Frenkel and B. Smit, Understanding Molecular Simulation: from Algorithms to Applications, Academic press, 2001, vol. 1 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Ultrashort mean free path; Bonding nature in perovskites; origins of low acoustic mode group velocities; perturbation of electronic charge distribution due to Pb/Si displacement; softening of optical modes on diatomic chains with second-nearest-neighbor interactions. See DOI: 10.1039/c8ee02820f |
| This journal is © The Royal Society of Chemistry 2019 |