Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Quantifying lithium concentration gradients in the graphite electrode of Li-ion cells using operando energy dispersive X-ray diffraction†
Koffi P. C.
Yao
 ab,
John S.
Okasinski
ab,
John S.
Okasinski
 c,
Kaushik
Kalaga
c,
Kaushik
Kalaga
 a,
Ilya A.
Shkrob
a,
Ilya A.
Shkrob
 a and
Daniel P.
Abraham
a and
Daniel P.
Abraham
 *a
*a
aChemical Sciences and Engineering Division, Argonne National Laboratory, 9700 Cass Avenue, Argonne, Illinois 60439, USA. E-mail: abraham@anl.gov
bUniversity of Delaware, 334 Spencer Lab, Newark, DE 19716, USA
cAdvanced Photon Source, Argonne National Laboratory, 9700 Cass Avenue, Argonne, Illinois 60439, USA
First published on 9th January 2019
Abstract
Safe, fast, and energy efficient cycling of lithium ion batteries is desired in many practical applications. However, modeling studies predict steep Li+ ion gradients in the electrodes during cycling at the higher currents. Such gradients introduce heterogeneities in the electrodes, which make it difficult to predict cell lifetimes as different portions of the cell age at different rates. There is a dearth of experimental methods to probe these concentration gradients across the depth of the electrode. Here we use spatially resolved energy dispersive X-ray diffraction to obtain a “movie” of lithiation and delithiation in different sections of the cell and quantify lithium gradients that develop in a porous graphite electrode during cycling at a 1C rate. Inhomogeneity in the total Li content, and in the individual ordered LixC6 phases formed during lithium insertion into (and extraction from) the graphite, has been observed in an operando fashion. The complex dynamics of lithium-staging in graphite with the distinct front propagation of phase changes have been characterized and new features of these dynamics are highlighted here. As large Li+ ion gradients contribute to cell polarization, our results suggest that Li plating conditions can be met near the graphite electrode surface, even when the cell is charged at a moderate (1C) rate.
Broader contextTo meet the expectations of today's consumers, charging of lithium-ion batteries in electric vehicles needs to become faster for these vehicles to become more widely adopted. A major obstacle to increasing the charging current is the steep gradient in lithium concentration that develops in the electrode matrix when the lithium ion flux into the active material, driven by the applied current, exceeds the transport capability of the electrolyte and/or the material. While numerous modeling studies have predicted such inhomogeneity, there are few experimental studies in which such concentration gradients are observed directly with the required temporal and spatial resolution. Here an in situ X-ray technique is used to obtain a “movie” of graphite electrode lithiation and delithiation during cycling of a cell at a ∼1C rate (full discharge in 1 hour). As lithium intercalates between the graphene layers, ordered LixC6 phases emerge in succession, which are identified and quantified through their X-ray diffraction patterns. Our results provide evidence for steep gradients in the LixC6 phase concentration, and in the total concentration of intercalated lithium, in the direction of the ionic current. Previously predicted behaviors, and surprising new features still awaiting an explanation, are revealed in this study. |
1. Introduction
Faster charging of Li-ion batteries (LIBs) would enable wider adoption of electric vehicles, as it would shorten the time needed to refill these vehicles bringing it closer to consumer's expectations informed by the use of gasoline-fueled cars. The current LIBs predominantly use porous graphite (Gr) anodes (negative electrodes) and layered metal oxide cathodes (positive electrodes). At cycling rates below 1C (full discharge in 1 hour), these LIBs can go through hundreds of cycles of operation with minimal performance degradation. However, at higher cycling rates, the capacity, cycle life, and thermal stability of these LIBs is known to degrade.1–9 Theoretical studies of lithium intercalation using Newman-type models10 attribute these effects to lithium plating, kinetic losses, and Li+ concentration gradients (causing polarization of the cell) occurring both in the electrolyte filling the matrix pores and in the graphite electrode itself.9,11,12 Our focus will be the latter gradients that are a complex function of Li+ diffusion coefficients, intercalation rates, ion transference numbers, and the electrode thickness (t), porosity (ε), and tortuosity (τ).9–11 For example, low porosity and high tortuosity in the electrode decrease the effective diffusion coefficient Deff = (ε/τ)Dbulk of the Li+ ions in the matrix relative to the solvent bulk.13,14 At high charge rates, this lower mobility leads to greater differentials in lithium concentration in the direction of the flowing Li+ ion current (that we take as the z-direction of the laboratory frame with z = 0 corresponding to the electrode surface near the separator between the electrodes).10,12,15,16Such Li+ ion gradients are problematic on at least three counts. First, they impose gradients in the lithium intercalation rates and the corresponding electrode overpotentials.1,17,18 The latter causes polarization of the cell, so the cut-off voltage can be reached prematurely before Li is fully extracted from the cathode, resulting in a lower capacity. Second, this heterogeneous lithiation can lower the (negative) electrode potential creating conditions facilitating lithium plating, especially in regions adjacent to the separator.9,18 Third, these Li+ gradients facilitate structural stresses within the graphite particles (causing their fracture)17,19–21 and in the electrode matrix at large (causing the coating to peel off the current collector).18,20 The higher the current flowing through the cell, the steeper the Li+ gradients, and greater their effect on cell performance and life.
Graphite electrodes have particularly high tortuosities due to the high aspect ratio of the pancake-shaped flakes.13 The effects of the packing of such particles on a cell's electrochemical performance have been demonstrated by Billaud et al.22 Out-of-plane alignment of graphite flakes in a strong magnetic field resulted in tripling of the specific discharge capacity at 1C rate, as the axial tortuosity of the electrode matrix decreased from ∼14 to ∼3.8 after this alignment.22 This problem is compounded by another concern inherent to the lithiated graphite as a charge storage medium: the potential for Li insertion into the graphite (85 to 220 mV vs. Li/Li+) is perilously close to the Li plating potential,23–26 so even a relatively small electrode overpotential can result in Li deposition on the graphite particles competing with Li intercalation into the particles.
While there have been many modeling studies of concentration gradients developing in LIBs during high-current cycling,10 the experiments directly observing and quantifying these gradients are still lacking. With this study, we seek to close this gap in knowledge. To this end, we use energy dispersive X-ray diffraction (EDXRD) to spatially resolve Li concentration profiles during cycling of a Li-ion cell at 1C rate. With this technique, narrowly focused polychromatic (“white light”) beams of synchrotron photons are used to obtain diffraction patterns at a fixed angle θ, so the Bragg condition, 2d![[thin space (1/6-em)]](https://www.rsc.org/images/entities/i_char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ = n × λ, is satisfied for some wavelengths λ in the light continuum. This method is complementary to the commonly used angle-dispersive XRD method, which uses monochromatic X-ray beams and scans the angle θ to satisfy the Bragg condition. As lithium intercalates into the graphite crystal, it fills layers between the graphene sheets (“staging of the graphite”) yielding distinctive, ordered LixC6 phases (0 ≤ x ≤ 1) that can be easily recognized even from a single Bragg peak. The intensities of these peaks can be used to quantify the concentration of each LixC6 phase, and through such quantification we determine the exact phase composition of each probed layer in the solid matrix. As only ordered LixC6 phases contribute to the diffraction signal, this method is blind to Li+ ions in the electrolyte and/or potential disordered solid compounds in the matrix. Using the EDXRD technique, the succession of LixC6 phases formed during the electrochemical lithiation and delithiation of graphite has been studied with a spatial resolution of 20 μm and a time resolution of one minute. Below we describe how this technique helps to quantify and visualize lithium gradients in the electrode and discuss the insights obtained from these data. Figures and tables with index S (e.g. Fig. S1) are contained in the ESI.†
θ = n × λ, is satisfied for some wavelengths λ in the light continuum. This method is complementary to the commonly used angle-dispersive XRD method, which uses monochromatic X-ray beams and scans the angle θ to satisfy the Bragg condition. As lithium intercalates into the graphite crystal, it fills layers between the graphene sheets (“staging of the graphite”) yielding distinctive, ordered LixC6 phases (0 ≤ x ≤ 1) that can be easily recognized even from a single Bragg peak. The intensities of these peaks can be used to quantify the concentration of each LixC6 phase, and through such quantification we determine the exact phase composition of each probed layer in the solid matrix. As only ordered LixC6 phases contribute to the diffraction signal, this method is blind to Li+ ions in the electrolyte and/or potential disordered solid compounds in the matrix. Using the EDXRD technique, the succession of LixC6 phases formed during the electrochemical lithiation and delithiation of graphite has been studied with a spatial resolution of 20 μm and a time resolution of one minute. Below we describe how this technique helps to quantify and visualize lithium gradients in the electrode and discuss the insights obtained from these data. Figures and tables with index S (e.g. Fig. S1) are contained in the ESI.†
2. Experimental
2.1. Materials
A standard 2032-type coin cell, containing a Gr based anode and a Li1.03(Ni0.5Co0.2Mn0.3)O2 (NCM523) based cathode, was used in our experiments. The detailed composition, sources, and properties of the cell materials are given in Table S1 (ESI†). Briefly, the anode contained 92 wt% graphite, 2 wt% conductive carbon particles, and 6 wt% polymer binder, while the NCM523 cathode contained 90 wt% oxide, 5 wt% conductive carbon particles, and 5 wt% polymer binder. The slurries were prepared by mixing the particles in a planetary centrifugal mixer using N-methyl-2-pyrrolidone as a solvent. Electrode laminates were fabricated by casting these slurries onto a 10 μm battery grade copper foil for the Gr electrode and 20 μm battery grade aluminum foil for the NCM523 counter electrode, using a battery coater at the Cell Analysis, Modeling and Prototyping (CAMP) facility at Argonne National Laboratory (ANL). After drying of the solvent, the Gr electrode was calendered to obtain uniform thickness. The NCM523 cathode was not calendered, in order to retain maximum porosity in the matrix and ensure minimal interference during the high rate cycling. Before cell assembly, the electrodes were dried at 120 °C for 12 h, and the separator was dried at 70 °C for 24 h, both in a vacuum oven. The assembled cell contained 40 μL of 1.2 M LiPF6 in ethyl carbonate/ethyl methyl carbonate mixture (3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 7 w/w). This electrolyte filled a microporous Celgard 2325 separator sandwiched between the two electrodes (1.58 cm2 areas). The Gr electrode had an areal capacity of ∼5 mA h cm−2; a positive-to-negative electrode capacity ratio of 1.13 was chosen to enable deep lithiation and delithiation of the graphite electrode.
7 w/w). This electrolyte filled a microporous Celgard 2325 separator sandwiched between the two electrodes (1.58 cm2 areas). The Gr electrode had an areal capacity of ∼5 mA h cm−2; a positive-to-negative electrode capacity ratio of 1.13 was chosen to enable deep lithiation and delithiation of the graphite electrode.
2.2. Cycling conditions
The cycling tests were conducted at 30 °C. The C-rates, state-of-lithiation, and cell capacities were calculated with respect to the theoretical capacity of the Gr, which is 372 mA h g−1. The applied current of 5.6 mA corresponded to a ∼1C rate for the full cell. Prior to the XRD experiment, the cell was cycled twice at a C/20 rate in the 3–4.1 V range (see Fig. S1, ESI†), in order to stabilize the solid electrolyte interphase (SEI) on the graphite electrode; this SEI protects the graphite from solvent intercalation and the electrolyte from runaway reduction reactions on the electrode. Three additional cycles were conducted during the XRD experiment: the cycling was performed in a galvanostatic regime until an upper cut voltage of 4.4 V or a lower cut voltage of 3.0 V were attained on charge (Gr lithiation) and discharge (Gr delithiation), respectively. Upon attainment of the set voltages, the cell operated in a potentiostatic regime for 30 min (referred to as “potentiostatic hold”).2.3. Energy dispersive X-ray diffraction (EDXRD)
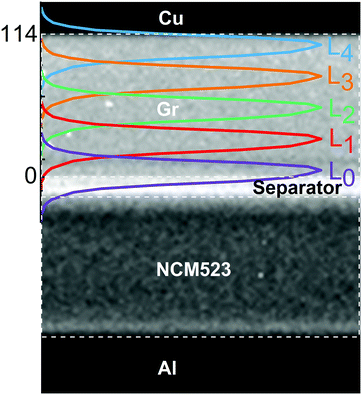
The EDXRD setup at beamline 6BM-A of the Argonne's Advanced Photon Source was used to observe the diffraction patterns of the pristine graphite and ordered LixC6 phases in an operating Gr/NCM523 cell described above. The X-ray photons with energies between 5 and 250 keV (that corresponds to 47 to 1 Å in d-spacing) readily transmit through the stainless-steel casing of the coin cell. A Ge detector placed at a fixed angle θ ≈ 3° in the vertical plane with respect to the incident X-ray beam collected and averaged the diffraction patterns at a rate of 1 min per acquisition for a total period of 3 h per charge/discharge cycle. The probe X-ray beam was 18.3 μm (fwhm) × 1045 μm; this beam propagated along the plane of the Gr electrode “slicing” it in steps of 25 μm, to give a total of five minimally-overlapping layers numbered from L0 to L4 in Fig. 1 (see Section S1, ESI† for calculation of layer centroids). The X-ray power in the overlapping region was calculated to be ∼12% of the total beam power. The absolute position of the coin cell with respect to the X-ray beam in the transverse direction was controlled using a stepper motor, and care was exercised to perfectly align the beam with the plane of the Cu current collector. As shown in Fig. 1, layer L0 was adjacent to the separator and layer L4 was adjacent to the Cu current collector.In order to establish the position of the 10 μm thick Cu current collector supporting the Gr coating within the reference frame of the X-ray diffractometer stage, we took the following steps. First, the current collector was located using a coarse scanning of the incident X-ray beam along the entire thickness of the cell noting the stage position and the intensity (or absence thereof) of the Cu(002) peak at ∼1.808 Å d-spacing. Upon identifying a strong presence of the Cu(002) peak, a fine 5 μm step scan in a narrow 30 μm span around the Cu position was collected. By fitting a Gaussian shape to the collected intensities of the (002) peak during the scan, the estimated position of maximum intensity was taken as the midsection of the foil and used as reference in positioning the slices across the graphite electrode. To obtain the profile of the beam as it crosses the Gr matrix, a radiograph through the cell was collected (Fig. 1). The pixel intensity map represents the beam intensity distribution, which is overlaid onto the radiograph. The five layers were sampled in a round-robin fashion. To obtain the gradient plots discussed later, linear interpolation was used to bring the elucidated LixC6 concentrations found in the successive measurements to the same points in time.
The Li–Gr intercalation system exhibits several phases (commonly referred to as stages). Through literature review, five main stages are identified and deconvoluted from the spectra collected using their reported d-spacing ranges: dilute stage I (denoted I′), stage IV/III, stage IIL, stage II, and stage I.26–29 The following equation is used to estimate the average lithium content x of each layer (expressed in Li atoms per C6):
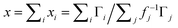 | (1) |
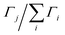 represent the normalized average concentration of phase j in the probed volume, whereas fj in eqn (1) gives the Li content in each phase j (per C6 units in the graphite matrix). These quantities are independent of the material distribution, porosity, and masking of the X-ray beam by non-graphitic materials. The stoichiometry of stages I′ and IV/III which are solid solution stages (the average Gr interlayer spacing increases with lithiation) varies with cell capacity. For these stages, a linear fit to d-spacing vs. capacity (fj ≈ 1.53·d − 5.11) was used to estimate the Li content.26
represent the normalized average concentration of phase j in the probed volume, whereas fj in eqn (1) gives the Li content in each phase j (per C6 units in the graphite matrix). These quantities are independent of the material distribution, porosity, and masking of the X-ray beam by non-graphitic materials. The stoichiometry of stages I′ and IV/III which are solid solution stages (the average Gr interlayer spacing increases with lithiation) varies with cell capacity. For these stages, a linear fit to d-spacing vs. capacity (fj ≈ 1.53·d − 5.11) was used to estimate the Li content.26
3. Results
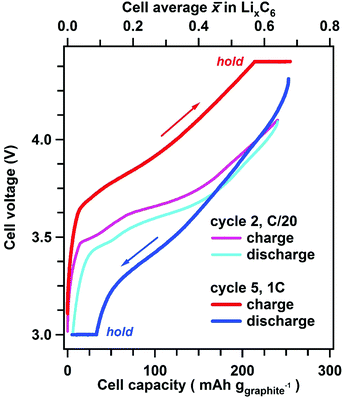
The voltage–capacity curves from the Gr/NCM523 cell during cycling at a C/20 rate (cycle 2, 3–4.1 V) and a 1C rate (cycle 5, 3–4.4 V) are shown in Fig. 2. From the measured specific capacity, one can calculate the cell average lithium content![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) that we express in Li atoms per C6 unit of the graphite present in the electrode; the
that we express in Li atoms per C6 unit of the graphite present in the electrode; the ![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) value is given at the top of Fig. 2. During 1C galvanostatic charging, the upper cut-off voltage of 4.4 V was attained at
value is given at the top of Fig. 2. During 1C galvanostatic charging, the upper cut-off voltage of 4.4 V was attained at ![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) = 0.58, which increased to
= 0.58, which increased to ![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) = 0.68 at the end of the 30 min potentiostatic hold. During the 1C discharge, the lower cut voltage of 3.0 V was attained at
= 0.68 at the end of the 30 min potentiostatic hold. During the 1C discharge, the lower cut voltage of 3.0 V was attained at ![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) = 0.1, which decreased to
= 0.1, which decreased to ![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) = 0.02 at the end of the 30 min hold.
= 0.02 at the end of the 30 min hold.
Typical XRD patterns collected during the continuing cycling are shown in Fig. 3. Only X-ray data collected during the fifth cycle are given below to highlight the major features and trends observed during cell cycling; data from cycles 3 and 4 showed similar features and are included in Fig. S2 (ESI†). In the d-spacing range shown, only the major Bragg peak for each one of the LixC6 phases is visible. The d-spacings corresponding to these peaks are shown in Fig. 4 and their Miller indices are listed in Table S2 (ESI†). For example, stage I (LiC6) is represented by (001) peak, stage II (LiC12) by (002) peak, and stage IIL (LiC18) by (004) peak. The peaks of stage I′, stage IV/III, and stage IIL overlap in d-spacing (Fig. 3). An uncertainty is introduced during deconvolution of the XRD pattern into pseudo-Voigt profiles that was used for integration; the associated errors in the quantification of lithium content can become significant especially after the formation of stage IIL (LiC18). Another source of error arises from uncertainties in the scattering factors themselves (see Section S2, ESI†). For convenience, the concentrations of the LixC6 phases reported below have been adjusted by the fractional Li content fj of the phases; therefore these concentrations reflect the availability of Li in each phase averaged in a given layer.
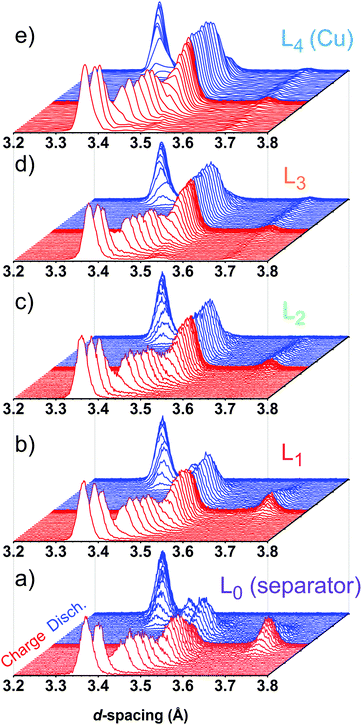 | ||
| Fig. 3 XRD patterns in the 3.2–3.8 Å d-spacing region collected during charge and discharge of the cell at a 1C rate (cycle 5 shown in Fig. 2). Panels (a) to (e) correspond to layers L0 to L4, respectively, as labeled in Fig. 1. The diffraction intensities have been normalized by the initial intensity of the graphite in each layer and shown on the same scale. The red color corresponds to charge and the blue color corresponds to the discharge of the cell. Different Bragg peaks in this plot correspond to different “stages” of graphite lithiation, as explained in the text. | ||
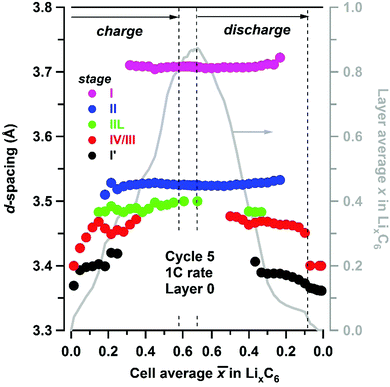 | ||
Fig. 4 Experimental d-spacing (filled circles, axis to the left) for LixC6 phases present in layer L0, observed during cycling at 1C rate and plotted as a function of the cell average lithium content ![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) in the matrix. The lithiation stages are color-coded as shown in the inset. The vertical dashed lines indicate the potentiostatic hold. Shown to the right in grey is the layer average lithium content x calculated using eqn (1). in the matrix. The lithiation stages are color-coded as shown in the inset. The vertical dashed lines indicate the potentiostatic hold. Shown to the right in grey is the layer average lithium content x calculated using eqn (1). | ||
For the slow C/20 cycle, the voltage–capacity curves shown in Fig. 2 reveal characteristic steps attributable to the graphite electrode (known as “stages”); the stages of graphite correspond to progressive filling of spaces between the adjacent graphene sheets. As the cycling rate increases to 1C, these steps become blurred due to Li heterogeneity in the matrix, but the distinct LixC6 phases are seen in the X-ray diffraction patterns during layer-by-layer sectioning as shown in Fig. 3. In particular, a well-separated Bragg peak at 3.7 Å is observed, which originates from the LiC6 phase (stage I in Fig. 4) that is formed in the final stages of lithiation. Excess Li transported to the graphite matrix beyond this final stage can become deposited as Li metal. Also clearly distinguished at the outset of charging is the rapid disappearance of dilute LixC6 phases that correspond to a solution of Li in graphite (stage I′ in Fig. 4). For this stage I′ (x < 1/8) and stage IV/III (1/4 < x < 1/3) peaks, the d-spacing changes with the extent of the lithiation x (as the unit cell dilates when the lithium content increases), whereas for stages I (x = 1), II (x = 1/2), and IIL (x = 1/3) this dependence is weak. The gaps seen in Fig. 4 correspond to lithiation regimes in which the peak positions cannot be determined due to weakness of the corresponding Bragg peaks relative to the prevalent LixC6 phases. For ![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) > 0.3, the two prevalent phases, LiC6 and LiC12, yield almost all of the diffraction signal. At peak charge (
> 0.3, the two prevalent phases, LiC6 and LiC12, yield almost all of the diffraction signal. At peak charge (![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) ≈ 0.68, Fig. 4) the layer average lithiation x for layer L0 as positioned in Fig. 1 is ∼0.87; as the LiC6 phase permeates this layer, relatively little LiC12 is observed.
≈ 0.68, Fig. 4) the layer average lithiation x for layer L0 as positioned in Fig. 1 is ∼0.87; as the LiC6 phase permeates this layer, relatively little LiC12 is observed.
Due to this pinning of lattice parameters and relatively strong scattering factors of LiC6 and LiC12 phases, their concentrations can be determined more accurately than those of the other LixC6 phases. In Fig. 5 we show the time progression of the LiC6 and LiC12 phase concentrations during cycling; the changes in the other stages/phases are included in Fig. S3 and S4 (ESI†). Near the electrode surface, the concentration profiles for lithiation and delithiation mirror each other, whereas deeper into the matrix they become asymmetric as it takes time for the formation and depletion fronts to reach the back of the electrode matrix during charging and discharging of the cell, respectively. The onset of LiC12 formation in layer L0 is at ![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) > 0.2; for
> 0.2; for ![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) > 0.4 this phase begins to convert to LiC6 that reaches the maximum concentration of 0.72 at the peak charge. Conversely, at this peak charge, the concentration of LiC6 in L4 at the back of the Gr electrode is lower than 0.1, indicating a steep gradient of the LiC6 phase in the cell.
> 0.4 this phase begins to convert to LiC6 that reaches the maximum concentration of 0.72 at the peak charge. Conversely, at this peak charge, the concentration of LiC6 in L4 at the back of the Gr electrode is lower than 0.1, indicating a steep gradient of the LiC6 phase in the cell.
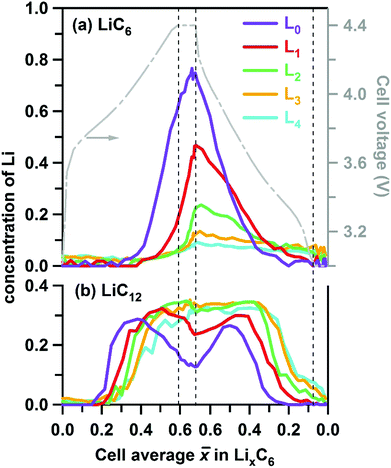 | ||
| Fig. 5 Layer average Li content of (a) LiC6 and (b) LiC12 phases given in atoms per C6 units in the graphite matrix (to the left) and plotted as a function of the cell average lithium content in this matrix during charge and discharge at 1C rate. The vertical dashed lines indicate the 30 min potentiostatic hold periods. The cell voltage is shown by the grey line (see axis to the right). The five layers are in the order of increasing depth and color coded as in Fig. 1 above. | ||
These differences are more clearly seen in Fig. 6, in which we show the concentrations of all stages in layers L0 and L4. On lithiation, the extrema stages I′ and I decrease from a maximum value or grow from a minimum value, respectively. In layer L0 where almost complete lithiation is observed, stage I reached a maximum concentration of ∼0.75 in good agreement with the initial concentration of stage I′ of 0.76. The intermediary stages IV/III, IIL, and II all show concentration peaks reflecting their formation, growth, and conversion to subsequent stages. Note that each of these three stages peak at a delayed time (that is, greater ![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) ) in the back layer L4 relative to their counterpart in the surface layer L0. As the lithiation progresses, the LiC12 phase arises. Even in layer L0 this LiC12 phase is not fully replaced by LiC6, and residual LiC12 remains in layer L4 even at the peak of charge. In this deepest layer, during discharge of the cell (delithiation of graphite) the LiC6 and LiC12 phases also persist much longer than in the surface layer; it takes time for the lithium to flow out of the electrode before the depletion front reaches the back of the cell. Intriguingly, some of these LixC6 phases persist in the electrode even after the 30 min potentiostatic hold at 3 V.
) in the back layer L4 relative to their counterpart in the surface layer L0. As the lithiation progresses, the LiC12 phase arises. Even in layer L0 this LiC12 phase is not fully replaced by LiC6, and residual LiC12 remains in layer L4 even at the peak of charge. In this deepest layer, during discharge of the cell (delithiation of graphite) the LiC6 and LiC12 phases also persist much longer than in the surface layer; it takes time for the lithium to flow out of the electrode before the depletion front reaches the back of the cell. Intriguingly, some of these LixC6 phases persist in the electrode even after the 30 min potentiostatic hold at 3 V.
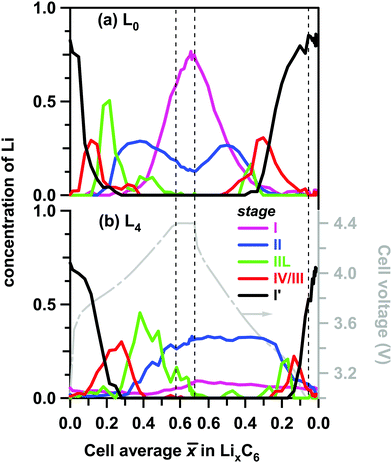 | ||
| Fig. 6 Layer average Li content in the ordered LixC6 phases (to the left) plotted as a function of the cell average Li content in the graphite matrix during charge and discharge at 1C rate. The color scheme for the lithiation stages in the inset follows the conventions of Fig. 4 above. Panel (a) is for layer L0 (near the separator) and panel (b) is for layer L4 (near the Cu current collector). Shown to the right in grey is the cell voltage. Stages I, II, IIL, IV/III and I′ are distinguished by their XRD patterns and associated with the LixC6 phases with x = 1, x = 1/2, x = 1/3, 1/6 < x < 1/4, and 0 < x < 1/8, respectively. | ||
Using the concentration of each phase, the layer average Li content of layers L0 through L4 can be determined using eqn (1) and compared with the cell average Li content ![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) determined electrochemically (see Fig. 7 and Table S3, ESI†). We reason that for sufficiently smooth concentration profiles the arithmetic average of these layers would be sufficiently close to the cell average (open circles in Fig. 7), i.e. the two metrics are expected to be close to each other (straight black lines in Fig. 7). This is indeed the case during charge, and this validation gives us certain confidence in our use of eqn (1). It is also seen from these plots that at the peak of charge, x for L0 is considerably above the cell average
determined electrochemically (see Fig. 7 and Table S3, ESI†). We reason that for sufficiently smooth concentration profiles the arithmetic average of these layers would be sufficiently close to the cell average (open circles in Fig. 7), i.e. the two metrics are expected to be close to each other (straight black lines in Fig. 7). This is indeed the case during charge, and this validation gives us certain confidence in our use of eqn (1). It is also seen from these plots that at the peak of charge, x for L0 is considerably above the cell average ![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) , whereas x for L4 is significantly below
, whereas x for L4 is significantly below ![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) . The inhomogeneity in the quantity of individual phases in each layer across the graphite electrode (greater amount of LiC6 at the electrode surface compared to deeper layers for example) as shown in Fig. 5 and 6 is reflected in the calculated Li content of the layers, with significant difference observed only when
. The inhomogeneity in the quantity of individual phases in each layer across the graphite electrode (greater amount of LiC6 at the electrode surface compared to deeper layers for example) as shown in Fig. 5 and 6 is reflected in the calculated Li content of the layers, with significant difference observed only when ![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) > 0.2. A surprising feature of Fig. 7 is the asymmetry of the traces: the delithiation of the electrode does not mirror the lithiation run “in reverse”; this asymmetry becomes even more noticeable for the deepest layers. Most strikingly, during the rapid discharge (in contrast to charge) the arithmetic mean of layer averages (open symbols in Fig. 7) strongly deviates from
> 0.2. A surprising feature of Fig. 7 is the asymmetry of the traces: the delithiation of the electrode does not mirror the lithiation run “in reverse”; this asymmetry becomes even more noticeable for the deepest layers. Most strikingly, during the rapid discharge (in contrast to charge) the arithmetic mean of layer averages (open symbols in Fig. 7) strongly deviates from ![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) for
for ![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) > 0.3, suggesting (among other possibilities) that the Li concentration profile may have sharp features, so our averaging of the layer Li contents becomes a poor estimate of the actual average Li concentration.
> 0.3, suggesting (among other possibilities) that the Li concentration profile may have sharp features, so our averaging of the layer Li contents becomes a poor estimate of the actual average Li concentration.
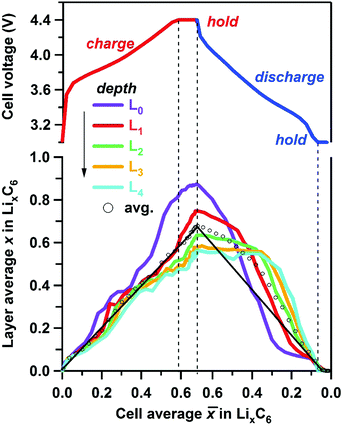 | ||
Fig. 7 Layer average lithium content x in the ordered LixC6 phases estimated using eqn (1) plotted as a function of the cell average lithium content of the graphite matrix determined electrochemically. The layers are color coded as shown in the inset. The vertical dashed lines correspond to the potentiostatic hold periods (see voltage plot at the top). The arrow shows the direction of increasing depth. The open circles indicate the five-layer average, and the straight line is ![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) . . | ||
To better visualize the inhomogeneities across the electrode, in Fig. 8 we plot Li content in each layer at different states of charge as a function of the centroid depth; this information is also given in Table S3 (ESI†). The smooth lines drawn through these symbols are B-splines added as a guide to the eye. In the initial stages of charging (Fig. 8a), the Li content is nearly uniform across the electrode. As the cell is charged further, a concentration gradient develops, with more lithium present near the surface (L0) than at the back (L4). This transformation nearly coincides with the moment when LiC6 becomes the prevalent phase near the surface in this particular graphite electrode. During cell charge (Fig. 8a), the gradient d[Li]/dz remains negative across the electrode depth. During cell discharge (Fig. 8b), there is Li depletion near the surface that gradually spreads deeper into the matrix until it reaches the back of the cell. After that, the Li gradients once again become lower, and in the advanced stages of delithiation they become too small to observe. The complex shape of Li profiles during the cell discharge (Fig. 8b) compared to the profiles during the cell charge (Fig. 8a) is the primary reason for the asymmetries seen in Fig. 7, including the behavior of the arithmetic average of layer averages.
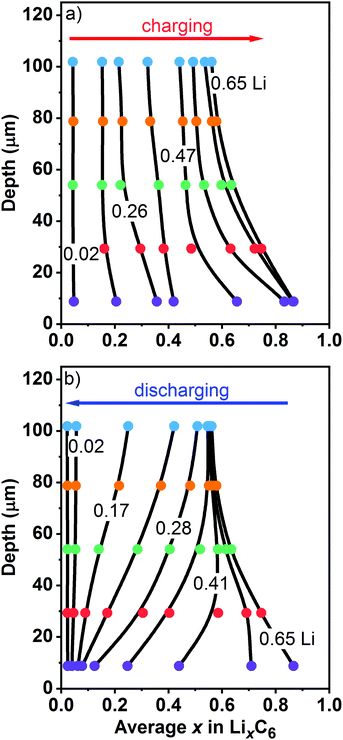 | ||
| Fig. 8 Layer average Li content x in the ordered phases (filled circles, to the bottom) plotted vs. the median depth of these layers (to the left). Panel (a) is for charge and panel (b) is for discharge of the cell at 1C rate vs. the graphite electrode capacity. On charge, Li-content lines are shown for of 0.02, 0.18, 0.26, 0.34, 0.47, 0.58, 0.63, and 0.65. On discharge, Li-content lines are shown for of 0.65, 0.52, 0.41, 0.33, 0.28, 0.23, 0.17, 0.10, and 0.02. The layers are color coded as in Fig. 1 and 7 above. The smooth lines are guides to the eye. The numbers in the plot give the overall cell average lithium content of the graphite matrix calculated based on the electrochemically measured cell capacity. | ||
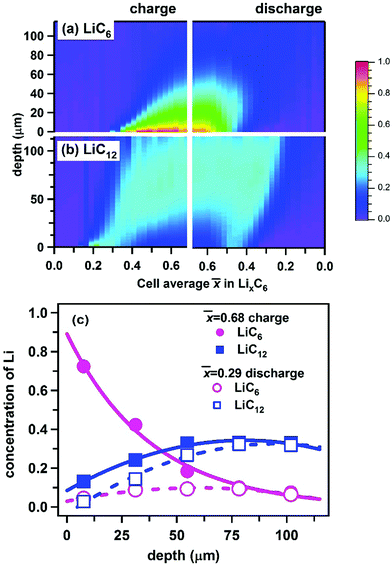
In Fig. 9, we use polynomial fits to extrapolate the concentration profiles over the entire range of depth (see Section S1, ESI† for more detail). Fig. 9a and b give the color maps of Li content in LiC6 and LiC12 phases obtained in this manner, and Fig. 9c shows the profiles obtained at two states of charge (more of such profiles are shown in Fig. S5, ESI†). At the peak charge, a nearly exponential LiC6 profile and an almost complete lithiation of the graphite at the electrode surface are observed. As the LiC6 phase grows from surface towards deeper layers, there is a complementary depletion zone for LiC12. This observation is made more obvious in Fig. 9c and also from comparison of Fig. 9a and b: the crest of high concentrations of LiC6 in Fig. 9a maps exactly onto the trough of low concentrations of LiC12 in Fig. 9b, suggesting the complementarity of these two phases through the cell, as expected. The same behavior is also seen in Fig. 5, where the maxima of the LiC6 concentration in Fig. 5a nearly coincide in position with the minima of the LiC12 concentration in Fig. 5b. The complementarity of these two phases is the consequence of the binary nature of the phase diagram for the Li–graphite system after more than 50% Li is inserted per C6 units of graphite: as the two phases undergo spinodal decomposition to their equilibrium fractions, at each states of charge the concentration of each phase is fully determined by the net Li content. As LiC6 replaces LiC12 across the matrix, the LiC12 profile develops the characteristic shape shown in Fig. 9c; this shape persists during the electrode delithiation, as seen from Fig. 9c and Fig. S5 (ESI†).
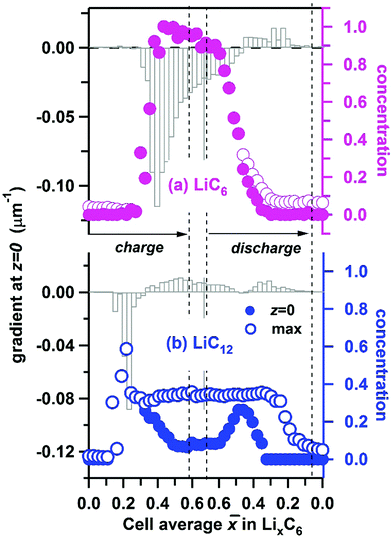
Using the interpolated concentrations for LiC6 and LiC12 phases, in Fig. 10 we provide the extrapolated concentrations and gradients of these two phases at the electrode surface (z = 0). The error bars of the gradients are given in Fig. S6 (ESI†). For LiC6, during the cell charge there is an abrupt increase of the surface concentration at ![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) ≈ 0.35, as the concentration rapidly approaches unity, and it stays close to unity until discharge is initiated. The maximum gradient for LiC6 (−0.120 ± 0.003 μm−1) is observed during the onset of conversion of LiC12 to LiC6, when the penetration depth is small. As the LiC6 phase spreads over preceding LiC12 phase, the surface gradient decreases, becoming −0.012 ± 0.002 μm−1 at the peak charge. During the discharge, the decrease of the LiC6 surface gradient continues, and at some point the gradient changes sign as the LiC6 phase becomes depleted near the surface. As the depletion zone extends into the bulk, the gradient decreases once again. For a greater part of the cycle the highest concentration of the LiC6 phase is at the surface. Only for
≈ 0.35, as the concentration rapidly approaches unity, and it stays close to unity until discharge is initiated. The maximum gradient for LiC6 (−0.120 ± 0.003 μm−1) is observed during the onset of conversion of LiC12 to LiC6, when the penetration depth is small. As the LiC6 phase spreads over preceding LiC12 phase, the surface gradient decreases, becoming −0.012 ± 0.002 μm−1 at the peak charge. During the discharge, the decrease of the LiC6 surface gradient continues, and at some point the gradient changes sign as the LiC6 phase becomes depleted near the surface. As the depletion zone extends into the bulk, the gradient decreases once again. For a greater part of the cycle the highest concentration of the LiC6 phase is at the surface. Only for ![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) < 0.46 during the discharge does the maximum concentration somewhat exceed this surface concentration. As seen in Fig. 5a, the formation of LiC6 during charge and depletion of this phase during discharge are generally faster near the surface as compared to the bulk. The persistence of LiC6 near the surface during discharge is caused by its preferential formation in this region during charge.
< 0.46 during the discharge does the maximum concentration somewhat exceed this surface concentration. As seen in Fig. 5a, the formation of LiC6 during charge and depletion of this phase during discharge are generally faster near the surface as compared to the bulk. The persistence of LiC6 near the surface during discharge is caused by its preferential formation in this region during charge.
As seen from Fig. 9c and 10b, for the LiC12 phase, where the maximum concentration is reached at the surface only in a narrow range of ![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) (0.16–0.24) which corresponds to the initial stages of LiC12 formation near the surface. Subsequently, the maximum relocates deeper into the matrix (see Fig. S5, ESI†), as the LiC6 phase takes over. The evolution of the gradient for LiC12 resembles that for LiC6 with the entire pattern shifted to lower
(0.16–0.24) which corresponds to the initial stages of LiC12 formation near the surface. Subsequently, the maximum relocates deeper into the matrix (see Fig. S5, ESI†), as the LiC6 phase takes over. The evolution of the gradient for LiC12 resembles that for LiC6 with the entire pattern shifted to lower ![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) . The maximum absolute gradient is observed at
. The maximum absolute gradient is observed at ![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) ≈ 0.22, which corresponds to the formation of a narrow wedge of LiC12 phase near the surface. As LiC12 transforms to LiC6, the sign of the gradient changes, and it reaches a positive maximum near
≈ 0.22, which corresponds to the formation of a narrow wedge of LiC12 phase near the surface. As LiC12 transforms to LiC6, the sign of the gradient changes, and it reaches a positive maximum near ![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) ≈ 0.54. Subsequently it decreases (as the LiC12 depletion zone becomes wider) only to increase again when LiC12 becomes the main source of recovered lithium during the discharge.
≈ 0.54. Subsequently it decreases (as the LiC12 depletion zone becomes wider) only to increase again when LiC12 becomes the main source of recovered lithium during the discharge.
Put together, our data indicate strong inhomogeneity of Li insertion and de-insertion, both in the net Li content and in the individual LixC6 phases.
4. Discussion
Previous in situ and operando approaches to visualization of LixC6 gradients in graphite used optical microscopy to distinguish between the colors of the lithiated grains: gold for stage I lithiation, red for stage II, and blue-grey for dilute stages.30 This method yields qualitative insight in the succession of LixC6 phases, but only bands of the corresponding zones were determined. The method has particular difficulty in separating contributions from mixed phases, and it can give misleading results if the composition varies across the individual Gr particles. In our approach using X-rays, the concentration profiles of the LixC6 phases correspond to their bulk averages, integrating over the individual particles and quantifying the fraction of each ordered phase in these particles.Presently, dynamic modeling of phase composition for individual Gr particles and the porous matrix on the whole are still in the development stages, and many aspects of phase transformations remain insufficiently understood. Bazant's phase-field periodic bilayer model appears to be particularly promising for description of stage I–stage II transitions captured in our experiments.31 This model predicts rapid spinodal decomposition in the individual lithiated Gr particles into well-defined LiC6 and LiC12 subdomains which may explain why our “mixed phase” analysis works so remarkably well on the quantitative level. Bazant and co-workers have recently combined these models with the distributed-resistance models of the matrix to include multiple particles.32 Another approach for describing these phase transitions combined Newman-type models with the heuristic Avrami equations for growth of the LixC6 phases.33 Now, both of these approaches can be tested against the experimental data. The more traditional Newman-type models consider the LixC6 phases as a continuum (a solid solution, e.g., ref. 10 and 34) skipping over the details of the phase dynamics seen in our experiments. This limitation is the reason why many of our results have been presented using the net Li content of the solid matrix, which can be compared with the model simulations. The latter routinely yield sloping concentration profiles seen in Fig. 8 (e.g., ref. 35), yet for lack of observational input such models are continued to be tested and validated mainly through the electric potential measurements. Our study opens a new way in which these models can be tested, verified, and improved.
One of the less anticipated features observed in our experiments is the surprisingly long time the diffraction peaks persist in the back layer (L4) during the potentiostatic hold after reaching the lower limit of 3 V (see Fig. 6), suggesting incomplete Li extraction. As seen from Fig. 5 and 6 the residual signals from LiC6 and LiC12 can be observed at the end of the hold period; as shown in Fig. S7 (ESI†), these signals were observed at the end of each one of the 1C delithiation half-cycles. A possible explanation may be relatively poor connectivity of some Gr particles at the end of the cell discharge, as the matrix contracts after swelling.
As mentioned in the Introduction, one of the greatest concerns with operation of LIBs at high currents is Li plating, which occurs when the rate of Li deposition exceeds the rate of Li intercalation. The latter rate is typically expressed using the Butler–Volmer equation in which the exchange current density is proportional to [(1 − x)x]1/2, approaching zero as x nears unity.34 In contrast, the exchange current density of Li plating does not depend on x, so it can overtake Li intercalation in the “red zone” shown in Fig. 9a, where x is close to unity. This condition persists for ![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) > 0.4 during charge and for
> 0.4 during charge and for ![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) > 0.5 during discharge, i.e. the surface of the cell enters this perilous regime at a much lower Li content than is predicted by modeling when neglecting inhomogeneity. While the saturation of the solid matrix with Li is important for plating, equally important is the overpotential η(x) = ϕa(x) − Vfilm, where the first term corresponds to the anode potential vs. the electrolyte and the second term corresponds to the potential drop on the resistive SEI film.34 As the current increases, so does the latter term; the overpotential becomes negative and the lithiation rate increases dramatically. Since for x > 1/2, the potential ϕa(x) is small (see Fig. S8a, ESI†), even moderate currents can cause this “thermodynamic” Li plating condition to occur. Again, while at low current the cell average ϕa(x) can be close to ϕa(
> 0.5 during discharge, i.e. the surface of the cell enters this perilous regime at a much lower Li content than is predicted by modeling when neglecting inhomogeneity. While the saturation of the solid matrix with Li is important for plating, equally important is the overpotential η(x) = ϕa(x) − Vfilm, where the first term corresponds to the anode potential vs. the electrolyte and the second term corresponds to the potential drop on the resistive SEI film.34 As the current increases, so does the latter term; the overpotential becomes negative and the lithiation rate increases dramatically. Since for x > 1/2, the potential ϕa(x) is small (see Fig. S8a, ESI†), even moderate currents can cause this “thermodynamic” Li plating condition to occur. Again, while at low current the cell average ϕa(x) can be close to ϕa(![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) ), when steep gradients are present (see Fig. S8b, ESI†), the front and the back of the cell can correspond to different lithiation stages, and the condition is not met uniformly across the cell. A preference for near surface Li deposition during high-current charging of the cells has been observed in the optical operando experiments of Harris and co-workers.30 Our study suggests that due to the concentration heterogeneity Li plating can be difficult to avoid near the surface even when care is taken to keep the average lithiation sufficiently low during the rapid charge.
), when steep gradients are present (see Fig. S8b, ESI†), the front and the back of the cell can correspond to different lithiation stages, and the condition is not met uniformly across the cell. A preference for near surface Li deposition during high-current charging of the cells has been observed in the optical operando experiments of Harris and co-workers.30 Our study suggests that due to the concentration heterogeneity Li plating can be difficult to avoid near the surface even when care is taken to keep the average lithiation sufficiently low during the rapid charge.
5. Conclusions
Speciation of ordered LixC6 phases in a porous electrode containing graphite flakes during cycling of a full cell at a (moderately high) 1C rate has been studied both in time and space using energy dispersive X-ray diffraction. The X-ray “slicing” of a 114 μm thick graphite electrode reveals steep gradients in the net and phase specific lithium content. The greatest inhomogeneity is observed for the LiC6 phase. Under certain charging conditions, this phase accounts for all Li present at the surface; deeper in the electrode, the concentration exponentially falls towards the current collector. This Li inhomogeneity can have detrimental effects on cell performance, including low utilization of the active material and Li plating in the regions that are close to the electrode surface. Our data on concentration profiles in the individual phases LixC6 as a function of lithiation can serve as a benchmark for modeling of electrochemical processes in LIBs. While some of the features observed have been anticipated by modelers, other features are less expected, such as the surprising persistence of LixC6 phases during the potentiostatic hold at the end of discharge. Another peculiarity that awaits full explanation is the striking asymmetry between the charge and discharge, which suggests that the complex character of phase transitions during the high-rate delithiation may involve less ordered phases. While our method is eminently suitable to characterize phase dynamics on the scale of tens of microns, it does not provide sufficient insight into the processes occurring in the individual graphite particles, where different phase domains can coexist and affect each other. In fact, it is somewhat surprising that our analysis (neglecting such complexities) appears to adequately capture the phase dynamics under strongly nonequilibrium conditions.To summarize, we present an experimental methodology for quantifying spatial and phase heterogeneity of lithium intercalation into graphite during rapid cycling. We hope that the insight this approach provides into electrochemical processes in practical lithium-ion cells, will spark renewed interest in validation and improvement of the cell models. In particular, a greater emphasis on understanding intraparticle and coarse-scale phase dynamics would be highly conducive to taking full advantage of this new approach.
Conflicts of interest
The authors declare no financial competing interests.Acknowledgements
Support from the U.S. DOE's Office of Vehicle Technologies, is gratefully acknowledged. Use of the Advanced Photon Source (APS) at Argonne is supported by the U.S. Department of Energy, Office of Science, Office of Basic Energy Sciences, under Contract No. DE-AC02-06CH11357. The electrodes used in this article are from Argonne's Cell Analysis, Modeling and Prototyping (CAMP) Facility, which is supported within the core funding of the Applied Battery Research (ABR) for Transportation Program. We are grateful to our many colleagues (Stephen Trask, Bryant Polzin, Andrew Jansen, Dennis Dees, Jonathan Almer and Andrew Chuang) for their support and guidance during this effort. The submitted manuscript has been created by UChicago Argonne, LLC, Operator of Argonne National Laboratory (“Argonne”). Argonne, a U.S. Department of Energy Office of Science laboratory, is operated under Contract No. DE-AC02-06CH11357. The U.S. Government retains for itself, and others acting on its behalf, a paid-up nonexclusive, irrevocable worldwide license in said article to reproduce, prepare derivative works, distribute copies to the public, and perform publicly and display publicly, by or on behalf of the Government.References
- S. J. Harris and P. Lu, J. Phys. Chem. C, 2013, 117, 6481–6492 CrossRef CAS.
- A. Zhou, W. Wang, Q. Liu, Y. Wang, X. Yao, F. Qing, E. Li, T. Yang, L. Zhang and J. Li, J. Power Sources, 2017, 362, 131–139 CrossRef CAS.
- P. Ramadass, B. Haran, R. White and B. N. Popov, J. Power Sources, 2002, 111, 210–220 CrossRef CAS.
- G. Ning, B. Haran and B. N. Popov, J. Power Sources, 2003, 117, 160–169 CrossRef CAS.
- H. Zheng, J. Li, X. Song, G. Liu and V. S. Battaglia, Electrochim. Acta, 2012, 71, 258–265 CrossRef CAS.
- W. Fang, J. Kwon Ou and C. Y. Wang, Int. J. Energy Res., 2010, 34, 107–115 CrossRef CAS.
- Y. Ye, L. H. Saw, Y. Shi and A. A. O. Tay, Appl. Therm. Eng., 2015, 86, 281–291 CrossRef CAS.
- M. Keyser, A. Pesaran, Q. Li, S. Santhanagopalan, K. Smith, E. Wood, S. Ahmed, I. Bloom, E. Dufek, M. Shirk, A. Meintz, C. Kreuzer, C. Michelbacher, A. Burnham, T. Stephens, J. Francfort, B. Carlson, J. Zhang, R. Vijayagopal, K. Hardy, F. Dias, M. Mohanpurkar, D. Scoffield, A. N. Jansen, T. Tanim and A. Markel, J. Power Sources, 2017, 367, 228–236 CrossRef CAS.
- K. G. Gallagher, S. E. Trask, C. Bauer, T. Woehrle, S. F. Lux, M. Tschech, P. Lamp, B. J. Polzin, S. Ha, B. Long, Q. Wu, W. Lu, D. W. Dees and A. N. Jansen, J. Electrochem. Soc., 2016, 163, A138–A149 CrossRef CAS.
- M. Doyle and J. Newman, J. Appl. Electrochem., 1997, 27, 846–856 CrossRef CAS.
- M. F. Hasan, C.-F. Chen, C. E. Shaffer and P. P. Mukherjee, J. Electrochem. Soc., 2015, 162, A1382–A1395 CrossRef CAS.
- D. W. Dees, S. Kawauchi, D. P. Abraham and J. Prakash, J. Power Sources, 2009, 189, 263–268 CrossRef CAS.
- C. Ding-Wen, E. Martin, R. E. David, W. Vanessa and R. E. García, Modell. Simul. Mater. Sci. Eng., 2013, 21, 074009 CrossRef.
- E. E. Petersen, AIChE J., 2004, 4, 343–345 CrossRef.
- A. Nyman, T. G. Zavalis, R. Elger, M. Behm and G. Lindbergh, J. Electrochem. Soc., 2010, 157, A1236–A1246 CrossRef CAS.
- R. Zhao, J. Liu and J. Gu, Appl. Energy, 2015, 139, 220–229 CrossRef CAS.
- S. J. Harris, E. K. Rahani and V. B. Shenoy, J. Electrochem. Soc., 2012, 159, A1501–A1507 CrossRef CAS.
- Y. Qi and S. J. Harris, J. Electrochem. Soc., 2010, 157, A741–A747 CrossRef CAS.
- K. Zhao, M. Pharr, J. J. Vlassak and Z. Suo, J. Appl. Phys., 2010, 108, 073517 CrossRef.
- J. Christensen, J. Electrochem. Soc., 2010, 157, A366–A380 CrossRef CAS.
- P. Barai and P. P. Mukherjee, J. Electrochem. Soc., 2013, 160, A955–A967 CrossRef CAS.
- J. Billaud, F. Bouville, T. Magrini, C. Villevieille and A. R. Studart, Nat. Energy, 2016, 1, 16097 CrossRef CAS.
- M. Klett, J. A. Gilbert, K. Z. Pupek, S. E. Trask and D. P. Abraham, J. Electrochem. Soc., 2017, 164, A6095–A6102 CrossRef CAS.
- R. Yazami and P. Touzain, J. Power Sources, 1983, 9, 365–371 CrossRef CAS.
- C. Wang, X.-w. Zhang, A. J. Appleby, X. Chen and F. E. Little, J. Power Sources, 2002, 112, 98–104 CrossRef CAS.
- J. R. Dahn, Phys. Rev. B: Condens. Matter Mater. Phys., 1991, 44, 9170–9177 CrossRef CAS.
- A. Missyul, I. Bolshakov and R. Shpanchenko, Powder Diffr., 2017, 32, S56–S62 CrossRef CAS.
- N. A. Cañas, P. Einsiedel, O. T. Freitag, C. Heim, M. Steinhauer, D.-W. Park and K. A. Friedrich, Carbon, 2017, 116, 255–263 CrossRef.
- M. D. Levi, E. A. Levi and D. Aurbach, J. Electroanal. Chem., 1997, 421, 89–97 CrossRef CAS.
- S. J. Harris, A. Timmons, D. R. Baker and C. Monroe, Chem. Phys. Lett., 2010, 485, 265–274 CrossRef CAS.
- R. B. Smith, E. Khoo and M. Z. Bazant, J. Phys. Chem. C, 2017, 121, 12505–12523 CrossRef CAS.
- K. E. Thomas-Alyea, C. Jung, R. B. Smith and M. Z. Bazant, J. Electrochem. Soc., 2017, 164, E3063–E3072 CrossRef CAS.
- K. G. Gallagher, D. W. Dees, A. N. Jansen, D. P. Abraham and S.-H. Kang, J. Electrochem. Soc., 2012, 159, A2029–A2037 CrossRef CAS.
- P. Arora, M. Doyle and R. E. White, J. Electrochem. Soc., 1999, 146, 3543–3553 CrossRef CAS.
- M. M. Forouzan, B. A. Mazzeo and D. R. Wheeler, J. Electrochem. Soc., 2018, 165, A2127–A2144 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c8ee02373e |
| This journal is © The Royal Society of Chemistry 2019 |