Open Access Article
Open Access ArticleThermal energy grid storage using multi-junction photovoltaics†
Caleb
Amy
 a,
Hamid Reza
Seyf
a,
Hamid Reza
Seyf
 b,
Myles A.
Steiner
b,
Myles A.
Steiner
 c,
Daniel J.
Friedman
c,
Daniel J.
Friedman
 c and
Asegun
Henry
c and
Asegun
Henry
 *abde
*abde
aDepartment of Mechanical Engineering, Massachusetts Institute of Technology, Cambridge, MA 02139, USA. E-mail: ase@mit.edu
bGeorge W. Woodruff School of Mechanical Engineering, Georgia Institute of Technology, Atlanta, GA 30332, USA
cNational Renewable Energy Laboratory, Golden, CO 80401, USA
dSchool of Materials Science and Engineering, Georgia Institute of Technology, Atlanta, GA 30332, USA
eHeat Lab, Georgia Institute of Technology, Atlanta, GA 30332, USA
First published on 19th November 2018
Abstract
As the cost of renewable energy falls below fossil fuels, the key barrier to widespread sustainable electricity has become availability on demand. Energy storage can enable renewables to provide this availability, but there is no clear technology that can meet the low cost needed. Thus, we introduce a concept termed thermal energy grid storage, which in this embodiment uses multi-junction photovoltaics as a heat engine. We report promising initial experimental results that suggest it is feasible and could meet the low cost required to reach full penetration of renewables. The approach exploits an important tradeoff between the realization of an extremely low cost per unit energy stored, by storing heat instead of electricity directly, and paying the penalty of a lower round trip efficiency. To understand why this tradeoff is advantageous, we first introduce a general framework for evaluating storage technologies that treats round trip efficiency, as well as cost per unit energy and power, as variables.
Broader contextEven though the cost of solar and wind has dropped dramatically, the extent to which they can be used on the grid is limited by the need for some form of energy storage. As a result the storage problem has emerged as one of the most important technological hurdles to mitigating climate change. Current and future predictions for battery prices are too expensive to enable full penetration of renewables, which has necessitated a search for alternatives. Here, we introduce a somewhat non-intuitive approach termed thermal energy grid storage, which stores electricity as heat and then converts it back to electricity on demand. It is well known that the conversion of heat to electricity is thermodynamically limited and therefore results in a significant efficiency penalty. However, the storage of energy as heat instead of electricity can be 50–100× cheaper, and as a result the 15–40% efficiency penalty becomes a worthwhile tradeoff. In this article, we introduce a new embodiment that stores heat at extremely high temperatures (>1900 °C) in order to maximize the conversion efficiency and it also enables usage of a different type of heat engine (i.e., specially designed photovoltaics) instead of a turbine, to achieve even lower cost. |
Introduction
In the last decade the cost of electricity derived from renewables, i.e., solar photovoltaics (PV) and wind, has fallen dramatically,1,2 making renewables cheaper or competitive with fossil derived electricity in many locations. This is a remarkable achievement, but it is based purely on an assessment of the levelized cost per unit energy (LCOE) (i.e., the total cost divided by the lifetime electricity output, $ per kWh-e). Although this is an important quantity, it does not account for the fact that renewable electricity is not necessarily available when desired, since it is inherently tied to the weather. Thus, providing energy on demand remains a key necessity provided by existing fossil-based technologies. Consequently, as Denholm3,4 and others5–7 have shown, renewable penetration into the grid will be limited to <10–15% without grid level storage. Thus, “the storage problem” i.e., how to store/buffer energy at the grid scale cheaply, has emerged as one of the most important technological barriers to decarbonization of the grid and mitigating climate change.Currently the cheapest grid storage technology is pumped hydroelectric storage (PHS), which has a high roundtrip efficiency (RTE) ∼80–90%, as well as a low cost per unit energy (CPE) ∼$60 per kWh-e and cost per unit power (CPP) ∼$1 per W-e.8 Here, CPE indicates all the costs related to the storage of energy (e.g. water reservoir), while CPP represents the costs that scale with power output (e.g. water pump/turbine). The issue with PH, and also compressed air energy storage (CAES), however, is that they are geographically limited, and in the case of PH the prime locations have already been exploited.7,9–11 Electrochemical batteries, on the other hand, have promising new chemistries,7,12 but it is unclear if any will displace Li-ion batteries whose prices continue to drop from $300–400 per kWh-e down to a predicted asymptote ∼$150 per kWh-e.7 There is significant concern nonetheless, that even this lower asymptote for Li-ion is still not cheap enough to enable the eventual 100% penetration of renewables. In this respect, alternative solutions to the storage problem are needed, and it is likely that costs closer to $50 per kWh-e and below13,14 will be needed to eventually realize 100% penetration and full abatement of CO2 emissions from the stationary power sector. This low cost requirement arises from the fact that the storage cost, i.e., levelized cost of storage (LCOS), should be below the $0.06 per kWh current average electricity price15 and 10 or more hours16 of storage are needed to reliably and cost-effectively supply the grid.
Thermal energy grid storage
In thinking about lower cost storage, one class of technologies that has not received much attention is thermal energy storage (TES). This is because the final form of energy needed is electricity, necessitating the conversion of heat back to electricity, which tends to occur at low efficiency (∼35–40%) and high cost (∼$1 per W-e) for conventional turbine-based heat engines. However, even though the low efficiency is off-putting, when one considers the entire economic proposition, it can actually prove quite attractive if new embodiments that achieve somewhat higher RTEs or very low CPEs17 and/or CPPs are considered.Several embodiments18,19 are under development involving the conversion of electricity to heat, which is then stored and later converted back on demand, such that we have generally termed this class of technologies thermal energy grid storage (TEGS) herein. What these various incarnations share is the storage of heat, which is exploited to be as inexpensive as possible and can be 1–2 orders of magnitude cheaper than electrochemical batteries. The simplest embodiment that is arguably closest to commercialization, is to use molten salt as is currently done in concentrated solar power (CSP) plants,20 except that one would need to replace the solar heat input with joule heating. With this approach, one can today achieve a CPE < $100 per kWh-e,21 but the problem would be the low RTE (∼35–40%) and significant CPP (∼$1 per W-e). A more clever approach introduced by Laughlin18 involves the usage of a heat pump instead of joule heating, which can in theory almost double the RTE to ∼72%, perhaps at similar CPP, and makes TEGS a very attractive option. Other interesting and potentially attractive embodiments also exist, but to determine the best option, the value of RTE must be assessed with respect to CPE and CPP. It is therefore important to have a framework for quantitatively evaluating the tradeoffs between RTE, CPE and CPP, which ultimately dictates the economics and value to the grid. In what follows, we briefly introduce a simple framework for assessing such tradeoffs, followed by an introduction and discussion of our own incarnation of TEGS, which our analysis shows may be one of the few solutions to the storage problem that is inexpensive enough to eventually enable a fully renewable grid.
A general framework for comparison of storage technologies
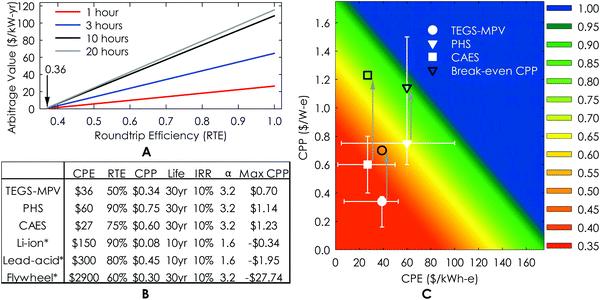
For a given storage technology, the total capital expenditure (CAPEX) can be thought of as a sum of two main components, CAPEX = CPE + CPP/t, where t is the time that the resource can be discharged at maximum power. In the simplest terms, CAPEX is compared to the two primary unsaturated sources of revenue, namely capacity payments ($ per kW) paid annually, which scale with the power output promised/supplied, and arbitrage ($ per kW) earned annually, which is where the RTE plays a critical role. Notably, we do not assume any intervention from governments or otherwise to incentivize sustainable energy despite the positive externalities so that these results stand on economic drivers alone. Sioshansi et al.4 have quantified how much value a storage resource would receive from arbitrage, as a function of the RTE and t, by using the Pennsylvania New Jersey Maryland (PJM) grid as an example. Their work showed that there would be a diminishing increase in value for large t resources on the 2007 PJM grid and they quantified how the value of storage changes with RTE, which we have used as an input in Fig. 1A. This plot shows that a storage technology with RTE ≤ 36% would not have generated any value from arbitrage on the 2007 PJM grid. Fundamentally, this is because the input energy must be purchased and therefore the ratio between on-peak and off-peak pricing sets a lower efficiency limit, ηmin, to earn arbitrage profit, as shown in eqn (1). That is, if a technology must buy three times as much energy as it sells, it must sell that energy for at least three times the purchase price to derive positive value from arbitrage. Because these devices cannot charge or discharge instantaneously, the closer their efficiency is to ηmin, the less frequently they can profitably engage in arbitrage.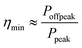 | (1) |
To assess the value of RTE relative to CPE and CPP, we can use the simple relation in eqn (2). Here, the CPP for zero net present value (NPV) is evaluated where total cost is equal to total revenue earned during the system's life, discounted with an internal rate of return (IRR) of 10%, denoted by r. This rate is based on typical interest rates of energy storage systems,22 although the effect of variability is explored in extended data Table S2, ESI.† Here, L is the lifetime in years, and Varb (RTE) is the arbitrage value in $ per kW per year, which is a function of RTE, as shown in Fig. 1A. The capacity payment (CP) is estimated based on the average net cost of new entry (Net CONE) of peaking gas turbines. Net CONE is the cost of a peaking gas turbine minus its anticipated energy and ancillary revenue, and therefore represents the capacity payment needed for it to break even.23,24 For the results in Fig. 1, CP is taken to be $95 per kW per year (see ESI†). Future revenue is discounted with the factor α as shown in eqn (3), which assumes revenue is accrued uniformly over time.
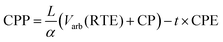 | (2) |
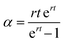 | (3) |
Using this simple relationship, the maximum CPP value allowed, i.e., to break-even, was estimated for various technologies, assuming the values given in the table of Fig. 1B, which are detailed in ESI,† where alternative IRRs are considered. Using this framework, any storage technology can be evaluated by knowing its RTE, CPE and CPP. By using its actual CPE (horizontal axis) and corresponding RTE (color) from Fig. 1C, one can read off the maximum allowable CPP for the technology on the vertical axis. If it turns out that a given technology's actual CPP is lower than the corresponding max CPP in Fig. 1C, then it would be profitable under the stated financial assumptions. The max CPP and actual CPP values for different technologies are then indicated in Fig. 1C, as well as the estimated values for the technology introduced herein, which could be profitable based on the conservative “high” results of the following Cost estimation section.
The results in Fig. 1C show that although it is initially non-intuitive to operate at low RTE, economically it makes sense to still consider low RTE technologies that have very low CPE and CPP values. For example, a storage technology with an RTE of 50%, CPE < $50 per kWh-e and CPP < $0.5 per W-e can be profitable like PH, while batteries would not be profitable under the stated assumptions in Fig. 1B. This is largely due to the limited cycle-life of batteries compared to the storage of energy via bulk mechanical/thermal methods. To consider the coordinates of batteries on Fig. 1C their costs must be multiplied by 3α10/α30 ≅ 1.5 (e.g. resulting in CPE = $230 per kWh-e and CPP = $0.12 per kW-e), where discount factor α accounts for the shorter loan/payback period of batteries as shown in eqn (3). Thus, based on this economic motivation, we introduce a new TEGS concept termed TEGS-MPV that employs ultra-high temperatures and multi-junction photovoltaics (MPV) to achieve a profitable combination of CPE, CPP, and RTE as described in the following sections. With this approach, a storage technology that is not geographically limited, yet has similar cost effectiveness to PH, could be realized and could become the most cost-effective embodiment of TEGS.
A new system concept
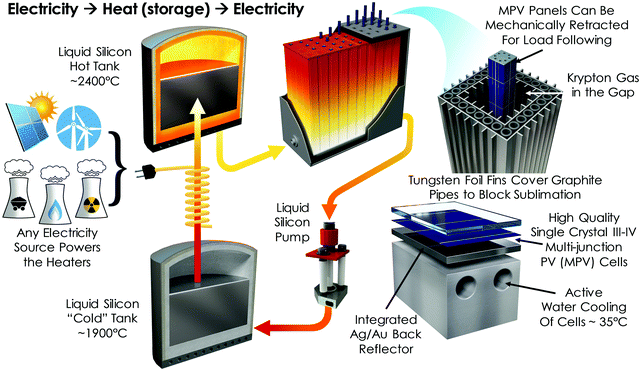
The new TEGS-MPV system concept is illustrated in Fig. 2 and consists of a low cost thermal storage fluid, nominally 553 metallurgical grade (98.5% pure) silicon, which costs ∼$1.6 per kg at high volume. The liquid Si is stored in a “cold” tank, nominally at 1900 °C, in the discharged state. To charge the system, the 1900 °C Si is pumped, using an all graphite seal-less sump pump, through a series of pipes that are externally irradiated by tungsten or graphite heaters which draw electricity from the grid. In this heater sub-system, the temperature of the Si is nominally raised to ∼2400 °C as it is pumped into the “hot” tank, where it is stored. The tanks are large, with diameters on the order of 10 m, which allows the surface area to volume ratio to be small enough that it is feasible for less than 1% of the energy stored to be lost each day, which is similar to CSP plants using molten salt TES.25 In this extreme temperature case, the insulation is more expensive as detailed in the Cost modeling section, but heat loss can still be minimal. Assuming such a storage resource were to be discharged once a day, this leads to an almost negligible penalty on the RTE. When electricity is desired, the 2400 °C Si is pumped out of the hot tank and through a MPV power cycle. The MPV power cycle is envisioned to consist of an array of graphite pipes that are covered in tungsten (W) foil. The W foil acts as a lower vapor pressure barrier between the graphite pipes and the MPV cells, which are mounted on an actively cooled block that keeps their temperature near the ambient temperature (i.e., ∼40 °C as described in the ESI†). The W foil therefore serves as a photon emitter, almost identical to an incandescent lightbulb,26 that emits light to the MPV cells which convert a fraction to electricity. As the Si passes through the power cycle piping network it cools as energy is extracted and converted to electricity, returning to the “cold” tank to await later recharging. Here, it is important to note that for this temperature range, 25–33% of the light being converted is in the visible spectrum, and materials with band gaps similar to or higher than Si are envisioned. Therefore, these cells are arguably just PV cells, as opposed to thermophotovoltaic (TPV) cells. For this reason, we’ve elected to use the term multi-junction PV (MPV) instead of TPV, to highlight the fact that the envisioned cells bear resemblance to and use many of the advances that have been made for MPV, in the context of concentrated PV (CPV).It should be appreciated that the temperature regime chosen here represents a rather practical limit for industrially manufactured refractories, namely graphite and W. Although both materials melt/decompose at even higher temperatures, at 2400 °C, a substantial vapor pressure develops, which can lead to emitter material deposition onto the MPV cells—degrading their optical performance. Nonetheless, the most extreme temperatures possible are employed to achieve the highest possible RTE.
To the best of our knowledge, the efficiency of PV that converts light from a high temperature heat source, most commonly referred to as TPV, has not exceeded ∼29%, which was achieved using single junction Si cells and a 2000 °C emitter.27 However, more recent work using an InGaAs cell achieved almost the same efficiency (28.2%),28 but only required an emitter temperature of 1256 °C. This is because the single most important loss in such cells is the voltage, which is usually ∼0.3–0.4 V for III–V materials.29 However, this loss is worse for a material such as silicon, because of its indirect band gap, as well as Auger recombination at the high photon fluxes in this application. Given that this voltage loss tends to be almost constant when practical devices are made (neglecting a small bandgap dependence), it suggests that the most important pathway to reaching higher efficiencies (>40%) with a terrestrial light source is to utilize higher band gap materials than have been pursued previously. In this way, the rather fixed voltage loss becomes a smaller fraction of the band gap voltage and the overall device efficiency improves. However, higher band gaps require higher temperatures so that a substantial portion of the emitted spectrum is above the band gap and can be converted. This is important, because achieving a low CPP requires that the cells be operated at high power density, so that their cost, which scales with the total cell area, can remain low. Furthermore, although photons below the band gap can be returned to the emitter by mounting the cells on a back surface reflector (BSR), this recycling is imperfect, so the proportion of photons above the band gap must be substantial to outweigh the parasitic below band gap absorption. It is for these reasons that the most extreme temperatures are considered in this TEGS embodiment.
Although it is appreciated that such a concept may seem unrealistic, our recent work30 and the initial experiments above 2000 °C described herein have laid the foundation for the high temperature infrastructure in Fig. 2, by addressing some of the most critical risks. Key to this approach is the use of a flowing liquid as a heat storage and heat transfer medium. This is because, unlike the large thermal resistance present conducting through a large solid, transferring heat via convection minimizes thermal resistance. Usage of a solid or formation of a solid (i.e., via phase change) can become problematic because a sensible heat discharge from a solid will inherently cause a conductive resistance to build up, which will lower the power output and efficiency over time. Besides direct cost implications, this issue is undesirable for grid operation because capacity payments are based on a rated power that can be supplied/promised (see ESI†). However, since a liquid/fluid can be pumped, it enables straightforward designs that can achieve a steady state power output and RTE.
For the MPV power cycle, some of the important system level considerations have been addressed in previous work by Seyf and Henry,31 such as the need for the power cycle to be large (MW scale, with length scales ∼10 m) in order to overcome the losses associated with heat leakage to the environment by minimizing the ratio of surface area to volume. Their prior work also identified the BSR reflectivity, or more specifically the net amount of below band gap cell absorption, as the most critical parameter. However, while their initial predictions for the cell efficiency are theoretically justified, they do not fully capture the realistic voltage losses that tend to occur in real cells. Thus, a more realistic consideration of practical cell losses would drive the system towards operation at much higher temperatures than their initial work indicated,31 as will be discussed in more detail in the next section. Nonetheless, the MPV cells considered herein are still envisioned to incorporate a BSR, but for this temperature regime, higher band gap materials as well as multiple junctions are expected to be optimal. Furthermore, by using cells grown on GaAs as opposed to InP substrates and by using hydride vapor phase epitaxy (HVPE) instead of metal–organic chemical vapor deposition (MOCVD), the cell costs could be much lower than estimated.
One critical question that arises with the TEGS-MPV approach, however, is why MPV is chosen as the heat engine instead of a turbine, which could likely be more efficient at lower temperatures. There are three reasons for this: (1) turbines that take an external heat input and operate at high efficiencies (>50%) do not currently exist. Although it may be possible to develop such a system, a large barrier to commercial deployment exists, as it would require a large OEM to undertake an expensive (>$100 million) development effort for a high-risk application. On the other hand, existing III–V cell manufacturers are positioned to facilitate the commercialization and deployment of the described MPV power cycle with much less investment. (2) The cost of our proposed MPV system can be much lower than that of a turbine. (3) The speed with which turbine-based heat engines can ramp from zero to full power is on the order of tens of minutes to an hour. However, with this TEGS-MPV approach, as is illustrated in Fig. 2, the MPV modules can be actuated in and out of the light on the order of seconds, which could provide much greater value to the grid via load following, thereby increasing revenue.
Modeling and experimental results on feasibility
One inescapable component needed to realize the TEGS-MPV system is the storage medium tank. If there is no conceivable way to make the tanks, then there is no path towards realizing the system. Using a liquid storage medium requires that the tank be impermeable, and the options for materials at these temperatures are severely limited. One of the only cost effective options is graphite, but it would be infeasible to fabricate the entire ∼10 m diameter tank from a single monolithic piece. This necessitates that the tank be formed from sections, with sealed interfaces that do not leak.A first and highly encouraging result that suggests this problem can be easily and cost effectively solved is shown in Fig. 3. In this experiment, a dense (1.85 g cc−1) graphite (KYM-20) miniature “tank” filled with 553 grade Si was heated above 2000 °C for 60 minutes. The tank was made from two sections and sealed with a thin grafoil face seal that was compressed by carbon fiber composite (CFC) threaded rods and nuts. The tank was insulated with graphite felt and aluminum silicate insulation inside a quartz tube, under high purity argon gas (<1 × 10−6 atm O2). The tank was heated by induction and its temperature was measured using a C-type thermocouple. It is well known that graphite and Si(l) react to form SiC,32 and a protective SiC scale that prevents further reaction can form, if the graphite has the right microstructure. In this experiment, as shown in Fig. 3E, Si penetrated the graphite tank approximately 400 μm, and created a dense 20 μm thick SiC layer at the interface, preventing further penetration. Initial experiments showed that if a thicker grafoil seal is used, the expansive reaction could break apart the entire “tank”. Thus, this preliminary result is rather non-trivial, as it offers initial proof and confidence that Si can be contained at these temperatures in a multi-section tank.
Another feasibility issue concerns the need to pump liquid Si at temperatures as high as 2400 °C. On this issue, recent experiments by Amy et al.30 have shown that it is feasible to use brittle ceramics as mechanical pumps, as they pumped liquid tin at temperatures up to 1400 °C. Here, the temperature is ∼1000 °C higher, which would be a major concern for infrastructure made from solid metal components. However, for ceramics and refractories, such as graphite, this is much less of a concern, since the materials tend to be covalently bonded and therefore tend to exhibit weak dependence of their mechanical properties on temperature. In fact, the strength of graphite actually increases with temperature, up to 2600 °C.33 For these reasons, although pumping at 2400 °C has not been done before, the testing above 2000 °C and pumping30 at 1400 °C renders the notion now feasible, as there are no obvious issues that should prevent operation at the higher temperatures.
Another potential issue with the TEGS-MPV system is that the heater efficiency is a non-trivial matter, since it would require power conditioning electronics that could have substantial losses that ultimately detract from the RTE. This issue is discussed in more detail in ESI,† but the conclusion is that existing power electronics can supply the necessary input at low cost with less than 1% parasitic loss.34 This loss is small and almost negligible, which shifts our focus to the primary loss in the system, which occurs in the MPV power block.
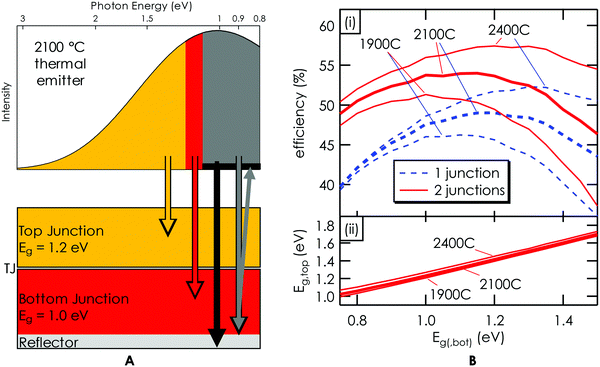
The PV cell which converts photons radiated from the thermal emitter to electricity plays a crucial role in the system efficiency and almost entirely dictates the RTE. The energy in a photon (eVphoton) incident on the cell can suffer several types of losses, which are very strongly dependent on the spectrum of light, and on the design of the cell itself. The most significant is the voltage loss, where an incident photon is absorbed by the cell and converted into electrical current, at a cell open-circuit voltage VOC < Vphoton. This energy loss Eloss = eVphoton − eVOC can be partitioned into two individual losses related to the junction bandgap (Eg): Eloss = (eVphoton − Eg) + (Eg − eVOC). The first loss, referred to as thermalization loss, arises because the thermally-radiated spectrum contains a wide range of photon energies, and the energy above the bandgap is lost. To mitigate this loss, we envision using a two-junction photovoltaic device, with the two bandgaps chosen to optimally convert a band of the spectrum. This MPV approach, illustrated schematically in Fig. 4A, is well established for solar CPV, and is the only effective approach that has been demonstrated to mitigate thermalization losses.
The second aspect of the voltage loss, which is typically ∼0.3–0.4 eV for high-quality (Ga,In)(As,P)-based III–V devices at conventional operating conditions of ∼25 °C and one-sun photon flux, is also unavoidable. This loss is largely due the large solid angle of photon emission,35 and has been demonstrated to be representative of the best III–V cells across a wide range of bandgaps,29 and including lattice-mismatched alloys.36 An additional voltage penalty occurs, due to non-radiative recombination, and this penalty is greater for cells made from silicon than from III–V materials, due to silicon's indirect bandgap. It should be noted nonetheless that silicon was used in the experiments that led to the highest reported TPV efficiency we’re aware of (∼29%27), and therefore using III–V materials is an important step toward mitigating this penalty and reaching higher efficiencies. Most importantly, however, is the fact that the Eg − eVOC penalty is proportionally smaller for higher bandgap materials than for lower bandgap materials. The very high emitter temperatures used in the TEGS-MPV concept generate correspondingly high-energy photons for which relatively high-bandgap PV cells are suitable, thus mitigating the Eg − eVOC penalty. Similarly, the high temperatures proposed also result in a very high flux of photons, which increases eVOC, further suppressing this penalty.37
A type of absorption loss also occurs at the system level and results from the free carrier absorption of sub-bandgap photons, either at the BSR or in the semiconductor itself. The BSR should be as reflective as possible, so unusable sub-bandgap photons are reflected back to the thermal emitter, which is a critically enabling feature for this system concept.31 A reflectivity of 98%, as illustrated in gray in Fig. 4A, is necessary to realize the high performance predicted in Fig. 4B, but has been previously demonstrated.38 The additional losses associated with series resistance and shadowing are discussed in ESI.†
The modeled efficiencies of 1-junction and series-connected 2-junction cells as a function of junction bandgap, for a range of thermal emitter temperatures, are shown in Fig. 4B. The cell modeling was performed using the very well experimentally validated model of Geisz et al.39 including a conservative, but realistic, Eg/e − VOC = 0.4 V penalty. The incident spectrum was computed using W's emissivity40 and the diffuse gray band approximation was used to account for the MPV cell's high absorptivity above the band gap and low absorptivity below the band gap. Consistent with the cell measurements, we assumed 2% of the light below the cell's band gap is absorbed, which is illustrated in the 2100 °C spectrum as shown in Fig. 4A. The integrated power from this 2100 °C spectrum is 689 kW m−2. The fraction of this incident power absorbed by the cell, including sub-bandgap absorption due to imperfect 98% sub-bandgap reflectivity, depends on the cell's bottom-junction bandgap Eg,bot, and is 150 kW m−2 for Eg,bot = 1.4 eV and 367 kW m−2 for Eg,bot = 1.0 eV. Every above-bandgap photon which is absorbed is assumed to be collected as current, an idealization that can later be replaced with actual measured cell performance. Nonetheless, this assumption is close to the measured performance of many previous cells. The cell's current–voltage characteristics and maximum-power output are then computed, with junction voltages adding for multi-junction devices. The ratio of this power output to the integrated net input power, including a static 4.6 kW m−2 convection loss (see ESI†) through the inert gas between the emitter and cell, yields the net cell efficiency. Practical cell efficiencies are typically ∼85–90% of the efficiencies modeled at this level of idealization.39Fig. 4B shows that practical efficiencies of well over 40% are achievable for 1-junction cells, and ≥50% is possible with 2-junction cells. For the 2100 °C emitter, the optimal junction bandgaps are roughly 1.0–1.2 eV for the 1-junction cell, and {1.2, 1.0} eV to {1.4, 1.2} eV for the {top, bottom} junctions of a 2-junction cell.
As described in further detail in the ESI,† a dual junction PV device could be fabricated using the inverted metamorphic multijunction (IMM) cell architecture. The cell is grown on a GaAs substrate, but first the lattice constant is slowly increased by means of a compositionally step-graded buffer so as to enable strain-free deposition of (Al)GaInAs films with bandgaps of 1.0–1.2 eV. Years of development of lattice-mismatched epitaxy, and the IMM cell specifically, have lead to defect densities <106 cm−2 and Woc < 0.4 V,36 despite the mismatch with the substrate. The junctions in the tandem are separated by a tunnel diode.
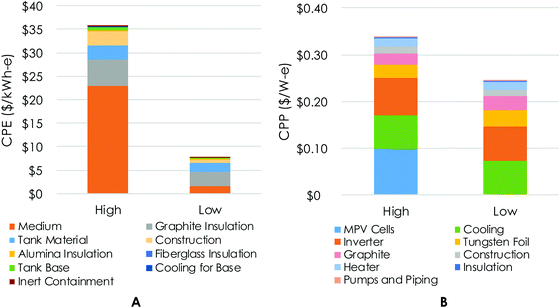
Cost estimation
The major advantages of TEGS-MPV over other grid level energy storage technologies are its expected low cost and geographically flexibility. Thus, it is important to demonstrate the basis of the cost estimates provided, as summarized in Fig. 5. As a nominal design point, we considered a 100 MW-e output system with 10 hours of storage. The CPE includes the storage medium, tank, insulation, auxiliary components, and construction, using a similar procedure to Glatzmaier17 and Wilk et al.41 The CPP includes the heater, MPV cells, inverter, emitter, insulation, construction, and cooling system. Following a summary of the basis of these costs, the ESI† describes the methodology used to generate these estimates and associated sources.In the base case, 553 grade (98.5% pure) Si is used at a market price of $1.60 per kg. The tank wall is made from isostatic molded graphite (e.g. KYM-20) of density 1.8 g cm−3, at a cost of $7 per kg based on multiple quotes from large suppliers. The insulation for all components consists of graphite felt ($7000 per m3), surrounded by an aluminum silicate blanket, surrounded by a fiberglass blanket. The cost of the graphite felt dominates, so its use is constrained to the region above the 1350 °C temperature limit of aluminum silicate. Construction costs are based on the cost of molten-salt CSP plants,41 plus the labor cost of assembling additional components as detailed in ESI.† The cost of the heater includes graphite heating elements, graphite pipes and headers, insulation, and inert containment. The MPV power block contains similar elements, although the cost is dominated by the $0.08 per W-e inverter cost,1 $0.10 per W-e MPV cell cost, and $0.07 per W-e cooling cost. This cell cost is based on an assumed power density of 100 kW m−2 and a cell cost31 of $10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 per m2. In reality, this cost may be much lower if the aforementioned cell manufacturing developments are realized (i.e., GaAs substrates and HVPE). Similarly, an alternative embodiment of interest is Fe partially or fully replacing Si as the storage medium. In this scenario, the cost of the medium becomes extremely low if one uses scrap steel, and the other tank costs, especially insulation and construction, dominate. In this less conservative lower cost case, we also assume a lower grade extruded ($2 per kg) graphite is used for the tank and a higher heat loss of 2% per day, instead of 1%. The effect of these changes is shown in Fig. 5.
000 per m2. In reality, this cost may be much lower if the aforementioned cell manufacturing developments are realized (i.e., GaAs substrates and HVPE). Similarly, an alternative embodiment of interest is Fe partially or fully replacing Si as the storage medium. In this scenario, the cost of the medium becomes extremely low if one uses scrap steel, and the other tank costs, especially insulation and construction, dominate. In this less conservative lower cost case, we also assume a lower grade extruded ($2 per kg) graphite is used for the tank and a higher heat loss of 2% per day, instead of 1%. The effect of these changes is shown in Fig. 5.
Discussion
Based on the analysis presented herein, the TEGS-MPV concept offers an attractive value proposition as a grid storage technology. In this study, a simplified framework was presented that enables one to compare and assess the economic viability of new grid storage solutions. Of particular importance is the tradeoff between RTE, CPE and CPP. The analysis showed that some TEGS embodiments have the potential to significantly exceed the expected 36% RTE lower bound,4 while also achieving extremely low CPE and CPP. A new TEGS embodiment was then presented based on ultra-high temperature storage media, in liquid form, and that uses MPV as the converter. This new approach has several noteworthy benefits including the ability to reach ≥50% RTE with a CPP < $0.5 per W-e, and the potential to offer load following capabilities to grid operators. These benefits strongly suggest that, if realized, the TEGS-MPV approach could be one of the few grid storage approaches that are inexpensive enough to enable the eventual 100% penetration of renewables onto the grid. However, there are a number of practical challenges that must be overcome to realize the TEGS-MPV approach. Most notably, a prototype system is needed to confirm that the storage medium can be reliably pumped without leaks and that the MPV cells can be reliably fabricated and perform as modeled under realistic conditions. Towards this end, two first experiments were presented that strongly suggest some of the most risky aspects of the TEGS-MPV system can be resolved. First, experiments above 2000 °C showed that a tank for Si with dimensions on the order of 10 m could conceivably be made out of smaller (i.e., order 1 m) sections that are sealed and bolted together. These experiments showed that grafoil gaskets can be used to successfully seal against liquid silicon without leakage. Additionally, the most important property of the MPV cells is their absorptivity for below band gap radiation. Calculations herein assumed this parasitic absorption to be 2% and measurements of the reflectivity of cells that were backed by a gold or silver layer have confirmed that this is indeed possible.38 For these reasons, it seems feasible, although challenging, to realize the cost and performance described herein (i.e., CPE < $40 per kWh-e, CPP < $0.4 per W-e, and RTE ≥ 50%) using TEGS-MPV.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was authored in part by the National Renewable Energy Laboratory, operated by Alliance for Sustainable Energy, LLC, for the U.S. Department of Energy (DOE) under Contract No. DE-AC36-08GO28308. Funding provided by the U.S. Department of Energy Office of Energy Efficiency and Renewable Energy Solar Energy Technologies Office. The views expressed herein do not necessarily represent the views of the DOE or the U.S. Government. The U.S. Government retains and the publisher, by accepting the article for publication, acknowledges that the U.S. Government retains a nonexclusive, paid-up, irrevocable, worldwide license to publish or reproduce the published form of this work, or allow others to do so, for U.S. Government purposes.References
- R. Fu, D. Feldman, R. Margolis, M. Woodhouse and K. Ardani, U.S. Solar Photovoltaic System Cost Benchmark: Q1 2017, Report No. NREL/TP-6A20-68925 (National Renewable Energy laboratory, 2017).
- T. Stehly, D. Heimiller and G. Scott, 2016 Cost of Wind Energy Review, Report No. NREL/TP-6A20-70363, (National Renewable Energy Laboratory, 2017).
- P. Denholm, J. Jorgenson, M. Hummon, T. Jenkin and D. Palchak, The Value of Energy Storage for Grid Applications, Report No. NREL/TP-6A20-58465, 45 (National Renewable Energy Laboratory, 2013).
- R. Sioshansi, P. Denholm, T. Jenkin and J. Weiss, Estimating the value of electricity storage in PJM: Arbitrage and some welfare effects, Energ. Econ., 2009, 31, 269–277, DOI:10.1016/j.eneco.2008.10.005.
- K. Bradbury, L. Pratson and D. Patiño-Echeverri, Economic viability of energy storage systems based on price arbitrage potential in real-time U.S. electricity markets, Appl. Energy, 2014, 114, 512–519, DOI:10.1016/j.apenergy.2013.10.010.
- A. H. Slocum, et al., Ocean Renewable Energy Storage (ORES) System: Analysis of an Undersea Energy Storage Concept, Proc. IEEE, 2013, 101, 906–924, DOI:10.1109/JPROC.2013.2242411.
- O. Schmidt, A. Hawkes, A. Gambhir and I. Staffell, The future cost of electrical energy storage based on experience rates, Nat. Energy, 2017, 6, 17110, DOI:10.1038/nenergy.2017.110.
- S. Schoenung, Energy Storage Systems Cost Update Report No. SAND2011-2730 (Sandia National Laboratories 2011).
- R. Uría-Martínez, P. W. O’Connor and M. M. Johnson, 2014 Hydropower Market Report, (DOE EERE Wind and Water Power Technologies Office, 2015).
- R. Bowers, Energy storage and renewables beyond wind, hydro, solar make up 4% of U.S. power capacity, (U.S. Energy Information Administration, 2017).
- Challenges and Opportunities For New Pumped Storage Development. (NHA's Pumped Storage Development Council, 2012).
- M. Park, J. Ryu, W. Wang and J. Cho, Material design and engineering of next-generation flow-battery technologies, Nat. Rev. Mater., 2016, 2, 16080, DOI:10.1038/natrevmats.2016.80.
- Y.-M. Chiang, L. Su, M. S. Pan and Z. Li, Lowering the Bar on Battery Cost, Joule, 2017, 1, 212–219, DOI:10.1016/j.joule.2017.09.015.
- Z. Li, et al., Air-Breathing Aqueous Sulfur Flow Battery for Ultralow-Cost Long-Duration Electrical Storage, Joule, 2017, 1, 306–327, DOI:10.1016/j.joule.2017.08.007.
- S. M. Schoenung and W. V. Hassenzahl, Long- vs. Short-Term Energy Storage Technologies Analysis, Report No. SAND2003-2783 (Sandia National Laboratories Albuquerque, New Mexico, 2003).
- C. Budischak, et al., Cost-minimized combinations of wind power, solar power and electrochemical storage, powering the grid up to 99.9% of the time, J. Power Sources, 2013, 225, 60–74, DOI:10.1016/j.jpowsour.2012.09.054.
- G. Glatzmaier, Developing a Cost Model and Methodology to Estimate Capital Costs for Thermal Energy Storage. (National Renewable Energy Laboratory, 2011).
- R. B. Laughlin, Pumped thermal grid storage with heat exchange, J. Renewable Sustainable Energy, 2017, 9, 044103, DOI:10.1063/1.4994054.
- A. Dietrich, Assessment of Pumped Heat Electricity Storage Systems through Exergoeconomic Analyses, University of Darmstadt, 2017 Search PubMed.
- U. Pelay, L. Luo, Y. Fan, D. Stitou and M. Rood, Thermal energy storage systems for concentrated solar power plants, Renewable Sustainable Energy Rev., 2017, 79, 82–100, DOI:10.1016/j.rser.2017.03.139.
- C. S. Turchi, J. Vidal and M. Bauer, Molten salt power towers operating at 600–650 °C: Salt selection and cost benefits, Sol. Energy, 2018, 164, 38–46, DOI:10.1016/j.solener.2018.01.063.
- Lazard's Levelized Cost of Storage Analysis – Version 3.0. (Lazard and Enovation Partners, 2017).
- 2018/2019 RPM Base Residual Auction Planning Period Parameters, 14 (PJM, 2015).
- T. Jenkin, P. Beiter and R. Margolis, Capacity Payments in Restructured Markets under Low and High Penetration Levels of Renewable Energy, Report No. NREL/TP-6A20-65491, (National Renewable Energy Laboratory, 2016).
- R. Sioshansi and P. Denholm, The Value of Concentrating Solar Power and Thermal Energy Storage, IEEE Trans. Sustain. Energy, 2010, 1, 173–183, DOI:10.1109/TSTE.2010.2052078.
- A. Leroy, et al., Combined selective emitter and filter for high performance incandescent lighting, Appl. Phys. Lett., 2017, 111, 094103, DOI:10.1063/1.4989522.
- R. M. Swanson, 1978 International Electron Devices Meeting, 70–73.
- Z. Omair, et al., Conference on Lasers and Electro-Optics. AW3O.7, Optical Society of America.
- R. R. King, et al., 40% efficient metamorphic GaInP/GaInAs/Ge multijunction solar cells, Appl. Phys. Lett., 2007, 90, 183516, DOI:10.1063/1.2734507.
- C. Amy, et al., Pumping liquid metal at high temperatures up to 1,673 kelvin, Nature, 2017, 550, 199–203, DOI:10.1038/nature24054.
- H. R. Seyf and A. Henry, Thermophotovoltaics: a potential pathway to high efficiency concentrated solar power, Energy Environ. Sci., 2016, 9, 2654–2665, 10.1039/C6EE01372D.
- S. Kawanishi, T. Yoshikawa and T. Tanaka, Equilibrium Phase Relationship between SiC and a Liquid Phase in the Fe–Si–C System at 1523–1723 K, Mater. Trans., 2009, 50, 806–813, DOI:10.2320/matertrans.MRA2008404.
- C. Malmstrom, R. Keen and L. Green, Some Mechanical Properties of Graphite at Elevated Temperatures, J. Appl. Phys., 1951, 22, 593–600, DOI:10.1063/1.1700013.
- T. Nagel, S. Kosik and D. Fuhlbohm, How SCR Controllers Help Boost Energy Efficiency, Report No. ENG-SCRControllers-EnergyEfficiency-270-01 11.15, (Advanced Energy Industries, Inc., 2015).
- E. D. Kosten, J. H. Atwater, J. Parsons, A. Polman and H. A. Atwater, Highly efficient GaAs solar cells by limiting light emission angle, Light: Sci. & Appl., 2013, 2, e45, DOI:10.1038/lsa.2013.1.
- R. M. France, F. Dimroth, T. J. Grassman and R. R. King, Metamorphic epitaxy for multijunction solar cells, MRS Bull., 2016, 41, 202–209, DOI:10.1557/mrs.2016.25.
- Concentrator Photovoltaics, ed. Antonio L. Luque and Andreev Viacheslav, Springer, Berlin Heidelberg, 2007, pp. 175–197 Search PubMed.
- T. Xiao, et al., Conference on Lasers and Electro-Optics. ATu1K.2, Optical Society of America.
- J. F. Geisz, et al., Generalized Optoelectronic Model of Series-Connected Multijunction Solar Cells, IEEE J. Photovolt., 2015, 5, 1827–1839, DOI:10.1109/JPHOTOV.2015.2478072.
- W. W. Coblentz, The Reflecting Power of Various Metals, Bulletin of the Bureau of Standards, Washington, 1910 Search PubMed.
- G. Wilk, A. DeAngelis and A. Henry, Estimating the cost of high temperature liquid metal based concentrated solar power, J. Renewable Sustainable Energy, 2018, 10, 023705, DOI:10.1063/1.5014054.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c8ee02341g |
| This journal is © The Royal Society of Chemistry 2019 |