The good, the neutral, and the positive: buffer identity impacts CO2 reduction activity by nickel(ii) cyclam†
Abstract
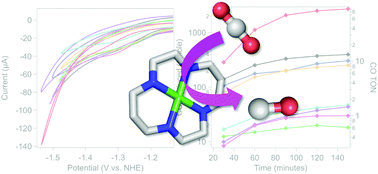
Development of new synthetic catalysts for CO2 reduction has been a central focus of chemical research efforts towards mitigating rising global carbon dioxide levels. In parallel with generating new molecular systems, characterization and benchmarking of these compounds across well-defined catalytic conditions are essential. Nickel(II) cyclam is known to be an active catalyst for CO2 reduction to CO. The degree of selectivity and activity has been found to differ widely across electrodes used and upon modification of the ligand environment, though without a molecular-level understanding of this variation. Moreover, while proton transfer is key for catalytic activity, the effects of varying the nature of the proton donor remain unclear. In this work, a systematic investigation of the electrochemical and light-driven catalytic behaviour of nickel(II) cyclam under different aqueous reaction conditions has been performed. The activity and selectivity are seen to vary widely depending on the nature of the buffering agent, even at a constant pH, highlighting the importance of proton transfer for catalysis. Buffer binding to the nickel center is negatively correlated with selectivity, and cationic buffers show high levels of selectivity and activity. These results are discussed in the context of molecular design principles for developing increasingly efficient and selective catalysts. Moreover, identifying these key contributors towards activity has implications for understanding the role of the conserved secondary coordination environments in naturally occurring CO2-reducing enzymes, including carbon monoxide dehydrogenase and formate dehydrogenase.


 Please wait while we load your content...
Please wait while we load your content...