Open Access Article
Open Access ArticleHigh relaxation barrier in neodymium furoate-based field-induced SMMs†
E.
Bartolomé
 *a,
A.
Arauzo
*a,
A.
Arauzo
 bc,
J.
Luzón
bc,
J.
Luzón
 bd,
S.
Melnic
e,
S.
Shova
bd,
S.
Melnic
e,
S.
Shova
 f,
D.
Prodius
f,
D.
Prodius
 g,
I. C.
Nlebedim
g,
I. C.
Nlebedim
 g,
F.
Bartolomé
g,
F.
Bartolomé
 b and
J.
Bartolomé
b and
J.
Bartolomé
 b
b
aEscola Universitària Salesiana de Sarrià (EUSS), Passeig Sant Joan Bosco 74, 08017-Barcelona, Spain. E-mail: ebartolome@euss.es
bInstituto de Ciencia de Materiales de Aragón, CSIC-Universidad de Zaragoza, Pedro Cerbuna 12, 50009 Zaragoza, Spain
cServicio de Medidas Físicas. Universidad de Zaragoza, Pedro Cerbuna 12, 50009 Zaragoza, Spain
dCentro Universitario de la Defensa. Academia General Militar, Zaragoza, Spain
eInstitute of Chemistry, Academy of Sciences of Moldova, Academiei 3, MD-2028, Chisinau, Republic of Moldova
f“Petru Poni” Institute of Macromolecular Chemistry, Alea Gr. Ghica Voda 41A, 700487 Iasi, Romania
gAmes Laboratory, US Department of Energy and Critical Materials Institute, Ames, IA-50011-3020, USA
First published on 24th June 2019
Abstract
Two new neodymium molecular magnets of formula {[Nd(α-fur)3(H2O)2]·DMF}n (1) and {[Nd0.065La0.935(α-fur)3(H2O)2]}n (2), α-fur = C4H3OCOO, have been synthesized. In (1) the furoate ligands, in bidentate bridging mode, consolidate zig-zag chains running along the a-direction. Compound (2) is a magnetically diluted complex of a polymeric chain along the b-axis. Heat capacity, dc magnetization and ac susceptibility measurements have been performed from 1.8 K up to room temperature. Ab initio calculations yielded the gyromagnetic factors gx* = 0.52, gy* = 1.03, gz* = 4.41 for (1) and gx* = 1.35, gy* = 1.98, gz* = 3.88 for (2), and predicted energy gaps of Δ/kB = 125.5 K (1) and Δ/kB = 58.8 K (2). Heat capacity and magnetometry measurements agree with these predictions, and confirm the non-negligible transversal anisotropy of the Kramers doublet ground state. A weak intrachain antiferromagnetic interaction J′/kB = −3.15 × 10−3 K was found for (1). No slow relaxation is observed at H = 0, attributed to the sizable transverse anisotropy component, and/or dipolar or exchange interactions enhancing the quantum tunnelling probability. Under an external applied field as small as 80 Oe, two slow relaxation processes appear: above 3 K the first relaxation mechanism is associated to a combination of Orbach process, with a sizeable activation energy U/kB = 121 K at 1.2 kOe for (1), Raman and direct processes; the second, slowest relaxation mechanism is associated to a direct process, affected by phonon-bottleneck effect. For complex (2) a smaller U/kB = 61 K at 1.2 kOe is found, together with larger g*-transversal terms, and the low-frequency process is quenched. The reported complexes represent rare polymeric Nd single-ion magnets exhibiting high activation energies among the scarce Nd(III) family.
1. Introduction
Single-ion magnets (SIMs), single-molecule magnets (SMMs) and single-chain magnets (SCMs) are being intensively investigated owing to their interesting physics (including slow relaxation of the magnetization, magnetic hysteresis and quantum tunneling), and potential application in high-density data storage or quantum information.Some heavy lanthanide(III) ions are especially well suited for the design of molecular magnets because of their large magnetic moment (Gd, Tb, Dy, Ho, Er, Tm and Yb), on one hand, and the unquenched orbital moment, which leads to a strong magnetic anisotropy (Tb, Dy, Ho), on the other, when the ions are placed in an anisotropic ligand field.1 The light rare earth are less likely to present SMM behavior since their magnetic moment is lower, although anisotropy may also be present in Pr, Nd and Sm. The quantum number J is L + S for heavy-Ln(III) ions and L–S for light-Ln(III) ions. Therefore, research of Ln-SMMs has hitherto focused on complexes based on heavy lanthanide ions, mainly Dy3+ (L = 5, S = 5/2, J = 15/2), Tb3+ (L = 3, S = 3, J = 6) and Er3+ (L = 6, S = 3/2, J = 15/2).
Work on light Ln-SMMs is still rare.2 However, they are receiving growing attention given that earlier lanthanide ions are substantially more abundant, cheaper and thus more interesting for the sustainable development of applications3 (e.g. they are used in the production of most commercial permanent magnets like Nd2Fe14B and SmCo5).
In particular, Nd(III) Kramers ion, with an oblate electron density and a 4I9/2 (L = 6, S = 3/2, J = 9/2) free ion ground state, may introduce a significant anisotropy, if the crystal field is designed such that the ground ±MJ doublet is stabilized well below the first-excited one.4,5 Neodymium single molecule magnets are however relatively rare (see review in Table 1). The first Nd-SIM reported in 2012, [NdTp3], exhibited field-induced relaxation with a small thermal activation energy of U/kB = 4.1 K (100 Oe).6 Eight field-induced Nd-SIMs3,7–12 and three dimeric {Nd2} complexes13–15 with higher barrier energies have been reported ever since, with POM derivative [Na9Nd(W5O18)2]9− holding at present the record U/kB = 73.9 K (1 kOe).16
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−U/kBT)
exp(−U/kBT)
| Complex | g x * | g y * | g z * | H (kOe) | U/kB (K) | τ 0 (s) | C (s−1 K−n) | n | τ QT −1 (s−1) | A (s−1 K−1) | Ref. | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0-D | ||||||||||||
| Na9[Nd(W5O18)2] | 1 | 73.9 | 3.55 × 10−10 | 16 | ||||||||
| Cp*2Nd(BPh4) | 1 | 41.7 | 1.4(4) × 10−6 | 0.0286 | 5.2 | 1.1 | 3 | |||||
| [L2Nd(H2O5]-[I]3·L2(H2O) | 0 | 16.08 | 2.64 × 10−4 | 7 | ||||||||
| 24.69 | 5.03 × 10−6 | |||||||||||
| Ab initio | 0.02 | 0.02 | 6.3 | 302 | ||||||||
| 2 | 39.21 | 8.98 × 10−7 | ||||||||||
| (NH2Me2)3{[Nd(Mo4O13)(DMF)4]3(BTC)2}8·(DMF) | 0.5 | 34.06 | 4.69 × 10−8 | 8 | ||||||||
| [NdL(NO3)2]PF6·MeCN | 1 | 34(1) | 1.1(4) × 10−8 | 2.8(2) | 5 | 9 | ||||||
| 10(2) | 2.0(6) × 10−4 | 0.081(2) | 9 | |||||||||
| [Nd(NO3)3(18-crown-6)] | 1 | 30.9(4) | 2.2(3) × 10−9 | 4.1(3) | 5 | 10 | ||||||
| Nd(fdh)3(bpy) | Exp. | 1.04 | 1.43 | 4.31 | 2 | 28.7 | 9.2 × 10−8 | 11 | ||||
| Ab initio | 0.56 | 1.06 | 4.78 | 106.42 | ||||||||
| [Li(DME)3][Nd(COT′′)2] | 1 | 21 | 5.5 × 10−5 | 12 | ||||||||
| [NdTp3] | 0.1 | 4.1 (100%) | 4.2(2) × 10−5 | 6 | ||||||||
| 5.46 (3.8%) | 2.6(2) × 10−4 | |||||||||||
| Nd 2 | ||||||||||||
| [Nd2 (2-FBz)4-(NO3)2(phen)2] | 13.67 | 7.4 × 10−6 | 0.02 | 9 | 265.21 | 13 | ||||||
| [Nd2(L)4(H2O)6](L)2(H2O)14 | 6.2 | 2.2 × 10−5 | 15 | |||||||||
| [Nd2(μ2-9-AC)4(9-AC)2(bpy)2] | — | — | 1.03 | 6 | 823.60 | 14 | ||||||
| 1-D | ||||||||||||
| {[Nd(pzdo)(H2O)4][Co(CN)6]}·0.5(pzdo)·4H2O | 1 | 51(2) | 4.5(9) × 10−8 | 0.09(6) | 5.6(9) | 2.2(9) | — | 20 | ||||
| [Nd(NO3){Zn(L)(SCN)}2] | 1 | 38.5(5) | 2.07(1) × 10−7 | 4 | ||||||||
| [Nd2(CNCH2COO)6(H2O)4]·2H2O | 1.5 | 26.6 | 1.75 × 10−7 | 17 | ||||||||
| {[Nd(μ2-L1)3(H2O)2]·MeCN}n | 1.021 | 2.012 | 3.514 | 2 | 27 | 4.1 × 10−7 | 18 | |||||
| [Nd(μ2-L2)(L2)(CH3COO)(H2O)2]n | 0.622 | 1.730 | 4.122 | 3.5 | 29 | 3.1 × 10−7 | 18 | |||||
| [Nd(μ2-L1)3(H2O)2]·H2O | 2.0 | 28(2) | 7.29(3) × 10−7 | 0.014(2) | 19 | |||||||
| [Nd(μ2-L2)2(CH3COO)(H2O)2]n | 2.0 | 19.7(2) | 3.43(2) × 10−6 | 0.0026(2) | ||||||||
| {Nd(α-fur)3(H2O)2} (1) | Exp. | 1.2 | 121(2) | 1.04 × 10−13 | 1.41 × 102 | 3.7 | 3.5 × 102 | 1.9 × 103 | This work | |||
| Ab initio | 0.52 | 1.03 | 4.41 | 125.0 | ||||||||
| {Nd0.065La0.935(α-fur)3(H2O)2}n (2) | Exp | 1.2 | 61(2) | 3.63 × 10−11 | 2.89 × 10−3 | 9.9 | 7.82 | 0.247 | This work | |||
| Ab initio | 1.35 | 1.98 | 3.88 | 58.8 | ||||||||
On the other hand, our group reported in 2014 the first polymeric Nd complex, based on cyanoacetate ligands, [Nd2(CNCH2COO)6(H2O)4]·2H2O, showing field-induced slow relaxation with U/kB = 26 K (1.5 kOe).17 In recent years a few more 1D nanomagnets have been reported,4,18,19 the complex {[Nd(pzdo)(H2O)4][Co(CN)6]}·0.5(pzdo)·4H2O showing the highest U/kB = 51.2 K (1 kOe) to date.20
There are also a few examples of heterometallic SMMs, combining [Mn/Nd],21–23 [Ni/Nd],24 [Co/Nd],25 [Zn/Nd],4 in which the neodymium atom plays a secondary role, increasing the anisotropy. Notably, slow relaxation under zero dc bias field has been observed only in one case.7 This may be explained in terms of the large transversal components of the Nd g*-factor, favoring fast relaxation through quantum tunneling at H = 0.17
Herein we present the synthesis, structural and magneto-thermal characterization of two new Nd-based polymeric complexes, {[Nd(α-fur)3(H2O)2]·DMF}n (1), and the non-isostructural, magnetically diluted {[Nd0.065La0.935(α-fur)3(H2O)2]}n (2), where α-fur = C4H3OCOO. Compound (2) is designed to determine single-ion relaxation in absence of Nd–Nd interaction, in contrast to (1) where Nd–Nd interaction may play a role.
In previous works we demonstrated that furoate ligand, in bridging mode, can be successfully used to form 1D polymeric chains of rare earths. This allowed us to synthesize different isostructural homonuclear {Ln(α-fur)3(H2O)3}n complexes with either Kramers (Dy)29 or non-Kramers (Tb)30 ions, and heteronuclear complexes, such as {[Dy2Sr(α-fur)8(H2O)4]}n·2H2O26 and {Ln2Ba(α-fur)8(H2O)4}n (Ln = Dy,27 Tb28). As a result, we were able to elucidate their different dynamic behavior depending on the Kramers or non-Kramers character of the magnetic Ln and the Ln–Ln interactions.
In this work, the crystal structure, static and dynamic magnetic properties of the two new Nd molecular magnets (1) and (2) are determined and discussed under the light of ab initio calculations of the energy level distribution.
2. Methods
2.1. Synthesis
All chemicals were used as received. Syntheses were performed under aerobic conditions.2.2. Experimental methods
Elemental analyses (C, H, N) were performed on an Elemental Analyzer vario EL(III). IR spectra of polycrystalline samples were recorded on a Perkin Elmer spectrum 100 FT IR Spectrometer in the range 4000–400 cm−1. The X-ray fluorescence technique (XRF, Bruker M4 TORNADO Micro-XRF spectrometer operated at 50 kV and 300 μA with Rh as target) was used to determine the purity and ratio between neodymium and lanthanum in complex (2).Single crystal X-ray analysis was performed on the crystal with a size of 100 μm specimens selected from the bulk. Sets of single-crystal X-ray intensity data were collected at room temperature (∼298 K) with Mo-Kα radiation (APEX CCD diffractometer Bruker Inc., Madison, USA, λ = 0.71073 Å) in φ- and ω-scan modes with at least 700 frames and exposures of 20 s per frame. The reflection intensities were integrated with the aid of the SAINT program of the SMART31 software package over the entire reciprocal space. Empirical absorption corrections were accomplished using the program SADABS.32 The structure was solved by direct methods using Olex2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 33 software with the SHELXS34 structure solution program and refined by full-matrix least-squares based on and refined by full-matrix least-squares on F2 with SHELXL-97
33 software with the SHELXS34 structure solution program and refined by full-matrix least-squares based on and refined by full-matrix least-squares on F2 with SHELXL-97![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 34 using an anisotropic model for non-hydrogen, atoms. All H atoms attached to carbon were introduced in idealized positions (dCH = 0.96 Å) using the riding model with their isotropic displacement parameters fixed at 120% of their riding atom. Positional parameters of the H (water) atoms were obtained from difference Fourier syntheses and verified by the geometric parameters of the corresponding hydrogen bonds.
34 using an anisotropic model for non-hydrogen, atoms. All H atoms attached to carbon were introduced in idealized positions (dCH = 0.96 Å) using the riding model with their isotropic displacement parameters fixed at 120% of their riding atom. Positional parameters of the H (water) atoms were obtained from difference Fourier syntheses and verified by the geometric parameters of the corresponding hydrogen bonds.
The magnetization, dc and ac susceptibility of powdered samples were measured, above 1.8 K, using a Quantum Design superconducting quantum interference device (SQUID) magnetometer. Ac measurements were done at an excitation field of 4 Oe, and under dc fields between 0–30 kOe, while sweeping the frequency between 0.1 and 1000 Hz. Additional ac measurements at 1.2 kOe, at temperatures in the range 2.2 K < T > 5.6 K in an extended frequency range, 90 < f < 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 Hz, were performed in a Quantum Design PPMS ACMS magnetometer. Measurements on powdered samples were done with the addition of Daphne oil, introduced to fix the grains at low temperatures.
000 Hz, were performed in a Quantum Design PPMS ACMS magnetometer. Measurements on powdered samples were done with the addition of Daphne oil, introduced to fix the grains at low temperatures.
Heat capacity C(T) under different applied fields (0–30 kOe) was measured on a powder pressed pellet fixed with Apiezon N grease, using the same PPMS.
2.3. Simulation methods
Relativistic ab initio calculations were performed using the CASPT2/RASSI-SO35 method as implemented in the MOLCAS 7.8 package.36 This relativistic quantum-chemistry approach has proven suitable to analyse the magnetic anisotropy and direction of the easy axis of magnetization (EAM) of lanthanide ions.37 The atomic positions were extracted from the X-ray crystal structure. The cluster model for complex (1) includes the studied Nd ion, its ligands, 5 furoate molecules and two waters, and the closest C3H7NO moiety. The model also includes two La(III) ions in the position of the two neighbour Nd(III) ions and the ligands of these two Nd(III) ions, where the furoate moieties have been replaced by formate ions. As for complex (2), the cluster model includes the Nd(III) ion, its surrounding furoate and water molecules and the three closest La(III) ions. The model also includes formate molecules replacing the furoate ligands of the previous La(III) ions. For both complexes, all atoms were represented by basis sets of atomic natural orbitals from the ANO RCC library. The following contractions were used: [9s8p6d4f2g1h] for the Nd ion; [4s3p1p] for the O and C atoms in the three first shells around the Nd ion; [3s2p] for the rest of the N, C and O atoms, [7s6p4d2f] for the La ion and [2s] for the H atoms. Finally, the chosen CASSCF active space consisted of the Nd 4f orbitals, containing three electrons in seven orbitals [CASSCF(3,7)].3. Structural characterization
The main crystallographic data together with refinement details are summarized in Table 2. The supplementary crystallographic data for this contribution are contained in CCDC-1914212 (1) and CCDC-1914213 (2).†| a R 1 = ∑||Fo| − |Fc||/∑|Fo|. b wR2 = {∑[w(Fo2 − Fc2)2]/∑[w(Fo2)2]}1/2. c GOF = {∑[w(Fo2 − Fc2)2]/(n − p)}1/2, where n is the number of reflections and p is the total number of parameters refined. | ||
|---|---|---|
| Compound | 1 | 2 |
| CCDC | 1914212 | 1914213 |
| Empirical formula | C18H20NNdO12 | C15H13La0.935Nd0.065O11 |
| Molecular weight | 586.59 | 508.51 |
| Temperature (K) | 298 | 296 |
| Wavelength (Å) | 0.71073 | 0.71073 |
| Crystal system | Triclinic | Monoclinic |
| Space group |
P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) |
P21/c |
| a (Å) | 9.8094(6) | 10.3803(5) |
| b (Å) | 11.1662(6) | 16.8316(9) |
| c (Å) | 11.2979(6) | 9.4569(5) |
| α (°) | 76.439(3) | 90 |
| β (°) | 69.609(3) | 92.7144(15) |
| γ (°) | 75.440(3) | 90 |
| V (Å3) | 1107.89(11) | 1650.43(15) |
| Z, Z′ | 2 | 4 |
| D calc (g cm−3) | 1.758 | 2.047 |
| μ (mm−1) | 2.406 | 2.687 |
| Reflections collected | 38![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 486 486 |
26![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 563 563 |
| Independent | 8697 (Rint = 0.0425) | 2879 (Rint = 0.0147) |
| Crystal size (mm) | 0.12 × 0.10 × 0.10 | 0.15 × 0.10 × 0.10 |
R
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a a |
0.0322 | 0.0140 |
wR2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) b b |
0.0692 | 0.0380 |
| GOFc | 0.995 | 1.014 |
| Δρmax and Δρmin (e Å−3) | 1.24/−0.74 | 0.32/−0.39 |
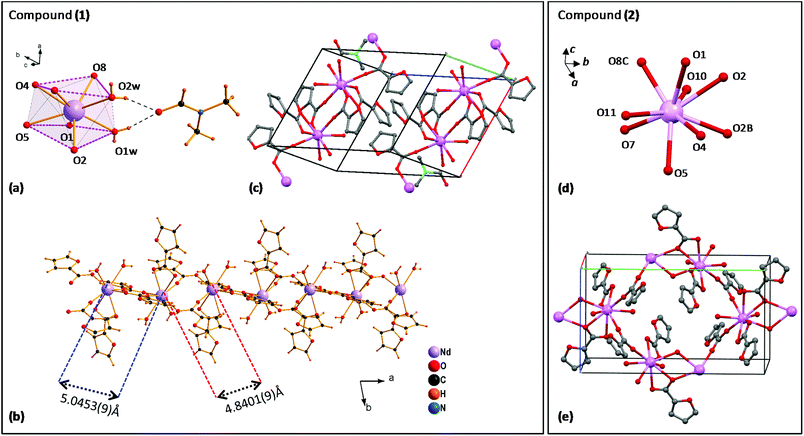
Fig. 1 (left) shows the structure of complex (1). The distorted square-antiprism coordination environment of each Nd(III) ion is shown in Fig. 1a. Each Nd is coordinated to 8 oxygen atoms, supporting five α-furoates in different coordination modes: one furoate is a bidentate-chelating ligand coordinating O4,O5, while two pairs of furoates in bridging mode, coordinated with O1,O2 and O7,O8, consolidate the Nd ions into a chain, running along the a-direction (Fig. 1b).
The Nd–Nd distance between O1,O2-bridged and O7,O8-bridged Nd pairs is slightly different, 5.0453(9) Å and 4.8401(9) Å. The coordination sphere is completed by two O1w,O2w; these water molecules are linked through H bridges to a C3H7NO moiety. The structure of the complex unit cell is shown in Fig. 1c. The 1D polymeric chains running along the a-direction are contained within the ab-planes, separated by an inter-chain distance of 11.292 Å. It is noted that the structure of this polymeric complex is slightly different from that of our previously reported linear Dy29 and Tb30 furoates, and that in complex (1) all Nd sites are equivalent.
The diluted furoate complex of neodymium (6.5%)–lanthanum (93.5%), complex (2) shown in Fig. 1 (right), is isostructural to previously described [Ln(α-fur)3(H2O)2]n, for large lanthanide ions Ln = Pr,38,39 Ce39 and La.39 Each Nd is nine-coordinated to 9 oxygen atoms: the pairs (O4,O5) and (O1,O2) support two α-furoates in bidentate mode, while O7 and O8C support each an α-furoate in bridging mode coordinating with a neighbor Ln atom; O2, O2B provide coordination with the closest Ln ion, and O10, O11 are free (Fig. 1d). The resulting structure of complex (2) is a polymeric chain running along the b-axis, where two Ln–Ln atoms are coupled through two branches to the next two Ln–Ln atoms, where Ln = La or Nd (see Fig. 1e).
4. Ab initio calculations
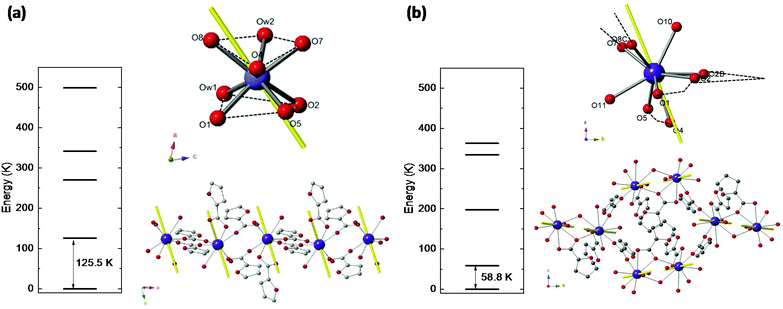
Nd(III) has a free ion 4I9/2 ground state (S = 3/2, L = 6, J = 9/2), which is split by ligand field into five Kramers doublets. The lowest doublet is the only one populated at temperatures of the order of a few K. Relativistic ab initio calculations were performed to determine the energy level structure of Nd(III) in the two studied complexes, the main axes of the g*-tensor for its doublet ground state, and the direction of the Easy Axis of Magnetization (EAM).Ab initio calculations yield an energy multiplet structure composed by five Kramers doublets in a range of 500 K for the two complexes, as shown in Fig. 2. The calculated eigenstates of Nd(III) in the two complexes, in terms of the weighted contribution of the free ion ±MJ states, is given in Table S1.†
The Hamiltonian of the polymers, consisting of a Nd chain of identical ions is:
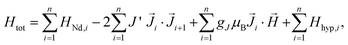 | (1) |
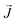 , the third is the Zeeman interaction with the external field
, the third is the Zeeman interaction with the external field 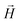 , and:
, and: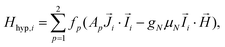 | (2) |
Although the ab initio calculations and their predictions have been done using the full J, MJ states, the calculated values for the ground state anisotropic g* factors, are expressed in terms of an effective spin S* = 1/2 restricted basis. The interaction constant expressed in terms of the S* = 1/2 model is related to the J = 9/2 basis by the relation J′* = 81J′. In terms of the effective S* = 1/2 description, the first term of eqn (2) for a given isotope transforms into:
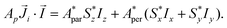 | (3) |
The results in terms of S* = 1/2 model are: for complex (1) the first excited doublet is at Δ/kB = 125.5 K, and the g* factors are gx* = 0.52, gy* = 1.03, gz* = 4.41. For complex (2) the energy gap is smaller, Δ/kB = 58.8 K, as a result of a less anisotropic ground state: gx* = 1.35, gy* = 1.98, gz* = 3.88. The EAM of magnetization in the two compounds are depicted in Fig. 2.
Besides, the Nd–Nd dipolar interaction for complex (1) is calculated with the Nd moment as a classical vector oriented along the predicted direction (see Fig. 2a). The calculation predicts the value J′dip/kB = −6.5 × 10−4 K or −1.3 × 10−3 K, for the Nd–Nd distances 5.045 Å and 4.840 Å, respectively, when the dipolar interaction contribution to the Hamiltonian is expressed as 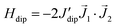 . For complex (2), the Nd–Nd interaction is neglected because of the strong magnetic dilution.
. For complex (2), the Nd–Nd interaction is neglected because of the strong magnetic dilution.
5. Static results
5.1. Magnetic properties
The field-dependence of the magnetization measured for the two complexes at T = 1.8 K is shown in Fig. 3. The M(H) data could be well fitted within the Hamiltonian model in eqn (1), with the magnetic states calculated by ab initio method (Table S1†), and the intrachain Nd–Nd interaction J′/kB = −3.15 × 10−3 K.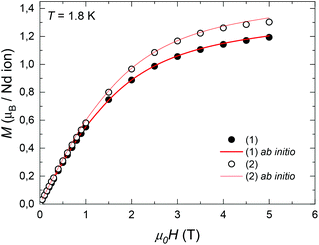 | ||
| Fig. 3 Field-dependence of the magnetization per formula unit M(H) measured for complexes (1) and (2) at T = 1.8 K. Red line: ab initio fits. | ||
The equilibrium dc susceptibility as a function of the temperature for complex (1) from T = 1.8 K to 300 K is shown in Fig. 4. The room temperature saturation value, χT(300 K) = gJ2J(J + 1)/8 = 1.289 emu K mol−1, with J = 9/2, yields an experimental gyromagnetic factor gJ = 0.65 smaller than the value for a free Nd(III) ion, gJ = 0.727.40χT decreases as the temperature is reduced, as a result of the thermal depopulation of the excited doublets, and reaches 0.59 emu K mol−1 at 1.8 K. A good fit of the χT data is achieved using the ab initio calculated wavefunctions and intrachain interaction J′/kB = −3.15 × 10−3 K (J′*/kB = −0.255 K in S* = 1/2). For the highly diluted complex (2), χT(T) was measured with low accuracy due to the difficulty in subtracting accurately the sample holder signal (Fig. S1†).
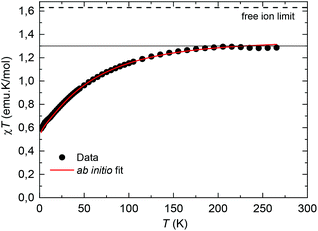 | ||
| Fig. 4 Temperature dependence of χT for complex (1). The dotted line marks the predicted χT (300 K) value for a Nd(III) free ion with gyromagnetic value gJ = 0.727.40 Red line: fit within a chain model of Nd ions, with ab initio calculated wavefunctions and intrachain interaction J′/kB = −3.15 × 10−3 K. | ||
5.2. Heat capacity
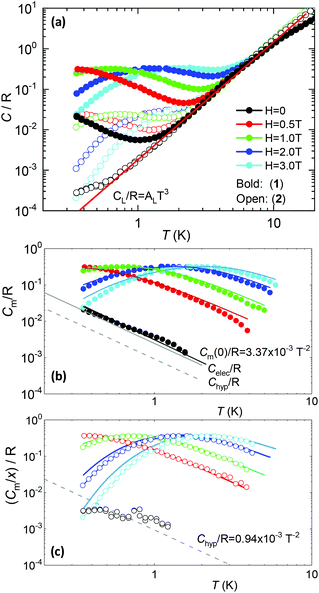
Fig. 5a shows the heat capacity (HC) as a function of temperature measured at different fields, for the two complexes. The lattice contribution to the heat capacity produces the upraise at high temperature, which follows the expected law, CL/R = ALT3, with AL = 1.7 × 10−3 R K−3. The magnetic contribution to the heat capacity, after subtracting the lattice contribution, is shown in Fig. 5b and c for complexes (1) and (2), respectively.For complex (1) at H = 0, the magnetic contribution to the low temperature HC is just a high temperature tail, Cm/R ≈ BT−2 (B = 3.37 × 10−3 R K−2), with an electronic contribution caused by the interaction with other Nd nearest neighbors, and a spin-nucleus hyperfine contribution, Chyp/R ≈ bnT−2. An estimate of the constant bn ≈ 9.37 × 10−4 R K−2 was obtained from: 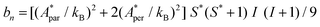 , with S* = 1/2, and values of
, with S* = 1/2, and values of 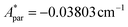 ,
, 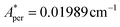 for 143Nd, and
for 143Nd, and 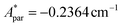 ,
, 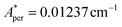 for 145Nd, corresponding to diluted Nd ethylsulphate, used as reference,40 and natural abundancies of 143Nd, 145Nd (see section 4). The estimated hyperfine contribution is represented by the dashed line in Fig. 5b.
for 145Nd, corresponding to diluted Nd ethylsulphate, used as reference,40 and natural abundancies of 143Nd, 145Nd (see section 4). The estimated hyperfine contribution is represented by the dashed line in Fig. 5b.
For the 6.5%Nd complex (2), where Nd–Nd interactions are negligible, the observed HC at H = 0 is indeed compatible with the existence of such a hyperfine contribution, as shown in Fig. 5c.
The electronic contribution associated to Nd–Nd coupling in complex (1) after subtracting the hyperfine contribution is Celec/R ≈ 2.46 × 10−3T−2, depicted in Fig. 5b.
At H ≠ 0, Schottky type anomalies show up. The in-field heat capacity data could be well fit under the model described by eqn (1), with the ab initio-calculated gyromagnetic values, neglectable hyperfine term, and intrachain interaction of J′/kB = −3.15 × 10−3 K (J′*/kB = −0.255 K in S* = 1/2) for complex (1) and J′/kB = 0 K for the diluted complex (2), see Fig. 5b, c. According to the ab initio calculations, about 30% of the J′ Nd–Nd interaction in (1) is caused by the dipolar one.
6. Dynamic results
AC susceptibility measurements at varying frequency, as a function of temperature and magnetic field, were performed to study the dynamic behavior of (1) and (2).For the two complexes, at H = 0, no contribution to χ′′ could be observed above 1.8 K, implying that there exists a relaxation process, related to Quantum Tunneling (QT) with τQT < 10−5 s faster than the frequency window of our experiment (0.01 < f < 10 kHz). In a Kramers Nd(III)-based complex, QT would be in principle forbidden, however, it can be enabled by the existence of a non-zero dipolar field that splits the Kramers degeneracy, and/or by the transverse components of the g* tensor. The application of an external field H ≠ 0 detunes the QT process, and allows the observation of slow relaxation dynamics.
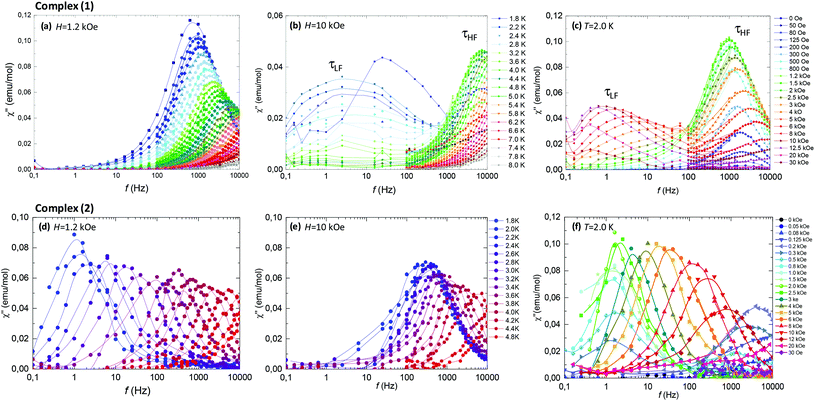
Fig. 6 (top panel) summarizes the ac results for complex (1). Fig. 6c shows the imaginary susceptibility χ′′(f) data measured at T = 2.0 K and different fields. The application of a field as small as 50–80 Oe sets on a slow relaxation process at high frequencies (τHF), whose associated peak χ′′ grows in intensity till reaching a maximum at 1.2 kOe, and then decreases again for higher fields. At H > 2.5 kOe a second relaxation process (τLF) with smaller intensity at lower frequencies appears. The double-peaked χ′′(f) data observed at constant field H = 10 kOe and varying temperatures, Fig. 6b, evidence the existence of two different slow relaxation paths above 1.8 K, (τHF) and (τLF). At H = 1.2 kOe, however, only one χ′′(f) peak appears, corresponding to the higher frequency process (τHF), see Fig. 6a.
Fig. 6 (bottom panel) shows the ac results for complex (2). The χ′′(f, T) data at constant field H = 1.2 kOe (Fig. 6d) and H = 10 kOe (Fig. 6f) evidence that in the 6.5% Nd-diluted sample the τHF peak appears at lower frequencies, whereas the τLF peak is not observed.
Fig. 7 shows the dependence of the relaxation time with the inverse temperature, τ(1/T), and the magnetic field, τ(H), for the different observed processes, determined from the position of the χ′′(f) peaks, for the two complexes.
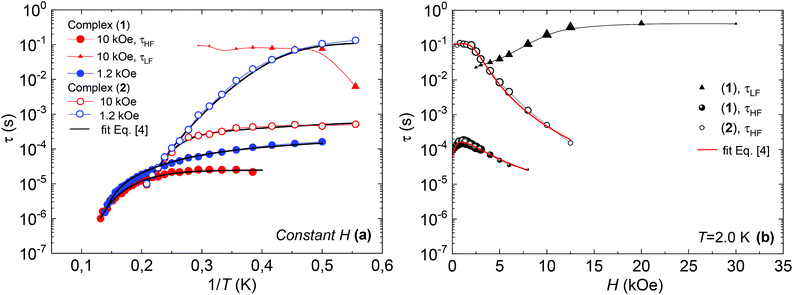 | ||
| Fig. 7 (a) Relaxation time vs. inverse of the temperature, at H = 1.2 kOe and H = 10 kOe, and fits with eqn (4); (b) relaxation time as a function of the applied field, at constant T = 2 K, and fits with eqn (4), for complex (1) (bold symbols) and complex (2) (open symbols). | ||
The high frequency relaxation process, τHF(1/T), in the 6–8 K temperature range follows an Arrhenius law, τ = τ0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(U/kBT), indicative of thermally activated spin-reversal over an energy barrier, with an estimated value U/kB = 74.6 K (τ0 = 5.19 × 10−11 s) for (1) and U/kB = 52.1 K (τ0 = 1.90 × 10−10 s) and for (2). However, a pronounced curvature in τHF with decreasing temperature is observed, revealing the presence of additional relaxation pathways, also facilitated by phonons. Besides, the fast decay of the relaxation time observed for growing fields, especially for (2), points towards a relevance of direct processes. Therefore, we analysed altogether the field and temperature dependence of the relaxation data using the equation:
exp(U/kBT), indicative of thermally activated spin-reversal over an energy barrier, with an estimated value U/kB = 74.6 K (τ0 = 5.19 × 10−11 s) for (1) and U/kB = 52.1 K (τ0 = 1.90 × 10−10 s) and for (2). However, a pronounced curvature in τHF with decreasing temperature is observed, revealing the presence of additional relaxation pathways, also facilitated by phonons. Besides, the fast decay of the relaxation time observed for growing fields, especially for (2), points towards a relevance of direct processes. Therefore, we analysed altogether the field and temperature dependence of the relaxation data using the equation:
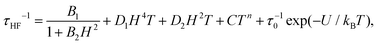 | (4) |
To avoid over parametrization, we first fit the τHF(H) data to determine B1, B2, D1, D2; then fit the τHF(1/T) curves at two fixed fields (H = 1.2 kOe and 10 kOe) to obtain the Raman (C, n) and Orbach (τ0, U) parameters.41 The τ(H,T) curves could be well reproduced, see Fig. 7, using the fitting parameters summarized in Table 3. For both compounds, the determined Orbach activation energies, U/kB = 121 K (1) and U/kB = 61 K (2), are close to the ab initio calculations. The Raman exponent for the two compounds was n ≈ 5 (1) and n ≈ 9 for (2), within the range of values usually reported for Nd ions.3,10,13,20
| # | Dependence | B 1 (s−1) | B 2 (Oe−2) | D 1 (s−1K−1Oe−4) | D 2 (s−1K−1Oe−2) | C (s−1 K−n) | n | τ 0 (s) | U/kB (K) |
|---|---|---|---|---|---|---|---|---|---|
| (1) | τ HF −1(H) | (11 ± 1) × 10+3 | (21 ± 1) × 10−6 | 0 | (2.7 ± 0.2) × 10−4 | (1.57 ± 0.05) × 10+2 | 5.0 ± 0.2 | (2.56 ± 0.01) × 10−13 | 121 ± 2 |
| τ HF −1(1/T),1.2 kOe | (11 ± 1) × 10+3 | (21 ± 1) × 10−6 | 0 | (13.7 ± 0.4) × 10−4 | (1.41 ± 0.05) × 10+2 | 3.7 ± 0.5 | (1.04 ± 0.01) × 10−13 | 121 ± 2 | |
| τ HF −1(1/T), 10 kOe | (11 ± 1) × 10+3 | (21 ± 1) × 10−6 | 0 | (1.67 ± 0.2) × 10−4 | 9.9 ± 0.5 | 5.3 ± 0.2 | (2.56 ± 0.01) × 10−13 | 121 ± 2 | |
| (2) | τ HF −1(H, 1/T) | 8.0 ± 0.5 | (1.6 ± 0.2) × 10−8 | (1.19 ± 0.06) × 10−13 | 0 | (2.89 ± 0.01) × 10−3 | 9.9 ± 0.5 | (3.63 ± 0.01) × 10−11 | 61 ± 2 |
Regarding the τ(H) dependence, some distinct differences are found for the two complexes: the τQT term is much smaller for the diluted compound (2) than for (1), as a result of the reduced interactions. Yet, even for (2) it is necessary to apply a small field to suppress completely QT, which is still favored by the transversal component of the ground state. The field strength at which slow processes appear allows us to estimate the internal dipolar field. Indeed, the tunneling time depends on the distribution of dipolar (or exchange) energy bias P(ξdip) and on the quantum tunnel splitting ΔT:42
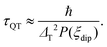 | (5) |
The energy bias distribution may be approximated to a Gaussian, with 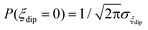 , where the width σξdip can be estimated from the condition σξdip ≈ kBTN. At H ≠ 0, the QT probability decreases as the Zeeman energy bias moves the tunneling energy window out of the dipolar energy bias distribution. We may consider that for an external field given by H ≈ 2σdip,z, QT is suppressed. In complex (1), the slow relaxation process appears at about 50–80 Oe. Therefore, the width of the bias field is estimated to be σdip,z = Hdip,z ≈ 25–40 Oe Note that this dipolar field would imply that magnetic ordering transition, if present, would occur at kBTN = σξdip =σdip,z/gz*μB ≈ 0.01 K, i.e. below the range of our measurements. Indeed, no ordering was observed in the Cm(T) curves down to the smallest measured temperature, 0.3 K.
, where the width σξdip can be estimated from the condition σξdip ≈ kBTN. At H ≠ 0, the QT probability decreases as the Zeeman energy bias moves the tunneling energy window out of the dipolar energy bias distribution. We may consider that for an external field given by H ≈ 2σdip,z, QT is suppressed. In complex (1), the slow relaxation process appears at about 50–80 Oe. Therefore, the width of the bias field is estimated to be σdip,z = Hdip,z ≈ 25–40 Oe Note that this dipolar field would imply that magnetic ordering transition, if present, would occur at kBTN = σξdip =σdip,z/gz*μB ≈ 0.01 K, i.e. below the range of our measurements. Indeed, no ordering was observed in the Cm(T) curves down to the smallest measured temperature, 0.3 K.
At high fields the QT is effectively suppressed and the direct process becomes dominant. For compound (2), it is found that eqn (4) is nicely verified in both H and T dependences. Indeed, τHF decreases as H−4, as predicted for a Kramers doublet with a negligible effect due to hyperfine interaction (D1 ≠ 0, D2 = 0).
In contrast, for compound (1), either the τHF(H) or the τHF(1/T) dependencies with (D1 = 0, D2 ≠ 0) could be fit, but not with the same set of parameters (Table 3). We note that also in previously reported Nd compounds the relaxation field dependence was not well explained by eqn (4).4,10 Since from compound (2) we may conclude that hyperfine effects are weak or negligible, the τHF decrease with H−2 cannot be caused by this effect. The discrepancy in the H and T parameters for compound (1) is probably caused by the effect of Nd–Nd interactions, which are completely neglected in the approximations implicit in eqn (4). For example, considering interactions as an additional effective internal field, its effect, according to eqn (4), would be the decrease of τHF(H) of (1) compared to the diluted (2), as is qualitatively found.
On the other hand, the τLF(1/T) and τLF(H) dependencies of the very slow process observed for complex (1) are characteristic of a direct process affected by phonon-bottleneck (PB) effect, a mechanism that we have commonly encountered in polymeric furoate complexes.27–30,43 The PB effect was indeed demonstrated through relaxation measurements performed under different pressure conditions of the bath on complex (1) (S3): the χ′′(f) peak shifted to higher frequencies by increasing the pressure, and moved back reversibly by lowering the pressure (Fig. S2†). However the very slow process τLF is not observed in (2). This fact is in agreement with previously reported results showing that PB processes are released upon magnetic dilution.29,43
7. Conclusion
In Nd complexes two mechanisms cooperate in favoring fast tunneling at H = 0: the non-zero dipolar field that splits the Kramer's degeneracy and allows new relaxation pathways between the ground and the excited levels, and transversal components in the g* tensor. Our literature survey indicates that this may be the principle reason for the absence of slow relaxation under H = 0 in most reported homonuclear Nd complexes above 5 K.In this work we have reported the synthesis of two new Nd-based complexes, coordinated by furoate ligands, displaying field-induced relaxation behavior. The application of a small field of ca. 80 Oe is enough to quench QT and allow relaxation through slower paths. The temperature and field dependencies of the relaxation rates indicate that relaxation proceeds not only through an Orbach process, but also through Raman and direct processes. In the polymeric complex (1), a sizeable energy barrier of energy U/kB = 121 K at 1.2 kOe was measured, close to the ab initio predicted difference between the ground and first excited doublet Δ/kB = 125.5 K. In (2), despite magnetic dilution was introduced so as to reduce dipolar interactions, which favour QT, a factor of two smaller relaxation barrier of U/kB = 61 K at 1.2 kOe was found. The larger SIM energy barrier for (1) than for (2) is a reflect of the different Nd(III) coordination environment and symmetry: indeed, although in both compounds transversal components gx*, gy* appear, preventing the observation of slow relaxation under H = 0, (1) presents a more anisotropic ground-state than (2): gz*2/(gx*2 + gy*2) = 14.6 (1), 2.6 (2). The stronger relaxation time τHF(H) field dependence and higher values, by at least two orders of magnitude at H = 10 kOe, in compound (2) with respect to (1) is most probably caused by the absence of Nd–Nd interactions.
The two new furoate-based complexes enlarge the still scarce family of Nd(III) based compounds. The energy barrier of compound (1) is the highest ever reported for a Nd complex.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work has been financed by MINECO DWARFS project MAT2017-83468-R and Gobierno de Aragón (RASMIA group, E12-17R). This work was supported in part (XRF and SXRD analysis) by the Critical Materials Institute, an Energy Innovation Hub funded by the U.S. Department of Energy, Office of Energy Efficiency and Renewable Energy, Advanced Manufacturing Office. Ames Laboratory is operated for the U.S. Department of Energy by Iowa State University of Science and Technology under contract No. DE-AC02-07CH11358.References
- E. Bartolomé, A. Arauzo, J. Luzón, J. Bartolomé and F. Bartolomé, in Handbook of Magnetic Materials, ed. E. Brück, Elsevier, 2017, pp. 1–289 Search PubMed.
- F. Pointillart, O. Cador, B. Le Guennic and L. Ouahab, Coord. Chem. Rev., 2017, 346, 150–175 CrossRef CAS.
- S. Demir, K. R. Meihaus and J. R. Long, J. Organomet. Chem., 2018, 857, 164–169 CrossRef CAS.
- C. Takehara, P. L. Then, Y. Kataoka, M. Nakano, T. Yamamura and T. Kajiwara, Dalton Trans., 2015, 44, 18276–18283 RSC.
- J. Rinehart and J. Long, Chem. Sci., 2011, 2, 2078–2085 RSC.
- J. D. Rinehart and J. R. Long, Dalton Trans., 2012, 41, 13572–13574 RSC.
- S. K. Gupta, T. Rajeshkumar, G. Rajaraman and R. Murugavel, Chem. Commun., 2016, 52, 7168–7171 RSC.
- H. L. Zhang, X. Y. Wu, J. Z. Liao, X. F. Kuang, W. Yang and C. Z. Lu, Dalton Trans., 2018, 47, 1796–1800 RSC.
- H. Wada, S. Ooka, D. Iwasawa, M. Hasegawa and T. Kajiwara, Magnetochemistry, 2016, 2, 43 CrossRef.
- H. Wada, S. Ooka, T. Yamamura and T. Kajiwara, Inorg. Chem., 2017, 56, 147–155 CrossRef CAS PubMed.
- M.-X. Xu, Y.-S. Meng, J. Xiong, B.-W. Wang, S.-D. Jiang and S. Gao, Dalton Trans., 2018, 47, 1966–1971 RSC.
- J. J. Le Roy, S. I. Gorelsky, I. Korobkov and M. Murugesu, Organometallics, 2015, 34, 1415–1418 CrossRef CAS.
- B. Casanovas, M. Font-Bardía, S. Speed, M. S. El Fallah and R. Vicente, Eur. J. Inorg. Chem., 2018, 1928–1937 CrossRef CAS.
- B. Casanovas, S. Speed, O. Maury, S. El Fallah, M. Font-Bardía and R. Vicente, Eur. J. Inorg. Chem., 2018, 3859–3867 CrossRef CAS.
- G. Huang, G. Calvez, Y. Suffren, C. Daiguebonne, S. Freslon, O. Guillou and K. Bernot, Magnetochemistry, 2018, 4, 1–14 CrossRef.
- J. J. Baldoví, J. M. Clemente-Juan, E. Coronado, Y. Duan, A. Gaita-Ariño and C. Giménez-Saiz, Inorg. Chem., 2014, 53, 9976–9980 CrossRef PubMed.
- A. Arauzo, A. Lazarescu, S. Shova, E. Bartolomé, R. Cases, J. Luzón, J. Bartolomé and C. Turta, Dalton Trans., 2014, 43, 12342–12356 RSC.
- A. K. Jassal, N. Aliaga-Alcalde, M. Corbella, D. Aravena, E. Ruiz and G. Hundal, Dalton Trans., 2015, 44, 15774–15778 RSC.
- A. K. Jassal, B. S. Sran, Y. Suffren, K. Bernot, F. Pointillart, O. Cador and G. Hundal, Dalton Trans., 2018, 47, 4722–4732 RSC.
- S. Chorazy, T. Charytanowicz, J. Wang, S. Ohkoshi and B. Sieklucka, Dalton Trans., 2018, 47, 7870–7874 RSC.
- H. Ke, L. Zhao, Y. Guo and J. Tang, Dalton Trans., 2012, 41, 2314–2319 RSC.
- V. Mereacre, D. Prodius, A. M. Ako, N. Kaur, J. Lipkowski, C. Simmons, N. Dalal, I. Geru, C. E. Anson, A. K. Powell and C. Turta, Polyhedron, 2008, 27, 2459–2463 CrossRef CAS.
- A. Mishra, W. Wernsdorfer, K. A. Abboud and G. Christou, J. Am. Chem. Soc., 2004, 126, 15648–15649 CrossRef CAS PubMed.
- M. X. Yao, Q. Zheng, K. Qian, Y. Song, S. Gao and J. L. Zuo, Chem. – Eur. J., 2013, 19, 294–303 CrossRef CAS PubMed.
- P. Vrábel, M. Orendác, A. Oredácová, E. Cizmár, R. Tarasenko, S. Zvyagin, J. Wosnitza, J. Prokleska, V. Sechovský, V. Pavlík and S. Gao, J. Phys.: Condens. Matter, 2013, 25, 186003–186012 CrossRef PubMed.
- C. Turta, S. Melnic, M. Bettinelli, S. Shova, C. Benelli, A. Speghini, A. Caneschi, M. Gdaniec, Y. Simonov, D. Prodius and V. Mereacre, Inorg. Chim. Acta, 2007, 360, 3047–3054 CrossRef CAS.
- E. Bartolomé, J. Bartolomé, S. Melnic, D. Prodius, S. Shova, A. Arauzo, F. Luis, J. Luzón, C. Turta and S. Page, Dalton Trans., 2014, 43, 10999–11013 RSC.
- E. Bartolomé, A. Arauzo, J. Luzón, S. Melnic, S. Shova, D. Prodius, J. Bartolomé, A. Amann, M. Nallaiyan and S. Spagna, Dalton Trans., 2019, 48, 5022–5034 RSC.
- E. Bartolomé, J. Bartolomé, S. Melnic, D. Prodius, S. Shova, A. Arauzo, J. Luzón, F. Luis and C. Turta, Dalton Trans., 2013, 42, 10153–10171 RSC.
- E. Bartolome, J. Bartolome, A. Arauzo, J. Luzón, L. Badía, R. Cases, F. Luis, S. Melnic, D. Prodius, S. Shova and C. Turta, J. Mater. Chem. C, 2016, 4, 5038–5050 RSC.
- SMART: SMART, Bruker AXS, Madison, WI, 1996 Search PubMed.
- R. Blessing, Acta Crystallogr., Sect. A: Found. Crystallogr., 1995, 51, 33–38 CrossRef PubMed.
- O. V. Dolomanov, L. J. Bourhis, R. J. Gildea, J. A. K. Howard and H. Puschmann, J. Appl. Crystallogr., 2009, 42, 339–341 CrossRef CAS.
- G. M. Sheldrick, Acta Crystallogr., Sect. A: Found. Crystallogr., 2008, 64, 112–122 CrossRef CAS PubMed.
- B. O. Roos and P. A. Malmqvist, Phys. Chem. Chem. Phys., 2004, 6, 2919 RSC.
- F. Aquilante, L. de Vico, N. Ferré, G. Ghigo, P.-Å. Malmqvist, P. Neogrády, T. Pedersen, M. Pitonák, M. Reiher, B. O. Roos, L. Serrano-Andrés, M. Urban, V. Verzayov and R. Lindh, J. Comput. Chem., 2010, 31, 224–247 CrossRef CAS PubMed.
- G. Cucinotta, M. Perfetti, J. Luzon, M. Etienne, P. E. Car, A. Caneschi, G. Calvez, K. Bernot and R. Sessoli, Angew. Chem., Int. Ed., 2012, 51, 1606–1610 CrossRef CAS PubMed.
- A. E. Koziol, W. Brzyska, B. Klimek, A. Krol and K. Stepniak, J. Coord. Chem., 1987, 15, 367 CrossRef CAS.
- B. Klimek, A. E. Koziol and K. Stepniak, Z. Kristallogr., 1986, 174, 305 CrossRef CAS.
- A. Abragam and B. Bleaney, in Electron Paramagnetic Resonance of Transition Ions, 1970, pp. 4, 42, 133–163, 398–406, 417–430, 541–547, 583–599 Search PubMed.
- E. Lucaccini, L. Sorace, M. Perfetti, J.-P. Costes and R. Sessoli, Chem. Commun., 2014, 50, 1648–1651 RSC.
- N. V. Prokof'ev and P. C. E. Stamp, Phys. Rev. Lett., 1998, 80, 5794–5797 CrossRef.
- E. Bartolomé, J. Bartolomé, A. Arauzo, J. Luzón, R. Cases, S. Fuertes, V. Sicilia, A. I. Sánchez-Cano, J. Aporta, S. Melnic, D. Prodius and S. Shova, J. Mater. Chem. C, 2018, 6, 5286–5299 RSC.
Footnote |
| † Electronic supplementary information (ESI) available. CCDC 1914212 and 1914213. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c9dt02047k |
| This journal is © The Royal Society of Chemistry 2019 |