Open Access Article
Open Access ArticleOptical fingerprint of bright and dark localized excitonic states in atomically thin 2D materials†
Maja
Feierabend
 *,
Samuel
Brem
*,
Samuel
Brem
 and
Ermin
Malic
and
Ermin
Malic
Chalmers University of Technology, Department of Physics, 412 96 Gothenburg, Sweden. E-mail: maja.feierabend@chalmers.se
First published on 13th November 2019
Abstract
Point defects, local strain or impurities can crucially impact the optical response of atomically thin two-dimensional materials as they offer trapping potentials for excitons. These trapped excitons appear in photoluminescence spectra as new resonances below the bright exciton that can even be exploited for single photon emission. While large progress has been made in deterministically introducing defects, only little is known about their impact on the optical fingerprint of 2D materials. Here, based on a microscopic approach we reveal direct signatures of localized bright excitonic states as well as indirect phonon-assisted side bands of localized momentum-dark excitons. The visibility of localized excitons strongly depends on temperature and disorder potential width. This results in different regimes, where either the bright or dark localized states are dominant in optical spectra. We trace back this behavior to an interplay between disorder-induced exciton capture and intervalley exciton–phonon scattering processes.
1 Introduction
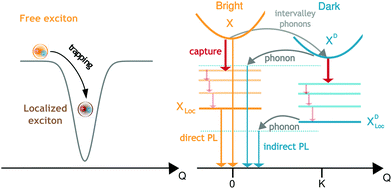
Monolayer transition metal dichalcogenides (TMDs) are remarkable materials, among others due to their exceptional optical properties.1,2 Their optical response at room temperature is dominated by optically accessible bright excitons and the resulting resonances in optical spectra are well understood based on strong Coulomb and light-matter interactions.3,4 The excitonic resonances were shown to be controllable by strain, chemical functionalization and doping.5–8 However, at low temperatures the optical response is much more complicated. It is dominated by a variety of resonances energetically below the bright excitons, which have not been fully understood yet. While some of those peaks can be explained by trions,9,10 biexcitons11 or momentum- and spin-dark excitons,12–17 little is known about the origin of defect-determined emission. The latter appears at holes,18 etched surfaces,19 edges,20 nanopillars,21 areas of local strain,22 nanobubbles23 or similar. Moreover, defect-related emission resonances have great potential as sources for single-photon emitters20,24–27 and hence a more fundamental understanding of the origin of these peaks is crucial.In this work, we shed light on the temperature-dependent optical fingerprint of TMDs spectrally below the bright exciton in presence of defects. We include direct photoluminescence (PL) from the bright exciton X and its localized states XLoc as well as phonon-assisted PL from momentum-dark excitons XD and the corresponding localized states XDLoc, cf.Fig. 1. We model both free and localized excitons on the same microscopic footing. While free excitons are formed by a Coulomb potential leading to the quantization of the relative motion of electron and hole, localized excitons are formed due to trapping into a disorder potential giving rise to a quantization of the exciton center-of-mass motion. We show that depending on the width of the trapping potential, the existence of localized states as well as exciton capture and recombination rates can be controlled. The calculated optical spectra agree well with recent experiments, observing localized states due to local strain18,22 or in presence of nanopillars.21,28 Moreover, depending on temperature and disorder potential characteristics we predict phonon- or localization-dominated regimes in PL spectra of TMDs.
2 Theoretical approach
To describe the optical fingerprint of free and localized excitonic states on a microscopic level, we exploit the density matrix formalism,29–31 where we apply the cluster expansion approach in excitonic basis.4,32,33 This allows us to describe the entire exciton landscape including bright and dark exciton states, their binding energies, wavefunctions and signatures in PL spectra. The main goal of our study is to investigate under which conditions a disorder potential can trap excitons and how it influences the optical fingerprint of TMDs including signatures of bright and momentum-dark excitonic states.To obtain access to the optical response of these materials, the knowledge of the number of emitted photons 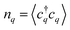 is crucial as it determines the steady-state photoluminescence
is crucial as it determines the steady-state photoluminescence 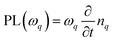 . The dynamics of the photon number nq on the other side depends on the photon-assisted polarization17,34
. The dynamics of the photon number nq on the other side depends on the photon-assisted polarization17,34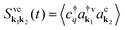 resulting in
resulting in 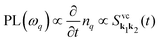 . This microscopic quantity is a measure for optically induced transitions from the state (v,k1) to the state (c,k2) under annihilation (creation) of a photon
. This microscopic quantity is a measure for optically induced transitions from the state (v,k1) to the state (c,k2) under annihilation (creation) of a photon 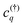 . The states are characterized by the electronic momentum ki, and the band index λ = v, c denoting valence or conduction band, respectively. Note that we take into account the conduction band minima at the K, Λ, and K′ valley, which are crucial for the formation of momentum-dark exciton states.12
. The states are characterized by the electronic momentum ki, and the band index λ = v, c denoting valence or conduction band, respectively. Note that we take into account the conduction band minima at the K, Λ, and K′ valley, which are crucial for the formation of momentum-dark exciton states.12
To account for excitonic effects, which are dominant in these materials,1,4,35,36 we project the photon-assisted polarization into an excitonic basis. We use the relation 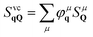 , where our original observable SvcqQ is projected to a new excitonic quantity SμQ that is weighted by the excitonic wave function φμq. Here, we have introduced the center-of-mass momentum Q = k2 − k1 and the relative momentum q = αk1 + βk2 with
, where our original observable SvcqQ is projected to a new excitonic quantity SμQ that is weighted by the excitonic wave function φμq. Here, we have introduced the center-of-mass momentum Q = k2 − k1 and the relative momentum q = αk1 + βk2 with 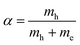 and
and 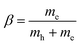 with the electron (hole) mass me(h). The free excitonic eigenfunctions φq and eigenenergies εμ are obtained by solving the Wannier equation, which presents an eigenvalue problem for excitons.4,12,17,29,30 The corresponding Coulomb matrix elements are calculated using a Keldysh potential.4,37,38
with the electron (hole) mass me(h). The free excitonic eigenfunctions φq and eigenenergies εμ are obtained by solving the Wannier equation, which presents an eigenvalue problem for excitons.4,12,17,29,30 The corresponding Coulomb matrix elements are calculated using a Keldysh potential.4,37,38
To obtain the temporal evolution of SμQ(t), we exploit the Heisenberg equation of motion iħṠμQ(t) = [H,SμQ(t)],29,31 which requires the knowledge of the many-particle Hamilton operator H. The latter reads in this work H = H0 + Hc-l + Hc-phon + Hc-dis including the free carrier contribution H0, the carrier-light interaction Hc-l, the carrier-phonon coupling Hc-phon and the carrier-disorder interaction Hc-dis. To calculate the matrix elements, we apply the nearest-neighbor tight-binding approach39,40 including fixed (not adjustable) input parameters from DFT calculations of the electronic bandstructure.41
The crucial part of the Hamilton operator in this work is the carrier-disorder matrix element 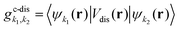 with a Gaussian disorder potential
with a Gaussian disorder potential 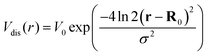 with σ denoting the full-width half maximum in real space, V0 the depth of the potential and R0 the position of the disorder. Assuming disorder centers far away from each other, R0 only leads to a phase in the momentum space. Although the Gaussian disorder potential is a simple approximation,42–44 in certain situations experimentally measured potential traps show a Gaussian-like behavior.19,22 Note that our theory is not limited to Gaussian potentials but could be extended to other potential forms, such as elliptical45 or nanobubbles.46 The investigated Gaussian potential in its general form can have its origin in a variety of physical phenomena, such as local strain gradients stemming e.g. from nanopillars on TMD monolayers21,22,28 but also in defect- or impurity-induced potentials on atomic level.47 In our work, we do not take into account variations in the trapping potential due to the atomic structure nor defect-induced changes in phonon characteristics. The main focus lies on providing qualitative microscopic insights into the impact of localized bright and dark exciton states on the optical response of monolayer TMDs.
with σ denoting the full-width half maximum in real space, V0 the depth of the potential and R0 the position of the disorder. Assuming disorder centers far away from each other, R0 only leads to a phase in the momentum space. Although the Gaussian disorder potential is a simple approximation,42–44 in certain situations experimentally measured potential traps show a Gaussian-like behavior.19,22 Note that our theory is not limited to Gaussian potentials but could be extended to other potential forms, such as elliptical45 or nanobubbles.46 The investigated Gaussian potential in its general form can have its origin in a variety of physical phenomena, such as local strain gradients stemming e.g. from nanopillars on TMD monolayers21,22,28 but also in defect- or impurity-induced potentials on atomic level.47 In our work, we do not take into account variations in the trapping potential due to the atomic structure nor defect-induced changes in phonon characteristics. The main focus lies on providing qualitative microscopic insights into the impact of localized bright and dark exciton states on the optical response of monolayer TMDs.
By transforming the disorder potential into momentum space we find that disorder leads to a quantization of the exciton center-of-mass momentum, i.e. excitons are trapped into the disorder potential and cannot move freely anymore.43 Then, we project the phonon-assisted polarization into a localized excitonic basis with 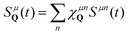 , where χμnQ are the localized excitonic wavefunctions. Note that all types of free excitons including bright KK or momentum-dark intervalley KΛ and KK′ excitons48 can be localized in a disorder potential, each with the localization quantum number n = 1s, 2s,…, cf.Fig. 1. The center-of-mass localization approach leading to new states below the free excitons is consistent with the observed mid-bandgap states in the electron–hole picture in density functional theory studies on defects.49–51
, where χμnQ are the localized excitonic wavefunctions. Note that all types of free excitons including bright KK or momentum-dark intervalley KΛ and KK′ excitons48 can be localized in a disorder potential, each with the localization quantum number n = 1s, 2s,…, cf.Fig. 1. The center-of-mass localization approach leading to new states below the free excitons is consistent with the observed mid-bandgap states in the electron–hole picture in density functional theory studies on defects.49–51
To obtain access to the wavefunctions and eigenenergies of localized excitons, we solve the eigenvalue problem
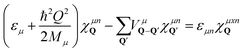 | (1) |
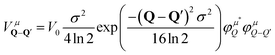 , including the formfactor
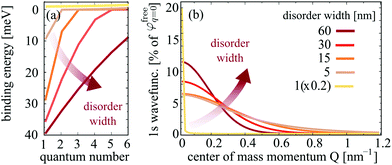
, including the formfactor 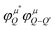 stemming from the change into free exciton basis. Depending on the exact form of the disorder potential, we find bound or free solutions of this eigenvalue problem, corresponding to trapped or free excitons, respectively. In this study, we fix the disorder potential to a typical value of V0 = 40 meV and vary the disorder width between 1 and 60 nm, cf.Fig. 2. For a very narrow potential in real space, excitons cannot be trapped due to their finite Bohr radius of approximately 1 nm.52 As soon as the potential is broad enough, trapping occurs and bound states appear (Fig. 2(a)). The broader the disorder potential in real space, the more bound eigenenergies fit into the potential. However, we also observe that the binding energies show a non-linear increase, i.e. when increasing from 30 to 60 nm the binding energy changes only slightly. If the potential is very wide in real space, it does not act as a strong local confinement anymore: excitons can be trapped inside but since the potential is so wide, excitons tend to behave more like free excitons, i.e. become broad in real space. In momentum space, the wavefunctions become narrower and higher (Fig. 2(b)) resembling more and more the shape of free excitons. The actual position of excitonic resonances in PL spectra strongly depends on the characteristics of the trapping potential. In the ESI,† we have included excitonic binding energies, wavefunctions as well as PL spectra for a deeper disorder potential of V0 = 160 meV that has been estimated in recent photoluminescence excitation measurements.27
stemming from the change into free exciton basis. Depending on the exact form of the disorder potential, we find bound or free solutions of this eigenvalue problem, corresponding to trapped or free excitons, respectively. In this study, we fix the disorder potential to a typical value of V0 = 40 meV and vary the disorder width between 1 and 60 nm, cf.Fig. 2. For a very narrow potential in real space, excitons cannot be trapped due to their finite Bohr radius of approximately 1 nm.52 As soon as the potential is broad enough, trapping occurs and bound states appear (Fig. 2(a)). The broader the disorder potential in real space, the more bound eigenenergies fit into the potential. However, we also observe that the binding energies show a non-linear increase, i.e. when increasing from 30 to 60 nm the binding energy changes only slightly. If the potential is very wide in real space, it does not act as a strong local confinement anymore: excitons can be trapped inside but since the potential is so wide, excitons tend to behave more like free excitons, i.e. become broad in real space. In momentum space, the wavefunctions become narrower and higher (Fig. 2(b)) resembling more and more the shape of free excitons. The actual position of excitonic resonances in PL spectra strongly depends on the characteristics of the trapping potential. In the ESI,† we have included excitonic binding energies, wavefunctions as well as PL spectra for a deeper disorder potential of V0 = 160 meV that has been estimated in recent photoluminescence excitation measurements.27
3 Photoluminescence of localized excitons
The approach of disorder-induced center-of-mass localization allows us to write the equations of motion in a localized exciton basis. The advantage is that we can exploit the TMD Bloch equations for phonon-assisted photoluminescence derived in our previous work,17 transfer the PL equation in the localized exciton basis and obtain the PL intensity IbPL for localized states belonging to the bright exciton X: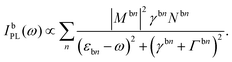 | (2) |
Here, we use the index b for the bright KK excitons within the light cone and n for the quantum number of the localized state. The equation resembles the well-known Elliott formula.53 The position of excitonic peaks is determined by the energy εbn, while the peak width is given by radiative (γbn) and non-radiative dephasing (Γb,n) due to phonons. The oscillator strength is determined by the optical matrix element, which reads in the new basis 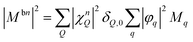 with localized and free exciton wave functions χ and φ, respectively, as well as the original momentum-dependent optical matrix element Mq.4 The delta distribution assures that only bright excitons within the light cone with Q = 0 are visible. In the limit of no localized excitons, we find
with localized and free exciton wave functions χ and φ, respectively, as well as the original momentum-dependent optical matrix element Mq.4 The delta distribution assures that only bright excitons within the light cone with Q = 0 are visible. In the limit of no localized excitons, we find 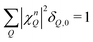 , which results in the free-exciton photoluminescence formula.17
, which results in the free-exciton photoluminescence formula.17
Moreover, our calculations show that the wave functions of localized excitons are an order of magnitude weaker compared to free excitons (Fig. 2(b)), and hence the oscillator strength of localized excitons |Mbn|2 becomes rather small. On the other side, the exciton occupation Nbn of the energetically lower localized states is high at low temperatures. The occupation is determined by the capture rate of excitons into the considered disorder potential. The capture process has been treated microscopically taking into account exciton–phonon scattering processes between free and localized excitonic states within the second-order Born–Markov approximation54 and applying the basis of orthogonal plane waves for localized states.55,56 More details can be found in the ESI.†
Interestingly, the reports in literature show that localized excitons are most pronounced in tungsten-based TMDs.16,57 The latter are characterized by the presence of momentum-dark KΛ and KK′ excitons that are located below the bright KK excitons.12,48 Their role in presence of disorder has not been investigated yet. Depending on their energetic position and the ratio between capture and phonon-assisted intervalley scattering rates, the free KK excitons can either first be captured in a disorder potential or first scatter into a dark intervalley exciton state (KΛ, KK′) and then be captured, cf.Fig. 1. To account for these additional dark exciton scattering channels, we extend eqn (2) including now phonon-assisted PL IdPL from the states ν = KK, KΛ, KK′:17
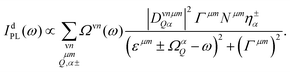 | (3) |
Here, we have introduced the abbreviation 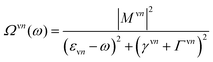 . The position of excitonic resonances in the PL spectrum is now determined by the energy of the exciton εμm and the energy of the involved phonon ±ΩαQ. The sign describes either the absorption (+) or emission (−) of phonons. We take into account all in-plane optical and acoustic phonon-modes. Moreover, the appearing phonon occupation
. The position of excitonic resonances in the PL spectrum is now determined by the energy of the exciton εμm and the energy of the involved phonon ±ΩαQ. The sign describes either the absorption (+) or emission (−) of phonons. We take into account all in-plane optical and acoustic phonon-modes. Moreover, the appearing phonon occupation 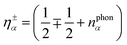 is assumed to correspond to the Bose equilibrium distribution according to a bath approximation.58 Since dark states can not decay radiatively, the peak width is only determined by non-radiative dephasing processes Γμn. The oscillator strength of phonon-assisted peaks scales with the exciton–phonon scattering element
is assumed to correspond to the Bose equilibrium distribution according to a bath approximation.58 Since dark states can not decay radiatively, the peak width is only determined by non-radiative dephasing processes Γμn. The oscillator strength of phonon-assisted peaks scales with the exciton–phonon scattering element 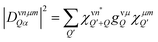 , where gνμQ is the exciton–phonon coupling element including free exciton wavefunctions.17,32
, where gνμQ is the exciton–phonon coupling element including free exciton wavefunctions.17,32
In this study, we focus on processes involving the bright KK excitons as initial states, as those states are expected to be the most dominant in PL. Note that in eqn (3), the sum over n describes the additive contribution of excited localized excitonic states. However, our microscopic calculations show that the intraexcitonic scattering of localized excitonic states (μn → μn′) appears on a much faster timescale than the capture processes itself. Hence, it is sufficient to take into account only the ground 1s state for the calculation of the optical response. This reduces the complexity to determine the exciton occupations Nνn appearing in eqn (2) and (3). Taking into account all scattering processes on a microscopic footing, we calculate the exciton densities within the states X, XLoc, XD, XDLoc, cf.Fig. 1. We would like to emphasize that we calculate both the exciton decay via intervalley scattering X → XD and the capture process X(D) → X(D)Loc on a microscopic level driven by the exciton–phonon coupling strength 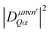 , cf. the ESI,† for more details.
, cf. the ESI,† for more details.
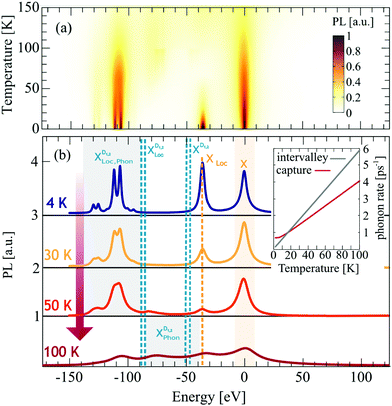
Now we have all ingredients to investigate the photoluminescence of free and localized bright and dark excitonic states, i.e. IPL(ω) = IbPL(ω) + IdPL(ω). Fig. 3 shows the time-integrated and temperature dependent PL spectra for the exemplary material tungsten diselenide (WSe2) choosing a fixed disorder width of 30 nm and a disorder depth of V0 = 40 meV. These values are chosen by taking into account recent experimental measurements on nanopillars and deterministic local strain in TMD samples.21 The temperature dependence enters through exciton and phonon occupations in eqn (3). We observe a variety of peaks at low temperatures, which we can microscopically ascribe to: (i) the bright KK exciton X, (ii) the localized KK exciton XLoc (located about 40 meV below the X resonance), (iii) a series of peaks around 100–130 meV below the X resonance reflecting phonon-assisted PL from dark localized states 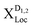 (D1,2 = KΛ, KK′). In particular, we predict pronounced phonon side bands from the energetically lowest KK′ exciton involving TO/LO phonons (around 130 meV) and TA/LA phonons (around 115 meV). Our findings support the hypothesis of recent experimental findings, predicting photoluminescence resonances stemming from dark localized excitons.59,60
(D1,2 = KΛ, KK′). In particular, we predict pronounced phonon side bands from the energetically lowest KK′ exciton involving TO/LO phonons (around 130 meV) and TA/LA phonons (around 115 meV). Our findings support the hypothesis of recent experimental findings, predicting photoluminescence resonances stemming from dark localized excitons.59,60
We find that with the increasing temperature the linewidth of all peaks increases (Fig. 3(b)) due to the enhanced exciton–phonon scattering. For free excitons, this is intuitive and well established in literature.61 However, for localized excitons the temperature behavior is still not well understood. Our calculations show (i) a temperature-independent contribution due to radiative decay and (ii) an linear increase in the linewidth due to the enhanced exciton–phonon scattering. The radiative part is determined by the wavefunction overlap and we find γ0 ≈0.5–1.0 meV, which is in good agreement with the experimental obtained value of 0.9 meV.60 The increase with temperature stems from the temperature dependence of the phonon-driven capture rate, cf. the inset in Fig. 3. Even at 0 K we find a contribution to the capture rate due to phonon emission processes. This agrees well with the overall temperature behavior of localized excitons observed in experiments, revealing stable localized excitons up to 100 K.60,62
Furthermore, we find that the localized bright exciton XLoc shows a fast intensity decrease with temperature. This can be explained by the behavior of the capture rate (cf. the inset in Fig. 3(b)): For temperatures below 20 K the capture of excitons is faster than the intervalley scattering with phonons, and hence the intensity of XLoc is high. The calculated capture rates are in good agreement with other theoretical studies.63 For temperatures above 20 K, the intervalley exciton–phonon scattering becomes faster, which means that excitons are more likely to scatter to the KΛ and KK′ states first, before they are captured in the respective localized states. This presents a crucial difference between bright and dark localized states, and their temperature behavior could be used to trace back their origin. Moreover, as XLoc signature disappears with temperature, the probability to occupy the dark states XD increases and from about 50 K we can see traces of phonon side17,32 bands from these actually dark states. We find additional peaks between 100 and 50 meV reflecting phonon emission and absorption processes from KK′ and KΛ excitons. To sum up, at low temperatures (<100 K) the PL is dominated by disorder-driven signatures, while at higher temperatures phonon-dominated signatures determine the optical response.
4 Disorder-induced control of PL
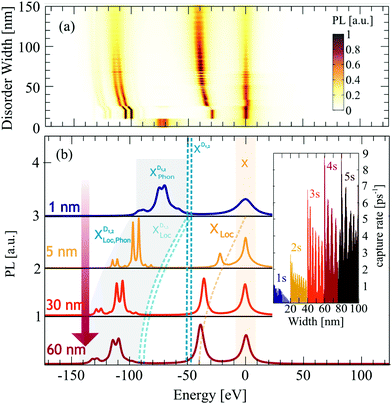
Having understood the origin of different resonances in low-temperature PL spectra in presence of disorder, the goal now is to investigate to what extent the spectra can be tuned by the characteristics of the disorder potential. We keep the temperature fixed at 4 K, as this is the temperature with the most pronounced localized states, and vary the width of the potential. For a better understanding of the underlying processes, we keep the disorder depth constant (V0 = const = 40 meV). Changing the disorder depth would not change the qualitative behavior, since the crucial quantity is the product of width σ2 and depth V0 appearing in the Fourier-transformed disorder potential, cf.eqn (1). The strength of our approach is that we can describe different regimes including very narrow and deep disorder potentials and as well as disorders of width and height in the range of 100 nm and more. In the ESI,† we also show the results for a deeper disorder potential of V0 = 160 meV.As expected from the calculated eigenenergies in Fig. 2(a), we observe clear spectral shifts of localized excitons towards lower energies with increasing disorder width, cf.Fig. 4. However, at about 60 nm a saturation is reached and the position of the peaks remains constant. This behavior can be understood as follows: for very narrow disorder potentials (in the range of 1 nm and below), i.e. σ < rB with rB as the exciton Bohr radius, excitons do not get trapped and hence we only observe phonon side bands (50–100 meV below X) from the free dark excitons 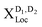 (Fig. 4(b) upper panel). Here, we are in the phonon-dominated regime. As soon as the disorder potential is broad enough, excitons can be captured and localized bright excitons XLoc as well as phonon side bands of localized dark excitons
(Fig. 4(b) upper panel). Here, we are in the phonon-dominated regime. As soon as the disorder potential is broad enough, excitons can be captured and localized bright excitons XLoc as well as phonon side bands of localized dark excitons 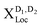 appear (Fig. 4(b) lower panels). Here, we enter a disorder-dominated regime in the PL. When increasing the disorder width in real space, first excitons become stronger localized, however at some width a saturation is reached. This is due to the fact that with very wide potentials, excitons are not tightly confined anymore and tend to behave like free excitons again. They are characterized by a broad wavefunction in real space (and hence a narrow wavefunction in momentum space, cf.Fig. 2(b)).
appear (Fig. 4(b) lower panels). Here, we enter a disorder-dominated regime in the PL. When increasing the disorder width in real space, first excitons become stronger localized, however at some width a saturation is reached. This is due to the fact that with very wide potentials, excitons are not tightly confined anymore and tend to behave like free excitons again. They are characterized by a broad wavefunction in real space (and hence a narrow wavefunction in momentum space, cf.Fig. 2(b)).
Beside the spectral shift discussed above, we also observe a clear disorder-induced increase of the resonance linewidth of localized excitons. This is due to narrower exciton wavefunctions (cf.Fig. 2(b)) and hence stronger radiative dephasing, as the latter directly scales with |χμn|2. Interestingly, we also find that the intensity of localized dark and bright states clearly changes with the disorder width. This can be ascribed to the width dependence of capture processes, cf. the inset in Fig. 4(b). We find an overall enhanced capture efficiency at larger disorder widths due to enhanced overlap of the free and localized wavefunctions. As we increase the disorder width, the localized wavefunctions become narrower and hence more similar to the free exciton wavefunction resulting in a larger overlap. However, the capture rate is not only determined by the wavefunctions, but it also crucially depends on the energetic position of the highest localized state. At low temperatures, free excitons can scatter only by emission of a phonon into the energetically lower localized state. Therefore, the energetic difference between free and localized state has to be in the range of the phonon energy (≈20–30 meV). For larger disorder widths, the spectral distance between free and localized state increases and hence phonon-driven scattering becomes less probable. However, at some disorder width, an additional localized state emerges, which offers new scattering channels for phonons. Whenever this occurs, we observe a new peak in the capture rate (cf. different colors in the inset in Fig. 4(b)).
In conclusion, we have developed a microscopic approach to describe trapping processes of excitons in atomically thin 2D materials. We have calculated wavefunctions and energies of localized excitons depending on characteristics of the disorder potential. Using this knowledge, we have determined the optical fingerprint of the exemplary tungsten-based TMDs. We find a variety of pronounced peaks below the bright exciton stemming from both bright and momentum-dark localized states. The predicted signatures are strongly sensitive to temperature. We find a disorder-dominated regime at low temperatures and a free exciton phonon-dominated regime at higher temperatures. The gained insights can be extended to a broader class of 2D materials and might help to design tailored trapping potentials.
Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
This project has received funding from the Swedish Research Council (VR, project number 2018-00734) and the European Union's Horizon 2020 research and innovation programme under grant agreement No. 785219 (Graphene Flagship).References
- T. Mueller and E. Malic, npj 2D Mater. Appl., 2018, 2, 29 CrossRef.
- G. Wang, A. Chernikov, M. M. Glazov, T. F. Heinz, X. Marie, T. Amand and B. Urbaszek, Rev. Mod. Phys., 2018, 90, 021001 CrossRef CAS.
- K. F. Mak, C. Lee, J. Hone, J. Shan and T. F. Heinz, Phys. Rev. Lett., 2010, 105, 136805 CrossRef PubMed.
- G. Berghäuser and E. Malic, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 125309 CrossRef.
- J. O. Island, A. Kuc, E. H. Diependaal, R. Bratschitsch, H. S. van der Zant, T. Heine and A. Castellanos-Gomez, Nanoscale, 2016, 8, 2589 RSC.
- H. J. Conley, B. Wang, J. I. Ziegler, R. F. Haglund Jr, S. T. Pantelides and K. I. Bolotin, Nano Lett., 2013, 13, 3626 CrossRef CAS PubMed.
- J. S. Ross, P. Klement, A. M. Jones, N. J. Ghimire, J. Yan, D. Mandrus, T. Taniguchi, K. Watanabe, K. Kitamura and W. Yao, et al. , Nat. Nanotechnol., 2014, 9, 268 CrossRef CAS PubMed.
- S. Mouri, Y. Miyauchi and K. Matsuda, Nano Lett., 2013, 13, 5944 CrossRef CAS PubMed.
- T. Godde, D. Schmidt, J. Schmutzler, M. Aßmann, J. Debus, F. Withers, E. Alexeev, O. Del Pozo-Zamudio, O. Skrypka and K. Novoselov, et al. , Phys. Rev. B, 2016, 94, 165301 CrossRef.
- J. Jadczak, J. Kutrowska-Girzycka, P. Kapuściński, Y. Huang, A. Wójs and L. Bryja, Nanotechnology, 2017, 28, 395702 CrossRef CAS PubMed.
- P. Nagler, M. V. Ballottin, A. A. Mitioglu, M. V. Durnev, T. Taniguchi, K. Watanabe, A. Chernikov, C. Schüller, M. M. Glazov and P. C. Christianen, et al. , Phys. Rev. Lett., 2018, 121, 057402 CrossRef CAS PubMed.
- E. Malic, M. Selig, M. Feierabend, S. Brem, D. Christiansen, F. Wendler, A. Knorr and G. Berghäuser, Phys. Rev. Mater., 2018, 2, 014002 CrossRef CAS.
- M. Molas, C. Faugeras, A. Slobodeniuk, K. Nogajewski, M. Bartos, D. Basko and M. Potemski, 2D Mater., 2017, 4, 021003 CrossRef.
- Y. Zhou, G. Scuri, D. S. Wild, A. A. High, A. Dibos, L. A. Jauregui, C. Shu, K. De Greve, K. Pistunova and A. Y. Joe, et al. , Nat. Nanotechnol., 2017, 12, 856 CrossRef CAS PubMed.
- J. Lindlau, C. Robert, V. Funk, J. Förste, M. Förg, L. Colombier, A. Neumann, E. Courtade, S. Shree and T. Taniguchi, et al., arXiv preprint arXiv:1710.00988, 2017.
- X.-X. Zhang, Y. You, S. Y. F. Zhao and T. F. Heinz, Phys. Rev. Lett., 2015, 115, 257403 CrossRef PubMed.
- S. Brem, A. Ekman, D. Christiansen, F. Katsch, M. Selig, C. Robert, X. Marie, B. Urbaszek, A. Knorr and E. Malic, arXiv preprint arXiv:1904, 2019, 04711.
- S. Kumar, A. Kaczmarczyk and B. D. Gerardot, Nano Lett., 2015, 15, 7567 CrossRef CAS PubMed.
- M. R. Rosenberger, C. K. Dass, H.-J. Chuang, S. V. Sivaram, K. M. McCreary, J. R. Hendrickson and B. T. Jonker, ACS Nano, 2019, 13, 904 CrossRef CAS PubMed.
- M. Koperski, K. Nogajewski, A. Arora, V. Cherkez, P. Mallet, J.-Y. Veuillen, J. Marcus, P. Kossacki and M. Potemski, Nat. Nanotechnol., 2015, 10, 503 CrossRef CAS PubMed.
- C. Palacios-Berraquero, D. M. Kara, A. R.-P. Montblanch, M. Barbone, P. Latawiec, D. Yoon, A. K. Ott, M. Loncar, A. C. Ferrari and M. Atatüre, Nat. Commun., 2017, 8, 15093 CrossRef CAS PubMed.
- J. Kern, I. Niehues, P. Tonndorf, R. Schmidt, D. Wigger, R. Schneider, T. Stiehm, S. Michaelis de Vasconcellos, D. E. Reiter and T. Kuhn, et al. , Adv. Mater., 2016, 28, 7101 CrossRef CAS PubMed.
- G. D. Shepard, O. A. Ajayi, X. Li, X. Zhu, J. Hone and S. Strauf, 2D Mater., 2017, 4, 021019 CrossRef.
- C. Chakraborty, L. Kinnischtzke, K. M. Goodfellow, R. Beams and A. N. Vamivakas, Nat. Nanotechnol., 2015, 10, 507 CrossRef CAS PubMed.
- Y.-M. He, G. Clark, J. R. Schaibley, Y. He, M.-C. Chen, Y.-J. Wei, X. Ding, Q. Zhang, W. Yao and X. Xu, et al. , Nat. Nanotechnol., 2015, 10, 497 CrossRef CAS PubMed.
- A. Srivastava, M. Sidler, A. V. Allain, D. S. Lembke, A. Kis and A. Imamoğlu, Nat. Nanotechnol., 2015, 10, 491 CrossRef CAS PubMed.
- P. Tonndorf, R. Schmidt, R. Schneider, J. Kern, M. Buscema, G. A. Steele, A. Castellanos-Gomez, H. S. van der Zant, S. M. de Vasconcellos and R. Bratschitsch, Optica, 2015, 2, 347 CrossRef CAS.
- A. Branny, S. Kumar, R. Proux and B. D. Gerardot, Nat. Commun., 2017, 8, 15053 CrossRef CAS PubMed.
- H. Haug and S. W. Koch, Quantum Theory of the Optical and Electronic Properties of Semiconductors, World Scientific Publishing Co. Pre. Ltd, Singapore, 5th edn, 2004 Search PubMed.
- M. Kira and S. Koch, Prog. Quantum Electron., 2006, 30, 155 CrossRef.
- E. Malic and A. Knorr, Graphene and Carbon Nanotubes: Ultrafast Optics and Relaxation Dynamics, John Wiley & Sons, 2013 Search PubMed.
- M. Selig, G. Berghäuser, M. Richter, R. Bratschitsch, A. Knorr and E. Malic, 2D Mater., 2018, 5, 035017 CrossRef.
- S. Brem, M. Selig, G. Berghaeuser and E. Malic, Sci. Rep., 2018, 8, 8238 CrossRef PubMed.
- A. Thränhardt, S. Kuckenburg, A. Knorr, T. Meier and S. Koch, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 62, 2706 CrossRef.
- A. Chernikov, T. C. Berkelbach, H. M. Hill, A. Rigosi, Y. Li, O. B. Aslan, D. R. Reichman, M. S. Hybertsen and T. F. Heinz, Phys. Rev. Lett., 2014, 113, 076802 CrossRef PubMed.
- A. Arora, M. Koperski, K. Nogajewski, J. Marcus, C. Faugeras and M. Potemski, Nanoscale, 2015, 7, 10421 RSC.
- L. V. Keldysh, JETP Lett., 1978, 29, 658 Search PubMed.
- P. Cudazzo, I. V. Tokatly and A. Rubio, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 085406 CrossRef.
- M. Hirtschulz, F. Milde, E. Malic, S. Butscher, C. Thomsen, S. Reich and A. Knorr, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 035403 CrossRef.
- E. Malic, J. Maultzsch, S. Reich and A. Knorr, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 115439 CrossRef.
- A. Kormanyos, G. Burkard, M. Gmitra, J. Fabian, V. Zolyomi, N. D. Drummond and V. Falko, 2D Mater., 2015, 2, 022001 CrossRef.
- X. Wen-Fang, Chin. Phys. Lett., 2005, 22, 1768 CrossRef.
- A. Hichri, I. Ben Amara, S. Ayari and S. Jaziri, J. Appl. Phys., 2017, 121, 235702 CrossRef.
- J. Adamowski, M. Sobkowicz, B. Szafran and S. Bednarek, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 62, 4234 CrossRef CAS.
- R. Rosati, F. Lengers, D. E. Reiter and T. Kuhn, Phys. Rev. B, 2018, 98, 195411 CrossRef CAS.
- M. Brooks and G. Burkard, Phys. Rev. B, 2018, 97, 195454 CrossRef CAS.
- T. T. Tran, S. Choi, J. A. Scott, Z.-Q. Xu, C. Zheng, G. Seniutinas, A. Bendavid, M. S. Fuhrer, M. Toth and I. Aharonovich, Adv. Opt. Mater., 2017, 5, 1600939 CrossRef.
- G. Berghäuser, P. Steinleitner, P. Merkl, R. Huber, A. Knorr and E. Malic, Phys. Rev. B, 2018, 98, 020301 CrossRef.
- S. Salehi and A. Saffarzadeh, Surf. Sci., 2016, 651, 215 CrossRef CAS.
- S. Zhang, C.-G. Wang, M.-Y. Li, D. Huang, L.-J. Li, W. Ji and S. Wu, Phys. Rev. Lett., 2017, 119, 046101 CrossRef PubMed.
- S. Refaely-Abramson, D. Y. Qiu, S. G. Louie and J. B. Neaton, Phys. Rev. Lett., 2018, 121, 167402 CrossRef CAS PubMed.
- T. C. Berkelbach, M. S. Hybertsen and D. R. Reichman, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 88, 045318 CrossRef.
- W. Hoyer, C. Ell, M. Kira, S. Koch, S. Chatterjee, S. Mosor, G. Khitrova, H. Gibbs and H. Stolz, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 075324 CrossRef.
- D. F. Walls and G. J. Milburn, Quantum optics, Springer Science & Business Media, 2007 Search PubMed.
- C. Herring, Phys. Rev., 1940, 57, 1169 CrossRef.
- H. Schneider, W. Chow and S. W. Koch, Phys. Status Solidi B, 2003, 238, 589 CrossRef CAS.
- F. Cadiz, E. Courtade, C. Robert, G. Wang, Y. Shen, H. Cai, T. Taniguchi, K. Watanabe, H. Carrere and D. Lagarde, et al. , Phys. Rev. X, 2017, 7, 021026 Search PubMed.
- V. Axt, K. Victor and A. Stahl, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 53, 7244 CrossRef CAS PubMed.
- L. N. Tripathi, O. Iff, S. Betzold, Ł. Dusanowski, M. Emmerling, K. Moon, Y. J. Lee, S.-H. Kwon, S. Hofling and C. Schneider, ACS Photonics, 2018, 5, 1919 CrossRef CAS.
- Y.-M. He, S. Höfling and C. Schneider, Opt. Express, 2016, 24, 8066 CrossRef CAS.
- M. Selig, G. Berghäuser, A. Raja, P. Nagler, C. Schüller, T. F. Heinz, T. Korn, A. Chernikov, E. Malic and A. Knorr, Nat. Commun., 2016, 7, 13279 CrossRef CAS PubMed.
- J. Klein, M. Lorke, M. Florian, F. Sigger, J. Wierzbowski, J. Cerne, K. Müller, T. Taniguchi, K. Watanabe and U. Wurstbauer, et al., arXiv preprint arXiv:1901.01042, 2019.
- S. Ayari and S. Jaziri, Phys. Status Solidi B, 2019, 256, 1800682 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c9cp05763c |
| This journal is © the Owner Societies 2019 |