Open Access Article
Open Access ArticleStructure and dynamics of water in molecular models of hydrated polyvinylamine membranes†
Pierre
Fayon
 * and
Lev
Sarkisov
* and
Lev
Sarkisov
School of Engineering, Institute for Materials and Processes, The University of Edinburgh, Edinburgh, UK. E-mail: p.fayon@ed.ac.uk
First published on 20th November 2019
Abstract
Facilitated transport membranes (FTMs) constitute an emerging class of polymer materials with promising properties for carbon capture applications. The key feature of these membranes is the presence of chemical groups which, in the presence of water, engage in a reaction with dissolved carbon dioxide, thus enhancing the permeability and selectivity of the membrane. Currently, little is known about the organization of these membranes on a molecular level, reaction mechanisms and detailed chemical balance, transport of water, ion species and dissolved gas molecules. The nature of the actual facilitation mechanism and the factors responsible for this effect remain unclear. Here, we use a case of polyvinylamine (PVAm), one of the most studied fixed carrier material for FTMs, to propose molecular models of the hydrated polymers. We aim to understand how transport of water is governed by structural properties of the membrane, such as the free volume, pore limiting diameter, and degree of protonation. We observe that even at the highest experimentally used hydration level, the mobility of water in PVAm matrices is significantly lower than that in bulk water; unlike in bulk systems, chloride ions exhibit much slower diffusion in confined water; this, in turn, affects the diffusion of water, which also diminishes in the presence of chloride ions.
1 Introduction
Facilitated transport membranes (FTMs) constitute an emerging class of materials with promising properties for carbon capture applications.1 The main feature of FTMs is the reactive moieties (amine, imide) either present as fixed-site surface groups or as mobile species, often called carriers, which react with the adsorbed carbon dioxide. Let us briefly summarize what is known so far about FTMs and their performance with the focus on the fixed-site carriers, polyamine systems (for a more extensive review, the reader is referred to the recent articles by Tong and Ho1 and by Rafiq et al.,2). Firstly, FTMs function only in the hydrated state and their performance strongly depends on the degree of hydration. In separation applications, to keep membranes hydrated, the feed gas must be saturated with water, while steam should be used as a sweep gas on the permeate side. This imposes additional challenges in using FTMs in practice. Polymers, typically employed as fixed-site carriers, include polyvinylamine (PVAm), polyallylamine (PAAm) and polyethylenimine (PEI). In particular, Hägg and co-workers carried out extensive studies of the performance of PVAm membranes as a function of temperature, degree of hydration, pH and other conditions.3–11 In the presence of water, the amine groups of polyamines are expected to react with dissolved carbon dioxide, leading to the formation of several new species, i.e. carbamate (RNHCOO−) and bicarbonate (HCO3−) ions. It is believed that the carbamate ion is hydrolyzed with water leading to further formation of bicarbonate ions.Despite several promising experimental observations regarding the performance of the FTMs in gas separations, little is known about the actual transport mechanisms in FTMs or their structure on a molecular level. The precise speciation and the ionic state of polyamine are also not known. In the description of the transport in FTMs systems, a schematic is often invoked showing the carbon dioxide molecule “hopping” from one reactive surface amine group to another in a series of presumed reactive steps; however, there is no direct experimental evidence for this process.12
Lack of understanding of the actual processes in FTMs presents a significant challenge in the further development of these materials and separation processes based on them. In principle, the construction of a detailed picture of the absorption and transport phenomena in FTMs can be significantly aided by using molecular simulations. Previous studies indicate that molecular models can provide several useful insights on the structural organization of water confined in polymeric systems. Without trying to be exhaustive, here we mention just a few studies that have been particularly influential on the current work. Specifically, Müller-Plathe considered a molecular model of a closely related polymer, polyvinyl alcohol (PVA), made out of a single chain of 400 monomers hydrated with various amounts of water.13 Later, Zhang et al.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 14 employed molecular dynamics to explore the diffusion of water and ethanol mixtures in model PVA systems, based on oligomers of 50 monomers. Diffusion of water and benzene in model PVA systems was also considered by Noorjahan et al.15 The behavior of water confined in polyelectrolytes systems has also been explored using molecular simulations in the context of perfluorinated membranes (i.e. Nafion), reverse osmosis and desalination.16–23 In general, all these studies provide a wealth of guidance on required simulation times, scenarios for the diffusion behavior as a function of polymer volume fraction and water content and other parameters.
14 employed molecular dynamics to explore the diffusion of water and ethanol mixtures in model PVA systems, based on oligomers of 50 monomers. Diffusion of water and benzene in model PVA systems was also considered by Noorjahan et al.15 The behavior of water confined in polyelectrolytes systems has also been explored using molecular simulations in the context of perfluorinated membranes (i.e. Nafion), reverse osmosis and desalination.16–23 In general, all these studies provide a wealth of guidance on required simulation times, scenarios for the diffusion behavior as a function of polymer volume fraction and water content and other parameters.
One of the main questions to address in molecular simulation studies of transport in the hydrated polymer systems is how actually water diffuses in these systems as a function of the degree of hydration and other parameters. Let us briefly explore the key issues that we might encounter when approaching the analysis of diffusion under confinement. The conventional approach to the analysis of transport phenomena in molecular simulations is to extract the self-diffusion coefficient using either the Einstein or Green–Kubo formulas, assuming a normal (in other words, Gaussian) diffusion process. However, many complex systems, including diffusion in porous materials and polymers, do not follow normal diffusion. For example, in one of the proposed mechanisms, a diffusing molecule is trapped in a cage formed by slowly moving obstacles (or trapped by some other out-of-equilibrium environment). The obstacles may rearrange with time, allowing the particle to escape. However, this leads to long waiting times and a sub-diffusion process. Crowded colloidal environments, such as biological cells, fall into this category of sub-diffusive systems. From the theoretical point of view, continuous time random walk (CTRW) model with a heavy-tailed distribution of waiting times describes this mechanism.24 In another model, a molecule diffuses in a porous space (or generally speaking through a system of obstacles) featuring numerous structural dead-ends, also leading to obstructed diffusion. A theoretical model of a random walk on fractal porous supports has been shown to exhibit sub-diffusive behavior of this type.24 The hallmark of anomalous diffusion is a non-linear time dependence of the mean-squared displacement (MSD). Over the years, several theories have been proposed to describe various anomalous regimes.24
One can imagine that for a solvent confined in a non-rigid polymer matrix, complex and anomalous diffusion behavior may also take place. Indeed, Müller-Plathe observed in his early studies that water molecules would spend a significant amount of time in a particular cage formed by the polymer, before jumping to another cage when thermal fluctuations open a transient channel between the two cages.13 Sub-diffusive behavior of solvent in a system of charged polymer chains has been observed by Pandey et al.,25 Savage et al.26 described persistent sub-diffusive proton transport in hydrated perfluorosulfonic acid. Influence of chain length and polymer concentration on the extent of sub-diffusive behavior has been explored by Kozanecki et al.27 Sub-diffusion behavior of gas molecules in polymer matrices of different composition and morphology has been also observed and characterized by Anderson et al.28 More recently, Zhang et al.29 proposed a general model of transport in glassy polymers, carefully characterizing different regimes of diffusion and their relation to the behavior of polymer permeability and selectivity on the Robeson plot.30
The objective of this study is to propose a plausible molecular model of an FTM, elucidate its structural organization on a molecular level, and explore properties of water confined in these structures as a function of the degree of hydration and the protonation state of the membrane. We focus specifically on PVAm as the most studied system and also corresponding to the highest density of amine moieties per monomer in the chain. Ultimately, we are aiming to shed some light on the nature of transport phenomena in these materials.
2 Methodology
This article explores the diffusion of water and ions in a model of hydrated PVAm membranes as a function of the degree of hydration and degree of protonation using molecular dynamics (MD) simulations. Here, we treat the hydrated PVAm membrane as a binary system of polymer chains and water molecules. The first step encompasses the preparation of a system containing polymer chains and the appropriate number of water molecules and ions if required. The system is equilibrated through a series of molecular dynamics steps, varying in temperature and pressure. The resulting structure serves as an initial configuration for the subsequent studies of the dynamics of water and other properties. We use several alternative perspectives to discuss the possible correlations between the structure of the membrane on a molecular level and the mobility of water and ions. To characterize the membrane structure and pore morphology we determine the free volume, pore limiting diameter, pore size distribution, and surface area. The propensity of water molecules to form clusters and connected networks through the entire polymer structure as a function of the degree of hydration and protonation is analyzed using several complementary computational tools. We explore the behavior of the MSD and several other functions obtained from molecular dynamics to understand the nature of the diffusion mechanism of water and ions in these systems. In the following subsections, we describe the details of the methods and parameters associated with the different stages of the model construction and provide the definitions of the properties involved.2.1 Generation of hydrated polymer systems
Little is known about the organization of hydrated PVAm membranes on a molecular level, except that they are disordered, amorphous structures. Construction of realistic molecular models of disordered porous materials remains a challenging problem. In the studies of porous polymers, several strategies have been proposed to model the process of polymerization and cross-linking.31–33 In the case of hydrated polymers, several approaches can be encountered in the literature. For example, Müller-Plathe13 and Noorjahan et al.15 used a single polymer chain of 400 monomer units to model the hydrated PVA structure. To relax and equilibrate the structure, the chain is subjected to a separate molecular dynamics run at an elevated temperature. In the context of hydrated polyelectrolyte ion or proton exchange membranes (i.e., Nafion), the polymer structure is often modelled as a system of polymer chains (15–80) of 10–70 monomers.16,34–36In this work, the polymer is represented as a system of 25 polymer chains of 20 monomers each (see Section 2.8 on further discussion of the appropriateness of the model). To equilibrate the initial configuration of the system containing the polymer component and the required amount of water, the 21-step compression–relaxation scheme of Larsen et al.37 is executed. Several steps in this scheme involve simulation of a system at a high pressure, which is likely to have very little impact on the hydrated systems (as its behavior is akin to that of an incompressible liquid under most of the conditions). Possibly, simpler protocols or a reduced version of the protocol of Larsen et al.37 could have been used to arrive at the same initial structures. We reported the number of water molecules of all systems studied in Table S2 of the ESI.†
2.2 Molecular dynamics simulation
Molecular dynamics simulations are performed with the GROMACS software.38–44 We consider a cubic box, with periodic boundary conditions imposed in all directions, and the size of the box varying between 31.0 and 42.0 Å depending on the composition and conditions. Simulations are performed in the isothermal–isobaric (NPT) ensemble at P = 1 bar T = 300 K. The temperature and pressure are maintained constant using the Nosé–Hoover thermostat,45 and the Parrinello–Rahman barostat46 with the coupling constant equal to 2.0 ps for both. The time step for the equilibration and the production run is 1 fs. The Particle-Mesh Ewald (PME) method,47 is used for electrostatic interaction, with a cut-off of 9 Å. A cutoff of 9 Å is also set for the Lennard-Jones interactions, with the use of long-range dispersion corrections for energy and pressure. For structural characterization of model polymer systems, we perform a series of fourteen molecular dynamics runs of 5 ns, with each run starting from a new set of initial velocities of the components of the system. The structural properties are analyzed and averaged using the last configuration from each run. To obtain self-diffusion coefficients of water and chloride ions we perform 200 ns simulations and explore long-time behavior of the mean-squared displacement (MSD) function, see further details on this analysis in Section 2.7.2.3 Force field parameters
Here we summarize the essential details of the force field parameters in this study. We employ TIP4P/200548 model for water, as it exhibits a good agreement of static (density) and dynamic (self-diffusion coefficient) properties with the experimental data under conditions of interest. The bonded and non-bonded interaction parameters for the polymer chains and the monovalent ions (Cl−) are obtained from the AMBER99 force field.49 Initially, we obtained the partial charges for the unprotonated system using ab initio calculations. For this, we employed B3LYP density functional theory50 with the 6-31G* basis set, followed by the restrained electrostatic potential (RESP)51 charge fitting using AmberTools.52 Further investigations revealed that the values obtained are in a good agreement with the partial charges calculated by Kondinskaia et al.53 using a similar methodology. Therefore, for the protonated systems (P20 and P50), rather than performing DFT studies ourselves, we adopted the partial charges provided by Kondinskaia et al.53 Additional details about the model for partial charges and force field parameters can be found in the ESI.†2.4 Systems
The systems under consideration are binary mixtures of polymer and water components. Each system is considered in twelve states of hydration from 0% to 90%, with the degree of hydration defined as: | (1) |
In summary, we consider three protonation states with each of them investigated at twelve different levels of hydration. To designate a particular system, we use the notation PxxWxx, where Pxx denotes the degree of protonation and Wxx the degree of hydration; for example, P20W40 will refer to the 20% protonated system with 40% water content (when W = 40) according to eqn (1). The complete summary of the compositions of all thirty-six systems is provided in the ESI.†
2.5 Structural characterization of polymer matrix
In this section, we provide details of the methods employed for the structural characterization of the polymer matrix. Several computational tools, such as Zeo++56 and MOFOMICS/ZEOMICS,57 have been recently developed for structural characterization of porous materials. Here we employ Poreblazer, a Fortran 90 code developed by Sarkisov and Harrison.58 All calculations presented in this study are carried out with the v3.0.7 version available on GitHub.59Fig. 1 illustrates specific properties obtained using Poreblazer and their relevance to the dynamics of confined water molecules. The free volume is the porous space available within the polymer structure. This property plays a central role in many theories of diffusion in polymer materials.60 Yet, it seems there is still no consensus on how to rigorously define and calculate this property using either geometric or thermodynamic methods.61 In this study, the free volume of the polymer is the volume enclosed by the so-called Connolly surface left by the edge of the probe molecule rolling over the atoms of the polymer structure (see Fig. 1). The probe particle has the size of 3.1589 Å, which is the value of the σ Lennard-Jones parameter for the oxygen atom in the TIP4P/2005 water model we employ. Fractional free volume (FFV) is then defined as: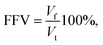 | (2) |
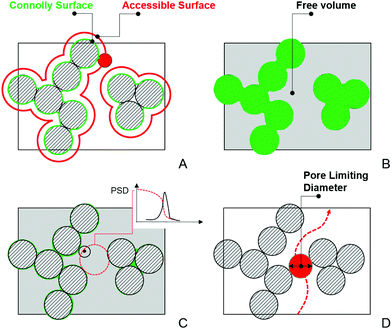 | ||
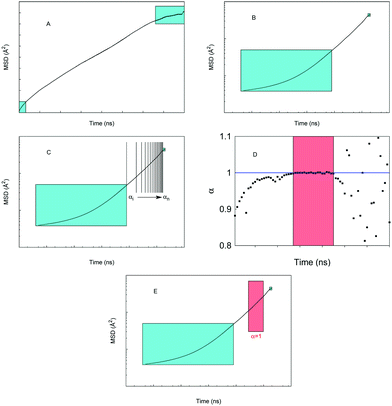
| Fig. 1 Schematic description of the structural properties calculated by Poreblazer. In this schematic, striped circles represent atoms of the structure. (A) The definition of the Connolly (green) and accessible (red) surfaces. The red circle represents a probe particle “rolling” on the surface of the atoms of the structure. (B) Free volume, shown as the grey area, defined as the volume enclosed by the Connolly surface. (C) Within the free volume, geometric methods can be used to obtain pore size distribution.62 As an example, a test point (shown as a black dot) is assumed to belong to a pore of a particular diameter (and all pores of smaller diameter) if a spherical probe of this diameter is the largest sphere that contains the point, without overlapping with any framework atoms. This sphere is schematically depicted as a dashed red circle in the figure. This analysis produces a cumulative pore volume distribution as a function of pore size, and pore size distribution, shown schematically in the inset. (D) Schematic illustration of the pore limiting diameter, shown as a red circle. It is the size of the largest probe that can traverse from one side of the system to the other. | ||
Within the disordered structure of the polymer matrix, the ability of a molecule to move from one cavity or pore to another (and ultimately diffuse through the membrane) will depend on the size of windows and openings between the porous compartments. Pore limiting diameter (PLD) is the size of the largest probe molecule that can traverse or diffuse through from one side of the simulation cell to the other. A PLD smaller than the size of the water molecule (≈3 Å) would indicate that the system consists of the pores isolated from each other, from the perspective of this molecule, by impassable windows. The water molecules in such a system will be largely confined to staying within the pores indefinitely. Poreblazer uses a lattice representation of porous space and the Hoshen–Kopelman percolation algorithm to obtain PLD.63 The accessible surface area (ASA), defined as the area formed by center the probe molecule rolling over the atoms of the polymer structure (see Fig. 1) is analogous to the surface area obtained experimentally using, for example, the Brunauer–Emmett–Teller method.64 The surface area is a key property of porous materials in the adsorption studies. Here we employ it to characterize hydrated polymers in terms of the surface exposed to water molecules. To this end, Poreblazer implements a Monte Carlo algorithm also described by Gelb and Gubbins in the context of porous glasses.62,64,65
2.6 Structural characterization of confined water
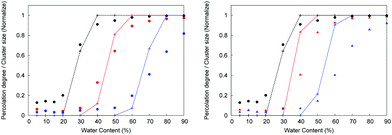
We now switch to the structural characterization of the confined water phase. In particular, we are interested in the size and number of water clusters as a function of the degree of hydration and the presence of ions. We are also interested in identifying the degree of hydration at which the water phase forms a fully percolated network spanning the membrane. We intuit that this condition will help us define two regimes of water diffusion, i.e., bulk-like diffusion of water molecules surrounded by other water molecules and a hopping mechanism,13 where water molecules are confined within separated pores and can only diffuse when a transient void in the polymer is formed. Analysis of the water clusters is performed according to the following methodology. Two water molecules are considered to be connected if the distance between their oxygen atoms is less than 3.5 Å (this distance corresponds to the first minimum in the oxygen–oxygen radial distribution function (RDF) for the bulk liquid TIP4P/2005 water at ambient conditions48). A pathway, consisting of these pairwise connections can be constructed for any two water molecules within a cluster. A simple recursive algorithm is used to calculate the distribution of the clusters in the system given the xyz coordinates of the oxygen atoms, with the mean cluster size Mcl obtained using:66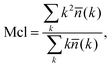 | (3) |
![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) (k) is the mean number of clusters of size k. Throughout the article we use the normalized cluster size by dividing properties such as the mean cluster size in eqn (3) by the total number of water molecules in the system. In the case of the largest cluster in the system, this number then indicates the proportion of molecules in the system associated with this cluster. A cluster is considered to be percolating the system if it completely spans (forms a connected network) the system in at least one dimension. We characterize the propensity of the system to be in this percolated state by calculating the percolation probability, in other words, the frequency of observing the percolating cluster in several independent runs. In these calculations, observing no percolating cluster has a numerical value of zero; observing a percolated cluster in one dimension has a numerical value of 1/3; in two dimensions 2/3 and in three dimensions, 1. This property is closely related to the pore limiting diameter, described earlier. However, PLD indicates the simple geometric possibility for water molecules to diffuse across the system (which may or may not happen at the specific level of hydration), whereas the percolation analysis of the water cluster indicates whether continuous water network is present in the system. In the calculation of all the structural properties above a question emerges on how to treat the mobile ions present in the protonated systems. As we will show later, the mobility of chloride ions in this study is lower than that of water and higher than the mobility of polymer chains. Thus, in the case of protonated systems, where ions are present, the structural properties of both the polymer and water are calculated in two different ways: treating ions as a part of the polymer matrix and as part of the mobile solvent.
(k) is the mean number of clusters of size k. Throughout the article we use the normalized cluster size by dividing properties such as the mean cluster size in eqn (3) by the total number of water molecules in the system. In the case of the largest cluster in the system, this number then indicates the proportion of molecules in the system associated with this cluster. A cluster is considered to be percolating the system if it completely spans (forms a connected network) the system in at least one dimension. We characterize the propensity of the system to be in this percolated state by calculating the percolation probability, in other words, the frequency of observing the percolating cluster in several independent runs. In these calculations, observing no percolating cluster has a numerical value of zero; observing a percolated cluster in one dimension has a numerical value of 1/3; in two dimensions 2/3 and in three dimensions, 1. This property is closely related to the pore limiting diameter, described earlier. However, PLD indicates the simple geometric possibility for water molecules to diffuse across the system (which may or may not happen at the specific level of hydration), whereas the percolation analysis of the water cluster indicates whether continuous water network is present in the system. In the calculation of all the structural properties above a question emerges on how to treat the mobile ions present in the protonated systems. As we will show later, the mobility of chloride ions in this study is lower than that of water and higher than the mobility of polymer chains. Thus, in the case of protonated systems, where ions are present, the structural properties of both the polymer and water are calculated in two different ways: treating ions as a part of the polymer matrix and as part of the mobile solvent.
Another approach to characterize the structure of the confined water versus the polymer and the ions (if present) is to compute the radial distribution function (RDF) and the coordination number (CN). The RDF gives the probability of finding an atom/molecule at a particular distance from another atom of the molecule. The CN indicates how many atoms or molecules can be found in the range of a coordination sphere of a particular radius.
2.7 Diffusion mechanisms
To characterize the mobility of species in model molecular systems, conventionally the self-diffusion coefficient D is obtained from the linear regime of the mean-squared displacement (MSD), according to the Einstein relation:| 〈r2(t)〉 = (2d)Dt, | (4) |
The most significant challenge in the case of the confined systems is whether the diffusion behavior follows the Einstein relation. In the systems under consideration, we may encounter molecules stuck in isolated cavities, diffusing sporadically from one compartment to the other because of the energy barriers, or molecules diffusing freely in the time frame of the simulation. The evaluation of the self-diffusion coefficient from the Einstein relation implies that this equation and regime is appropriate for the system of interest. Deviation from this value would indicate some other regimes of diffusion or much longer time scales needed to establish the normal self-diffusive regime if it is possible. A more general expression which encompasses possible deviations from the normal diffusion can be formulated as follows:
| 〈r2(t)〉 = (2d)Dαtα, | (5) |
The sub-diffusive regime can be identified by plotting the MSD versus time on the log–log scale. It corresponds to the region where the MSD linearly increases with a slope α < 1. If α = 1 then we recover the original normal diffusion regime, eqn (4). Hereafter, we use D to denote the self-diffusion coefficient for normal diffusion, obtained from eqn (4) and Dα to indicate the diffusion coefficient or sub-diffusion coefficient obtained from eqn (5). What is more challenging is to determine whether the observed (and if observed) sub-diffusive behavior is a transient phenomenon and simply longer times are required to establish a proper Gaussian regime, or indeed the deviation of α from 1 is a sign of anomalous diffusion mechanism present in the system. To establish this picture, typically more advanced analysis is required, using properties such as non-Gaussian parameter α2(t) = 3〈r4(t)〉/(5〈r2(t)〉2) − 1. As a function of time, this property goes through a peak, with the height of the peak corresponding to the degree of sub-diffusive behavior in the system and the position corresponding to the time scales where diffusion deviates most significantly from the Gaussian process.68 Other properties one might consider to provide a more complete picture of sub-diffusive regimes is the probability distribution function of waiting times in the pores and probability distribution function of single particle displacement.29 Here we limit ourselves to extracting self-diffusion coefficients in the regimes that are reasonably close to the Gaussian processes, while deeper characterization of the nature deviations from these regimes will be explored in further studies. At the end of the next section on the sensitivity and error analysis, we provide more details on the specific protocol employed to estimate these properties in different systems.
2.8 Sensitivity and error analysis
This section deals with the sensitivity of the predicted trends to the properties of the model and the statistical uncertainty of the observed results. We begin with the accuracy of the model employed. The first issue one may want to discuss is the selection of the force field. In the absence of direct comparison with the experimental data, the choice of the force field becomes somewhat arbitrary. Our approach is guided by previous studies and compatibility of the selected force fields with the chemistry of the systems.53Previous simulation studies on hydrated polymers encompass a range of strategies in the construction of model systems.16,69,70 When using short polymer chains as building blocks of the membrane, a question naturally arises as to whether these oligomers can adequately represent the structure of real polymers based on much longer molecules. The sensitivity of the predictions of the model (for both structural and dynamic properties) was tested in a series of preliminary studies on the unprotonated system. Specifically, systems based on 25 chains of 20 and 50 monomers, were investigated at 300 K at nine different water contents. In this analysis, we followed the same protocol as described in Section 2.1. As summarized in the ESI,† we observed no significant difference in the dynamics and structural properties between the systems with polymers of different lengths at the same water content.
The second factor deals with insufficient sampling and statistical uncertainty of the observed structural and dynamic properties. Typically, in the models based on the representation of the polymer as a system of finite chains, the diffusion of oligomers is considered to be so slow that it is not taken into account and only the diffusion of water and other components of the solvent is investigated. What is important, however, is that the polymer chains remain flexible as the movement of the polymer segments plays an important role in the diffusion of water molecules.14,16,36 In a sense, these models consider water confined in a disordered matrix of obstacles (polymer chains), with some internal degrees of freedom (chain flexibility). This, however, poses the question of whether the observed dynamic properties of the confined water are specific to a particular matrix configuration. In principle, this issue can be addressed either by taking a system large enough, so it is sufficiently representative of possible polymer chain configurations (further increase in the system size does not change the results), or by averaging the properties of the confined species over several matrix realizations (the results should agree with the results for macroscopically large matrix structure and should not be affected by the change in system size). Here, we probe the sensitivity of the obtained results to matrix realization by considering structural and dynamic properties in several independently generated polymer matrices. The results are summarized in the ESI.† They do not reveal significant sensitivity of the results, indicating that we are likely to be close to a matrix of sufficient size for the properties to become independent of the matrix realization.
Reliable estimation of the self-diffusion coefficient from the Einstein relation can often be challenging and comes with significant uncertainties.71 To understand this, let us consider the simplest case: the self-diffusion coefficient for bulk liquids under ambient conditions. Calculation of the self-diffusion coefficient relies on finding a linear fit to the mean-squared displacement (MSD) as a function of time. In this process, it is important to recognize that the first part of the curve may correspond to the regimes deviating from the linear Einstein relation and should be excluded from the analysis. Furthermore, the Einstein relation is supposed to describe the long-time behavior of the system. MSD values evaluated at longer times of the simulation suffer from poor statistics, because of the small number of samples available. Therefore, the self-diffusion coefficient is typically evaluated at a specific time interval, skipping the short-time and long-time regions of the MSD versus time plot.
In the case of systems with a relatively small number of particles present, the situation is further complicated: since the MSD is now averaged over a small number of particles and trajectories it suffers from poor statistics and noise. As a result, it is difficult and computationally expensive to estimate the slope of the MSD line reliably. For example, to obtain a reliable result for carbon dioxide self-diffusion coefficient in water, Moultos et al.72 performed twelve independent simulations, considering different configurations and velocities for the initial conditions in each case. Wang et al.73 proposed to average MSD trajectories from several independent runs to obtain a more statistically reliable representation of the MSD behavior as a function of time. Pranami et al.71 also recommended conducting multiple independent simulations to obtain reliable estimates of the dynamic properties and their uncertainties.
Here we adopted the following protocol. Each system (corresponding to particular hydration and protonation states) is simulated using 14 independent runs, with 5 ns of the production run for each simulation, unless otherwise specified. Structural properties of the matrices (FFV, PLD, surface area, etc.) are obtained as averages of the properties at the end of each of the 14 runs.
The MSD values as a function of time averaged over these runs indicate that in the short time scales (5 ns) most of the systems and conditions under considerations follow anomalous diffusion. Characteristic time scale analysis suggests that more appropriate time scales required for the Gaussian diffusion regime to develop exceed tens of nanoseconds. Here we perform 200 ns simulations for a selection of systems, given the significant computational cost of these simulations. Furthermore, also because of the computational cost, it is not feasible at the moment to perform multiple simulations to obtain an averaged MSD as was proposed in the previous studies. Our protocol for obtaining properties of interest from this long run simulation is schematically depicted in Fig. 2.
Specifically, panel (A) shows a typical MSD trajectory as a function of time. At shorter time scales the MSD is known to deviate from the normal linear behavior. At very long times, the statistics and accuracy of the MSD values suffer from limited number of time segments available to obtain MSD. Hence, in panel (A) we indicate as cyan squares the regions of MSD discarded from further analysis; this truncation became standard practice in the studies of MSD trajectories. In our cases, we discard the 1 ns at the beginning and the end of the MSD, obviously this is specific for the system under consideration, and other systems may require longer exclusion times. Panel (B) shows the same data in log–log coordinates. The trajectory beyond the short-time exclusion region is divided into small 3 ns time segments and for each segment, eqn (5) is fitted, giving the value of the anomalous diffusion coefficient α of the segment, panel (C). The values of α are then plotted as a function of time. Schematically, this is shown in the panel (D). From this illustration (which qualitatively reflects a typical behavior we observed in the system) at shorter length scales α < 1, signifying deviation from the normal diffusion regime. At long times, beyond a certain threshold, the trajectories suffer from poor statistics, and the values of α become scattered. In between these two regions, a steady regime is observed, with α approaching one. This segment of time is identified and eqn (5) and (4) are refitted to this segment to obtain diffusion characteristics, as schematically depicted in panel (E). In the results below, we explicitly specify what segment was used in the final fitting process.
3 Results and discussion
The result section consists of two parts. We first focus on the structural characteristics of the model membrane systems as a function of the degree of hydration and protonation. In the second section, this analysis is used to aid the interpretation of the diffusion behavior of water and chloride ions in these systems.3.1 Structural analysis of the model membranes and confined water phase
We begin this section by showing in Fig. 3, several computer visualizations of model P00 membranes, corresponding to different degrees of hydration and swelling at 300 K. These visualizations already provide some insight into the structure (and hence possible diffusion behavior) of water confined in these structures. At 10% hydration level (W10), we observe either individual water molecules or very small clusters (2–3 molecules as seen in the visualization). At 50% hydration level, clusters of water molecules form; they seem to be separated from each other by constrictions formed by polymer chains. At the highest hydration level, 90%, water appears to form a continuous phase. Below we develop a more quantitative analysis of these features. | ||
| Fig. 3 Molecular visualizations of the model PVAm membrane, P00 at different levels of water content. From left to right: W10, W50, and W90 as defined in the text. Polymer chains are shown in grey; for water molecules, red is used for oxygen atoms and white for hydrogen atoms. The green lines indicate the size of the simulation box in the periodic boundary conditions: from left to right 32.0 Å, 35.6 Å, and 38.9 Å, respectively. The computer visualizations were generated using the VMD software.74,75 | ||
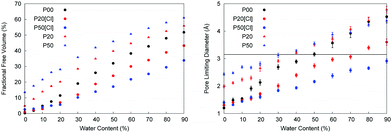
The mobility of molecules inside a porous matrix is governed by the available free volume. Fig. 4 shows the behavior of FFV in the systems under consideration as a function of hydration level.
As shown in Fig. 4, the FFV increases linearly with the water content and the diffusion coefficient is also expected to increase as a function of the hydration levels. The protonated systems, shown in blue and red symbols, present an interesting case. These systems contain chloride ions. At this stage, we have not yet presented the simulation results for the mobility of these ions. However, we can consider two extreme hypothetical scenarios. In the first scenario, the mobility of chloride ions is the same as the mobility of water molecules. The space available for the diffusion of water molecules is essentially the space not occupied by the polymer chains. To consider this scenario, we ignore chloride ions in the calculation of the FFV and PLD, with the resulting values shown as triangles in Fig. 4. The FFV of the protonated systems is significantly higher than that of the unprotonated systems at the same levels of hydration. This is a result of the coulombic repulsion and the charged polymer chains being more stretched than the uncharged polymer chains (this is confirmed by the analysis of the average radius of gyration, see the ESI†). The effect is particularly strong at low water content (the FFV for the P50W05 system is ten times larger than that for the P00W05 system) and increases with the level of protonation. As the hydration level increases, this opens more opportunities for the rearrangement of chloride ions and for screening of the charged groups by water. However, in the P50W90 system, the FFV is 1.2 times larger than in the P00W90 system. Therefore, under the scenario where mobility of chloride ions is the same as the mobility of water one would expect higher diffusion coefficients for water in the protonated systems compared to the unprotonated systems. In the second scenario, we hypothesize that the mobility of the chloride ions is significantly lower than that of water. In the extreme case, we can assume that the chloride ions have the same mobility as the polymer chains (in other words, essentially immobile on the time scales characteristic for water diffusion). In this situation, chloride ions play a role of obstacles for the mobility of water in the same way polymer chains do and should be considered as a part of the polymer structure. The space available for the diffusion of water molecules is then the space not occupied by the polymer chains and chloride ions. The FFV values obtained under these assumptions are shown as blue and red circles in Fig. 4 and, not surprisingly, are now substantially lower than that for the unprotonated system. Hence, if the chloride ions do not move on the time scale of the simulations (or move very slowly), the diffusion coefficient for water is expected to be lower in the protonated systems compared to the unprotonated ones.
In the same figure, we also show the analysis of the pore limiting diameter. The significance of this property is as follows. The diameter of water molecule can be taken as 3.1589 Å based on the value of σ Lennard-Jones parameter for the oxygen atom in the TIP4P/2005 model. If the pore limiting diameter is below this value, it indicates that the diffusion of water is either limited to diffusion within the isolated pores in the structure; or is hampered by water molecules having to cross windows smaller than the water diameter, which is an activated process. If the pore limiting diameter is above this value, it opens a possibility for water diffusion across the whole system without having to pass the constrictions (which involves a high energy barrier) or to wait for the voids to form. Of course, this is only an idealized, simplified picture. In reality, some water molecules will be located in the isolated clusters, some will be located in the cavities with occasional opportunity to escape and some will belong to a connected percolated cluster of water molecules. From the Fig. 4 one can see that the P00 system reaches the threshold at around 50% hydration level. In the case of the protonated systems, again the results will be different, depending on whether chloride ions are included in the analysis as part of immobile polymer structure or not. However, the results are consistent with the corresponding FFV trends. Indeed, if the chloride atoms are considered as immobile obstacles, the PLD shifts to lower values at the same level of hydration. For example, in the case of the P50 system, the PLD is below 3 Å even at 90% hydration. On the other hand, if we consider only the polymer chains as the structure forming component, the protonated structures appear as more open and the values of PLD are higher at the same level of hydration, compared to the P00 system.
3.2 Diffusion in molecular models of hydrated PVAm systems
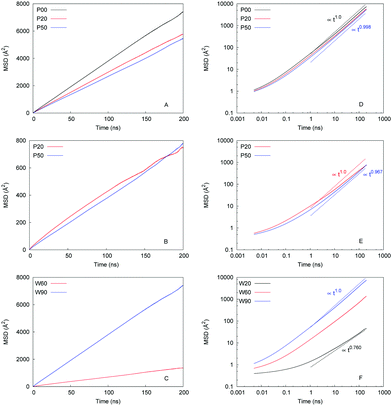
MSD as a function of time is one of the central properties in the analysis of the molecular diffusion phenomena. We begin our study into how water and ions diffuse in model hydrated structures by showing several examples of MSDs under various conditions in Fig. 6.Preliminary conclusions can be obtained simply from visual inspection of this figure. As panel (A) shows, the presence of the ions has a detrimental effect on the diffusion of water and this effect is enhanced with the degree of protonation. By inspecting the actual values of MSD in panel (B) it is evident that diffusion of ions is significantly slower compared to water (on the same timescale of 200 ns, the MSD values for chloride are about ten times lower, compared to water). Panel (C) explores the effect of hydration on the water diffusion in the unprotonated systems. Specifically, change of water content from 90% to 60% results in a significant drop in water mobility as evident from the MSD behaviour; even more dramatic change occurs when the water content is further reduced to 20%, it is not possible to show this MSD in panel (C), however, it is shown in log–log coordinates in panel (F). Panels on the right show the same data as the graphs on the left in log–log coordinates along with the estimates of the MSD slopes, we provide the MSD values for polymer, water, and ion in the ESI.†
Table 1 summarizes the numerical values of the dynamic properties extracted from the data shown in Fig. 6, and in particular compare the impact of confinement to the bulk diffusion coefficients for water and chloride ions at the same temperature. Firstly, we note that none of the anomalous diffusion exponents is strictly one, which could be related to statistical accuracy of our MSD data, the procedure to obtain the dynamic properties from MSD, or some underlying physical processes indeed making the diffusion in these systems slightly non-Gaussian (i.e. small number of molecules, indefinitely stuck in certain regions of the system). We will further comment on this later in this section. The closer is the numerical value of the anomalous diffusion exponent to one, the closer is the agreement between the anomalous diffusion Dα and Einstein diffusion coefficient D, as expected.
| Water | |||||
|---|---|---|---|---|---|
| Bulk | 0.217 (Å2 ps−1) | ||||
| Systems | Range (ns) | α | D α (Å2 ps−α 10−3) | D (Å2 ps−1 10−3) | |
| W20 | 132–136 | 0.976 | 0.0574 | 0.0427 | |
| P00 | W60 | 110–128 | 0.973 | 1.57 | 1.12 |
| W90 | 25–148 | 0.990 | 7.07 | 6.28 | |
| P20 | W90 | 43–121 | 0.983 | 5.99 | 4.91 |
| P50 | W90 | 58–127 | 0.998 | 4.52 | 4.45 |
| Chloride | |||||
|---|---|---|---|---|---|
| Bulk | 0.0932 (Å2 ps−1) | ||||
| Systems | Range (ns) | α | D α (Å2 ps−α 10−3) | D (Å2 ps−1 10−3) | |
| P20 | W90 | 106–112 | 0.904 | 2.09 | 0.629 |
| P50 | W90 | 58–127 | 0.967 | 0.908 | 0.609 |
Taking these values as reasonable estimates of the properties in question, this is our interpretation of the results in Table 1. Even at the highest level of hydration (W90), self-diffusion coefficient of water under confinement is several tens of times lower than that for bulk diffusion. Reducing hydration level to W60 (after the percolation threshold is reached for water cluster connectivity for all systems under consideration) in the unprotonated system, reduces the self-diffusion coefficient further four-five fold compared to the highest hydration regime. The self-diffusion of water at the conditions preceding the percolation threshold (i.e. W20) become difficult to estimate due to the statistical uncertainty and further deviation of the system from the Einstein regime. However, our data indicates one-two orders of magnitude decrease in the diffusion rate compared to W60–90 hydration regimes and three orders of magnitude compared to bulk. This also suggests that a reliable estimation of self-diffusion coefficients in these regimes and a more rigorous analysis of possible anomalous diffusion mechanisms in the system may require much longer trajectories (based on characteristic time scale analysis, in the vicinity of tens of microseconds and longer).
Reliable estimation of numerical values of the self-diffusion coefficient for chloride is also challenging for the same reasons as for water under low hydration regimes: our data indicate that chloride ions diffuse one order of magnitude slower than water and as a result of their presence also hinders diffusion of water around them. This is different from the relative mobility of water and chloride ions in bulk water solutions. According to Lyubartsev et al.,77 the diffusion coefficient chloride ions is approximately 1.6 time lower than the value of that for water in sodium chloride solutions under ambient conditions (300 K, 1 atm). As the concentration of salt increases (up to 4 M), mobility of both water and ions diminishes but the ratio of values remains the same, more or less. Here at similar conditions 300 K and 1 bar, and 0.54 M concentration of sodium chloride, we observe self-diffusion coefficient 2.3 lower than that for water. Compared to the bulk behavior, diffusion of chloride is two orders of magnitude lower under confinement even at the highest hydration regime.
Here we investigate diffusion mechanisms in these systems in more detail. As has been already discussed in Section 3.1.1 earlier, in case of complex structures, such as the model polymer systems considered here we can envision three possible scenarios for solvent and ion diffusion. A molecule trapped in a spatially isolated pore clearly cannot diffuse the distance larger than the size of the pore, thus violating linear scaling of the MSD with time. On the opposite side, is a scenario where molecule diffuses in a bulk-like fashion, surrounded by other molecules of solvent; this is a regime expected at very high hydration levels. In between these two extreme scenarios we deal with a situation of a molecule spending an extended time in a pore before jumping to another pore. At this stage, we do not invoke the complete set of tools and properties required to properly assert the nature of the diffusion mechanism in these systems (as this may require even longer trajectories, more complete statistics, and will be pursued in further studies). Here we are trying to answer a simpler question: what proportion of molecules under different conditions remains confined in the isolated pores even at the longest simulation times, thus potentially leading to apparent sub-diffusive behavior? For this we can compare the MSD trajectories as a function of time against several characteristic length scales present in the system: they are an average pore diameter (APD), maximum pore diameter (MPD), size of the simulation box (BOX). MSD histograms (these are essentially simplified distributions of displacements) are shown in Fig. 7. Let us first consider the case for the W20 hydration regime shown on the left. At 10 ns none of the molecules, effectively, manage to diffuse beyond the box size, although some molecules covered the distances compared to the largest pore present in the system (≈6 Å). At 200 ns, although a significant proportion of molecules traveled distances compared to the box size, about 45% of molecules effectively remain in the original pore. The situation is very different at W90 hydration regime (shown in Fig. 7 on the right) where even at 10 ns all the molecules traveled the distance comparable to the size of the box (≈39 Å).
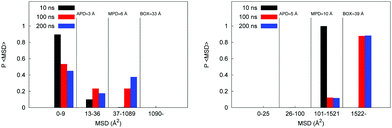 | ||
| Fig. 7 Probability distribution of MSD after 10, 100 and 200 ns for the P00W20 system on the left and the P00W90 system on the right. | ||
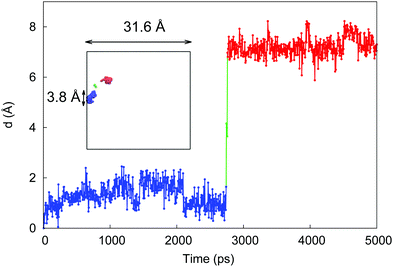
To provide further insight on how molecules travel at low hydration via a hopping mechanism, we tracked the behavior of one particle as shown in Fig. 8. Here a molecule of water spends ≈2.5 ns of the simulation time in one pore (blue line), before rapid transfer into another pore (red line) where it resides till the end of the simulation (5 ns). The location and the sizes of the pores are also provided in the figure, relative to the total system size. This hopping mechanism has been indeed linked to the sub-diffusive behavior in various systems and has also been described in the context of diffusion in polymers.27
4 Conclusions
In this study, we presented a simple molecular model of an FTM membrane comprising a mixture of polymer chains, water and, depending on the state of the polymer chains, ions. Using this model, we investigated structural and dynamical characteristics of the systems as a function of water content and degree of protonation. Our findings can be summarized as follows.At low hydration levels, water confined in these polymer structures exists in the form of clusters of few molecules in size, separated from each other by essentially impassable barriers. For the porous space to become fully accessible by water, with water in the structure forming a single continuous phase, the water content must reach at least 40–50%. Presence of ions shifts this threshold to even higher hydration levels. This picture is consistent with the experimental observations indicating that for the optimal performance FTMs must be operated at 60% water content.8 Mobility of water and ions has been investigated using molecular dynamics and a range of complementary analytical techniques. Under these conditions, we estimated that the self-diffusion coefficient of water is still 200 times lower than that of bulk water and self-diffusion coefficient of chloride ion is two orders of magnitude lower than in low concentration bulk water solutions under the same conditions of pressure and temperature.
These results are a clear manifestation of the very constrained mobility of water and ions under confinement in polymer systems and a plausible physical reason for the high levels of water content and degree of swelling required for an FTM to function properly. This may also suggest that the strategy for further improvement of the performance of FTMs can be associated with the systematic increase of the available free volume. For example, a PIM (polymer of intrinsic microporosity) featuring amine groups would combine both the high and stable free volume of a PIM with the chemical functionality of an FTM. In fact, an amine functionalized PIM has been reported by Mason et al.,78 however, it had not been investigated under humid conditions. According to Fang et al.79 the FFV of PIM-1 is 47% at 300 K which is comparable with the value of 51% of the P00W90 system at 300 K. Recently, more advanced treatments of the diffusive regimes in polymer systems started to emerge.29 These studies recognize that a new theoretical framework is required for systems operating in sub-diffusive regimes which would allow making quantitative predictions about the mobility of species using some morphological characteristics of the structure. These theoretical approaches combined with other tools already available for quantification of sub-diffusive regimes will be required to provide a more complete picture of the nature of diffusion mechanisms in these systems, particularly at lower hydration regimes. In the context of the FTM properties and functionality, further studies are needed to understand the mobility of the ions and dissolved gases and, in particular, the dependence of the diffusion mechanisms on temperature.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
We would like to thank Dr Abbie Trewin, Dr Matthew Borg and his colleagues, Dr Santiago Romero-Vargas Castrillion, and Mr Odin Kvam for very useful discussions of the manuscript. This work was supported by the European Union's Horizon 2020 Research and Innovation program [Grant Agreement No. 727734]. This work has made use of the resources provided by the Edinburgh Compute and Data Facility (ECDF) (http://www.ecdf.ed.ac.uk/).Notes and references
- Z. Tong and W. W. Ho, Sep. Sci. Technol., 2017, 52, 156–167 CrossRef CAS.
- S. Rafiq, L. Deng and M.-B. Hägg, ChemBioEng Rev., 2016, 3, 68–85 CrossRef CAS.
- M.-B. Hägg and A. Lindbråthen, Ind. Eng. Chem. Res., 2005, 44, 7668–7675 CrossRef.
- M. Sandru, T.-J. Kim and M.-B. Hägg, Desalination, 2009, 240, 298–300 CrossRef CAS.
- L. Deng, T.-J. Kim, M. Sandru and M.-B. Hägg, Proceedings of the 1st Annual Gas Processing Symposium, 2009, pp. 247–255.
- L. Deng, T.-J. Kim and M.-B. Hägg, J. Membr. Sci., 2009, 340, 154–163 CrossRef CAS.
- M. Sandru, S. H. Haukebø and M.-B. Hägg, J. Membr. Sci., 2010, 346, 172–186 CrossRef CAS.
- L. Deng and M.-B. Hägg, J. Membr. Sci., 2010, 363, 295–301 CrossRef CAS.
- M. W. Uddin and M.-B. Hägg, J. Membr. Sci., 2012, 423, 143–149 CrossRef.
- M. W. Uddin and M.-B. Hägg, J. Membr. Sci., 2012, 423, 150–158 CrossRef.
- T.-J. Kim, H. Vrålstad, M. Sandru and M.-B. Hägg, J. Membr. Sci., 2013, 428, 218–224 CrossRef CAS.
- Y. Li, S. Wang, G. He, H. Wu, F. Pan and Z. Jiang, Chem. Soc. Rev., 2015, 44, 103–118 RSC.
- F. Müller-Plathe, J. Membr. Sci., 1998, 141, 147–154 CrossRef.
- Q. G. Zhang, Q. L. Liu, Y. Chen, J. Y. Wu and A. M. Zhu, Chem. Eng. Sci., 2009, 64, 334–340 CrossRef CAS.
- A. Noorjahan and P. Choi, Chem. Eng. Sci., 2015, 121, 258–267 CrossRef CAS.
- A. Vishnyakov and A. V. Neimark, J. Phys. Chem. B, 2001, 105, 9586–9594 CrossRef CAS.
- R. Devanathan, A. Venkatnathan and M. Dupuis, J. Phys. Chem. B, 2007, 111, 8069–8079 CrossRef CAS PubMed.
- R. Devanathan, A. Venkatnathan and M. Dupuis, J. Phys. Chem. B, 2007, 111, 13006–13013 CrossRef CAS PubMed.
- K. P. Lee, T. C. Arnot and D. Mattia, J. Membr. Sci., 2011, 370, 1–22 CrossRef CAS.
- M. Ding, A. Ghoufi and A. Szymczyk, Desalination, 2014, 343, 48–53 CrossRef CAS.
- M. Shen, S. Keten and R. M. Lueptow, J. Membr. Sci., 2016, 506, 95–108 CrossRef CAS.
- E. Harder, D. E. Walters, Y. D. Bodnar, R. S. Faibish and B. Roux, J. Phys. Chem. B, 2009, 113, 10177–10182 CrossRef CAS PubMed.
- M. Kotelyanskii, N. Wagner and M. Paulaitis, J. Membr. Sci., 1998, 139, 1–16 CrossRef CAS.
- R. Metzler and J. Klafter, Phys. Rep., 2000, 339, 1–77 CrossRef CAS.
- R. Pandey, A. T. Bernardes, G. M. Foo and D. Stauffer, J. Chem. Phys., 1996, 105, 1682–1690 CrossRef CAS.
- J. Savage and G. A. Voth, J. Phys. Chem. Lett., 2014, 5, 3037–3042 CrossRef CAS PubMed.
- M. Kozanecki, K. Halagan, J. Saramak and K. Matyjaszewski, Soft Matter, 2016, 12, 5519–5528 RSC.
- L. R. Anderson, Q. Yang and A. M. Ediger, Phys. Chem. Chem. Phys., 2018, 20, 22123–22133 RSC.
- K. Zhang, D. Meng, F. Müller-Plathe and S. K. Kumar, Soft Matter, 2018, 14, 440–447 RSC.
- L. M. Robeson, J. Membr. Sci., 2008, 320, 390–400 CrossRef CAS.
- J. M. Thomas and A. Trewin, J. Phys. Chem. C, 2014, 118, 19712–19722 CrossRef CAS.
- L. J. Abbott, K. E. Hart and C. M. Colina, Theor. Chem. Acc., 2013, 132, 1334 Search PubMed.
- L. J. Abbott and C. M. Colina, Macromolecules, 2011, 44, 4511–4519 CrossRef CAS.
- S. Urata, J. Irisawa, A. Takada, W. Shinoda, S. Tsuzuki and M. Mikami, J. Phys. Chem. B, 2005, 109, 4269–4278 CrossRef CAS PubMed.
- K. B. Daly, J. B. Benziger, P. G. Debenedetti and A. Z. Panagiotopoulos, J. Phys. Chem. B, 2013, 117, 12649–12660 CrossRef CAS PubMed.
- S. Sengupta, R. Pant, P. Komarov, A. Venkatnathan and A. V. Lyulin, Int. J. Hydrogen Energy, 2017, 42, 27254–27268 CrossRef CAS.
- G. S. Larsen, P. Lin, K. E. Hart and C. M. Colina, Macromolecules, 2011, 44, 6944–6951 CrossRef CAS.
- M. J. Abraham, T. Murtola, R. Schulz, S. Páll, J. C. Smith, B. Hess and E. Lindahl, SoftwareX, 2015, 1, 19–25 CrossRef.
- S. Pall, M. J. Abraham, C. Kutzner, B. Hess and E. Lindahl, International Conference on Exascale Applications and Software, 2014, pp. 3–27.
- S. Pronk, S. Páll, R. Schulz, P. Larsson, P. Bjelkmar, R. Apostolov, M. R. Shirts, J. C. Smith, P. M. Kasson and D. Van Der Spoel, et al. , Bioinformatics, 2013, 29, 845–854 CrossRef CAS PubMed.
- B. Hess, C. Kutzner, D. Van Der Spoel and E. Lindahl, J. Chem. Theory Comput., 2008, 4, 435–447 CrossRef CAS PubMed.
- D. Van Der Spoel, E. Lindahl, B. Hess, G. Groenhof, A. E. Mark and H. J. Berendsen, J. Comput. Chem., 2005, 26, 1701–1718 CrossRef CAS PubMed.
- E. Lindahl, B. Hess and D. Van Der Spoel, Molecular Modeling Annual, 2001, vol. 7, pp. 306–317 Search PubMed.
- H. J. Berendsen, D. van der Spoel and R. van Drunen, Comput. Phys. Commun., 1995, 91, 43–56 CrossRef CAS.
- D. J. Evans and B. L. Holian, J. Chem. Phys., 1985, 83, 4069–4074 CrossRef CAS.
- M. Parrinello and A. Rahman, Phys. Rev. Lett., 1980, 45, 1196 CrossRef CAS.
- T. Darden, D. York and L. Pedersen, J. Chem. Phys., 1993, 98, 10089–10092 CrossRef CAS.
- J. L. Abascal and C. Vega, J. Chem. Phys., 2005, 123, 234505 CrossRef CAS PubMed.
- J. Wang, P. Cieplak and P. A. Kollman, J. Comput. Chem., 2000, 21, 1049–1074 CrossRef CAS.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS.
- C. I. Bayly, P. Cieplak, W. Cornell and P. A. Kollman, J. Phys. Chem., 1993, 97, 10269–10280 CrossRef CAS.
- D. Case, T. Darden, S. Gusarov, A. Kovalenko and P. Kollman, Amber 2015 (AmberTools15 and Amber14), 2015 Search PubMed.
- D. A. Kondinskaia, A. Y. Kostritskii, A. M. Nesterenko, A. Y. Antipina and A. A. Gurtovenko, J. Phys. Chem. B, 2016, 120, 6546–6554 CrossRef CAS PubMed.
- A. Katchalsky, J. Mazur and P. Spitnik, J. Polym. Sci., Part A: Polym. Chem., 1957, 23, 513–532 CAS.
- R. Pelton, Langmuir, 2014, 30, 15373–15382 CrossRef CAS PubMed.
- T. F. Willems, C. H. Rycroft, M. Kazi, J. C. Meza and M. Haranczyk, Microporous Mesoporous Mater., 2012, 149, 134–141 CrossRef CAS.
- E. L. First and C. A. Floudas, Microporous Mesoporous Mater., 2013, 165, 32–39 CrossRef CAS.
- L. Sarkisov and A. Harrison, Mol. Simul., 2011, 37, 1248–1257 CrossRef CAS.
- poreblazer v3.0.7 Polymer, https://github.com/pfayon/Poreblazer.
- L. Masaro and X. Zhu, Prog. Polym. Sci., 1999, 24, 731–775 CrossRef CAS.
- R. P. White and J. E. Lipson, Macromolecules, 2016, 49, 3987–4007 CrossRef CAS.
- L. D. Gelb and K. Gubbins, Langmuir, 1999, 15, 305–308 CrossRef CAS.
- J. Hoshen and R. Kopelman, Phys. Rev. B: Condens. Matter Mater. Phys., 1976, 14, 3438 CrossRef CAS.
- L. D. Gelb and K. Gubbins, Langmuir, 1998, 14, 2097–2111 CrossRef CAS.
- S. Figueroa-Gerstenmaier, J. Bonet Avalos, L. D. Gelb, K. E. Gubbins and L. F. Vega, Langmuir, 2003, 19, 8592–8604 CrossRef CAS.
- J. Essam, in Phase Transitions Critical Phenomena, ed. C. Domb and M. S. Green, Academic Press, New-York, 1972, vol. 2, p. 197 Search PubMed.
- K. Hahn, J. Kärger and V. Kukla, Phys. Rev. Lett., 1996, 76, 2762 CrossRef CAS PubMed.
- B. Vorselaars, A. V. Lyulin, K. Karatasos and M. Michels, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2007, 75, 011504 CrossRef PubMed.
- F. Müller-Plathe and W. F. van Gunsteren, Polymer, 1997, 38, 2259–2268 CrossRef.
- D. Romero Nieto, A. Lindbråthen and M.-B. Hägg, ACS Omega, 2017, 2, 8388–8400 CrossRef CAS PubMed.
- G. Pranami and M. H. Lamm, J. Chem. Theory Comput., 2015, 11, 4586–4592 CrossRef CAS PubMed.
- O. A. Moultos, I. N. Tsimpanogiannis, A. Z. Panagiotopoulos and I. G. Economou, J. Phys. Chem. B, 2014, 118, 5532–5541 CrossRef CAS PubMed.
- J. Wang and T. Hou, J. Comput. Chem., 2011, 32, 3505–3519 CrossRef CAS PubMed.
- W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graphics, 1996, 14, 33–38 CrossRef CAS PubMed.
- J. Stone, MSc thesis, Computer Science Department, University of Missouri-Rolla, 1998.
- D. Venturi, private communication, Universita di Bologna, 2018.
- A. P. Lyubartsev and A. Laaksonen, J. Phys. Chem., 1996, 100, 16410–16418 CrossRef CAS.
- C. R. Mason, L. Maynard-Atem, K. W. Heard, B. Satilmis, P. M. Budd, K. Friess, M. LancÌ, P. Bernardo, G. Clarizia and J. C. Jansen, Macromolecules, 2014, 47, 1021–1029 CrossRef CAS PubMed.
- W. Fang, L. Zhang and J. Jiang, Mol. Simul., 2010, 36, 992–1003 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c9cp05399a |
| This journal is © the Owner Societies 2019 |