 Open Access Article
Open Access ArticleNear dissociation states for H2+–He on MRCI and FCI potential energy surfaces†
Debasish
Koner
 a,
Juan Carlos
San Vicente Veliz
a,
Ad
van der Avoird
a,
Juan Carlos
San Vicente Veliz
a,
Ad
van der Avoird
 b and
Markus
Meuwly
b and
Markus
Meuwly
 *a
*a
aDepartment of Chemistry, University of Basel, Klingelbergstrasse 80, CH-4056 Basel, Switzerland. E-mail: m.meuwly@unibas.ch
bTheoretical Chemistry, Institute for Molecules and Materials, Radboud University Nijmegen, Nijmegen, The Netherlands
First published on 25th October 2019
Abstract
New potential energy surfaces (PES) have been constructed for H2+–He using a reproducing kernel Hilbert space (RKHS) representation from an extensive number of ab initio energies computed at the multi reference and full configuration interaction levels of theory. For the MRCI PES the long-range interaction region of the PES is described by analytical functions and is connected smoothly to the short range interaction region, represented as a RKHS. All bound ro-vibrational states for the ground electronic state of H2+–He are calculated using two different methods to determine quantum bound states. Comparing transition frequencies for the near-dissociation states for ortho- and para-H2+–He allows assignment of the 15.2 GHz line to a J = 2 e/f parity doublet of ortho-H2+–He whereas the experimentally determined 21.8 GHz line is only consistent with a (J = 0) → (J = 1) e/e transition in para-H2+–He.
I. Introduction
The interaction between ions and neutral atoms or molecules is of central importance in atmospheric and astronomical processes and environments. Prominent species in the interstellar environment include H3+, CH2+, HCO+ and N2H+, among others.1 Additionally, ions are also considered to play an important role in the formation of atmospheric aerosols.2Very recently,3 the HeH+ ion, which was the first molecule of the primordial universe,4 has been detected in interstellar space and means for the direct detection of H2+ have been discussed.5 However, although H2+ is most likely formed and present in space, e.g. through the HeH+ + H → H2+ + He reaction,3 (which is believed to be the first atom–diatom reaction in the universe6) collisions with H and H2 are also important loss channels of the ion. Nevertheless, with H2+ present in the interstellar medium, it is also likely that the H2+–He complex is formed. Hence, H2+–He plays an important role already in the early stages of the Molecular Universe.
The interaction between He and H2+ is also important for the rotational cooling of H2+ through collisions with Helium as the buffer gas.7 This is an attractive way to generate translationally and internally cold H2+ ions suitable for precision measurements.8,9 With even further increased precision and quantum state control of the ions, fundamental natural constants such as the ratio of the electron to the proton mass, me/mp, can be determined with unprecedented accuracy.
Another process of interest which has been recently investigated is the Penning ionization of 3S excited He colliding with H2.10 This process produces H2+–He with sufficient energy to dissociate into ground state and rovibrationally excited He and H2+ fragments. Such rovibrationally inelastic half-collisions are particularly sensitive to the long-range part of the intermolecular potential, which is dominated by polarization interactions induced by the charge and quadrupole of H2+. Furthermore, several long-range states for H2+–He have been characterized from microwave spectroscopy and by using electric field extraction.11,12 However, the interpretation of these spectra has remained elusive, in part due to the limited accuracy of the available potential energy surfaces.
In the past, several PESs have been constructed at different levels of theory to investigate the spectroscopy and dynamics of the H2+–He complex.13–18 To characterize spectral transitions in the microwave region, an accurate long-range potential is required.14,15 However, the level of theory used for the electronic structure calculations in these earlier efforts was rather modest by today's standards. Full configuration interaction (FCI) with the cc-pVQZ basis has been used more recently but no explicit analytical representation was included.17 Later, using the ab initio data of ref. 17 a new PES was constructed by including an explicit analytical formula only for the diatomic potentials.18
In the present work high-level electronic structure methods combined with advanced representation techniques for global potential energy surfaces and accurate representation of the long-range potential are used. With these PESs quantum calculations of all bound states of H2+–He with H2+ in its ground electronic and vibrational state are then carried out. As the near-dissociative states are particularly sensitive to the long range part of the PES, two different, advanced electronic structure techniques are used: Multireference configuration interaction (MRCI) with Davidson correction (+Q) and full configuration interaction calculations, in order to compare their performance. Also, both PESs are augmented with the analytical long range electrostatics for validating the long-range part computed with the two electronic structure methods. First, the computational methods are presented, followed by the discussion of the bound states computed and their interpretation in view of the near-dissociative states.
II. Computational methods
A. The potential energy surfaces
Two different levels of theory – (a) multi reference configuration interaction level including the Davidson correction (MRCI+Q)19,20 with the augmented Dunning-type correlation consistent polarized hexaple zeta (aug-cc-pV6Z)21 basis set and (b) full configuration interaction22,23 with the augmented Dunning type correlation consistent polarized quintuple zeta (aug-cc-pV5Z)24,25 basis set – are used in the present work to calculate the ab initio energies. Initial orbitals for the MRCI calculations were obtained using the complete active space self-consistent field (CASSCF)26–28 method with three 1s orbitals of H and He in the active space. The Molpro29 software was used to perform all electronic structure calculations.The grids for the ab initio energy calculations are set up in Jacobi coordinates (R,r,θ). Here, r is the H2+ bond length, R is the distance between He and the center of mass of the H2+ ion, and θ is the angle between ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) and
and ![[R with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0052_20d1.gif) . The angular grid is defined by Gauss-Legendre quadrature points chosen in the range between 0 ≤ θ ≤ 90° given the spatial symmetry of the system. Details of the angular and radial grids for the MRCI+Q and FCI calculations are given in Tables S1 and S2 in the ESI.†
. The angular grid is defined by Gauss-Legendre quadrature points chosen in the range between 0 ≤ θ ≤ 90° given the spatial symmetry of the system. Details of the angular and radial grids for the MRCI+Q and FCI calculations are given in Tables S1 and S2 in the ESI.†
The complete adiabatic surface for H2+–He can be expressed as a many-body expansion30
 | (1) |
In general, two body interaction energies, i.e., the diatomic potential, for a molecule AB can be expressed as18,31
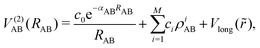 | (2) |
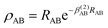 . The long range part, Vlong(
. The long range part, Vlong(![[r with combining tilde]](https://www.rsc.org/images/entities/i_char_0072_0303.gif) ), can be written as14
), can be written as14 | (3) |
![[r with combining tilde]](https://www.rsc.org/images/entities/i_char_0072_0303.gif) is defined as33
is defined as33![[r with combining tilde]](https://www.rsc.org/images/entities/i_char_0072_0303.gif) = r + rl = r + rl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−(r−re)), exp(−(r−re)), | (4) |
| H | He | |
|---|---|---|
| Dipole polarizability αd | 4.5 | 1.384 |
| Quadrupole polarizability αq | 15.0 | 2.275 |
| Octopole polarizability αo | 131.25 | 10.620 |
| First hyperpolarizability βddq | 159.75 | 20.41 |
| Second hyperpolarizability γd | 1333.125 | 37.56 |
| H2+ | HeH+ | |
|---|---|---|
| r l | 10.0 | 8.0 |
| r eq | 2.005815 | 1.4633 |
The linear parameters ci and the nonlinear parameters αAB and β(2)AB in eqn (3) are determined by fitting the expression with the ab initio energies using the Levenberg–Marquardt nonlinear multidimensional fitting method.34 The optimized linear and nonlinear parameters for the diatomic potentials calculated via fitting are given in Tables S3 and S4 (ESI†).
The three-body interaction energies, V(3)(rHeH,rHeH′,rHH′) = V(3)(r,R,θ) are calculated from eqn (1). For a particular configuration of H2+–He, V(3)(r,R,θ) can be calculated using the reproducing kernel Hilbert space35 (RKHS) approach.
The procedure for computing the analytical energy of a given configuration from a set of known ab initio energies is briefly described here. According to the RKHS theorem, the value of a function f(x) can be evaluated from a set of known values f(xi) at positions xi as a linear combination of kernel products
 | (5) |
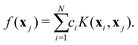 | (6) |
![[f with combining tilde]](https://www.rsc.org/images/entities/i_char_0066_0303.gif) (x) can be calculated analytically from the kernel functions K(x,x′). For a multidimensional function the D-dimensional kernel can be constructed as the product of D 1-dimensional kernels k(x,x′)
(x) can be calculated analytically from the kernel functions K(x,x′). For a multidimensional function the D-dimensional kernel can be constructed as the product of D 1-dimensional kernels k(x,x′) | (7) |
For the radial dimensions (r and R) a reciprocal power decay kernel35
 | (8) |
 | (9) |
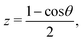 | (10) |
Finally, the 3-dimensional kernel is
| K(x,x′) = k[2,4](R,R′)k[2,4](r,r′)k[2](z,z′), | (11) |
To represent the long range part of the H2+–He interaction the analytical form from ref. 14
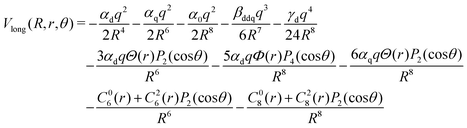 | (12) |
For configurations with R ≳ 9.0 a0 the MRCI+Q/aug-cc-pV6Z calculations are discontinuous along the R-coordinate, see Fig. 1, where MRCI+Q/aug-cc-pV6Z energies are given fixed values of θ and r. For large values of R, MRCI+Q/aug-cc-pV6Z energies are discontinuous which originates from the Davidson correction of the MRCI energies because the order of the states along a potential energy scan can swap. This then leads to discontinuities in the Davidson-corrected energies. Hence, for the long range part of the PES the explicit analytical long-range expression (see eqn (12)) was used to construct the full 3D PES which is referred to as MRCI+Q+LR in the following. In order to smoothly connect the short- and long-range parts of the MRCI+Q PES a Fermi (switching) function is used (see also ref. 37 for a different switching function), see Fig. 2
 | (13) |
| Vtot = fsVRKHS + (1 − fs)Vlong, | (14) |
 | ||
| Fig. 1 MRCI+Q/aug-cc-pV6Z and FCI/aug-cc-pV5Z energies as a function of R for fixed θ = 172.935° and r = 2.0 a0. The black line is the RKHS interpolation of the FCI energies. | ||
Full CI calculations are smooth out to R ∼ 50 a0, contrary to MRCI+Q, see Fig. 1. Hence, the full 3-dimensional PES was also calculated using FCI using a somewhat smaller basis set, i.e., aug-cc-pV5Z. This PES, called FCI in the following, was again represented as a RKHS. Although the FCI energies are smooth in the R-long range, a third PES (FCI+LR) was constructed by using the same long range expression used for the MRCI+Q+LR PES. For the FCI+LR PES the parameter values in the switching function were R0 = 13.5 a0 and δR = 0.25 a0 in eqn (13).
B. Bound state calculations
Ro-vibrational bound state calculations for different J states with e and f symmetries are carried out in scattering coordinates using the 3D discrete variable representation (DVR) method with the DVR3D program suite.38 The radial Gauss-Laguerre quadrature grids consist of 86 and 32 points along the R and r coordinates, respectively. For the Jacobi angle θ, a grid of 36 Gauss-Legendre points was used and for the radial grids (r, R) the wavefunctions were constructed using Morse oscillator functions. For the diatom (H2+), re = 2.5 a0, De = 0.1026 Eh and ωe = 0.018 Eh are used and with these parameters the r-grid covered points between 0.92 to 3.8 a0. As the wave functions for the near-dissociation states need to cover large values along R, the corresponding values were Re = 11.5 a0, De = 0.08 Eh, and ωe = 0.00065 Eh which defined the R grid between 1.82 and 20.87 a0. The r2 embedding38 is used to calculate the rotationally excited states, where the z-axis is parallel to R in body-fixed Jacobi coordinates. For the J > 0 calculations, the Coriolis couplings are included. In the r2 embedding, calculations with ipar = 1 and 0 correspond to the ortho and para H2+, respectively. The e and f symmetries are assigned by the parity operator p.Another method by which we calculated the bound states is the coupled-channels variational method (CCVM). It is similar to a coupled-channels (CC) scattering calculation, but instead of propagating the radial coordinate R to solve the CC differential equations it uses a basis also in R and obtains the desired number of eigenstates of the Hamiltonian matrix with the iterative Davidson algorithm.39 For the angular motion of H2+ in the H2+–He complex we used a free rotor basis with  ranging from 0 to 14 (or 16, in tests). The basis in the H2+ vibrational coordinate r contains the v = 0–7 eigenfunctions of the free H2+ Hamiltonian for
ranging from 0 to 14 (or 16, in tests). The basis in the H2+ vibrational coordinate r contains the v = 0–7 eigenfunctions of the free H2+ Hamiltonian for  on a grid of 110 equidistant points with r = 0.25–5.5 a0. The basis in R was obtained by solving a one-dimensional (1D) eigenvalue problem with the radial kinetic energy and a potential Veff(R). This potential is a cut through the full 3D potential of H2+–He with θ and r fixed at the equilibrium values, to which we added a term linear in R with a slope that was variationally optimized by using the R basis in full 3D calculations of the lower H2+–He levels. The 1D radial eigenvalue problem was solved with sinc-DVR40 on a 357-point grid with R = 2 to 50 a0. In order to converge also near-dissociative states we finally included 120 radial basis functions in the 3D full direct product basis.
on a grid of 110 equidistant points with r = 0.25–5.5 a0. The basis in R was obtained by solving a one-dimensional (1D) eigenvalue problem with the radial kinetic energy and a potential Veff(R). This potential is a cut through the full 3D potential of H2+–He with θ and r fixed at the equilibrium values, to which we added a term linear in R with a slope that was variationally optimized by using the R basis in full 3D calculations of the lower H2+–He levels. The 1D radial eigenvalue problem was solved with sinc-DVR40 on a 357-point grid with R = 2 to 50 a0. In order to converge also near-dissociative states we finally included 120 radial basis functions in the 3D full direct product basis.
In all bound state calculations the atomic masses were mH= 1.00782503 and mHe = 4.00260325 amu, respectively,41 which differ slightly from those used in earlier bound state and scattering calculations which employed mH = 1.00727647 amu and mHe = 4.00234755 amu.42 These differences lead to shifts in the bound states by ∼ 0.5 cm−1, see Table S6 (ESI†). The states in the present work are labeled with respect to the H2+ quantum numbers v and j for the vibrational and rotational state of the diatomic, and J for the spin-free orbital angular momentum of the complex. The fine and hyperfine splittings due to coupling of electron and total nuclear spin, and coupling of the resultant to the rotational angular momentum of the nuclei are both less than 100 MHz, so are several orders of magnitude smaller than the separation between rotational levels of the complex. Thus, identification of N (used in experiments12) with J is a meaningful approximation. It is also worthwhile to mention that for ortho- and para-H2+ the dissociation limits for the complex differ due to the different nuclear spins for the two spin isomers (0 for para and 1 for ortho). For para-H2+ only even j-states are allowed and the complex dissociates to E = 0 whereas for ortho-H2+ only odd j-states exist and the complex dissociates to the j = 1 state of H2+ with an energy of 2B, where B is the rotational constant. For the MRCI+Q and FCI PESs the dissociation limits for ortho-H2+ are 58.2320 cm−1 and 58.2336 cm−1, respectively.
III. Results and discussion
A. Quality of the PESs
First, the quality of the ab initio calculations and their RKHS representation is considered. In Fig. 3 the analytical energies are compared with the ab initio energies for a few selected Jacobi angles at r = 2.0 a0 for the MRCI+Q+LR PES. A similar comparison is also shown for the FCI PES in Fig. S1 (ESI†). Excellent agreement between the two sets of data is found, see Fig. 3. Fig. S2 (ESI†) presents the contour plot of the analytical energies for the H2+–He system for r = 2.0 a0.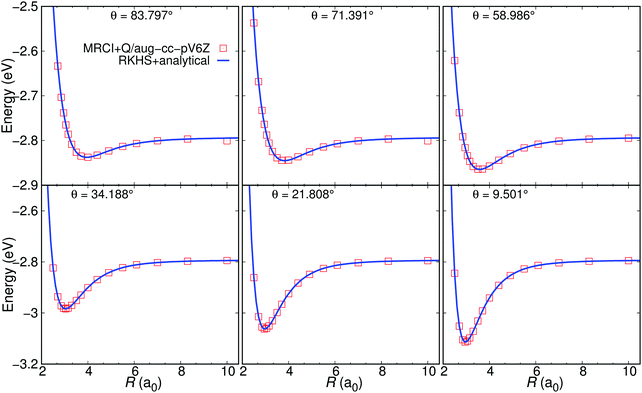 | ||
| Fig. 3 The analytical energies at off-grid points from the MRCI+Q+LR PES (solid line) and the MRCI+Q/aug-cc-pV6Z ab initio energies (open symbols) as a function of R for several Jacobi angles and at fixed r = 2.0 a0. The two points at long range (R ∼ 10 a0 for θ = 83.797° and θ = 71.391°) are due to convergence problems with MRCI+Q, see also Fig. 1. | ||
The quality of the RKHS representation of the MRCI+Q+LR and FCI PES is reported in Fig. S3 (ESI†). For the grid points used to generate the RKHS representation, the agreement between reference points and the reproducing kernel is excellent with R2 values of (1.0–8 × 10−10) and (1.0–2 × 10−12) for MRCI+Q+LR and FCI PESs, respectively. The root mean squared errors (RMSE) for the training data set are 0.67 and 0.02 cm−1 for the MRCI+Q+LR and FCI PESs, respectively. In addition, ab initio energies were also calculated at the MRCI+Q/aug-cc-pV6Z and FCI/aug-cc-pV5Z level of theory for off-grid geometries. They are also reported in Fig. S4 (ESI†) together with the RKHS energies evaluated at these geometries. Again, the agreement between the electronic structure calculations and the RKHS representation is good with RMSEs of 2.16 cm−1 for the MRCI+Q+LR PES and 0.92 cm−1 for the FCI PES.
The equilibrium geometry of the FCI/aug-cc-pV5Z surface is a linear He–H–H configuration (re = 2.07494 a0 and Re = 2.97120 a0), with an energy of −2735.11 cm−1 below the H2+ asymptote. This compares with the MRCI+Q+LR calculations for which r = 2.07447 a0, R = 2.97127 a0 and depth −2736.17 cm−1 and the earlier QCISD(T)/aug-cc-pvQz PES15 (r = 2.0750 a0, R = 2.9720 a0 and depth −2717.0 cm−1) values. For comparison, the refined PES from ref. 18 supports a linear equilibrium structure with a depth of −2732.34 cm−1 and re = 2.07792 a0 and Re = 2.96596 a0. Hence, the structures of all PESs differ by less than 0.01 a0 but the energetics varies over a range of ∼20 cm−1 whereas the dissociation energies for the two PESs from the present work only differ by 1.1 cm−1.
B. Bound states
The ground state energy of H2+(v = 0, j = 0)–He computed from the MRCI+Q+LR surface for ortho-H2+–He using DVR3D and CCVM are −1795.1567 and −1795.3328 cm−1, respectively. The same energies, are obtained from the FCI PES as −1793.7632 and −1793.9067 cm−1, using DVR3D and CCVM, respectively. These values are ∼40 cm−1 lower compared to those reported previously15 (−1754.269 cm−1) on the QCISD(T) PES. In ref. 15 only 3 quadrature points along r were used for the 3D bound state calculations, which may not be sufficient to fully converge the energies. The ground state energy is also calculated in the present work following a time dependent wave packet approach43 on a 2D potential fixing r at 2.0 a0. These ground state energies are in fair agreement with previous results (−1603 vs. −1593 cm−1).15For para-H2+–He the ground state energies obtained from the MRCI+Q+LR PES using DVR3D and CCVM are −1795.1575 and −1795.3352 cm−1, respectively. For the FCI surface the ground state energies of para-H2+–He are calculated as −1793.7639 and −1793.9091 cm−1 using DVR3D and CCVM, respectively. The difference between DVR3D and CCVM is less than 0.17 cm−1 for both, ortho and para-H2+–He. For the FCI+LR PES all the bound states obtained from different methods for both, ortho and para-H2+–He are within 0.02 cm−1 or less of the FCI PES results. Hence, only the results obtained from the MRCI+Q+LR and FCI PESs are reported.
A direct comparison for all and the near-dissociative (within 20 cm−1 of dissociation) bound e states for ortho-H2+–He and J = 0 to J = 6 from DVR3D calculations and using the MRCI+Q+LR (red) and FCI (black) PESs is given in Fig. 4 and 5. All states up to the dissociation limit of v = 0, j = 1 state of H2+ are reported. The level pattern for the two PESs is nearly identical. The distribution of the energy difference ΔE between the MRCI+Q+LR and the FCI PESs for calculations with DVR3D or CCVM is given in Fig. S5 (ESI†).
 | ||
| Fig. 5 Same as Fig. 4 except for the near dissociation states. States within ∼20 cm−1 of the dissociation are reported. | ||
The transitions that were probed by the microwave experiments lie close to dissociation. Hence, a particular focus here is on accurately computing these stationary states and to determine whether any candidate transitions can be identified from using the MRCI+Q+LR and the FCI PESs. A tentative assignment in particular for the 15.2 GHz and 21.8 GHz transitions has been given previously based on experiments using electric field dissociation.12 They were analyzed using an effective Hamiltonian. The 15.2 GHz transition was assigned to a low-N transition (in the terminology of ref. 12, N is the spin-free angular momentum which is J in the present work) with ΔN = 0 with N = 3 or N = 4 in ortho-H2+–He. In the following, N is used when referring to the analysis of the experiments12 whereas J is used when discussing the present calculations.
For the 21.7 GHz transition on the other hand the analysis led to an assignment involving ΔN = 1 with N = 11 and N′ = 10 in para-H2+–He. While the analysis leading to a ΔN = 1 transition involving para-H2+ is based on physical grounds, that to a high-N state involves fitting of the Zeeman pattern which is more approximate. The selection rules for these transitions are e ↔ f for ΔJ = 0 and e ↔ e or f ↔ f for ΔJ = ±1, respectively.
First, the near-dissociative states for ortho-H2+–He are discussed. All near-dissociative states from the MRCI+Q+LR and FCI PESs using the DVR3D and CCVM methods are reported in Fig. 6a–d. All energies for J = 0 to 6 are also reported in Tables 2 and 3. There is one e/f parity doublet with ΔJ = 0 with a transition frequency between 10 and 18 GHz, involving the J = 2 state for ortho-H2+–He. Using DVR3D the transition frequency is 14.4(5) GHz whereas with the CCVM code the transition is at 9.3 GHz. The parity doublet in both cases is within 2 cm−1 of dissociation which makes it a pair of near-dissociative states. This is also confirmed by considering the expectation value for the R-coordinate for the two states involved which are 〈R〉 = 13.1 a0 for the e state and 〈R〉 = 12.7 a0 for the f state which confirms their long range character as suggested from the experiments.
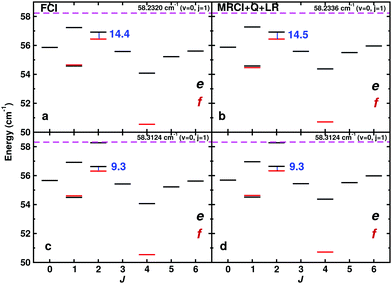 | ||
| Fig. 6 Near dissociation ortho-H2+–He states (in cm−1) and predicted transition frequencies in (GHz) using the FCI (left, panels a and c) and MRCI+Q+LR (right, panels b and d) PESs. States with e (black) and f symmetry (red) are reported separately. Results from DVR3D and CCVM are in the top and bottom row, respectively. The 14.4 GHz (MRCI+Q+LR, DVR3D), 14.5 GHz (FCI, DVR3D) and 9.3 (both PESs, CCVM) GHz parity doublet is a candidate for the 15.2 GHz line observed experimentally which had been assigned to a parity doublet with ΔN = 0.12 | ||
| J | ortho | para | ||||||
|---|---|---|---|---|---|---|---|---|
| e | f | e | f | |||||
| CCVM | DVR3D | CCVM | DVR3D | CCVM | DVR3D | CCVM | DVR3D | |
| 0 | 39.896 | 40.321 | −15.641 | −15.719 | ||||
| 55.689 | 55.876 | −1.509 | −1.137 | |||||
| 1 | 43.199 | 43.668 | 54.629 | 54.464 | −13.965 | −14.035 | ||
| 54.514 | 54.582 | −0.954 | −0.430 | |||||
| 56.959 | 57.273 | |||||||
| 2 | 49.345 | 49.755 | 56.329 | 56.439 | −10.712 | −10.766 | ||
| 56.639 | 56.923 | −0.061 | 0.895 | |||||
| 58.272 | 59.186 | |||||||
| 3 | 44.938 | 44.941 | 41.798 | 41.783 | −6.082 | −6.109 | ||
| 55.443 | 55.588 | |||||||
| 4 | 46.022 | 45.971 | 50.718 | 50.712 | −0.587 | −0.540 | ||
| 54.375 | 54.375 | |||||||
| 5 | 40.655 | 40.711 | 40.682 | 40.680 | −7.877 | −7.799 | ||
| 55.518 | 55.507 | |||||||
| 6 | 55.985 | 55.959 | −13.897 | −13.746 | ||||
| J | ortho | para | ||||||
|---|---|---|---|---|---|---|---|---|
| e | f | e | f | |||||
| CCVM | DVR3D | CCVM | DVR3D | CCVM | DVR3D | CCVM | DVR3D | |
| 0 | 39.575 | 40.036 | −16.005 | −16.067 | ||||
| 55.662 | 55.860 | −1.527 | −1.150 | |||||
| 1 | 42.934 | 43.438 | 54.601 | 54.648 | −14.315 | −14.368 | ||
| 54.494 | 54.575 | −0.969 | −0.448 | |||||
| 56.916 | 57.232 | |||||||
| 2 | 49.213 | 49.647 | 56.314 | 56.437 | −11.021 | −11.058 | ||
| 56.623 | 56.916 | −0.061 | 0.881 | |||||
| 58.271 | 59.162 | |||||||
| 3 | 44.497 | 44.513 | 41.473 | 41.473 | −6.311 | −6.320 | ||
| 55.422 | 55.577 | |||||||
| 4 | 45.652 | 45.611 | 50.538 | 50.547 | −0.680 | −0.619 | ||
| 54.067 | 54.084 | |||||||
| 5 | 40.565 | 40.626 | 40.854 | 40.860 | −8.092 | −8.005 | ||
| 55.219 | 55.220 | |||||||
| 6 | 55.626 | 56.610 | −11.890 | −11.742 | ||||
Next, the near-dissociative states for para-H2+–He are discussed for the two PESs and the two methods to compute bound states, see Fig. 7a–d. The only near-dissociative states involving either an e/e or an f/f transition with a transition frequency around 20.1(2) and 16.7(6) GHz from DVR3D and CCVM involves a J = 0 and a J = 1 state. The 〈R〉 = 15.0 a0 for the J = 0, e state and 〈R〉 = 16.0 a0 for the J = 1, f state, show the long range nature of the wave functions. The potential candidate for the 21.8 GHz transition is not found for the high J states sufficiently close to dissociation to be part of a suitable candidate transition.
IV. Discussion and conclusions
Two new PESs at the MRCI+Q+LR and FCI level of theory with large basis sets and represented as a reproducing kernel have been used to determine all bound and near-dissociative states for ortho- and para-H2+–He. Although MRCI+Q is already a high level of electronic structure theory, it was found to break down for H2+–He separations longer than R ∼ 10 a0, see Fig. 1 and 3. For this part of the MRCI PES an analytical long range potential was used. In order to establish that such an approach is meaningful, the full 3d PES was calculated at the even higher full CI level of theory. It is found that at both levels of theory the bound states compare to within fractions of a wavenumber when stationary states are determined from the same nuclear quantum code, see Table S5 (ESI†). Moreover, the stationary states on one and the same PES determined from two different quantum bound state codes (DVR3D and CCVM) also agree closely, typically within less than fractions of one cm−1.The need for such new PESs can also be gleaned from Table S6 (ESI†) which compares the J = 0 bound states for para-H2+–He on the FCI PES with three different methods and compares them with results on the earlier, high-quality PES used in previous work.18,42 The dissociation energies between the present and previous18 PESs differ only by about 3 cm−1 whereas the lower bound states differ rather by 20 cm−1. This suggests that the shape of the PESs away from the minimum differs also due to the different long range behaviour of the present and previous PESs. This is also supported by the observation that the total number of bound states on the present and previous PESs differs by one, i.e. one near-dissociative state is missing. Furthermore, the table also shows that three different methods for computing bound states (DVR3D, CCVM and time-dependent wave packet (TDWP)43) yield stationary states that differ by ∼0.3 cm−1 or less.
The present computations provide stringent benchmarks on potential transitions that have been observed experimentally. One such assignment is for the 15.2 GHz transition which corresponds to ortho-H2+–He. The transition found in the present work involves an e/f parity doublet with J = 2. This compares with a tentative assignment to an e/f parity doublet involving either a J = 3 or J = 4 state. For the 21.8 GHz transition which had been tentatively assigned to an e/e or f/f transition in para-H2+–He the candidate, near-dissociation states are J = 0 and J = 1, both of which are within less than 2 cm−1 of dissociation and the transition frequencies range from 16 to 22 GHz. However, no high-J candidate states suitable to assign the experimentally observed transition were found.
This work presents the generation and representation of two high-accuracy, full dimensional PESs for H2+–He together with quantum bound state calculations that provide first potential assignments of experimentally characterized, near-dissociation states. The results from both, MRCI+Q+LR and full CI PESs, using two different approaches for calculating the quantum bound states are largely consistent. It will be interesting to use the present PESs in future inelastic scattering calculations.
Code availability
The code for the RKHS PESs has been made available on github.44Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
This work was supported by the Swiss National Science Foundation through grants 200021-117810, the NCCR MUST and the AFOSR (to MM). The authors thank Prof. J. Tennyson for exchange on the DVR3D program.References
- A. G. G. M. Tielens, Rev. Mod. Phys., 2013, 85, 1021 CrossRef CAS.
- Q. Li, J. Jiang and J. Hao, KONA Powder Part. J., 2015, 57–74 CrossRef CAS.
- R. Güsten, H. Wiesemeyer, D. Neufeld, K. M. Menten, U. U. Graf, K. Jacobs, B. Klein, O. Ricken, C. Risacher and J. Stutzki, Nature, 2019, 568, 357–359 CrossRef PubMed.
- B. Zygelman, P. C. Stancil and A. Dalgarno, Astrophys. J., 1998, 508, 151–156 CrossRef CAS.
- J. H. Black, Philos. Trans. R. Soc., A, 2012, 370, 5130–5141 CrossRef CAS PubMed.
- S. Lepp, P. C. Stancil and A. Dalgarno, J. Phys. B: At., Mol. Opt. Phys., 2002, 35, R57–R80 CrossRef CAS.
- M. H. Vera, F. A. Gianturco, R. Wester, H. da Silva, Jr., O. Dulieu and S. Schiller, J. Chem. Phys., 2017, 146 Search PubMed.
- J. C. J. Koelemeij, B. Roth, A. Wicht, I. Ernsting and S. Schiller, Phys. Rev. Lett., 2007, 98, 173002 CrossRef.
- S. Schiller, D. Bakalov and V. I. Korobov, Phys. Rev. Lett., 2014, 113, 023004 CrossRef CAS PubMed.
- A. Klein, Y. Shagam, W. Skomorowski, P. S. Zuchowski, M. Pawlak, L. M. C. Janssen, N. Moiseyev, S. Y. T. van de Meerakker, A. van der Avoird, C. P. Koch and E. Narevicius, J. Chem. Phys., 2017, 13, 35–38 CAS.
- A. Carrington, D. I. Gammie, A. M. Shaw, S. M. Taylor and J. M. Hutson, Chem. Phys. Lett., 1996, 260, 395–405 CrossRef CAS.
- D. I. Gammie, J. C. Page and A. M. Shaw, J. Chem. Phys., 2002, 116, 6072 CrossRef CAS.
- T. Joseph and N. Sathyamurthy, J. Chem. Phys., 1987, 86, 704–714 CrossRef CAS.
- M. F. Falcetta and P. E. Siska, Mol. Phys., 1999, 97, 117–125 CrossRef CAS.
- M. Meuwly and J. M. Hutson, J. Chem. Phys., 1999, 110, 3418 CrossRef CAS.
- P. Palmieri, C. Puzzarini, V. Aquilanti, G. Capecchi, S. Cavalli, D. de Fazio, A. Aguilar, X. Giménez and J. M. Lucas, Mol. Phys., 2000, 98, 1835–1849 CrossRef CAS.
- C. Ramachandran, D. D. Fazio, S. Cavalli, F. Tarantelli and V. Aquilanti, Chem. Phys. Lett., 2009, 469, 26–30 CrossRef CAS.
- D. de Fazio, M. de Castro-Vitores, A. Aguado, V. Aquilanti and S. Cavalli, J. Chem. Phys., 2012, 137, 244306 CrossRef PubMed.
- H.-J. Werner and P. J. Knowles, J. Chem. Phys., 1988, 89, 5803–5814 CrossRef CAS.
- P. J. Knowles and H.-J. Werner, Chem. Phys. Lett., 1988, 145, 514–522 CrossRef CAS.
- A. K. Wilson, T. van Mourik and T. H. Dunning, THEOCHEM, 1996, 388, 339–349 CrossRef CAS.
- P. J. Knowles and N. Handy, Chem. Phys. Lett., 1984, 111, 315–321 CrossRef CAS.
- P. J. Knowles and N. C. Handy, Comput. Phys. Commun., 1989, 54, 75–83 CrossRef CAS.
- T. H. Dunning, J. Chem. Phys., 1989, 90, 1007–1023 CrossRef CAS.
- D. E. Woon and T. H. Dunning, J. Chem. Phys., 1994, 100, 2975–2988 CrossRef CAS.
- H.-J. Werner and P. J. Knowles, J. Chem. Phys., 1985, 82, 5053–5063 CrossRef CAS.
- P. J. Knowles and H.-J. Werner, Chem. Phys. Lett., 1985, 115, 259–267 CrossRef CAS.
- H.-J. Werner and W. Meyer, J. Chem. Phys., 1980, 73, 2342–2356 CrossRef CAS.
- H.-J. Werner, P. J. Knowles, G. Knizia, F. R. Manby and M. Schütz, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 242–253 CAS.
- A. J. C. Varandas, Intermolecular and Intramolecular Potentials: Topographical Aspects, Calculation, and Functional Representation via A Double Many-Body Expansion Method, John Wiley & Sons, Inc., 2007, pp. 255–338 Search PubMed.
- A. Aguado and M. Paniagua, J. Chem. Phys., 1992, 96, 1265–1275 CrossRef CAS.
- D. M. Bishop and J. Pipin, Chem. Phys. Lett., 1995, 236, 15 CrossRef CAS.
- L. Velilla, B. Lepetit, A. Aguado, A. Beswick and M. Paniagua, J. Chem. Phys., 2008, 129, 084307 CrossRef PubMed.
- W. H. Press, S. A. Teukolsky, W. T. Vetterling and B. P. Flannery, Numerical Recipes in Fortran 77, Cambridge University Press, New York, 1992 Search PubMed.
- T.-S. Ho and H. Rabitz, J. Chem. Phys., 1996, 104, 2584 CrossRef CAS.
- O. T. Unke and M. Meuwly, J. Chem. Inf. Model, 2017, 57, 1923–1931 CrossRef CAS PubMed.
- B. Yang, P. Zhang, C. Qu, X. H. Wang, P. C. Stancil, J. M. Bowman, N. Balakrishnan, B. M. McLaughlin and R. C. Forrey, J. Phys. Chem. A, 2018, 122, 1511–1520 CrossRef CAS PubMed.
- J. Tennyson, M. A. Kostin, P. Barletta, G. J. Harris, O. L. Polyansky, J. Ramanlal and N. F. Zobov, Comput. Phys. Commun., 2004, 163, 85–116 CrossRef.
- E. R. Davidson, J. Comput. Phys., 1975, 17, 87 CrossRef.
- G. C. Groenenboom and D. T. Colbert, J. Chem. Phys., 1993, 99, 9681–9696 CrossRef CAS.
- P. Linstrom and W. Mallard, NIST Webbook (NIST Chemistry Webbok, NIST Standard Reference Database Number 69), ed. P. J. Lindstrom and W. G. Mallard, http://webbook.nist.gov, National Institute of Standards and Technology, Gaithersburgh MD, 20899, 2019.
- T. Szidarovszky and K. Yamanouchi, Mol. Phys., 2017, 115, 1916–1926 CrossRef CAS.
- D. Koner, L. Barrios, T. González-Lezana and A. N. Panda, J. Chem. Phys., 2016, 144, 034303 CrossRef PubMed.
- https://github.com/MeuwlyGroup/H2pHe .
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c9cp05259c |
| This journal is © the Owner Societies 2019 |



