Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Assignment of the solid state spectra of the group VI hexacarbonyls by inelastic neutron scattering spectroscopy†
Stewart F.
Parker
 *a and
Upali A.
Jayasooriya
b
*a and
Upali A.
Jayasooriya
b
aISIS Facility, STFC Rutherford Appleton Laboratory, Chilton, Didcot, Oxon OX11 0QX, UK. E-mail: stewart.parker@stfc.ac.uk
bSchool of Chemical Sciences, University of East Anglia, Norwich NR4 7TJ, UK
First published on 4th November 2019
Abstract
The solid state vibrational spectra of M(CO)6, (M = Cr, Mo, W) in the region below 800 cm−1 have been assigned by a combination of infrared, Raman and the first reported inelastic neutron scattering (INS) spectra from homoleptic metal carbonyls. This region comprises of the lattice modes, the OC–M–CO deformations, the M–C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) O bends and the M–C stretches. Three modes that are forbidden in both the infrared and Raman spectra of the parent Oh symmetry gas phase molecule occur in this region. The absence of selection rules for INS spectroscopy means that all three modes are clearly seen for the first time, all previous work has relied on overtone and combination modes. Periodic density functional theory calculations of the complete orthorhombic structure support the assignments.
O bends and the M–C stretches. Three modes that are forbidden in both the infrared and Raman spectra of the parent Oh symmetry gas phase molecule occur in this region. The absence of selection rules for INS spectroscopy means that all three modes are clearly seen for the first time, all previous work has relied on overtone and combination modes. Periodic density functional theory calculations of the complete orthorhombic structure support the assignments.
Introduction
The group VI metal hexacarbonyls M(CO)6, (M = Cr, Mo, W) have been extensively studied over the years.1 Their uses are as diverse as precursors for organometallic reagents in synthetic chemistry2 and as metal sources in chemical vapour deposition processes.3–5 The vibrational spectroscopy of the compounds in the gas phase has been comprehensively investigated6–9 and empirical6,7,9 and ab initio10–12 force fields derived. In contrast, the solid state spectra have been much less investigated, the most complete study was by Adams and Taylor13 who recorded polarised infrared and Raman spectra from single crystals at 77 K. The spectra in the carbonyl stretch region have also been interpreted using a novel approach.14However, there are still uncertainties in some of the assignments and these relate to modes that are both infrared and Raman forbidden under the gas phase molecule's Oh symmetry. Knowledge of these modes is largely based on overtone and combination modes and also that they become weakly allowed in the solid state. In the present work we use a combination of inelastic neutron scattering (INS) spectroscopy15 and periodic density functional theory16,17 (periodic-DFT) to provide complete assignments of the solid state spectra.
Experimental
The INS spectra were recorded using TOSCA.18 10–15 g of the compound (Cr(CO)6 98%, Mo(CO)6 99.9%, W(CO)6 97%, all from Aldrich and used as received) was loaded into a sealed can in an argon-filled dry box. The sample was then cooled to ∼20 K and the spectrum recorded for ∼12 hours. Raman spectra were recorded at 7 K using an upgraded version of a Renishaw InVia spectrometer, that has been previously described.19 The upgrade consists of an additional laser operating at 532 nm and improved laser rejection filters with a low energy cut-off of ∼40 cm−1. Room temperature infrared spectra were recorded using a Bruker Vertex70 FTIR spectrometer, over the range 20 to 4000 cm−1 at 4 cm−1 resolution with a DLaTGS detector using 64 scans and the Bruker Diamond ATR. The use of the ultra-wide range beamsplitter enabled the entire spectral range to be recorded without the need to change beamsplitters. Spectra at 150 K were recorded using the same spectrometer with a SpecAc Golden Gate low temperature ATR accessory. The accessory limits the attainable, lowest energy to 350 cm−1. As the low temperature data is significantly sharper, this is shown where possible, unfortunately, only room temperature data is available for the region below 150 cm−1. The spectra have been corrected for the wavelength-dependent variation in path length using the Bruker software.Dispersion corrected periodic DFT calculations of the crystalline structures were carried out using the plane-wave pseudopotential method implemented in the CASTEP code.16,17 Exchange and correlation were approximated using the Perdew–Burke–Ernzerhof (PBE) functional,20 with the Tkatchenko–Scheffler (TS) dispersion correction scheme21 within the generalized gradient approximation (GGA). Norm-conserving pseudopotentials were generated using the kinetic-energy optimised method22 with a plane-wave cut-off energy of 830 (Cr, Mo) or 900 eV (W). Brillouin-zone sampling of electronic states was performed on a 6 × 6 × 8 Monkhorst–Pack grid (36 k-points). The equilibrium structure, an essential prerequisite for lattice dynamics calculations was obtained by Broyden–Fletcher–Goldfarb–Shanno (BFGS) geometry optimization after which the residual forces were converged to zero within ±0.0017 eV Å−1. Phonon frequencies were obtained by diagonalization of dynamical matrices computed using density-functional perturbation theory23 (DFPT). An analysis of the resulting eigenvectors was used to map the computed modes to the corresponding irreducible representations of the point group and assign IUPAC symmetry labels. DFPT was also used to compute the dielectric response and the Born effective charges, and from these the mode oscillator strength tensor and infrared absorptivity were calculated. In addition to the direct evaluation of frequencies and intensities at zero wavevector, phonon dispersion was also calculated along high symmetry directions throughout the Brillouin zone. For this purpose, dynamical matrices were computed on a regular grid of wavevectors throughout the Brillouin zone and Fourier interpolation was used to extend the computed grid to the desired fine set of points along the high-symmetry paths.24 The INS spectra were generated from the CASTEP output using ACLIMAX.25
Results and discussion
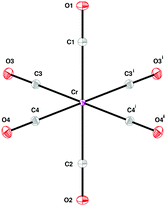
All three metal hexacarbonyls crystallise in space group Pnma (D162h number 62) with four molecules in the unit cell, each occupying a site of Cs symmetry, (Cr(CO)6,26 Mo(CO)6,27 W(CO)628).In the gas phase, the Oh symmetry results in 13 modes: three C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) O stretches (A1g, Eg, T1u), three M–CO stretches (A1g, Eg, T1u), four M–C
O stretches (A1g, Eg, T1u), three M–CO stretches (A1g, Eg, T1u), four M–C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) O bends (T1g, T1u, T2g, T2u) and three OC–M–CO deformations (T1u, T2g, T2u). The C
O bends (T1g, T1u, T2g, T2u) and three OC–M–CO deformations (T1u, T2g, T2u). The C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) O stretch modes occur at ∼2000–2150 cm−1, the M–CO stretches and M–C
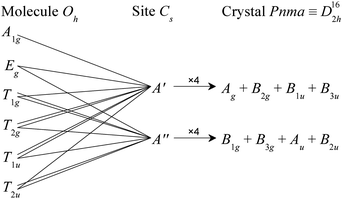
O stretch modes occur at ∼2000–2150 cm−1, the M–CO stretches and M–C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) O bends at ∼300–700 cm−1, and the OC–M–CO deformations below 150 cm−1. The A1g, Eg and T2g modes are Raman active, the T1u are infrared active and the T1g and T2u are inactive in both forms of spectroscopy. The effect of the Cs site symmetry is to formally remove all the degeneracies and the factor group splitting results in a quadrupling of the modes, as shown in Fig. 1. However, in all three cases, the geometry is that of a near-regular octahedron, Table 1, and for most of the modes both the site group and factor group splitting is small.13
O bends at ∼300–700 cm−1, and the OC–M–CO deformations below 150 cm−1. The A1g, Eg and T2g modes are Raman active, the T1u are infrared active and the T1g and T2u are inactive in both forms of spectroscopy. The effect of the Cs site symmetry is to formally remove all the degeneracies and the factor group splitting results in a quadrupling of the modes, as shown in Fig. 1. However, in all three cases, the geometry is that of a near-regular octahedron, Table 1, and for most of the modes both the site group and factor group splitting is small.13
| Cr(CO)6 | Mo(CO)6 | W(CO)6 | ||||
|---|---|---|---|---|---|---|
| Experimental ref. 25@11 K | CASTEP | Experimental ref. 26 | CASTEP | Experimental ref. 27 | CASTEP | |
| Distance/Å | ||||||
| M–C1 | 1.9121 | 1.934 | 2.062 | 2.074 | 2.029 | 2.052 |
| M–C2 | 1.9171 | 1.938 | 2.065 | 2.077 | 2.022 | 2.049 |
| M–C3 | 1.9152 | 1.940 | 2.055 | 2.079 | 2.020 | 2.055 |
| M–C4 | 1.9201 | 1.937 | 2.053 | 2.077 | 2.033 | 2.052 |
| C1–O1 | 1.1432 | 1.151 | 1.120 | 1.151 | 1.135 | 1.145 |
| C2–O2 | 1.1421 | 1.150 | 1.113 | 1.150 | 1.157 | 1.147 |
| C3–O3 | 1.1412 | 1.149 | 1.130 | 1.149 | 1.155 | 1.140 |
| C4–O4 | 1.1399 | 1.150 | 1.137 | 1.150 | 1.138 | 1.145 |
| Angle/° | ||||||
| M–C1–O1 | 179.94 | 179.32 | 179.45 | 179.28 | 179.42 | 179.36 |
| M–C2–O2 | 179.45 | 179.91 | 179.04 | 179.84 | 178.78 | 179.69 |
| M–C3–O3 | 179.38 | 179.53 | 179.27 | 179.51 | 179.20. | 179.40 |
| M–C4–O4 | 179.19 | 179.30 | 179.43 | 179.44 | 178.71 | 179.50 |
| C1–M–C2 | 179.45 | 179.34 | 179.81 | 179.47 | 179.56 | 179.21 |
| C1–M–C3 | 90.36 | 90.14 | 90.48 | 90.11 | 89.34 | 90.17 |
| C1–M–C4 | 90.09 | 89.57 | 89.92 | 89.55 | 89.44 | 89.65 |
| C2–M–C3 | 90.03 | 90.33 | 89.65 | 90.26 | 90.97 | 90.39 |
| C2–M–C4 | 89.53 | 89.97 | 89.95 | 90.08 | 90.26 | 89.81 |
| C3–M–C3i | 89.54 | 89.60 | 90.67 | 89.87 | 89.75 | 89.24 |
| C3–M–C4 | 89.79 | 89.77 | 89.90 | 89.84 | 89.98 | 90.00 |
| C3–M–C4i | 179.20 | 179.30 | 179.30 | 179.55 | 178.74 | 179.22 |
| C4–M–C4i | 90.88 | 90.85 | 89.53 | 90.46 | 90.27 | 90.75 |
In the solid state, all the modes have components that are infrared or Raman allowed, in reality, the forbidden modes give, at best, very weak transitions and they have usually been obtained from overtone or combination bands.29 INS spectroscopy has no selection rules, thus all modes are allowed. The resolution of INS spectrometers in the C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) O stretch region is insufficient to resolve the modes, however, in the region below 800 cm−1, the modes are more widely separated and the spectral resolution is much better. Fortunately, this is also the region where the forbidden modes occur and these are the focus of this paper.
O stretch region is insufficient to resolve the modes, however, in the region below 800 cm−1, the modes are more widely separated and the spectral resolution is much better. Fortunately, this is also the region where the forbidden modes occur and these are the focus of this paper.
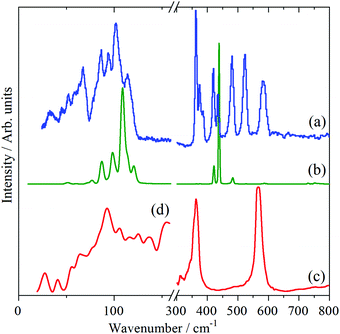
The INS, Raman and infrared spectra of Cr(CO)6, Mo(CO)6 and W(CO)6 in the 0–800 cm−1 region are shown in Fig. 2–4 respectively. In the 300–800 cm−1 region, seven modes are expected: three Raman active, two infrared active and two forbidden (in Oh symmetry) modes. Comparison of the spectra immediately identifies the forbidden modes at 365 and 511 cm−1 (Cr), 343 and 510 cm−1 (Mo) and 362 and 523 cm−1 (W).
In the very low energy region, 0–150 cm−1, the three OC–M–CO deformations occur, one of which is forbidden under Oh symmetry. However, the 12 translational (three acoustic and nine optic) and 12 librational modes also occur (three of each type for each of the four molecules in the primitive cell) in this region. This results in the INS spectra being very congested, since all of these will contribute to the INS spectrum. However, it can be seen that in all the INS spectra there are two main areas of intensity: 0–80 and 80–150 cm−1.
In the case of Cr(CO)6, there are three clear peaks at 91, 105 and 115 cm−1. The infrared and Raman spectra show that there are (relatively) strong modes at 90–100 and 110–115 cm−1 respectively, which are assigned to the allowed modes,9,13 accordingly the lowest energy peak at 91 cm−1 is assigned to the forbidden mode. The only previous9 assignment of this mode was at 68 cm−1 and was based on a very weak combination mode in the infrared spectrum of the gas phase molecule. The +23 cm−1 shift on going from the gas phase to the solid state is consistent with the other two OC–M–CO deformation modes which shift by +8 cm−1 and +24 cm−1. These three modes probably account for most of the intensity in the 80–150 cm−1 range in the INS spectra, suggesting that the lattice modes result in the 0–80 cm−1 massif.
For Mo(CO)6 and W(CO)6, the 0–150 cm−1 regions are almost superimposable and strongly resemble a “squashed” version of that of Cr(CO)6, as shown in Fig. 5. Accordingly, the OC–M–CO deformation modes are as for Cr(CO)6, with the forbidden mode observed at 85 and 86 cm−1 for Mo(CO)6 and W(CO)6 respectively. Table 2 lists the assignments.
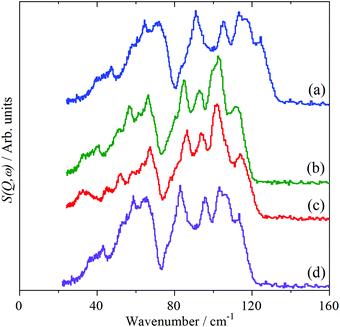 | ||
| Fig. 5 INS spectra of: (a) Cr(CO)6, (b) Mo(CO)6, (c) W(CO)6 and (d) Cr(CO)6 scaled by 0.91 in the lattice mode and OC–M–CO bend region. | ||
| Mode | Cr/cm−1 | Mo/cm−1 | W/cm−1 | Descriptionb | |||
|---|---|---|---|---|---|---|---|
| Solid (INS) | Gas | Solid (INS) | Gas | Solid (INS) | Gas | ||
| a Ref. 9. b δ = bend, ν = stretch. | |||||||
| T2u | 91 | 67.9 | 85 | 60 | 86 | 61.4 | δ(C–M–C) |
| T1u | 105 | 97.2 | 93 | 81.6 | 94 | 82.0 | δ(C–M–C) |
| T2g | 117 | 89.7 | 103 | 79.2 | 102 | 81.4 | δ(C–M–C) |
| T1g | 367 | 364.1 | 344 | 341.6 | 362 | 361.6 |
δ(M–C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) O) O) |
| A1g | 391 | 379.2 | 410 | 391.2 | 434 | 426 | ν(M–C) |
| Eg | 400 | 390.6 | 393 | 381 | 419 | 410 | ν(M–C) |
| T1u | 446 | 440.5 | 370 | 367.2 | 376 | 374.4 |
δ(M–C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) O) O) |
| T2u | 511 | 510.9 | 512 | 507.2 | 523 | 521.3 |
δ(M–C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) O) O) |
| T2g | 533 | 532.1 | 475 | 477.4 | 481 | 482.0 |
δ(M–C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) O) O) |
| T1u | 660 | 668.1 | 590 | 595.6 | 583 | 586.6 | ν(M–C) |
In order to confirm these assignments, periodic density functional theory (DFT) calculations of the complete unit cell are required. Comparison of observed and calculated INS spectra is an exacting test15 of the accuracy of such studies.
The results of a series of calculations for Cr(CO)6 are shown in Fig. 6 and summarised in Table 3. All of these are generated from calculations across the complete Brillouin zone, so as to include the effects of vibrational dispersion (variation of transition energy with wavevector). As may be seen from Fig. 7, this is significant in the region below 200 cm−1, but less so for the stretch and deformation region. (The dispersion curves for the C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) O stretch region and the corresponding sets for Mo(CO)6 and W(CO)6 are shown in Fig. S1–S7 of the ESI†). From Fig. 6, it can be seen that the agreement between observed and calculated spectra, is very sensitive to the details of the method used for the lattice mode region, but less so for the stretch and deformation region. The calculations with the experimental lattice parameters result in poor agreement, allowing the lattice lengths to optimise (but not the angles, so as to maintain the orthorhombic symmetry), results in much better agreement.
O stretch region and the corresponding sets for Mo(CO)6 and W(CO)6 are shown in Fig. S1–S7 of the ESI†). From Fig. 6, it can be seen that the agreement between observed and calculated spectra, is very sensitive to the details of the method used for the lattice mode region, but less so for the stretch and deformation region. The calculations with the experimental lattice parameters result in poor agreement, allowing the lattice lengths to optimise (but not the angles, so as to maintain the orthorhombic symmetry), results in much better agreement.
| Method | Metal | Relativea total energy/eV | Lattice parameters/Å | Cell volume | |||
|---|---|---|---|---|---|---|---|
| Å3 | Δ % | ||||||
| a | b | c | |||||
| a Relative to lowest energy structure. b % difference in cell volume. c Cell angles fixed at 90° in order to maintain the Pnma symmetry, but cell lengths are allowed to optimise. | |||||||
| Fixed at experimental lattice parameters (no TS correction) | Cr | 4.3259 | 11.474 | 10.894 | 6.188 | 773.549 | 0 |
| Mo | 6.514 | 12.019 | 11.415 | 6.488 | 890.133 | 0 | |
| W | 6.579 | 11.944 | 11.370 | 6.459 | 877.153 | 0 | |
| Lattice optimisedc (no TS correction) | Cr | 3.4015 | 12.770 | 11.833 | 6.868 | 1037.894 | +34.2 |
| Fixed at experimental lattice parameters with the TS correction included | Cr | 0.0951 | 11.474 | 10.894 | 6.188 | 773.549 | 0 |
| Mo | 0 | 12.019 | 11.415 | 6.488 | 890.133 | 0 | |
| W | 0 | 11.944 | 11.370 | 6.459 | 877.153 | 0 | |
| Lattice optimised with the TS correction included | Cr | 0 | 11.741 | 11.117 | 6.308 | 823.284 | +6.4 |
| Mo | 0 | 11.970 | 11.374 | 6.438 | 876.610 | −1.5 | |
| W | 0 | 11.875 | 11.360 | 6.417 | 865.540 | −1.3 | |
 | ||
Fig. 7 Calculated dispersion curves of Cr(CO)6 in the Cr–C stretch and Cr–C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) O bend region (upper panel) and the lattice mode and OC–Cr–CO bend region (lower panel). The calculations are for the lattice optimised structure with the TS correction and correspond to Fig. 5d. O bend region (upper panel) and the lattice mode and OC–Cr–CO bend region (lower panel). The calculations are for the lattice optimised structure with the TS correction and correspond to Fig. 5d. | ||
As these compounds have essentially zero permanent dipole moment, it follows that the solids are largely stabilised by van der Waals interactions. These are not included in conventional DFT functionals, so to compensate for this an empirical correction is added to the functional. There are a variety of such methods, the most comprehensive currently available is that of Tkatchenko and Scheffler21 (TS). Inclusion of the TS dispersion correction does not greatly change the fixed lattice results, but it does significantly modify the optimised lattice calculations in several respects: the change in cell volume is reduced from +34% to +6.4%, the acoustic modes (the bands below 50 cm−1 in Fig. 6c) harden and the profile of the 80–150 cm−1 feature is in excellent agreement with that found experimentally, Fig. 6e. Table 1 compares selected observed and calculated bond distances and angles for the lattice and geometry optimised structures with inclusion of the TS dispersion correction.
A calculation of an Oh symmetry Cr(CO)6 molecule in 10 × 10 × 10 Å cell, (which simulates a gas phase molecule) found that only the lowest three modes underwent a downshift of >5 cm−1 (solid–gas phase), consistent with our assignment.
Fig. 8 and 9 show the comparison of the observed and calculated INS spectra for Mo(CO)6 and W(CO)6 respectively. Both calculated spectra are from lattice and geometry optimisations with the TS correction. It can be seen that the result for Mo(CO)6 is in good agreement with the observed spectrum, while that for W(CO)6 is in poor agreement for the region <150 cm−1. We have no explanation for this event. It is noticeable that the lattice optimisation resulted in a small shrinkage of the lattice, Table 2, rather than an expansion as seen for Cr(CO)6. The contraction would harden the modes, but it does not explain why there is a difference between the Mo and W case.
The calculations confirm the assignments derived above. Tables S1–S3 (ESI†) list the calculated modes with their assignments for all three molecules.
Conclusions
The solid state vibrational spectra of M(CO)6, (M = Cr, Mo, W) in the region below 800 cm−1 have been assigned by a combination of infrared, Raman and the first reported inelastic neutron scattering (INS) spectra from homoleptic metal carbonyls. This has enabled the three modes that are forbidden in both the infrared and Raman spectra of the parent Oh symmetry gas phase molecule to be directly observed for the first time. Periodic density functional theory calculations of the complete orthorhombic structure support the assignments, although the agreement is not exact in the region below 100 cm−1, which highlights the difficulty of obtaining reliable assignments for the external modes (translations and librations) even for fairly simple molecules.Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
The STFC Rutherford Appleton Laboratory is thanked for funding and access to neutron beam facilities. Computing resources (time on the SCARF compute cluster for the CASTEP calculations) were provided by STFC's e-Science facility.References
- H. Werner, Angew. Chem., Int. Ed. Engl., 1990, 29, 1077 CrossRef.
- L. S. Hegedus, Pure Appl. Chem., 1990, 62, 691 CAS.
- C.-L. Chen and W.-C. J. Wei, J. Eur. Ceram. Soc., 2002, 22, 2883 CrossRef CAS.
- J. S. Cross and G. L. Schrader, Thin Solid Films, 1995, 259, 5 CrossRef CAS.
- K. K. Lai and H. H. Lamb, Thin Solid Films, 2000, 370, 114 CrossRef CAS.
- L. H. Jones, J. Chem. Phys., 1962, 36, 2375 CrossRef CAS.
- L. H. Jones, Spectrochim. Acta, 1963, 19, 329 CrossRef CAS.
- J. M. Smith and L. H. Jones, J. Mol. Spectrosc., 1966, 20, 248 CrossRef CAS.
- L. H. Jones, R. S. McDowell and M. Goldblatt, Inorg. Chem., 1969, 8, 2349 CrossRef CAS.
- V. Jonas and W. Thiel, J. Chem. Phys., 1995, 102, 8474 CrossRef CAS.
- V. Jonas and W. Thiel, Organometallics, 1998, 17, 353 CrossRef CAS.
- V. Jonas and W. Thiel, J. Phys. Chem., 1999, 103, 1381 CrossRef CAS.
- D. M. Adams and I. D. Taylor, J. Chem. Soc., Faraday Trans., 1982, 78, 1051 RSC.
- U. A. Jayasooriya, J. Chem. Soc., Faraday Trans., 1994, 90, 1265 RSC.
- P. C. H. Mitchell, S. F. Parker, A. J. Ramirez-Cuesta and J. Tomkinson, Vibrational Spectroscopy with Neutrons, World Scientific, Singapore, 2005 Search PubMed.
- S. J. Clark, M. D. Segall, C. J. Pickard, P. J. Hasnip, M. J. Probert, K. Refson and M. C. Payne, Z. Kristallogr., 2005, 220, 567 CAS.
- K. Refson, S. J. Clark and P. R. Tulip, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 155114 CrossRef.
- S. F. Parker, F. Fernandez-Alonso, A. J. Ramirez-Cuesta, J. Tomkinson, S. Rudic, R. S. Pinna, G. Gorini and J. Fernández Castañon, J. Phys.: Conf. Ser., 2014, 554, 012003 CrossRef.
- M. A. Adams, S. F. Parker, F. Fernandez-Alonso, D. J. Cutler, C. Hodges and A. King, Appl. Spectrosc., 2009, 63, 727–732 CrossRef CAS PubMed.
- J. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS PubMed.
- A. Tkatchenko and M. Scheffler, Phys. Rev. Lett., 2009, 102, 073005 CrossRef PubMed.
- A. M. Rappe, K. M. Rabe, E. Kaxiras and J. D. Joannopoulos, Phys. Rev. B: Condens. Matter Mater. Phys., 1990, 41, 1227 CrossRef PubMed.
- V. Milman, A. Perlov, K. Refson, S. J. Clark, J. Gavartin and B. Winkler, J. Phys.: Condens. Matter, 2009, 21, 485404 CrossRef PubMed.
- X. Gonze, J.-C. Charlier and M. P. Teter, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 13035–13038 CrossRef CAS PubMed.
- A. J. Ramirez-Cuesta, Comput. Phys. Commun., 2004, 157, 226 CrossRef CAS.
- B. N. Figgis and A. N. Sokolev, Acta Crystallogr., Sect. E: Struct. Rep. Online, 2004, 60, i9 CrossRef.
- T. C. W. Mak, Z. Kristallogr., 1984, 166, 277 CAS.
- F. Heinemann, H. Schmidt, K. Peters and D. Thiery, Z. Kristallogr., 1992, 198, 123 CrossRef CAS.
- T. Shimanouchi, J. Phys. Chem. Ref. Data, 1977, 6, 993 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c9cp05191k |
| This journal is © the Owner Societies 2019 |