Computational study of aromaticity, ¹H NMR spectra and intermolecular interactions of twisted thia-norhexaphyrin and its multiply annulated polypyrrolic derivatives

Abstract

The recently synthesized twisted thia-norhexaphyrin and its multiply annulated polypyrrolic derivatives have been studied computationally. Gauge-including magnetically induced current calculations predict a global nonaromatic character of the initial thia-norhexaphyrin due to the highly-twisted conformation of the macrocycle. Upon the oxidation of the thia-norhexaphyrin four multiply annulated polypyrrolic aromatic macrocycles are formed for which the global aromatic character is confirmed in agreement with experimentally measured ¹H NMR spectra. The calculation of the proton chemical shifts for the studied compounds by direct comparison with the tetramethylsilane standard leads to a significant mean absolute error. At the same time a linear regression procedure for the two selected groups of protons (CH and NH protons) provides much better values of calculated chemical shifts and tight correlation with experiment. The separate consideration of NH protons is motivated by the numerous intermolecular hydrogen bonds in which the protons are involved, which induce considerable upfield shifts, leading to a significant underestimation of the corresponding chemical shifts. Such a selected correlation can be used for accurate estimation of proton chemical shifts of the related porphyrinoids. Bader's theory of Atoms in Molecules has been applied for the studied twisted thia-norhexaphyrin and its multiply annulated polypyrrolic derivatives to characterize intramolecular H-bonds and other non-covalent interactions.

---

1. Introduction

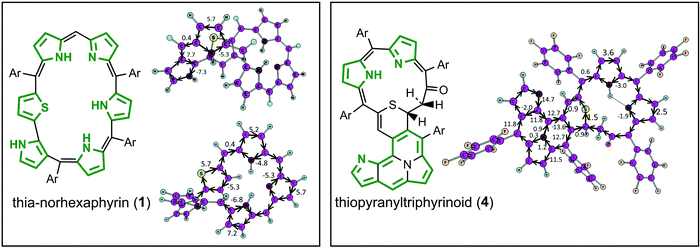
Porphyrinoids represent a large extended class of porphyrins that have found practical application as active materials for photovoltaic cells, field-effect transistors, and organic electronics devices.^1–3 Also, porphyrinoids can be used as sensitizers in photodynamic therapy and bioimaging.^4,5 It follows that the electronic structure and aromaticity of numerous porphyrinoids have been investigated intensively during the last decade.^6–14 Particularly, it has been shown that the isophlorines are strongly antiaromatic and are air-stable at the same time.¹⁴ On the other hand, the chemical and tautomeric transformations of them can lead to purely aromatic species,¹² meaning that porphyrinoids can be used as molecular aromatic/antiaromatic switches. Generally, porphyrinoid systems can demonstrate aromatic, antiaromatic or nonaromatic character depending on the type of heteroatoms included in the macrocycle, linkage moieties and outer substitutes.^15,16 The (non/anti)aromatic properties of expanded porphyrins, carbaporphyrinoids and other porphyrinoids determine their specific spectroscopic and photophysical properties,^6–8 which is a good case for computational studies.

In the present work we focus on the electronic structure and ¹H NMR spectra of five recently synthesized¹⁷ unique porphyrinoids (Fig. 1) – core-modified norhexaphyrin (1) containing a thiophene ring and four products of its oxidation: thiopyrrolo-pentaphyrin with an embedded pyrrolo[1,2]isothiazole (2), a sulfur-free pentaphyrin incorporating an indolizine moiety (3), thiopyranyltriphyrinoid containing a 2H-thiopyran unit (4) and a fused pentaphyrin containing a pyrrolizine moiety (5) which is formed upon desulfurization reaction of compound (2).

Fig. 1 The structure of the porphyrinoids studied in this work including the principal scheme of their synthesis starting from norhexaphyrin (1). Details about the synthetic procedure are published in ref. 17.

Due to the extended and complicated structure of the studied systems there are multiple pathways of magnetically induced ring currents which can exist and compete between each other. In such cases gauge-including magnetically induced current (GIMIC) calculations can provide a solid explanation of the real distribution of ring currents and make it possible to determine the global (non/anti)aromaticity. Accurate calculations of proton chemical shifts for extended porphyrins and porphyrinoids remain an important task because they help to assign the experimentally observed ¹H NMR signals, especially for close-positioned signals, and to support the (non/anti)aromatic behavior of these species. Such calculations are still a challenge for computational chemistry because of the large size of the porphyrinoids and the variety of proton types (aromatic, aliphatic, methine protons of CH bonds, NH protons of pyrrole rings, etc.). In this paper we have analyzed the applicability of a linear regression procedure for the accurate calculation of chemical shifts for two separate groups of protons (CH and NH protons). The proposed technique works well within both the gauge-independent atomic orbital (GIAO) and continuous set of gauge transformation (CSGT) computational approaches at the DFT level, demonstrating tight correlations with experiment (R² up to 0.995). Finally, we have analyzed the electronic density distribution function for the studied molecules (1)–(5) within Bader's quantum theory of “Atoms in Molecules” (QTAIM) in order to identify and characterize the intermolecular non-covalent interactions and H-bonds that significantly affect the ¹H NMR signal position for the corresponding protons involved in these contacts.

2. Computational details

The ground electronic singlet state (S₀) structures of the studied porphyrinoids 1–5 have been optimized using the B3LYP/6-31G(d)^18–20 method at the DFT level starting from the initial molecular geometries obtained by the single-crystal X-ray diffraction technique.¹⁷ Based on the optimized geometries QTAIM analysis²¹ of the electronic density distribution functions has been carried out. The non-covalent interactions have been identified by the presence of (3, −1) type critical points and bond paths between the interacting atoms. The energy of the found non-covalent contacts was estimated through the Espinosa–Molins–Lecomte (EML) relationship:^22,23E_bond = 0.5ν(r), where ν(r) is the potential energy density (a.u.) at the corresponding (3, −1) bond critical point. The calculations of nuclear magnetic shielding tensors for the hydrogen atoms have been performed within the GIAO²⁴ and CSGT²⁵ methods at the B3LYP/6-311++G(d,p) level^18,19,26 of DFT. The role of solvent in the shielding constants was considered using the polarizable continuum model (PCM)²⁷ taking CHCl₃ as a model solvent. The final proton chemical shift values (δ_i(theor), ppm) were estimated by: (1) the direct comparison of computed isotropic shielding constants (σ_i(iso), ppm) with the TMS standard (σ_TMS, ppm) calculated at the same level of theory: δ_i(theor) = σ_TMS − σ_i(iso); and (2) the linear regression method according to the following expression: δ_i(theor) = (σ_TMS − σ_i(iso) − b)/a, where the slope (a) and intercept (b) coefficients are estimated from the linear correlation between δ_i(theor) = σ_TMS − σ_i(iso) and δ_i(exp.).^28,29 All the above discussed calculations at the DFT level were performed using Gaussian16 software.³⁰ The QTAIM calculations were carried out using the AIMAll program package.³¹ Magnetically induced current densities and current strengths have been calculated using the GIMIC code.^32–35 The NMR shielding calculations required for the GIMIC computations have been performed at the B3LYP/def2-TZVP^18,19,36 level of theory using the Turbomole program package.³⁷ The strength of the global magnetically induced current for the case of planarized porphyrinoids 2, 3 and 5 was estimated by applying an external magnetic field along the z axis perpendicular to the molecular xy plane. In the case of compound 4, the magnetic field was oriented perpendicular to the plane of the cyclopenta[a]pyrrolo[2,1,5-de]quinolizine 14π-electron system, while the rest of the molecule is almost coplanar with this fragment. In the case of compound 1 we have used the approach described in ref. 38. The current strengths were computed by the rotation of the applied magnetic field in the xz plane (assuming that the macrocycle is oriented in the imaginary xy plane) in the range 0–180° with a step of 30°. The maximal values of total current strength and corresponding current pathways for compound 1 are only discussed in the text.

Ring-current strengths (I, nA T⁻¹) and current strength pathways for selected chemical bonds have been obtained by integrating the current density that flows through planes intersecting the chemical bonds.

3. Results and discussion

3.1. GIMIC calculations of global aromaticity

As follows from the optimized and X-ray structure, thia-norhexaphyrin (1)¹⁷ possesses a highly-twisted conformation of the macrocycle that prevents efficient π-conjugation and electron delocalization. GIMIC calculations indeed provide a very weak net diatropic ring current (0.4 nA T⁻¹) for the twisted macrocycle of thia-norhexaphyrin (1) (Fig. 2). At the same time each pyrrole and thiophene ring sustains significant local diatropic ring currents (the current strength varies in the range 5.2–7.2 nA T⁻¹). It means that thia-norhexaphyrin (1) can be considered as a globally nonaromatic twisted porphyrinoid containing six locally aromatic coupled heterocycles (five pyrroles and one thiophene). Moving to the thiopyranyltriphyrinoid (4) containing a 2H-thiopyran unit, two different cyclic subsystems can be classified. The first one is a cyclopenta[a]pyrrolo[2,1,5-de]quinolizine 14π-electron system which possesses aromatic character (the net diatropic current strength is 14.7 nA T⁻¹). The calculated currents along the three N–C bonds inside this fragment are very small (1.2, 0.3 and 0.9 nA T⁻¹) meaning that the inner N atom is not involved in the aromatic system. The remainder of the molecule (second subsystem) containing the 2H-thiopyran cycle sustains a net non-aromatic character because of the broken π-conjugation within the saturated –CO–CH₂–CH[double bond splayed right] fragment (Fig. 2). As a result only a weak local aromaticity can be postulated for the two pyrrole rings.

Fig. 2 The current pathways (black arrows) and corresponding current strengths (numbers in nA T⁻¹) for the globally non-aromatic porphyrinoids 1 and 4. Green frameworks mean the global current pathways predicted by GIMIC.

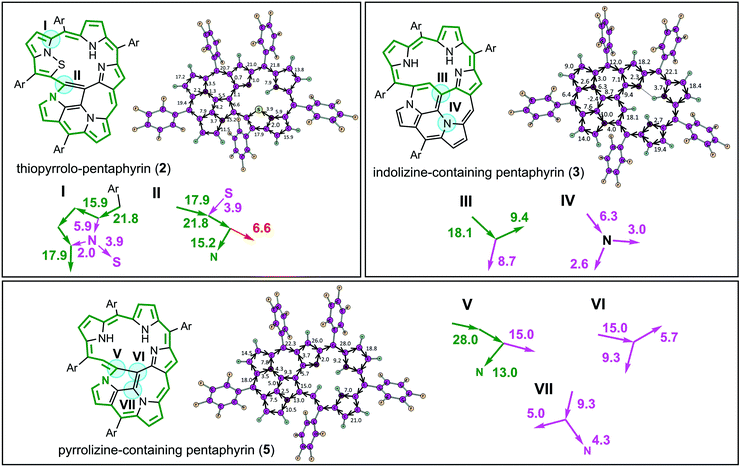
In contrast to compounds 1 and 4, porphyrinoids 2, 3 and 5 demonstrate clear global aromatic character and significant net diatropic ring currents (21.8, 22.1 and 28 nA T⁻¹, respectively) in agreement with the previously reported ACID and NICS calculations.¹⁷ However, our GIMIC calculations make it possible to determine the multiple global aromatic pathways within each porphyrinoid molecule (2, 3 and 5) based on the absolute value of the current strength along the selected bond and quantitative splitting of this current at the bifurcation points (marked by turquoise spots in Fig. 3). For instance, for thiopyrrolo-pentaphyrin (2) there are two most important bifurcation points (I and II, Fig. 3). The first one (I) represents a splitting of the incoming current (21.8 nA T⁻¹) into two flows that circulate through the outer perimeter (15.9 nA T⁻¹) and through the inner subperimeter (5.9 nA T⁻¹) (Fig. 3). Surprisingly, at the bifurcation point (II) the main part of the diatropic current circulates along the C–N bond (15.2 nA T⁻¹) and only a small amount (6.6 nA T⁻¹) goes to the C–C bond (Fig. 3). This fact actually means that the nitrogen atom in the pyrrolizine fragment is involved in the global aromatic electronic structure of thiopyrrolo-pentaphyrin (2). The same situation (i.e. involvement of the nitrogen atom in the pyrrolizine fragment in the global aromatic pathway) is also observed for the fused pentaphyrin containing a pyrrolizine moiety (5), which is similar to thiopyrrolo-pentaphyrin (2) but does not contain the –S– linker (Fig. 1). Despite the fact that the initial strong diatropic current (28.0 nA T⁻¹) is almost equally split at the bifurcation point (V), at the next two points (VI) and (VII) this current (15.0 nA T⁻¹) continues to split onto equivalent branches, so it is hard to distinguish the global aromatic pathway in this case. At the same time, the diatropic current in the outer perimeter (15.0 nA T⁻¹, green lines and arrows in Fig. 3) does not change significantly and becomes even higher because of the combination with the smaller currents from the inner π-delocalized system. Interestingly, compound 3, being very similar to compounds 2 and 4, demonstrates a short global aromatic pathway avoiding the multiply annulated fragment (Fig. 3). In the bifurcation point (III) the initial diatropic current (18.1 nA T⁻¹) splits almost equally – the first pathway (8.7 nA T⁻¹) gradually dissipates over the multiply annulated part, while the second pathway (9.4 nA T⁻¹) circulates through the inner perimeter forming a short global aromatic pathway (Fig. 3, green perimeter in compound 3).

Fig. 3 Current pathways (black arrows) and corresponding current strengths (numbers in nA T⁻¹) for the globally aromatic porphyrinoids 2, 3 and 5. Green frameworks denote the global current pathways predicted by GIMIC. Pink and red arrows denote different streams of the magnetically induced currents.

It is notable that the global aromatic pathways calculated by the GIMIC method (marked by green in Fig. 2 and 3) cannot be identified with the conjugation circuits usually presented for the porphyrinoid systems.^17,39–41 The conjugation circuits are based on general chemical principles and single-crystal X-ray information about single/double bond alternation. Rather, the current pathways predicted by GIMIC demonstrate the real distribution of the magnetic currents due to the perturbation of the delocalized π-electronic molecular shell by the external magnetic field (usually applied perpendicular to the molecular plane). Actually, the number of electrons in the conjugation circuit and its satisfaction or unsatisfaction to the Hückel (4n + 2) rule need not be fulfilled strictly for complicated porphyrinoids because all of the delocalized π-electrons interact with the external magnetic field (not only those marked by the conjugation circuit). One should stress that our GIMIC results do not contradict but excellently confirm the rise of the aromaticity degree in the series of multiply annulated molecules 2 < 3 < 5 based on a comparison of the total diatropic current strength (21.8 < 22.1 < 28 nA T⁻¹) and the difference in the chemical shifts of the inner and outer protons Δδ_out–in (7.19 < 10.70 < 12.51 ppm).¹⁷ The GIMIC results are also in excellent agreement with the previously published NICS(0) local aromaticity indices for all studied porphyrinoids 1–5.¹⁷

3.2. ¹H chemical shift calculations

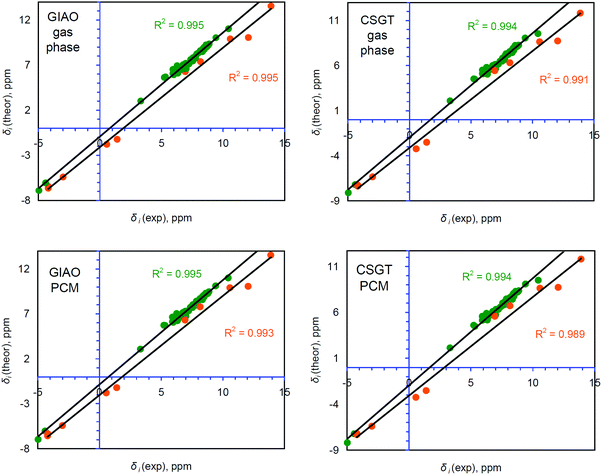
Generally, accurate calculations of the proton chemical shifts of porphyrinoid molecules still pose a challenge for computational chemistry. Actually, only a limited number of reports have been published^{10,12,14,42–45} in which the ¹H chemical shifts of porphyrin and some porphyrinoids are calculated and discussed. In most previous studies the direct comparison of the calculated isotropic shielding constants with the TMS standard was used to predict the ¹H chemical shifts. Generally, this approach provides significant mismatch between the experimental and theoretically estimated chemical shifts (up to 1 ppm for the CH protons and up to 4 ppm for NH protons). For our systems we observe the same trend (Table S1, ESI†). Analyzing Fig. 4, one finds that the GIAO/B3LYP/6-311++G(d,p) calculations demonstrate very good agreement between δ_i(theor) and δ_i(exp) only in the narrow region around 7.3 ppm. At this point the idealized δ_theor = δ_exp function (black line) is crossed with the linear regression function (green trend line). However, the significant slope parameter (1.164) and R² = 0.981 indicate that this particular correlation exhibits a fair amount of systematic and random errors (Table 1).²⁸ Especially, it relates to the low- and high-field regions (around (−5) to (−4) ppm and 10–14 ppm). The CSGT/B3LYP/6-311++G(d,p) approximation demonstrates a slightly smaller slope parameter (1.155) and thus a smaller contribution of systematic error, but the correlation coefficient is even smaller relative to the GIAO approach (R² = 0.975), meaning a larger random error contribution (Table 1). Additionally, the intercept parameter is almost two times higher in absolute value for the CSGT/B3LYP/6-311++G(d,p) approximation relative to the GIAO one (−2.2078 vs. −1.2072, Table 1), which also indicates a stronger systematic underestimation of ¹H chemical shifts computed by the CSGT scheme.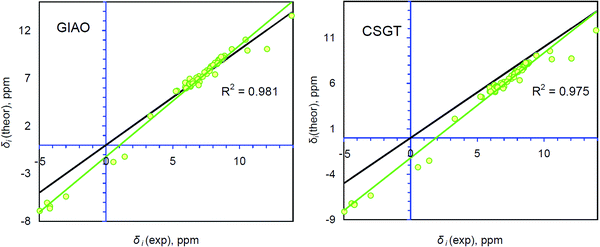

Fig. 4 Comparison between the theoretically calculated and experimentally determined ¹H chemical shifts for the single group of protons containing 63 atoms of NH and CH types. The R² parameter corresponds to the linear correlation (green line) between δ_i(exp) and δ_i(theor). The idealized correlation δ_i(theor) = δ_i(exp) (black line) is presented for comparison. Experimental data are taken from ref. 17.

Table 1 Parameters of the linear correlations δ_i(exp) = (σ_TMS − σ_i(iso) − b)/a for the different groups of protons of porphyrinoids 1–5 and related values of the mean absolute errors (MAEs)

	R ^2	Slope (a)	Intercept (b)	MAE, ppm	MAE(CH), ppm	MAE(NH), ppm
CH + NH (GIAO gas phase)	0.981	1.164	−1.207	0.330	0.208	0.980
CH + NH (CSGT gas phase)	0.975	1.155	−2.208	0.373	0.238	1.090
CH + NH (GIAO PCM)	0.980	1.170	−1.148	0.333	0.206	1.003
CH + NH (CSGT PCM)	0.974	1.161	−2.156	0.386	0.249	1.111
CH (GIAO gas phase)	0.995	1.152	−0.905	—	0.138	—
NH (GIAO gas phase)	0.995	1.102	−2.086	—	—	0.391
CH (CSGT gas phase)	0.994	1.157	−1.985	—	0.149	—
NH (CSGT gas phase)	0.991	1.073	−3.122	—	—	0.512
CH (GIAO PCM)	0.995	1.162	−0.864	—	0.126	—
NH (GIAO PCM)	0.993	1.103	−2.038	—	—	0.437
CH (CSGT PCM)	0.994	1.166	−1.952	—	0.143	—
NH (CSGT PCM)	0.989	1.075	−3.072	—	—	0.573
CH + NH (GIAO gas phase) direct	—	—	—	0.553	0.345	1.654
CH + NH (CSGT gas phase) direct	—	—	—	1.194	0.889	2.812
CH + NH (GIAO PCM) direct	—	—	—	0.612	0.426	1.602
CH + NH (CSGT PCM) direct	—	—	—	1.104	0.838	2.766

---

The estimated MAEs for the combined number of 63 protons (53 CH and 10 NH atoms) equal 0.330 and 0.373 ppm, respectively, by the GIAO and CSGT schemes (Table 1 and Table S2, ESI†). However, the MAEs for the particular groups of CH and NH protons within these combined correlations are very different (0.208 vs. 0.980 ppm and 0.238 vs. 1.090 ppm, Table 1) meaning that only the linear relation between δ_i(exp) and δ_i(theor) cannot explain accurately the chemical shifts for the NH protons.

The correlation between δ_i(exp) and δ_i(theor) can be improved by separating NH and CH protons into two different groups (53 and 10 atoms, respectively, Table S3, ESI†) for which each particular correlation is more tight (Fig. 5) relative to those for the overall 63 hydrogen atoms. Indeed, for the CH protons the R² parameter within the GIAO and CSGT schemes is around 0.995, which is an acceptable value for a well-performing computational method.^28,29 The slope parameter is still around 1.15–1.16, demonstrating a considerable contribution of systematic error, but the intercept parameter becomes significantly smaller for CH protons, indicating a decrease of systematic underestimation (Table 1). At the same time, the R², slope and intercept values for the linear correlation between δ_i(exp) and δ_i(theor) of NH protons are a bit worse compared to those for CH protons but much better compared to the generalized correlation for all 63 protons (Fig. 4). The resulting MAE values for the computed chemical shifts of NH protons are also much better relative to those obtained by the combined linear regression method as well as with a direct comparison with the TMS standard scheme (Table 1). It means that separating the different types of protons provides much better agreement between δ_i(exp) and δ_i(theor) values for the CH and NH protons in terms of a linear regression procedure, while the direct comparison with the TMS reference is much worse by the MAE criterion (Table 1, especially for NH protons).

Fig. 5 Comparison between the theoretically calculated and experimentally found ¹H chemical shifts for the two groups of CH (52 atoms, green spots) and NH (11 atoms, orange spots) types, calculated by both the GIAO and CSGT schemes with and without accounting for solvent effects at the PCM level. The R² parameter corresponds to the linear correlation (black line) between δ_i(exp) and δ_i(theor).

Accounting for solvent effects by the polarizable continuum model (PCM) almost does not affect the R² and slope parameters of the proposed correlations at all (Table 1), but definitely improves the intercept parameter. More precise calculations considering the influence of zero-point and thermal vibrations, and dynamic and relativistic effects^46–49 on the ¹H chemical shifts of porphyrinoid molecules should improve the correlation parameters in the future, however, such calculations are very time and resource consuming for large porphyrinoid systems.

Finally, we conclude that gas phase B3LYP/6-311++G(d,p) calculations of shielding constants by both the GIAO and CSGT schemes using the linear regression procedure for the different groups of protons (NH and CH in our case) demonstrate a sufficiently good accuracy of predicted chemical shifts as well as an optimal balance between accuracy and time/resource expenses. As an additional remark we can suppose that intramolecular non-covalent interactions affect significantly the chemical shifts of NH protons and generally provide a significant underestimation trend (the intercept parameter is large) in contrast to the CH protons, which are less sensitive and less active with respect to the inter- and intramolecular non-covalent interactions. Due to this reason, we will focus in the next section on the particular non-covalent interactions and their electronic parameters calculated at the QTAIM level for the studied porphyrinoid molecules 1–5.

3.3. Validation of ¹H chemical shift calculations

Several previous studies have demonstrated that functionals with a low percentage of Hartree–Fock exchange (HFE) should not be employed for conjugated (and, particularly, aromatic) systems.^50–52 More recently, in the context of porphyrins, it has been also commented by Casademont-Reig et al.⁵³ and Torrent-Sucarrat et al.⁵⁴ That is why, in order to validate the applicability of the B3LYP/6-311++G(d,p) technique (20% HFE) with respect to the role of the HFE amount, we have recalculated ¹H chemical shifts by the hybrid meta generalized gradient M06-2X(54% HFE) approach using the same 6-311++G(d,p) basis set. The M06-2X/6-31G(d) optimized geometries were used for the ¹H chemical shift calculations discussed next in this section. All the results are summarized in Fig. S1 and S2 and in Table S4–S7 (ESI†). One should stress that one can see from Table S4 that the R² parameter for all correlations based on the M06-2X functional does not exceed 0.988, meaning the higher contribution of random error within the applied computational scheme. It should be noted that by the R² criterion none of the M06-2X based correlations satisfy the minimal acceptable value (R² = 0.995) for a well-performing computational method.^28,29 However, the slope and intercept values are much closer to the ideal 1 and 0 values, respectively, meaning the much smaller contribution of systematic error for the M06-2X based correlations. Comparing the MAE values in Table 1 and Table S4 (ESI†), one should stress that the CSGT approach demonstrates much better performance for the direct and generalized (CH + NH) schemes when combined with the M06-2X/6-311++G(d,p) method rather than with the B3LYP/6-311++G(d,p) approach. However, comparing the particular correlations for the ¹H chemical shifts within the CH and NH manifolds, B3LYP/6-311++G(d,p) provides the better performance by the MAE criterion (no more than 0.149 ppm for CH protons and no more than 0.573 ppm for NH protons) relative to the M06-2X/6-311++G(d,p) approach (the minimal MAE equals 0.211 and 0.585 ppm for CH and NH protons, respectively, Table S4, ESI†). It means that the proposed differentiation scheme for the evaluation of ¹H chemical shifts within separate sorts of CH and NH protons works adequately at the B3LYP/6-311++G(d,p) level and the considerable systematic error within this approach can be effectively reduced by the linear regression procedure.

3.4. Intramolecular non-covalent interactions and tautomerism

Before we start the analysis of non-covalent interactions in the studied porphyrinoids we have investigated the possible tautomerism of these molecules by changing the position of the NH proton within the porphyrinoid macrocycle. The results are collected in Fig. S3 (ESI†). We have found that for all cases the structure of porphyrinoids 1–5 established by single-crystal X-ray diffraction corresponds to the lowest energy tautomer presented in Fig. 1. All other tautomers for compounds 1–3 and 5 are higher in energy by no less than 3.9 kcal mol⁻¹, which implies that the lowest ratio between the main tautomer and another one is only 1000 : 1 (if one considers the Boltzmann distribution at room temperature). Only in the case of compound 4 are the two possible tautomers (4 and 4a in Fig. S3, ESI†) quite close in energy, giving a distribution ratio 12 : 1, but accounting for the energy barrier for direct proton transfer along the NH⋯N coordinate this ratio should be much higher. Indeed, in all cases for compounds 1–5 only the main tautomer was isolated in the single crystal state and no additional signals were identified in the ¹H NMR spectra of the studied porphyrinoids.¹⁷ Therefore in this section we focus our attention only on the intramolecular interactions occurring in the main tautomer form of porphyrinoids 1–5 (Fig. 1).

All the non-covalent interactions identified in the investigated porphyrinoids (Fig. 6) can be generally classified into two main groups: H-bonds and van der Waals (vdW) interactions. A few types of H-bonds can be identified in the studied porphyrinoids (NH⋯N, NH⋯S, CH⋯N, CH⋯O, CH⋯F, and CH⋯C) and many sorts of vdW contacts (F⋯C, N⋯C, F⋯F, N⋯S, O⋯C, and H⋯H) exist in these molecules. The electronic characteristics of all these interactions are collected in Table S4 (ESI†). We have performed QTAIM analysis both for the B3LYP/6-31G(d) optimized geometries and for the experimental geometries taken from X-ray analysis. Generally, intramolecular H-bonds of only the NH⋯N and CH⋯N types occur in molecules 2, 3 and 5, while S-containing porphyrinoids 1 and 4 also possess CH⋯O and NH⋯S interactions. The main parameters of these H-bonds only slightly depend on the initial geometry (optimized or X-ray, Table S4, ESI†), which is why only the data for B3LYP/6-31G(d) optimized geometries are presented in Table 2. Accounting for the positive values of the Laplacian (∇²ρ(r)) and electron energy densities (h_e(r)), one can formally classify all the found non-covalent interactions (Table 2 and Table S4, ESI†) as closed-shell interactions (in the framework of the QTAIM formalism), which are characterized by the minor sharing of electron density in the interatomic space.

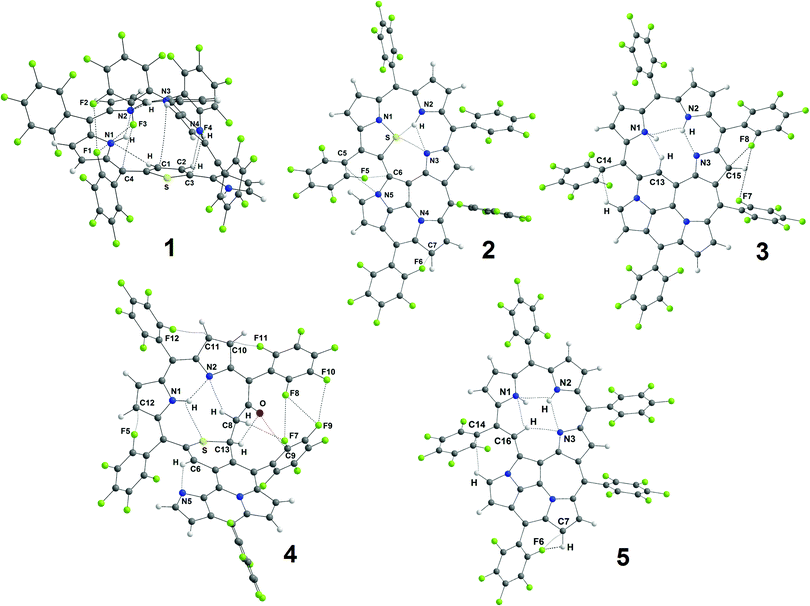Fig. 6 The structure of porphyrinoids 1–5 with the identified non-covalent interactions (dashed lines) identified by QTAIM analysis.

Table 2 Topological characteristics^a of selected (strongest) non-covalent interactions calculated by the QTAIM method for porphyrinoids 1–5 of different initial geometries

Bond	d, Å	ρ(r), e a0^−3^a	ν(r), a.u.	g(r), a.u.	h e(r), a.u.	∇^2ρ(r), e a0^−5	ε	E, kcal mol^−1	E(curr),^b kcal mol^−1 [Jdia, nA T^−1]
a d – interatomic distance, ρ(r) – electron density at the bond critical point (BCP), ν(r) – potential energy density at the BCP, g(r) – kinetic energy density at the BCP, he(r) – electronic energy density at the BCP (ν(r) + g(r)), ∇^2ρ(r) – Laplacian of the electron density at the BCP, E – EML bond energy, ε – bond ellipticity; a0 – Bohr radius. b E(curr) was estimated from the linear relation Jdia = aE(curr) + b, where a and b are dimension coefficients equal to −0.078 (nA T^−1)/(kcal mol^−1) and 0.345 nA T^−1, respectively, at the B3LYP/def2-TZVP level of theory.^56
1
N1H⋯N2	2.083	0.0241	−0.0185	0.0188	0.0003	0.0763	0.029	−5.8	−6.1 [0.81]
N3H⋯N2	2.058	0.0254	−0.0196	0.0198	0.0002	0.0804	0.034	−6.1	−6.2 [0.82]
2
N2H⋯S	2.360	0.0199	−0.0157	0.0165	0.0008	0.0697	0.193	−4.9	−5.9 [0.79]
N2H⋯N3	2.068	0.0246	−0.0193	0.0197	0.0004	0.0807	0.063	−6.1	−6 [0.8]
N3⋯S	3.027	0.0166	−0.0105	0.0114	0.0009	0.0495	0.063	−3.3	−2.1 [0.5]
3
N3⋯HN2	1.909	0.0348	−0.0283	0.0278	−0.0005	0.1094	0.056	−8.9	−9.5 [1.06]
N1⋯HC13	2.288	0.0167	−0.0118	0.0145	0.0027	0.0689	0.457	−3.7	−2 [0.5]
4
N1H⋯N2	1.946	0.0315	−0.0253	0.0251	−0.0002	0.0996	0.025	−7.9	−8.1 [0.96]
N1H⋯S	2.751	0.0106	−0.0062	0.0080	0.0018	0.0391	0.430	−1.9	−4 [0.65]
O⋯HC13	2.225	0.0191	−0.0155	0.0172	0.0017	0.0754	0.709	−4.9	−6.1 [0.81]
N5⋯HC6	2.126	0.0227	−0.0166	0.0175	0.0009	0.0735	0.051	−5.2	−7 [0.88]
5
N1⋯HN2	2.352	0.0149	−0.0109	0.0139	0.0030	0.0676	0.769	−3.4	−1 [0.43]
N2H⋯N3	2.268	0.0166	−0.0120	0.0130	0.0010	0.0561	0.143	−3.8	−1.9 [0.49]
N3⋯HC16	2.234	0.0185	−0.0129	0.0135	0.0006	0.0571	0.024	−4.0	−4 [0.65]

---

However, the h_e(r) values are very close to zero for most contacts (up to order 10⁻⁴), meaning a close balance between the potential ν(r) and kinetic g(r) energy densities, which are negative and positive, respectively, by definition.⁵⁵ In such cases, the absolute values of electron density ρ(r) and potential energy density ν(r) at the corresponding bond critical points (BCPs) should be considered and used for the estimation of the bond strengths. The EML bond energies based on the ν(r) values are predicted to be in the range 3.8–8.9 kcal mol⁻¹ for NH⋯N bonds, 3.7–5.2 kcal mol⁻¹ for CH⋯N bonds, and 1.9–4.9 kcal mol⁻¹ for NH⋯S and CH⋯O contacts. It means that all the NH protons in the studied porphyrinoids are involved in a network of strong intramolecular bonds, which causes significant electron cloud depletion around these H atoms. This could be a reason why the conventional DFT approach strongly underestimates the corresponding shielding constants used for the ¹H chemical shift prediction. In this case, the linear regression scheme discussed above seems to be a reasonable way to exclude such systematic effects.

The fact itself that accounting for solvent effects within the PCM model improves the intercept parameters of the δ_i(exp) vs. δ_i(theor) correlations (Table 1) also supports the idea that the correct polarization of NH protons (but not only) is a proper way to accurately estimate δ_i(theor) ¹H chemical shifts. The vdW interactions presented in Table 2 and Table S4 (ESI†) are expectedly less strong than the H-bonds, but they are very important for the stabilization of the conformational structure of the studied porphyrinoids. Particularly, C₆F₅-groups form numerous weak vdW interactions (mainly of F⋯C nature) with the central macrocycle, stabilizing the positions of these side substituents.

In order to validate the EML calculated energies of hydrogen bonds presented in Table 2 we have applied the technique proposed by Kaila et al.,⁵⁶ which is based on the linear correlation between the diamagnetic part of the magnetically induced current density (J_dia) along a selected hydrogen bond and the energy of this bond (E_curr). The results are summarized in Table 2. One can observe excellent agreement between the EML calculated bond energies and those estimated by the E(curr) ∝ J_dia dependence. It is interesting to note that the agreement is better for strong hydrogen bonds (generally, the deviation is no more than 1 kcal mol⁻¹) but for weak interactions the deviation can reach 2.4 kcal mol⁻¹. It can be explained by the fact that the E(curr) ∝ J_dia relation by Kaila et al.⁵⁶ was calibrated using reference H-bond energies no less than 3 kcal mol⁻¹.

Table 2 and Table S4 (ESI†) also consist of ellipticity (ε) values, which characterize the curvature of the bond path between the interacting atoms. Actually, a high ellipticity (more than 0.5) represents a dynamic instability of these interactions,^21,57i.e. these bonds are stable only upon the fixed position of atoms. It explains why in moving from B3LYP/6-31G(d) optimized to X-ray taken geometries the main electronic parameters (that are distance-dependent) are changed only slightly except for the ellipticity, which is interatomic disposition dependent. Concluding shortly, we should note that QTAIM analysis cannot be considered as a chemically accurate method for electronic structure calculations but with respect to the characterization of non-covalent interactions it seems to be the most powerful tool developed until now. Our QTAIM calculations also shed light on the very complicated electronic surroundings of the NH protons in the studied porphyrinoids, which become even more sophisticated in the presence of external magnetic field induced magnetic dia- or paratropic currents.

4. Conclusions

In the present paper the electronic structure, aromaticity and ¹H chemical shifts have been computationally studied for five recently synthesized porphyrinoids – multiply annulated polypyrrolic derivatives 2–5 of twisted thia-norhexaphyrin (1). The magnetically induced current density calculations predict a non-aromatic character of thia-norhexaphyrin (1), partial aromatic character of thiopyranyltriphyrinoid (4), which contains a 2H-thiopyran unit, and strong global aromaticity of pentaphyrin with an embedded pyrrolo[1,2]isothiazole (2), a sulfur-free pentaphyrin (3) incorporating an indolizine moiety and fused pentaphyrin (5) containing a pyrrolizine moiety. These results are in excellent agreement with previously published experimental observations. Rather surprisingly, for compounds 2 and 5 we found that the pyrrolizine nitrogen atom is involved in the global aromatic pathway, implying significant electronic delocalization over the pyrrolizine fragment. Such a phenomenon has never been observed before despite the fact that a pyrrolizine fragment frequently appears in porphyrinoid systems.^39,40

Considering the groups of CH and NH protons as distinct, calculations using the GIAO/B3LYP/6-311++G(d,p) method, and analyzed using a linear regression scheme, made it possible to estimate the ¹H chemical shift values with high accuracy (the MAE is 0.138 and 0.391 ppm, respectively) and with an acceptable correlation criterion (R² = 0.995). Computations within the continuous set of gauge transformations (CSGT) scheme provide comparable results relative to the GIAO method but gave slightly worse results. Accounting for solvent effects on the isotropic shielding constants did not improve the correlation tightness, but reduced the systematic underestimation of the computed chemical shifts. We assign this effect to the fact that all the NH protons of the studied molecules are involved in moderate or strong H-bonds and in weak van der Waals interactions. This provides a stronger depletion of electron density around the NH protons compared to the CH protons, which usually are inactive with respect to inter- and intramolecular interactions.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by the Ministry of Education and Science of Ukraine (project no. 0117U003908), and by the Olle Engkvist Byggmästare foundation (contract no. 189-0223). The calculations were performed with computational resources provided by the High Performance Computing Center North (HPC2N) in Umeå, Sweden, through the project ‘‘Multiphysics Modeling of Molecular Materials’’ SNIC 2018-2-38. The GIMIC calculations were carried out using the SKIF supercomputer at the Tomsk State University. The work at ECUST was financially supported by Shanghai Municipal Science and Technology Major Project (Grant No. 2018SHZDZX03) and the international Cooperation Program of Shanghai Science and Technology Committee (17520750100), NSFC (21772041, 21702062, 21811530005), and Program of Introducing Talents of Discipline to Universities (B160170). R. R. Valiev thanks the Academy of Finland (1325369) and is personally thankful to the Tomsk Polytechnic University Competitiveness Enhancement Program (VIU-RSCABS-142/2019).

References

1. C. Wang, H. Dong, W. Hu, Y. Liu and D. Zhu, Chem. Rev., 2012, 112, 2208.
2. M. Jurow, A. E. Schuckman, J. D. Batteas and C. M. Drain, Coord. Chem. Rev., 2010, 254, 2297.
3. T. Tanaka and A. Osuka, Chem. Soc. Rev., 2015, 44, 943.
4. R. K. Pandey and G. Zheng, Porphyrin Handbook, Academic Press, San Diego, CA, 2000, vol. 6, p. 157.
5. J. R. H. Huang, W. Song and J. F. Lovell, Front. Phys., 2015, 3(23), 1.
6. R. R. Valiev, I. Benkyi, Y. V. Konyshev, H. Fliegl and D. Sundholm, J. Phys. Chem. A, 2018, 122, 4756.
7. R. R. Valiev, H. Fliegl and D. Sundholm, Phys. Chem. Chem. Phys., 2017, 19, 25979.
8. M.-C. Yoon, S. Cho, M. Suzuki, A. Osuka and D. Kim, J. Am. Chem. Soc., 2009, 131, 7360–7367.
9. I. Benkyi, H. Fliegl, R. R. Valiev and D. Sundholm, Phys. Chem. Chem. Phys., 2016, 18, 11932.
10. R. R. Valiev, H. Fliegl and D. Sundholm, J. Phys. Chem. A, 2015, 119, 1201.
11. R. R. Valiev, H. Fliegl and D. Sundholm, Phys. Chem. Chem. Phys., 2015, 17, 14215.
12. R. R. Valiev, H. Fliegl and D. Sundholm, Phys. Chem. Chem. Phys., 2014, 16, 11010.
13. T. D. Lasha, Org. Biomol. Chem., 2015, 13, 7846.
14. R. R. Valiev, H. Fliegl and D. Sundholm, J. Phys. Chem. A, 2013, 117(37), 9062.
15. J. I. Wu, I. Fernández and P. v. R. Schleyer, J. Am. Chem. Soc., 2013, 135, 315.
16. H. Fliegl, R. Valiev, F. Pichierri and D. Sundholm, Chem. Modell., 2018, 14, 1.
17. Q. Li, M. Ishida, H. Kai, T. Gu, C. Li, X. Li, G. Baryshnikov, X. Liang, W. Zhu, H. Ågren, H. Furuta and Y. Xie, Angew. Chem., Int. Ed., 2019, 58, 5925.
18. A. D. Becke, J. Chem. Phys., 1993, 98, 5648.
19. C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785.
20. M. M. Francl, W. J. Pietro, W. J. Hehre, J. S. Binkley, D. J. DeFrees, J. A. Pople and M. S. Gordon, J. Chem. Phys., 1982, 77, 3654.
21. R. F. W. Bader, Atoms in Molecules. A Quantum Theory, Calendon Press, Oxford, 1990.
22. E. Espinosa, E. Molins and C. Lecomte, Chem. Phys. Lett., 1998, 285, 170.
23. E. Espinosa, I. Alkorta and I. Rozas, Chem. Phys. Lett., 2001, 336, 457.
24. K. Wolinski, J. F. Hilton and P. Pulay, J. Am. Chem. Soc., 1990, 112, 8251.
25. T. A. Keith and R. F. W. Bader, Chem. Phys. Lett., 1992, 194, 1.
26. K. Raghavachari, J. S. Binkley, R. Seeger and J. A. Pople, J. Chem. Phys., 1980, 72, 650.
27. J. Tomasi, B. Mennucci and R. Cammi, Chem. Rev., 2005, 105, 2999.
28. M. W. Lodewyk, M. R. Siebert and D. J. Tantillo, Chem. Rev., 2012, 112, 1839.
29. G. K. Pierens, J. Comput. Chem., 2014, 35, 1388.
30. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, Revision A.03, Gaussian, Inc., Wallingford CT, 2016.
31. T. A. Keith, http://www.aim.tkgristmill.com, 2010.
32. H. Fliegl, S. Taubert, O. Lehtonen and D. Sundholm, Phys. Chem. Chem. Phys., 2011, 13, 20500.
33. J. Jusélius and D. Sundholm, J. Chem. Phys., 2004, 121, 3952.
34. D. Sundholm, H. Fliegl and R. J. F. Berger, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2016, 6, 639.
35. Gauge-Including Magnetically Induced Currents (GIMIC) program is distributed on GitHub platform and can be downloaded through the link: https://github.com/qmcurrents/gimic.
36. F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297.
37. TURBOMOLE V7.2 2017, a development of University of Karlsruhe and Forschungszentrum Karlsruhe GmbH, 1989–2007, TURBOMOLE GmbH, since 2007, available from http://www.turbomole.com.
38. H. Fliegl, D. Sundholm, S. Taubert and F. Pichierri, J. Phys. Chem. A, 2010, 114, 7153.
39. M. Suzuki, T. Hoshino and S. Neya, Org. Lett., 2014, 16, 327.
40. T. Higashino and A. Osuka, Chem. Sci., 2012, 3, 103.
41. T. Stuyver, M. Perrin, P. Geerlings, F. De Proft and M. Alonso, J. Am. Chem. Soc., 2018, 140, 1313.
42. T. Woller, J. Contreras-García, P. Geerlings, F. De Proft and M. Alonso, Phys. Chem. Chem. Phys., 2016, 18, 11885.
43. H. Cybulski, M. Pecul, T. Helgaker and M. M. Jaszuński, J. Phys. Chem. A, 2005, 109, 4162.
44. R. M. Gomila, C. Garau, A. Frontera, D. Quiñonero, P. Ballester, A. Costa and P. M. Deyà, Tetrahedron Lett., 2004, 45, 9387.
45. M. Stępień, L. Latos-Grażyński, N. Sprutta, P. Chwalisz and L. Szterenberg, Angew. Chem., Int. Ed., 2007, 46, 7869.
46. J. Vaara, Phys. Chem. Chem. Phys., 2007, 9, 5399.
47. K. Ruud, P.-O. Åstrand and P. R. Taylor, J. Am. Chem. Soc., 2001, 123, 4826.
48. J. N. Woodford and G. S. Harbison, J. Chem. Theory Comput., 2006, 2, 1464.
49. R. Faber, J. Kaminsky and S. P. A. Sauer, Gas Phase NMR, 2016, 218.
50. C. S. Wannere, K. W. Sattelmeyer, H. F. Schaefer III and P. v. R. Schleyer, Angew. Chem., Int. Ed., 2004, 43, 4200.
51. J. C. Sancho-García and J. Cornil, J. Chem. Phys., 2004, 121, 3096.
52. S. Refaely-Abramson, R. Baer and L. Kronik, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 075144.
53. I. Casademont-Reig, T. Woller, J. Contreras-García, M. Alonso, M. Torrent-Sucarrat and E. Matito, Phys. Chem. Chem. Phys., 2018, 20, 2787.
54. M. Torrent-Sucarrat, S. Navarro, F. P. Cossio, J. M. Anglada and J. M. Luis, J. Comput. Chem., 2017, 38, 2819.
55. D. Cremer and E. Kraka, Croat. Chem. Acta, 1984, 57, 1259.
56. H. Fliegl, O. Lehtonen, D. Sundholm and V. R. I. Kaila, Phys. Chem. Chem. Phys., 2011, 13, 434.
57. R. F. W. Bader, T. S. Slee, D. Cremer and E. Kraka, J. Am. Chem. Soc., 1983, 105, 5061.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c9cp04819g

---