Open Access Article
Open Access ArticleSpin-dependent charge transfer at chiral electrodes probed by magnetic resonance†
Felix
Blumenschein
a,
Mika
Tamski
 a,
Christophe
Roussel
a,
Christophe
Roussel
 ab,
Eilam Z. B.
Smolinsky
c,
Francesco
Tassinari
c,
Ron
Naaman
ab,
Eilam Z. B.
Smolinsky
c,
Francesco
Tassinari
c,
Ron
Naaman
 c and
Jean-Philippe
Ansermet
c and
Jean-Philippe
Ansermet
 *a
*a
aInstitute of Physics, Ecole Polytechnique Federale de Lausanne (EPFL), 1015 Lausanne, Switzerland. E-mail: jean-philippe.ansermet@epfl.ch; Tel: +41 21 69 33320
bSCGC, Ecole Polytechnique Federale de Lausanne (EPFL), 1015 Lausanne, Switzerland
cDepartment of Chemical and Biological Physics, Weizmann Institute of Science, Rehovot 76100, Israel
First published on 28th October 2019
Abstract
Chirality-induced spin selectivity is evidenced by exciting the spin resonance of radicals in an electrochemical cell where the working electrode is covered with a chiral self-assembled monolayer. Because the electron transfer to and from the paramagnetic radical is spin dependent, the electrochemical current changes at resonance. This electrically-detected magnetic resonance (EDMR) is monitored by a lock-in detection based on electrode voltage modulation, at a frequency that optimizes the sensitivity of the differential conductance to the electrode charge transfer process. The method is validated using p-doped GaAs electrodes in which the conduction band electrons are hyperpolarized by a well-known method of optical spin pumping with circularly polarized light. Gold electrodes covered with peptides consisting of 5 alanine groups (Al5) present a relative current change of up to 5 × 10−5 when the resonance condition is met, corresponding to a spin filtering efficiency between 6 and 19%.
1 Introduction
Spin effects in electrochemistry had been rarely examined until developments in spintronics prompted a growing interest in spin-dependent processes taking place at electrode surfaces.1–4 Spin-dependent charge recombination was identified in radical pairs (RPs) much sooner.5 This mechanism was also evidenced in organic light emitting diodes (OLEDs) and solar cells.6,7In pioneering experiments, Chazalviel first,8 and Modestov and Kazarinov later,9 found spin effects at the surface of optically polarized bare p-doped GaAs. Chazalviel relied on the spin polarization of the p-GaAs conduction band electrons that can be achieved by optical excitation with circularly polarized light.10,11 About a 100 pA change in electrochemical photocurrents was observed when the light polarization was modulated.8 Light helicity modulation was used to remove spurious magnetohydrodynamic effects known to change the electrochemical current.12–14 This method however requires great care to avoid light intensity modulation.
In 1995, Tacken and Janssen reviewed the effects of magnetic fields on cathodic crystallization, anodic dissolution and magnetohydrodynamic mass transport. They concluded that the effect of magnetic field on electron transfer was controversial.15 In 1998, Timmel et al. observed the effect of weak magnetic fields on reaction kinetics in the liquid phase and accounted for it by a radical pair recombination mechanism which included hyperfine interactions.16,17 Schwartz investigated spin-dependent reaction efficiencies in the gas phase.18
In the case of electrochemical processes, a breakthrough was achieved by functionalizing electrode surfaces with chiral molecules, giving rise to a chirality-induced spin selectivity (CISS).19–21 Using chiral self-assembled monolayers (SAMs) and a magnetic electrode, the spin effects thus obtained were so large that they could be readily detected by standard electrochemical techniques.19,22–24 The spin effects could be distinguished from magnetohydrodynamic effects by observing electrodes of opposite chiralities. CISS was also characterized using electrochemical near-field probe techniques, thus avoiding magnetohydrodynamics altogether because in this case, the detection happens on a nanometer scale.25
In this paper, we show that we can reveal spin-dependent charge transfer at bulk electrodes and avoid magnetohydrodynamic effects by using electrically-detected magnetic resonance (EDMR). This technique has been used to study spin-dependent transport in inorganic semiconductors,26,27 fullerene thin films,7 organic conductors,28 solar cells29 and light-emitting diodes.30 Recently, EDMR has been extended into a time-resolved technique that allowed distinction between spin-dependent charge transport and spin-dependent carrier recombination in organic light emitting diodes.31 As EDMR in solid state systems is sensitive enough to detect a single spin,32 it ought to be able to detect surface processes at an electrode/electrolyte interface, even if the requirements of electrochemistry render the samples far from optimal for signal detection.
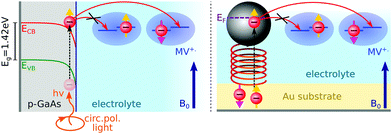
Here, we report EDMR evidence for spin-dependent charge transfer rates at two types of electrodes: optically pumped p-GaAs and Au electrodes functionalized with chiral molecules (Fig. 1). For this purpose we excited the spin resonance of methyl viologen free radicals (MV+˙) dissolved in an organic solvent. The detection scheme is based on the Pauli exclusion principle: a radical cannot be reduced by an electron which has the same spin as the radical. At resonance, the radical spins are flipped and the reduction current is changed. The radical spin polarization in our experiment is of about 8 × 10−4. Therefore, exciting the resonance cannot produce a relative current change any greater than this. We validate our methodology using optically pumped p-GaAs and then proceed by showing EDMR signals when using chiral electrodes.
2 Experimental
2.1 Electrochemistry
Self-assembled monolayers of chiral molecules were deposited on Au-covered GaN substrates. The chiral molecules were α-helical oligopeptides of composition NH2-{alanine-Aib}5-CONH2CH2CH2SH, where Aib stands for α-aminoisobutyric acid. Contacts were established with the Au layer on top of the undoped GaN. Therefore, in the experiments presented here, the conductive properties of the GaN substrate are irrelevant. A thin silicon rubber covered these contacts so as to isolate them from the electrolyte. Polypeptides were terminated on the electrolyte side by Ag nanoparticles, about 3 nm in diameter. These particles have a negligible effect on the spin polarization obtained by driving electrons through the chiral molecules since their diameter is far less than the spin diffusion length of Ag. The spin diffusion length is known from giant magnetoresistance (GMR) measurements to be quite large in silver.33 Using lateral non-local magnetoresistive structures, it was found to be greater than 100 nm at room temperature.34Epitaxially grown p-type GaAs (UniversityWafer Inc., Item 2178), Zn-doped to 2.9 × 1017 cm−3, were used as a working electrode with the polished (111) surface exposed to the sample solution. As-received p-GaA wafers were oxygen-plasma-etched on both sides to obtain a clean surface. A 200 nm thick polycrystalline layer of Au was electron-beam evaporated on the backside of the wafer to establish an electrical contact. This contact preparation has been found to be adequate in previous work for electrochemical and impedance measurements on p-GaAs.35–37 A connection with Cu wire was established using silver paste. This contact was then insulated from the sample solution with a silicon sealant.
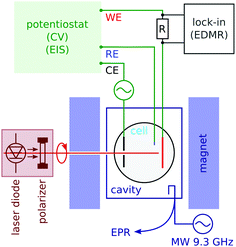
An electrolyte of 2 mM methyl viologen radicals MV+˙ in an acetonitrile (ACN) solution was prepared with 200 mM tetrabutylammonium perchlorate (TBAP) as the supporting electrolyte (see the ESI†). The experiments were performed in a 4 mm inner diameter NMR tube using either chiral electrodes or p-GaAs as the working electrodes. The reference electrode was a Pt pseudo reference, while Pt wire, 0.5 mm in diameter, served as the counter electrode. The electrochemical cell was assembled and filled with the sample solution and sealed with a two-part epoxy adhesive inside a glove box, and then taken out of it to perform EDMR experiments. An Autolab potentiostat (PGSTAT302N) was used for electrochemical measurements.
2.2 EPR and EDMR
We carried out conventional continuous wave electron paramagnetic resonance (CW EPR) spectroscopy by monitoring the microwave reflection of an X-band (9.4 GHz) cavity while sweeping the field (see Fig. 2). EPR detects the signal of radicals in the bulk of the electrolyte. The cavity was a Varian V-4531, which has TE 102 mode that allowed us to introduce conductors along the cavity axis. The quality factor (Q) was between 1000 and 2000 in the presence of an electrolytic cell; 4000 when the cell was removed.In order to detect the spin effect in the charge transfer at the working electrode, we used electrically-detected magnetic resonance (EDMR). Its principle, when applied to electrochemistry, is described in Section 3.
We carried out EDMR with a lock-in detection based on voltage modulation. The modulation frequency (of the order of 100 to 2000 Hz) was chosen near the dip in the Nyquist plot of the electrochemical impedance, which is the point most sensitive to the charge transfer process at the electrode (see the ESI†). In order to decouple the lock-in detection from the potentiostat, we measured the current with a series resistance of two thirds of the cell resistance.
3 Resonant detection of spin-dependent charge transfer
Here we describe how magnetic resonance modifies the electrochemical current when the charge transfer is spin-dependent. The total electron current density je resulting from a reduction process of the oxidized species Ox at the surface concentration [Ox] and charge transfer rate kRed combined with an oxidation process of the reduced species Red at the charge transfer rate kOx is given by,| je = nF(kOx[Red] − kRed[Ox]), | (1) |
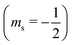 or antiparallel
or antiparallel 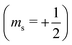 to the external field. Here, kRed− describes the transport, from the electrode to the radical, of an electron with
to the external field. Here, kRed− describes the transport, from the electrode to the radical, of an electron with 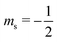 . Due to the Pauli exclusion principle, the transferred electron spin must be antiparallel to the radical spin (Fig. 1), i.e., kRed−NOx− and kRed+NOx+ are vanishingly small.
. Due to the Pauli exclusion principle, the transferred electron spin must be antiparallel to the radical spin (Fig. 1), i.e., kRed−NOx− and kRed+NOx+ are vanishingly small.
Therefore, for a pure reduction process and taking spins into account, eqn (1) reads as,
| je = −kRed+NOx− − kRed−NOx+. | (2) |
In order to examine how the electrode processes are affected by the spin polarization of the radicals at the surface, we write (2) as:
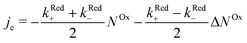 | (3) |
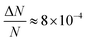 .
.
When microwave power is applied at resonance, electron spins are excited and counterbalance the spin–lattice relaxation. As a consequence, ΔNOx changes, and in view of eqn (3), je changes from its value far from resonance to its value jrese at resonance. When the microwave power is near saturation, the relative change in the current regarding on and off resonance is given by (see the ESI†),
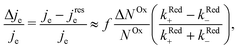 | (4) |
The relative change in the current given by eqn (4) is the principle of our electrochemical EDMR experiment. It is proportional to the radical spin polarization
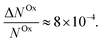 | (5) |
According to eqn (4), the relative current change is directly proportional to the relative spin dependence of the charge transfer rates.
During an oxidation process of the MV+˙ radical, electrons are transferred to the electrode from both possible radical spin polarizations, NOx− and NOx+. Therefore, the spin-dependence of the oxidation process is either due to the CISS effect (chiral electrodes) or the valence band and surface state spin dependent electron hole recombination (p-GaAs).
4 Results
4.1 Cyclic voltammetry
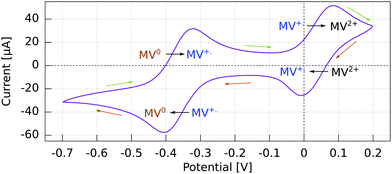
The cyclic voltammogram (CV) for the Al5 working electrode presents four regions clearly distinguishable by their peaks (Fig. 3).The potential ranges of interest are the ones where the MV+˙ radicals are consumed, i.e., where an electron either goes from a spin polarized electrode to a spin polarized radical or vice versa. In the reduction range (a negative current), this is the MV+˙ → MV0 process, and in the oxidation range, this is the MV+˙ → MV2+ process. For the other two processes, MV2+ → MV+˙ reduction and MV0 → MV+˙ oxidation, the reactant is diamagnetic. Therefore, when using spin-polarized p-GaAs or chiral electrodes in combination with the spin polarized MV+˙ radical, we expect the charge transfer rates to depend on the spin, whereas we expect no influence on the charge transfer rate for non-radical reactants. In other words, the electrochemical current spin dependency is strongly potential dependent.
For p-GaAs, the CV is in part light-dependent (Fig. 4). The MV+˙ → MV0 reduction and MV0 → MV+˙ oxidation appear only upon laser excitation, indicating that at least the reduction process is brought about by photogenerated electrons in the conduction band and/or surface states within the band gap. The MV2+ → MV+˙ reduction and MV+˙ → MV2+ oxidation were essentially independent of the illumination conditions, which is contrary to what is expected for a photo-cathode. This dark process is likely to originate from the valence band, with a hole transfer mediated by surface states.38 A laser light power of 80 μW was chosen to maximize the current while staying away from the diffusion-limited regime.
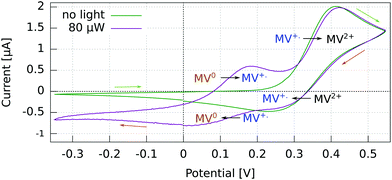 | ||
| Fig. 4 Cyclic voltammogram in the dark and under light at 830 nm of a p-GaAs electrode vs. Pt using a 2 mM MV+˙ solution in acetonitrile with 200 mM TBAP. Recorded at 50 mV s−1 with a Pt rod CE. | ||
4.2 EDMR spectra
We could not obtain EDMR spectra by sweeping the field through resonance at a fixed voltage. The reason for this is the following. When the current is measured as a function of time at a fixed voltage (chronoamperometry), a current decay is observed which is due to the depletion of the redox mediator at the interface, and at longer times the current is diffusion-limited. It is very difficult to measure EDMR under these conditions, though the feasibility of this measurement has been demonstrated.39Here, we resolved to measure the current while scanning the potential at a constant magnetic field, increasing the field stepwise after every linear potential sweep. After a full set of data was acquired, we extracted the spectra as line cuts at a fixed potential through the two-dimensional data sets (see the ESI†). Thus, it was necessary to carry out cyclic voltammetry and electron spin resonance simultaneously. The combination of EPR and electrochemistry has been reported by others. An elegant design has been proposed for an electrochemical cell compatible with microwave electron spin resonance spectroscopy.40 It has been pointed out that EPR can bring much information about electron transfer processes, such as during the electropolymerization of aniline.41,42 However, the combination, which consists in detecting resonance using the electrochemical current itself, is new.
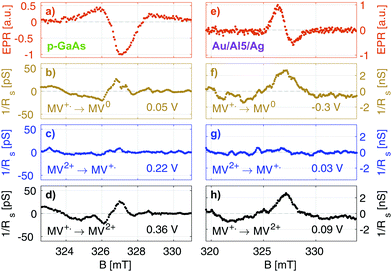
In Fig. 5, we summarize our results for the p-GaAs electrode (left) and for the chiral Al5 electrode (right). All spectra were obtained from cross sections at a constant potential of the matrices obtained by continuously sweeping the potential and increasing the field stepwise (see the ESI†).
Our EPR signals, such as those shown in Fig. 5(a and e), are found at any value of the electrode potential, since they correspond to radicals located everywhere in the solution. These EPR spectra are consistent with the results obtained in the literature.43 Grampp et al. attributed the broad featureless resonance of MV+˙ to the fast rate of electron exchange due to the comproportionation reaction.44 In our case, the broadening is due to the field inhomogeneity with respect to the size of the sample and modulation broadening.45 We recall that these EPR spectra are not acquired in the normal way. They result from line cuts at a fixed voltage in data arrays that were acquired in about 4 to 12 hours, depending on the matrix size. Thus, they attest to the great stability of our electrodes.
Fig. 5(b–d) and (f, g) present EDMR spectra obtained as line cuts at a constant potential in our 2 dimensional data arrays. We report our EDMR spectra in conductivity units (Siemens), since they directly reflect the outcome of the potential modulation lock-in detection. The following potentials were selected:
– (b and f): potentials at which the MV+˙ → MV0 reduction takes place.
– (c and g): potentials at which MV+˙ radicals are produced, i.e., the MV2+ → MV+˙ reduction. As expected, no EDMR signal was observed, since the reactant is not spin-polarized.
– (d and h): potentials at which the MV+˙ → MV2+ oxidation takes place, i.e., the unpaired electron spin of the radical is transferred to the electrode.
In summary, we have detected a conductivity change at resonance only in the potential regions in which the radical MV+˙ is consumed by a reduction process (f and b) or an oxidation process (d and h). This is expected because MV+˙ is the only oxidation state of methyl viologen which is spin polarized. As expected, we do not obtain EDMR signals at potentials corresponding to MV2+ → MV+˙ reduction (Fig. 5) and MV0 → MV+˙ oxidation, since the reactant does not have a spin in these cases.
4.3 Charge-transfer-rate spin-dependence
We now proceed to estimate the order of magnitude of the spin dependence we have observed by EDMR. The relative change in current density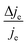 can be deduced from the lock-in data (see the ESI†). Using eqn (4), we can estimate the relative spin-dependent charge transfer rate difference as,
can be deduced from the lock-in data (see the ESI†). Using eqn (4), we can estimate the relative spin-dependent charge transfer rate difference as,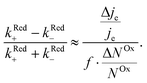 | (6) |
In the case of Al5, we find the relative spin-dependent charge transfer rate difference and therefore the chiral molecule spin filtering efficiency to be 6 to 19%. This range of values is determined mostly by the uncertainty of the value of f. Electrochemical measurements carried out with Al5 on top of gold covered nickel electrodes yielded a spin filtering efficiency of 8%.24 EDMR measurements, which are quite different since they consist of acting on the radical spins directly, give therefore a value which is consistent with previous observations.
For p-GaAs, we express the charge transfer rate using a chemical rate constant kc and an effective spin-dependent electrode charge carrier density D, k = kcD. The relative spin dependent charge transfer rate difference is then written as,
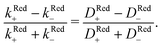 | (7) |
Thus, we find for optically spin pumped p-GaAs, a spin polarization value of 2 to 5%, while the literature reports 10%, as found in a solid state device at room temperature.46 Our value is less than half of the literature value, which can be expected, since our experiment is of a totally different nature. The literature value is obtained for the bulk of a solid, whereas our value corresponds to the spin polarization after crossing the solid/liquid interface where spin relaxation may occur. At the p-GaAs surface, surface states are to be expected, which can accept additional electrons.38 These surface states can act as additional intermediate transfer states, ultimately leading to a slower transfer or even spin trapping. Chiral molecules, in contrast, suppress dangling bond terminations. Therefore, chiral electrodes are less prone to this problem.
5 Conclusion
We have used a direct action on the spin of radicals in an electrolyte to demonstrate a spin-dependent charge transfer process taking place at two types of electrodes: (1) semiconducting III–V electrodes which are optically pumped with circularly polarized light and (2) gold electrodes functionalized with a polypeptide (5 units of alanine) terminated with Ag nanoparticles. In both cases, the spin-dependence is visible at potentials at which the radical is reduced or oxidized. The effect is weak in both cases simply because the spin polarization of radicals in solution is only about 8 × 10−4 at room temperature in a field of 330 mT. As far as we know, this is the first time that EDMR has been used to demonstrate spin-dependent charge transfers at an electrode/electrolyte interface, i.e., using electrical detection of electron spin resonance of a radical in solution.In the case of optically pumped p-GaAs, we find a relative spin-dependent charge transfer rate difference (eqn (6)) of only 2 to 5%, with a possible complication due to the presence of surface states.38
When using Al5 chiral molecules, we have found a strong spin dependence, indicating a spin-polarization after passing the chiral molecules of 6 to 19%, which is consistent with the idea that chiral molecules act as spin filters.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
We gratefully acknowledge funding from the Templeton Foundation, the Swiss National Science Foundation (Grants 200021-160182 and 200020-169515) and the Rothschild Caesarea Foundation, Caesarea Business Park, 38900 Caesarea, Israel (Grant 6115).References
- S. Sanvito, Nat. Phys., 2010, 6, 562–564 Search PubMed.
- X. Li, O. E. Tereshchenko, S. Majee, G. Lampel, Y. Lassailly, D. Paget and J. Peretti, Appl. Phys. Lett., 2014, 105, 052402 CrossRef.
- B. Göhler, V. Hamelbeck, T. Z. Markus, M. Kettner, G. F. Hanne, Z. Vager, R. Naaman and H. Zacharias, Science, 2011, 331, 894–897 CrossRef.
- C. Barraud, P. Seneor, R. Mattana, S. Fusil, K. Bouzehouane, C. Deranlot, P. Graziosi, L. Hueso, I. Bergenti, V. Dediu, F. Petroff and A. Fert, Nat. Phys., 2010, 6, 615–620 Search PubMed.
- R. Kaptein, J. Am. Chem. Soc., 1972, 94, 6251–6262 CrossRef CAS.
- C. Boehme and K. Lips, Phys. Rev. Lett., 2003, 91, 246603 CrossRef.
- T. Eickelkamp, S. Roth and M. Mehring, Mol. Phys., 1998, 95, 967–972 CrossRef CAS.
- J. Chazalviel, J. Chem. Phys., 1985, 83, 401–412 CrossRef.
- A. Modestov and V. Kazarinov, J. Eectroanal. Chem., 1993, 346, 353–366 CrossRef CAS.
- G. Lampel, Phys. Rev. Lett., 1968, 20, 491 CrossRef CAS.
- Optical Orientation, ed. F. Meier and B. Zakharchenya, North Holland, 1984 Search PubMed.
- F. M. F. Rhen, D. Fernandez, G. Hinds and J. M. D. Coey, J. Electrochem. Soc., 2006, 153, J1 CrossRef CAS.
- L. Monzon and J. Coey, Eletrochem. Commun., 2014, 38, 106–116 Search PubMed.
- B. F. Gomes, P. F. da Silva, C. M. S. Lobo, M. S. Santos and L. A. Colnago, Anal. Chim. Acta, 2017, 983, 91–95 CrossRef CAS.
- R. Tacken, J. Appl. Electrochem., 1995, 25, 1–5 CrossRef CAS.
- C. R. Timmel, U. Till, B. Brocklehurst, K. A. McLauchlan and P. J. Hore, Mol. Phys., 1998, 95, 71–89 CrossRef CAS.
- U. E. Steiner, T. Ulrich, C. Universitat, K. Konstanz and W. Germany, Chem. Rev., 1989, 89, 51–147 CrossRef CAS.
- H. Schwarz, Int. J. Mass Spectrom., 2004, 237, 75–105 CrossRef CAS.
- P. Mondal, C. Fontanesi, D. Waldeck and R. Naaman, ACS Nano, 2015, 9, 3377–3384 CrossRef CAS.
- W. Mtangi, F. Tassinari, K. Vankayala, A. V. Jentzsch, B. Adelizzi, A. Palmans, C. Fontanesi, E. Meijer and R. Naaman, J. Am. Chem. Soc., 2017, 139, 2794–2798 CrossRef CAS.
- F. Tassinari, D. Jayarathna, N. Kantor-Uriel, K. Davis, V. Varade, C. Achim and R. Naaman, Adv. Mater., 2018, 30, 1–6 CrossRef.
- D. Mishra, T. Z. Markus, R. Naaman, M. Kettner, B. Göhler, H. Zacharias, N. Friedman, M. Sheves and C. Fontanesi, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 14872–14876 CrossRef CAS.
- P. C. Mondal, C. Fontanesi, D. H. Waldeck and R. Naaman, Acc. Chem. Res., 2016, 49, 2560–2568 CrossRef CAS.
- M. Kettner, B. Göhler, H. Zacharias, D. Mishra, V. Kiran, R. Naaman, C. Fontanesi, D. H. Waldeck, S. Sek, J. Pawowski and J. Juhaniewicz, J. Phys. Chem. C, 2015, 119, 14542–14547 CrossRef CAS.
- A. C. Aragones, E. Medina, M. Ferrer-Huerta, N. Gimeno, M. Teixido, J. L. Palma, N. Tao, J. M. Ugalde, E. Giralt, I. Diez-Perez and V. Mujica, Small, 2017, 13, 1–6 CrossRef.
- I. Solomon, D. Biegelsen and J. Knights, Solid State Commun., 1977, 22, 505–508 CrossRef CAS.
- C. Boehme and K. Lips, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 68, 245105 CrossRef.
- D. Sun, K. J. van Schooten, M. Kavand, H. Malissa, C. Zhang, M. Groesbeck, C. Boehme and Z. V. Vardeny, Nat. Mater., 2016, 15, 863–869 CrossRef CAS.
- J. Behrends, A. Schnegg, M. Fehr, A. Lambertz, S. Haas, F. Finger, B. Rech and K. Lips, Philos. Mag., 2009, 89, 2655–2676 CrossRef CAS.
- F. Comande and J.-P. Ansermet, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, R201201 CrossRef.
- M. Kavand, D. Baird, K. van Schooten, H. Malissa, J. M. Lupton and C. Boehme, Phys. Rev. B, 2016, 94, 075209 CrossRef.
- M. Xiao, I. Martin, E. Yablonovitch and H. W. Jiang, Nature, 2004, 430, 435–439 CrossRef CAS.
- J. Bass and W. P. Pratt Jr, J. Phys.: Condens. Matter, 2007, 19, 183201 CrossRef.
- R. Godfrey and M. Johnson, Phys. Rev. Lett., 2006, 96, 136601 CrossRef.
- W. H. Laflère, R. L. Van Meirhaeghe, R. Cardon and W. P. Gomes, Surf. Sci., 1976, 59, 401–412 CrossRef.
- W. H. Laflère, F. Cardon and W. P. Gomes, Surf. Sci., 1974, 44, 541–552 CrossRef.
- F. R. F. Fan and A. J. Bard, J. Am. Chem. Soc., 1980, 102, 3677–3683 CrossRef CAS.
- M. Tamski, F. Blumenschein, C. Roussel and J. P. Ansermet, J. Photochem. Photobiol., A, 2019, 382, 111894 CrossRef.
- A. Kumar, E. Capua, C. Fontanesi, R. Carmieli and R. Naaman, ACS Nano, 2018, 12, 3892–3897 CrossRef CAS.
- P. R. Murray, D. Collison, S. Daff, N. Austin, R. Edge, B. W. Flynn, L. Jack, F. Leroux, E. J. L. McInnes, A. F. Murray, D. Sells, T. Stevenson, J. Wolowska and L. J. Yellowlees, J. Magn. Reson., 2011, 213, 206–209 CrossRef CAS.
- J. Tang, R. D. Allendoerfer and R. A. Osteryoung, J. Phys. Chem., 1992, 96, 3531–3536 CrossRef CAS.
- M. A. Tamski, J. V. Macpherson, P. R. Unwin and M. E. Newton, Phys. Chem. Chem. Phys., 2015, 17, 23438–23447 RSC.
- C. S. Johnson and H. S. Gutowsky, J. Chem. Phys., 1963, 39, 58 CrossRef CAS.
- G. Grampp, B. Y. Mladenova, D. R. Kattnig and S. Landgraf, Appl. Magn. Reson., 2006, 30, 145–164 CrossRef CAS.
- G. R. Eaton, S. S. Eaton, D. P. Barr and R. T. Weber, Quantitative EPR, Springer Vienna, Vienna, 2010, pp. 1–185 Search PubMed.
- C. Weisbuch and C. Hermann, Phys. Rev. B: Solid State, 1977, 15, 816–822 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c9cp04681j |
| This journal is © the Owner Societies 2020 |