Binding modes of carboxylic acids on cobalt nanoparticles

Abstract

Owing to their high saturation magnetisation, cobalt nanoparticles hold significant potential for the hyperthermia treatment of tumours. Covalent binding of carboxylic acids to the nanoparticles can induce biocompatibility, whilst also preventing the formation of surface oxides which reduce the magnetic properties of cobalt. Understanding the origin of the acid–metal interaction is key, yet probably the most experimentally challenging step, for the rational design of such entities. In this density functional theory study, we use static calculations to establish that a 57-atom Co cluster is the smallest model able to reproduce the adsorption behaviour of carboxylic acids, and ab initio metadynamics to obtain the structure and the free energy landscape for its interaction with valeric acid. Our simulations show that a bridging bidentate binding mode has a stronger affinity compared to monodentate binding, with energetically high transition barriers between the two. A chelate interaction mode of two carboxyl oxygen atoms can be formed as an intermediate. These results clarify the organic–inorganic interactions in the cobalt–acid system, providing a basis for the rational design of biocompatible metallic nanoparticles.

---

1. Introduction

With increasing numbers of cancer cases suffering from drug resistance and severe side effects as corollaries of commonly used chemotherapy, the development of materials for hyperthermia as a treatment, where a moderate degree of tissue warming results in malignant cell destruction with minimal collateral damage and no drug consumption, is becoming a priority.¹ The high saturation magnetisation and large anisotropy field of pure cobalt nanoparticles give them an intrinsic advantage within the strict requirements of hyperthermia over commonly tested iron oxides and ferrites.^2,3 However, biocompatibility is the key for their integration into biomedicine, and while titanium implants owe their biocompatibility to thin oxide layers formed on the surface in the presence of air and water,^4,5 the same phenomenon is a substantial drawback when magnetic cobalt nanoparticles transform into non-magnetic oxide compounds.⁶ In order to obtain biocompatibility and prevent oxidation, a surfactant which is effective in adjusting the reactivity of the nanoparticles without affecting their magnetic properties is usually employed.^7–9 Understanding the surface chemistry and the interaction between the surfactant and the nanoparticle therefore plays a major role in tuning the properties and the performance of the final nanocomposite.^10,11 While many chemical reactions at nanoparticle surfaces are very well understood experimentally, with strategies for the control of the surfactant architecture developed accordingly, atomic-level details about bond formation and charge transfer remain difficult to explore.

Atomic understanding of the underlaying interaction mechanisms requires for the comprehension of structure, morphology, and size, but also physiochemical properties and reactivity of both metal of interest and capping agent. From structural point of view, cobalt can exist in three crystal phases, namely hcp, fcc, and ε-phase.^12–14 With an hcp → fcc phase transition occurring at temperatures around 450 °C,^15,16 the hcp phase is the one of interest from a biomedical standpoint. When considering the morphology of nanostructures, attractive possibilities of improving the catalytic power by increasing the area of reactive metal surfaces have led to intensive research in synthesis methods, ranging from nanospheres, nanodiscs, and nanosheets, over hollow structures or pellets, to unusual and less ordered geometries, such as snowflakes and leaf-shapes.^17–22 Similarly, the shape and size of the nanoparticles can strongly affect the material uptake and biodistribution as well as their reactivity. Since the main interest in hyperthermia is to maximise magnetisation and mobility while minimising oxidation, small spherical nanoparticles are preferred, as after ligand functionalisation the overall diameter should be enough to circulate throughout the blood vessel network for a sustained period of time with minimal surface-to-volume ratio to avoid reacting with the surroundings. Cobalt nanoparticles have been shown experimentally and theoretically to favour a non-crystalline icosahedral morphology for the smallest sizes, with large nanoparticles expected to adopt hcp-bulk geometry.^23–25

A variety of ligands have so far been tested to enhance biocompatibility, improve growth control, stabilise the particle dispersions, prevent agglomeration, provide functionality, and limit the surface reactions. By now it is known that metallic nanoparticles experience strong van der Waals and magnetic dipole interactions, hence only the surfactants which covalently bond to the metal can considerably promote their stability. Carboxylic acids can bind strongly to the surface metal atoms through carboxyl group, and they are therefore an excellent choice as capping agents. Among them, oleic acid (OA), which has a C18 tail with a cis-double-bond in the middle, is the most common, since it can form the kink necessary for effective stabilisation. OA forms a dense protective monolayer, thereby producing nanocomposites in a highly uniform size range.^7,26,27

The interaction between the carboxylate head and the metal atoms can adopt four different modes.^28–30 If one metal atom binds with one oxygen atom, the mode is called monodentate. If both oxygen atoms are involved, they can form complexes with either one or two different metal atoms, referred to as chelate and bidentate, respectively. The final possible interaction is of ionic nature. Which motif is dominating for a specific ligand–metal pair depends on the properties of the metal surface and the structure of the adsorbed carboxylic acid. Experimentally, the actual binding interaction may be distinguished by infrared (IR) spectroscopy due to the characteristically shifted carbonyl band.

The bonding nature of OA can have a critical effect on the magnetisation³¹ and a detailed knowledge of the type of interaction between OA and cobalt nanoparticles hence allows fine-tuning of the size, morphology, and magnetic properties. It is therefore a crucial step in the characterisation of this nanocomposite for biomedical applications. However, experimental results are, so far, inconclusive on the binding mode between OA and cobalt nanoparticles. Older investigations gave a uniform conclusion on oleic^12,27,32 and elaidic³³ acid chemisorption onto cobalt surfaces, yielding nanoparticles in a narrow distribution, but they did not provide the exact binding mode. To the best of our knowledge, there exist only two such works that suggested a type of interaction between the cobalt atoms and carboxylate head of oleic acid. According to Wu et al.³⁴ oleic acid is chemisorbed as a carboxylate onto the Co nanoparticles, and the two oxygen atoms are coordinated symmetrically to the Co atoms. They interpreted the shift of the carbonyl's IR band to be due to a bridging bidentate adsorption. Similarly, Ansari et al.³⁵ presented an IR spectrum that demonstrated the chemisorption of the acid as a carboxylate onto the nanoparticles. However, they attributed the shift of the carbonyl band to a monodentate interaction.

In this work, we have first performed static density functional theory (DFT) calculations to establish a 57-atom cluster as the minimum size that reproduces the adsorption properties of larger Co nanoparticles. Next, we have performed metadynamics simulations of valeric acid (VA), a convenient model for OA, on the Co cluster. We have efficiently explored the free energy landscape of the system, evaluating in particular the most relevant energy minima and the barriers appearing in the corresponding transition pathways.

2. Models and methods

2.1 Optimising the size of the cluster

The use of atomically flat surfaces can be appropriate when exploring the arrangement and properties of small molecules since the effects of irregular, curved, stepped, porous, and otherwise deformed nanoparticle surfaces can be largely excluded. However, changes in the reactivity become notable for large surfactants, i.e., when the nanoparticle diameter is less than 20 times the length of the surfactants in their extended conformation. For example, the length of a C18 alkyl ion is about 3 nm, and the nanoparticle diameter then needs to be at least 60 nm for curvature effects to become marginal. However, the maximum size of a nanoparticle allowed for biomedical applications should not exceed 20 nm, including the protective coating, which significantly magnifies the effects of surface curvature, edges, and vertices. To determine the optimal cluster size in terms of reactivity and computational cost, the adsorption characteristics of one oxygen atom, formic acid, and acetic acid have been investigated on hcp-shaped cobalt clusters, as the most stable morphology of larger clusters, going from 6 to 323 atoms, and compared with those on the extended slabs.

These calculations were carried out using the DFT Vienna Ab Initio Simulation Package (VASP) code,³⁶ with a spin-polarized formalism and the exchange–correlation functional developed by Perdew, Burke, and Ernzerhof (PBE).³⁷ The core electrons up to and including the 3p levels of cobalt were kept frozen and their interaction with the valence electrons was described by the projector augmented wave (PAW) method.³⁸ The DFT-D3 method with Becke–Johnson damping was used to include the long-range dispersion interactions.³⁹ The kinetic energy cutoff of the wave functions was set to 400 eV. The Monkhorst–Pack k-point grid for the cluster calculations included only Γ-point. For the (0001) and (101̄1) surfaces, 3 × 3 and 3 × 2 supercells with 4 layers of atoms (top two relaxed, bottom two constrained in the bulk-relaxed positions) were used, with k-point meshes of 5 × 5 × 1 and 5 × 4 × 1, respectively. Structural optimisations were carried out without any constraints, with convergence criteria of 1.0 × 10⁻⁶ eV per atom and 1.0 × 10⁻² eV Å⁻¹ for the electronic energy and the atomic forces, respectively. The vacuum space in the unit cell was set to be 12 Å in the z-direction to avoid interactions between periodic images of the surface slabs, while clusters were positioned in the centre of a box with sizes adjusted such that there is at least 12 Å of vacuum between neighbouring clusters in each direction. The adsorption energy, E_ads, was calculated as follows:

E_ads = E_surf+mol − (E_surf + E_mol), (1)

where E_surf+mol, E_surf, and E_mol are the DFT energies of the system with the adsorbed molecule, the clean surface or cluster, and the isolated molecule, respectively.

2.2 Choice of carboxylic acid

Earlier studies of the interactions of primary carboxylic and mercapto-carboxylic acids^40,41 with zeolites and ZnO surfaces have shown that adsorption modes and dielectric properties of the hybrid systems are rather insensitive to the chain length, since the interaction state is localised on the specific atom (either carboxyl oxygen or mercapto-sulphur). Structural and electronic properties of OA, as the experimental compound of interest, and VA, as a segment of OA cut at the fourth carbon atom of the alkyl chain where the distance from the carboxyl group is larger than three bonds thus diminishing the inductive effect, have been compared by DFT calculations using the computational details specified in Section 2.1. We anticipate that the carbon chain size does not affect significantly the properties of interest and the computational cost of the metadynamics can therefore be substantially reduced by using the shorter VA.

2.3 Metadynamics simulations

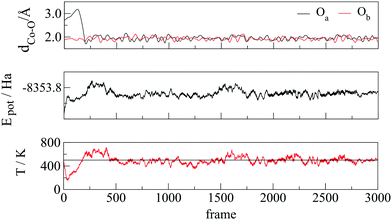
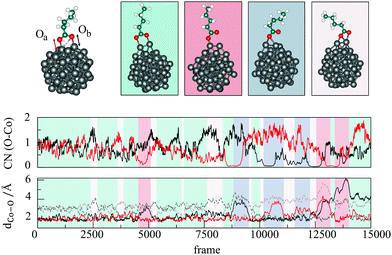
Ab initio metadynamics^42,43 of a single molecule of VA on a 57-atom cobalt cluster was performed using CP2K^44,45 with the PBE exchange–correlation functional and the Goedecker, Teter, and Hutter (GTH) Gaussian basis set.⁴⁶ The whole system was placed in a cubic box of 25 Å a side and equilibrated in the NVT ensemble during 3 ps of Born–Oppenheimer molecular dynamics. A Nosé–Hoover thermostat⁴⁷ was set to 500 K, in accordance with the temperature of experiments (160–250 °C),^27,34,35 and a time step of 1 fs was used for the integration of the equations of motion. Fluctuations in temperature, potential energy, and Co–O bonds during the equilibration are shown in Fig. 1.

Fig. 1 Co–O distances (top), potential energy (middle), and temperature (bottom, with horizontal line representing the temperature of the thermostat, T = 500 K) during the ab initio molecular dynamics equilibration of valeric acid on the 57-atom Co cluster.

The most recent experimental study conducted on the OA-cobalt nanoparticle system by Ansari et al.³⁵ suggested a monodentate-type interaction, which was hence taken as the starting structure. During the equilibration, we observed that the oxygen atom which was not bound to the nanoparticle surface attached to a neighbouring cobalt atom within less than 0.25 ps (Fig. 1, top), yielding a bidentate interaction with both oxygen atoms atop two neighbouring cobalt surface atoms.

After equilibration, metadynamics was performed. The two collective variables for the projection of the metadynamics free energy landscape were chosen to be the coordination numbers (CNs) of the two oxygen atoms of VA. Both Co–O distances during the equilibration period oscillated around 2.0 Å, as shown in Fig. 1, top. Accordingly, this value was used in the definition of CNs, together with exponents n = 8 and m = 14.⁴² Gaussian hills with height of 0.01 Hartree and width of 0.05 were deposited every 50 fs. The metadynamics simulation was carried out for 15 ps, after which one of the oxygen atoms bound to a new Co atom that was not included in the binding states observed thus far, hence reproducing previously formed interaction modes on a different site of the nanoparticle. This was considered to be a terminating event, as it indicates that the molecule has exhausted all the binding possibilities with the initially assigned pair of cobalt atoms. VMD was used for postprocessing.⁴⁸

2.4 Infrared spectroscopy

Infrared spectra of free VA and VA adsorbed on a cobalt cluster have been calculated within the perturbation theory at the PBE level. The PHONOPY code⁴⁹ was used to derive the associated intensities based on the Born effective charges tensor which yields information on the change in the dipole moment under atomic displacements. The intensity of a given mode can be evaluated as a square of all transition moments of the mode and expressed in terms of the Born effective charge matrix and eigenvectors of the mass-weighted Hessian. It is well-known that vibrational frequencies obtained by quantum-chemical calculations are typically larger than those evaluated experimentally, and thus, empirical scaling factors are often used for obtaining better match. However, since the current work focuses on the changes in the ligand spectra induced by binding to the nanoparticle rather than on the absolute values of the frequencies, the scaling was not carried out.

3. Results

3.1 Adsorption behaviour with the nanoparticle size

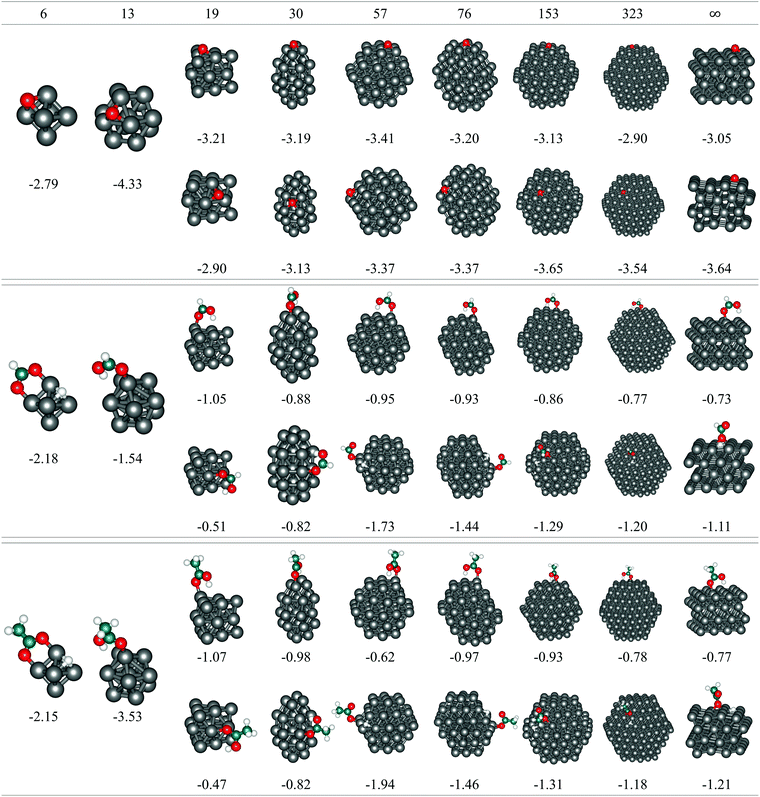
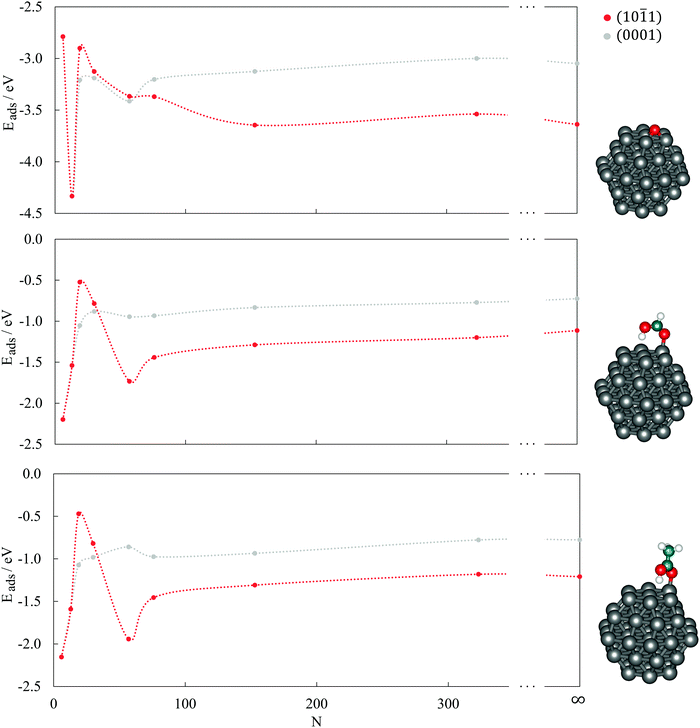
The Co model clusters studied for the size-dependent adsorption consisted of 6, 13, 19, 30, 57, 76, 153, and 323 atoms arranged in an hcp-like atomic packing to mimic the behaviour of larger nanoparticles that are expected to perform well in cancer treatments. All clusters, except for the smallest 6 and 13-atom ones, exhibit facets of (0001) and (101̄1) orientations to minimise the overall surface energy. Size-dependent adsorption of O, HCOOH, and CH₃COOH was therefore examined on both surfaces.

3.1.1 Oxygen adsorption. Fig. 2, top, shows the optimised structures of clusters with a single adsorbed O atom and the corresponding adsorption energies, E_ads, which are plotted in Fig. 3, top. For comparison, the structures of the periodic (0001) and (101̄1) surfaces are also shown (N = ∞). The oxygen atom, regardless of the cluster size or the surface stacking, adsorbs in the hollow position which allows binding to three different cobalt atoms of the (0001) surface. On the (101̄1) surface, clusters with more than 19 atoms can accommodate oxygen in the centre of four cobalt atoms, while the smaller surface area of the 19-atom cluster limits the interaction to three cobalt atoms. However, despite the similarities in the adsorption sites, there are still noticeable differences in the energetical aspects of the single oxygen atom adsorption on different clusters. On the (0001) surface, the interaction becomes stronger with shrinking cluster size but begins to weaken from 30-atom cluster downwards, with an exception for the adsorption on 13-atom cluster, which is the most favoured (E_ads = −4.33 eV). A similar behaviour can be observed for the adsorption on the (101̄1) surface of the clusters, with lessening of E_ads already triggered on the 76-atom cluster. The E_ads values of the largest clusters considered, N = 153 and 323, differ only slightly from those of the periodic slab models. The initial trend of a strengthening interaction with decreasing cluster size prevails for larger particles only and reflects the decrease in the average CN of cobalt atoms as a consequence of the higher surface-to-volume ratio.

Fig. 2 Optimised geometries of O (top), HCOOC (middle), and CH₃COOH (bottom) adsorbed on the (0001) – top row and (101̄1) – bottom row surfaces of Co_N (N = 6, 13, 19, 30, 57, 76, 153, 323) clusters and on the extended surfaces (N = ∞). Adsorption energies in eV are also shown. Grey, turquoise, red, and white spheres represent cobalt, carbon, oxygen, and hydrogen atoms, respectively.

Fig. 3 Calculated adsorption energies, E_ads, of O (top), HCOOH (middle), and CH₃COOH (bottom) adsorption on the (0001) and (101̄1) surfaces of Co_N clusters as a function of the cluster size, N. Results for surface slabs are shown as N = ∞. Lines are to guide an eye only.

Fig. 4 shows the d-band energies calculated following the definition by Hammer et al.,⁵⁰ for both the 3d spin-up and spin-down electrons of cobalt atoms in differently sized clusters and the infinite surfaces. The spin-up (3 unpaired electrons per Co atom which are responsible for oxygen-binding) d-band energy sequence mirrors the trend of oxygen adsorption, with the 13-atom cluster having the most positive d-band energy and, accordingly, the strongest interaction.

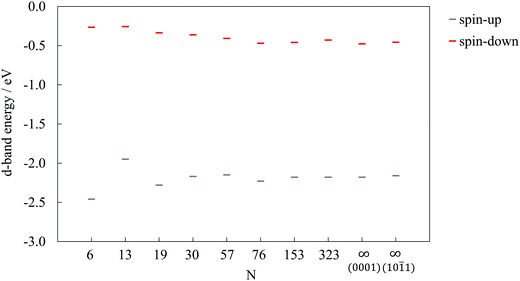Fig. 4 d-Band energies for 3d spin-up and spin-down electrons of Co as a function of cluster size, N. Results for surface slabs are shown as N = ∞.

Small clusters experience the influence of quantum effects, with a resulting non-scalable regime which often makes it hard to find a detailed quantitative dependence of the adsorption energy on the cluster size. However, it is evident that even with a single atom adsorbate the two surfaces behave differently, which might have a more pronounced influence when it comes to the adsorption of larger molecular entities. In order to capture the main features of the cobalt cluster–oxygen atom systems, small 19- or 30-atom clusters may be used efficiently, although this may not be the case for carboxylic acids.

3.1.2 HCOOH and CH₃COOH adsorption. Fig. 2 illustrates the optimised structures and Fig. 3 the energy trends as a function of the cluster size for the adsorption of HCOOH and CH₃COOH (middle and bottom, respectively). Compared to the single oxygen atom, where electronic effects make for the biggest change in the adsorption capabilities of differently sized clusters, the adsorption of acid molecules depends on the geometry of the clusters as well as on their electronic properties. On the (0001) surface, we observed dissociation only on the 6-atom cluster, where the preferred binding is with an oxygen atop one cobalt atom and the dissociated hydrogen atom in the bridging position over the two surface cobalt atom closest to the oxygen binding site. When the carboxyl oxygen was situated in the hollow as the most favourable adsorption site for a single oxygen atom adsorption, the interaction was weaker, probably due to the inconvenience of accommodating the –OH hydrogen atom. Adsorption of a carboxylic acid on the extended slab of the (101̄1) surface, on the other hand, shows a clear tendency toward dissociation. One of the oxygen atoms of the carboxyl group as well as the dissociated hydrogen tend to be located in the hollow sites on the largest clusters, while the remaining oxygen binds in the bridge position between two edge Co atoms on the 57- and 76-atom clusters. However, due to the limited (101̄1) surface areas of smaller clusters with 19 and 30 atoms, this dissociative behaviour is inhibited. It is important to note that dissociation was not manually forced and all initial structures of the acids prior to the adsorption process were undissociated.

For large clusters, the energy of HCOOH and CH₃COOH adsorption on both the (0001) and (101̄1) surface slowly progresses towards the asymptotic value for the infinite surface slabs. When adsorbed on the (0001) surface on clusters with less than 30 atoms, the adsorption energy reduces quickly with decreasing cluster size, yielding values well below the extended surface value. The opposite trends seen in large and small cobalt clusters meet at an intermediate size range of 15–50 atoms for the (0001) surface, with the 19-atom cluster exhibiting the least negative adsorption energies of −0.52 eV and −0.47 eV for HCOOH and CH₃COOH, respectively. On the (101̄1) surface, the 57-atom cluster is the smallest of the tested sizes that showed the dissociative behaviour of an infinite slab model and, consequently, the adsorption energies of both carboxylic acids grow considerably with the reduction in size of the cluster. This trend is only interrupted with the 6- and 13-atom clusters, where the two surfaces cannot be distinguished.

As illustrated previously in the case of the oxygen atom, the strengthening of the adsorption as the cluster size shrinks is governed by the upward shift in the d-band centre throughout the whole range of clusters. However, for HCOOH and CH₃COOH, this occurs only for large clusters, whereas the resemblance disappears once the clusters become smaller than 57 atoms, when the increase in the number of corner and edge sites with lower CNs leads towards stronger adsorptions. It can therefore be concluded that clusters with ∼50 atoms are precisely at the border where the domination of the electronic effects of large clusters vanishes and the ascendency of geometric effects of small clusters onsets.

3.2 Chain length dependence on the adsorption behaviour

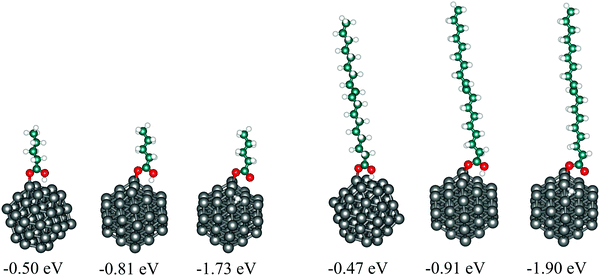
To assess the suitability of VA as a model for OA when adsorbed on cobalt nanoparticles, both molecules were adsorbed on the 57-atom Co cluster and their structural, energetic, and electronic properties have been compared.

3.2.1 Structures and adsorption energies. Fig. 5 depicts the structures and adsorption energies of VA and OA adsorbed on the 57-atom cluster. Qualitatively, the positioning of the shorter chain of VA resembles the shape of the first few carbon atoms of OA. The adsorption energies on the surface of the cluster differ only by 0.03 eV, while undissociative and dissociative modes on the (101̄1) surface give adsorption energies of OA lower by 0.10 and 0.17 eV than VA, respectively.

Fig. 5 Structures of valeric (left panel) and oleic acid (right panel) undissociated on the (0001) surface (left) and both undissociated (middle) and dissociated (right) on the (101̄1) surface of the 57-atom Co cluster. Adsorption energies are also shown below each structure.

3.2.2 Electronic properties. For comparison of the electronic properties, the densities of states (DOS) of VA and OA adsorbed on the (0001) and (101̄1) surfaces of the 57-atom cluster are presented in Fig. 6, together with their projection on the carbon chains and the carboxyl oxygen atoms. In all three cases of adsorption, VA and OA show similar electronic structures, with bonding hybridisation mainly occurring at ∼−5.0 eV for undissociative adsorption and at ∼−3.5 eV for dissociative adsorption.

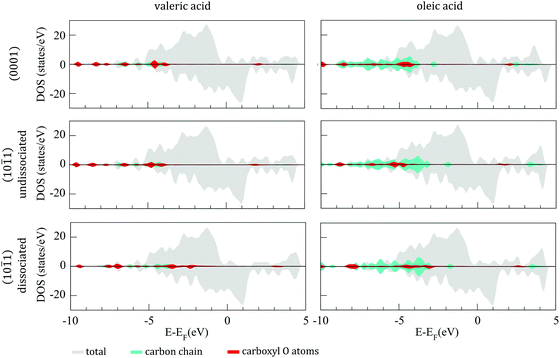Fig. 6 DOS of undissociated and dissociated valeric (left panel) and oleic (right panel) acid on the (0001) and (101̄1) surfaces of 57-atom Co cluster.

To estimate the share of carbon-chain charge transfer in the overall bonding process, the Bader charge difference⁵¹ was calculated as

Δq_c = q_ads − q_vac, (2)

where q_ads and q_vac are the number of electrons of all the atoms in the carbon-chain of the adsorbate on the cluster and in vacuum, respectively. Δq_c represents the charge gained or lost in the process of adsorption. If it is positive, the electrons are lost from the carbon-chain, and vice versa, if it is negative, the carbon-chain drains electrons from the atoms of the cluster. In the case of adsorption on the (0001) surface, the carbon chain of VA, namely –(CH₂)₃CH₃, experiences a charge transfer of Δq_c = +0.062 eV, which increases to +0.086 eV for the –(CH₂)₇C=C(CH₂)₇CH₃ carbon-chain of OA. For undissociative adsorption on the (101̄1) surface, carbon-chain charge transfers are equal to +0.060 and +0.057 eV, while for dissociative adsorption they are equal to −0.011 and −0.008 eV for VA and OA, respectively. No appreciable electron transfer occurs during the adsorption, with carbon chains of both acid molecules losing or, in the case of dissociation, gaining a negligible amount of charge during the process. Importantly, the differences between the two acids are minimal. Combined with the findings on the energetics of adsorption, the comparison of the electronic properties suggests that the carboxyl group plays the dominant role and interaction with the surface is not significantly affected by the size of the carbon-chain. Accordingly, VA has been used in the continuation of the study.

3.3 Free energy landscape of valeric acid on a Co cluster

Now that we have identified a system that can accurately represent the OA–cobalt nanoparticle interaction at affordable computational cost, the stability and the likelihood of the possible binding modes can be explored. To provide insight in the mechanisms and barriers of the transitions while taking into account temperature effects, we have employed metadynamics, which enforces the process of sampling between different minima by adding a small repulsive Gaussian potential in a steady manner.

The most prominent differences between the well-known experimentally defined modes of interaction are the CNs of the two oxygen atoms, O_a and O_b, of carboxyl group with respect to surface metal atoms. By going from a bidentate mode, for which both CN (O_a–Co) and CN (O_b–Co) equal one (1,1), to a monodentate, the CN of one oxygen decreases to zero, while the other oxygen can bind to one, two, or three cobalt atoms, yielding combinations of (0,1), (0,2), and (0,3), respectively. Transition to a chelate interaction induces binding of both oxygen atoms to the same cobalt atom, which would at the first sight give exactly the same combination of CNs of bidentate binding, namely (1,1). However, the oxygen–oxygen repulsion results in an increased distance between the oxygen atoms in the chelate configuration, making the chelating Co–O bonds longer than in the bidentate, giving an approximate CN combination of (0.5,0.5). Thus, being able to distinguish between the most relevant structures, CN (O_a–Co) and CN (O_b–Co) make a good choice for collective variables.

Co–O distances and CNs of O_a and O_b have been presented for the whole metadynamics trajectory in Fig. 7, alongside the most representative structures. The starting structure was bridging bidentate with each oxygen bonded to one Co atom, as continued from the ab initio molecular dynamics equilibration. After 2.5 ps of metadynamics run, O_a formed a bridge in between neighbouring cobalt atoms, resulting in a chelating form which was stable for a short period. Around 0.5 ps later, O_b created a mirroring structure which persisted for a similar amount of time. The first monodentate interaction with a single O_b–Co bond occurred after approximately 4.75 ps, but the second bond between O_a and Co was formed again in less than 0.25 ps. Before the next monodentate appearance, both oxygen atoms formed a chelate structure with two neighbouring cobalt atoms three more times. The next time that the monodentate was formed, O_a bonded with two cobalt atoms rather than one for the duration of about 0.5 ps. The same type of bridging monodentate interaction, with O_a and O_b alternating in the bond formation during the run, could have been seen twice before the original atop monodentate mode with single Co–O bond was again established. In most of the transitions between bridging bidentate and monodentate or vice versa, a chelating interaction behaved as an intermediate state. No desorption of VA was observed on the time scale of the entire simulation. After 15 ps, instead of desorption of the molecule, O_b bonded to the third different surface cobalt atom. Ultimately, four distinct interaction modes were captured: atop monodentate where one of carboxyl oxygen atoms binds one cobalt atom; bridging monodentate where one O atom has two bonds with a pair of neighbouring Co atoms; bridging bidentate where each carboxyl oxygen binds a single Co atom from a neighbouring pair; and, finally, chelate, where one O atom forms two bonds, one with each atom from Co pair, while the other O atom forms a single bond with one of the Co atoms from the same pair. The bridging bidentate mode was formed for more than half of the time, ∼54%, with the bridging monodentate, atop monodentate, and chelate mode having a similar share of ∼18, ∼15 and ∼13%, respectively.

Fig. 7 Representative structures sampled during the metadynamics run (top). Changes in the coordination numbers CN (middle), and Co–O bond distances d_Co–O (bottom) throughout the metadynamics trajectory. O_a and O_b CNs and distances, as well as windows across the simulation are coloured according to the colours associated in the top panel.

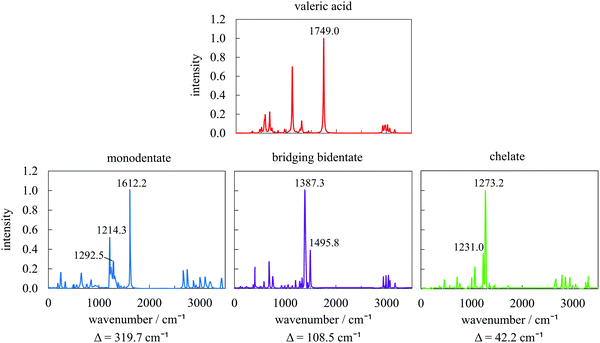
The type of interaction between the carboxylate head and the metal atoms can be confirmed by the wavenumber separation (Δ) between the asymmetric (ν_as(COO⁻)) and symmetric (ν_s(COO⁻)) stretches of COO⁻:^34,52,53 the largest Δ (∼200–320 cm⁻¹) corresponds to the monodentate interaction, medium Δ (∼140–190 cm⁻¹) to bridging bidentate interaction, and the smallest Δ (∼<110 cm⁻¹) to chelate interaction. We have selected three geometries corresponding to the main binding modes resulting from the metadynamics trajectory and simulated their IR spectra, together with that of VA in vacuum (Fig. 8). The IR spectrum of the pure acid shows good agreement with the positions of the fundamental frequencies of carboxylic acids. After adsorption, the intense peak at 1749 cm⁻¹, typical of the C=O stretch, disappears and two new peaks as features of carboxylate are formed at ∼1200 and 1650 cm⁻¹ instead. The obtained wavenumber separations Δ between the asymmetric and symmetric stretches are 320, 108, and 42 cm⁻¹, respectively, which, following the experimental trends discussed above, confirms our assignment of the type of interactions to monodentate, bridging bidentate, and chelate. A low Δ value obtained for the chelate mode is probably a consequence of an additional Co–O bond compared to the traditional chelating form.

Fig. 8 Simulated IR spectra of valeric acid in vacuum (top) and adsorbed on the 57-atom Co nanoparticle (bottom) as monodentate, bridging bidentate, and chelate, with accompanying wavenumber separations (Δ) between the asymmetric and symmetric stretches of COO⁻. Both axes are the same for all spectra.

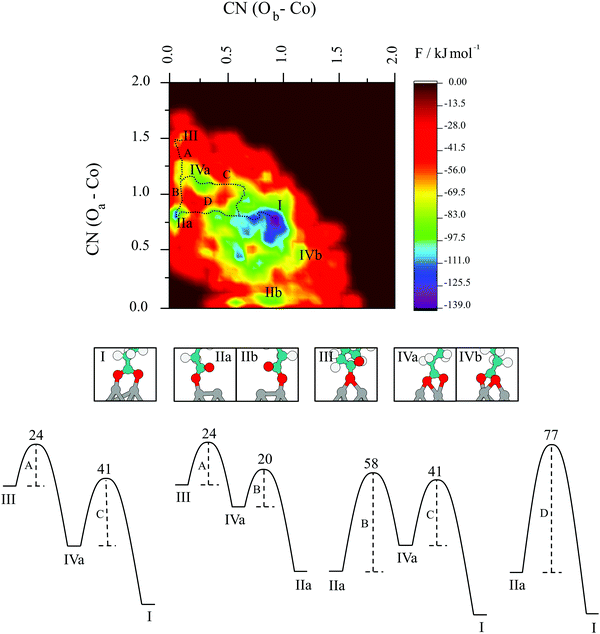
The next question that arises is to what extent does the change from bidentate to monodentate interaction happen; i.e., what are the pathways and barriers taking place, considering finite-temperature effects at the appropriate thermodynamic conditions. To investigate the underlying mechanisms in pertinent detail, the reconstructed free energy surface projected onto the plane spanning the two collective variables has been plotted in Fig. 9. Several minima beyond the one that defines the starting structure are readily identified and denoted using Roman numbers. Minimum I represents the bridging bidentate and is by far the most stable structure with an energy of −139 kJ mol⁻¹. The minima denoted as IIa and IIb are atop monodentate structures with O_a and O_b attached to one surface cobalt atom, respectively. They are higher in energy with respect to bridging bidentate and sit at around −115 kJ mol⁻¹. Chelates are represented by IVa and IVb and are energetically less favourable at −90 kJ mol⁻¹. Bridging monodentate, III, is least likely to be formed with an energy of around −60 kJ mol⁻¹. A wide area in energy up to −70 kJ mol⁻¹ around the global minimum can be assigned to exhaustive efforts of the system to stay in the bidentate mode with both oxygen atoms of carboxyl group bonded to a single cobalt atom, even when one or both bonds do not reach the ideal value of 2.0 Å. What clearly emerges from Fig. 9 is that the bridging bidentate is the most favourable mode of interaction between carboxylic acids and cobalt nanoparticles.

Fig. 9 Free energy surface for the adsorption process of valeric acid on the 57-atom Co cluster; Roman numbers denote different minima, with accompanying letters a and b standing for the configurations differing only by the oxygen atom, O_a or O_b, to which the surface cobalt atom is bonded. All structures are visually represented in the middle panel. Upper case letters illustrate the lowest energy paths whose mechanisms are proposed together with the free energy barriers for individual processes in the bottom panel. All energy barriers are given in kJ mol⁻¹.

Fig. 9 also illustrates that the transition of the system from the minima II to the global minimum I has two possible pathways, i.e. one with a chelating mode as an intermediate (B, C) and another direct pathway (D). The formation of the intermediate chelating state IV allows the molecule to access a lower energy pathway. In particular, the shift from atop monodentate directly to the bridging bidentate global minimum following route D, requires the system to overcome an energy barrier of 77 kJ mol⁻¹. However, the inclusion of the chelate interaction in the transition separates the process into two major steps (B and C), for which the two barriers of 58 and 41 kJ mol⁻¹ are both lower than in the direct route D.

Other possible pathways include bridging monodentate as a starting point, with two possible final destinations – atop monodentate (A, B), or the global minimum – bridging bidentate (A, C). Starting with a bridging monodentate and going towards the atop analogue requires an energy of 24 kJ mol⁻¹ to overcome the rate-determining step, which increases to 41 kJ mol⁻¹ if bridging bidentate is the final structure. In general, all transitions between minima are moderately energetically costly, with the rate-determining steps depending on the pathway.

4. Conclusion

We have presented a theoretical investigation which clarifies the interaction modes of cobalt nanoparticles with carboxylic acids. On the basis of DFT calculations, we suggest that a 57-atom cluster is the smallest cluster that can be adopted to model the interaction of carboxylic acids with Co nanoparticles. In addition, our ab initio metadynamics simulations have provided important insights into the free energy landscape around the two experimentally observed binding modes, namely monodentate and bridging bidentate. In particular, we found that the free energies of the two modes differ by 24 kJ mol⁻¹ in favour of the bridging bidentate, with the barrier allowing for the direct transition being moderately high, i.e. 77 kJ mol⁻¹. A chelating interaction was detected as a possible intermediate state, in a transition mechanism with an energy barrier of 58 kJ mol⁻¹ for the rate-limiting step. We also observed the formation of a fourth possible mode, bridging monodentate, but its high free energy makes it even more unlikely to be present under experimental conditions.

Thus, it is conceivable that the majority of the carboxylic acid molecules attached to cobalt nanoparticles would maintain a bridging bidentate interaction on the surface under synthesis conditions. Determination of the binding mode between the two modalities was a first step towards simulating the organic acid coatings on cobalt nanoparticles and their behaviour in an in vivo environment. The next set of issues to be addressed are the possible density of the adsorbed molecules and whether the introduction of the coating would be sufficient to prevent further chemical reactions, such as oxidation, to take place at the nanoparticles’ surface. Work along these directions is in progress.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

BF is grateful to Cardiff University for support through a Research Scholarship from the School of Chemistry. We acknowledge the Engineering and Physical Sciences Research Council (Grant no. EP/R512503/1 and EP/K009567/2) for funding. This work was performed using the computational facilities of the Advanced Research Computing @ Cardiff_(ARCCA) Division, Cardiff University. Via our membership of the UK's HPC Materials Chemistry Consortium, which is funded by EPSRC (EP/L000202), this work made use of the facilities of ARCHER, the UK's national high-performance computing service, which is funded by the Office of Science and Technology through EPSRC's High End Computing Programme. Information on the data underpinning the presented results, including how to access them, can be found in the Cardiff University data catalogue at http://doi.org/10.17035/d.2019.0081261776.

References

1. C. S. S. R. Kumar and F. Mohammad, Magnetic nanomaterials for hyperthermia-based therapy and controlled drug delivery, Adv. Drug Delivery Rev., 2011, 63, 789–808.
2. L. Kafrouni and O. Savadogo, Recent progress on magnetic nanoparticles for magnetic hyperthermia, Prog. Biomater., 2016, 5, 147–160.
3. M. Zeisberger, et al., Metallic cobalt nanoparticles for heating applications, J. Magn. Magn. Mater., 2007, 311, 224–227.
4. J. Pan, D. Thierry and C. Leygraf, Electrochemical impedance spectroscopy study of the passive oxide film on titanium for implant application, Electrochim. Acta, 1996, 41, 1143–1153.
5. C. Larsson, et al., Bone response to surface-modified titanium implants: studies on the early tissue response to machined and electropolished implants with different oxide thicknesses, Biomaterials, 1996, 17, 605–616.
6. B. Farkaš, D. Santos-Carballal, A. Cadi-Essadek and N. H. A. de Leeuw, DFT+U study of the oxidation of cobalt nanoparticles: implications for biomedical applications, Material, 2019, 7, 100381.
7. W. Wu, Q. He and C. Jiang, Magnetic iron oxide nanoparticles: synthesis and surface functionalization strategies, Nanoscale Res. Lett., 2008, 3, 397–415.
8. V. Georgakilas, et al., Functionalization of Graphene: Covalent and Non-Covalent Approaches, Derivatives and Applications, Chem. Rev., 2012, 112, 6156–6214.
9. T. Kang, et al., Surface design of magnetic nanoparticles for stimuli-responsive cancer imaging and therapy, Biomaterials, 2017, 136, 98–114.
10. J. Fouineau, et al., Synthesis, Mössbauer characterization, and Ab initio modeling of iron oxide nanoparticles of medical interest functionalized by dopamine, J. Phys. Chem. C, 2013, 117, 14295–14302.
11. M. Patitsa, et al., Magnetic nanoparticles coated with polyarabic acid demonstrate enhanced drug delivery and imaging properties for cancer theranostic applications, Sci. Rep., 2017, 7, 1–8.
12. S. Sun and C. B. Murray, Synthesis of monodisperse cobalt nanocrystals and their assembly into magnetic superlattices (invited), J. Appl. Phys., 1999, 85, 4325–4330.
13. V. A. De La Peña O’Shea, P. R. De la Piscina, N. Homs, G. Aromí and J. L. G. Fierro, Development of hexagonal closed-packed cobalt nanoparticles stable at high temperature, Chem. Mater., 2009, 21, 5637–5643.
14. V. F. Puntes, K. M. Krishnan and P. A. Alivisatos, Colloidal Nanocrystal Shape and Size Control: The Case of Cobalt, Science, 2001, 291, 2115–2117.
15. W. Betteridge, The properties of metallic cobalt, Prog. Mater. Sci., 1980, 24, 51–142.
16. C. Yoo, P. Soederlind and H. Cynn, The phase diagram of cobalt at high pressure and temperature: the stability of γ (fcc)-cobalt and new epsilon’(dhcp)-cobalt, J. Phys.: Condens. Matter, 1998, 10, L311–L318.
17. R. Deshmukh, A. Mehra and R. Thaokar, Formation and shape-control of hierarchical cobalt nanostructures using quaternary ammonium salts in aqueous media, Beilstein J. Nanotechnol., 2017, 8, 494–505.
18. M. Liu, L. Chen, C. Lin, L. Zhang and H. Song, Cobalt chains composed of hexagonal intercrossed microplatelets: shape-controlled synthesis, growth mechanism, and magnetic properties, J. Colloid Interface Sci., 2013, 410, 116–123.
19. C. He, et al., Facile synthesis of hollow porous cobalt spheres and their enhanced electromagnetic properties, J. Mater. Chem., 2012, 22, 22160–22166.
20. S. L. Wen, Y. Liu, X. C. Zhao, J. W. Cheng and H. Li, Synthesis, dual-nonlinear magnetic resonance and microwave absorption properties of nanosheet hierarchical cobalt particles, Phys. Chem. Chem. Phys., 2014, 16, 18333–18340.
21. H. I. Won, H. H. Nersisyan and C. W. Won, Cobalt powders and porous cobalt particles prepared by co-reduction of hydrazine and sodium phosphate and its formation mechanism, Mater. Chem. Phys., 2012, 133, 225–231.
22. Z. T. Liu, X. Li, Z. W. Liu and J. Lu, Synthesis and catalytic behaviors of cobalt nanocrystals with special morphologies, Powder Technol., 2009, 189, 514–519.
23. M. Pellarin, et al., Evidence for icosahedral atomic shell structure in nickel and cobalt clusters. Comparison with iron clusters, Chem. Phys. Lett., 1994, 217, 349–356.
24. J. Souto-Casares, M. Sakurai and J. R. Chelikowsky, Structural and magnetic properties of large cobalt clusters, Phys. Rev. B: Condens. Matter Mater. Phys., 2016, 93, 1–6.
25. F. Baletto, R. Ferrando, A. Fortunelli, F. Montalenti and C. Mottet, Crossover among structural motifs in transition and noble-metal clusters, J. Chem. Phys., 2002, 116, 3856–3863.
26. A. T. Le, et al., Synthesis of oleic acid-stabilized silver nanoparticles and analysis of their antibacterial activity, Mater. Sci. Eng., C, 2010, 30, 910–916.
27. H. T. Yang, et al., Stable cobalt nanoparticles passivated with oleic acid and triphenylphosphine, Nanotechnology, 2004, 15, 70–74.
28. L. H. Dubois, B. R. Zegarski and R. G. Nuzzo, Spontaneous Organization of Carboxylic Acid Monolayer Films in Ultrahigh Vacuum. Kinetic Constraints to Assembly via Gas-Phase Adsorption, Langmuir, 1986, 2, 412–417.
29. M. Wühn, J. Weckesser and C. Wöll, Bonding and orientational ordering of long-chain carboxylic acids on Cu(111): Investigations using X-ray absorption spectroscopy, Langmuir, 2001, 17, 7605–7612.
30. A. Weddemann, et al., Review and outlook: from single nanoparticles to self-assembled monolayers and granular GMR sensors, Beilstein J. Nanotechnol., 2010, 1, 75–93.
31. V. R. Reddy, et al., High coercivity of oleic acid capped CoFe₂O₄ nanoparticles at room temperature, J. Phys. Chem. B, 2009, 113, 9070.
32. Y. Su, X. OuYang and J. Tang, Spectra study and size control of cobalt nanoparticles passivated with oleic acid and triphenylphosphine, Appl. Surf. Sci., 2010, 256, 2353–2356.
33. Y. Lu, X. Lu, B. T. Mayers, T. Herricks and Y. Xia, Synthesis and characterization of magnetic Co nanoparticles: a comparison study of three different capping surfactants, J. Solid State Chem., 2008, 181, 1530–1538.
34. N. Wu, et al., Interaction of Fatty Acid Monolayers with Cobalt Nanoparticles, Nano Lett., 2004, 4, 383–386.
35. S. M. Ansari, et al., Cobalt nanoparticles for biomedical applications: facile synthesis, physiochemical characterization, cytotoxicity behavior and biocompatibility, Appl. Surf. Sci., 2017, 414, 171–187.
36. G. Kresse and J. Furthmüller, Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set, Comput. Mater. Sci., 1996, 6, 15–50.
37. J. P. Perdew, K. Burke and M. Ernzerhof, Generalized Gradient Approximation Made Simple, Phys. Rev. Lett., 1996, 77, 3865–3868.
38. P. E. Blöchl, Projector augmented-wave method, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979.
39. S. Grimme, S. Ehrlich and L. Goerigk, Effect of the damping function in dispersion corrected density functional theory, J. Comput. Chem., 2011, 32, 1456–1465.
40. X. Li, Y. Zhao, S. Wang, Y. Zhu and G. Yang, DFT-D2 Study of the Adsorption of Bio-Oil Model Compounds in HZSM-5: C₁–C₄ Carboxylic Acids, Catal. Lett., 2016, 146, 2015–2024.
41. D. Franke, M. Lorke, T. Frauenheim and A. L. Rosa, Hybrid Density-Functional Theory Calculations of Electronic and Optical Properties of Mercaptocarboxylic Acids on ZnO(1010) Surfaces, J. Phys. Chem. C, 2018, 122, 24838–24842.
42. A. Laio and F. L. Gervasio, Metadynamics: a method to simulate rare events and reconstruct the free energy in biophysics, chemistry and material science, Rep. Prog. Phys., 2008, 71, 126601.
43. A. Laio, A. Rodriguez-Fortea, F. L. Gervasio, M. Ceccarelli and M. Parrinello, Assessing the accuracy of metadynamics, J. Phys. Chem. B, 2005, 109, 6714–6721.
44. J. Vandevondele, et al., Quickstep: fast and accurate density functional calculations using a mixed Gaussian and plane waves approach, Comput. Phys. Commun., 2005, 167, 103–128.
45. J. Hutter, M. Iannuzzi, F. Schiffmann and J. Vandevondele, CP2K: atomistic simulations of condensed matter systems, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2014, 4, 15–25.
46. J. VandeVondele and J. Hutter, Gaussian basis sets for accurate calculations on molecular systems in gas and condensed phases, J. Chem. Phys., 2007, 127, 114105.
47. S. Nosé, A unified formulation of the constant temperature molecular dynamics methods, J. Chem. Phys., 1984, 81, 511–519.
48. W. Humphrey, A. Dalke and K. Schulten, VMD: visual molecular dynamics, J. Mol. Graphics, 1996, 14, 33–38.
49. A. Togo and I. Tanaka, First principles phonon calculations in materials science, Scr. Mater., 2015, 108, 1–5.
50. B. Hammer and J. K. Norskov, Theoretical Surface Science and Catalysis—Calculations and Concepts, Adv. Catal., 2000, 45, 71–129.
51. G. Henkelman, A. Arnaldsson and H. Jónsson, A fast and robust algorithm for Bader decomposition of charge density, Comput. Mater. Sci., 2006, 36, 354–360.
52. L. Zhang, R. He and H. C. Gu, Oleic acid coating on the monodisperse magnetite nanoparticles, Appl. Surf. Sci., 2006, 253, 2611–2617.
53. U. Terranova and D. R. Bowler, Coating TiO₂ anatase by amorphous Al₂O₃: effects on dyes anchoring through carboxyl groups, J. Phys. Chem. C, 2012, 116, 4408–4415.

---