Periodically-arrayed ferroelectric nanostructures induced by dislocation structures in strontium titanate†
Abstract
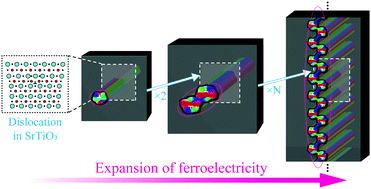
A dislocation induces ferroelectricity around it in incipient ferroelectric SrTiO3 due to some reasons such as electro-mechanical coupling and it being a one-dimensional ferroelectric nanostructure. Furthermore, this microstructure is arrayed periodically in the material and dislocation structures such as a dislocation wall are formed. Due to these facts, periodically-arrayed ferroelectric nanostructures, which show various intriguing polarization configurations and functionalities depending on the internal periodic structure, may be fabricated by dislocations. The phase-field simulation exhibits that a ferroelectric nano-region induced by the strain concentration and incidental electric field around a dislocation connects with each other in a dislocation wall. As a result, a periodic ferroelectric nano-region, which is a periodically-arrayed ferroelectric nanostructure embedded in paraelectric matrices, is formed. Our findings provide a new pathway for the fabrication of novel functional nanodevices in ferroelectric systems.
- This article is part of the themed collection: 2019 PCCP HOT Articles


 Please wait while we load your content...
Please wait while we load your content...