Open Access Article
Open Access ArticleMachine learning prediction of coordination energies for alkali group elements in battery electrolyte solvents†
Atsushi
Ishikawa
 *abcd,
Keitaro
Sodeyama
*abcd,
Keitaro
Sodeyama
 *acd,
Yasuhiko
Igarashi
ae,
Tomofumi
Nakayama
*acd,
Yasuhiko
Igarashi
ae,
Tomofumi
Nakayama
 e,
Yoshitaka
Tateyama
e,
Yoshitaka
Tateyama
 bce and
Masato
Okada
bce and
Masato
Okada
 e
e
aPRESTO, Japan Science and Technology Agency (JST), 4-1-8 Honcho, Kawaguchi, Saitama 333-0012, Japan
bCenter for Green Research on Energy and Environmental Materials (GREEN), and International Center for Materials Nanoarchitectonics, National Institute for Materials Science (NIMS), 1-1 Namiki, Tsukuba, Ibaraki 305-0044, Japan. E-mail: ISHIKAWA.Atsushi@nims.go.jp; SODEYAMA.Keitaro@nims.go.jp
cCenter for Materials Research by Information Integration (cMI2), Research and Services Division of Materials Data and Integrated System (MaDIS), National Institute for Materials Science (NIMS), 1-2-1 Sengen, Tsukuba, Ibaraki 305-0047, Japan
dElements Strategy Initiative for Catalysts & Batteries (ESICB), Kyoto University, 1-30 Goryo-Ohara, Nishikyo-ku, Kyoto 615-8245, Japan
eGraduate School of Frontier Sciences, The University of Tokyo, 5-1-5, Kashiwanoha, Kashiwa, Chiba 277-8561, Japan
First published on 18th November 2019
Abstract
We combined a data science-driven method with quantum chemistry calculations, and applied it to the battery electrolyte problem. We performed quantum chemistry calculations on the coordination energy (Ecoord) of five alkali metal ions (Li, Na, K, Rb, and Cs) to electrolyte solvent, which is intimately related to ion transfer at the electrolyte/electrode interface. Three regression methods, namely, multiple linear regression (MLR), least absolute shrinkage and selection operator (LASSO), and exhaustive search with linear regression (ES-LiR), were employed to find the relationship between Ecoord and descriptors. Descriptors include both ion and solvent properties, such as the radius of metal ions or the atomic charge of solvent molecules. Our results clearly indicate that the ionic radius and atomic charge of the oxygen atom that is connected to the metal ion are the most important descriptors. Good prediction accuracy for Ecoord of 0.127 eV was obtained using ES-LiR, meaning that we can predict Ecoord for any alkali ion without performing quantum chemistry calculations for ion–solvent pairs. Further improvement in the prediction accuracy was made by applying the exhaustive search with Gaussian process, which yields 0.016 eV for the prediction accuracy of Ecoord.
Introduction
Electrolytes are indispensable components of rechargeable secondary batteries, and finding good electrolytes is a key issue in the development of next-generation batteries.1,2 Currently, electrolyte solvents for Li ion batteries (LIBs) have been established, such as ethylene carbonate, propylene carbonate, dimethyl carbonate, diethyl carbonate, and ethyl methyl carbonate. However, we still have only limited knowledge about electrolyte solvents for other metal ions (Na, K, Mg, Ca, etc.). Considering the limited Li resources in the Earth's crust, it is necessary to develop alternative batteries that use more abundant metal ions. Thus, extending our knowledge of LIBs to other systems, such as Na or K ion batteries, is critical for future battery technology.3,4 Ideal batteries should possess high voltage and high capacity, as well as fast charging/recharging. From an atomistic perspective, in the charging/recharging processes the ions are transferred between the anode and cathode, and thus ion diffusion between the electrode and electrolytes determines the charge–discharge rate.The ion transfer between the electrolyte and the electrode has a large impact on the ion transport of the whole battery. The overall process of ion transfer between electrolyte and electrode is complicated, mainly because of the formation of the solid–electrolyte interface layer. Therefore, finding the direct relationship between ion transfer efficiency and the properties of isolated molecules is quite a challenging task.
In spite of these difficulties, several studies have shown that the character of the single ion–solvent pair is useful for understanding the tendencies in the ion transfer at the electrolyte/electrode interface. For example, the activation energy of electrolyte–electrode Li transfer is largely influenced by the desolvation energy of the ion from the electrolyte molecule.5,6 This suggests that ion–solvent interaction is one of the important factors governing the ion transfer phenomenon. In this context, the coordination energy of the ion to the solvent (Ecoord) can be a good indicator for ion transfer at the electrolyte/electrode interface. Indeed, several studies have investigated Ecoord of Li, Na, and K with various solvent molecules using quantum chemistry methods.7,8 For this reason, the search for battery electrolytes based on Ecoord would be an efficient and important approach.
Recently, great advances have been made in machine learning-based or data science-driven approaches. These approaches, in combination with high-throughput theoretical calculations, have also been applied to battery electrolytes.9–15 For example, a computational screening of over 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 materials has been reported for solid electrolytes in LIBs.16,17 Existing studies have mainly focused on solid electrolytes, while investigations on liquid electrolytes are limited.18,19 This is mainly because a solid system has a rather rigid structure, thus extracting structural, electronic, and energetic information from it is straightforward. By comparison, a liquid system is much more flexible in terms of molecular structure, making the extraction of structural information more challenging.
000 materials has been reported for solid electrolytes in LIBs.16,17 Existing studies have mainly focused on solid electrolytes, while investigations on liquid electrolytes are limited.18,19 This is mainly because a solid system has a rather rigid structure, thus extracting structural, electronic, and energetic information from it is straightforward. By comparison, a liquid system is much more flexible in terms of molecular structure, making the extraction of structural information more challenging.
In the present study, a machine learning-based technique, in combination with quantum chemistry calculations, was applied to the battery electrolyte problem, to derive an accurate and efficient method to predict values of Ecoord. Here, we consider coordination of alkali metal ions (Li, Na, K, Rb, and Cs) to electrolyte solvents, and use Ecoord calculated by quantum chemistry methods as the target properties. To the best of our knowledge, computational evaluation of Ecoord for such a wide range of alkali metals has not previously been reported. We expect that the combination of computational chemistry and data science-driven methods will be of great benefit in the search for electrolytes for next-generation batteries. Extending our knowledge of electrolyte solvents to metal ions other than Li would facilitate the computational screening of materials in post-LiBs.
Theoretical background
Data science method
Predicting Ecoord with simple physical or chemical properties of the solvent has two main advantages: (i) reduced cost of quantum chemistry calculations, since the computation for the ion–solvent complex is avoided, and (ii) it provides a fundamental understanding of the ion–solvent interaction, because it shows which solvent properties are critical for estimating the Ecoord value. In the present case, we can regard Ecoord and the solvent properties as the target properties and descriptors, respectively. Finding the relationship between these two sets is often called the variable selection problem.Among several approaches for variable selection, the simplest one is multiple linear regression (MLR). However, MLR often suffers from redundant descriptors when their number becomes large. The sparseness of the variable space is useful to alleviate this redundancy and avoids overfitting. Recently, sparse methods, such as the least absolute shrinkage and selection operator (LASSO), have been applied to many problems.20 Despite its success, LASSO gives only one combination of descriptors, which is not guaranteed to be the best among all possible pairs of descriptors. In order to analyze the stability of the chosen descriptor combination, examining combinations other than the optimal one is informative.
Recently, we showed that the exhaustive search with linear regression (ES-LiR) method, proposed and developed by Okada and co-workers, is quite useful in this context.21–23 In the ES-LiR method, all combinations of variable pairs are tested, guaranteeing that the best pair should be found. Thus, the ES-LiR method is a new and powerful solution for the variable selection.
Based on the above considerations, here, we applied the MLR, LASSO, and ES-LiR methods to find the relationship between Ecoord and solvent properties. The MLR was performed by minimizing the least-squares error
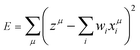 | (1) |
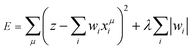 | (2) |
If λ is sufficiently large, some of the coefficients wi become zero. This makes the model sparse with respect to explanatory variables. To determine λ, we used the tenfold cross-validation error (CV error), that is, the whole data set was divided into training and validating data in ten different ways. The ES-LiR can be defined by introducing the indicator
| c = (c1, c2,…,cN) ⊂ {0, 1}N | (3) |
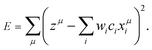 | (4) |
The exhaustive search with Gaussian process (ES-GP) is also an exhaustive search method, like ES-LiR.24 In ES-LiR, the regression method is linear regression, while in ES-GP it is a Gaussian process (GP).25 In the GP, the predicted value is written as
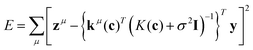 | (5) |
| kμ(c) = (k(x1,xμ),…,k(xn,xμ))T | (6) |
| k(xν,xμ) = exp(−β|xν(c) − xμ(c)|)2 | (7) |
| K(c) = {k(xν,xξ)}ν,ξ (1 ≤ ν, ξ ≤ n) | (8) |
Quantum chemistry calculation
For the electrolyte solvent database, we selected 70 solvents taken from commercialized battery-grade materials from KISHIDA Chemical Co., Ltd.26 The full list of electrolyte solvents examined is shown in Table S1 (ESI†). The electrolyte database is close to the one used in ref. 21. Some experimental data are included as descriptors here, namely, the melting point, boiling point, and density taken from ref. 26 The metal ions are described by their experimental ionic radii.In the present study, Ecoord was defined by the following formula
| Ecoord = Eion–solv − (Esolv + Eion) | (9) |
Density functional theory (DFT) was used in the electronic structure calculation. M06-2X was used for the exchange–correlation functional, since this functional is reported to accurately predict the thermodynamic properties of main group elements.27,28 The Def2-SVP basis set was used for all the elements, and the pseudo-potential was used for K, Rb, and Cs.29 Another alkali ion, Fr, is omitted in this work because it is unstable and radioactive, thus not relevant for batteries. Atomic charges were calculated by the natural population analysis method proposed by Weinhold et al., using the NBO 6 program.30 All the calculations were performed with Gaussian16.31
For the descriptors or explanatory variables, the following were used as ‘computational’ descriptors: energies of the highest occupied molecular orbital (HOMO) and the lowest unoccupied molecular orbital (LUMO), dipole moment, natural bond orbital (NBO) charge of the O atom that coordinates to the metal ion, total energy (i.e. electronic energy plus nuclear repulsion), and total dipole moment. From an atomic/molecular perspective, the ion–solvent interaction can be understood as an acid–base interaction, since the ion works as a hard acid and the solvent works as a hard or soft Lewis base. Common organic electrolyte solvents have alkoxy or carbonyl groups, and in these cases the O atom works as the Lewis base site. For this reason, we assumed that the ion coordinated to this O atom. Also, the NBO charge on the coordinating O atom was included in the descriptors. For the optimized geometries of the cation-coordinated system, see Fig. S1 in the ESI.† The computational properties of the solvent are obtained by DFT calculation of the pure solvent, i.e. without ions. All the experimental and computational descriptors for the solvent molecules are shown in Table 1.
| Experimental | Cations: ionic radius, electronegativity, atomic weight |
| Solvents: boiling point, melting point, flashing point, density | |
| Computational | Solvents: NBO charge on coordinating O atom, HOMO energy, LUMO energy, total dipole moment, total energy, molecular weight |
Results and discussion
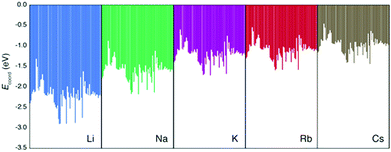
First, we discuss the accuracy of the three methods to estimate the true (i.e. DFT-calculated) Ecoord values. Here, the data set includes all the Ecoord data (i.e. coordination of Li, Na, K, Rb, and Cs to solvent molecule). In other words, solvent descriptors and ion descriptors were independently made and combined to form the whole data set. Since we have 70 solvents, the Ecoord data set consists of 5 × 70 = 350 points.32Our calculated Ecoord values for Li, Na, K, Rb, and Cs are summarized in the bar chart in Fig. 1, and the selected numerical values for Ecoord are shown in Table 2. The range of Ecoord for the five ions are: Li −1.32 to −2.91 eV (mean value: −2.20 eV), Na −0.88 to −2.18 (−1.60), K −0.61 to −1.73 (−1.20), Rb −0.55 to −1.60 (−1.11), and Cs −0.46 to −1.44 eV (−0.98). Thus, the Ecoord of metal ions can be ranked as Li > Na > K ∼ Rb > Cs.
| Solvent | E coord (eV) | ||||
|---|---|---|---|---|---|
| Li | Na | K | Rb | Cs | |
| Ethylene carbonate | −2.343 | −1.747 | −1.365 | −1.272 | −1.135 |
| Propylene carbonate | −2.399 | −1.789 | −1.397 | −1.307 | −1.165 |
| Vinylene carbonate | −2.179 | −1.610 | −1.246 | −1.157 | −1.025 |
| Fluoroethylene carbonate | −2.128 | −1.569 | −1.210 | −1.129 | −1.001 |
| Dimethyl carbonate | −2.068 | −1.454 | −1.078 | −0.968 | −0.842 |
| Diethyl carbonate | −2.130 | −1.492 | −1.106 | −1.010 | −0.877 |
| Ethyl methyl carbonate | −2.114 | −1.488 | −1.108 | −1.006 | −0.878 |
| Furan | −1.320 | −0.884 | −0.605 | −0.545 | −0.461 |
| Tetrahydrofuran | −2.047 | −1.454 | −1.065 | −0.978 | −0.851 |
| Ethyl acetate | −2.206 | −1.574 | −1.185 | −1.083 | −0.950 |
| Isopropyl acetate | −2.222 | −1.585 | −1.187 | −1.093 | −0.958 |
| Methyl propionate | −2.138 | −1.524 | −1.133 | −1.030 | −0.896 |
| Methyl formate | −2.011 | −1.444 | −1.082 | −0.981 | −0.861 |
| Vinyl acetate | −2.052 | −1.454 | −1.076 | −0.984 | −0.857 |
| Sulfolane | −2.481 | −1.879 | −1.450 | −1.350 | −1.200 |
| Dimethyl sulfoxide | −2.905 | −2.183 | −1.725 | −1.590 | −1.427 |
| Cyclohexanone | −2.259 | −1.654 | −1.265 | −1.158 | −1.025 |
| Benzaldehyde | −2.177 | −1.570 | −1.188 | −1.085 | −0.958 |
| Benzyl benzoate | −2.758 | −2.139 | −1.682 | −1.591 | −1.441 |
| Diphenyl ether | −1.625 | −1.120 | −0.758 | −0.738 | −0.638 |
| Acetone | −2.190 | −1.600 | −1.219 | −1.117 | −0.987 |
| Chloroacetone | −1.938 | −1.399 | −1.047 | −0.964 | −0.845 |
| Methyl acrylate | −2.195 | −1.570 | −1.178 | −1.069 | −0.938 |
Next, we examined the regression of Ecoord from the solvent and ion properties. Fig. 2 demonstrates a good correlation between Ecoord values calculated by DFT and those estimated by ES-LiR. The CV error for ES-LiR in Fig. 2 was 0.127 eV. This is only 5.7% for the average Li coordination energy, indicating that the regression formula from ES-LiR gives accurate results. We also observe that the prediction accuracy tends to be lower at Ecoord < −2.5 eV. As we shall see later, the important descriptors are the O charge and the total dipole. The deviation from this regression formula indicates other effects, for example, large distortion of the ion–solvent complex would contribute to large Ecoord values.
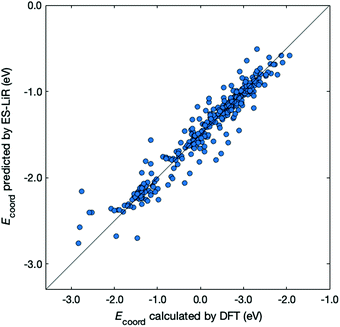 | ||
| Fig. 2 Comparison between Ecoord calculated by DFT (x-axis) and that predicted by ES-LiR (y-axis). The diagonal line corresponds to a perfect match. | ||
The accuracy of the estimation methods can be evaluated by the CV errors. The smallest CV error calculated with the MLR, LASSO, and ES-LiR methods was 0.1280, 0.1278, and 0.1271 eV, respectively. These values are shown in Table 3, together with selected combinations of descriptors. Values in Table 3 suggest that ES-LiR gives the smallest CV error and thus the best prediction accuracy, although the differences between the three methods are moderate. It is well known that the CV error is intimately related to the choice of descriptors. Since the ES-LiR examines all combinations of descriptors, it is always guaranteed to choose the best combination. In all three regression formulae, the ionic radius of the metal ion has the largest coefficient and thus it is the most important descriptor. This can be understood in terms of Pearson's hard–soft acid–base rule, which states that the smaller ion has hard acid character. The positive coefficient of ionic radius in Table 3 indicates that smaller ions give the smaller Ecoord values (thus the stronger ion–solvent interaction). After the ionic radius, the NBO charge on the O atom coordinating to the ion has the second largest coefficient. Since the ion–solvent interaction mainly has an electrostatic cationic–anionic character, a more negative O charge leads to a stronger interaction and thus a larger Ecoord value. This conclusion is the same as in our previous work, in which the O atomic charge is the most important descriptor for the Li coordination on electrolyte solvent molecules.21 We also found that the total dipole has a relatively large coefficient. This adds to the charge–charge electrostatic interaction via charge–dipole interaction, so this also contributes to the ion–solvent interaction.
| MLR | LASSO | ES-LiR | |
|---|---|---|---|
| Ionic radius | 0.6637 | 0.6542 | 0.6637 |
| Electronegativity | 0.1612 | 0.1569 | 0.1612 |
| Atomic weight | −0.0986 | −0.0930 | −0.0986 |
| NBO charge of Oatom | 0.1832 | 0.1751 | 0.1860 |
| HOMO energy | 0.0121 | 0.0111 | 0.0000 |
| LUMO energy | 0.0260 | 0.0248 | 0.0273 |
| Total dipole | −0.1467 | −0.1420 | −0.1475 |
| Total energy | −0.1384 | −0.1261 | −0.1476 |
| Boiling point | −0.0956 | −0.0941 | −0.0977 |
| Flashing point | 0.1154 | 0.1034 | 0.1182 |
| Melting point | −0.0202 | −0.0151 | 0.0000 |
| Molecular weight | −0.1156 | −0.1051 | −0.1215 |
| Density | 0.0249 | 0.0270 | 0.0000 |
| CV error | 0.1280 | 0.1278 | 0.1271 |
Another important difference among the three regression methods is the sparseness of the regression formula. In MLR and LASSO, all descriptors have some non-zero coefficients, and thus these methods are the least sparse among the three. Contrary to these two methods, ES-LiR gives a more sparse regression formula because three descriptors (HOMO energy, melting point, and density) have zero coefficients. This indicates that the regression formula given by ES-LiR is the most accurate of the three methods, and at the same time its physical and chemical meanings are the easiest to interpret.
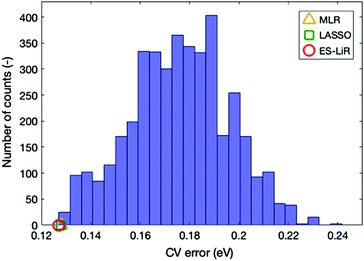
Up to now, our discussion is based on the optimal combination of descriptors that minimize the CV error. Estimation accuracy for other descriptor combinations can also be found using the ES-LiR, because this method examines all combinations of descriptors. The number of counts in the descriptor combination within a fixed CV error range can be summarized by the histogram in Fig. 3, where descriptor combinations that reduce CV error to below 0.14 are rather rare. From this, we can infer that the combination of particular descriptors is important for achieving accuracy.
This issue can be analyzed with the linear coefficient of the accurate regression formula. This is another important piece of information obtained by ES-LiR. The plot of linear coefficients for ten descriptor combinations that give low CV errors is shown in Fig. 4. We call this the ‘weight diagram’, where each color represents the magnitude of the fitted coefficient. Since we can find the contribution of descriptors for several combinations of them, the stability of the important descriptors can be found from the weight diagram. We consider that analysis with several regression formulae is important, because multicollinearity often occurs in the linear regression model; inspecting the descriptor weights for multiple combinations of regression models is more robust than analysis based on a single regression model.
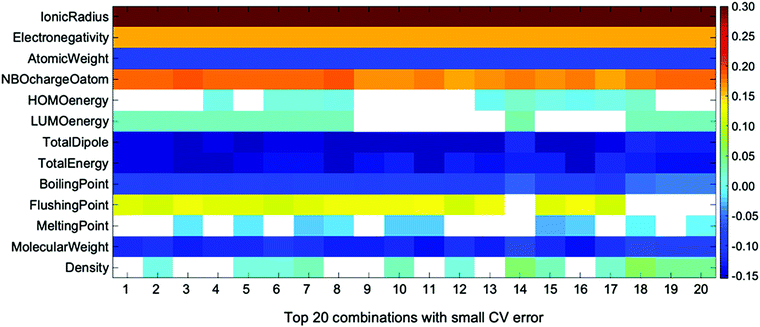 | ||
| Fig. 4 Weight diagram for the descriptors of top 20 combinations with small CV error in ES-LiR. Descriptors with coefficients smaller than 10−10 shown in white box. | ||
In the weight diagram, the ionic radius has the largest contribution to the regression formula in all descriptor combinations. Thus, this property is the most important and also most stable descriptor in the Ecoord prediction, as stated above. Since the ionic radius is the most important descriptor in all top 20 descriptor combinations, it is also the most stable one in the present descriptor set. The next important descriptor is the NBO charge of the coordinating O atom, which is also a stable descriptor among the 20 combinations. Other descriptors, such as dipole moment, boiling point, and density, are also important, but their stability is not as high as the ionic radius or the solvent O NBO charge.
We also note that the atomic weights of cation species have large weight. The atomic weight works as a secondary factor for the ionic radius, as can be confirmed by carrying out the ES-LiR without the ionic radius; in this case the atomic weights have the largest weight in the regression formula. However, the calculated CV error is considerably higher (0.2807 eV), indicating that the ionic radius does much better in the linear regression model.
Finally, we applied the ES-GP method for Ecoord prediction. The ES-GP method, like ES-LiR, examines all the possible combinations of descriptors, while regression of the target value is done with the Gaussian process. This includes the non-linear terms of the descriptors, which were not taken into account in the ES-LiR method. According to this feature, we can expect higher prediction accuracy with ES-GP, which was already shown in our previous study.24 Here, the same data set used for ES-LiR was used for ES-GP. We used the following seven descriptors in the ES-GP; ionic radius, NBO charge, total dipole moment, total energy, boiling point, melting point, and density. We selected these descriptors as they minimize the CV error of the ES-GP prediction; the dependence of the CV error on the number of descriptors is shown in Fig. S2 in the ESI.†
In Fig. 5, we compare the Ecoord values calculated by DFT and predicted by ES-GP. The CV error for ES-GP was 0.016 eV, which is significantly better than that for ES-LiR (0.127 eV). The accuracy of the ES-GP method is 1.54 in kJ mol−1 unit, which is sufficient for most purposes for battery-related study. From these results, we can conclude that the combined use of ES-LiR and ES-GP is advantageous in obtaining good physical or chemical intuition and achieving high prediction accuracy.
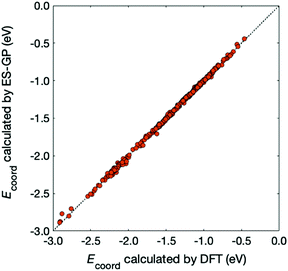 | ||
| Fig. 5 Comparison between Ecoord calculated by DFT (x-axis) and predicted by ES-GP (y-axis). The diagonal line corresponds to a perfect match. | ||
Conclusions
Exploration of new electrolyte solvents is key for next-generation batteries. To this end, data science-driven techniques combined with computational chemistry are an up and coming powerful tool. In the present study, the coordination energy (Ecoord) of alkali metal ions to battery electrolyte solvent was calculated by DFT for Li, Na, K, Rb, and Cs ions and 70 solvents. Additionally, the calculated Ecoord was used as the target property in the regression using MLR, LASSO, and ES-LiR methods. This enables the prediction of Ecoord for various ion species using only the properties of the ion and the solvent.E coord calculated with DFT using M06-2X show that the ion–solvent interaction is in the order of Li > Na > K ∼ Rb > Cs, with the mean Ecoord values of −2.20, −1.60, −1.20, −1.11, and −0.98 eV. We then constructed regression models to predict Ecoord from ion and solvent descriptors (melting point, flashing point, HOMO energy, LUMO energy, NBO atomic charge, total energy, total dipole moment, and metal ionic radius). We found that the ES-LiR gives the best accuracy for Ecoord, since its cross-validation error was 0.127 eV. Even higher accuracy (0.016 eV) can be obtained with ES-GP. This suggests that accurate prediction of Ecoord is possible even if solvent descriptors and ion descriptors are independently formed. The ionic radius is the most important descriptor since it has the largest coefficient in the regression formula. Other descriptors, such as NBO charge on the solvent O atom or total dipole, are also important. This result can be easily understood as the ion–solvent interaction is mainly electrostatic in nature. The weight diagram from ES-LiR revealed that the importance of the ionic radius and O atom NBO charge as descriptors is stable over many regression formulae.
This study has shown that combined use of computational chemistry and data-driven science can be an efficient and accurate tool for coordination energy prediction. We succeeded in showing that this approach can be applicable to any alkali metal ion coordination. The constructed regression models are accurate enough for practical use in the search for battery electrolytes. These features will be important in developing post-Li next-generation batteries.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported in part by JST “Materials research by Information Integration” Initiative (MI2I) project, by JSPS KAKENHI Grant Number JP15H05701, and by MEXT as “Priority Issue (No. 5) on Post K Computer”. The calculations were carried out at the supercomputer center of NIMS. The work also used computational resources of the K computer at the RIKEN through the HPCI System Research Projects (project IDs: hp160174, hp170198, and hp180134).Notes and references
- K. Xu, Nonaqueous Liquid Electrolytes for Lithium-Based Rechargeable Batteries, Chem. Rev., 2004, 104(10), 4303–4418 CrossRef CAS PubMed.
- M. D. Bhatt and C. O'Dwyer, Recent Progress in Theoretical and Computational Investigations of Li-ion Battery Materials and Electrolytes, Phys. Chem. Chem. Phys., 2015, 17(7), 4799–4844 RSC.
- N. Yabuuchi, K. Kubota, M. Dahbi and S. Komaba, Research Development on Sodium-Ion Batteries, Chem. Rev., 2014, 114(23), 11636–11682 CrossRef CAS.
- A. Eftekhari, Z. Jian and X. Ji, Potassium Secondary Batteries, ACS Appl. Mater. Interfaces, 2017, 9(5), 4404–4419 CrossRef CAS PubMed.
- Y. Yamada, F. Sagane, Y. Iriyama, T. Abe and Z. Ogumi, Kinetics of Lithium-Ion Transfer at the Interface between Li0.35La0.55TiO3 and Binary Electrolytes, J. Phys. Chem. C, 2009, 113(32), 14528–14532 CrossRef CAS.
- T. Abe, F. Sagane, M. Ohtsuka, Y. Iriyama and Z. Ogumi, Lithium-Ion Transfer at the Interface Between Lithium-Ion Conductive Ceramic Electrolyte and Liquid Electrolyte-A Key to Enhancing the Rate Capability of Lithium-Ion Batteries, J. Electrochem. Soc., 2005, 152(11), A2151–A2154 CrossRef.
- M. Okoshi, Y. Yamada, A. Yamada and H. Nakai, Theoretical Analysis on De-Solvation of Lithium, Sodium, and Magnesium Cations to Organic Electrolyte Solvents, J. Electrochem. Soc., 2013, 160(11), A2160–A2165 CrossRef CAS.
- M. Okoshi, Y. Yamada, S. Komaba, A. Yamada and H. Nakai, Theoretical Analysis of Interactions between Potassium Ions and Organic Electrolyte Solvents: A Comparison with Lithium, Sodium, and Magnesium Ions, J. Electrochem. Soc., 2017, 164(2), A54–A60 CrossRef CAS.
- R. Ramprasad, R. Batra, G. Pilania, A. Mannodi-Kanakkithodi and C. Kim, Machine Learning in Materials Informatics: Recent Applications and Prospects. npj Computational, Materials, 2017, 3(1), 54 Search PubMed.
- L. Cheng, R. S. Assary, X. Qu, A. Jain, S. P. Ong, N. N. Rajput, K. Persson and L. A. Curtiss, Accelerating Electrolyte Discovery for Energy Storage with High-Throughput Screening, J. Phys. Chem. Lett., 2015, 6(2), 283–291 CrossRef CAS PubMed.
- M. D. Halls and K. Tasaki, High-Throughput Quantum Chemistry and Virtual Screening for Lithium Ion Battery Electrolyte Additives, J. Power Sources, 2010, 195(5), 1472–1478 CrossRef CAS.
- G. Hautier, A. Jain and S. P. Ong, From the Computer to the Laboratory: Materials Discovery and Design using First-Principles Calculations, J. Mater. Sci., 2012, 47(21), 7317–7340 CrossRef CAS.
- S. Curtarolo, G. L. W. Hart, M. B. Nardelli, N. Mingo, S. Sanvito and O. Levy, The High-Throughput Highway to Computational Materials Design, Nat. Mater., 2013, 12, 191 CrossRef CAS PubMed.
- M. Korth, Large-Scale Virtual High-Throughput Screening for the Identification of New Battery Electrolyte Solvents: Evaluation of Electronic Structure Theory Methods, Phys. Chem. Chem. Phys., 2014, 16(17), 7919–7926 RSC.
- T. Husch, N. D. Yilmazer, A. Balducci and M. Korth, Large-Scale Virtual High-Throughput Screening for the Identification of New Battery Electrolyte Solvents: Computing Infrastructure and Collective Properties, Phys. Chem. Chem. Phys., 2015, 17(5), 3394–3401 RSC.
- Z. Ahmad, T. Xie, C. Maheshwari, J. C. Grossman and V. Viswanathan, Machine Learning Enabled Computational Screening of Inorganic Solid Electrolytes for Suppression of Dendrite Formation in Lithium Metal Anodes, ACS Cent. Sci., 2018, 4(8), 996–1006 CrossRef CAS PubMed.
- A. D. Sendek, Q. Yang, E. D. Cubuk, K. A. N. Duerloo, Y. Cui and E. J. Reed, Holistic Computational Structure Screening of More Than 12
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 Candidates for Solid Lithium-Ion Conductor Materials, Energy Environ. Sci., 2017, 10(1), 306–320 RSC.
000 Candidates for Solid Lithium-Ion Conductor Materials, Energy Environ. Sci., 2017, 10(1), 306–320 RSC. - X. Chen, X. Shen, B. Li, H.-J. Peng, X.-B. Cheng, B.-Q. Li, X.-Q. Zhang, J.-Q. Huang and Q. Zhang, Ion–Solvent Complexes Promote Gas Evolution from Electrolytes on a Sodium Metal Anode, Angew. Chem., Int. Ed., 2018, 57(3), 734–737 CrossRef CAS PubMed.
- X. Chen, H.-R. Li, X. Shen and Q. Zhang, The Origin of the Reduced Reductive Stability of Ion–Solvent Complexes on Alkali and Alkaline Earth Metal Anodes, Angew. Chem., Int. Ed., 2018, 57(51), 16643–16647 CrossRef CAS PubMed.
- R. Tibshirani, Regression Shrinkage and Selection via the Lasso, J. Roy. Stat. Soc. B, 1996, 58(1), 267–288 Search PubMed.
- K. Sodeyama, Y. Igarashi, T. Nakayama, Y. Tateyama and M. Okada, Liquid Electrolyte Informatics using an Exhaustive Search with Linear Regression, Phys. Chem. Chem. Phys., 2018, 20(35), 22585–22591 RSC.
- Y. Igarashi, K. Nagata, T. Kuwatani, T. Omori, Y. Nakanishi-Ohno and M. Okada, Three Levels of Data-Driven Science. In International Meeting on High-Dimensional Data-Driven Science, ed. T. Obuchi, T. Kasai, M. J. Miyama, M. Ohzeki and M. Uemura, 2016, vol. 699 Search PubMed.
- Y. Igarashi, H. Takenaka, Y. Nakanishi-Ohno, M. Uemura, S. Ikeda and M. Okada, Exhaustive Search for Sparse Variable Selection in Linear Regression, J. Phys. Soc. Jpn., 2018, 87, 4 CrossRef.
- T. Nakayama, Y. Igarashi, K. Sodeyama and M. Okada, Material Search for Li-ion Battery Electrolytes Through an Exhaustive Search with a Gaussian Process, Chem. Phys. Lett., 2019, 731, 136622 CrossRef CAS.
- C. E. Rasmussen and C. K. I. Williams, Gaussian Processes for Machine Learning, The MIT Press, Cambridge, MA, 2005 Search PubMed.
- KISHIDA CHEMICAL Co., L., KISHIDA Product Information. 2016.
- N. Mardirossian and M. Head-Gordon, How Accurate Are the Minnesota Density Functionals for Noncovalent Interactions, Isomerization Energies, Thermochemistry, and Barrier Heights Involving Molecules Composed of Main-Group Elements?, J. Chem. Theory Comput., 2016, 12(9), 4303–4325 CrossRef CAS PubMed.
- Y. Zhao and D. G. Truhlar, The M06 Suite of Density Functionals for Main Group Thermochemistry, Thermochemical Kinetics, Noncovalent Interactions, Excited States, and Transition Elements: Two New Functionals and Systematic Testing of Four M06-Class Functionals and 12 Other Functionals, Theor. Chem. Acc., 2008, 120(1-3), 215–241 Search PubMed.
- F. Weigend and R. Ahlrichs, Balanced Basis Sets of Split Valence, Triple Zeta Valence and Quadruple Zeta Valence Quality for H to Rn: Design and Assessment of Accuracy, Phys. Chem. Chem. Phys., 2005, 7(18), 3297–3305 RSC.
- A. E. Reed, R. B. Weinstock and F. Weinhold, Natural-Population Analysis, J. Chem. Phys., 1985, 83(2), 735–746 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, Ö. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, Revision A.03, Gaussian Inc, Wallingford, CT, 2016 Search PubMed.
- In our calculation, descriptors are not fully independent because solvent descriptors are same with five cations. However, Ecoord values were individually calculated for all the solvent-cation pairs (i.e. 350 systems). Therefore the whole dataset (descriptors and target values) is independent and identically distributed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c9cp03679b |
| This journal is © the Owner Societies 2019 |