Soft experimental constraints for soft interactions: a spectroscopic benchmark data set for weak and strong hydrogen bonds

Abstract

An experimental benchmark data base on rotational constants, vibrational properties and energy differences for weakly and more strongly hydrogen-bonded complexes and their constituents from the spectroscopic literature is assembled. It is characterized in detail and finally contracted to a more compact, discriminatory set (ENCH-51, for Experimental Non-Covalent Harmonic with 51 entries). The meeting points between theory and experiment consist of equilibrium rotational constants and harmonic frequencies and energies, which are back-corrected from experimental observables and are very easily accessible by quantum chemical calculations. The relative performance of B3LYP-D3, PBE0-D3 and M06-2X density functional theory predictions with a quadruple-zeta basis set is used to illustrate systematic errors, error compensation and selective performance for structural, vibrational and energetical observables. The current focus is on perspectives and different benchmarking methodologies, rather than on a specific theoretical method or a specific class of compounds. Extension of the data base in chemical, observable and quantum chemical method space is encouraged.

---

1 Introduction

Quantum chemical methods need guidance from multiple experiments, because they involve approximations which have different implications for different experimental observables. In the absence of highly accurate theoretical reference methods for large molecular systems, the popular route of benchmarking against more rigorous theoretical calculations^1–12 is often less viable or not fully sufficient. Experimental benchmark data sets offer alternatives.^13,14 They have to make educated selections in the chemical space and in the space of observables, to be practical. Furthermore, they should offer back-correction to easily computable equilibrium and harmonically evaluated quantities to be applicable without major computational barriers. This perspective explores such alternatives. We pick a relatively small subspace of compounds and observables, to illustrate some strategies and limitations of experimental benchmarking. Specifically, we focus on five well-studied strong hydrogen bond donors (hydrogen fluoride HF,^15–29 formic acid FA,^30–37 acetic acid AA,^{30,32,38–40} trifluoroethanol TE,^41–43 and hexafluoroisopropanol HP^44–47) and on some of their hydrogen-bonded dimers and trimers as well as complexes with very weak hydrogen bond acceptors (dinitrogen NN^48–51 and dioxygen OO^52–54). We thus span the weakest and the strongest among the regular hydrogen bonds and initially include closely related systems to discover potential outliers in the experimental characterization. In terms of observables, we concentrate on rotational constants A, B, C for structure, on OH (and analogous FH) fundamental stretching wavenumbers [small nu, Greek, tilde]_OH as well as their shifts and splittings Δ[small nu, Greek, tilde]_OH for dynamics, and on conformational preferences ΔE and dissociation energies D for the energetics of hydrogen bonding.⁵⁵ Energies are often the least accessible observables in spectroscopic experiments, if they do not correspond to allowed one-quantum transitions. This is usually the case for dissociation and isomerization energies. We analyze possible strategies to include them, trying to account for anharmonic effects with realistic error bounds. Rotational constants and fundamental wavenumbers also suffer from anharmonicity and we describe suggestions how to cope with this in a standardized back-correction procedure, necessarily sacrificing experimental accuracy. The intention is to make electronic structure and harmonically estimated dynamics calculations directly comparable to experiment, such that a large number of quantum chemical methods can be easily explored. By selecting and summarizing a set of experimental reference data with realistic error bars from back-correction, we invite computational chemists to systematically test the performance of their preferred methods in describing these energetic, structural and vibrational benchmark data on strong and weak hydrogen bonding.⁵⁶ Once a few successful methods have been identified, the next step will be to extend the data base to other systems and to other observables for further method discrimination. To prepare for such data base extensions, the reduction of the data set to non-redundant representative entries without loss in discriminatory power is exemplified.

Our simple approach complements the more sophisticated strategy to directly and accurately predict experimental anharmonic observables for very small molecules with high level methods.^57–61 By focusing on the smallest molecules with 1–3 vibrational degrees of freedom, no significant compromise in the vibrational treatment is required, such that the quality of the electronic structure approach can be directly assessed. For the smallest hydrogen-bonded complexes, minor compromises in the electronic structure level and in the vibrational treatment still provide excellent matches between theory and experiment.^57,61 Such matches are very encouraging for the success of modern numerical quantum chemistry, but they lack the scalability to chemically more relevant system sizes with potentially new binding contributions such as many-body dispersion effects or chirality-selective forces.

Our proposal also complements the strategies for medium-sized molecules of, say, 5–20 atoms, to assume the correctness of vibrational perturbation theory⁶² or to limit the expansion of the anharmonic force field to its leading terms.⁶³ These and related methods are very valuable and powerful tools for well-chosen systems and degrees of freedom, but they quickly fail whenever secondary minima on the potential energy hypersurface come into reach. Adding a methyl rotor can deteriorate their performance even for apparently unrelated degrees of freedom or at least demands tailored computational treatment.

Our approach avoids the high computational and man-power barrier associated with such detailed calculations and is meant to replace the frequent but unsatisfactory practice of directly matching harmonic predictions with anharmonic experiment in a “comparing apples-to-oranges”-fashion. The proposed back-correction rules are designed to be generally valid and sufficiently conservative, but occasional exceptions are to be expected for very floppy systems such as quasistructural molecules⁶⁴ and complexes.⁶⁵ However, outliers could also be due to experimental error. To give just a few examples, direct absorption measurements of hydrogen-bonded clusters may not always provide unambiguous size and conformation assignments.⁶⁶ The omnipresent methyl groups in organic complexes may complicate the unique rotational constant determination by microwave spectroscopy⁶⁷ and also the dissociation energy determination by stimulated-emission-pumping/resonant 2-photon ionization.¹⁴ Multi-experimental approaches are particularly promising in this context.^68,69 It is crucial to remain skeptical on the experimental and the theoretical side⁷⁰ in such benchmark comparisons and both sides profit from a critical discussion.

2 Strategy

Many aspects determine the outcome of such benchmarking efforts and there is some degree of subjectiveness, but also a certain amount of common sense involved. It is essential to select benchmark observables which have an adequate discriminatory power. To give an example, the energy ranking between the doubly hydrogen-bonded dimer of FA and its most stable singly hydrogen bonded isomer³⁰ will be predicted correctly by essentially any theoretical model, even the most elementary ones which often fail for hydrogen bonding such as AM1. On the other hand, the experimental wavenumber of the lowest mode of the metastable cis FA monomer⁷¹ is known to 8 significant digits⁷² and no theoretical model will be able to come close to this accuracy in the foreseeable future.⁷³ For benchmarking purposes, it is more meaningful to provide a number of FA monomer modes^31,74 to, say, 1% accuracy and an experimental binding energy of the formic acid dimer.³⁶ It is essential that these data refer to molecules in the gas phase, rather than in matrix isolation,^75,76 because matrix shifts will likely be of similar size and unknown direction as residual errors in modern quantum chemical methods. The same is true for packing and cooperative effects in X-ray crystal structure determination.^77,78 Meeting experiment at the level of anharmonic modes is often challenging⁷⁹ and we make several suggestions how this can be avoided, evidently at the cost of losing accuracy.

Standard Newtonian molecular dynamics simulations are not an option for anharmonic high frequency vibrations, although this is frequently claimed in the literature.^80–82 There will always be a specific simulation temperature for which the average classical frequency matches the quantum mechanical anharmonic value for a specific mode, but this temperature exceeds several 1000 K for a hydride stretching fundamental and changes from mode to mode.⁴⁴ At room temperature or even below,⁸⁰ hardly any high frequency mode anharmonicity is probed by Newtonian dynamics. Agreement with experiment is then the result of a fortuitous cancellation between electronic structure error and vibrational error without any benchmarking insight. We note that a more elaborate procedure based on time-integrated normal modes⁸³ claims to recover a larger fraction of the anharmonicity of high frequency modes from classical trajectories even at room temperature.

A meeting point at the harmonic level is much more universal to explore, because any quantum chemical method which can provide minimum structures of molecular systems also allows for the computation of the Hessian matrix of local second derivatives. Rigorous anharmonic calculations, on the other hand, fall short of being routine for any system with more than 4 atoms.^84,85 Vibrational perturbation theory⁶² may represent an alternative particularly for stiff high frequency modes, where it appears to be quite successful even in hydrogen-bonded situations.⁸⁶ However, this is difficult to prove rigorously in the absence of analogous results from fully converged wavefunction methods and potential energy hypersurfaces of spectroscopic accuracy for the same systems. This is particularly true whenever large amplitude motion like methyl rotation comes into play. Vibrational CI methods also partially lose their intrinsically high performance when it comes to large amplitude motion.⁸⁷ A similar situation applies to rotational constants, which are much harder to predict including anharmonic zero point motion than at equilibrium.⁸⁸ It has been remarked more than 15 years ago⁸⁹ that “one of the traditional tasks of rotational spectroscopy, to provide unambiguous benchmarking data for the development of theoretical descriptions is considerably hindered, in particular for the most weakly bound clusters.” To a large extent, this is still true today, although there are several very accurate theory-experiment comparisons for small systems⁹⁰ and semiexperimental non-covalent bond lengths have recently been proposed.⁹¹ Rotational constants are likely to involve less methodical bias than singled-out bond distances in a polyatomic molecule and we therefore concentrate on these collective observables. Again, a meeting point at the equilibrium structure level would be very helpful for the theoretical community, but it comes at the price of losing the enormously high accuracy of rotational spectroscopy, which includes zero-point motion. As long as the shift of the meeting point and its resulting accuracy loss does not spoil the discriminatory power of the experimental benchmark, we consider this acceptable. In the end, a large number of soft experimental constraints can be more useful for a ranking of approximate methods than a small number of too rigorous ones, which theory cannot meet, anyway.

We propose the following classes Xn of fairly conservative constraints for the systems under investigation for back-correction of experimental, intrinsically anharmonic data to harmonic or equilibrium structure estimates (see Fig. 1):

Fig. 1 Illustration of the back-correction procedures Xn proposed in the text with a microwave spectrum of jet-cooled HP and its dimer,⁴⁶ an FTIR spectrum of jet-cooled HP/NN mixtures,⁴⁷ and schematic energy diagrams for the dissociation of NN from a hydrogen bond donor like HP or HF and for two interconvertible HPHPNN isomers.²⁶

• R1: Experimental ground state rotational constants of rigid molecules are back-corrected to equilibrium values by +1(±1)% to account for typical harmonic and anharmonic averaging effects, building on previous suggestions and evidence.^90,92,93 For diatomics, extrapolation of constants in vibrationally excited states allows for much more accurate equilibrium values (denoted R1D) than polyatomic molecules (R1P).

• R2: Experimental rotational constants of weakly bound complexes are back-corrected by +1(±3)% to account for potentially more pronounced anharmonic effects in both directions.

• V1: Experimental fundamental OH stretching wavenumbers of monomers ν₁ are corrected for diagonal anharmonicity x₁₁ from an overtone measurement and given an additional error bar of ±20% of the diagonal anharmonicity constant due to off-diagonal contributions, which are often small and relatively unsystematic for isolated OH modes. Again, diatomics (V1D) represent a special case because of the absence of off-diagonal corrections, as opposed to polyatomic molecules (V1P).

• S1: Complexation shifts of OH stretching wavenumbers relative to the monomer should involve a high degree of anharmonic cancellation between the monomer and the complex. Nevertheless, we add a safety margin of 50% in both directions, because it is known from an analysis of the simplest organic hydrogen bond that diagonal and off-diagonal effects tend to cancel but are individually quite large.⁹⁴

• S2: Spectral shifts between different isomers of a complex (or of a flexible molecule) or of different components in a degenerate mode coupling pattern are likely to involve little anharmonic correction due to systematic cancellation, because the messenger is the same. If the complexation shift (S1) is small, it is unlikely that it induces very different anharmonicities. If the complexation shift is large, the uncertainty in the isomer shifts also becomes larger. Therefore, we introduce a S1-proportional error bar of ±10% for back-correction to harmonic isomer shifts. Within a flexible molecule, a proper experimental reference point is usually missing and one has to resort to S2 between isomers instead of S1 for the error estimation.

• E1: Dissociation energies of OH-bonded dimers are typically too small in the harmonic limit and anharmonic treatments bring them closer to the infinite nuclear mass limit, but intramolecular effects may counteract this trend. We back-correct experimental dimer dissociation values to harmonically estimated ones by subtracting up to 10% and adding up to 5%, which should cover the expected variation for typical hydrogen bonds.

• E2: Energy differences between different isomers of a complex can be affected strongly by anharmonic corrections. Even if the total energy difference is small, it can be the net effect of rather different and thus differently anharmonic interactions. Also, experiment often can only provide the sign of the energy difference with some certainty. Tentatively, we add an error bar of ±50% to the anharmonic value, although well-designed cases of isomerism are likely to involve smaller errors⁹⁵ and worst cases will not be covered by this uncertainty.

All these back-conversion errors are added to the individual experimental error bar, which can be significant for low resolution and more indirect observables but is usually negligible for high resolution spectroscopy data. We emphasize that these back-correction rules do not depend on the theory level to be tested but rather apply to the experimental data themselves. Due to the dependence of even the most straightforward anharmonicity corrections for diatomics on the employed model Hamiltonian, the Born–Oppenheimer approximation and other subtleties, we somewhat arbitrarily set a lower limit for the experimental error bar at 1 MHz for rotational constants (which is certainly conservative for polyatomic molecules⁹⁶) and 1 cm⁻¹ for vibrational term values.

There is always the possibility that the error bar for an individual back-correction from experiment to the meeting point with theory is not conservative enough. Single outliers must be compensated for by a sufficiently large size of the benchmark database. A few examples of well-characterized experimental outliers for small molecular systems shall be briefly discussed.

The ground state rotational constant of H₂ is lower than the equilibrium constant⁹⁷ by 2.5%, whereas R1 assumes 0–2%. For molecular complexes, mixed theoretical-computational analyses which rigorously connect the equilibrium value of rotational constants with the ground state value are not very abundant.⁸⁹ An extreme example is Ar-HBr, which, according to the analysis in ref. 98 has a qualitatively different preferred structure at equilibrium (Ar-BrH) than at zero point level (Ar-HBr), which leads to ZPVE effects on the order of 30% for rotational constants. Complexes with several equivalent accessible minima such as HCl–H₂O may show similar deviations.⁸⁹ Also, the A rotational constant of quasilinear complexes may experience large ZPVE corrections due to centrifugal effects and the asymptotic divergence at linear configurations.²⁰ Furthermore, there are cases where molecular rotation couples to internal rotation, occasionally leading to enormous deviations between the experimental A constant and the equilibrium one.⁶⁵ The R2 constraint used in this work may thus encounter exceptions, but should still be valid as a rule for not too floppy and not too linear polyatomic complexes.

Experimental OH stretching wavenumbers for monomers usually have a narrow range of anharmonicity contributions, unless there is significant intramolecular hydrogen bonding. Even in the latter case, diagonal and off-diagonal shift contributions tend to attenuate each other. Furthermore, the OH stretching mode only shows major resonances once shifted below about 3 μm. Therefore, it is actually difficult to find molecules where off-diagonal anharmonicity contributions exceed 10% of the diagonal correction. Formic acid is a case where the 10% are reached for the net effect, because all off-diagonal corrections point in the same direction.³⁰ Complexation shifts in OH stretching wavenumbers are particularly difficult to assess, because rigorous analyses are scarce. In the case of the methanol dimer,⁹⁹ there is a near cancellation of different contributions which have an individual magnitude up to 30% of the total shift. Formic acid dimer is an extreme case,³⁰ where diagonal and off-diagonal terms also tend to cancel, but framework resonances contribute very significantly to the OH stretching intensity in a shift range of (500 ± 200) cm⁻¹. For weaker hydrogen bonds, cancellation also appears to be active.¹⁰⁰ Thus, the safety margin of 50% in S1 appears generally justified.

Dimer dissociation energies are among the most fundamental quantities which a computational method for non-covalent interactions must reproduce, but unfortunately they are rarely accessible to experiment.^36,55,101 Dissociation changes six low frequency intermolecular modes into ZPVE-free degrees of freedom. Therefore it is particularly susceptible to anharmonic effects and there can be qualitative effects such as in the He dimer which is not bound in the harmonic approximation, being barely bound in experiment and in accurate anharmonic calculations. In the field of classical hydrogen bonding, the dimer of HF is a pronounced case with an anharmonic contribution to the dissociation energy of about 9%. Anharmonicity typically increases the dissociation energy, as those modes created by the interaction usually have negative anharmonicities. This may be amplified by intramolecular stretching modes involved in the interaction, whose anharmonicity typically increases by the interaction. However, for the formic acid dimer, there are indications that the net effect of anharmonicity on the dissociation energy may only be on the order of 1%^30,102 despite diverging earlier assumptions.¹⁰³ Finally, there are even rare cases where the anharmonic dissociation energy is larger than the electronic dissociation energy.¹⁰⁴

The main purpose of this perspective is to provide an initial experimental benchmark set and not so much to test a large number of theoretical methods against it. The latter is left to interested theory groups and we provide cartesian coordinates for all investigated systems in the ESI.† However, as a start, we compare the performance of two established hybrid functionals for structural, energetic and vibrational properties of hydrogen bonds, PBE0 and B3LYP, both with Grimme's D3 dispersion correction,¹⁰⁵ as well as the popular M06-2X hybrid functional with heavy empirical fitting. The D3 correction or some other way of including long range dispersion is essential for hydrogen-bonded systems once they reach a certain size and it would be easy to demonstrate poor performance by leaving it away.^46,66

Once a theoretical value (x_Q) at computational level Q for an observable rotational constant, wavenumber or energy based on electronic structure and harmonic curvature is available for a compound C, it is compared with the recommended best experimental back-corrected value (x_exp.) for the same quantity. The difference is divided by the estimated experimental uncertainty (Δx_exp.) based on the back-correction strategy Xn and on experimental errors. The ratio between the theoretical deviation and the experimental error is squared. This removes the sign of the deviation and at the same time weighs small deviations (which might still suffer from limitations of experimental back-correction) much less than large deviations:

The resulting individual dimensionless δ_Xn²(C,Q) values can be averaged over different compounds C and different back-correction classes for observables Xn (R1, R2, V1, S1, S2, E1, E2) for a given method Q (B = B3LYP-D3, P = PBE0-D3, M = M06-2X, all employing the def2-QZVP basis set, using the Gaussian09 program suite¹⁰⁶), or over all compounds (providing their number #, optionally followed by a D for diatomics and a P for polyatomics). Such averages are further marked with a bar, 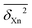. Furthermore, averages over all classes 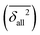or families of classes (e.g.) may be formed. These overall rankings can only be reasonably balanced if the different classes have similar discriminatory power. Therefore, diatomics usually have to be treated separately, as they would otherwise dominate the benchmark due to their straightforward, much more rigorous modeling of anharmonicity. Alternatively, for a given set of m methods Q to be compared, one can normalize each individual δ²(Q) by the value averaged over all m investigated methods. The resulting Δ²(Q) values are close to 0 for outstandingly good and fall between 1 and m for the poorer methods. However, the assessment of the experimental and back-correction error bar and thus a key ingredient of the present approach is lost, whereas the best estimate for the back-correction is kept. Another possible approach, still widely used, is to compare apples to oranges by directly taking the anharmonic experimental value as a reference for the computed harmonic or even electronic (in the case of rotational constants) value. We discourage this practice for obvious reasons, but provide some results for the popular shortcut, denoted as ω²(Q) and Ω²(Q). Given the bold approximation involved, a careful assessment of experimental error bar is superfluous in this case and we thus focus on Ω²(Q) values normalized by all considered methods.

By partial averaging, one can identify methods which are particularly successful for, e.g., structural or vibrational benchmarks and also remove classes with strongly deviating discriminatory power. In this way, rather comprehensive and detailed judgements of the performance of theoretical methods for growing benchmark datasets can be obtained. For example denotes the relative performance of M06-2X for 30 rotational constants in molecular complexes. If it is less than 1, M06-2X performs better than the average of all investigated methods.

In terms of the size of the benchmark database, the strategy is to start with some similarities in the considered systems to identify experimental outliers. In the present case, we start with a database size of 82 entries. After validation and analysis, it is compactified to 51 entries with enhanced discriminatory power based on a total of only 5 molecules and their complexes. Because the quantum chemical effort typically scales sublinearly with the number of benchmarked observables, a small number of systems with a large number of observables offers a computational advantage. In particular, harmonic frequency shifts and dissociation energies draw from the same Hessian calculations. Future efforts may focus on such cost-effective extensions to other observables related to intermolecular interactions such as electric moments, polarizabilities¹⁰⁷ or spectral intensities,¹⁰⁸ but should always be open for the addition of new systems with different method-discriminating properties.

3 Results and discussion

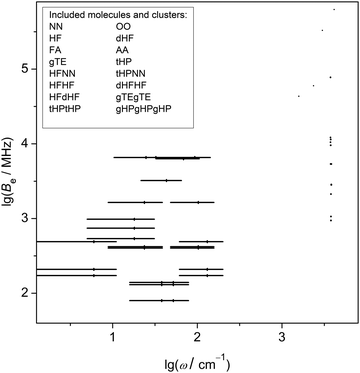
Table 1 lists the systems in the experimental benchmark and the number of observables included in the different back-correction categories R1/R2, V1, S1, S2, E1, E2. The systems include the 7 compounds which were labelled in the introduction with capital two-letter acronyms (NN, OO, HF, FA, AA, TF, HP). O-deuteration (d), gauche (g) and trans (t) isomerism is specified in front with a small case letter, if needed. Complexes are listed in donor–acceptor sequence, so tHPtHPNN means a complex in which a dimer of two trans hexafluoroisopropanol units is capped at the free OH end by a nitrogen molecule. 50% of the 82 entries are rotational constants, 40% are vibrational properties (13% stretching vibrations, 27% vibrational shifts and splittings), and 10% are dissociation energies and energy splittings. The included rotational and vibrational quantities are correlated in Fig. 2 to show remaining gaps in the frequency coverage. While the rotational constants cover the range from 10² to 10⁶ MHz, there is a gap for mid-IR wavenumbers. This is in part explainable by the low sensitivity of that spectral range to hydrogen bonding, but future extensions of the database can improve the coverage to some extent. Note that Fig. 2 does not include systems for which either the vibrational or the rotational data are missing, such as OO complexes.

Table 1 List of molecules and molecular complexes and the number of included observables in the individual back-correction categories, including their partial and total sums Σ. See text for the abbreviations. The values in parentheses correspond to a reduced, highly discriminatory database, where it differs from the large database

System	R1/R2	V1	S1	S2	E1	E2	Σ
NN	1	1	—	—	—	—	2
OO	1	1	—	—	—	—	2
HF	1	1	—	—	—	—	2
dHF	1	1	—	—	—	—	2
FA	3	1	—	—	—	—	4
dFA	—	1(0)	—	—	—	—	1(0)
AA	3(0)	1(0)	—	—	—	—	4(0)
dAA	—	1(0)	—	—	—	—	1(0)
gTE	3(0)	1(0)	—	—	—	—	4(0)
tHP	3	1	—	—	—	—	4
gHP	—	1(0)	—	1(0)	—	—	2(0)
HFNN	1	—	1	—	1	—	3
FANN	—	—	1	—	—	—	1
dFANN	—	—	1(0)	—	—	—	1(0)
AANN	—	—	1(0)	—	—	—	1(0)
dAANN	—	—	1(0)	—	—	—	1(0)
tHPNN	3	—	1	—	—	—	4
FAOO	—	—	1	—	—	—	1
AAOO	—	—	1(0)	—	—	—	1(0)
tHPOO	—	—	1	—	—	—	1
HFHF	1	—	2	—	1	—	4
dHFHF	1(0)	—	1(0)	—	1(0)	—	3(0)
HFdHF	1	—	1	—	1	1	4
FAFA	6(3)	—	—	—	1	—	7(4)
AAAA	—	—	—	—	1(0)	—	1(0)
gTEgTE	3(0)	—	2(0)	—	—	—	5(0)
tHPtHP	3	—	2	—	—	—	5
gHPtHP	3(0)	—	—	—	—	—	3(0)
tHPtHPNN	—	—	—	2	—	1	3
gHPgHPgHP	3	—	—	2	—	—	5
Σ	41 (25)	11 (6)	17 (10)	5 (4)	6 (4)	2	82 (51)

---

Fig. 2 Double-logarithmic representation of the rotational constant vs. vibrational wavenumber coverage contained in the database. Back-corrected (R1, R2/V1, S1, S2) pairs are shown together with their error bars. The gap in the fingerprint range is related to the lower sensitivity of the corresponding vibrations to aggregation but can be partially filled in future extensions.

3.1 Relative unweighted DFT performance

We start with an analysis of the relative performance of the three DFT methods in reproducing the back-corrected experimental observables (see ESI†). All three average values are 1.0, so the overall performance of the three functionals is very similar when all entries are equally weighted. There are, however, large performance differences in detail. For the small sample of diatomic vibrations, Q = P (PBE0-D3) performs significantly better , for the 7 polyatomic OH stretching vibrations, B (B3LYP-D3) is vastly superior and for hydrogen bond-induced downshifts, M (M06-2X) makes the closest predictions . For rotational constants, P is still the best method for diatomics 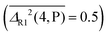, whereas M and B swap their role as best performers for polyatomic molecules and complexes . For energetical quantities, the poor performance of M for relative energies stands out (1.9), but the sample size is far too small to allow for firm conclusions, although this matches growing evidence from intermolecular energy balances.^109,110 The overall performance for energies is very similar for the three methods .

3.2 Comparing apples to oranges

For comparison purposes, we now tentatively leave away the back-correction, thus directly comparing apples (experimental anharmonic values) to oranges (harmonic or equilibrium structure predictions), as is still common practice. Now, B3LYP is clearly superior to the other two methods . This is largely due to a better performance for polyatomic and in particular diatomic rotational constants and vibrations. Ultimately it reflects the fact that the vibrations are somewhat too soft and that the bond lengths slightly too small at B3LYP level, in particular when the element F is involved. A significant deterioration without back-correction is only found for OH stretching vibrations of polyatomic molecules, where harmonic predictions of this popular hybrid functional should better not be compared to anharmonic experiment, as is widespread practice in the DFT community. For PBE0, such deteriorations for the right reason are instead found for diatomic vibrations and rotational constants of molecules. For M06-2X, the effect of back-correction is non-systematic for vibrations but clearly improving for rotational constants.

3.3 Error-weighted comparisons

Next we turn on the back-correction error estimates Δx_exp. proposed in this work, which allow to assess individual methods over several observables by providing best estimate weighting factors. Observables which are poorly defined by experiment and by anharmonic uncertainty are given smaller weights than those with well-defined anharmonic corrections. When doing this, the 8 diatomic bond lengths and harmonic curvatures have to be removed from the analysis due to their orders of magnitude better defined reference values. For such systems, one would anyway employ much higher levels of theory and not fall back to the sometimes erratic and sometimes systematic errors of DFT. We only note the substantial failure of all three DFT-approaches in reproducing these quantities. The theoretical error is always at least one, but typically two or more orders of magnitude larger than the experimental error despite back-correction uncertainties. For example, the HF equilibrium rotational constant at B3LYP level is 1% too small, whereas the PBE0 value is an order of magnitude more accurate but still orders of magnitude outside the experimental error bar, even allowing for model errors.

The following discussion thus focuses on the 74 polyatomic benchmark entries from Table 1. Here, experimental and back-correction errors are much closer to the model deviations for the three investigated DFT functionals. The largest outliers are found in the dissociation energy of HFNN, the weakly bound complex between HF and NN. It was experimentally determined by the Miller group at 4.76(2) kJ mol⁻¹,²⁶ obviously including the anharmonic zero point energy of the complex. Based on the back-correction rule E1, we add 5% and subtract 10% of the value to obtain a best estimate for the harmonically corrected dissociation energy of the complex at 4.64(36) kJ mol⁻¹, or 4.64(38) kJ mol⁻¹ after adding the experimental error. The harmonically corrected B value for the dissociation energy of 5.9 kJ mol⁻¹ is thus far too high, resulting in δ_E1²(HFNN,B) = 10.2. This is actually the largest of all 74 × 3 δ² entries in the present data base, all other values being single digit all the way down to less than 0.1. There is other experimental evidence that B overbinds hydrogen-bonded complexes of NN,⁵⁵ even without correction for anharmonicity.

Table 2 lists 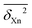values for different sub-categories Xn. They range from 0.1 (perfect match between back-corrected experiment and theory within the back-correction uncertainty) to about 3. Characteristically, the two extremes are often covered by the same methods. M describes rotational constants of polyatomic molecules best (0.1) and OH vibrational frequencies worst (3.2). B describes polyatomic OH vibrations best (0.1) and hydrogen bond dissociation energies of their complexes worst (3.1). This underscores the large extent of error cancellation in such methods, because a method which gives the right answers for the right reasons should perform systematically well for different observables with such a close relationship as it does exist for bond lengths and bond vibrations. It is noteworthy that on average , all methods show the smallest deviations for rotational properties (0.8) and the largest errors for energetical quantities (2.2). This suggests that energetical quantities are particularly helpful for benchmarking, but unfortunately also the hardest to obtain by experiment. The best discrimination ([small pi, Greek, macron]) between the three methods is found to behave similarly. For rotational properties, the average standard deviation is smallest (0.9), for energetical and vibrational properties it is larger (1.7 and 1.5, respectively). It will be interesting to see in the future whether accurate wave function based methods perform more systematically for the different properties and corresponding studies are invited.⁷ All relevant back correction data are available in the ESI.†

Table 2 Performance of DFT methods B, P, M for polyatomic properties in terms of . Also given is their average performance 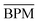and the average discriminatory power [small pi, Greek, macron] (standard deviation among methods) of a given property to distinguish between the three methods. Values in bold mark the best-performing method for a given property class. Values in parentheses correspond to the reduced data set ENCH-51

#	Xn	B	P	M		[small pi, Greek, macron]
12 (6)	R1P	2.0 (2.2)	0.4 (0.7)	0.1 (0.2)	0.9 (1.0)	1.5 (1.6)
25 (15)	R2	0.6 (0.7)	0.9 (1.0)	1.0 (0.8)	0.8 (0.8)	0.7 (0.5)
37 (21)	R1P, R2	1.0 (1.2)	0.7 (0.9)	0.7 (0.6)	0.8 (0.9)	0.9 (0.8)
7 (2)	V1P	0.1 (0.2)	2.1 (3.3)	3.2 (4.7)	1.8 (2.7)	2.3 (3.4)
17 (10)	S1	1.7 (2.0)	2.8 (2.8)	0.7 (0.7)	1.7 (1.8)	1.5 (1.6)
5 (4)	S2	0.4 (0.3)	0.5 (0.6)	0.3 (0.4)	0.4 (0.4)	0.5 (0.5)
29 (16)	V1P, S1, S2	1.1 (1.3)	2.2 (2.3)	1.2 (1.1)	1.5 (1.6)	1.5 (1.5)
6 (4)	E1	3.1 (4.1)	2.6 (3.3)	1.6 (1.6)	2.3 (3.0)	0.6 (1.9)
2	E2	1.5	1.4	2.2	1.7	0.6
8 (6)	E1, E2	2.7 (3.2)	2.3 (2.6)	1.6 (1.8)	2.2 (2.6)	1.7 (1.5)
74 (43)	All	1.3 (1.5)	1.5 (1.7)	1.0 (1.0)	1.3 (1.6)	1.2 (1.5)

---

After these general observations, a few specific findings deserve discussion, because they can help to condense and later also to extend the present benchmark. The poor performance of B for rotational constants for fluorinated alcohols has already been remarked. The corresponding δ² values are an order of magnitude larger than for carboxylic acids and for the other DFT methods. M misses the harmonic OH stretching frequencies most prominently. These poor performances disappear when moving to molecular complexes, where B performs particularly well for rotational constants and M for vibrational shifts. This is related to the well-known general overestimation of hydrogen bond-induced downshifts of the OH stretching frequency for most density functionals. The M functional compensates partly for this overestimate, but at the price of missing the monomer values. Unless one adopts a very pragmatic attitude, this is not satisfactory. Returning to the initial discussion of HFNN, we back-correct the observed downshift²² of the HF stretching mode of 43 cm⁻¹ to a loose harmonic estimate of 43 ± 22 cm⁻¹, because of diagonal and off-diagonal anharmonic contributions (rule S1). Nevertheless, this back-correction window is missed badly by B (92) and P (102 cm⁻¹), somewhat in line with the overestimated dissociation energy. Already two decades ago, it was shown that such deviations should be blamed more on DFT than on anharmonic corrections.¹¹¹ The best harmonic CCSD(T) estimate for the downshift at that time was 64 cm⁻¹, within our experimental back correction and significantly below the B and P predictions. At the time, the harmonically corrected dissociation energy was predicted at 3.9 kJ mol⁻¹, somewhat below our back correction estimate of 4.6(4) kJ mol⁻¹. Nowadays, one could carry these calculations to even higher level to see whether our back-correction is applicable to such a highly anharmonic system.

A more recent test of the back-correction reliability is possible for HFHF.^57,112 For this system, a combination of harmonic CCSD(T) basis set limit estimate and vibrational perturbation theory has yielded a surprisingly accurate match for the two HF stretching downshifts, within a few cm⁻¹. While there may still be some error compensation at play, it will not be very large. The underlying harmonic downshifts are less than 30% larger than the anharmonic ones, well within the S1 back-correction window of ±50% despite a substantial floppiness of this dimer. For the dissociation energy, an elaborate theoretical study⁶¹ suggests that the anharmonic zero point energy correction to the dissociation energy is on the order of +6(1)%, again well within the +10% error margin of the E1 criterion.

We note that the difference in performance of the tested DFT functionals for the open shell complexes of OO as compared to the closed shell system NN is not very significant, despite the simple UHF treatment in the former. This may deserve further investigation and extension of the open shell database to more sensitive quantities.¹¹³

3.4 Downsizing of the benchmark

To prepare the present benchmark approach for a much wider coverage of molecular complexes, it appears indicated to remove some redundancies, which were introduced to check the soundness of the experimental data base and to identify highly discriminatory systems. For this purpose, one may look at the individual [small pi, Greek, macron] values in the ESI,† which provide the standard deviation of the three methods and also at the average value () of the three methods. As an example, the rotational constants of FA³³ deviate somewhat more from experiment than those of AA.³⁹ The same is the case for the OH stretching fundamental^30,31,38 and for the dimer dissociation energy^36,40 as well as for the NN downshifts.³⁰ Considering that FA will be much more amenable to high level harmonic and anharmonic calculations, it makes sense to drop the AA entries in favour of FA. As the difference between rotational constants of FAFA with Coriolis coupling³⁴ or without³⁵ is not very significant in relation to the back-correction error, we drop the latter. The performance of TE data is quite similar to that of HP data, whereas HP offers more diversity in the experimental characterization. Therefore, TE is also dropped. With similar arguments and the weakness of the S2 criterion for intramolecular isomerism in mind (vide supra), we drop the monomer and dimer entries of gHP. The resulting more compact benchmark dataset (see Table 1, values in parentheses) comprises 51 entries for 14 species and some of their isotopologues, which are built from 5 different monomers, summarized in Fig. 5. For this compact set, the performance of B, P and M is still nearly identical (1.0(1)) without including the rule-based error estimates. From Table 2 (values in parentheses), one can see that the database reduction has several implications upon inclusion of the back-correction error. The average deviation () and the discriminatory power [small pi, Greek, macron] both increase. The overall superior performance of functional M relative to B, P increases somewhat, but it has significant outliers. Polyatomic OH stretching vibrations show the poorest performance whereas the performance for rotational properties and also for vibrational shifts is best for the same functional.

These performance details are graphically summarized in Fig. 3. For rotational (top panel), vibrational (central panel) and energy quantities (bottom panel), the values from Table 2 are plotted for each of the methods and the results for subcategories are connected with those for the full category. The poor performance for monomer rotational constants for method B is evident, as is the poor performance of M for monomer vibrational fundamentals and the generally poorer performance for energies. In some sense, P yields the most balanced performance within a category – its polygons are best centered and of intermediate size.

Fig. 3 ENCH-51 polyatomic values from Table 2 for the R, V and E categories (from top to bottom) and corresponding subcategories for each of the three tested DFT methods. A large deviation from the origin represents a poor performance of the method.

Fig. 4 is also instructive. In the top panel, it compares the overall rotational, vibrational and energy performance of the different methods. M, although quite erratic in detail (Fig. 3), has the best overall performance, as its polygon is inscribed in those of the others. The lower panel compares the average BPM performance over all methods with the standard deviation [small pi, Greek, macron] among the methods. They match quite well, indicating a moderate discriminatory power of the investigated observables for the three functionals. Only for energies, the average deviation is larger than the standard deviation. This may hint at a systematic error, either in the experiment or in the functionals, but the E data base is currently too small for significant conclusions. A general conclusion from these figures is that future efforts to broaden the data base should probably focus on energies and vibrational properties.

Fig. 4 ENCH-51 polyatomic 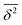summary performance for all, R-only, V-only, and E-only observables for the three tested DFTs (top) and method-averaged performance as well as standard deviation [small pi, Greek, macron] among the methods (bottom panel), all from Table 2.

3.5 Future extensions

Fig. 5 summarizes the systems included in the compact 51-entry benchmark and suggests the previously unstudied FA/HP complexes as a meaningful extension. Extension to other aggregation-sensitive vibrational modes beyond the hydride stretches does not increase the evaluation effort of the benchmark and is thus planned in particular for formic acid. New observables such as dipole moments could be included, whenever experimental data and realistic back-correction errors are available. New molecular constituents should be added to cover further intermolecular interaction types. Phenol or another aromatic hydrogen bond donor could be such a candidate.⁵⁵ Wherever reliable experimental energy differences become available for the investigated systems, they should be added to the benchmark data set due to the sparseness of such quantities.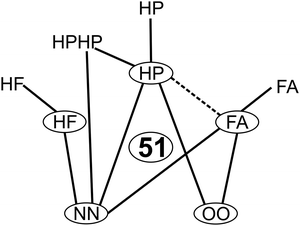

Fig. 5 Systems covered by the compactified benchmark database. Monomers are circled and complexes are represented by connecting lines. The dashed line marks a meaningful next extension.

The current data set should thus be seen as the first step into a continuous refinement procedure. We denote it ENCH-51 for Experimental Non-Covalent Harmonic database with currently 51 entries. As long as future extensions make sure that the number of entries is never repeated, this allows for a unique identification. Once these proposed experimental extensions gain momentum, an online repository of the experimental benchmark values is planned in the context of a local research training group on benchmarking. It should be open to external suggestions for systems and experimental data corrections and it could be extended to performance compilations of quantum-chemical methods contributed by interested theoretical groups based on the cartesian coordinates of starting structures provided in the ESI.†

4 Conclusions and outlook

We have presented the initial step for an extensive data base series ENCH which enables the testing of quantum chemical methods with experimental data. It establishes the easily accessible equilibrium structure and harmonic characterization level for not too floppy intermolecular complexes as a meeting point between theory and experiment. This allows for the inclusion of larger molecular systems, where the popular theory-internal benchmarking reaches its limits. The price to pay is that experimental data have to be back-corrected to this reference with realistic error bounds. Rules for such back-corrections are presented. They are compromise suggestions, trying to maximize discriminatory power without generating too many exceptions. The relative weight of data base entries grows quadratically with decreasing back-correction error bounds. Very small error bounds are unlikely in the field of non-covalent interactions between large molecules but if they occur such as in constituent diatomic molecules, these entries are removed from the weighted average to avoid imbalance. Very large error bounds typically disqualify a data base entry due to a lack of discriminatory power. Outliers must be carefully studied and may indicate a problem on the experimental side, a systematic deficiency of the included theoretical methods or an overly optimistic back-correction error estimate. Extension of the data base should minimize the number and similarity of chemical systems, at the same time maximizing the type of interactions and the number of experimental observables. ENCH is not meant to replace very systematic and careful comparisons between theory and experiment at high electronic structure and nuclear dynamics level for small systems. The latter are extremely useful and provide valuable input for the set of back-correction rules.

Most of the error bars used in this work to translate experimental quantities into easily accessible electronic structure data rely on a reasonably systematic cancellation between different vibrational contributions which can sometimes be as large as or even larger than the combined error bar. Therefore, outliers are unavoidable. The ENCH strategy is to compensate for such potential outliers by a large number of carefully chosen benchmark data.

We recommend ENCH for a simple test of the suitability of new or old quantum chemical models to describe noncovalent interactions.¹¹⁴ A side use could be to focus on a certain type of observable and to pragmatically choose the best suited method for this observable, irrespective of its performance for other observables. This is still more satisfactory than the popular scaling for or ignoring of anharmonic nuclear motion effects. However, a method which provides a balanced and reasonably good description of several observables is to be preferred over a method which performs very well for a specific observable only. The latter is most likely due to fortuitous error cancellation which should not be relied upon, although it can be useful as a spectroscopic assignment aid.

ENCH relies on experimentalists providing more reference data for its molecular entries^14,40,107 and on computational chemists adding quantum chemical models to its performance tables.^{6–8,12,60,92} In particular, an investigation of the current 51 data entries at the highest consistently affordable wave function theory level would be instructive to test the degree of realism of the back-correction rules in a more rigorous way.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We thank Z. Kisiel for valuable discussions and the Fonds der Chemischen Industrie for a generous scholarship for S. O. This work was supported by Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) – 389479699/GRK2455.

Notes and references

1. T. Takatani, E. G. Hohenstein, M. Malagoli, M. S. Marshall and C. D. Sherrill, J. Chem. Phys., 2010, 132, 144104.
2. L. Goerigk and S. Grimme, J. Chem. Theory Comput., 2010, 6, 107–126.
3. L. Goerigk and S. Grimme, J. Chem. Theory Comput., 2011, 7, 291–309.
4. L. Goerigk and S. Grimme, Phys. Chem. Chem. Phys., 2011, 13, 6670–6688.
5. J. Řezáč, K. E. Riley and P. Hobza, J. Chem. Theory Comput., 2012, 8, 4285–4292.
6. L. A. Burns, M. S. Marshall and C. D. Sherrill, J. Chem. Theory Comput., 2014, 10, 49–57.
7. J. C. Howard, J. D. Enyard and G. S. Tschumper, J. Chem. Phys., 2015, 143, 214103.
8. J. G. Brandenburg, J. E. Bates, J. Sun and J. P. Perdew, Phys. Rev. B, 2016, 94, 115144.
9. D. E. Taylor, J. G. Ángyán, G. Galli, C. Zhang, F. Gygi, K. Hirao, J. W. Song, K. Rahul, O. A. von Lilienfeld, R. Podeszwa, I. W. Bulik, T. M. Henderson, G. E. Scuseria, J. Toulouse, R. Peverati, D. G. Truhlar and K. Szalewicz, J. Chem. Phys., 2016, 145, 124105.
10. J. Řezáč and P. Hobza, Chem. Rev., 2016, 116, 5038–5071.
11. L. Goerigk, A. Hansen, C. Bauer, S. Ehrlich, A. Najibi and S. Grimme, Phys. Chem. Chem. Phys., 2017, 19, 32184–32215.
12. N. Mardirossian and M. Head-Gordon, Mol. Phys., 2017, 115, 2315–2372.
13. N. O. C. Winter, N. K. Graf, S. Leutwyler and C. Hättig, Phys. Chem. Chem. Phys., 2013, 15, 6623–6630.
14. R. Knochenmuss, R. K. Sinha and S. Leutwyler, J. Chem. Phys., 2019, 150, 234303.
15. G. Guelachvili, Opt. Commun., 1976, 19, 150–154.
16. R. M. Talley, H. M. Kaylor and A. H. Nielsen, Phys. Rev., 1950, 77, 529–534.
17. R. S. Ram, Z. Morbi, B. Guo, K.-Q. Zhang, P. F. Bernath, J. van der Auwera, J. W. C. Johns and S. P. Davis, Astrophys. J., Suppl. Ser., 1996, 103, 247.
18. G. Cazzoli and C. Puzzarini, J. Mol. Spectrosc., 2005, 231, 124–130.
19. P. D. Soper, A. C. Legon, W. G. Read and W. H. Flygare, J. Chem. Phys., 1982, 76, 292–300.
20. W. J. Lafferty, R. D. Suenram and F. J. Lovas, J. Mol. Spectrosc., 1987, 123, 434–452.
21. T. R. Dyke, B. J. Howard and W. Klemperer, J. Chem. Phys., 1972, 56, 2442–2454.
22. C. M. Lovejoy and D. J. Nesbitt, J. Chem. Phys., 1987, 86, 3151–3165.
23. M. A. Suhm, J. T. Farrell, A. McIlroy and D. J. Nesbitt, J. Chem. Phys., 1992, 97, 5341–5354.
24. M. Hippler, L. Oeltjen and M. Quack, J. Phys. Chem. A, 2007, 111, 12659–12668.
25. J. T. Farrell, M. A. Suhm and D. J. Nesbitt, J. Chem. Phys., 1996, 104, 9313–9331.
26. R. J. Bemish, E. J. Bohac, M. Wu and R. E. Miller, J. Chem. Phys., 1994, 101, 9457–9468.
27. E. J. Bohac, M. D. Marshall and R. E. Miller, J. Chem. Phys., 1992, 96, 6681–6695.
28. W. Klopper, M. Quack and M. A. Suhm, J. Chem. Phys., 1998, 108, 10096–10115.
29. D. H. Zhang, Q. Wu, J. Z. H. Zhang, M. von Dirke and Z. Bačić, J. Chem. Phys., 1995, 102, 2315–2325.
30. S. Oswald, E. Meyer and M. A. Suhm, J. Phys. Chem. A, 2018, 122, 2933–2946.
31. M. Freytes, D. Hurtmans, S. Kassi, J. Liévin, J. van der Auwera, A. Campargue and M. Herman, Chem. Phys., 2002, 283, 47–61.
32. H. Morita and S. Nagakura, J. Mol. Spectrosc., 1972, 41, 54–68.
33. R. G. Lerner, B. P. Dailey and J. P. Friend, J. Chem. Phys., 1957, 26, 680–683.
34. Y. Zhang, W. Li, W. Luo, Y. Zhu and C. Duan, J. Chem. Phys., 2017, 146, 244306.
35. K. G. Goroya, Y. Zhu, P. Sun and C. Duan, J. Chem. Phys., 2014, 140, 164311.
36. F. Kollipost, R. Wugt Larsen, A. V. Domanskaya, M. Nörenberg and M. A. Suhm, J. Chem. Phys., 2012, 136, 151101.
37. J. van der Auwera, J. Mol. Spectrosc., 1992, 155, 136–142.
38. K. R. Lange, N. P. Wells, K. S. Plegge and J. A. Phillips, J. Phys. Chem. A, 2001, 105, 3481–3486.
39. B. P. van Eijck, J. van Opheusden, M. van Schaik and E. van Zoeren, J. Mol. Spectrosc., 1981, 86, 465–479.
40. M. Goubet, P. Soulard, O. Pirali, P. Asselin, F. Réal, S. Gruet, T. R. Huet, P. Roy and R. Georges, Phys. Chem. Chem. Phys., 2015, 17, 7477–7488.
41. T. Scharge, C. Cézard, P. Zielke, A. Schütz, C. Emmeluth and M. A. Suhm, Phys. Chem. Chem. Phys., 2007, 9, 4472–4490.
42. L.-H. Xu, G. T. Fraser, F. J. Lovas, R. D. Suenram, C. W. Gillies, H. E. Warner and J. Z. Gillies, J. Chem. Phys., 1995, 103, 9541–9548.
43. J. Thomas and Y. Xu, J. Phys. Chem. Lett., 2014, 5, 1850–1855.
44. M. A. Suhm and F. Kollipost, Phys. Chem. Chem. Phys., 2013, 15, 10702–10721.
45. A. Shahi and E. Arunan, J. Phys. Chem. A, 2015, 119, 5650–5657.
46. S. Oswald, N. A. Seifert, F. Bohle, M. Gawrilow, S. Grimme, W. Jäger, Y. Xu and M. A. Suhm, Angew. Chem., Int. Ed., 2019, 58, 5080–5084.
47. S. Oswald and M. A. Suhm, Angew. Chem., Int. Ed., 2017, 56, 12672–12676.
48. J. Bendtsen and F. Rasmussen, J. Raman Spectrosc., 2000, 31, 433–438.
49. R. Z. Martínez and D. Bermejo, J. Raman Spectrosc., 2013, 44, 727–730.
50. M. L. Orlov, J. F. Ogilvie and J. W. Nibler, J. Mol. Spectrosc., 1997, 185, 128–141.
51. A. Lofthus and P. H. Krupenie, J. Phys. Chem. Ref. Data, 1977, 6, 113–307.
52. G. Rouillé, G. Millot, R. Saint-Loup and H. Berger, J. Mol. Spectrosc., 1992, 154, 372–382.
53. K. K. Irikura, J. Phys. Chem. Ref. Data, 2007, 36, 389–397.
54. S. Oswald, PhD thesis, Georg-August-University, Göttingen, 2019.
55. R. Knochenmuss, R. K. Sinha and S. Leutwyler, J. Chem. Phys., 2018, 148, 134302.
56. Q. Ma and H.-J. Werner, J. Chem. Theory Comput., 2019, 15, 1044–1052.
57. J. C. Howard, J. L. Gray, A. J. Hardwick, L. T. Nguyen and G. S. Tschumper, J. Chem. Theory Comput., 2014, 10, 5426–5435.
58. O. L. Polyansky, R. I. Ovsyannikov, A. A. Kyuberis, L. Lodi, J. Tennyson and N. F. Zobov, J. Phys. Chem. A, 2013, 117, 9633–9643.
59. A. Shee, S. Knecht and T. Saue, Phys. Chem. Chem. Phys., 2015, 17, 10978–10986.
60. D. P. Tew, W. Klopper, M. Heckert and J. Gauss, J. Phys. Chem. A, 2007, 111, 11242–11248.
61. J. Řezáč and P. Hobza, J. Chem. Theory Comput., 2014, 10, 3066–3073.
62. V. Barone, M. Biczysko and J. Bloino, Phys. Chem. Chem. Phys., 2014, 16, 1759–1787.
63. A. G. Császár, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 273–289.
64. C. Fábri and A. G. Császár, Phys. Chem. Chem. Phys., 2018, 20, 16913–16917.
65. L. Evangelisti, G. Feng, Q. Gou, J.-U. Grabow and W. Caminati, J. Phys. Chem. A, 2014, 118, 579–582.
66. T. Forsting, H. C. Gottschalk, B. Hartwig, M. Mons and M. A. Suhm, Phys. Chem. Chem. Phys., 2017, 19, 10727–10737.
67. C. L. Lugez, F. J. Lovas, J. T. Hougen and N. Ohashi, J. Mol. Spectrosc., 1999, 194, 95–112.
68. A. A. Fokin, T. S. Zhuk, S. Blomeyer, C. Pérez, L. V. Chernish, A. E. Pashenko, J. Antony, Y. V. Vishnevskiy, R. J. F. Berger, S. Grimme, C. Logemann, M. Schnell, N. W. Mitzel and P. R. Schreiner, J. Am. Chem. Soc., 2017, 139, 16696–16707.
69. D. Bernhard, F. Dietrich, M. Fatima, C. Pérez, H. C. Gottschalk, A. Wuttke, R. A. Mata, M. A. Suhm, M. Schnell and M. Gerhards, Beilstein J. Org. Chem., 2018, 14, 1642–1654.
70. R. A. Mata and M. A. Suhm, Angew. Chem., Int. Ed., 2017, 56, 11011–11018.
71. W. H. Hocking, Z. Naturforsch., A: Phys. Sci., 1976, 31, 1113–1121.
72. O. I. Baskakov, V.-M. Horneman, J. Lohilahti and S. Alanko, J. Mol. Struct., 2006, 795, 49–53.
73. J. Demaison, M. Herman and J. Liévin, J. Chem. Phys., 2007, 126, 164305.
74. K. A. E. Meyer and M. A. Suhm, Chem. Sci., 2019, 10, 6285–6294.
75. M. Pettersson, J. Lundell, L. Khriachtchev and M. Räsänen, J. Am. Chem. Soc., 1997, 119, 11715–11716.
76. S. Lopes, A. V. Domanskaya, R. Fausto, M. Räsänen and L. Khriachtchev, J. Chem. Phys., 2010, 133, 144507.
77. J. Moellmann and S. Grimme, Phys. Chem. Chem. Phys., 2010, 12, 8500–8504.
78. A. Gavezzotti, New J. Chem., 2016, 40, 6848–6853.
79. E. L. Sibert, J. Chem. Phys., 2019, 150, 090901.
80. S. Wang, ACS Omega, 2019, 4, 9271–9283.
81. M. Thomas, M. Brehm, R. Fligg, P. Vöhringer and B. Kirchner, Phys. Chem. Chem. Phys., 2013, 15, 6608–6622.
82. J. P. Beck, A. Cimas, J. M. Lisy and M.-P. Gaigeot, Spectrochim. Acta, Part A, 2014, 119, 12–17.
83. A. Petrone, D. B. Lingerfelt, D. B. Williams-Young and X. Li, J. Phys. Chem. Lett., 2016, 7, 4501–4508.
84. T. Carrington, J. Chem. Phys., 2017, 146, 120902.
85. M. Sibaev and D. L. Crittenden, Comput. Phys. Commun., 2016, 203, 290–297.
86. T. Forsting, J. Zischang, M. A. Suhm, M. Eckhoff, B. Schröder and R. A. Mata, Phys. Chem. Chem. Phys., 2019, 21, 5989–5998.
87. C. Qu and J. M. Bowman, Phys. Chem. Chem. Phys., 2019, 21, 3397–3413.
88. P. B. Changala and J. H. Baraban, J. Chem. Phys., 2016, 145, 174106.
89. Z. Kisiel, J. Mol. Spectrosc., 2003, 218, 58–67.
90. C. Puzzarini, M. Heckert and J. Gauss, J. Chem. Phys., 2008, 128, 194108.
91. P. Kraus and I. Frank, J. Phys. Chem. A, 2018, 122, 4894–4901.
92. S. Grimme and M. Steinmetz, Phys. Chem. Chem. Phys., 2013, 15, 16031–16042.
93. T. Risthaus, M. Steinmetz and S. Grimme, J. Comput. Chem., 2014, 35, 1509–1516.
94. M. Heger, M. A. Suhm and R. A. Mata, J. Chem. Phys., 2014, 141, 101105.
95. A. Poblotzki, H. C. Gottschalk and M. A. Suhm, J. Phys. Chem. Lett., 2017, 8, 5656–5665.
96. G. Czakó, E. Mátyus and A. G. Császár, J. Phys. Chem. A, 2009, 113, 11665–11678.
97. F. Pawłowski, P. Jørgensen, J. Olsen, F. Hegelund, T. Helgaker, J. Gauss, K. L. Bak and J. F. Stanton, J. Chem. Phys., 2002, 116, 6482–6496.
98. F. F. Willaert, B. A. McElmurry, R. R. Lucchese and J. W. Bevan, Chem. Phys. Lett., 2008, 460, 525–530.
99. M. Heger, J. Andersen, M. A. Suhm and R. Wugt Larsen, Phys. Chem. Chem. Phys., 2016, 18, 3739–3745.
100. M. Heger, R. A. Mata and M. A. Suhm, Chem. Sci., 2015, 6, 3738–3745.
101. J. A. Frey, C. Holzer, W. Klopper and S. Leutwyler, Chem. Rev., 2016, 116, 5614–5641.
102. E. Miliordos and S. S. Xantheas, J. Chem. Phys., 2015, 142, 094311.
103. R. Kalescky, E. Kraka and D. Cremer, J. Chem. Phys., 2014, 140, 084315.
104. C. Stein, R. Oswald, P. Botschwina and K. A. Peterson, J. Phys. Chem. A, 2015, 119, 5158–5164.
105. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104.
106. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09 Revision E.01, Gaussian Inc., Wallingford CT, 2009.
107. U. Hohm, J. Mol. Struct., 2013, 1054–1055, 282–292.
108. A. P. Charmet, P. Stoppa, N. Tasinato, S. Giorgianni, V. Barone, M. Biczysko, J. Bloino, C. Cappelli, I. Carnimeo and C. Puzzarini, J. Chem. Phys., 2013, 139, 164302.
109. H. C. Gottschalk, J. Altnöder, M. Heger and M. A. Suhm, Angew. Chem., Int. Ed., 2016, 55, 1921–1924.
110. G. Karir, N. O. B. Lüttschwager and M. A. Suhm, Phys. Chem. Chem. Phys., 2019, 21, 7831–7840.
111. D. E. Woon, T. H. Dunning and K. A. Peterson, J. Chem. Phys., 1996, 104, 5883–5891.
112. J. Huang, D. Yang, Y. Zhou and D. Xie, J. Chem. Phys., 2019, 150, 154302.
113. M.-L. Dubernet, D. Flower and J. M. Hutson, J. Chem. Phys., 1991, 94, 7602–7618.
114. M. Korth and W. Thiel, J. Chem. Theory Comput., 2011, 7, 2929–2936.

---

Footnote

† Electronic supplementary information (ESI) available: Keywords for calculations, spreadsheets connecting the experimental data with benchmark parameters and cartesian coordinates of the benchmark structures. See DOI: 10.1039/c9cp03651b

---