Brownian dynamics assessment of enhanced diffusion exhibited by ‘fluctuating-dumbbell enzymes’

Abstract

Recent experiments have reported that diffusion of enzymes can be enhanced in the presence of their substrates. Using a fluctuating dumbbell model of enzymes, it has been argued that such an enhancement can be rationalized by the reduction of the enzyme size and by the suppression of the hydrodynamically coupled conformational fluctuations, induced by binding a substrate or an inhibitor to the enzyme [Nano Lett. 2017, 17, 4415]. Herein, we critically examine these expectations via extensive Brownian dynamics simulations of a similar model. The numerical results show that neither of the two mechanisms can cause an enhancement comparable to that reported experimentally, unless very large, physically counter-intuitive, enzyme deformations are invoked.

---

Enzymes play a key role in living systems and have numerous biotechnological applications. While often the apparent rates of enzyme-catalysed reactions depend on the diffusion of enzymes and their substrates,^1,2 it has been reported recently that, surprisingly, the diffusion of enzymes could also be enhanced by the chemical reactions they catalyze.^3–9 For instance, a fluorescence correlation spectroscopy (FCS) study reported that the diffusion of urease is enhanced by about 30% in the presence of urea (the substrate of urease).³ Similar catalysis-induced enhancements of the diffusion constants have been mentioned for catalase,^4,5 DNA polymerase,⁶ alkaline phosphatase⁵ and aldolase.⁷ Interestingly, for aldolase the diffusion enhancement was observed also in the presence of pyrophosphate, which is a competitive inhibitor of aldolase;⁷ this indicates, as pointed out in ref. 7, that a chemical reaction is not necessary for this phenomenon to occur.

Various mechanisms have been suggested to rationalize the enhanced enzyme diffusion.^{3,5,7,10–12} For instance, in ref. 3 an electrophoretic mechanism was invoked, owing to the generation of ionic species in the hydrolysis of urea, while in ref. 5 it was proposed that the heat released during reaction could create an asymmetric pressure wave ‘propelling’ the enzyme. A lucid analysis of four possible mechanisms (self-thermophoresis, boost in kinetic energy or pressure waves, stochastic swimming, and collective heating) has been carried out by Golestanian,¹⁰ who concluded that only collective heating and stochastic swimming could lead to changes in the diffusion constant comparable to the reported ∼30% values.

Observing that the enhanced diffusion could also occur in the presence of competing inhibitors, Illien et al. have suggested that this phenomenon may be understood in terms of changes in the internal degrees of freedom of enzymes induced by reversible binding of substrates or inhibitors.⁷ They considered a simple fluctuating-dumbbell model of enzymes, in which the binding step was represented as reduction in the average length of the dumbbell as well as stiffening of the ‘spring’ connecting the subunits. Via approximate analytical calculations, it was inferred that “the reduction of enzyme's hydrodynamic radius and suppression of internal modes of fluctuations of enzymes can yield significant diffusion enhancement.”⁷

Such a flexible-dumbbell enzyme is a very compelling model, owing to its conceptual simplicity and to the possibility for a straightforward implementation in numerical simulations. The latter can provide a benchmark for validating the approximate analytical estimates,⁷ and it can serve as a platform for studies of collective behaviour. Herein, we perform extensive Brownian dynamics (BD) simulations of an enzyme model compatible with the analysis in ref. 7 and 12. The results of these simulations provide direct numerical estimates of the various contributions to diffusion enhancement, arising from changes in the enzyme's shape and from suppression of internal fluctuations, and thereby allow a critical assessment of the proposed model against the available experimental results.

We first succinctly recall the details of the model enzyme and of the corresponding contributions to the diffusion constant from ref. 7. In an idealized coarse description, an enzyme can be found in one of the following three states: open (o), closed (c), and closed with a substrate (or inhibitor) bound to its active site (cs). The closed state accounts for possible shape/size changes of an enzyme;¹³ in general, an enzyme can be in the closed state with or without a substrate. Additionally, as pointed out in ref. 7, binding a substrate (or inhibitor) may hinder internal (conformational) fluctuations of the enzyme. Both effects may contribute to deviations of the diffusion coefficient from its value in the absence of substrates.

Assuming that the time taken by the o ⇌ c and o + s ⇌ cs transitions is negligible, as compared to typical ‘life times’ of these states, one can present the (long-time) diffusion coefficient D in the form

D = D_op_o + D_cp_c + D_csp_cs, (1)

where p_α is the probability that the enzyme is in the state α = {o,c,cs} and D_α is the corresponding diffusion coefficient. Further assuming that the shapes of an enzyme in the states c and cs are similar (however, in general they may differ, cf.Fig. 1), one can write D_cs = D_c + ΔD^fluct_cs to identify ΔD^fluct_cs as the contribution to the diffusion coefficient solely due to the reduction of internal (conformational) fluctuations caused by binding a substrate.

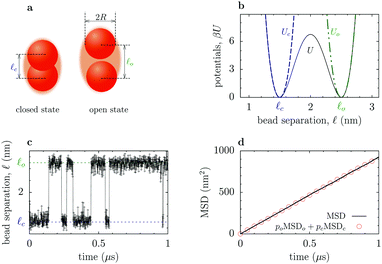
Fig. 1 Effect of stiffness of the interaction potential on the diffusion of flexible dumbbell enzymes. (a) Flexible dumbbell enzyme consisting of two spherical beads (subunits) of radii R₁ and R₂. The enzyme is depicted by the orange area and the beads by red spheres. The spring depicts schematically the interaction potential U([small script l]) between the beads. (b) Interaction potential, eqn (5), between the beads. The closed states with (cs) and without (c) a substrate correspond to the spring constants κ_cs and κ_c, respectively; two spring constants for the c state are considered. The grey area denotes the region inaccessible to the beads due to the hard core repulsion (for the results without hard core repulsion and smaller separations, see Fig. S1 and S2 in the ESI,† respectively). (c) Brownian dynamics results for the separation [small script l]. The fluctuations and the average separations between the beads are both significantly enlarged when the spring constant is reduced. (d) Average bead–bead separations as a function of the spring constant κ. (e) Mean square displacement of the center of mass of the dumbbell enzyme in the cs (κ_cs) and c (κ_c) states. (f) Diffusion coefficient from Brownian dynamics simulations (symbols) and from the approximate analytical estimates based on ref. 12 (Section S3 in the ESI†). The squares and the circles in (d) and (f) correspond to the spring constants from (b), (c) and (e). The results in panels (b–f) correspond to the following values: the radii R₁ = 1.5 nm and R₂ = 1 nm, and the parameters of the interaction potential [small script l]_o = 6 nm and [small script l]_c = 5 nm. The results shown in (d), (e), and (f) are averages over 4000 independent runs.

The relative change in the diffusion coefficient, δD(ρ_S) = [D(ρ_S) − [scr D, script letter D]]/[scr D, script letter D], where ρ_S is the substrate concentration and [scr D, script letter D] = D(ρ_S = 0), can then be presented as a sum of contributions coming from the change in size and from conformational fluctuations (Section S1 in the ESI†):

δD(ρ_S) = g(ρ_S)[δD^size + δD^fluct], (2)

wherethe substrate-dependent function,has a Michaelis–Menten form, with the Michaelis–Menten constant of the enzymatic reaction, K_M, rescaled by the probability p⁽⁰⁾ of an enzyme to be in the open state in the absence of substrates (Section S1 in the ESI†). Note that g ≤ 1 for ρ_S ≤ ∞, hence δD^size and δD^fluct describe the maximum enhancements.

The arguments leading to eqn (2) are quite general and should hold for a variety of enzyme models, including the flexible dumbbell model with hydrodynamic interactions between its subunits.⁷ We have analyzed via numerical simulations such enzyme models (cf.Fig. 1 and 2), defined by an interaction between spherical subunits given by a single or double-well potential; the former was used to study the effects due to suppression of fluctuations, while the latter was employed to test the assumption of additivity, eqn (1). The Brownian dynamics simulations have been carried out for a single dumbbell enzyme by using a customized version of the package BD_BOX¹⁴ (Section S2A in the ESI†) and the hydrodynamic interactions were approximated via the generalized Rotne–Prager–Yamakawa tensor.^15,16 To calculate the diffusion coefficient, D, we computed the mean-square displacement (MSD) of the center of mass r(t) of the dumbbell, MSD(t) = 〈|r(t) − r(0)|²〉, and fitted it to MSD(t) = 6Dt.

Fig. 2 Two beads interacting via a double-well potential as a model for an enzyme fluctuating between ‘open’ and ‘closed’ states. (a) Fluctuating dumbbell model with different average separations between the subunits in the closed and open states. (b) Interaction potentials between the beads in a double-well model (U) and when the system is only in the closed (U_c) or open (U_o) state; note that there is no hard core repulsion between the beads. (c) Separation between the beads as a function of time from Brownian dynamics simulations. Only the system with interaction potential U([small script l]) is shown (see (b)). (d) Mean square displacement for the system with interaction potential U([small script l]), compared with the weighed sum of the MSDs for the open and closed states; p_α is the probability of an enzyme to be in state α. The interaction constant κ ≈ 6.8k_BT, the separations at the minima were [small script l]_c = 1.5 nm and [small script l]_o = 2.5 nm in the closed and open states, respectively, and the bead radii R = R₁ = R₂ = 1 nm.

The role played by suppression of fluctuations can be assessed by considering the dumbbell model depicted in Fig. 1a, with the following single-well interaction potential (the 4th order polynomial was chosen because of a straightforward extension to a two-state model, cf.eqn (6) and Fig. 2a and b):

where [small script l] is the center-to-center distance between the beads, [small script l]_c and [small script l]_o are two parameters (see below) and κ the “spring” constant defining the characteristic energy scale (we considered U_c with and without the hard-core repulsion between the beads, see Fig. 1, and Fig. S1, S2 in the ESI,† respectively). The closed states with and without a substrate can then be modeled by varying κ, while keeping [small script l]_c and [small script l]_o unchanged. In this way, the role played by suppression of fluctuations can be singled out.

Fig. 1c shows the time dependence of the separation between the enzyme subunits. It demonstrates a significant reduction in the amplitude of fluctuations, which is accompanied by a decrease in the average bead–bead separation (Fig. 1d), caused by increasing the spring constant from κ_c to κ_cs ≈ 4 × 10⁴κ_c (this models the binding of a substrate to the enzyme⁷). However, such a suppression of fluctuations and the size reduction lead to only small changes in the diffusion constant. Fig. 1e and f show that the diffusion is enhanced by at most about 5%, even though the spring constant was varied over four orders of magnitude (see also Fig. S1 and S2 in the ESI†). This behaviour is in good agreement with the theoretical estimates, obtained by adapting the calculations from ref. 12 (the blue line in Fig. 1f; Section S3 in the ESI†). Furthermore, when the stiffness of the potential becomes sufficiently large, such that the average bead–bead separation [small script l] ≈ [small script l]_at−min = 6 nm (Fig. 1d), which also reduces the probability of physically counter-intuitive large separations, the value of the diffusion coefficient becomes virtually independent of the further increases in stiffness (the gray star in Fig. 1f). To clearly isolate the effect of fluctuations, we also compared models with the same average bead–bead separation, but with significant differences in the amplitude of fluctuations; the results indicate less than 2% difference in the diffusion coefficients (see Fig. S3 in the ESI†). One can thus conclude that the suppression of internal fluctuations due to stiffening of the potential in the cs state is unlikely to enhance significantly the diffusion of such a flexible dumbbell enzyme.

We have also used the dumbbell model to test the assumption of additivity of diffusion constants (eqn (1)), and to estimate the role played by the size changes. We chose the following double-well interaction potential

where [small script l]_o and [small script l]_c < [small script l]_o correspond to the equilibrium separations in the ‘open’ and ‘closed’ states, respectively (Fig. 2a); here, the characteristic energy set by the spring constant, κ, corresponds to the height of the energy barrier separating the two states (Fig. 2b). Fig. 2b shows that U([small script l]) (solid line) interpolates between two single-well potentials U_c (eqn (5)) and U_o (eqn (S11) in the ESI†), which have minima at [small script l]_c and [small script l]_o, with the shapes at the minima coinciding with the shape of U.

We have performed BD simulations for each of the three potentials (for computational efficiency, we did not consider the hard-core repulsion between the beads). Fig. 2c shows that the system with the double-well potential has a dynamics that indeed exhibits long periods of fluctuations around one minimum with rapid jumps between the wells (i.e., between the open and closed states). From the simulations, we extracted the frequency of jumps f ≈ 15 μs⁻¹ (a jump was defined as crossing of the mid-point, ([small script l]_c + [small script l]_o)/2). The probabilities of the dumbbell to be in the open and close states were found to be p_o ≈ 72% and p_c = 1 − p_o(0) ≈ 28%, which agree well with the equilibrium probabilities obtained from the Boltzmann distribution (Section S2B in the ESI†). Fig. 2d shows the MSD for the system with the interaction potential U([small script l]), which is compared with the weighted sum p_cMSD_c + p_oMSD_o, in the spirit of eqn (1). The agreement is excellent, confirming that eqn (1) provides an accurate description (at long observation times t ≫ f⁻¹).

The model with the potential U([small script l]) can be interpreted as corresponding to a system in the absence of substrates. Then, from the slope of the MSD, we have estimated the diffusion coefficient [scr D, script letter D] = D(ρ_S = 0) ≈ 1.55 × 10⁻¹⁰ m² s⁻¹; similarly, we obtained the diffusion coefficient in the closed state to be D_c ≈ 1.72 × 10⁻¹⁰ m² s⁻¹. Eqn (3) then gives δD^size ≈ 11% for the maximum possible enhancement of the diffusion coefficient due to size change (for the dumbbell model with the parameters as in Fig. 2).

Although this value of δD^size is comparable to those reported experimentally, it is clear that our model involved significant changes in the shape of an enzyme (Fig. 2a). To get additional physical insight into the effect of conformational changes, we consider a toy model of an enzyme as a sphere of radius R in the closed state and as a prolate spheroid with the largest semi-axes γR in the open state (Fig. 3a). Then D_c = k_BT/(6πηR), where η is the viscosity, while in the open state^17,18

Using eqn (3) we have obtained the maximum possible enhancement due to the size changeFor small extensions (γ ≳ 1), the enhancement is linear in the size-changein agreement with Illien et al.¹² (The factor 1/3 in eqn (9) accounts for the deformation occurring solely along one direction; this factor is 2/3 for an oblate spheroid and unity if an enzyme deforms along all three directions.) Fig. 3b illustrates that small, experimentally relevant (see below) size reductions can lead to merely few percent enhancement in the diffusion coefficient;¹⁹ this is inconsistent with most experiments, which have reported about 30% (or even 80%) enhancements.^3–9

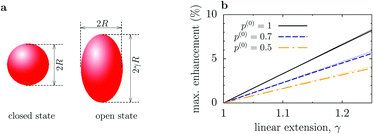Fig. 3 Enhancement of enzyme diffusion due to size change of enzymes. (a) Enzyme is a sphere of radius R in the closed state, while in the open state it is a prolate spheroid with the largest semi-axes γR (linear extension γ). (b) Maximum enhancement of the enzyme diffusion as a function of γ. p⁽⁰⁾ = p_o(ρ_S = 0) is the probability that the enzyme is in the open state in the absence of substrates. Thin dotted lines show the linear approximation given by eqn (9).

The maximal reduction of enzyme's hydrodynamic radius in the closed state, as reported so far,²⁰ is for F₁-ATPase and amounts to about 15%. In this case, the maximum increase in the diffusion coefficient could also be up to 15%, assuming that F₁-ATPase enlarges in all three directions and that it is in the open state most of the time (i.e., p⁽⁰⁾ ≈ 1). This seems to be in agreement with the FCS study of Börsch et al.²¹, who reported about 14% diffusion increase.¹⁹ For other enzymes, however, conformational changes are much less pronounced; for instance, for hexokinase it is about 3.6%.¹⁹ Employing the dmatrix program from the BD_BOX package,¹⁴ which is based on rigid-body hydrodynamic calculations of the diffusion matrix,^22,23 we have computed the diffusion coefficients of K. aerogenes urease using the open and closed state conformations from Protein Data Base (PBD) taken from the BRENDA database (1ejx and 1fwj, respectively¹³). The result is D_o ≈ 61.73 μm² s⁻¹ and D_c ≈ 61.1 μm² s⁻¹ for the urease in water at room temperature; such miniscule changes imply that the diffusion of enzymes should be practically insensitive to their catalytic activity.

In summary, Brownian dynamics simulations of a fluctuating dumbbell model of enzymes, similar to the one proposed by Illien et al.,^7,12 indicate that suppression of the hydrodynamically coupled conformational fluctuations is unlikely to produce a diffusion enhancement comparable to that reported experimentally (Fig. 1). In agreement with previous analyses,¹² an enhancement can be induced by the reduction of enzyme's size due to binding a substrate or competitive inhibitor; this enhancement is proportional to the change in the hydrodynamic radius (eqn (8) and (9), and Fig. 3). It is worth noting, however, that recent reports have pointed out that FCS studies, used to measure the enzyme diffusion coefficients, may be affected by spurious factors, such as fluorescence quenching by substrates,¹¹ catalysis-induced enzyme decomposition, or enzyme binding to a surface.¹⁹ Interestingly, very recent dynamic light scattering²⁴ and NMR²⁵ studies have indicated no enhancement of aldolase in the presence of its substrate, in contrast to the FCS studies. It appears that a thorough revisit of the experimental results, preferably by other, complementary, techniques is necessary. Thus, the questions as to whether enzyme diffusion can be enhanced by catalysis, and what is its physical mechanism, if so, still remain open.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

S. K. was supported by NCN grant No. 2017/25/B/ST3/02456. We acknowledge insightful discussions with R. Golestanian and J. A. Canalejo regarding the theoretical analysis in ref. 7 and 12. We thank an anonymous referee for suggesting to isolate the effect of fluctuations (Fig. S3 in the ESI†).

Notes and references

1. J. Schurr, Biophys. J., 1970, 10, 717–727.
2. I. Pastor, L. Pitulice, C. Balcells, E. Vilaseca, S. Madurga, A. Isvoran, M. Cascante and F. Mas, Biophys. Chem., 2014, 185, 8–13.
3. H. S. Muddana, S. Sengupta, T. E. Mallouk, A. Sen and P. J. Butler, J. Am. Chem. Soc., 2010, 132, 2110–2111.
4. S. Sengupta, K. K. Dey, H. S. Muddana, T. Tabouillot, M. E. Ibele, P. J. Butler and A. Sen, J. Am. Chem. Soc., 2013, 135, 1406–1414.
5. C. Riedel, R. Gabizon, C. A. M. Wilson, K. Hamadani, K. Tsekouras, S. Marqusee, S. Pressé and C. Bustamante, Nature, 2015, 517, 227–230.
6. S. Sengupta, M. M. Spiering, K. K. Dey, W. Duan, D. Patra, P. J. Butler, R. D. Astumian, S. J. Benkovic and A. Sen, ACS Nano, 2014, 8, 2410–2418.
7. P. Illien, X. Zhao, K. K. Dey, P. J. Butler, A. Sen and R. Golestanian, Nano Lett., 2017, 17, 44154420.
8. A.-Y. Jee, S. Dutta, Y.-K. Cho, T. Tlusty and S. Granick, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, 14–18.
9. X. Zhao, H. Palacci, V. Yadav, M. M. Spiering, M. K. Gilson, P. J. Butler, H. Hess, S. J. Benkovic and A. Sen, Nat. Chem., 2018, 10, 311–317.
10. R. Golestanian, Phys. Rev. Lett., 2015, 115, 108102.
11. X. Bai and P. G. Wolynes, J. Chem. Phys., 2015, 143, 165101.
12. P. Illien, T. Adeleke-Larodo and R. Golestanian, EPL, 2017, 119, 40002.
13. B. P. Roberts, B. R. Miller, A. E. Roitberg and K. M. Merz, J. Am. Chem. Soc., 2012, 134, 9934–9937.
14. M. Dlugosz, P. Zielinski and J. Trylska, J. Comput. Chem., 2011, 32, 2734–2744.
15. J. Rotne and S. Prager, J. Chem. Phys., 1969, 50, 4831–4838.
16. H. Yamakawa, J. Chem. Phys., 1970, 53, 436–444.
17. F. Perrin, J. Phys. Radium, 1934, 5, 497.
18. A. K. Wright and J. E. Baxter, Biophys. J., 1976, 16, 931.
19. J.-P. Günther, M. Börsch and P. Fischer, Acc. Chem. Res., 2018, 51, 1911–1920.
20. B. Böttcher, I. Bertsche, R. Reuter and P. Gräber, J. Mol. Biol., 2000, 296, 449–457.
21. M. Börsch, P. Turina, C. Eggeling, J. R. Fries, C. A. Seidel, A. Labahn and P. Gräber, FEBS Lett., 1998, 437, 251–254.
22. B. Carrasco and J. G. de la Torre, Biophys. J., 1999, 76, 3044–3057.
23. M. X. Fernandes and J. G. de la Torre, Biophys. J., 2002, 83, 3039–3048.
24. Y. Zhang, M. J. Armstrong, N. M. B. Kazeruni and H. Hess, Nano Lett., 2018, 18, 8025–8029.
25. J.-P. Günther, G. Majer and P. Fischer, J. Chem. Phys., 2019, 150, 124201.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c9cp02842k

---