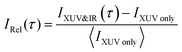Ultrafast nuclear dynamics of the acetylene cation C₂H₂⁺ and its impact on the infrared probe pulse induced C–H bond breaking efficiency

Abstract

The ultrafast nuclear dynamics of the acetylene cation C₂H₂⁺ following photoionization of the neutral molecule is investigated using an extreme-ultraviolet pump/infrared probe setup. The observed modulation of the C₂H⁺ fragment ion yield with pump–probe delay is related to structural changes induced by the extreme-ultraviolet pump pulse taking place on the femtosecond timescale. High-level simulations suggest that the trans-bending and C–C bond stretching motion of the C₂H₂⁺ cation govern the observed interaction with the infrared pulse. Depending on the molecular configuration at arrival of the infrared pulse, it either transfers population to higher-lying states or to the C₂H₂⁺ ground state, thereby enhancing or lowering the C₂H⁺ yield. Our ultrafast pump–probe scheme can thus be used to track excited state nuclear dynamics with a resolution of a few femtoseconds, leading the way to studying fast dynamics also in larger hydrocarbon molecules.

---

Introduction

Hydrocarbon molecules are the basic building blocks of organic matter. Thus, it is of fundamental importance to understand the mechanisms and pathways underlying chemical reactions of these molecules. The most basic reaction step is the formation and breaking of bonds between the individual atoms constituting a hydrocarbon. These processes are mediated by nuclear and electronic rearrangements on atomic length scales that may happen on an ultrafast timescale within ∼100 fs. In order to study these fundamental rearrangement mechanisms a correspondingly high time resolution is required.¹ To this end time-resolved pump–probe spectroscopy has proven to be an ideal tool.^2–6 In recent years, with the advent of high-harmonic generation technologies, especially the extreme-ultraviolet (XUV)-infrared (IR) pump–probe methods have yielded valuable insights into the fastest of these processes.^7–9 Most of these studies, combining advanced experimental and theoretical methods, investigated diatomic systems^10,11 and the excited state dynamics of larger, polyatomic systems remain to be fully understood.

The acetylene molecule C₂H₂ is a prototypical hydrocarbon system and the simplest molecule containing a carbon triple bond. Thus, it has been widely used to examine fundamental processes, such as charge migration, structural rearrangement, dissociation and isomerization on ultrafast timescales.^12–20 In a recent study, the nuclear dynamics following strong-field ionization of the acetylene molecule was investigated using the Coulomb explosion technique.¹⁸ The elaborated experimental setup and advanced calculations allowed the extraction of information about bond length oscillations on the ground state of the acetylene cation initiated by the excitation process and to connect them with the observed fragment yields. In the present work, the ultrafast molecular dynamics in acetylene following photoexcitation to an excited state is studied with few-femtosecond resolution in a pump–probe experiment using an attosecond XUV pump and a few-cycle IR probe pulse. In contrast to most recent studies performed on the acetylene cation, an IR beam of moderate intensity (∼10¹² W cm⁻²) was used. As elaborated by Cörlin et al.⁸ this prevents strong deformations of the potential energy surface (PES) and allows the investigation of the molecular dynamics within the linear regime of perturbation.

It is known that the variations of the yields of different fragmentation channels with pump–probe delay reflect the fast nuclear motion occurring on the few-tens-of-femtosecond timescale.^{3–5,18,19,21} This letter focuses on the nuclear motion after ionization leading to the modulation of the C₂H⁺ fragment yield probed by IR irradiation. Using electronic structure computations and dynamical simulations, we were able to identify the different reaction pathways leading to C–H dissociation and assess the impact of nuclear rearrangements on the different IR-induced mechanisms leading to either an enhancement or a quenching of the C₂H⁺ fragment yield. The investigations reveal that the C₂H⁺ fragment yield not only contains all the characteristic vibrational frequencies governing the excited state dynamics but also confirm that the delay-dependent yield is an indicator of the position of the wave packet on the PES at the respective instant of time.

Results

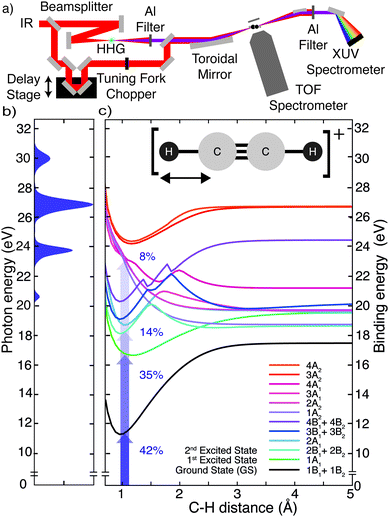
The experimental work was conducted with an XUV-pump/IR-probe setup²² (Fig. 1a), described in more detail in the ESI.† The pump pulse was obtained via high-harmonic generation (HHG) in xenon, yielding an XUV attosecond pulse train (APT) spectrally extending from 20 to 35 eV (Fig. 1b). From a cross-correlation trace obtained by ionizing argon, the XUV pump and IR probe pulse durations were estimated to be 7 and 13 fs, respectively. A mixture of gaseous acetylene and helium, introduced into the interaction region via a steel nozzle, was excited by the XUV pump pulse and subsequently probed at variable delays using an IR probe pulse (hν_IR ≈ 1.6 eV). The IR intensity could be adjusted in a range from 1 to 5 × 10¹² W cm⁻² using a motorized iris. The ion fragments resulting from the pump and probe interaction were detected with a time-of-flight (TOF) spectrometer. To improve the signal-to-noise ratio, the experiment was referenced shot-to-shot using a tuning fork chopper, which blocked every second IR probe pulse, enabling a direct subtraction of the XUV induced background.²³ From two consecutive shots the delay-dependent relative change of the fragment ion yield I_Rel(τ) was extracted according to:

Fig. 1 (a) Extreme-ultraviolet (XUV) pump and infrared (IR) probe setup, where the XUV results from high harmonic generation (HHG) in xenon. (b) Normalized XUV spectrum used to photoionize the acetylene molecules. (c) The 16 lowest electronic states of the acetylene cation C₂H₂⁺ as a function of the single C–H bond stretching coordinate. The probability to access the electronic states of the cation with the recorded XUV spectrum is given next to the arrows indicating the corresponding transitions from the ground state of the neutral molecule (set to 0 eV).

To interpret the delay-dependent relative change of the fragment ion yields, we first determined the electronic states of the acetylene cation that are accessed by the XUV pump pulse alone. The XUV photons were energetic enough to populate not only the ground state but also several excited states of the acetylene cation. A cut of its PES along the C–H bond distance was computed at the XMS-CASPT2²⁴ level. The lowest 16 electronic states from this calculation are shown in Fig. 1c (see ESI,† for full computational details). An estimate of the initial population of these states after XUV excitation was calculated based on the measured XUV spectrum and the absolute partial photoionization cross-sections from literature.²⁵ Due to the small photoionization cross sections of the higher lying states²⁶ most of the excited state population is found in the five lowest cationic states, as has been pointed out previously.¹³ As indicated in Fig. 1c, after photoionization by the XUV pump pulse, 42% of the initial electron population is found in the doubly degenerate cationic ground state. 35% and 14% of the initial population is excited to the first and doubly degenerate second excited state, respectively. 8% populate dissociative states, leaving 1% population in all other states. This initial state population can explain the stationary ion yield observed experimentally (Fig. 2a).

Fig. 2 (a) Measured normalized stationary ion yield recorded by the TOF spectrometer using the XUV beam only. Helium gas was added as a buffer gas to avoid cluster formation. (b) Relative change of the fragment ion yields as a function of pump–probe delay, recorded with delay steps of 2 fs within a 140 fs time window. The relative change of the yield of the molecular ion C₂H₂⁺ is multiplied by a factor of four to compensate for the difference in absolute yields between the C₂H₂⁺ and the C₂H⁺channels and to facilitate the observation of the anticorrelation. The IR probe intensity is 1.6 × 10¹² W cm⁻². (c) A Fourier analysis of the temporal evolution of the measured molecular and dehydrogenated fragment ion yields (f = A_C2H2⁺(τ) and f = A_C2H2⁺(τ)) and of the temporal evolution of the computed energy gap between the ground (D₀) and first excited (D₂) state (f = ΔE_D2–Do(τ)).

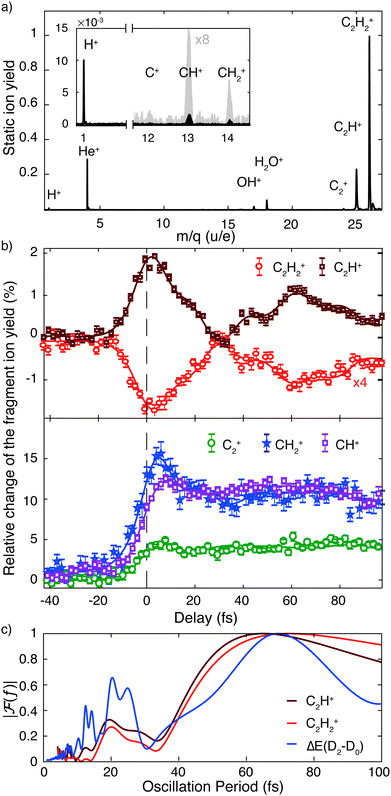
The addition of an IR probe pulse results in the delay-dependent changes of the fragment ion yields (Fig. 2b). They were extracted from multiple series of TOF spectra and subsequently fitted using an exponentially modified Gaussian (EMG) function, multiplied with a term describing two damped oscillations²⁷ (see ESI†). Our investigation focuses on the anti-correlated modulation in the yield of the molecular and dehydrogenated fragment ion (C₂H₂⁺ and C₂H⁺, respectively). Since the overall yield of the molecular ion C₂H₂⁺ is about four times as large as the C₂H⁺ fragment ion yield (Fig. 2a), the relative change of the former, given in percent of the total fragment yield, is multiplied by a factor of four to clearly show the anti-correlation. A Fourier analysis of the temporal variations of the relative change of the fragment ion yields reveals two oscillations with a period of 74 ± 2 fs and 22 ± 1 fs for the molecular ion yield and 72 ± 2 fs and 22 ± 1 fs for the dehydrogenated ion yield, respectively (Fig. 2c). The errors indicate the standard deviation of these oscillation periods extracted from three individual sets of six scans each. Calculations²⁸ indicate that the observed oscillation periods could be associated with a trans-bending (70.1 ± 0.7 fs) and a C–C bond stretching (23.0 ± 0.5 fs) motion in the ground state of the acetylene cation. The dependence of the observed features on the pump and probe pulse parameters was investigated and is discussed in more detail in the ESI.† By comparing measurements taken at different IR intensities (Fig. S2a, ESI†) and with different XUV spectra (Fig. S2b, ESI†), we could exclude any qualitative dependence of the observed dynamics on these pulse parameters. An increase in IR intensity resulted in a larger amplitude of the observed fragment yield oscillations, while leaving the temporal behavior unchanged (Fig. S2a, ESI†).

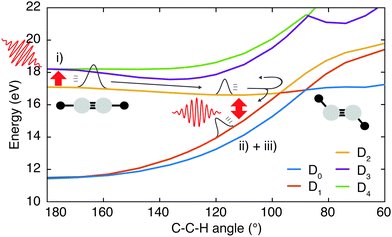
To shed light on the possible mechanisms involved in the modulation of the C₂H⁺ fragment yield, we performed static electronic structure calculations as well as a series of advanced dynamics simulations. Since the ground state is very tightly bound along the C–H bond stretching coordinate (Fig. 1c), our investigations focused on the dynamics of the first and second excited state of the cation. We followed the non-adiabatic excited state dynamics of the system upon pump laser excitation to the first excited state using Tully's fewest switches trajectory surface hopping (FSSH) simulations at the SA(5)-CAS(9,8)-SCF/6-31G** level (see ESI† for full details). During these dynamics simulations no symmetries are retained. In the following, we thus label the states according to their instantaneous energy order. We will refer to the ith energy ordered state as D_i. Therefore, at the Franck–Condon point, D₀ and D₁ correspond to the degenerate ground state, and the first excited state 1A₁ is D₂.

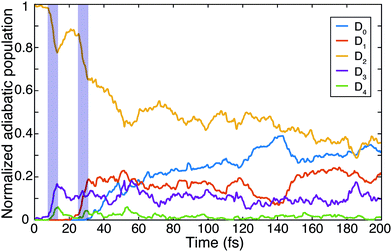
The non-adiabatic dynamics simulations (Fig. 3) show a transfer of population from the initially populated state D₂ to D₃ around 10 fs after photoexcitation (first blue shaded area), which corresponds to roughly half the C–C bond stretching period as discussed above. Indeed, the cut of the static PES along the C–C bond stretching coordinate shows a conical intersection (CI) between these two states (Fig. S4a, ESI†). Further, in agreement with previous studies,^15,16,29,30 the wave packet on D₂ was observed to reach another CI in about 30 fs (second blue shaded area). Here the D₂ state crosses the D₁ state and relaxation of the wave packet can occur. This CI is reached along the trans-bending coordinate of the molecule (Fig. S4b, ESI†). The energy difference between D₂ and its neighboring states is strongly modulated by these two characteristic molecular vibrations. A Fourier transformation of the temporal evolution of the energy difference between D₂ and D₀, for example, is shown in Fig. 2c. It reveals a qualitative agreement of the energy gap's modulations and the observed oscillations of the fragment ion yields. The observed oscillation periods correspond to above-mentioned molecular vibrations. Additionally, it was found that in 5% of the simulated trajectories direct dissociation, leading to the formation of the C₂H⁺ fragment, occurs spontaneously within the first 200 fs of the propagation.

Fig. 3 Time-dependent population of the lowest five adiabatic electronic states during the non-adiabatic dynamics simulations up to 200 fs. The shaded blue areas indicate t ≈ 10 fs and t ≈ 30 fs, where efficient transfer of population from the D₂ state to the D₃ and D₁ states occurs, respectively.

Discussion

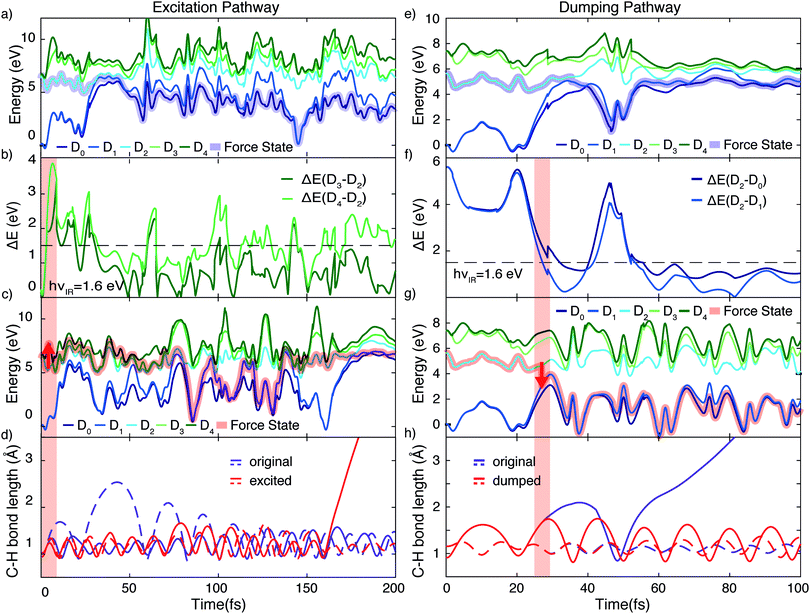
Using the gained insights about the dynamics of the system upon XUV excitation, we investigated how a delayed IR probe pulse can affect the molecular dynamics and thus the observed C₂H⁺ fragment yield. First of all, the spontaneous dissociation described above can be enhanced by an IR pulse irrespective of the instantaneous molecular arrangement due to the extra energy deposited in the system. We thus expect an enhancement of the C₂H⁺ yield for all delays of the probe pulse. The amplitude of this IR induced increase of spontaneous dissociation follows on the amount of population on the D₂ state, which decays with pump–probe delay (Fig. 3). Additionally, during the pump–probe overlap an enhanced ionization yield or a different initial population distribution can result from the combined presence of both beams. Further, we consider three mechanisms, shown in Fig. 4, whose probabilities depend on the instantaneous structural arrangement of the molecule: (i) photoexcitation of population from D₂ to higher-lying states, (ii) dumping of population from D₂ to the ground states and (iii) re-excitation of relaxed population from the ground states to the D₂ state.

Fig. 4 Sketch outlining three mechanisms considered to possibly cause the observed IR-induced delay-dependent modulation of the C₂H⁺ yield and their dependence on the instantaneous molecular configuration at the moment of the probe pulse arrival: (i) photoexcitation, (ii) dumping of and (iii) re-excitation of the wave packet.

In the following sections these pathways are discussed in more detail and their interplay is unraveled. Even though enhanced dissociation from a bound state due to a strong external field has also been observed,^31,32 this mechanism can be neglected for the present experimental study as the IR probe beam intensities are not large enough.^33,34 We first focus on the photoexcitation from D₂ to higher-lying states. We chose a typical, non-dissociative trajectory from the FSSH simulations to show the possibility of such a mechanism. In the absence of an IR probe pulse the wave packet evolves along the trajectory indicated as force state in the energy profile (Fig. 5a) without showing C–H bond dissociation within 200 fs (Fig. 5d). Immediately following the XUV photoionization, the energy gap to the D₄ state is small (Fig. 5b). The promotion of the trajectory upon reaching the resonance condition for one-photon excitation by the IR pulse leads to the evolution on a new trajectory (Fig. 5c), facilitating C–H bond breaking (Fig. 5d). The interaction with the IR probe pulse close to zero delay can thus enhance the dissociation probability through these resonant transitions to higher-lying states in agreement with the peak in the C₂H⁺ yield observed experimentally. The same mechanism can also account for the peak around 70 fs when the molecular trans-bending oscillations has completed a full period and the molecule has returned to a linear configuration. Since part of the excited state population from the D₂ state relaxes to the lower states, see Fig. 3, this peak is expected to be smaller in amplitude.

Fig. 5 Demonstration of the proposed mechanisms modulating the C–H dissociation efficiency via excitation (a)–(d) or dumping (e)–(h) of a wave packet. (a) Energy profile of a non-dissociative trajectory. (b) Corresponding energy gap from the D₂ to the higher-lying D₃ and D₄ states. The IR photon energy (hν_IR ≈ 1.6 eV) is indicated as the black dashed line. (c) Energy profile of the trajectory from (a) when being excited by the IR pulse at 3.2 fs from D₂ to D₄, designated by the red arrow. (d) Evolution of C–H bond lengths for both C–H bonds. Promotion by the IR pulse causes C–H dissociation. (e) Energy profile of a spontaneously dissociating trajectory. (f) Corresponding energy gaps between D₂ and the ground states (D₁ and D₀), which become resonant with the IR photon energy in the vicinity of the conical intersection. (g) Energy profile of the same trajectory shown in (e), but encountering a dumping from the D₂ to the D₁ state at 27 fs, designated by the red arrow. (h) Evolution of the two C–H bond lengths of the C₂H₂⁺ cation for the two trajectories, exhibiting quenching of C–H bond dissociation in the dumped one.

During the first 30 fs of the molecular dynamics, a stretching of the C–C bond as well as a strong bending of the molecule occur (Fig. S5 in the ESI†). This combined nuclear motion results in an increase of the energy gap between the D₂ and the higher-lying states and a decrease of the energy gap to the D₁ state, eventually leading the system to the mentioned CI. On one hand this inhibits excitation to higher-lying states. On the other hand it has been shown that in the vicinity of a CI a probe-pulse-induced resonant coupling between two states can result in an efficient wave packet dumping to the lower state.³⁵ To demonstrate this mechanism a spontaneously dissociating trajectory from the FSSH simulations is chosen (Fig. 5e). Around 27 fs, when the wave packet approaches the CI, the energy gap between the D₂ and the D₁ state becomes resonant with the IR photon energy (Fig. 5f). Thus, the arrival of the probe pulse at this instant of time can cause stimulated emission and the dumping of the wave packet to the D₁ state (Fig. 5g). Since 1.6 eV of electronic energy are freed in form of radiation during this transition, C–H bond dissociation is prevented (Fig. 5h). This is consistent with the experimentally observed quenching of the C₂H⁺ yield around 30 fs (Fig. 2b). A Fourier analysis of the relevant energy gap between the D₂ and the D₀ states (Fig. 2c) reveals oscillations that coincide with the temporal oscillations in the experimentally observed fragment yields. In the same manner, also the third proposed IR-induced mechanism can be observed in our simulations. Here, the wave packet first relaxes non-radiatively from the D₂ to the ground state and is re-excited by the IR probe pulse at later times to a dissociative channel (see ESI,† Fig. S6 for details). This mechanism could further contribute to the measured enhancement of C₂H⁺ around 60 fs.

Conclusions

In conclusion, we have conducted an extensive study of the nuclear dynamics in the acetylene cation C₂H₂⁺ initiated by photoionization to an excited state. After excitation by an XUV pulse train from HHG, the fragment ions were recorded for different delays of an IR probe pulse, revealing strong modulations of fragmentation yields on ultrashort timescales. The dehydrogenated fragment yield originating from C–H bond breaking was found to be modulated with two superimposed oscillations whose periods correspond to the trans-bending and C–C bond stretching motion of the cation. We showed that these pump–probe delay-dependent modulations of the C₂H⁺ yield can be explained as a result of a configuration dependent effect driven by the IR pulse. Depending on the position of the wave packet on the multidimensional surface, the IR pulse can either cause photoexcitation to higher-lying states or dumping to the ground state, leading to an increase or a decrease of the observed ion yield, respectively. The relative C₂H⁺ yield thus reflects the instantaneous molecular geometry at the moment of IR incidence. The modulation of the C–H bond breaking efficiency can thus be used to investigate nuclear dynamics on a manifold of electronic states of hydrocarbon molecules on the femtosecond timescale in the weak perturbation limit.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This research was supported by the NCCR MUST, funded by the Swiss National Science Foundation. Z. Schumacher gratefully acknowledges the support by the ETH Zurich Postdoctoral Fellowship. We thank B. Mignolet and F. Remacle for extensive discussions concerning the interpretation of the experimental results and acknowledge T. Martinez’ insightful remarks.

References

1. A. H. Zewail, Angew. Chem., Int. Ed., 2000, 39, 2586–2631.
2. I. V. Hertel and W. Radloff, Rep. Prog. Phys., 2006, 69, 1897.
3. I. Fischer, M. J. J. Vrakking, D. M. Villeneuve and A. Stolow, Chem. Phys., 1996, 207, 331–354.
4. F. Légaré, K. F. Lee, I. V. Litvinyuk, P. W. Dooley, A. D. Bandrauk, D. M. Villeneuve and P. B. Corkum, Phys. Rev. A: At., Mol., Opt. Phys., 2005, 72, 052717.
5. T. Ergler, A. Rudenko, B. Feuerstein, K. Zrost, C. D. Schröter, R. Moshammer and J. Ullrich, Phys. Rev. Lett., 2006, 97, 193001.
6. S. De, M. Magrakvelidze, I. A. Bocharova, D. Ray, W. Cao, I. Znakovskaya, H. Li, Z. Wang, G. Laurent, U. Thumm, M. F. Kling, I. V. Litvinyuk, I. Ben-Itzhak and C. L. Cocke, Phys. Rev. A: At., Mol., Opt. Phys., 2011, 84, 043410.
7. F. Kelkensberg, C. Lefebvre, W. Siu, O. Ghafur, T. T. Nguyen-Dang, O. Atabek, A. Keller, V. Serov, P. Johnsson, M. Swoboda, T. Remetter, A. L’Huillier, S. Zherebtsov, G. Sansone, E. Benedetti, F. Ferrari, M. Nisoli, F. Lepine, M. F. Kling and M. J. J. Vrakking, Phys. Rev. Lett., 2009, 103, 123005.
8. P. Cörlin, A. Fischer, M. Schönwald, A. Sperl, T. Mizuno, U. Thumm, T. Pfeifer and R. Moshammer, Phys. Rev. A: At., Mol., Opt. Phys., 2015, 91, 43415.
9. F. Calegari, D. Ayuso, A. Trabattoni, L. Belshaw, S. D. Camillis, S. Anumula, F. Frassetto, L. Poletto, A. Palacios, P. Decleva, J. B. Greenwood, F. Martín and M. Nisoli, Science, 2014, 336, 336–339.
10. P. Ranitovic, C. W. Hogle, P. Riviere, A. Palacios, X.-M. Tong, N. Toshima, A. Gonzalez-Castrillo, L. Martin, F. Martin, M. M. Murnane and H. Kapteyn, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 912–917.
11. A. Trabattoni, M. Klinker, J. González-Vázquez, C. Liu, G. Sansone, R. Linguerri, M. Hochlaf, J. Klei, M. J. J. Vrakking, F. Martín, M. Nisoli and F. Calegari, Phys. Rev. X, 2015, 5, 041053.
12. A. Hishikawa, A. Matsuda, E. J. Takahashi and M. Fushitani, J. Chem. Phys., 2008, 128, 084302.
13. Y. H. Jiang, a. Rudenko, O. Herrwerth, L. Foucar, M. Kurka, K. U. Kühnel, M. Lezius, M. F. Kling, J. Van Tilborg, a. Belkacem, K. Ueda, S. Düsterer, R. Treusch, C. D. Schröter, R. Moshammer and J. Ullrich, Phys. Rev. Lett., 2010, 105, 1–4.
14. M. E.-A. Madjet, O. Vendrell and R. Santra, Phys. Rev. Lett., 2011, 107, 263002.
15. Y. H. Jiang, A. Senftleben, M. Kurka, A. Rudenko, L. Foucar, O. Herrwerth, M. F. Kling, M. Lezius, J. V. Tilborg, A. Belkacem, K. Ueda, D. Rolles, R. Treusch, Y. Z. Zhang, Y. F. Liu, C. D. Schröter, J. Ullrich and R. Moshammer, J. Phys. B: At., Mol. Opt. Phys., 2013, 46, 164027.
16. H. Ibrahim, B. Wales, S. Beaulieu, B. E. Schmidt, N. Thiré, E. P. Fowe, E. Bisson, C. T. Hebeisen, V. Wanie, M. Giguére, J.-C. Kieffer, M. Spanner, A. D. Bandrauk, J. Sanderson, M. S. Schuurman and F. Légaré, Nat. Commun., 2014, 5, 4422.
17. B. Wolter, M. G. Pullen, A.-T. Le, M. Baudisch, K. Doblhoff-Dier, A. Senftleben, M. Hemmer, C. D. Schröter, J. Ullrich, T. Pfeifer, R. Moshammer, S. Gräfe, O. Vendrell, C. D. Lin and J. Biegert, Science, 2016, 354, 308–312.
18. C. Burger, A. Atia-Tul-Noor, T. Schnappinger, H. Xu, P. Rosenberger, N. Haram, S. Beaulieu, F. Légaré, A. S. Alnaser, R. Moshammer, R. T. Sang, B. Bergues, M. S. Schuurman, R. D. Vivie-Riedle, I. V. Litvinyuk and M. F. Kling, Struct. Dyn., 2018, 5, 044302.
19. Z. Li, L. Inhester, C. Liekhus-Schmaltz, B. F. E. Curchod, J. W. Snyder, N. Medvedev, J. Cryan, T. Osipov, S. Pabst, O. Vendrell, P. Bucksbaum and T. J. Martinez, Nat. Commun., 2017, 8, 453.
20. R. C. Gillen, B. Ostojic and W. Domcke, Chem. Phys., 2001, 272, 1–14.
21. H. Tao, T. K. Allison, T. W. Wright, A. M. Stooke, C. Khurmi, J. van Tilborg, Y. Liu, R. W. Falcone, A. Belkacem and T. J. Martinez, J. Chem. Phys., 2011, 134, 244306.
22. R. Locher, M. Lucchini, J. Herrmann, M. Sabbar, M. Weger, A. Ludwig, L. Castiglioni, M. Greif, M. Hengsberger, L. Gallmann and U. Keller, Rev. Sci. Instrum., 2014, 85, 013113.
23. A. Ludwig, E. Liberatore, J. Herrmann, L. Kasmi, P. Lopez-Tarifa, L. Gallmann, U. Rothlisberger, U. Keller and M. Lucchini, J. Phys. Chem. Lett., 2016, 7, 1902–1906.
24. T. Shiozaki, W. Győrffy, P. Celani and H.-J. Werner, J. Chem. Phys., 2011, 135, 081106.
25. J. Berkowitz, Atomic and Molecular Photoabsorption, Elsevier, Amsterdam, 2015, ch. 5.3, pp. 423–441 DOI:10.1016/B978-0-12-801943-6.00005-8.
26. M. Wells and R. R. Lucchese, J. Chem. Phys., 1999, 110, 6365.
27. S. A. Trushin, K. Kosma, W. Fuß and W. E. Schmid, Chem. Phys., 2008, 347, 309–323.
28. C. Burger, N. G. Kling, R. Siemering, A. S. Alnaser, B. Bergues, A. M. Azzeer, R. Moshammer, R. de Vivie-Riedle, M. Kubel and M. F. Kling, Faraday Discuss., 2016, 194, 495–508.
29. M. E. A. Madjet, O. Vendrell and R. Santra, Phys. Rev. Lett., 2011, 107, 263002.
30. M. E. A. Madjet, Z. Li and O. Vendrell, J. Chem. Phys., 2013, 138, 094311.
31. J. H. Posthumus, Rep. Prog. Phys., 2004, 67, 623–665.
32. S. Larimian, S. Erattupuzha, E. Lötstedt, T. Szidarovszky, R. Maurer, S. Roither, M. Schöffler, D. Kartashov, A. Baltuška, K. Yamanouchi, M. Kitzler and X. Xie, Phys. Rev. A: At., Mol., Opt. Phys., 2016, 93, 053405.
33. S. Roither, X. Xie, D. Kartashov, L. Zhang, M. Schöffler, H. Xu, A. Iwasaki, T. Okino, K. Yamanouchi, A. Baltuska and M. Kitzler, Phys. Rev. Lett., 2011, 106, 163001.
34. S. Erattupuzha, C. L. Covington, A. Russakoff, E. Lötstedt, S. Larimian, V. Hanus, S. Bubin, M. Koch, S. Gräfe, A. Baltuška, X. Xie, K. Yamanouchi, K. Varga and M. Kitzler, J. Phys. B: At., Mol. Opt. Phys., 2017, 50, 125601.
35. J. Kim, H. Tao, J. L. White, V. S. Petrović, T. J. Martinez and P. H. Bucksbaum, J. Phys. Chem. A, 2012, 116, 2758–2763.

---

Footnote

† Electronic supplementary information (ESI) available: SupplementaryInfo.pdf containing further descriptions of the experimental and theoretical methods. See DOI: 10.1039/c9cp03138c

---