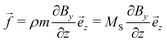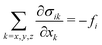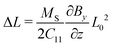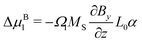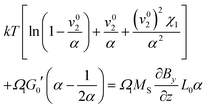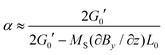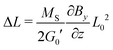Magnetically responsive composites: electron beam assisted magnetic nanoparticle arrest in gelatin hydrogels for bioactuation†
Received
22nd May 2019
, Accepted 6th June 2019
First published on 7th June 2019
Abstract
As emerging responsive materials, ferrogels have become highly attractive for biomedical and technical applications in terms of soft actuation, tissue engineering or controlled drug release. In the present study, bioderived ferrogels were fabricated and successfully deformed within moderate, heterogeneous magnetic fields. Synthesis was realized by arresting iron oxide nanoparticles in porcine gelatin by introduction of covalent crosslinks via treatment with energetic electrons for mesh refinement. This approach also allows for tuning thermal and mechanical stability of the gelatin matrix. Operating the bioferrogel in compression, magnetic forces on the nanoparticles are counterbalanced by the stiffness of the hydrogel matrix that is governed by a shift in thermodynamic equilibrium of swelling, as derived in the framework of osmosis. As gelatin and iron oxide nanoparticles are established as biocompatible constituents, these findings promise potential for in vivo use as contactless mechanical transducers.
1 Introduction
Smart biomaterials, capable of responding to external stimuli by shape changes, exhibit high potential in numerous sectors of biomedicine, for use in biomimetics and drug delivery systems or as simple switching devices in technical applications.1–4 A very promising material system along these lines is composites of gels and magnetic particles, viz. so called ferrogels. Arresting magnetic particles within the gel matrix enables realization of a direct coupling between sample shape and external magnetic field, viz. a magneto-mechanical transducer.5–7 The possibility of being controllable without the need for direct contacts renders ferrogels highly attractive candidates for use in medical tools,8 particularly if the constituents are biodegradable or -absorbable. Biopolymeric hydrogels are thus particularly good starting points due to their intrinsic biological nature. With this background, the present paper focuses on the synthesis and characterization of a bioferrogel, based on porcine gelatin as the hydrogel and superparamagnetic iron oxide nanoparticles (SPIONs). The particles are primarily geometrically arrested within the matrix by introducing covalent crosslinks due to exposure to high energy electrons. This approach constitutes a biocompatible procedure that also facilitates thermal stabilization and allows for tuning of mechanical properties to mimic, e.g., the desired extracellular matrix (ECM) properties.9–12
Gelatin itself is an advantageous material as it is biopolymer-derived and of very little complexity such that it exhibits less irregularities and is simple to handle. Compared to collagen of which it is a derivative, it also shows less antigenicity.13–15 As gelatin is furthermore already medically approved, inexpensive and highly available, it constitutes a favorable material of outstanding promise for applications. In fact, since 2000, gelatin based composites have been more and more applied to artificial skin, bone grafts and scaffolds for tissue engineering.2,3,16,17 Recent research showed that gelatin is tunable in its elastic and viscoelastic properties by different parameters such as gelatin concentration, crosslinking degree or temperature.18 Ferrogels in general have attracted increasing research interest since Zrínyi et al.19 first observed small deformations in external magnetic fields in 1996. Until today, ferrogels have been successfully fabricated to deform in external magnetic fields, however mostly in terms of elongation, bending or torsion.7,19,20 Zhao et al.,21 for instance, achieved large ferrogel compressions of up to 80% but with very low compression moduli around 2.5 kPa. A general problem in the comparability of most of these studies is given by the quantification of “shape change” that is frequently chosen as the sample end-to-end distance, while the sample performs complex shape changes (such as curling and bending) due to a lack of boundary constraints. Enforcing strictly affine sample deformations by suitable constraints is clearly advantageous for quantifying “real” dimensional change of the composite material itself for physical interpretation.
The current experiments will thus focus on the magneto-mechanical responses of electron beam synthesized gelatin-SPION based ferrogels with physiologically relevant compression moduli between 60 and 150 kPa and quantify affine deformations within moderate magnetic fields that are enforced using strong boundary constraints in a custom-built setup. We have previously evaluated the central properties of similar ferrogels, including homogeneous synthesis, strength of mechanical nanoparticle–matrix coupling and long-term stability, within an extensive previous study centered around magnetic particle spectroscopy (MPS) and magnetorelaxometry (MRX) assessment.9
The paper is organized as follows. Section 2 presents methods to synthesize, crosslink and deform ferrogels within external magnetic fields. In Section 3, the deformations of ferrogels in terms of elastic, viscoelastic and plastic responses are quantified. All experimental results are discussed in Section 4, followed by an in-depth contemplation of the underlying thermodynamic foundations in Section 5 and conclusion in Section 6.
2 Methods and materials
2.1 Ferrogel synthesis
Ferrogels were prepared from lauric acid coated superparamagnetic iron oxide nanoparticles (SPIONLAc) in solution and porcine gelatin type 300 A (Sigma Aldrich Life Science). The preparation method of SPIONLAc is included in the ESI.† 4 wt% gelatin powder was added to a magnetic nanoparticle solution with a concentration of 3–3.5 wt% Fe and left for swelling for an hour at room temperature. The mixture was subsequently annealed at 60 °C for about 10 minutes and pipetted into cylindrical molds with a diameter of 0.8 cm and a height of 5 cm. Samples were gelled and stored for a minimum of 24 hours at 10 °C before irradiation. Irradiated samples were kept within airtight bags flushed with nitrogen to prevent oxygen exposure.
2.2 Electron irradiation crosslinking
Samples were irradiated by a 10 MeV linear accelerator (Mevex, Ontario, Canada) using a moving stage at a rate of 1 m min−1. The accelerator had a pulse repetition rate of 180 Hz to 450 Hz and electron pulse lengths of 8 μs. The total dose was carried out in steps of 5 kGy with an uncertainty of 5% with respect to a graphite dosimeter. Samples were irradiated inside a cooled, thermocoupled, insulating box to minimalize heating effects. Irradiation time took up to an hour.
2.3 Mechanical characterization of compression moduli
The effective compression moduli were determined with a tensile stage (Hegewald & Peschke, Inspect Mini) using the compressive testing mode. Cylindrical samples of 8 mm diameter and about 6 mm height were cut out of the gel films with a metal punch. They were individually measured with a caliper for better accuracy of further calculations. The samples were blotted dry with filter paper to prevent slipping during measurements and subsequently positioned in the center between the two parallel plates. The top plate approached and compressed the sample with a velocity of 2 mm min−1. The measurement was terminated manually after fracture occurred within the samples. The linear elastic regime of the stress–strain curve was determined and its slope identified as the apparent compression modulus. Averages were calculated from five different samples per dose.
2.4 Magnetic characterization
We employed a SQUID-based (Superconducting Quantum Interference Device) MPMS-XL5 (Magnetic Property Measurement System, Quantum Design, USA) magnetometer to characterize the magnetization behavior of gelatin–nanoparticle composites that were treated with different electron doses, and dispersion as reference. The contributions of the sample holder and the pure gelatine were subtracted from the data. To this end, the purely diamagnetic contribution of the gelatin was approximated by the value of water, i.e. χd = 9.3 × 10−6. Furthermore, the field strength, calculated from the coil current, was corrected with respect to the remanent field originating from the mu-metal shield of the system.
2.5 Magnetically driven deformations
Ferrogel cylinders were taken out of the molds and incubated for swelling and accompanying softening in destilled water for at least 24 hours. Samples were subsequently inserted into new vessels of equal geometry and covered with destilled water. They were sited perpendicularly to the magnetic flux lines of a 1 Tesla electromagnet (Schueler Magnetic Ltd, Dortmund, Germany) and exposed to its heterogeneous magnetic field, while room temperature was maintained for all experiments. First, a test series was performed to find the position of maximum deformation. The magnetic field was successively increased from 0 to 0.89 T. Cyclic measurements were performed by applying and removing the field within 53 s, respectively, while three cycles were realized for each sample. Long-term measurements were conducted by applying a constant field for at least 16 hours. Samples were observed for a further six hours after the field was switched off. 0.5 frames per second were recorded with a high resolution camera and the software uEye cockpit.
2.5.1 Compression evaluation.
Absolute deformations were evaluated with the pixel counting measurement function of the software ImageJ. Mean and standard deviation were calculated from three measurements on each sample. Errors on subsequently calculated values were determined by the Gaussian error propagation. Curve progression for long-term deformation was evaluated with a Python script for digital image evaluation. Movies were fractionized into frames, cropped and converted into binary frames consisting of black and white pixels. Pixel counting enabled determination of the progression of sample compression.
2.5.2 Bending and curving.
Ferrogel cylinders were placed upwards, in line with the magnetic field gradient, and fixed at designated sample parts.
3 Results
3.1 Magnetic properties
The survey on the physical properties of our gelatin–nanoparticle composites starts with the assessment of magnetic properties, which we conduct in direct comparison to a nanoparticle dispersion as a reference. Fig. 1 presents the magnetization curves of the gels that have been treated with different electron doses, normalized to the dispersion reference of the same Fe concentration. The shapes of the M(H) curves of all gel samples are nearly identical. There are only very small coercitive fields that do not differ significantly among the different gel samples (Table 1). This shape deviates only slightly from that of the dispersion. The about 10% higher magnetization of the dispersion in the region around 10 kA m−1 can be attributed either to the Brownian mobility of the particles within the dispersion or to the onset of dipolar interaction among the MNP in the gels. In disordered systems, this interaction may lead to a reduction of the magnetization, depending on the interplay between interaction strength and thermal energy. Slight differences in the saturation magnetization (Table 1) might be due to uncertainties in preparation. Saturation magnetizations are found to be 5–10% lower than in gels irradiated with 5–60 kGy, which might be related to a loss of water in the dispersion, resulting in an increase of nanoparticle concentration.
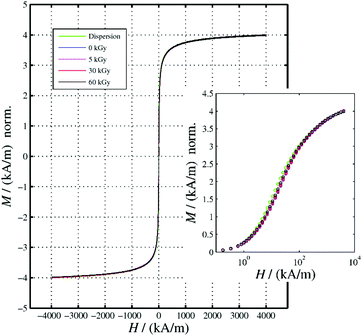 |
| | Fig. 1 Hysteresis curves and M(H) virgin curves (inset) of ferrogels subjected to the indicated irradiation dose. The data were normalized to that of the corresponding MNP-dispersion at H = 4000 kA m−1. | |
Table 1 Magnetic characterization (coercivity Hc and remanence MS) of gelatin–NP composites and a NP dispersion as a reference
| Sample |
Dose (kGy) |
H
c (kA m−1) |
M
S (kA m−1) |
| Dispersion |
0 |
0.0062 ± 0.0086 |
4.000 ± 0.001 |
| Gelatin/NP |
0 |
0.031 ± 0.016 |
4.390 ± 0.014 |
| Gelatin/NP |
5 |
0.023 ± 0.007 |
4.000 ± 0.005 |
| Gelatin/NP |
30 |
0.032 ± 0.013 |
3.950 ± 0.009 |
| Gelatin/NP |
60 |
0.030 ± 0.015 |
3.90 ± 0.01 |
3.2 Maximum magnetically induced deformations
To identify the optimum sample positions within the magnetic field that yielded maximum deformations, the total compression of the ferrogel was measured at different locations within the mirror plane of the 1 T electromagnet (Fig. 2a). The compression ratios ranged from 0.2% to 8.3% at different height h, defined as the distance between the axis of the magnetic setup and the upper sample edge prior to deformation. A plateau between 5.5 cm < h < 7.5 cm exhibiting maximum compressions of around 8% could be identified, as indicated by the dashed lines in Fig. 3. Both experimental setup (including a visualization of h) and magnetic field as a function of h (measured with a commercial Hall probe) are shown in Fig. 2. The field is almost homogeneous at h = 0 and decreases with further distance from the pole shoes, while the absolute magnetic field gradient increases. The range of the upper sample edge when yielding maximum deformation is indicated by dashed lines in Fig. 2b. As each sample was of about 5 cm size, we conclude that maximum deformations were observed when the sample was exposed to the highest absolute magnetic field gradients.
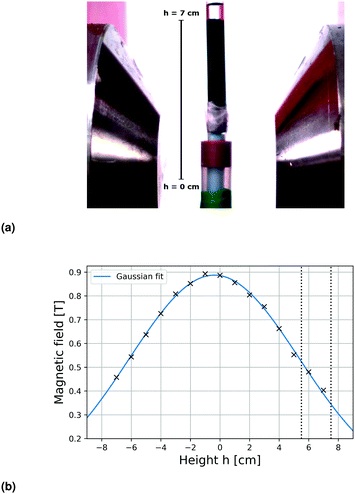 |
| | Fig. 2 (a) Photograph of the experimental setup. Height h describes the distance of the upper edge of the undeformed sample from the axis of the magnet. (b) Magnetic field gradient of utilized 1 T electromagnet measured with a Hall probe as a function of h. Maximum deformations are observed when the upper sample edge is positioned between the dashed vertical lines. | |
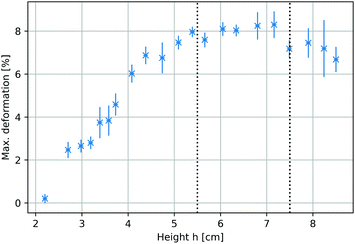 |
| | Fig. 3 Maximum sample compression as a response to cyclic magnetic fields as a function of the position within the electromagnet. Height h is defined in Fig. 2a. Each data point represents averaged results of three individual measurements. | |
3.3 Deformation on short timescales
Ferrogels with 4 wt% gelatin concentration, one day swelling and varying irradiation doses yielded compressions of (7.3 ± 0.6)%, (5 ± 0.7)% and (5 ± 1.0)% for doses of 5 kGy, 30 kGy and 60 kGy, respectively, within cyclic magnetic fields. Three samples treated with the 30 kGy dose were remeasured after 14 days swelling. Compressions of up to (9.1 ± 0.4)% could be achieved, which exhibit a relative increase of about 82%. These studies were performed with magnetic nanoparticles (MNPs) SPIONLAc3 (batch 3 of 3).
Prestudies on ferrogel deformations with the 30 kGy irradiation dose and varying gelatin concentrations were performed with a different batch of nanoparticles (SPIONLAc2) of approximately the same properties. They showed compressions of up to (7.4 ± 0.9)% and (14.5 ± 1.0)% for 3.8 wt% and 2 wt% gelatin concentrations, respectively. All results are summarized in Table 2. The given compression moduli refer to unswollen gels and the one day swelling results show a reduction of up to 35%.
Table 2 Ferrogel compressions as a response to cyclic magnetic fields for varying irradiation doses, swelling times, gelatin concentrations and magnetic nanoparticles (MNPs). Longer swelling times yielded significantly larger deformations under otherwise equal conditions. A prestudy with another batch of MNPs (SPIONLAc2) yielded higher compressions at similar gelatin concentrations and irradiation doses, respectively
| MNPs |
# Samples |
Gelatin concentration (wt%) |
Dose (kGy) |
Swelling time (d) |
Compression modulus (kPa) |
Compression (%) |
| SPIONLAc3 |
3 |
4.0 |
5 |
1 |
91 |
7.3 ± 0.6 |
| SPIONLAc3 |
8 |
4.0 |
30 |
1 |
149 |
5.0 ± 0.7 |
| SPIONLAc3 |
2 |
4.0 |
60 |
1 |
182 |
5.0 ± 1.0 |
| SPIONLAc3 |
3 |
4.0 |
30 |
14 |
— |
9.1 ± 0.4 |
| SPIONLAc2 |
2 |
3.8 |
30 |
1 |
— |
7.4 ± 0.9 |
| SPIONLAc2 |
1 |
2.0 |
30 |
1 |
— |
14.5 ± 1.0 |
Fig. 4 shows the ferrogel extension in response to three magnetic field cycles. The compression followed the external field almost without phase shift and was almost reversible, while maximum compressions were reached at maximum magnetic fields. Ferrogels revealed a slightly faster extension than compression as it is manifested in the slight asymmetry in each cycle's curve. After three cycles, the gel returned to its initial extension.
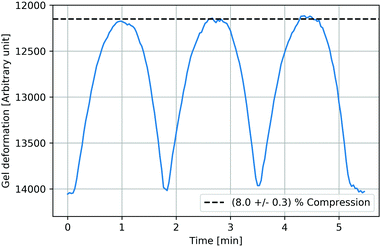 |
| | Fig. 4 Almost reversible ferrogel deformation as a response to cyclic magnetic fields (exemplarily shown for a ferrogel with 3.8% gelatin and SPIONLAc2 nanoparticles, irradiated with 30 kGy, after 24 hours of swelling). The compression followed the external field almost without phase shift, while maximum compressions were reached at maximum magnetic fields. Ferrogels revealed a slightly faster extension than compression as manifested in the slight asymmetry in each cycle's curve. | |
3.4 Deformation on long timescales
Ferrogels treated with two different irradiation doses were compressed within magnetic fields for about 16 hours and their recovery was subsequently observed for further six hours. Samples synthesized with SPIONLAc3 particles with doses of 30 kGy were compressed by about (10.1 ± 1.3)% and recovered to (96.4 ± 1.2)% of their initial extension. A sample with a 5 kGy dose was compressed by about (15.9 ± 0.4)% and recovered to (94.3 ± 0.9)%. These studies have been performed with magnetic nanoparticles (MNPs) SPIONLAc3.
A prestudy with a different batch of nanoparticles (SPIONLAc2) of approximately the same properties and 30 kGy dose showed compression and shape recovery of (15.5 ± 0.4)% and (95.6 ± 0.2)%, respectively. Total compressions of SPIONLAc2 samples exceeded the ones of SPIONLAc3 samples of the same dose and similar gelatin concentration by far. All results are summarized in Table 3. A minor correlation between total compressions and plastic deformations was observed, viz. more strongly compressed samples exhibited slightly larger plastic deformations. Shape recovery of all measured samples agreed within the second standard deviation, though.
Table 3 Long-term compressions of ferrogels within heterogeneous magnetic fields. A prestudy with another batch of MNPs (SPIONLAc2) yielded higher compression at similar gelatin concentrations and same irradiation doses
| MNPs |
# Samples |
Gelatin concentration (wt%) |
Dose (kGy) |
Compression modulus (kPa) |
Compression (%) |
Relaxation (%) |
| SPIONLAc3 |
1 |
4 |
5 |
91 |
15.9 ± 0.4 |
94.3 ± 0.9 |
| SPIONLAc3 |
3 |
4 |
30 |
149 |
10.1 ± 1.3 |
96.4 ± 1.2 |
| SPIONLAc2 |
1 |
3.8 |
30 |
— |
15.5 ± 0.4 |
95.6 ± 0.2 |
Fig. 5 shows an exemplary temporal evolution of strain response upon application of a magnetic field. The samples showed a strong and direct compression as a reaction to the applied external field. The compression was observed to continue, although slower, for all samples, as they were exposed to the field for a further 16 hours. Stepwise long-term compression was observed for all measured samples. When the magnetic field was turned off, the samples showed a pretty strong recovery as a direct response and further relaxed slowly. Recovery did not exhibit comparable discontinuities. After six hours of recovery, the samples had not returned to their initial extension. Larger total compressions entailed the tendency to be left with stronger remaining deformations. Stretched exponential functions, so called Kohlrausch fits, which are well-known to describe typical viscoelastic behavior in dynamically heterogeneous systems of the form
| | 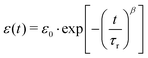 | (1) |
were fitted onto the data, with time
t, initial strain
ε0, retardation time
τr and stretching exponent
β. The data are in very good accordance with the fit, which represents the viscoelastic nature of the composite. The deviation of stretching exponent
β from 1 is typically associated with the degree of heterogeneity in a system. Stretching exponent
β ranged from 0.24 to 0.30 for all 30 kGy SPION
LAc3 samples. The 5 kGy SPION
LAc3 sample showed a lower value of
β = 0.15. The 30 kGy SPION
LAc2 sample showed a much higher value of
β = 0.43.
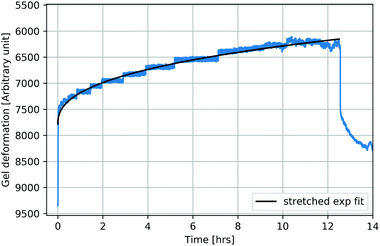 |
| | Fig. 5 Partly reversible ferrogel deformation as a response to long-term magnetic field exposure (exemplarily shown for ferrogels synthesized as in Fig. 4). After strong and direct compression with increasing magnetic field, further slow and stepwise compression at a constant field occurs. Recovery similarly reveals strong and direct relaxation as the field is turned off, followed by further slow but continuous relaxation witout full reversibility. A Kohlrausch fit can account for the observed viscoelastic behavior. | |
3.5 Bending actuators
Ferrogel cylinders were placed into the magnetic field. They were constrained only at designated sample parts. Different geometries of the systems yielded varying bending and curving of the samples as is exemplarily shown in Fig. 6. A straight upwards positioned sample was fixed within a sampleholder up to half of its height and positioned into the heterogeneous field. It showed strong bending to the right side.
 |
| | Fig. 6 Fully reversible bending of ferrogel cylinder located within the heterogeneous magnetic field of a 1 T electromagnet. The free edge is attracted by the magnetic pole. | |
4 Discussion of experimental observations
4.1 Driving force for deformations
Maximum deformations were obtained when the samples were exposed as much as possible to the highest absolute magnetic field gradients. As this behavior complies with the forces on individual magnetic dipoles in heterogeneous magnetic fields, which are proportional to the magnetic field gradient, this finding confirms the picture that the ensemble of individual magnetic nanoparticles exerts a force on the hydrogel matrix. Detailed inspection of the deformation reaction furthermore revealed a slight delay in response during the onset of deformation at low magnetic fields. Low magnetic fields occur at the beginning of the deformation cycle (when switching on the magnet) or at the very edge of the pole shoes (Fig. 5). As coercivity is too small to account for this behavior (Table 1), due to the virtual absence of magnetic coupling (Fig. 1 and our previous MRX/MPI studies on similar ferrogels9), we surmise that a stick-slip type of friction at the wall, combined with the viscoelastic response of the hydrogel matrix, might be the cause for this.
4.2 Elastic deformation on short timescales
Ferrogel deformation nevertheless followed almost instantaneously the applied magnetic field, yielding a greatly reversible mechanical response. This corresponds to a dominant elastic behavior. Maximum deformations within the magnetic field showed dependencies on irradiation dose, swelling time and gelatin concentration. All these parameters strongly affect material stiffness of the gelatin matrix, which induces stresses during deformation that balance magnetic forces on the arrested nanoparticles in equilibrium. Higher irradiation doses result in a higher degree of crosslinks and thus make it mechanically stiffer.18,22 Smaller deformations are thus achievable. As for gelatin concentrations, it was shown that deformations grew significantly larger with lower concentrations. Wisotzki et al.18 found that gelatin of lower concentrations was significantly softer in terms of shear response. It is suggested that the uniaxial response should be significantly softened as well, which would support again the previous hypothesis. Following the previous line of reasoning, a softening of the material with longer swelling times is suspected. We plan to corroborate this picture in future by performing tailored experiments for detailed assessment. We thus propose that the maximum compression should be tunable by the compression modulus that reflects the network's elasticity. This may be realized by irradiation dose, gelatin concentration or swelling time. The influence of the batch of nanoparticles on total deformations is going to be discussed seperately later in this paper.
4.3 Viscoelastic deformation on long timescales
It should not be neglected that the effect of long-term deformations is much more complex than their short-term counterpart, which is elastically dominated. First of all, time dependent deformation implies viscous contributions.23 Furthermore, the observed deformations were not fully reversible, which means that plastic deformations also occurred. Plastic contributions that were only observed for long-term compressions were simply quantified by irreversible deformations. The total mechanical response can thus be interpreted within a Burgers material model that consists of a Kelvin-Voigt and Maxwell element in series. We surmise that viscous contributions arise from structural changes of the polymer matrix that are possible in regions‡, where not enough covalent crosslinks have been inserted. Relaxed polymers, oriented straight upwards after irradiation, for instance, could be tilted after compression, accompanied by energy dissipation. There would be no force pulling them back during recovery. As plastic contributions that only occurred during long-term measurements were almost as large as the long-term response (excluding the instantaneous elastic response), we deduce that the major part of long-term compression is not reversible.
Total sample deformation showed dependencies on irradiation dose, gelatin concentration and batch of nanoparticles. Samples irradiated with 5 kGy showed much larger compressions than comparable samples irradiated with 30 kGy, which might be traced back to the lower compression modulus as discussed before.
4.3.1 Discontinuous shape transitions.
The discontinuous, avalanche-like mechanical response during compression was hypothesized to be rooted in the strong boundary constraints generating stick-slip behavior due to friction of the ferrogel at the wall of the surrounding plastic tube. Comparison measurements in oil instead of water as surrounding medium were performed to test the influence of friction on avalanche-like deformation. The discontinuity in shape transitions was clearly reduced manifested in softened steps compared to strictly angular ones. Corresponding images may be found in the ESI.† The friction hypothesis was furthermore supported by the increasing step-width with increasing compressions and by missing discontinuity during relaxation. Avalanches are thus assumed to be caused by friction.
4.3.2 Stretched exponential fits.
All samples revealed strains, whose temporal evolutions were in good agreement with stretched exponential Kohlrausch fits. Especially, quantification by stretching exponent β seems to be promising as it opens up the potential for deeper understanding of the impact of electron irradiation on polymeric systems. The deviation of stretching exponent β from 1 is typically associated with the degree of heterogeneity in a system. Linear electron irradiation is suspected to be able to change a system's heterogeneity. As for the performed measurements, the less irradiated sample showed stronger heterogeneity, it is conjecturable that irradiation would promote the system's mechanical homogeneity by increasing the amount of covalently bonded chains. Further evaluation will be the topic of our future research, since the potential to more deeply understand the impact of electron irradiation on such systems seems to be opened up.
We dare to propose the stretching exponent as a possible parameter to predict specific deformation behavior in the future. The retardation time τr showed extremely high values for all samples such that the fraction 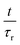 was very small, as has been observed before for stress retardation on critical gels.25 We would support their statement to take care in using stretched exponential functions in linear viscoelasticity, since only one out of three parameters seemed to give us explanations on our system. Nevertheless, we conclude that the stretched exponential function described our system in good approximation.
was very small, as has been observed before for stress retardation on critical gels.25 We would support their statement to take care in using stretched exponential functions in linear viscoelasticity, since only one out of three parameters seemed to give us explanations on our system. Nevertheless, we conclude that the stretched exponential function described our system in good approximation.
4.4 Differences in SPIONLAc2 and SPIONLAc3 samples
The prestudy based on SPIONLAc2 samples showed much greater effects for elastic and viscoelastic deformations than comparable SPIONLAc3 samples. This effect is hypothesized to be caused by a more favorable relation between magnetic driving force and material stiffness. This means that either SPIONLAc2 particles are magnetically stronger or the latter samples were softer despite equal parameters. Regarding the former aspect, the Fe concentration of SPIONLAc3 slightly exceeded the one of SPIONLAc2 while the susceptibility of SPIONLAc2 exhibited slightly higher values. The impact is not suspected to be very large, though. As for the material stiffness, varying aspects could have softened the SPIONLAc2 30 kGy samples. First of all, the slightly lower gelatin concentration of 3.8 wt% compared to 4 wt%. Previous studies showed that at least shear rheology significantly depended on the gelatin concentration in terms of stiffness being increased with increasing gelatin concentrations.18 However, the effect was not sufficiently high to fully explain the observed deviations. A further two experimental points originate on one hand from electron irradiation, precisely from thermal effects or strongly differing graphite calibration resulting in exposure to slightly different doses. The influence should not be prominent, though. Second, the SPIONLAc2 samples might have been unintentionally softened by oxygen exposure during the preparation process. The possible strength of the impact is not known. Combinations of the proposed points are possible.
Besides the mentioned points, gelatin is still a biopolymer, though much less complex than others, and it does not always behave in the same manner due to natural variation of properies.
4.5 Bending actuators
Ferrogel cylinders were bent and curved within magnetic fields. The results confirmed the field gradient as the driving force. Curving and bending were much larger with greater distance to the pole shoes where the gradient was shown to be higher. Additionally, there was almost no deformation observable within the homogeneous field between the pole shoes as predicted by several authors.5,7,26 It was thus shown that ferrogel deformations may be controlled by the geometries of the whole system or the sample itself.
5 Analytical model – elasticity vs. osmosis
Following Flory and Huggins,27,28 the free enthalpy of mixing water (index “1” in the following) with the electron beam crosslinked gelatin molecules (index “2”) is given within the “regular solution approach” by| | ΔGM = kT(n1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) v1 + χ1n1n2 − n01 v1 + χ1n1n2 − n01![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) v01 − χ1n01n02) v01 − χ1n01n02) | (2) |
where ni, vi and χ1 denote the molecular numbers, volume ratios and normalized interaction enthalpy between water and gelatin (χ = 0.497 for isoelectric gelatin29), respectively. Due to the applied boundary conditions and magnetic fields, the sample changes its volume by a uniaxial length change along its geometrical axis, as characterized by the reduced length, α = L/L0 (Fig. 7), where L0 denotes the reference state at which the crosslinks were introduced. Within the framework of rubber elasticity theory (employed in the revised version of ref. 30 and 31), this is associated with an entropy change that constitutes the elastic contribution to free enthalpy| | | ΔGE = (kTνe/2)(α2 − 1 − ln(α)) | (3) |
where νe denotes the effective number of chain segments. To address the resultant contribution to the solvent chemical potential| | 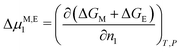 | (4) |
we follow Flory30 in assuming that (de)mixing occurs without any significant total volume change, i.e.| | | α = (V0 + (n1 − n01)Ω1)/V0 | (5) |
where Ω1 denotes the solvent molecule volume, yielding| | 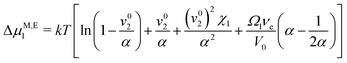 | (6) |
As the sample is placed within a heterogeneous magnetic field with spatially uniform 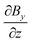 , the homogeneously distributed and arrested magnetic nanoparticles of magnetic moment m and volume density ρ exert a force density on the hydrogel network, given by
, the homogeneously distributed and arrested magnetic nanoparticles of magnetic moment m and volume density ρ exert a force density on the hydrogel network, given by| | 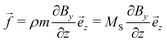 | (7) |
with the saturation magnetization MS ≥ 0. Requiring force equilibrium with sample stresses| | 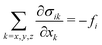 | (8) |
and enforcing free and supported, but sliding upper and lower boundaries (Fig. 7) lead to linearly increasing stresses towards the supportThe off-diagonal terms of the stress tensor vanish, while the other diagonal terms are generally non-zero. Despite the non-linear/non-Hookian behavior of our electron beam treated hydrogels, this stress profile can be employed to estimate a first guess of the expected deformation, if a suitable “effective” compression modulus C11 is available. As our experiments using a uniaxial compressive test indicate, an effective Young's modulus Y can be experimentally fitted (given in Table 2), which can be used to estimate C11 ≈ Y, neglecting volume change at the moment for a first guess. The length change can then be estimated as| | 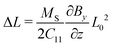 | (10) |
As, however, this treatment is surely only a crude approximation, we proceed with our more elaborate thermodynamic treatment. Both stresses and potential energy −fzzΩ1 contribute to the chemical potential of a solvent molecule. Assuming thermodynamic equilibrium, the sum of both contributions must be independent of z and is most conveniently calculated on the stress-free top surface of the sample, yielding the magnetic contribution to the free enthalpy per solvent molecule| | 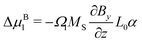 | (11) |
Bringing all contributions together and requiring chemical equilibrium, the contributions to the chemical potential need to cancel as direct exchange with surrounding water is ensured (assuming gravity is neglectable in comparison to magnetic forces), i.e.| | 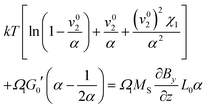 | (12) |
with G0′ denoting the shear modulus in the reference state. For sufficiently swollen samples (v02 → 0) and small deformations (α ≈ 1), this can be approximated by| | 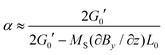 | (13) |
which (by further linearization) reduces to| | 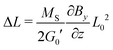 | (14) |
This final equation, which has now been derived on rigorous grounds, has the shape of eqn (10), but is based on a different physics (osmosis vs. linear elasticity) and thus involves the shear modulus as a measure for cross link density. Table 4 compares the prediction of the osmosis model and linear elasticity with the experimental results. Clearly, linear elasticity predicts strains an order of mangnitude lower than the experimental values, while the osmosis model overestimates the observable strain. Thus, linear elasticity is clearly at odds with the experiments, while the osmotic model can explain the experiment, as lower experimental strains can be rationalized with friction within the ferrogels (i.e. intrinsic viscoelasticity) or between the ferrogel and wall of the glassy sample tube. In fact, as friction with the wall occurs in a stick-slip-like manner in the experiments, it will constitute a more relevant contribution for soft ferrogels with large deformations, and will also show its manifestation in a slight hysteretic response of strain on field gradient, i.e. incomplete recovery after turning off the magnetic field. As can be seen in Table 4, this notion is in line with our experimental observations.
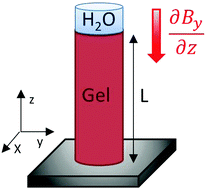 |
| | Fig. 7 Scheme of the model assumptions for analytical treatment. | |
Table 4 Comparison of the predictions of the osmosis model (eqn (14)) with linear elasticity (eqn (10)) and experiments. Parametrization has been taken from ref. 18, and the others are included in Tables 1 and 2
| Dose (kGy) |
(ΔL/L0)eqn (14) (%) |
(ΔL/L0)eqn (10) (%) |
(ΔL/L0)exp. (%) |
| 5 |
31 |
1.0 |
(7.3–15.9) |
| 30 |
9.1 |
0.6 |
(5.0–10.1) |
| 60 |
4.5 |
0.4 |
(5.0 ± 1.0) |
6 Conclusions
Crosslinked gelatin based ferrogels were significantly deformed within moderate magnetic fields. Strains of up to 8% and 15% for elastic and viscoelastic measurements were achieved, while the latter ones contained plastic contributions of about 4%. First results indicated that lowering gelatin concentrations or increasing swelling times could yield even higher deformations. The cylindrical sampleholder, into which the samples were placed, exhibited very strong boundary constraints during compression, which are favorable for detailed characterization of pure gel deformation, but also induced friction during deformation. The opportunity to easily achieve even larger compressions for a modified, boundary effect and friction minimizing system is evident. Samples locally fixed at pivot points only were demonstrated to show much more significant elastic deformations in terms of bending or curving, based on magnifying effects due to a lever geometry. The simplicity in controlling such deformations of desired shapes by choosing different geometries was illustrated.
To address the physical foundations of the deformation response due to magnetic forces on homogeneously dispersed nanoparticles in our gels, we have compared the predictions of a purely elastic model with a derived expression based on an equlibrium shift in osmosis. While only the latter one can be reconciled with the experimental observations, slightly lower strains observed in experiments hint at the presence of dissipation due to stick-slip type friction at the boundaries and viscoelasticity.
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
The authors gratefully acknowledge Dr E. Wisotzki, R. Konieczny, Dr W. Knolle and S. Riedel for their contributions to this research. This study was supported in part by the German Research Foundation (DFG) – Priority Program (SPP) 1681 (MA 2432/6-2, WI 4230/1-2 and AL 552/5-3), the Saxonian Department for Science and Arts (SMWK), Project BIOCOAT (via Sächsische Aufbaubank SAB 100259192) and the Emerging Fields Initiative BIGTHERA of the Friedrich-Alexander-Universität Erlangen-Nürnberg.
References
- J. P. Vacanti, M. A. Morse, W. M. Saltzman, A. J. Domb, A. Perez-Atayde and R. Langer, J. Clin. Pediatr. Surg., 1988, 23, 3–9 CrossRef CAS.
- A. Ito, A. Mase, Y. Takizawa, M. Shinkai, H. Honda, K.-I. Hata, M. Ueda and T. Kobayashi, J. Biosci. Bioeng., 2003, 95, 196–199 CrossRef CAS PubMed.
- F. Zhao, Y. Yin, W. W. Lu, J. C. Leong, W. Zhang, J. Zhang, M. Zhang and K. Yao, Biomaterials, 2002, 23, 3227–3234 CrossRef CAS PubMed.
- T.-Y. Liu, S.-H. Hu, T.-Y. Liu, D.-M. Liu and S.-Y. Chen, Langmuir, 2006, 22, 5974–5978 CrossRef CAS PubMed.
- M. Zrnyi, L. Barsi, D. Szabó and H.-G. Kilian, J. Chem. Phys., 1997, 106, 5685–5692 CrossRef.
- G. Filipcsei and M. Zrinyi, J. Phys.: Condens. Matter, 2010, 22, 276001 CrossRef PubMed.
- R. Weeber, S. Kantorovich and C. Holm, J. Magn. Magn. Mater., 2015, 383, 262–266 CrossRef CAS.
- S. Medeiros, A. Santos, H. Fessi and A. Elaissari, Int. J. Pharm., 2011, 403, 139–161 CrossRef CAS PubMed.
- E. I. Wisotzki, D. Eberbeck, H. Kratz and S. G. Mayr, Soft Matter, 2016, 12, 3908–3918 RSC.
- E. I. Wisotzki, R. P. Friedrich, A. Weidt, C. Alexiou, S. G. Mayr and M. Zink, Macromol. Biosci., 2016, 16, 914–924 CrossRef CAS PubMed.
- M. Tadsen, R. P. Friedrich, S. Riedel, C. Alexiou and S. G. Mayr, ACS Appl. Mater. Interfaces, 2019, 11, 7450–7458 CrossRef CAS PubMed.
- W. E. Hennink and C. F. van Nostrum, Adv. Drug Delivery Rev., 2012, 64, 223–236 CrossRef.
-
B. Brodsky, J. A. Werkmeister and J. A. Ramshaw, Biopolymers Online: Biology Chemistry Biotechnology Applications, 2005, vol. 8 Search PubMed.
- A. O. Elzoghby, J. Controlled Release, 2013, 172, 1075–1091 CrossRef CAS PubMed.
- S.-M. Lien, L.-Y. Ko and T.-J. Huang, Acta Biomater., 2009, 5, 670–679 CrossRef CAS.
- C.-H. Chang, H.-C. Liu, C.-C. Lin, C.-H. Chou and F.-H. Lin, Biomaterials, 2003, 24, 4853–4858 CrossRef CAS.
- K. Kawai, S. Suzuki, Y. Tabata, Y. Ikada and Y. Nishimura, Biomaterials, 2000, 21, 489–499 CrossRef CAS.
- E. I. Wisotzki, M. Hennes, C. Schuldt, F. Engert, W. Knolle, U. Decker, J. A. Käs, M. Zink and S. G. Mayr, J. Mater. Chem. B, 2014, 2, 4297–4309 RSC.
- M. Zrnyi, L. Barsi and A. Büki, J. Chem. Phys., 1996, 104, 8750–8756 CrossRef.
- M. Zrnyi, L. Barsi and A. Büki, Polym. Gels Networks, 1997, 5, 415–427 CrossRef.
- X. Zhao, J. Kim, C. A. Cezar, N. Huebsch, K. Lee, K. Bouhadir and D. J. Mooney, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 67–72 CrossRef CAS PubMed.
- E. I. Wisotzki, P. Tempesti, E. Fratini and S. G. Mayr, Phys. Chem. Chem. Phys., 2017, 19, 12064–12074 RSC.
-
S. P. Marques and G. J. Creus, Computational viscoelasticity, Springer Science & Business Media, 2012 Search PubMed.
- S. Riedel and S. G. Mayr, Phys. Rev. Appl., 2018, 9, 024011 CrossRef CAS.
- G. C. Berry and D. J. Plazek, Rheol. Acta, 1997, 36, 320–329 CrossRef CAS.
- D. Szabó, G. Szeghy and M. Zrnyi, Macromolecules, 1998, 31, 6541–6548 CrossRef.
- M. L. Huggins, J. Chem. Phys., 1941, 9, 440 CrossRef CAS.
- P. J. Flory, J. Chem. Phys., 1941, 9, 660 CrossRef CAS.
- S. Ma, M. Natoli, X. Liu, M. P. Neubauer, F. M. Watt, A. Fery and W. T. Huck, J. Mater. Chem. B, 2013, 1, 5128–5136 RSC.
-
P. Flory, Principles of Polymer Chemistry, Cornell University Press, 1953 Search PubMed.
- B. Erman and P. Flory, Macromolecules, 1986, 19, 2342–2353 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c9cp02910a |
| ‡ The presence of regions with large molecular degrees of freedom at moderate doses is, in fact, the basis of the electron beam induced shape memory effect in gelatin hydrogels.24 |
|
| This journal is © the Owner Societies 2019 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article ab,
Nils
Wilharm
ab,
Marina
Mühlberger
d,
Ralf P.
Friedrich
d,
Christoph
Alexiou
d and
Stefan G.
Mayr
*ab
ab,
Nils
Wilharm
ab,
Marina
Mühlberger
d,
Ralf P.
Friedrich
d,
Christoph
Alexiou
d and
Stefan G.
Mayr
*ab



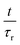 was very small, as has been observed before for stress retardation on critical gels.25 We would support their statement to take care in using stretched exponential functions in linear viscoelasticity, since only one out of three parameters seemed to give us explanations on our system. Nevertheless, we conclude that the stretched exponential function described our system in good approximation.
was very small, as has been observed before for stress retardation on critical gels.25 We would support their statement to take care in using stretched exponential functions in linear viscoelasticity, since only one out of three parameters seemed to give us explanations on our system. Nevertheless, we conclude that the stretched exponential function described our system in good approximation.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) v1 + χ1n1n2 − n01
v1 + χ1n1n2 − n01![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) v01 − χ1n01n02)
v01 − χ1n01n02)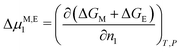
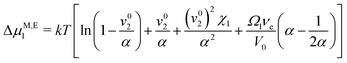
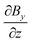 , the homogeneously distributed and arrested magnetic nanoparticles of magnetic moment m and volume density ρ exert a force density on the hydrogel network, given by
, the homogeneously distributed and arrested magnetic nanoparticles of magnetic moment m and volume density ρ exert a force density on the hydrogel network, given by