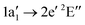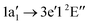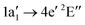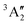Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Inner-shell X-ray absorption spectra of the cationic series NHy+ (y = 0–3)
Sadia
Bari†
*a,
Ludger
Inhester†
 bc,
Kaja
Schubert
ad,
Karolin
Mertens
bc,
Kaja
Schubert
ad,
Karolin
Mertens
 d,
Jan O.
Schunck
d,
Jan O.
Schunck
 ad,
Simon
Dörner
a,
Sascha
Deinert
a,
Lucas
Schwob
a,
Stefan
Schippers
ad,
Simon
Dörner
a,
Sascha
Deinert
a,
Lucas
Schwob
a,
Stefan
Schippers
 e,
Alfred
Müller
e,
Alfred
Müller
 f,
Stephan
Klumpp
f,
Stephan
Klumpp
 a and
Michael
Martins
a and
Michael
Martins
 d
d
aDeutsches Elektronen-Synchrotron (DESY), Notkestr. 85, 22607 Hamburg, Germany. E-mail: sadia.bari@desy.de; Fax: +49 040 8998 4475; Tel: +49 040 8998 5093
bCenter for Free-Electron Laser Science (CFEL), DESY, Notkestr. 85, 22607 Hamburg, Germany
cThe Hamburg Centre for Ultrafast Imaging (CUI), Luruper Chaussee 149, 22761 Hamburg, Germany
dDepartment Physik, Universität Hamburg, Luruper Chaussee 149, 22761 Hamburg, Germany. E-mail: michael.martins@desy.de
eJustus-Liebig-Universität Gießen, I. Physikalisches Institut, Heinrich-Buff-Ring 16, 35392 Gießen, Germany
fJustus-Liebig-Universität Gießen, Institut für Atom- und Molekülphysik, 35392 Gießen, Germany
First published on 22nd July 2019
Abstract
Ion yields following X-ray absorption of the cationic series NHy+ (y = 0–3) were measured to identify the characteristic absorption resonances in the energy range of the atomic nitrogen K-edge. Significant changes in the position of the absorption resonances were observed depending on the number of hydrogen atoms bound to the central nitrogen atom. Configuration interaction (CI) calculations were performed to obtain line assignments in the frame of molecular group theory. To validate the calculations, our assignment for the atomic cation N+, measured as a reference, was compared with published theoretical and experimental data.
Introduction
To understand the function of large biomolecules, like amino acids and peptides, one has to study the properties of their fundamental constituents, i.e. their electronic and geometric structure,1–4 as well as their dynamics.5–7 By exploiting the element specificity of inner-shell excitation, X-ray absorption spectroscopy (XAS) is an ideal tool to study the local electronic and geometric structure in the vicinity of a specific element within a molecule. Because of the rather large number of atoms within a biomolecule, photoabsoprtion spectra can be complex and sophisticated calculations are needed for their interpretation.8Thus, modelling accurate X-ray absorption spectra for biomolecules is very challenging.9,10 Instead of addressing an entire biomolecule, one can interpret the (measured) X-ray absorption spectrum as being composed of the contributions of smaller constituents or building blocks of larger molecules. For example, glycine (NH2–CH2–COOH), the simplest amino acid, connects the amino group NH2 and the carboxyl group COOH via a methylene bridge. Solved in water, like all amino acids, glycine is a zwitterion composed of a protonated amino group R–NH2+ and a de-protonated carboxylic acid COO− at its iso-electric point. Based on the assumption that the X-ray absorption is dominantly determined by the local chemical environment, knowing the XAS of NH2+ and COO− will facilitate the interpretation of more complicated XAS of e.g. glycine.
An inherent difficulty of this approach is that both of these building blocks of glycine are transient ionic molecules which are (almost) impossible to prepare as a solid or as a solution in water. However, an ion beam arrangement can be used to deliver ionic samples to the X-ray interaction region to address their absorption spectrum.11–15 Mass spectroscopy with high resolving power does not only offer the possibility to prepare a pure, transient molecular ion beam, but additionally provides control about the chemical environment of the molecular ion, enabling or disabling the interaction of chosen elements within the molecule (see Fig. 1). Depending on the number y of hydrogen atoms bound to the central nitrogen atom in NHy+, the electronic structure of the respective molecular ion and hence its absorption features will change. Especially inner-shell resonances, like the nitrogen 1s–2p resonances, are sensitive to the chemical environment of a molecule (see e.g.ref. 16–18), enabling us to probe the changes in the electronic structure of the respective molecular ions by performing a XAS-experiment.
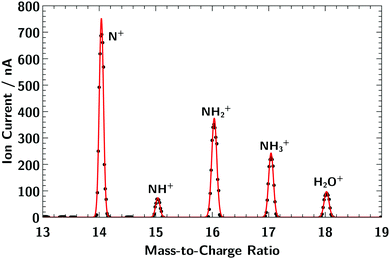 | ||
| Fig. 1 Mass spectrum of the molecular cation series of NHy+ (y = 0–3) showing clearly separated mass lines. | ||
Whereas there is plenty of previous work on the neutral species of the series NHy,19–30 little work on the cations NHy+ (y = 1–3) has been published. Theoretical work on the electronic structure of NH+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 31,32 and NH2+
31,32 and NH2+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 33 has been done calculating molecular potential curves and bonding angles. Experiments on molecular ions addressed the valence electronic structure of NH2+ using VUV photoionisation34 or the determination of the absolute cross section of NH+ using electron impact ionisation.35 Yet, there is no detailed information available on the inner-shell XAS of the cationic series NHy+ apart from the atomic cation, N+, which has been studied previously by Gharaibeh et al.36
33 has been done calculating molecular potential curves and bonding angles. Experiments on molecular ions addressed the valence electronic structure of NH2+ using VUV photoionisation34 or the determination of the absolute cross section of NH+ using electron impact ionisation.35 Yet, there is no detailed information available on the inner-shell XAS of the cationic series NHy+ apart from the atomic cation, N+, which has been studied previously by Gharaibeh et al.36
Furthermore, the role of NHy with different numbers y of hydrogen atoms has recently been studied in the liquid phase by Ekimova et al. for alkylamines in different solutions.37,38 They show a strong dependence of the N 1s X-ray spectra on the number y of H atoms and the solution itself.
Here, we report on our systematic investigations on the X-ray absorption for the cationic series NHy+ (y = 0–3) in a combined experimental and theoretical work.
Experiment
The PIPE merged-beams set-up39,40 at the XUV beamline P0441 of PETRA III, DESY, was used to record XAS spectra of NHy+ in the photon energy range of the nitrogen K-edge. Details of the preparation of a molecular ion beam at PIPE have been given in a previous publication.42As primary source for the production of the target molecular cations we have used gaseous NH3. The gas leaked into the plasma chamber of a 10 GHz Electron Cyclotron Resonance (ECR)43 ion source via an electronic needle valve keeping the gas pressure in the order of 2 × 10−5 hPa.
Fig. 1 shows the mass spectrum of the molecular cation series of NHy+ (y = 0–3). As can be seen, the resolving power of the preparation dipole-magnet mass spectrometer is sufficient to distinguish each single ion of the series. Both elements, nitrogen and hydrogen, have two naturally stable isotopes but the abundance ratio for both cases, 14N/15N and 1H/2H, is in the order of 0.99/0.01.44 Thus, the composition of the mass lines in Fig. 1 can be considered to be almost pure. A possible NH4+ molecular ion has the same mass-to-charge ratio as H2O+. However, the corresponding absorption spectrum did not show any nitrogen resonances, indicating that no NH4+ molecular ions were produced in our ion source.
A beam of singly charged molecular ions was prepared and accelerated to 6 keV kinetic energy, transported to the interaction region on ground potential and collinearly overlapped with the X-ray photons of P04 along an effective absorption length of 1.7 m. The vacuum chamber base pressure of the interaction region was in the order of 1 × 10−9 hPa.
At the nitrogen K-edge, the X-ray photons create an inner-shell hole in the ionic target which results in subsequent Auger decay. The excitation and ionisation is accompanied by possible shake-off processes and is followed by dissociation producing Nq+ (q = 2, 3) ions. These ions were separated from the target ionic beam with a second magnetic-dipole mass spectrometer. The Nq+ (q = 2, 3) ions have been counted with a channeltron as a function of the photon energy.
The yield of photoexcited ions of an atomic nitrogen ion N+ target was measured as a reference to help identifying the spectroscopic features for the molecular targets, as recently done for IH+.42 The X-ray photons delivered by the P04 beamline of PETRA III were dispersed by a 400 lines per mm variable line spacing grating (VLS) favouring high photon flux in the order of 1 × 1012 photons per s to 7.5 × 1013 photons per s for monochromator exit slits from 20 μm to 1500 μm. The molecular ion yields were measured with a monochromator exit slit of 500 μm and for the atomic ion yield a slit width of 50 μm was chosen. This results in an energy bandwidth in the order of ΔE = 0.5 eV for the molecular spectra and ΔE = 0.05 eV for the atomic spectrum. The energy axis of the P04 monochromator was calibrated with the known resonance positions of the atomic N+ 1s → 2p resonance group36 (see Fig. 3a). The resulting uncertainty of the experimental photon-energy scale is estimated to be approximately 0.1 eV.
Theory details
To assign the observed ion yield peaks with X-ray absorption resonances, we have conducted X-ray absorption cross section calculations with the XMOLECULE toolkit.45,46 The calculations are based on geometries obtained from geometry optimisation for the respective NHy+ cationic ground state using GAMESS47 on the ROHF/MP2 level employing a 6-311G(d,p) basis set.48 We have calculated the orientation-averaged X-ray absorption cross section,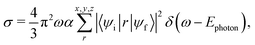 | (1) |
A similar approach for calculating X-ray absorption spectra has been employed in earlier works51,52 but with a slightly different configurational space. The mentioned energy shift relative to the experimental data could potentially be avoided by using an orbital set for the final core excited state that has been optimised in the presence of the core hole and might result in an improved modelling of core-hole relaxation effects. However, the calculation of electronic transitions (eqn (1)) becomes computationally very demanding with different orbital sets for initial and final state in combination with a large configuration space. We think that the resulting energy shift of 1 eV to 2 eV is acceptable for the purposes of our study and therefore decided keep a common orbital set.
Results and discussion
The normalised ion yields Y measured for the target ion series NHy+ (y = 0–3) are shown in Fig. 2 from y = 0 (panel a) to y = 3 (panel d). The curves consist of the N3+ ion yield for the atomic N+ target and the N2+ ion yield for the molecular targets NHy+ (y = 1–3). The N2+ and N+ product channels, for the N+ and NH+ primary beams, respectively, exhibited excessive backgrounds from collisions with residual gas targets such that no meaningful photoinduced ion yields could be measured in these product channels. | ||
| Fig. 2 Product ion yields Y (see eqn (2)) from photoionisation and/or photofragmentation of the target ion series NHy+ (y = 0–3) (a) N+ → N3+, (b) NH+ → N2+, (c) NH2+ → N2+, and (d) NH3+ → N2+ measured in the photon energy region of the nitrogen K-edge. The light blue vertical lines mark the energy region of the atomic nitrogen 1s → 2p resonance group in panel (a). For the panels (b)–(d) the shift of the respective molecular resonances to lower excitation energies can be seen. For details of the comparison of the different decay channels of the atomic and molecular targets see the main text. | ||
The normalised photoinduced ion yield Y is given by the background-subtracted ion count rate R measured with the channeltron detector divided by the target ion current Iion and photon current ϕph,
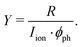 | (2) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) np configuration. For configurations where a two-step Auger cascade is energetically not allowed, i.e. for n = 2, in particular, a double Auger process is required. Such processes are known to appear with a probability of a few percent following atomic K shell ionisation of light elements.40,53–58 For the molecular ions NHy+ (y = 1–3) there are more pathways, resonant and non-resonant, to create the detected N2+ fragment compared to the two ionisation processes needed for the N+ target to reach N3+, since hydrogen partners can leave the system either as neutral atoms or as protons. N2+, for instance, can be created from NH+via single Auger decay and release of a neutral hydrogen or via double Auger decay and release of a proton. From NH2+ and NH3+ the creation of N2+ ions can be expected to be less likely, since it requires more hydrogen to leave the molecule as neutral atoms. This trend is reflected in our data by a steep drop of the N2+-count rate when gradually changing the molecular target from NH+ to NH3+ (with each additional hydrogen the ion yield drops by an order of magnitude). However, since our experimental set-up does not allow us to detect neutral fragments or N+ ions, we have no measure on competing fragmentation channels.
np configuration. For configurations where a two-step Auger cascade is energetically not allowed, i.e. for n = 2, in particular, a double Auger process is required. Such processes are known to appear with a probability of a few percent following atomic K shell ionisation of light elements.40,53–58 For the molecular ions NHy+ (y = 1–3) there are more pathways, resonant and non-resonant, to create the detected N2+ fragment compared to the two ionisation processes needed for the N+ target to reach N3+, since hydrogen partners can leave the system either as neutral atoms or as protons. N2+, for instance, can be created from NH+via single Auger decay and release of a neutral hydrogen or via double Auger decay and release of a proton. From NH2+ and NH3+ the creation of N2+ ions can be expected to be less likely, since it requires more hydrogen to leave the molecule as neutral atoms. This trend is reflected in our data by a steep drop of the N2+-count rate when gradually changing the molecular target from NH+ to NH3+ (with each additional hydrogen the ion yield drops by an order of magnitude). However, since our experimental set-up does not allow us to detect neutral fragments or N+ ions, we have no measure on competing fragmentation channels.
Distinct characteristic behaviour can be observed in the ion yield spectra of Fig. 2. On the one hand, below the 1s ionisation threshold a strong resonance group is observed in each spectrum which originates in the atomic case from the transition 1s → 2p. At higher energies, except for NH+, the first 1s ionisation threshold is visible together with Rydberg resonances. Increasing the photon energy and passing the ionisation threshold one may expect an increase in the ion yield, since the initial absorption leads to emission of an electron. For the N+, NH2+, and NH3+ cations, such an increase of the ion yield above the threshold is clearly seen. Remarkably, almost no increase in the ion yield is seen for NH+ (panel b in Fig. 2). This observation may indicate that the mechanisms that lead to creation of N2+ ions via emission of additional electrons and release of hydrogen atoms differ for the above and below threshold regions for NH+ and any other ion in the series NHy+.
The blue dashed lines in Fig. 2 mark the energy region of the atomic nitrogen 1s → 2p resonance group. As can be seen in the spectra for the molecular ionic series NHy (y = 1–3), the respective molecular resonance shifts towards lower energies depending on the number of hydrogen atoms bound to the central nitrogen atom. This is due to increasing hybridisation between the nitrogen valence and hydrogen orbitals. For the atomic nitrogen ion N+, we observe sharp Rydberg lines below and above the lowest 1s ionisation threshold (Fig. 3b), while for the molecular targets the resonance features are broader and overlap with one another. In the following we discuss the assignments of the X-ray absorption resonances for each target NHy+ (y = 0–3) in more detail.
Atomic target N+
The ground state of the N+ cation is 1s22s22p2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3P. Within the experimental ion beam, a non-statistical mixture of several meta-stable terms exists, as has been pointed out before.36 These various states result in a multitude of multiplet lines as observed in Fig. 3. For comparison of the measured N3+ ion yield (orange dots in Fig. 3) with the calculated X-ray absorption resonance positions (vertical light blue lines in Fig. 3) we take into account the terms 1s22s22p2
3P. Within the experimental ion beam, a non-statistical mixture of several meta-stable terms exists, as has been pointed out before.36 These various states result in a multitude of multiplet lines as observed in Fig. 3. For comparison of the measured N3+ ion yield (orange dots in Fig. 3) with the calculated X-ray absorption resonance positions (vertical light blue lines in Fig. 3) we take into account the terms 1s22s22p2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3P, 1s22s22p2
3P, 1s22s22p2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1D, 1s22s22p2
1D, 1s22s22p2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1S, and 1s22s12p3
1S, and 1s22s12p3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5S with the relative weights of 0.54, 0.11, 0.03, 0.32, respectively, as suggested by Gharaibeh et al.36 For a better comparison, we have shifted the calculated transition energies by 2.1 eV to higher energies for the region showing 1s → 2p excitations (below 405 eV) and by 1.1 eV for the region showing higher excitations above 405 eV. Overall, the calculated data show good agreement with the measured ion yield for the energy position of the resonances values below 427 eV. The discrepancies at photon energies above 427 eV are due to the limited capability of the employed basis set to adequatly describe the electronic continuum as discussed in the section Theory Details. For the region below 405 eV, the ion-yield peak heights coincide with the calculated absorption cross section. However, for the region above 415 eV the calculated absorption strength does not always agree with the measured abundance of ions. A particularly drastic disagreement is seen for the 1s22s12p3
5S with the relative weights of 0.54, 0.11, 0.03, 0.32, respectively, as suggested by Gharaibeh et al.36 For a better comparison, we have shifted the calculated transition energies by 2.1 eV to higher energies for the region showing 1s → 2p excitations (below 405 eV) and by 1.1 eV for the region showing higher excitations above 405 eV. Overall, the calculated data show good agreement with the measured ion yield for the energy position of the resonances values below 427 eV. The discrepancies at photon energies above 427 eV are due to the limited capability of the employed basis set to adequatly describe the electronic continuum as discussed in the section Theory Details. For the region below 405 eV, the ion-yield peak heights coincide with the calculated absorption cross section. However, for the region above 415 eV the calculated absorption strength does not always agree with the measured abundance of ions. A particularly drastic disagreement is seen for the 1s22s12p3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5S → 1s12s12p33p1
5S → 1s12s12p33p1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5P transition at 419 eV. The signal in the measured ion yield is remarkably low (magnified by a factor of 200 in Fig. 3b) in contrast to the relatively strong calculated absorption cross section. The 1s12s12p33p1
5P transition at 419 eV. The signal in the measured ion yield is remarkably low (magnified by a factor of 200 in Fig. 3b) in contrast to the relatively strong calculated absorption cross section. The 1s12s12p33p1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5P term, e.g., has a particularly high spin that may lead to blocking of certain Auger decay channels, since the spin of most electrons does not match the spin of the core hole. The production of N3+ ions might therefore be suppressed for this core excited configuration relative to other core excited configurations.
5P term, e.g., has a particularly high spin that may lead to blocking of certain Auger decay channels, since the spin of most electrons does not match the spin of the core hole. The production of N3+ ions might therefore be suppressed for this core excited configuration relative to other core excited configurations.
Our assignment of the individual resonances for the first resonance region is given in Table 1 and compared with previous calculations using the multi-configuration Dirac–Fock (MCDF) method and the R-matrix method.36 Most of our results match those of previous calculations, however, there is a slight discrepancy regarding the assignment of the 1s22s12p3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5S → 1s12s12p4
5S → 1s12s12p4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5P transition. In the previous work36 this line is, according to the R-matrix calculation, associated with the first resonance at 399.8 eV whereas we identify this transitions at ≃401.5 eV (in agreement with the previous MCDF calculation36).
5P transition. In the previous work36 this line is, according to the R-matrix calculation, associated with the first resonance at 399.8 eV whereas we identify this transitions at ≃401.5 eV (in agreement with the previous MCDF calculation36).
| Resonance transition | CI present work (eV) | MCDF (eV) | R-Matrix (eV) |
|---|---|---|---|
| Gharaibeh et al.36 | |||
1s22s22p2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3P → 1s12s22p3 3P → 1s12s22p3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3D 3D |
399.8 | 399.9 | 399.7 |
1s22s22p2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1S → 1s12s22p3 1S → 1s12s22p3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1P 1P |
400.1 | 400.6 | 400.2 |
1s22s22p2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3P → 1s12s22p3 3P → 1s12s22p3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3S 3S |
400.6 | 400.0 | 400.6 |
1s22s22p2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1D → 1s12s22p3 1D → 1s12s22p3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1D 1D |
400.6 | 400.0 | 400.7 |
1s22s12p3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5S → 1s12s12p4 5S → 1s12s12p4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5P 5P |
401.5 | 400.8 | 399.9 |
1s22s22p2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3P → 1s12s22p3 3P → 1s12s22p3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3P 3P |
402.5 | 402.3 | 401.3 |
1s22s22p2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1D → 1s12s22p3 1D → 1s12s22p3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1P 1P |
403.3 | 402.5 | 402.3 |
Overall we conclude that the applied calculation procedure is sufficient to conduct assignment of the resonant transitions.
Molecular target NH+
The NH+ cation has two close lying nearly degenerate terms31,32 that both result in an absorption signal from our ion beam: 1σ22σ23σ21π1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2Π and 1σ22σ23σ11π2
2Π and 1σ22σ23σ11π2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4Σ−.
4Σ−.
With our geometry optimisation we obtained a bond distance of 1.065 Å for the 2Π term and of 1.080 Å for the 4Σ− term. Fig. 4 shows the calculated absorption resonances (light blue vertical lines) for the NH+ cation compared to the measured N2+ ion yield (dark blue dots). In the figure we used 0.8 and 0.2 as weights for the 2Π and 4Σ− terms, respectively. The red dashed line in Fig. 4 is the result of a convolution of the calculated resonances characterised by their positions and absorption oscillator strengths with a 400 meV FWHM Gaussian function for the lower energy part (392 eV to 404 eV) and with 3 eV FWHM Gaussian function for the higher energy part. As for the spectrum of the atomic N+ ion, the calculated transition lines have been shifted by 2.1 eV for the region 390 eV to 405 eV and by 1.1 eV for the region above 405 eV.
In the region below 405 eV one can clearly identify four peaks in the experimental spectrum. The weak resonance at 395 eV can be assigned to a 1σ4Σ− → 3σ4Σ− excitation. In the region 397 eV to 400 eV our calculation predicts four excitation resonances 4Σ− → 4Π, 2Π → 2Δ, 2Π → 2Σ−, and 2Π → 2Σ+. However, in the measured ion yield one can clearly resolve three peaks, only. The calculation suggests that the 2Π → 2Δ transition is hidden between the 4Σ → 4Π and the 2Π → 4Σ− resonances. The remaining resonance peak at 399.5 eV can be associated with a 2Π → 2Σ− transition.
Above an excitation energy of 405 eV the resonance structures in the measured ion yield are very broad. This might be attributed to the large broadening due to a steep potential energy curve in the final state. The resonance at 411 eV is rather isolated. According to our calculation, the dominant broad peak around 411 eV can mainly be assigned to a 1σ → 4σ (2Π → 2Π) excitation. Above 415 eV we see the ion yield decreasing with photon energy, whereas the calculated convoluted absorption cross section suggests rather the opposite trend. The assignments for the dominant transitions in the NH+-XAS are summarised in Table 2.
| Resonance assignment | PIPE (experiment) (eV) | CI (theory) (eV) | |
|---|---|---|---|
| Initial state | |||
1σ22σ23σ11π2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4Σ− 4Σ− |
1σ → 3σ4Σ− | 394.9 | 394.8 |
| 1σ → 1π4Π | 397.8 | 398.0 | |
| 1σ → 4σ4Σ− | 409.3 | ||
| 1σ → 4σ4Σ− | 412.4 | ||
1σ22σ23σ21π1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2Π 2Π |
1σ → 1π2Δ | 398.8 | 398.2 |
| 1σ → 1π2Σ− | 398.8 | 398.6 | |
| 1σ → 1π2Σ+ | 399.6 | 399.7 | |
| 1σ → 4σ4Π | 411.4 | ||
| 1σ → 4σ4Π | 414.3 | ||
Molecular target NH2+
The NH2+ molecular cation has C2v symmetry, but has an almost linear geometry with a very flat bending potential in its ground state.59,60 The cationic ground level is (1a1)2(2a1)2(1b2)2(3a1)1(1b1)1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3B1. For the X-ray absorption calculation we also included the closed shell level (1a1)2(2a1)2(1b2)2(3a1)2
3B1. For the X-ray absorption calculation we also included the closed shell level (1a1)2(2a1)2(1b2)2(3a1)2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1A1.
1A1.
From geometry optimisation, we obtain an NH bond distance of 1.03 Å and a bond angle of 150° for the triplet level and a bond distance of 1.05 Å with a bond angle of 107° for the singlet level. Fig. 5 shows the calculated absorption resonance positions (light blue vertical lines) for the NH2+ cation compared to the measured N2+ ion yield (green dots). The orange dashed line is a convolution of the calculated resonance position and strength with a 1.0 eV FWHM Gaussian function. For better comparison, the calculated absorption lines have been shifted by 1.8 eV in the region below 405 eV and by 1.0 eV in the region above 405 eV. Because of the almost linear geometry of the molecular cation, the 1a1 → 3a1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3B1 and 1a1 → 1b1
3B1 and 1a1 → 1b1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3A1 excitations are almost degenerate. As can be seen in Fig. 5a, the calculated positions of these two resonances agree with the ion yield peak at 396 eV. The 1a1 → 1b1 resonance for the tilted geometry of the 1A1 cationic level is at distinguishably higher energies.
3A1 excitations are almost degenerate. As can be seen in Fig. 5a, the calculated positions of these two resonances agree with the ion yield peak at 396 eV. The 1a1 → 1b1 resonance for the tilted geometry of the 1A1 cationic level is at distinguishably higher energies.
For the higher excitation energies above 405 eV, the observed ion yield peaks can be assigned to calculated absorption lines of the 3B1 initial level into dipole-allowed higher excited levels of the irreducible representations 3B1 or 3A2. Overall good agreement can be seen for resonances up to 420 eV. The assignments are summarised in Table 3.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3B1) or excited level ((1a1)2(2a1)2(1b2)2(3a1)2
3B1) or excited level ((1a1)2(2a1)2(1b2)2(3a1)2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1A1). The assignment is done according to the dominant CI configuration. The uncertainty of the experimental values is ΔEph = 0.1 eV
1A1). The assignment is done according to the dominant CI configuration. The uncertainty of the experimental values is ΔEph = 0.1 eV
| Resonance assignment | PIPE (experiment) (eV) | CI (theory) (eV) | |
|---|---|---|---|
| Initial state (val. conf.) | |||
(3a1)1(1b1)1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3B1 3B1 |
1a1 → 3a1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3B1 3B1 |
396.4 | 396.1 |
1a1 → 1b1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3A1 3A1 |
396.4 | 396.5 | |
1a1 → 4a1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3B1 3B1 |
407.2 | 407.4 | |
1a1 → 2b2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3A2 3A2 |
409.6 | 409.8 | |
1a1 → 2b1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3A1 3A1 |
412.7 | 412.8 | |
1a1 → 5a1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3B1 3B1 |
412.7 | 412.8 | |
1a1 → 2b2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3A2 3A2 |
413.0 | ||
1a1 → 3b2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3A2 3A2 |
416.1 | 415.6 | |
1a1 → 2b1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3A1 3A1 |
416.1 | 416.4 | |
1a1 → 5a1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3B1 3B1 |
416.1 | 416.4 | |
(3a1)2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1A1 1A1 |
1a1 → 1b1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1B1 1B1 |
397.5 | |
1a1 → 4a1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1A1 1A1 |
410.2 | ||
1a1 → 2b2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1B2 1B2 |
411.4 | ||
1a1 → 2b1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1B1 1B1 |
415.4 | ||
1a1 → 5a1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1A1 1A1 |
415.6 | ||
Molecular target NH3+
The neutral NH3 molecule has a pyramidal geometry and hence its symmetry group is C3v.25,27 The cation NH3+ has a planar geometry and thus belongs to symmetry group D3h.61 The electronic ground state of the cation is . Geometry optimisation gives an NH bond length of 1.024 Å. Fig. 6 compares the calculated absorption lines (light blue vertical lines) for the NH3+ cation with the measured N2+ ion yield (red dots). The orange dashed line is a convolution of the calculated resonance position and strength with a 1.0 eV FWHM Gaussian function. The calculated transitions have been shifted by 1.6 eV for the region below 405 eV and by 1.2 eV above 405 eV.
. Geometry optimisation gives an NH bond length of 1.024 Å. Fig. 6 compares the calculated absorption lines (light blue vertical lines) for the NH3+ cation with the measured N2+ ion yield (red dots). The orange dashed line is a convolution of the calculated resonance position and strength with a 1.0 eV FWHM Gaussian function. The calculated transitions have been shifted by 1.6 eV for the region below 405 eV and by 1.2 eV above 405 eV.
Below 405 eV the single ion yield peak must be associated with the 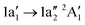 excitation, as indicated by the calculated transition. Above 405 eV several peaks can be observed in the measured ion yield. These peaks match with those of the calculated transitions into higher excited states up to excitation energies of 420 eV. The assignment of individual resonances is summarised in Table 4.
excitation, as indicated by the calculated transition. Above 405 eV several peaks can be observed in the measured ion yield. These peaks match with those of the calculated transitions into higher excited states up to excitation energies of 420 eV. The assignment of individual resonances is summarised in Table 4.
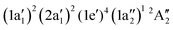 ) (see Fig. 6). The assignment is done according to the dominant CI configuration. The uncertainty of the experimental values is ΔEph = 0.1 eV
) (see Fig. 6). The assignment is done according to the dominant CI configuration. The uncertainty of the experimental values is ΔEph = 0.1 eV
Chemical shift
As indicated by the light blue dashed lines in Fig. 2, the respective 1s → 2p resonances shift to lower excitation energies when going from the atomic cation N+ to the molecular cation NH3+. For the energies of the 1s → 2p resonance peaks, we obtain a systematic sequence of 399.8 eV, 398.8 eV, 396.4 eV, 395.2 eV. With more hydrogen atoms in the molecule, additional electrons contribute to core-hole screening effects62 and lower the energy of the core excited state. As discussed previously,42 this effect leads to a systematic lowering of core excitation resonances. To further confirm this trend, we calculated the ionisation potential of the molecular cations using a Δ SCF calculation, in which the ionisation energy is obtained from separate SCF calculations for the initial and final electronic states, respectively (see Table 5). As can be seen, apart from the metastable configurations that involve vacancies in 2s/3σ orbitals (5S for N+ and 4Σ+ for NH+), the ionisation potential shifts systematically to lower energies with increasing number of hydrogen atoms.At 400 eV, in Fig. 2 a clear shift of the resonant structures to lower photon energies with increasing number y of H atoms is found for the series of free NHy+ ions. This is contrary to shifts found for the alkylamines,37 where the N 1s resonances are shifting to higher photon energy with increasing number of H atoms.
Absolute count rate for the lower and upper resonance regions
As indicated by the different scale on the calculated cross section axes in Fig. 3–6(a) and (b), the absorption lines for the higher Rydberg region (>415 eV) are weaker than for the first resonance region (390 eV to 405 eV). In contrast, the measured N2+ ion yield is significantly larger in the Rydberg region compared to the first resonance region. This clearly indicates that the relative probability for creating N2+ ions is larger for the more highly excited resonances than for the resonances with lower excitation energies. The relative production yields of N2+ subsequent to excitation into these two resonance regions can be read off the relative change of the ion yield/cross section scale in Fig. 3–6. For N+ we observe a factor ≃5 higher N2+ production rate, for NH+ the factor is ≃1.8, for NH2+ the factor is ≃3.7, and for NH3+ the factor is ≃2.3.Comparison with glycine
Fig. 7 shows a comparison between the absorption spectrum of glycine around the nitrogen K-edge63 and our measured ion yield of NH2+. The data of glycine was scaled to match the intensity at energies above the K-edge and the figure is drawn with two different energy axes, because of the different chemical environment of the two molecules. As can be seen, the first resonances below the K-edge are prominent in both spectra, but at higher energies the resonances are much smoother in glycine. The three resonances for glycine are assigned to excitations into virtual orbitals with the local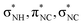 orbital character.63 This assignment matches the assignment for NH2+ attributing the three major resonances mainly to excitations into the 2b2, 2b1, and 5a1 orbitals, corresponding to local
orbital character.63 This assignment matches the assignment for NH2+ attributing the three major resonances mainly to excitations into the 2b2, 2b1, and 5a1 orbitals, corresponding to local  , px, and py orbital character, respectively.
, px, and py orbital character, respectively.
 | ||
| Fig. 7 Comparison of the ion yield of the molecular ion NH2+ (green dots) and the absorption spectrum of glycine63 (orange line) at the nitrogen K-edge. The photon energy and ion yield scale of glycine is shifted and scaled to match NH2+. The two photon energy axes have different step widths. | ||
In contrast, the spectra of glycine shows some significant differences compared to the spectra of NH3+ (see Fig. 6). Thus, this comparison between NH2+, NH3+ and glycine demonstrates that the spectra of ionic fragments can be useful to identify building blocks of more complex molecules.
Conclusions
The N2+ ion yields of the target molecular cations NHy+ (y = 1–3) have been measured in the energy range of the nitrogen K-edge and their absorption resonance structure has been determined. We have calculated X-ray absorption cross sections based on the configuration interaction method utilising the XMOLECULE toolkit. Our calculations show excellent agreement with the ion yield data. For most of the observed transitions, the ion yield seems to correlate with the calculated absorption strength. However, we quantify a trend for a lower abundance of N2+ ions for excitation in the first resonance region compared to higher resonances. This trend as well as particular deviations (e.g., the very low ion yield for the N+ 1s22s12p3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5S → 1s12s12p33p1
5S → 1s12s12p33p1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5P transition) indicate that the mechanism behind the production of the highly charged ions depends on the specific state populated by the X-ray absorption. In future studies, this effect will be further investigated by comparing the relative ion yields of different fragment charges.
5P transition) indicate that the mechanism behind the production of the highly charged ions depends on the specific state populated by the X-ray absorption. In future studies, this effect will be further investigated by comparing the relative ion yields of different fragment charges.
The measured ion yield resonances have been identified by the calculated absorption transitions (see Tables 2–4). Depending on the number of hydrogen atoms bound to the nitrogen atom we report characteristic structures in the X-ray absorption. Each additional hydrogen atom and its electron has a significant impact on the spectral features of the different absorption spectra (Fig. 2). These characteristic resonance structures in the NHy+ series might help to identify different molecular cationic (sub-)groups within larger molecular complexes such as the amino acid glycine, for example. Nevertheless, the comparison of the free ions NHy+ with the amine group in different solutions and molecular environments shows the tremendous influence also of the larger chemical surrounding.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This research was carried out at the synchrotron light source PETRA III at DESY, a member of the Helmholtz Association (HGF). We would like to thank J. Buck, G. Hartmann, F. Scholz, J. Seltmann, and J. Viefhaus for assistance in using beamline P04. The design and construction of PIPE and this work was funded by German ministry for education and research (BMBF) under contracts 05KS7RG1, 05KS7GU2, 05KS7KE1, 05KS7RF2, 05K10RG1, 05K10GUB, 05K10KEA, and 05K10RF2 within the “Verbundforschung” funding scheme. KM and MM acknowledge funding by the Deutsche Forschungsgemeinschaft (DFG) via SFB925/A3. AM acknowledges funding by Deutsche Forschungsgemeinschaft via grant Mu 1068/22. SK acknowledges the funding of the EUCALL project within the European Union's Horizon 2020 research and innovation programme under the grant agreement no. 654220. SDö, SDe, LS, KS, and SB were supported by the Helmholtz Initiative and Networking Fund through the Young Investigator Groups Program. KS and SB acknowledge support from the Deutsche Forschungsgemeinschaft, project B03/SFB755.Notes and references
- H. N. Chapman, P. Fromme, A. Barty, T. A. White, R. A. Kirian, A. Aquila, M. S. Hunter, J. Schulz, D. P. DePonte, U. Weierstall, R. B. Doak, F. R. N. C. Maia, A. V. Martin, I. Schlichting, L. Lomb, N. Coppola, R. L. Shoeman, S. W. Epp, R. Hartmann, D. Rolles, A. Rudenko, L. Foucar, N. Kimmel, G. Weidenspointner, P. Holl, M. Liang, M. Barthelmess, C. Caleman, S. Boutet, M. J. Bogan, J. Krzywinski, C. Bostedt, S. Bajt, L. Gumprecht, B. Rudek, B. Erk, C. Schmidt, A. Homke, C. Reich, D. Pietschner, L. Struder, G. Hauser, H. Gorke, J. Ullrich, S. Herrmann, G. Schaller, F. Schopper, H. Soltau, K.-U. Kuhnel, M. Messerschmidt, J. D. Bozek, S. P. Hau-Riege, M. Frank, C. Y. Hampton, R. G. Sierra, D. Starodub, G. J. Williams, J. Hajdu, N. Timneanu, M. M. Seibert, J. Andreasson, A. Rocker, O. Jonsson, M. Svenda, S. Stern, K. Nass, R. Andritschke, C.-D. Schroter, F. Krasniqi, M. Bott, K. E. Schmidt, X. Wang, I. Grotjohann, J. M. Holton, T. R. M. Barends, R. Neutze, S. Marchesini, R. Fromme, S. Schorb, D. Rupp, M. Adolph, T. Gorkhover, I. Andersson, H. Hirsemann, G. Potdevin, H. Graafsma, B. Nilsson and J. C. H. Spence, Nature, 2011, 470, 73 CrossRef CAS PubMed.
- H. N. Chapman, C. Caleman and N. Timneanu, Philos. Trans. R. Soc., B, 2014, 369, 20130313 CrossRef PubMed.
- J. Czapla-Masztafiak, J. Szlachetko, C. Milne, E. Lipiec, J. Sá, T. Penfold, T. Huthwelker, C. Borca, R. Abela and W. Kwiatek, Biophys. J., 2016, 110, 1304 CrossRef CAS PubMed.
- S. Bari, D. Egorov, T. L. C. Jansen, R. Boll, R. Hoekstra, S. Techert, V. Zamudio-Bayer, C. Bülow, R. Lindblad, G. Leistner, A. Ławicki, K. Hirsch, P. S. Miedema, B. von Issendorff, J. T. Lau and T. Schlathölter, Chem. – Eur. J., 2018, 24, 7631 CrossRef CAS PubMed.
- A. Barty, J. Küpper and H. N. Chapman, Annu. Rev. Phys. Chem., 2013, 64, 415 CrossRef CAS PubMed.
- C. Kupitz, S. Basu, I. Grotjohann, R. Fromme, N. A. Zatsepin, K. N. Rendek, M. S. Hunter, R. L. Shoeman, T. A. White, D. Wang, D. James, J.-H. Yang, D. E. Cobb, B. Reeder, R. G. Sierra, H. Liu, A. Barty, A. L. Aquila, D. Deponte, R. A. Kirian, S. Bari, J. J. Bergkamp, K. R. Beyerlein, M. J. Bogan, C. Caleman, T.-C. Chao, C. E. Conrad, K. M. Davis, H. Fleckenstein, L. Galli, S. P. Hau-Riege, S. Kassemeyer, H. Laksmono, M. Liang, L. Lomb, S. Marchesini, A. V. Martin, M. Messerschmidt, D. Milathianaki, K. Nass, A. Ros, S. Roy-Chowdhury, K. Schmidt, M. Seibert, J. Steinbrener, F. Stellato, L. Yan, C. Yoon, T. A. Moore, A. L. Moore, Y. Pushkar, G. J. Williams, S. Boutet, R. B. Doak, U. Weierstall, M. Frank, H. N. Chapman, J. C. H. Spence and P. Fromme, Nature, 2014, 513, 261 CrossRef CAS PubMed.
- I. D. Young, M. Ibrahim, R. Chatterjee, S. Gul, F. D. Fuller, S. Koroidov, A. S. Brewster, R. Tran, R. Alonso-Mori, T. Kroll, T. Michels-Clark, H. Laksmono, R. G. Sierra, C. A. Stan, R. Hussein, M. Zhang, L. Douthit, M. Kubin, C. de Lichtenberg, L. Vo Pham, H. Nilsson, M. H. Cheah, D. Shevela, C. Saracini, M. A. Bean, I. Seuffert, D. Sokaras, T.-C. Weng, E. Pastor, C. Weninger, T. Fransson, L. Lassalle, P. Bräuer, P. Aller, P. T. Docker, B. Andi, A. M. Orville, J. M. Glownia, S. Nelson, M. Sikorski, D. Zhu, M. S. Hunter, T. J. Lane, A. Aquila, J. E. Koglin, J. Robinson, M. Liang, S. Boutet, A. Y. Lyubimov, M. Uervirojnangkoorn, N. W. Moriarty, D. Liebschner, P. V. Afonine, D. G. Waterman, G. Evans, P. Wernet, H. Dobbek, W. I. Weis, A. T. Brunger, P. H. Zwart, P. D. Adams, A. Zouni, J. Messinger, U. Bergmann, N. K. Sauter, J. Kern, V. K. Yachandra and J. Yano, Nature, 2016, 540, 453 CrossRef CAS PubMed.
- T. J. Penfold, I. Tavernelli, C. J. Milne, M. Reinhard, A. E. Nahhas, R. Abela, U. Rothlisberger and M. Chergui, J. Chem. Phys., 2013, 138, 014104 CrossRef CAS PubMed.
- R. Kaschner and D. Hohl, J. Phys. Chem. A, 1998, 102, 5111 CrossRef CAS.
- N. Mardirossian and M. Head-Gordon, Mol. Phys., 2017, 115, 2315 CrossRef CAS.
- T. Andersen, H. Kjeldsen, H. Knudsen and F. Folkmann, J. Phys. B: At., Mol. Opt. Phys., 2001, 34, L327 CrossRef CAS.
- G. Hinojosa, A. M. Covington, R. A. Phaneuf, M. M. Sant'Anna, R. Hernandez, I. R. Covington, I. Domínguez, J. D. Bozek, A. S. Schlachter, I. Álvarez and C. Cisneros, Phys. Rev. A: At., Mol., Opt. Phys., 2002, 66, 032718 CrossRef.
- G. Hinojosa, M. M. Sant'Anna, A. M. Covington, R. A. Phaneuf, I. R. Covington, I. Domínguez, A. S. Schlachter, I. Alvarez and C. Cisneros, J. Phys. B: At., Mol. Opt. Phys., 2005, 38, 2701 CrossRef CAS.
- J.-P. Mosnier, E. T. Kennedy, P. van Kampen, D. Cubaynes, S. Guilbaud, N. Sisourat, A. Puglisi, S. Carniato and J.-M. Bizau, Phys. Rev. A, 2016, 93, 061401 CrossRef.
- A. Puglisi, T. Miteva, E. T. Kennedy, J.-P. Mosnier, J.-M. Bizau, D. Cubaynes, N. Sisourat and S. Carniato, Phys. Chem. Chem. Phys., 2018, 20, 4415 RSC.
- C. Nordling, E. Sokolowski and K. Siegbahn, Phys. Rev., 1957, 105, 1676 CrossRef CAS.
- O. Travnikova, K. J. Børve, M. Patanen, J. Söderström, C. Miron, L. J. Sæthre, N. Mårtensson and S. Svensson, J. Electron Spectrosc. Relat. Phenom., 2012, 185, 191 CrossRef CAS.
- N. Mårtensson, E. Sokolowski and S. Svensson, J. Electron Spectrosc. Relat. Phenom., 2014, 193, 27 CrossRef.
- J. Higuchi, J. Chem. Phys., 1956, 24, 535 CrossRef CAS.
- G. Wight and C. Brion, J. Electron Spectrosc. Relat. Phenom., 1974, 4, 25 CrossRef CAS.
- R. N. Sodhi and C. Brion, J. Electron Spectrosc. Relat. Phenom., 1985, 36, 187 CrossRef CAS.
- S. Y. T. van de Meerakker, I. Labazan, S. Hoekstra, J. Küpper and G. Meijer, J. Phys. B: At., Mol. Opt. Phys., 2006, 39, S1077 CrossRef CAS.
- B.-M. Cheng, H.-C. Lu, H.-K. Chen, M. Bahou, Y.-P. Lee, A. M. Mebel, L. C. Lee, M.-C. Liang and Y. L. Yung, ApJ, 2006, 647, 1535 CrossRef CAS.
- D. Edvardsson, P. Baltzer, L. Karlsson, B. Wannberg, D. M. P. Holland, D. A. Shaw and E. E. Rennie, J. Phys. B: At., Mol. Opt. Phys., 1999, 32, 2583 CrossRef CAS.
- J. Schirmer, A. B. Trofimov, K. J. Randall, J. Feldhaus, A. M. Bradshaw, Y. Ma, C. T. Chen and F. Sette, Phys. Rev. A: At., Mol., Opt. Phys., 1993, 47, 1136 CrossRef CAS PubMed.
- A. Jürgensen and R. G. Cavell, Chem. Phys., 2001, 273, 77 CrossRef.
- K. Jakubowska, G. Vall-llosera, A. Kivimäki, M. Coreno, E. M. García, M. Stankiewicz and E. Rachlew, J. Phys. B: At., Mol. Opt. Phys., 2007, 40, 1489 CrossRef CAS.
- N. Walsh, A. Sankari, J. Laksman, T. Andersson, S. Oghbaie, F. Afaneh, E. P. Mansson, M. Gisselbrecht and S. L. Sorensen, Phys. Chem. Chem. Phys., 2015, 17, 18944 RSC.
- Y.-J. Wu, H.-C. Lu, H.-K. Chen, B.-M. Cheng, Y.-P. Lee and L. C. Lee, J. Chem. Phys., 2007, 127, 154311 CrossRef PubMed.
- Y. Senba, T. Goya, H. Yoshida and A. Hiraya, J. Electron Spectrosc. Relat. Phenom., 2005, 144, 195 CrossRef.
- J. M. Amero and G. J. Vázquez, Int. J. Quantum Chem., 2004, 99, 353 CrossRef CAS.
- J. M. Amero and G. J. Vázquez, Int. J. Quantum Chem., 2005, 101, 396 CrossRef CAS.
- J. C. Stephens, Y. Yamaguchi and H. F. Schaefer III, THEOCHEM, 1999, 461, 41 CrossRef.
- S. Willitsch, F. Merkt, M. Kállay and J. Gauss, Mol. Phys., 2006, 104, 1457 CrossRef CAS.
- J. Lecointre, J. J. Jureta and P. Defrance, J. Phys. B: At., Mol. Opt. Phys., 2010, 43, 105202 CrossRef.
- M. F. Gharaibeh, J. M. Bizau, D. Cubaynes, S. Guilbaud, N. El Hassan, M. M. Al Shorman, C. Miron, C. Nicolas, E. Robert, C. Blancard and B. M. McLaughlin, J. Phys. B: At., Mol. Opt. Phys., 2011, 44, 175208 CrossRef.
- M. Ekimova, M. Kubin, M. Ochmann, J. Ludwig, N. Huse, P. Wernet, M. Odelius and E. T. J. Nibbering, J. Phys. Chem. B, 2018, 122, 7737 CrossRef PubMed.
- M. Ekimova, W. Quevedo, Ł. Szyc, M. Iannuzzi, P. Wernet, M. Odelius and E. T. J. Nibbering, J. Am. Chem. Soc., 2017, 139, 12773 CrossRef CAS PubMed.
- S. Schippers, S. Ricz, T. Buhr, A. B. Jr, J. Hellhund, K. Holste, K. Huber, H.-J. Schäfer, D. Schury, S. Klumpp, K. Mertens, M. Martins, R. Flesch, G. Ulrich, E. Rühl, T. Jahnke, J. Lower, D. Metz, L. P. H. Schmidt, M. Schöffler, J. B. Williams, L. Glaser, F. Scholz, J. Seltmann, J. Viefhaus, A. Dorn, A. Wolf, J. Ullrich and A. Müller, J. Phys. B: At., Mol. Opt. Phys., 2014, 47, 115602 CrossRef.
- A. Müller, D. Bernhardt, A. Borovik Jr., T. Buhr, J. Hellhund, K. Holste, A. Kilcoyne, S. Klumpp, M. Martins, S. Ricz, J. Seltmann, J. Viefhaus and S. Schippers, ApJ, 2017, 836, 166 CrossRef.
- J. Viefhaus, F. Scholz, S. Deinert, L. Glaser, M. Ilchen, J. Seltmann, P. Walter and F. Siewert, Nucl. Instrum. Methods Phys. Res., Sect. A, 2013, 710, 151 CrossRef CAS.
- S. Klumpp, A. A. Guda, K. Schubert, K. Mertens, J. Hellhund, A. Müller, S. Schippers, S. Bari and M. Martins, Phys. Rev. A, 2018, 97, 033401 CrossRef CAS.
- R. Trassl, P. Hathiramani, F. Broetz, J. B. Greenwood, R. W. McCullough, M. Schlapp and E. Salzborn, Phys. Scr., 1997, 1997, 380 CrossRef.
- M. Berglund and M. Wieser, Pure Appl. Chem., 2011, 83, 397 CAS.
- Y. Hao, L. Inhester, K. Hanasaki, S.-K. Son and R. Santra, Struct. Dyn., 2015, 2, 041707 CrossRef PubMed.
- L. Inhester, K. Hanasaki, Y. Hao, S.-K. Son and R. Santra, Phys. Rev. A, 2016, 94, 023422 CrossRef.
- M. W. Schmidt, K. K. Baldridge, J. A. Boatz, S. T. Elbert, M. S. Gordon, J. H. Jensen, S. Koseki, N. Matsunaga, K. A. Nguyen, S. Su, T. L. Windus, M. Dupuis and J. A. Montgomery, J. Comput. Chem., 1993, 14, 1347 CrossRef CAS.
- R. Krishnan, J. S. Binkley, R. Seeger and J. A. Pople, J. Chem. Phys., 1980, 72, 650 CrossRef CAS.
- K. Kaufmann, W. Baumeister and M. Jungen, J. Phys. B: At., Mol. Opt. Phys., 1989, 22, 2223 CrossRef CAS.
- Q. Sun, J. Comput. Chem., 2015, 36, 1664 CrossRef CAS PubMed.
- R. Arneberg, H. Ågren, J. Müller and R. Manne, Chem. Phys. Lett., 1982, 91, 362 CrossRef CAS.
- H. Ågren and R. Arneberg, Phys. Scr., 1983, 28, 80 CrossRef.
- T. A. Carlson and M. O. Krause, Phys. Rev. Lett., 1965, 14, 390–392 CrossRef CAS.
- T. A. Carlson and M. O. Krause, Phys. Rev. Lett., 1966, 17, 1079–1083 CrossRef CAS.
- N. Saito and I. H. Suzuki, Phys. Scr., 1994, 49, 80 CrossRef CAS.
- B. Kanngießer, M. Jainz, S. Brünken, W. Benten, C. Gerth, K. Godehusen, K. Tiedtke, P. van Kampen, A. Tutay, P. Zimmermann, V. F. Demekhin and A. G. Kochur, Phys. Rev. A: At., Mol., Opt. Phys., 2000, 62, 014702 CrossRef.
- A. Müller, A. Borovik, T. Buhr, J. Hellhund, K. Holste, A. Kilcoyne, S. Klumpp, M. Martins, S. Ricz, J. Viefhaus and S. Schippers, Phys. Rev. Lett., 2015, 114, 013002 CrossRef PubMed.
- S. Schippers, R. Beerwerth, L. Abrok, S. Bari, T. Buhr, M. Martins, S. Ricz, J. Viefhaus, S. Fritzsche and A. Müller, Phys. Rev. A, 2016, 94, 041401 CrossRef.
- S. T. Lee and K. Morokuma, J. Am. Chem. Soc., 1971, 93, 6863 CrossRef CAS.
- S. Willitsch, C. Jungen and F. Merkt, J. Chem. Phys., 2006, 124, 204312 CrossRef CAS PubMed.
- P. Hariharan and J. Pople, Mol. Phys., 1974, 27, 209 CrossRef CAS.
- L. Inhester, G. Groenhof and H. Grubmüller, J. Chem. Phys., 2013, 138, 164304 CrossRef CAS PubMed.
- O. Plekan, V. Feyer, R. Richter, M. Coreno, M. de Simone, K. C. Prince and V. Carravetta, J. Electron Spectrosc. Relat. Phenom., 2007, 155, 47 CrossRef CAS.
Footnote |
| † These authors contributed equally to this work. |
| This journal is © the Owner Societies 2019 |