Snowball formation for Cs⁺ solvation in molecular hydrogen and deuterium

Abstract

Interactions of atomic cations with molecular hydrogen are of interest for a wide range of applications in hydrogen technologies. These interactions are fairly strong despite being non-covalent, hence one can ask whether hydrogen molecules would form dense, solid-like, solvation shells around the ion (snowballs) or rather a more weakly bound compound. In this work, the interactions between Cs⁺ and H₂ are studied both experimentally and computationally. Isotopic substitution of H₂ by D₂ is also investigated. On the one hand, helium nanodroplets doped with cesium and hydrogen or deuterium are ionized by electron impact and the (H₂/D₂)_nCs⁺ (up to n = 30) clusters formed are identified via mass spectrometry. On the other hand, a new analytical potential energy surface, based on ab initio calculations, is developed and used to study cluster energies and structures by means of classical and quantum-mechanical Monte Carlo methods. The most salient features of the measured ion abundances are remarkably mimicked by the computed evaporation energies, particularly for the clusters composed of deuterium. This result supports the reliability of the present potential energy surface and allows us to recommend its use in related systems. Clusters with either twelve H₂ or D₂ molecules stand out for their stability and quasi-rigid icosahedral structures. However, the first solvation shell involves thirteen or fourteen molecules for hydrogenated or deuterated clusters, respectively. This shell retains its internal structure when extra molecules are added to the second shell and is nearly solid-like, especially for the deuterated clusters. The role played by three-body induction interactions as well as the rotational degrees of freedom is analyzed and they are found to be significant (up to 15% and 18%, respectively) for the molecules belonging to the first solvation shell.

---

Introduction

Interactions between molecular hydrogen and cations of metallic atoms (H₂–M⁺) are in general non-covalent but relatively strong, as they are dominated by charge-quadrupole electrostatic as well as charge-induced electric dipole forces.^1,2 Due to these characteristics, metallic cations can be expected to solvate in hydrogen, with the formation of one or more dense, solid-like, solvation shells, similar to the well-known Atkins snowballs formed by the solvation of ions in helium.³ Properties of hydrogen as a solvent^4–6 differ from those of helium (due to differences in mass, polarizability, onset of superfluidity, internal degrees of freedom, etc.), hence, it is worth exploring the impact of this alternative quantum solvent. There is also much interest in H₂–M⁺ interactions for applications of reversible storage of hydrogen in porous materials,^7–11 where dopant metal cations act as centers to which hydrogen molecules attach. Moreover, different nuclear quantum effects in H₂ and D₂ have been proposed to exploit selective adsorption¹² and isotope separation¹³ in metal-doped materials, processes of paramount importance for the development of new fusion reactors.

In contrast to the solvation of ions in helium,^14–23 studies on (H₂)_nM⁺ clusters are scarce and limited to small cluster sizes.^5,24–29 Clampitt and Jefferies²⁴ carried out mass spectrometry measurements of (H₂)_nLi⁺ clusters up to n = 7 and found indications that Li⁺ is solvated by six H₂ molecules, a conjecture that was later confirmed theoretically.^5,27–29 Interestingly, a study of the potential energy minima of these clusters⁵ led the authors to suggest that, while the first solvation shell of Li⁺ is solid-like, this shell screens the charge of the cation so that the outer shells become more diffuse. No further experiments explored these issues until the recent work by Kranabetter et al.,³⁰ who were able to produce (H₂)_nCs⁺ clusters with as many as 65 hydrogen molecules by means of electron ionization of large helium nanodroplets doped with Cs and hydrogen. Anomalies in the mass spectrum (maxima or abrupt drops in the cluster abundances) were found for n = 8, 12, 32, 44 and 52. Accompanying density functional theory (DFT) calculations for n = 1–14 found that the n = 12 cluster has icosahedral symmetry and exhibits a special stability, in agreement with the experiment. In this way, the authors attribute the anomalies at n = 12, 32 and 44 to the formation of three concentric, solid-like, solvation shells of icosahedral symmetry. More theoretical work was requested for the elucidation of the origin of these and the other magic numbers.

In the present work, previous experiments³⁰ are extended to deuterated clusters (D₂)_nCs⁺ (n ≤ 30). Moreover, classical and quantum Monte Carlo calculations of energies and structures of both hydrogenated and deuterated clusters are reported based on a new potential energy surface (PES) parametrized using high level ab initio calculations. As far as we are aware, this is the first combined experimental and theoretical work on the solvation of alkali cations by hydrogen that also includes a consistent study of the effects of isotopic substitution. Our goal is to investigate whether well-defined and compact shells are formed and what their structure is. In addition, since the H₂–Cs⁺ interaction is very anisotropic, we believe that it is worth studying the H₂/D₂ orientational effects^10,31,32 by explicitly taking into account their rotational degrees of freedom and comparing with the more widely used pseudoatom model. The importance of three-body (3B) induction forces^33–36 is assessed as well.

Experimental details

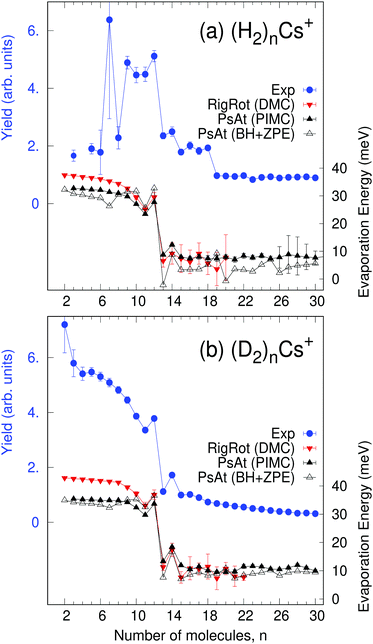
In the present experiments, large helium nanodroplets (≈10⁶ atoms) are successively doped with Cs and H₂ (or D₂) particles. Cs atoms are strongly heliophobic and occupy dimple sites at the surface of the He droplets whereas H₂ or D₂ submerges into the droplet as they are heliophilic. Then, the nanodroplets are exposed to an electron beam, which causes significant fragmentation with the formation of a variety of positively charged clusters, whose abundance is ultimately recorded with a high-resolution time of flight mass spectrometer. Electron bombardment causes formation of Cs⁺via Penning ionization of Cs by He*.³⁷ These cations undergo rather strong attractive forces with the remaining particles and consequently submerge into the droplet¹⁵ where association with hydrogen clusters occurs. Thorough descriptions of the experiments and data analysis are provided elsewhere^38,39 and, for details specific to the present system, see the ESI.† Measured ion abundances of (H₂)_nCs⁺ and (D₂)_nCs⁺ are displayed in Fig. 1. Both series clearly show an anomaly for n = 12 (local maximum and strong drop for n > 12) followed by a peak in the abundance of n = 14 clusters. We have noticed that, in a previous work,³⁰ the abundance of the (H₂)₈Cs⁺ cluster was assigned a value excessively large due to a residual gas contribution. In the present work, a corrected value is reported for this cluster size after removal of the effect of the contaminant.

Fig. 1 Measured abundances (in blue, refer to left ordinate) compared with computed evaporation energies (ΔE_n = E_n−1 − E_n, in meV, refer to right ordinate) of (a) (H₂)_nCs⁺ and (b) (D₂)_nCs⁺ clusters as a function of the number of molecules. Calculations correspond to DMC within the rigid rotor approximation (in red) as well as to BH + ZPE (open triangles) and PIMC (black) within the pseudoatom approximation. All theoretical models are able to clearly reproduce the behavior of the measured ion yields in the region n = 11–15. In many cases, error bars (associated with measurements or quantum calculations) are not seen because they are smaller than the symbol size.

Theoretical methods

Potential energy surface

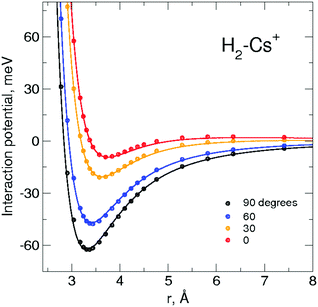
Two theoretical models are considered in this work, depending on whether the H₂ molecules are assumed to be rotating rigid rotors or pseudoatoms, referred to in what follows as “RigRot” and “PsAt” approaches, respectively. In both approaches, the PES is given as a sum of two-body (2B) terms, corresponding to the H₂–Cs⁺ and H₂–H₂ pairwise interactions, and 3B terms, associated with the interaction between the dipoles that the cation induces in the H₂ molecules. A detailed account of the building of these PESs is given in the ESI,† accompanied by Table S1, where all the PES parameters are gathered. A brief summary is given below.

Within the RigRot approximation, the H₂–Cs⁺ 2B interaction is given analytically as a sum of an electrostatic contribution – determined by interacting point charges – and a non-covalent component (including induction and van der Waals interactions) given by the atom-bond model⁴⁰ and the Improved Lennard Jones (ILJ) formulation.⁴¹ The relevant parameters are optimized by comparing the resulting interaction potential with ab initio estimations obtained at the CCSD(T) level⁴² using the d-aug-cc-pV6Z⁴³ and def2-AQVZPP⁴⁴ basis sets for H₂ and Cs⁺, respectively, and where the basis set superposition error was corrected by applying the counterpoise method.⁴⁵ As shown in Fig. 2, the analytical representation compares very well with the ab initio results. It can also be seen that the interaction is quite anisotropic, the minimum corresponding to a T-shaped configuration due to a leading charge-quadrupole interaction. Despite interactions between molecular hydrogen and the lighter alkalis have been previously studied,^2,46 we believe that this is the first time that a H₂–Cs⁺ PES is reported. Regarding the H₂–H₂ 2B potential, it is also given as a sum of an electrostatic contribution (using the same point charges) and a non-covalent (van der Waals) contribution. The latter is represented using the atom-bond ILJ formulation mentioned above, with parameters being fitted to the accurate PES of Patkowski et al.⁴⁷ (a comparison between the present and Patkowski's potentials is shown in Fig. S1, ESI†). Finally, the 3B component corresponds to the interaction between the dipoles that the cation induces on the hydrogen molecules.^23,34 For this, anisotropy in the H₂ polarizability is neglected; so this contribution is identical within both RigRot and PsAt approximations. Indeed, it is found that the anisotropic contribution just provides a difference of 0.1 meV to the total potential energy of (H₂)₂Cs⁺ at equilibrium. A comparison of the present PES with ab initio estimations for the case of the (H₂)₂Cs⁺ cluster is given in Fig. S2, ESI,† where the extent of 3B effects can be assessed.

Fig. 2 H₂–Cs⁺ interaction potential (in meV) as a function of intermolecular distance r (in Å) for various angular orientations θ, from linear (θ = 0) to T-shaped (θ = 90°). Filled circles correspond to CCSD(T) results whereas solid lines correspond to the analytical representation.

Finally, within the PsAt approximation, H₂–Cs⁺ and H₂–H₂ potentials are represented by atom-atom ILJ functions⁴¹ reproducing the spherical average of the RigRot potentials. It should be noted that the electrostatic contribution cancels out by means of averaging.

Calculation of cluster energies

Using either the RigRot or PsAt in the PESs, energies, E_n, and structures of the (H₂)_nCs⁺ and (D₂)_nCs⁺ clusters have been obtained by means of a combination of classical and quantum Monte Carlo methods, as in previous works.^23,48,49 First, within the PsAt model, putative global minima of the PESs were obtained by means of the basin-hopping (BH) method.^48–50 Quantum cluster energies, labelled as BH + ZPE, are then obtained by adding zero-point energies (in the harmonic approximation) to the BH minima. Geometrical arrangements of the clusters obtained from the BH approach are then used as initial seeds for running Path Integral Monte Carlo (PIMC) calculations,^48,51 where cluster energies are obtained at a temperature of 2 K using the thermodynamic estimator.⁵² On the other hand, within the RigRot model, cluster ground state energies and probability distributions were computed by applying the rigid body Diffusion Monte Carlo (DMC) approach developed by Buch.⁵³ Details of the implementation of these techniques are given in the ESI.†

Results and discussion

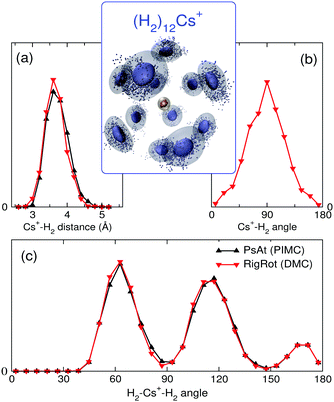
With the methods mentioned above, the stability of the complexes is studied by means of the evaporation energies, defined as ΔE_n = E_n−1 − E_n, i.e., the energy required to adiabatically remove the most weakly bound monomer from a (H₂/D₂)_nCs⁺ cluster. Results are reported in Fig. 1 in comparison with the experimental distribution of cluster abundances. It can be seen that all the computational approaches reproduce remarkably well the most important features of the experimental abundances, i.e., a maximum at n = 12 followed by a steep drop at n = 13 and a small peak at n = 14. This result provides a nice example for the theoretical predictions of a linear proportionality between cluster abundances and evaporation energies, within the model of the evaporative ensemble.^16,54 Moreover, agreement with experiment gives substantial support to the PES proposed here. It is noteworthy that all the theoretical approaches, ranging from BH + ZPE and PIMC within the PsAt model to the more elaborate RigRot DMC calculation, lead to very similar conclusions, as discussed below. For n > 14, the recorded abundances follow a smooth trend for both kinds of clusters except for a drop after (H₂)₁₈Cs⁺, which is not reproduced by the PsAt (PIMC) calculations, whereas PsAt (BH + ZPE) predicts a drop at n = 19 and uncertainties of the RigRot (DMC) energies do not allow a definite conclusion to be reached. For n < 11, comparison between experiment and theory is more satisfactory for the deuterated than for the hydrogenated clusters. For these sizes, the experimental distribution of (H₂)_nCs⁺ clusters is affected by larger error bars due to both shorter measurement times and overlapping with signals coming from the residual gas.

To understand the origin of the special stability of the n = 12 clusters, a study of the structure of (H₂)₁₂Cs⁺ is presented in Fig. 3 within the PsAt(PIMC) and RigRot(DMC) approaches. Upon examination of the distributions presented therein, it can be concluded that this cluster has an icosahedral structure, in agreement with the original experimental suggestion and DFT calculations therein.³⁰ Indeed, the PIMC three-dimensional representation of the cluster (top-central panel) reveals a relatively diffuse icosahedron. Also, the H₂–Cs⁺ radial distribution (Fig. 3(a)) shows a unique shell of radius ≈3.6 Å and the H₂–Cs⁺–H₂ angular distribution (Fig. 3(c)) exhibits three wide peaks centered around the values corresponding to an icosahedron (63.43°, 116.57° and 180°). Regarding the quantum H₂ rotational degrees of freedom studied within RigRot(DMC), the distribution of Fig. 3(b) indicates that the H₂ molecules behave as hindered rotors with a moderately large amplitude motion around the T-shaped configuration, as expected from the features of the H₂–Cs⁺ potential and found for related systems.^1,2 It is worth noticing that, despite this angular anisotropy, the distributions concerning the translational degrees of freedom of the molecule (Fig. 3(a) and (c)) are almost identical within the PsAt and the RigRot models. Concerning the structure of the smaller clusters (n < 12), it is found that the molecules arrange around the cation approximately filling in the positions of a nominal icosahedron (“icosahedral growth”), as could be expected from the fact that the equilibrium distances of H₂–Cs⁺ and H₂–H₂ pairwise interactions are rather similar (Table S1, ESI†). Analogous conclusions are reached for the deuterated clusters, with somewhat narrower distributions of the molecules as expected from their heavier mass.

Fig. 3 Structure of (H₂)₁₂Cs⁺, from PsAt(PIMC) (in black) and RigRot(DMC) (in red) calculations. Top-central panel: Representation of the three-dimensional PIMC probability distribution for specific snapshots of the quantum beads, depicting the corresponding average as a cloud (center of mass of H₂ and Cs⁺ symbolized by blue-gray and light brown colors, respectively). (a) Radial distribution (arb. units) of H₂ molecules around Cs⁺ (H₂–Cs⁺ distance in Å). (b) Distribution (arb. units) of the angle (in degrees) formed between the H₂ molecular axes and the vector joining the ion and the H₂ center of mass (only applicable to the RigRot model). (c) Distribution of the angle (in degrees) between vectors joining Cs⁺ with the center of mass of two different H₂ molecules.

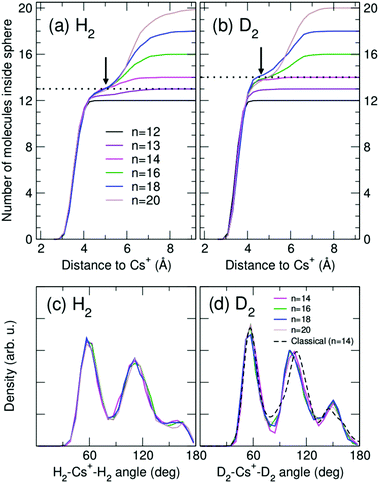
Analysis of cluster structures for larger sizes (n > 12) is shown in Fig. 4, corresponding to RigRot (DMC) calculations. First, inflection points in the accumulated radial distributions of Fig. 4(a) and (b) indicate that the first solvation shell is composed by 13 and 14 molecules for the hydrogenated and deuterated clusters, respectively (it should be noted however that (D₂)₁₄Cs⁺ clearly has a compact structure while (H₂)₁₃Cs⁺ is more diffuse). Therefore, despite the special stability of the n = 12 clusters, this magic number does not correspond to a solvation shell as could be expected.³⁰ Rather, n= 12 is a cluster with a special energetic stability (with respect to clusters of similar sizes), while n = 13 or 14 leads to maximum packing structures.⁵⁵ Hence, local maxima observed at n = 14 of Fig. 1 can be attributed to maximum packing or, in other words, solvation shells. The internal structure of the first solvation shell for n ≥ 14 is depicted in Fig. 4(c) and (d), by means of the distributions of H₂–Cs⁺-H₂ and D₂–Cs⁺–D₂ angles for molecules that reside within the first shell. The radius of that shell is defined by the inflection point indicated by arrows in Fig. 4(a) and (b). As can be seen, adding extra molecules to the second shell does not affect the structure of the first shell, which remains nearly constant.

Fig. 4 Upper panels (a and b): number of H₂ and D₂ molecules, respectively, inside a sphere defined by the distance between the molecules and Cs⁺ for cluster sizes n = 12, 13, 14, 16, 18 and 20. It can be seen that the first solvation layer has 13 and 14 molecules for hydrogenated and deuterated clusters, respectively. Lower panels (c and d): distribution of H₂–Cs⁺–H₂ and D₂–Cs⁺–D₂ angles (in degrees), respectively, for molecules residing in the first shell (defined by the radial distance indicated by arrows in the upper panels) for n = 14, 16, 18 and 20. All distributions correspond to RigRot (DMC) calculations. Angular distribution based on the classical minimum energy structure of the n = 14 cluster is also shown in (d) (black dashed lines).

More insight into the structure of these clusters is gained by means of some indicators at the PsAt (PIMC) level: the gyration radius and the Lindemann index, defined in the ESI and displayed in Fig. S3(a–d).† First, for (D₂)_nCs⁺ clusters, it can be seen that the n = 12, 14 and n > 16 complexes are rather rigid, with localized molecules in the first solvation shell. Indeed, deuterated clusters of these sizes can be considered to be solid-like since their corresponding Lindemann indexes (≈0.1) are below the critical value that discriminates between a solid-like and a liquid-like phase, which ranges between 0.1 and 0.2, depending on the authors.^56,57 The behavior of these indicators is qualitatively similar for the (H₂)_nCs⁺ clusters. However, with a few exceptions (such as that of n = 12), quantum delocalization and fluidity are larger as compared with the deuterated clusters.

Apart from a solid-like behavior, an enhancement of the H₂/D₂ density around the cation due to electrostriction is another common feature for the formation of snowballs.^14,19 As a measure of electrostriction, we have computed the percentage of H₂–H₂ density within the repulsive region of the H₂–H₂ potential.¹⁹ The results are shown in Fig. S3(e and f) (ESI†), where it can be seen that electrostriction is significant and steadily increases with n until the first shell is completed (n ∼ 15), decreasing thereafter. It should be noted that this index behaves quite similarly for the two isotopes. The analysis points to a snowball-like structure of the inner solvation shell of these clusters, especially the deuterated ones that are more rigid, as commented above.

It is worth noting that cluster sizes n = 12 and n = 14 already manifest special stability at a classical level, as can be seen in Fig. S4 (ESI†), where evaporation energies computed using the minima of the PES show the same kind of anomalies for these magic numbers. The classical structure of the n = 12 cluster corresponds to an icosahedron, in agreement with the quantum structure of both H₂ and D₂ clusters. For n = 14, the classical cluster has a D_6d symmetry within the PsAt approximation. Within the RigRot approach, this structure becomes distorted and lowers its symmetry. Using the latter structure, we have computed a “classical” D₂–Cs⁺–D₂ angular distribution (arbitrarily widening the classical sticks to emulate quantum effects) and the result is shown in Fig. 4(d). It can be seen that this classical “skeleton” is compatible with the quantum-mechanical results.

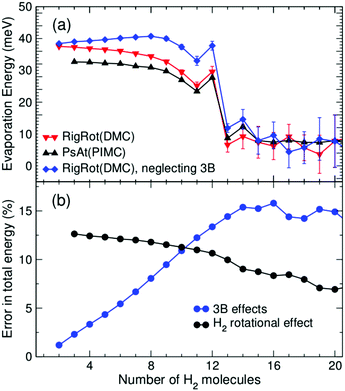
In addition, it is interesting to study in more detail the role of rotation of the H₂/D₂ molecules as well as of the explicit inclusion of 3B induction terms in the PES, as these effects are often neglected in related computational studies. The extent of 3B effects is explored by comparing RigRot calculations that include or neglect 3B terms in the PES. Analogously, PsAt and RigRot approaches (including 3B terms) are compared to study the orientational effects. (H₂)_nCs⁺ evaporation energies, obtained within these models, are depicted in Fig. 5(a) as functions of n. Fig. 5(b) shows relative errors (of the approximated approaches with respect to the most accurate one) in the determination of the total energy. As expected, rotational effects are significant for small cluster sizes (about 10–12% for n < 13), where the H₂ molecules close to the cation tend to orient perpendicularly to it, and become less important for larger cluster sizes. On the other hand, 3B effects steadily increase as the first solvation shell is being filled, reaching a maximum of about 15% for n = 14. This is due to the increase in the number of 3B partners as more polarizable molecules are attached to the cation. The extent of these effects does not continue to rise for larger cluster sizes because of the reduction in the polarization energy of molecules in the second shell due to their larger distance to the cation. Regarding (D₂)_nCs⁺ clusters, it has been found that, while 3B effects are nearly the same as those of hydrogenated clusters, rotational effects are somewhat larger, as they account for about 14–18% within the first solvation shell. As a consequence of the above, these two effects have a noticeable impact on the evaporation energies of small clusters (n < 13) but their role becomes negligible for larger cluster sizes, as can be seen in Fig. 5(a). In particular, it is worth noting that the more approximated models reproduce the behavior of the evaporation energies around the main anomalies quite well and thereby the experimental results.

Fig. 5 (a) Evaporation energies of (H₂)_nCs⁺ as functions of n, for various different approaches: rigid rotors (in red), pseudoatoms (in black) and rigid rotors with the removal of three-body terms in the PES (in blue). There are appreciable differences for small cluster sizes but the behavior near n = 12 and 14 is very similar, as well as for larger cluster sizes. (b) Relative errors in the total energy of the cluster due to neglecting 3B terms in the PES (blue) and not accounting for H₂ rotational degrees of freedom (black).

Finally, one may wonder about the sensitivity of the most salient results reported here with respect to variations of the PES parameters. To explore this aspect, some parameters of the non-covalent contribution of the H₂–Cs⁺ pair interaction have been artificially modified (see Table S2, ESI†) so as to make the total interaction either less or more attractive by ∼14%. As seen from Fig. S5(a) (ESI†), the peak in the evaporation energy at n = 12 is robust with respect to these variations while that at n = 14 disappears. Interestingly, in both cases, the shell structure is different to that reported above: the more attractive PES leads to a compact shell with 12 molecules whereas the less attractive one gives more diffuse structures with about 14–15 molecules in the first shell (Fig. S5(b), ESI†). It should be pointed out that possible inaccuracies of the present PES would imply much smaller modifications, which eventually should be tested against stringent spectroscopy measurements.¹

Conclusions

In conclusion, mass spectra of (H₂)_nCs⁺ and (D₂)_nCs⁺ clusters (n ≤ 30) have been measured and calculations of cluster evaporation energies-based on a new potential energy surface-have been able to reproduce the most important features of the experiment, namely, the anomalies for cluster sizes around n = 12 and n = 14. Icosahedral (H₂/D₂)₁₂Cs⁺ clusters are found to be specially stable, while the first solvation shell becomes closed for 13 or 14 hydrogen or deuterium molecules, respectively. Solvation layers exhibit the typical characteristics of the well-known Atkins snowballs, especially for the deuterated clusters. In addition, it is found that an explicit account for rotational motion as well as three body induction interactions is important for the description of the first solvation shell. Experimental and computational methods presented here appear to be very well suited for studying the solvation of other alkali or alkali earth ions in hydrogen as well as for an extension to studies of the adsorption of hydrogen on fullerenes or polyaromatic hydrocarbons doped with alkali atoms.^11,49 Work in these directions is in progress.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The work has been funded by Spanish MINECO grants (FIS2014-51993-P, FIS2016-79596-P, FIS2017-84391-C2-2-P and FIS2017-83157-P) and by the Austrian Science Fund, Wien (FWF Projects P26635, P31149, and W1259). Allocation of computing time by the CESGA (Spain) is also acknowledged. JOZ would like to acknowledge Programa Operativo de Empleo Juvenil 2014-2020 from the European Social Fund.

References

1. V. Dryza, B. Poad and E. Bieske, Phys. Chem. Chem. Phys., 2012, 14, 14954–14965.
2. V. Dryza and E. J. Bieske, Int. Rev. Phys. Chem., 2013, 32, 559–587.
3. K. R. Atkins, Phys. Rev., 1959, 116, 1339–1343.
4. S. Grebenev, B. Sartakov, J. P. Toennies and A. F. Vilesov, Science, 2000, 289, 1532–1535.
5. A. Ponzi, F. Marinetti and F. A. Gianturco, Phys. Chem. Chem. Phys., 2009, 11, 3868–3874.
6. H. Li, R. J. Le Roy, P. N. Roy and A. R. W. McKellar, Phys. Rev. Lett., 2010, 105, 133401.
7. P. Chen, X. Wu, J. Lin and K. Tan, Science, 1999, 285, 91–93.
8. I. Cabria, M. J. López and J. A. Alonso, J. Chem. Phys., 2005, 123, 377.
9. M. Dinca and J. R. Long, Angew. Chem., Int. Ed., 2008, 47, 6766–6779.
10. L. P. Lindoy, S. J. Kolmann, J. H. D'Arcy, D. L. Crittenden and M. J. T. Jordan, J. Chem. Phys., 2015, 143, 194302.
11. A. Kaiser, M. Renzler, L. Kranabetter, M. Schwärzler, R. Parajuli, O. Echt and P. Scheier, Int. J. Hydrogen Energy, 2017, 42, 3078–3086.
12. I. Savchenko, B. Gu, T. Heine, J. Jakowski and S. Garashchuk, Chem. Phys. Lett., 2017, 670, 64–70.
13. A. J. Physick, D. J. Wales, S. H. Owens, J. Shang, P. A. Webley, T. J. Mays and V. P. Ting, Chem. Eng. J., 2016, 288, 161–168.
14. S. Müller, M. Mudrich and F. Stienkemeier, J. Chem. Phys., 2009, 131, 044319.
15. M. Theisen, F. Lackner and W. E. Ernst, J. Chem. Phys., 2011, 135, 074306.
16. L. An der Lan, P. Bartl, C. Leidlmair, R. Jochum, S. Denifl, O. Echt and P. Scheier, Chem. – Eur. J., 2012, 18, 4411–4418.
17. A. Mauracher, O. Echt, A. M. Ellis, S. Yang, D. K. Bohme, J. Postler, A. Kaiser, S. Denifl and P. Scheier, Phys. Rep., 2018, 751, 1–90.
18. C. A. Brindle, M. R. Prado, K. C. Janda, N. Halberstadt and M. Lewerenz, J. Chem. Phys., 2005, 123, 064312.
19. E. Coccia, E. Bodo, F. Marinetti, F. A. Gianturco, E. Yildrim, M. Yurtsever and E. Yurtsever, J. Chem. Phys., 2007, 126, 124319.
20. P. Slavicek and M. Lewerenz, Phys. Chem. Chem. Phys., 2010, 12, 1152–1161.
21. D. E. Galli, D. M. Ceperley and L. Reatto, J. Phys. Chem. A, 2011, 115, 7300–7309.
22. N. Issaoui, K. Abdessalem, H. Ghalla, S. J. Yaghmour, F. Calvo and B. Oujia, J. Chem. Phys., 2014, 141, 174316.
23. M. Rastogi, C. Leidlmair, L. An der Lan, J. Ortiz de Zárate, R. Pérez de Tudela, M. Bartolomei, M. I. Hernández, J. Campos-Martínez, T. González-Lezana, J. Hernández-Rojas, J. Bretón, P. Scheier and M. Gatchell, Phys. Chem. Chem. Phys., 2018, 20, 25569–25576.
24. R. Clampitt and D. Jefferies, Nature, 1970, 226, 141–142.
25. J. E. Bushnell, P. R. Kemper and M. T. Bowers, J. Phys. Chem., 1994, 98, 2044–2049.
26. C. Emmeluth, B. L. J. Poad, C. D. Thompson, G. H. Weddle and E. J. Bieske, J. Chem. Phys., 2007, 126, 204309.
27. B. K. Rao and P. Jena, Europhys. Lett., 1992, 20, 307–312.
28. M. Barbatti, G. Jalbert and M. A. C. Nascimento, J. Chem. Phys., 2001, 114, 2213–2218.
29. K. R. S. Chandrakumar and S. K. Ghosh, Chem. Phys. Lett., 2007, 447, 208–214.
30. L. Kranabetter, M. Goulart, A. Aleem, T. Kurzthaler, M. Kuhn, E. Barwa, M. Renzler, L. Grubwieser, M. Schwärzler, A. Kaiser, P. Scheier and O. Echt, J. Phys. Chem. C, 2017, 121, 10887–10892.
31. M. Mella and E. Curotto, J. Phys. Chem. A, 2017, 121, 5005–5017.
32. F. Calvo and E. Yurtsever, J. Chem. Phys., 2018, 148, 102305.
33. A. J. Stone, The Theory of the Intermolecular Forces, Oxford University Press, 2013.
34. M. M. Liu, M. S. Wu, H. L. Han and T. Y. Shi, J. Chem. Phys., 2016, 145, 034304.
35. F. V. Prudente, J. M. C. Marques and F. B. Pereira, Phys. Chem. Chem. Phys., 2017, 19, 25707–25716.
36. W. S. Jesus, F. V. Prudente and J. M. C. Marques, J. Phys. Chem. A, 2019, 123, 2867.
37. A. Scheidemann, V. Kresin and H. Hess, J. Chem. Phys., 1997, 107, 2839–2844.
38. L. An der Lan, P. Bartl, C. Leidlmair, H. Schöbel, R. Jochum, S. Denifl, T. D. Märk, A. M. Ellis and P. Scheier, J. Chem. Phys., 2011, 135, 044309.
39. S. Ralser, J. Postler, M. Harnisch, A. M. Ellis and P. Scheier, Int. J. Mass Spectrom., 2015, 379, 194–199.
40. F. Pirani, M. Albertí, A. Castro, M. Moix Teixidor and D. Cappelletti, Chem. Phys. Lett., 2004, 394, 37–44.
41. F. Pirani, S. Brizi, L. Roncaratti, P. Casavecchia, D. Cappelletti and F. Vecchiocattivi, Phys. Chem. Chem. Phys., 2008, 10, 5489–5503.
42. H.-J. Werner, P. J. Knowles, R. Lindh, F. R. Manby, M. Schütz, P. Celani, T. Korona, G. Rauhut, R. D. Amos, A. Bernhardsson, A. Berning, D. L. Cooper, M. J. O. Deegan, A. J. Dobbyn, F. Eckert, C. Hampel, G. Hetzer, A. W. Lloyd, S. J. McNicholas, W. Meyer, M. E. Mura, A. Nicklass, P. Palmieri, R. Pitzer, U. Schumann, H. Stoll, A. J. Stone, R. Tarroni and T. Thorsteinsson, MOLPRO, Version2012.1, a Package of Ab Initio Programs, 2012, see http://www.molpro.net.
43. R. A. Kendall, T. H. Dunning and R. J. Harrison, J. Chem. Phys., 1992, 96, 6796.
44. F. Weigend, Phys. Chem. Chem. Phys., 2006, 8, 1057–1065.
45. S. Boys and F. Bernardi, Mol. Phys., 1970, 19, 553.
46. J. G. Vitillo, A. Damin, A. Zecchina and G. Ricchiardi, J. Chem. Phys., 2005, 122, 114311.
47. K. Patkowski, W. Cencek, P. Jankowski, K. Szalewicz, J. Mehl, G. Garberoglio and A. H. Harvey, J. Chem. Phys., 2008, 129, 094304.
48. R. Rodríguez-Cantano, R. Pérez de Tudela, M. Bartolomei, M. I. Hernández, J. Campos-Martínez, T. González-Lezana, P. Villarreal, J. Hernández-Rojas and J. Bretón, J. Chem. Phys., 2015, 143, 224306.
49. M. Bartolomei, R. Pérez de Tudela, T. González-Lezana, M. I. Hernández, J. Campos-Martínez, P. Villarreal, J. Hernández-Rojas, J. Bretón and F. Pirani, Phys. Chem. Chem. Phys., 2017, 19, 26358.
50. D. J. Wales and J. P. K. Doye, J. Phys. Chem. A, 1997, 101, 5111–5116.
51. D. Ceperley, Rev. Mod. Phys., 1995, 67, 279–355.
52. J. A. Barker, J. Chem. Phys., 1979, 70, 2914–2918.
53. V. Buch, J. Chem. Phys., 1992, 97, 726–729.
54. K. Hansen and U. Näher, Phys. Rev. A: At., Mol., Opt. Phys., 1999, 60, 1240–1250.
55. S. Acosta-Gutiérrez, J. Bretón, J. M. G. Llorente and J. Hernández-Rojas, J. Chem. Phys., 2012, 137, 074306.
56. J. E. Cuervo and P.-N. Roy, J. Chem. Phys., 2008, 128, 224509.
57. F. Calvo, J. Phys. Chem. A, 2015, 119, 5959–5970.

---

Footnotes

† Electronic supplementary information (ESI) available: Details on experimental setup, potential energy surface, classical and quantum Monte Carlo methods, plus two tables and five figures. See DOI: 10.1039/c9cp02017a

‡ All the authors contributed equally to this work.

---