Open Access Article
Open Access ArticleELDOR-detected NMR beyond hyperfine couplings: a case study with Cu(II)-porphyrin dimers†
Nino
Wili
 a,
Sabine
Richert‡
a,
Sabine
Richert‡
 b,
Bart
Limburg
c,
Simon J.
Clarke
d,
Harry L.
Anderson
b,
Bart
Limburg
c,
Simon J.
Clarke
d,
Harry L.
Anderson
 c,
Christiane R.
Timmel
c,
Christiane R.
Timmel
 b and
Gunnar
Jeschke
b and
Gunnar
Jeschke
 *a
*a
aLaboratorium für Physikalische Chemie, ETH Zürich, Vladimir-Prelog-Weg 2, 8093 Zürich, Switzerland. E-mail: gjeschke@ethz.ch
bCentre for Advanced Electron Spin Resonance (CÆSR), University of Oxford, South Parks Road, Oxford, OX1 3QR, UK
cChemistry Research Laboratory, University of Oxford, Mansfield Road, Oxford, OX1 3TA, UK
dInorganic Chemistry Laboratory, University of Oxford, South Parks Road, Oxford, OX1 3QR, UK
First published on 21st May 2019
Abstract
The pulse EPR method ELDOR-detected NMR (EDNMR) is applied to two Cu(II)-porphyrin dimers that are suitable building blocks for molecular wires. One of the dimers is meso–meso singly linked, the other one is β, meso, β-fused. We show experimentally and theoretically that EDNMR spectra contain information about the electron–electron couplings. The spectra of the singly linked dimer are consistent with a perpendicular arrangement of the porphyrin planes and negligible exchange coupling. In addition, the resolution is good enough to distinguish 63Cu and 65Cu in frozen glassy solution and to resolve a metal-ion nuclear quadrupole coupling of 32 MHz. In the case of the fused dimer, we observe so far unreported signal enhancements, or anti-holes, in the EDNMR spectra. These are readily explained in a generalized framework based on [Cox et al., J. Magn. Reson., 2017, 280, 63–78], if an effective spin of S = 1 is assumed, in accordance with SQUID measurements. The positions of the anti-holes encode a zero-field splitting with |D| = 240 MHz, which is about twice as large as expected from the point-dipole approximation. These findings demonstrate the previously unrecognized applicability and versatility of the EDNMR technique in the quantitative study of complex paramagnetic compounds.
1 Introduction
Electron–electron double resonance (ELDOR)-detected NMR (EDNMR) is a pulse EPR technique that was introduced by Schosseler et al. in 1994.1 It is intended for the measurement of hyperfine couplings to nuclei in the vicinity of unpaired electrons and works best for moderately sized couplings that are not resolved in EPR spectra, but may also be hard to access by electron spin echo envelope modulation (ESEEM) or electron nuclear double resonance (ENDOR) techniques. For weakly coupled, low-γ nuclei (e.g.14N), EDNMR is most useful at high fields and high frequencies, e.g. at W-band frequencies (≈95 GHz),2 and became popular only relatively recently.3–5 It proved to be an invaluable tool, for example, in the study of the oxygen-evolving complex of photosystem II6 and the spectroscopic investigation of ATP turnover in ABC exporters.7 EDNMR was also applied to investigate Mn(II) complexes inside cells.8 Only in a few cases was the technique applied at Q-band frequencies (≈35 GHz).9–12In contrast to their widespread use for ligand nuclei, hyperfine techniques have only in a few cases been applied to gain information about the central ions of metal complexes.9,13–19 Only the last two studies cited here made use of EDNMR, although it might be more sensitive than ENDOR if the lines are mainly inhomogeneously broadened – which is often the case for metal hyperfine couplings.
Several groups have introduced modifications and extensions in order to increase the information content of EDNMR spectra. An additional microwave (mw) or radio-frequency (rf) source is employed in the triple resonance techniques 2D-EDNMR20 and THYCOS,21 respectively, that correlate hyperfine couplings of several nuclei coupled to the same paramagnetic center. Alternatively, the nuclear frequency spectrum can be correlated to the EPR spectrum in order to gain information about the relative orientation of the tensors.2 With arbitrary waveform generator (AWG)-controlled spectrometers, it is possible to detect the complete hole pattern in one shot by the use of chirp pulses.22 In this context, it was also shown that it is possible to obtain hyperfine sublevel correlation (HYSCORE)-type information with hole burning experiments. The latter experiment can also be performed in a classical EDNMR fashion without chirp pulses.
In this study we highlight, on the example of two Cu(II)-porphyrin dimers, that even the basic form of EDNMR can provide more information than generally appreciated, in particular, on metal-ion nuclear quadrupole and on electron–electron couplings.
Porphyrins are suitable components for molecular wires that mediate long distance charge transport, because of their large delocalized π-systems, small HOMO–LUMO gaps, rigid frameworks, and small reorganization energies.23–27 The edge-fused porphyrin tapes, pioneered by Osuka and coworkers,28–30 exhibit particularly strong electronic coupling, leading to highly conductive molecular wires.31 Here we report an EDNMR investigation of two copper porphyrin dimers: the edge-fused dimer f-CuP2 and the meso–meso singly linked dimer CuP2; see chemical structures in Fig. 1. The dimers f-CuP2 and CuP2 are very similar to copper porphyrin dimers reported previously,29,32 except that the compounds investigated here have bulky 3,5-bis(trihexylsilyl)phenyl substituents to provide high solubility and prevent aggregation.33 Previous crystallographic studies29,32 have shown that the Cu–Cu distance in both of these dimers is in the range of 8.3–8.4 Å, and that the planes of the two porphyrin units are almost perpendicular in CuP2, whereas they are coplanar in f-CuP2. DFT studies of CuP2 revealed that the rigidity is much higher compared to ethyne or butadiyne-linked structures.34 The twisted conformation of CuP2 prevents orbital overlap between the π-systems of the porphyrin units.27 In a different study it was demonstrated that copper(II)-porphyrin dimers, similar to f-CuP2 and CuP2, exhibit anti-ferromagnetic coupling between the metal centers.35 Variable-temperature magnetic susceptibility measurements in the range 2–300 K on the fused dimer revealed that the value of χT drops sharply at temperatures below 20 K, and a Bleaney–Bowers fit to these data gave a J value of 1.43 cm−1 (for Ĥ = 2J![[S with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0053_20d1.gif) 1
1![[S with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0053_20d1.gif) 2). Recently, it was also shown that a doubly fused Cu(II)-porphyrin dimer exhibits electrocatalytic properties for hydrogen evolution.36
2). Recently, it was also shown that a doubly fused Cu(II)-porphyrin dimer exhibits electrocatalytic properties for hydrogen evolution.36
Here we demonstrate that the EDNMR spectra of CuP2 are consistent with a small exchange coupling between the Cu(II) centres and a perpendicular orientation of the porphyrin planes. The strong orientation selection of the experiment leads to a striking resolution of the copper hyperfine peaks and makes it possible to resolve the isotopes 63Cu and 65Cu at natural abundance in glassy frozen solution. Additionally, we determine the copper quadrupole coupling in a similar way as previously shown for nitroxides.37 A recently proposed fast simulation algorithm4 quantitatively reproduces the experiment in spectral regions where only copper signals contribute to the spectrum. In the case of a relatively strong exchange coupling in f-CuP2 (79 GHz for J![[S with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0053_20d1.gif) 1
1![[S with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0053_20d1.gif) 2, corresponding to 1.32 cm−1 for 2J
2, corresponding to 1.32 cm−1 for 2J![[S with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0053_20d1.gif) 1
1![[S with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0053_20d1.gif) 2), we observe anti-holes or signal enhancements in the EDNMR spectra. These anti-holes are in line with our previous general description of polarization changes in hole burning22 and their correlation to the EPR spectrum can be simulated with a generalized algorithm that can treat arbitrary spin systems. The correlation confirms the expected orientation of the dipolar coupling tensor with respect to the g- and A-tensors of the Cu(II)-porphyrin subsystems. In addition, the magnitude of the dipolar coupling is found to be significantly larger than expected from a simple point-dipole approximation, contradicting previous interpretations of the CW EPR spectra of similar Cu(II)-porphyrin dimers.35,36 Since the information content of the experiment goes beyond the nuclear frequencies, the NMR in ELDOR-detected NMR can be misleading.
2), we observe anti-holes or signal enhancements in the EDNMR spectra. These anti-holes are in line with our previous general description of polarization changes in hole burning22 and their correlation to the EPR spectrum can be simulated with a generalized algorithm that can treat arbitrary spin systems. The correlation confirms the expected orientation of the dipolar coupling tensor with respect to the g- and A-tensors of the Cu(II)-porphyrin subsystems. In addition, the magnitude of the dipolar coupling is found to be significantly larger than expected from a simple point-dipole approximation, contradicting previous interpretations of the CW EPR spectra of similar Cu(II)-porphyrin dimers.35,36 Since the information content of the experiment goes beyond the nuclear frequencies, the NMR in ELDOR-detected NMR can be misleading.
2 Theory
2.1 Description of ELDOR-detected NMR
The pulse sequence for ELDOR-detected NMR is shown in Fig. 2. A high turning angle (HTA) pulse burns a hole into an inhomogeneously broadened EPR line. The hole burned at νHTA = νObs is referred to as the central hole. This central hole obscures side holes at low frequencies. If a transition irradiated by the hole burning pulse shares a level with another transition that is either fully or weakly allowed, the polarization of the latter transition is changed and a side hole (or side anti-hole) is created. Anisotropic hyperfine couplings of the same order of magnitude as the nuclear Zeeman frequency lead to weakly allowed electron–nuclear transitions that correspond to side holes offset by the nuclear frequencies. By changing the frequency of the HTA pulse in a stepwise fashion, one can obtain the spectrum of the side holes if the variable echo intensity is plotted against νHTA–νObs. This experiment is usually applied for the detection of nuclear frequencies, hence the name EDNMR. The standard description of EDNMR uses a two-spin system consisting of one electron and one nucleus,4,5 usually also of spin-1/2. This four-level system corresponds to the subsystem {|1〉, |2〉, |3〉, |4〉} in Fig. 3. If the HTA pulse drives, for example, the transition (|1〉 → |4〉), which is formally forbidden, then the polarization, and thus the signal, of the formally allowed transitions (|1〉 → |3〉) and (|2〉 → |4〉) is also decreased. This results in the mentioned side holes offset by the NMR frequencies. In an inhomogeneously broadened EPR line, any of the allowed or forbidden EPR transitions in the mentioned subsystem can be driven by the HTA pulse. In this case, the peak intensity (i.e., the hole depth h) is described as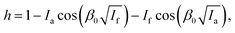 | (1) |
In the case of several unpaired electrons, the side holes and anti-holes will also contain information about the electron–electron coupling, or, if this coupling is very large, about the zero-field splitting. In these cases, we simply denote the method as ELDOR instead of ELDOR-detected NMR.
ELDOR was used before for the quantification of electron spectral diffusion.38 However, in this context, no anti-holes were observed, and the high concentration (10–40 mM) that was used makes electron spectral diffusion a bulk property, whereas we focus on interactions of isolated systems. Note that the pulse sequence is the same, but the parameters for the hole burning pulse are vastly different. Measurements of electron spectral diffusion are carried out with HTA pulses of about 100 ms, EDNMR normally uses pulses of about 5–50 μs, and some of the spectra shown in this work were even acquired with pulses as short as 50 ns.
Interestingly, the signal enhancement by inversion pulses on connected transitions that correspond to the anti-holes has already been used as a means of sensitivity enhancement in NMR39 and EPR.40,41 However, to the best of our knowledge, this kind of signal enhancement has not been used to date as a spectroscopic tool.
2.2 Simulation algorithm
The simulation algorithm used in this work is based on earlier work by Cox et al.4 Before we discuss our extensions, we need to recapitulate the important steps and comment on the validity of the approximations.1. Generate the Hamiltonian Ĥ0 for a particular orientation.
2. Diagonalize Ĥ0 to get the energy levels and transition frequencies.
3. Calculate transition probabilities between the eigenstates of the system.
4. Introduce orientation selection by weighting the transitions according to a Gaussian function centered at the detection frequency.
5. Calculate the inversion efficiency of each transition by assuming selective excitation by the HTA pulse and using a Bloch picture.
6. Check which transitions share a common level and calculate the intensity change of the observed transitions due to the polarization transfer induced by the HTA pulse.
7. Build the spectrum by adding up all possible peaks and orientations.
The approach is valid as long as the excitation is transition-selective within each three-level subsystem and spectral diffusion processes are negligible. It is orders of magnitudes faster than a full quantum-mechanical calculation of spin dynamics employing the Liouville–von Neumann equation. While EDNMR spectra including some 63,65Cu signals have been interpreted before taking into account off-resonance effects and relaxation,20,42 we will show here that the above algorithm can quantitatively reproduce our experimental EDNMR spectra.
In addition to the spin system, one needs to provide the program with the length and amplitude of the HTA pulse, tHTA and ν1, the phase memory time of the electron spins, Tm, and the quality factor of the resonator, Qres. These parameters can be determined experimentally.
The published implementation of Cox et al. cannot be used to simulate arbitrary spin systems, because it makes implicit assumptions about the structure of the Hamiltonian, namely the mS sub-blocks. Signal enhancements are not possible. In the general case, mS is not necessarily a good quantum number. Additionally, the published version only considers (mS = −1/2 → mS = 1/2) transitions, which does not exist at all in the case of f-CuP2. Therefore, we extended the published algorithm to an electron–nuclear spin system that may contain more than one unpaired electron. A more detailed description is given in the ESI† (see Section S.5) and the code is available online.
2.3 Description of the spin system
The structures of the compounds investigated in this work are shown in Fig. 1. While there are many nuclei with nuclear spin I > 0, we focus on the copper nuclei and the unpaired electrons, which contribute the dominating interactions.43The Hamiltonian that describes a system of two electrons S1 = S2 = 1/2 and two nuclei I1 = I2 = 3/2, with zero hyperfine coupling between S1 and I2 as well as between S2 and I1, reads in linear frequency units
 | (2) |
![[B with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0042_20d1.gif) 0 the external static magnetic field and g the electron g-tensor. The second term describes the nuclear Zeeman interaction, where γn is the gyromagnetic ratio of the respective nucleus. Ai denotes the hyperfine coupling between electron i and nucleus i. The last term in parentheses is the nuclear quadrupole interaction, which is given in its principal axis system by44
0 the external static magnetic field and g the electron g-tensor. The second term describes the nuclear Zeeman interaction, where γn is the gyromagnetic ratio of the respective nucleus. Ai denotes the hyperfine coupling between electron i and nucleus i. The last term in parentheses is the nuclear quadrupole interaction, which is given in its principal axis system by44 | (3) |
 | (4) |
 | (5) |
 . The term
. The term  describes the isotropic exchange coupling between the electron spins. Note that several other conventions exist in the literature. In this convention, J describes the energetic singlet–triplet separation, and a positive J describes an anti-ferromagnetic coupling with the singlet state at lower energy than the triplet state.
describes the isotropic exchange coupling between the electron spins. Note that several other conventions exist in the literature. In this convention, J describes the energetic singlet–triplet separation, and a positive J describes an anti-ferromagnetic coupling with the singlet state at lower energy than the triplet state.
 ). The singlet is EPR-silent, and the triplet state can be described by an effective spin 1.46 The effective hyperfine coupling in the triplet manifold is halved compared to the uncoupled case (see also Section 3.5, ESI†vide infra), but the effective electron spin couples to any nucleus with non-zero hyperfine coupling to one of the electron spins in the uncoupled representation, in the present case to both copper nuclei. The dipolar coupling in the uncoupled basis manifests itself as a zero-field splitting (ZFS) in the coupled basis with the Hamiltonian
). The singlet is EPR-silent, and the triplet state can be described by an effective spin 1.46 The effective hyperfine coupling in the triplet manifold is halved compared to the uncoupled case (see also Section 3.5, ESI†vide infra), but the effective electron spin couples to any nucleus with non-zero hyperfine coupling to one of the electron spins in the uncoupled representation, in the present case to both copper nuclei. The dipolar coupling in the uncoupled basis manifests itself as a zero-field splitting (ZFS) in the coupled basis with the Hamiltonian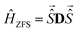 | (6) |
 | (7) |
| D = 3/2Dz E = (Dx − Dy)/2 | (8) |
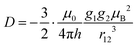 | (9) |
3 Results and discussion
The synthesis of CuP2 and f-CuP2 is described in the ESI† (see Section S.1). The samples were dissolved in toluene to give a final concentration of about 1 mM. We verified that the rather high concentration does not affect the EDNMR measurements by checking representative spectra at a concentration of 0.2 mM (see the ESI,† Section S.10). For both samples, 40 μl of solution was transferred to a 3 mm (outer diameter) quartz tube. A 3 mm Q-band resonator with large bandwidth (Qres ≈ 110) was used for the EDNMR measurements. Further details on the EPR spectrometers are presented in the ESI† (see Section S.2). A detailed description of the parameters and where to find the raw data is given for each figure at the end of the ESI† (see Section S.15).Note that the results for the copper hyperfine and quadrupole couplings are specified for the slightly more abundant isotope 63Cu. The parameters were scaled according to the natural constants (gyromagnetic ratio and quadrupole moment of the nucleus) of 65Cu to calculate the spectra of isotopologues. Isotope effects beyond this scaling were neglected. Natural isotope abundance was assumed.
3.1 CuP2: small exchange coupling
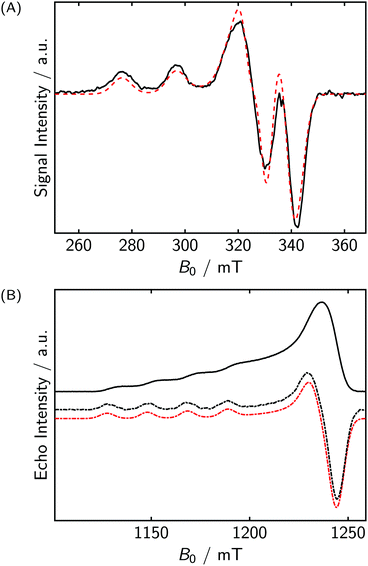
The X-band continuous wave (CW) spectrum and the Q-band echo-detected field sweep (EDFS) spectra of CuP2 are shown in Fig. 5(A and B). The spectra are typical for axially symmetric Cu(II) compounds. The nitrogen hyperfine couplings are not resolved. For simulating the spectra, we only included a single copper nucleus. No further hyperfine couplings or electron–electron couplings were included. Nevertheless, a rather good estimate of the g-values and of A‖,Cu (≈610 MHz) can be obtained. By including more parameters in the simulation, such as the nitrogen couplings and the exchange coupling, the fit could most likely be improved.43 However, the rather featureless character of the spectrum makes it difficult to assign quantitatively and confidently precise values to the different interactions, as all of these additional parameters only contribute to field-dependent line broadening in the present case. Note that similar, butadiyne-linked, compounds,43 exhibit an exchange coupling of about 50 MHz. But if the two porphyrin planes of CuP2 are perpendicular to each other, consistent with X-ray and DFT studies of similar compounds, the exchange coupling is expected to be close to zero. In this case, it is also reasonable to model the EDNMR spectra (vide infra) by only considering a single, isolated copper site.Q-band EDNMR spectra obtained at the low-field edge of the spectrum are shown in Fig. 6(A). The high resolution and information content of these spectra was surprising. In order to simulate the spectra quantitatively, it was necessary to include both copper isotopes (63Cu/65Cu, nat. abund. ≈ 70/30%, γ63/γ65 = 0.934) and also a substantial quadrupole coupling of e2qQ/h = 32 ± 7 MHz. The uncertainty is an estimate based on the linewidth of the peaks. The standard deviation σ of a Gaussian is related to the full width at half maximum Γ by  , and for these spectra Γ ≈ 15 MHz. The quadrupole tensor was assumed to be axial, but because of the rather low resolution in the high-field region, the fitting is not very sensitive to the asymmetry parameter η. The quadrupole coupling of the metal center is of considerable interest, as it gives information about the coordination environment. Since it depends on total electron density, particularly the charge distribution, rather than on spin density, we expect that computation with quantum chemical approaches is more reliable than that of metal hyperfine couplings. While quadrupole interactions of copper have been determined before, the approach used in the literature relied on second order shifts in the EPR spectra47 usually of single crystals.48,49 In the latter case, also ENDOR was used.50
, and for these spectra Γ ≈ 15 MHz. The quadrupole tensor was assumed to be axial, but because of the rather low resolution in the high-field region, the fitting is not very sensitive to the asymmetry parameter η. The quadrupole coupling of the metal center is of considerable interest, as it gives information about the coordination environment. Since it depends on total electron density, particularly the charge distribution, rather than on spin density, we expect that computation with quantum chemical approaches is more reliable than that of metal hyperfine couplings. While quadrupole interactions of copper have been determined before, the approach used in the literature relied on second order shifts in the EPR spectra47 usually of single crystals.48,49 In the latter case, also ENDOR was used.50
The approach used here to determine the quadrupole coupling is analogous to that employed for nitroxides at W-band, where the coupling can be determined by analyzing a series of spectra at the high-field edge of the EPR spectrum.37 An energy level diagram for our particular situation is shown in the ESI† (see Section S.7.1). Note that the spectra are asymmetric with respect to zero offset because the detection is selective with respect to the copper hyperfine components. In this particular case, there are no peaks at positive offsets at all, because there are no forbidden transitions at higher frequencies than the observed allowed transitions. The surprising resolution of the two copper isotopes is a result of the large and strongly anisotropic hyperfine coupling combined with the strong orientation selection of EDNMR.
EDNMR spectra acquired at various field positions spanning the whole EPR spectrum are shown in Fig. 6(B). A slightly shorter and softer HTA pulse was used because the effective nutation frequency is larger for EDNMR peaks at smaller resonator offsets. The strong correlation of the g-tensor to the A-tensor is clearly visible from the strong shift of the copper peaks when changing the field position. In regions where the copper peaks are isolated, the agreement between experiment and simulation is quantitative. If the copper peaks overlap with the proton and nitrogen peaks or with the central hole (shown in gray and scaled down for clarity), the agreement is worse. The main discrepancy is actually a slight asymmetry of the overall intensity between the right-hand side (RHS) and the left-hand side (LHS) of the spectrum. Note that we fitted the linewidth in the simulated spectra (excluding the gray part of the spectra) and found that it is correlated with the field position. The resolution decreases by going from the low-field to the high-field edge. We tentatively assigned this to the different effective microwave powers at higher offsets and increased spectral diffusion at the maximum of the EPR spectrum. Additionally, the neglected electron–electron coupling could influence the observed linewidth. Note that the model we used here, i.e. only a single electron and a single copper nucleus, fits the EDNMR data better than the CW data, especially those recorded at X-band frequencies. This is due to the reduced number of parameters that influence the copper EDNMR peaks. The nitrogen nuclei and the exchange coupling have nearly no influence on these EDNMR peaks, in contrast to their significant influence on the EPR spectrum.
Again, the spectra are asymmetric with respect to the central hole because the detection selects specific hyperfine components of the EPR spectrum. This is illustrated in Fig. 7(A), where we show only the left-hand side of the EDNMR spectrum for simplicity. The contributions of the different Cu-hyperfine components to the EPR or EDNMR spectrum at a particular field position are indicated. In this case, the mI = +3/2 component is not observed at all. Note that the different hyperfine components that are selected by the observer sequence have also different orientations with respect to the external magnetic field (see top right panel). In principle, the orientation selection is slightly different for the different isotopes, but this difference is very small here. The splitting induced by the nuclear quadrupole coupling and the nuclear Zeeman interaction depends on mI. Therefore, the contribution of the mI = +1/2 component (in red) to the EDNMR spectrum does not show any resolved splitting. The nuclear Zeeman interaction and the nuclear quadrupole interaction nearly cancel each other in this particular case.
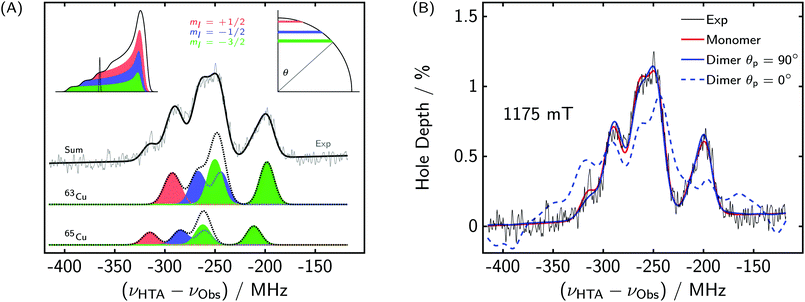 | ||
| Fig. 7 (A) Orientation selection in the EDNMR spectra of CuP2. νObs = 35.5 GHz, B0 = 1175 mT. The contributions of the different Cu-hyperfine components to the total EDNMR spectrum are shown. Top left inset: Contributions to the EPR spectrum. Top right inset: Observed orientations corresponding to the Gaussian in the top left panel. θ refers to the angle between the external magnetic field and the unique axis of the g-tensor. (B) Influence of the electron–electron coupling and relative porphyrin plane orientation on the EDNMR spectra of CuP2. The same parameters as in Fig. 6 were used for the simulation, but the blue spectra were simulated for a dimer including J = 50 MHz and d = 85 MHz. | ||
We also simulated some of the spectra assuming two copper sites and including a dipolar coupling of  and an exchange coupling with a somewhat arbitrary but illustrative value of J = 50 MHz. For a perpendicular orientation of the porphyrin planes, i.e. θp = 90°, no significant difference was found compared to a monomer simulation, see Fig. 7(B). On the other hand, if the porphyrin planes are assumed to be parallel (θp = 0°), the simulated EDNMR spectra look very different. In case of a non-parallel arrangement, the two copper centers have different effective g-values, and the perturbation by the electron–electron coupling is reduced compared to a parallel arrangement. In summary, the effect of the electron–electron couplings on the EDNMR spectra is strongly dependent on the other interactions present in the system. In the case of CuP2, the effect is marginal, which is in line with X-ray crystallography studies and DFT calculations demonstrating a perpendicular orientation and high rigidity of the two porphyrin planes.
and an exchange coupling with a somewhat arbitrary but illustrative value of J = 50 MHz. For a perpendicular orientation of the porphyrin planes, i.e. θp = 90°, no significant difference was found compared to a monomer simulation, see Fig. 7(B). On the other hand, if the porphyrin planes are assumed to be parallel (θp = 0°), the simulated EDNMR spectra look very different. In case of a non-parallel arrangement, the two copper centers have different effective g-values, and the perturbation by the electron–electron coupling is reduced compared to a parallel arrangement. In summary, the effect of the electron–electron couplings on the EDNMR spectra is strongly dependent on the other interactions present in the system. In the case of CuP2, the effect is marginal, which is in line with X-ray crystallography studies and DFT calculations demonstrating a perpendicular orientation and high rigidity of the two porphyrin planes.
3.2 f-CuP2: large exchange coupling
The X-band continuous wave (CW) spectrum and the Q-band EDFS spectrum of f-CuP2 are shown in Fig. 8(A and B). They clearly differ from the spectra of CuP2, with several additional splittings appearing. Nevertheless, the Q-band spectrum still indicates an axial g-tensor. In this case, both copper centers were included in the simulation and an effective spin-1 was assumed. This is justified if the exchange coupling constant J is much bigger than both the hyperfine coupling and the electron Zeeman anisotropy, or more precisely, if there is no significant singlet–triplet mixing. Agreement of the EPR spectrum with a simulated spectrum assuming the absence of singlet–triplet mixing poses a lower bound on the exchange coupling. This will be discussed below. The g- and A-values were assumed to be the same as for the CuP2 compound (apart from the fact that A has to be halved if the system is treated as a triplet). This is justified by the same local structure of the copper centers up to the third coordination sphere. The normal vectors of the two porphyrin planes were assumed to be parallel, implying θp = 0.A ZFS with |D| = 240 MHz had to be included in the simulation to obtain a satisfactory agreement with the experimental data. This value is about a factor of two higher than the expectation based on the dipole–dipole approximation (eqn (9)), which would be around 130 MHz for a distance of 8.4 Å. Note that the unique axis of the D-tensor is assumed to be collinear with the x-axes of the g-tensors, see Fig. 4.
Interestingly, because the ZFS splitting is roughly the same as the copper hyperfine splitting, one obtains an eight-line pattern along the parallel direction, clearly visible in the simulated Q-band spectrum and the inset. This is in contrast to the seven-line pattern expected if the ZFS is either much smaller or much larger than the hyperfine coupling. It is hard to claim the magnitude and orientation of the ZFS tensor from the field-swept spectra alone, since the signal-to-noise ratio of the low-field peaks is not sufficient in either case. However, we will provide additional support for the ZFS parameters by analysis of the field-correlated ELDOR spectra below.
In principle, one can gain additional information about the dipolar coupling and the relative orientation of the two copper centers by investigating the intensity and shape of the half-field transition.51 In the present case, the sample concentration we had available (1 mM) was only sufficient to just about distinguish the half-field transition from the noise. A reliable quantification was not possible (see the ESI,† Section S.8.1). This is consistent with the observation by Ikeue et al.35
The field-correlated ELDOR spectrum of f-CuP2 is shown in Fig. 9(A). Two features are striking compared to CuP2. First, the resolution is much worse, and second, there are clear signal enhancements (or anti-holes) visible (blue areas). Because we assign positive intensity to EDNMR side holes in agreement with previous work, the anti-holes correspond to negative intensities. In the spectrum shown in Fig. 9(A), the poor resolution could be ascribed to the settings used. The hole burning pulse was relatively short and strong, compared to the usual settings of EDNMR, where one generally uses long and soft pulses. Interestingly, softer and longer pulses did not lead to a better resolution (see the ESI,† Section S.8.2). The poor resolution is thus intrinsic to the spin system at hand, where the large exchange coupling leads to many side holes close to each other as verified by simulations (see the ESI,† Section S.12, for simulated single-orientation spectra, which are surprisingly complicated). Note that, in this case, the hole burning pulse predominantly excites allowed or only weakly disallowed transitions, in stark contrast to the usual EDNMR situation, where the side holes correspond to rather strongly disallowed transitions.
The positive part of the spectrum (red ridges) corresponds to side holes that increase in offset when going from higher to lower fields. These ridges roughly indicate the effective copper hyperfine coupling at a given field, similar to what is seen in the EDNMR spectra of CuP2. We find both ‘single quantum’ ridges, corresponding to an offset around 300 MHz (≈ACu/2) near the low-field edge and ‘double quantum’ ridges, corresponding to an offset around 600 MHz (≈ACu). In between these hole ridges, one can see signal enhancements or anti-holes (blue), which are due to the moderate ZFS and the exchange coupling. The strong anti-holes at positive and negative offsets around 1240 mT are due to the ZFS, which, for these orientations, is much larger than the hyperfine coupling.
The simulation program that we developed on the basis of the algorithm of Cox et al.4 was used to generate spectra for a multitude of possible spin Hamiltonian parameters, see Fig. 9(B–F). The comparison between the experimental spectrum and the simulated spectra led to the conclusions that (1) there must be a significant exchange coupling (>15 GHz). For lower exchange couplings, the splittings in the CW spectrum do not fit the experimental ones. (2) The ZFS is about |D| = 240 MHz, which is approximately twice as much as expected from the point-dipole approximation. If one assumes a smaller ZFS, again the splittings in the CW spectra do not match. On top of this, the strong anti-holes at the high-field edge in the 2D correlation plots are shifted to smaller offsets (see Fig. 9(E and F) at around 1240 mT). Note that changing the sign of the ZFS does not change the outcome of the simulations. However, if the ZFS is dominated by the dipole–dipole contribution, as we assume here, its sign is known. Note that it is difficult to predict the appearance of the field-correlated ELDOR spectra of f-CuP2 in an intuitive way, because the ZFS and the hyperfine couplings are in the same range. For the interested reader, we also simulated simpler model systems, and displayed the spectrum in Fig. 9(B) in terms of the individual EPR transitions, see the ESI,† Section S.11.
The agreement between experimental data and simulation obtained for our best parameter set is not as good as in the case of CuP2, but it is at the very least semi-quantitative. The main features are very well reproduced. The lower bound of the exchange coupling can be estimated with certainty, especially if the field-correlated ELDOR spectra and the CW spectra are inspected together. While the uncertainty in the ZFS is rather high (around 20 MHz, judged only by visual inspection of a range of simulations), it is still clear that the ZFS is much larger than estimated from the point-dipole approximation. This is not unexpected, since the large exchange coupling (vide infra) indicates significant spin density in the π-system in between the copper atoms. In all cases, we assumed that E = 0, and we did not obtain better fitting simulations by including a non-zero E.
We would like to emphasize that using CW EPR alone can lead to wrong conclusions regarding the spin Hamiltonian parameters. Ikeue et al.35 measured the exchange coupling of a very similar fused dimer by variable-temperature magnetometry, but they ignored the ZFS/dipolar coupling, stating that it is not resolved in the EPR spectrum. Accordingly, their fit gave very different g-values for the fused and the singly-linked dimer. Our ELDOR spectra contradict this interpretation. Khusnutdinova et al.36 investigated a fused dimer that was fused only at two points instead of three (the meso-position of one porphyrin was coupled to a β-position of the other porphyrin and vice versa, and the two porphyrin moieties were slightly shifted with respect to each other). They did not consider any dipolar electron–electron coupling and obtained a very different and rhombic g-tensor and approximately halved copper hyperfine constants. They also observed the shoulder at the high-field edge of the X-band CW spectrum, but did not reproduce it in their simulation (Khusnutdinova et al.,36Fig. 1(a) therein). We expect that similar problems will arise in other multi-nuclear complexes. ELDOR can give valuable information in these cases, where many parameters have to be fitted to a single spectrum and several local minima are possible.
3.3 Comparison of CuP2 and f-CuP2
Here we highlight the differences in the field-correlated ELDOR spectra of CuP2 and f-CuP2. Fig. 10 shows the two spectra as filled contour plots side by side. (1) As mentioned above, the resolution is much better in the case of CuP2 compared to f-CuP2. A contour plot is not the optimal representation for showing the high resolution for CuP2 (Fig. 10(A)). This can be judged from Fig. 6. (2) The ELDOR spectra of f-CuP2 show anti-holes, while the CuP2 spectra only show holes. This is due to the difference in electron spin state (S = 1 vs. S = 1/2). (3) The side holes arising from the Cu-hyperfine coupling are more pronounced in the case of f-CuP2, although the nominal flip angle of the hole burning pulse was smaller. For example, we could observe clear double-quantum peaks in the case of f-CuP2 (seen around ±600 MHz at the low-field edge), while we could not detect any double quantum peaks at all in the case of CuP2. This is due to the S = 1 spin state of f-CuP2: in the strong coupling regime, the transition moments for the forbidden transitions in the S = 1/2 case go towards zero if |A| ≫ |νI|, because the quantization axes of the nuclear spin in the two different electron spin manifolds are approximately (anti-)parallel to each other. The same is not true in the S = 1 case, because there is no hyperfine contribution in the MS = 0 manifold. This means that even if |A| ≫ |νI|, the quantization axes of the MS = ±1 and the MS = 0 manifold are not parallel and therefore the transition moments of the forbidden transitions do not vanish. A detailed discussion can be found in the ESI† (Section S.13). In addition to these considerations, the effective electron spin in f-CuP2 couples to two equivalent nuclei, which makes the holes more intense. | ||
| Fig. 10 Comparison of the field-correlated ELDOR spectra of CuP2 (A) and f-CuP2 (B). The data underlying (A) are the same as in Fig. 6(B). The asterisk indicates a field-independent spurious frequency which leads to a small and very sharp peak that is not visible in (B) because a larger step size was used. | ||
3.4 SQUID magnetometry
So far, all arguments regarding the exchange coupling of f-CuP2 were given on the basis of EPR data, but only a lower bound of roughly 15 GHz (or 0.5 cm−1) could be inferred that way. Additionally, we conducted SQUID magnetometry measurements of f-CuP2 and a corresponding Cu(II) monomer (see the ESI† for the structure). The data for the temperature-dependent susceptibility per mole Cu shown in Fig. 11 clearly show a maximum at about 2.4 K in the case of f-CuP2, which indicates an anti-ferromagnetic coupling of 79 GHz (for JS1S2, corresponding to 1.32 cm−1 for 2JS1S2). This is consistent with the measurements of Ikeue et al.35 The magnetization observed by SQUID is also consistent with thermal excitation of the triplet state at the temperatures of our EPR measurements. For a more accurate determination of J, lower temperatures would be needed. A detailed description of the SQUID measurements is given in the ESI† (see Section S.4).3.5 A comment on ENDOR of CuP2 and f-CuP2
It is a well known fact that, in the case of a system with large exchange coupling, the apparent hyperfine coupling is halved.46,52 Interestingly, this does not lead to different ENDOR spectra, as the spectra displayed in Fig. 12 clearly show.This was surprising to us at first and led us to the wrong assumption that the exchange coupling of f-CuP2 is of the order of a few hundred MHz at the most. On closer inspection, we found that the ENDOR spectra indeed do not change when going from the uncoupled to the strongly coupled case. In fact, this is straightforward to see, if one notes that ENDOR transitions inside the |αα〉 (T1 substate) and |ββ〉 (T−1 substate) manifolds of the electron spins are untouched by the exchange coupling, which mixes only the |αβ〉 with the |βα〉 state. Since, in the weak and strong exchange limits, ENDOR transitions are always within one MS manifold, ENDOR spectra for the |αα〉 and |ββ〉 electron spin states must be the same in the two limiting cases. In the strong exchange limit, the T0 triplet substate should, in principle, give rise to peaks at nuclear frequencies without hyperfine couplings (nuclear Zeeman and nuclear quadrupole), but for strongly hyperfine-coupled nuclei, the peaks in the other triplet substates will be much more intense due to hyperfine enhancement. A more detailed discussion is presented in the ESI† (see Section S.14).
4 Conclusion and outlook
We applied ELDOR-detected hole burning experiments to two Cu(II)-porphyrin dimers and interpreted the results with a generalization of the algorithm introduced by Cox et al.4 In the case of the singly-linked dimer with small exchange coupling and perpendicular orientation of the porphyrin planes, the EDNMR description is fully adequate and the experiment could resolve the two isotopes of copper as well as the nuclear quadrupole coupling constant in frozen solution. The simulation algorithm quantitatively reproduces these highly resolved experimental spectra. In the case of the fused dimer with large anti-ferromagnetic exchange coupling, anti-holes were observed in the ELDOR experiment. These anti-holes are due to allowed transitions that share a level. They are also well reproduced by simulations with the extended algorithm. From these experiments alone, a lower bound for the exchange coupling of about 15 GHz could be derived. SQUID measurements confirmed the presence of a significant exchange coupling of 79 GHz (singlet–triplet separation) at a distance of about 8.4 Å between the copper ions, in line with Ikeue et al.35 The EPR data also revealed a previously neglected dipolar coupling, which manifests as a ZFS in this strongly exchange-coupled system. The determined dipolar coupling is about twice as large as that expected based on a point-dipole approximation.Both findings, the large exchange and the large dipolar coupling, point to substantial spin delocalization and are thus consistent with an interaction of the copper d-orbitals with the delocalised π-system. The detailed experimental data presented here could serve as a starting point for in-depth quantum-chemical studies of the spin distribution in the fused system.
Our findings suggest that ELDOR experiments are even more useful than generally assumed: they can reveal more than “just” hyperfine and nuclear quadrupole couplings. By applying the extended simulation algorithm, a detailed understanding of systems with strong exchange and dipolar couplings can be achieved. Careful optimization of experimental parameters is needed, as much information comes from the connections between allowed transitions, i.e. much shorter pulses should be used compared to the usual setup of EDNMR.
Nevertheless, the interactions have to be accessible inside the resonator bandwidth, which might prevent the elucidation of very large ZFS or dipole–dipole couplings. This is where non-resonant setups, such as HiPER53 could have a dramatic advantage, provided they are combined with ultra-wideband frequency generation. While the bandwidth has to be large, the power does not need to be.
Surprisingly, anti-holes have not been reported before in EDNMR studies on Mn(II), although the polarization enhancement of the central transition by inversion of satellite transitions40 is based on the same effect. We can only speculate on the cause. For large ZFS and, accordingly, substantial second-order broadening, the anti-holes may be so strongly broadened that they go unnoticed or are considered baseline artefacts. In addition, they are less prominent compared to the nuclear-frequency holes if the flip angle of the hole-burning pulse is very high. Here we worked with lower nominal flip angles and shorter hole-burning pulses to enhance the anti-holes.
The emergence of anti-holes in exchange-coupled systems with rather large dipolar couplings also implies that ELDOR-detected NMR or related sequences with additional pulses might be useful to study biradicals with moderately strong dipole–dipole and exchange couplings that are commonly employed in dynamic nuclear polarization (DNP) experiments and are difficult to characterize only via their CW EPR spectra.54
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was financed by ETH Zürich (grant ETH-48 16-1), the EPSRC (grants EPL011972/1 and EP/N017188/1), the ERC (grant 320969) and the SCG Innovation Fund. We would like to thank Nick Cox et al. for making their simulation code available on the EasySpin forum, which was essential for us to simulate the spectra of f-CuP2. We hope that this example encourages other members of the scientific community to share their code if they employ simulations in their work.References
- P. Schosseler, T. Wacker and A. Schweiger, Chem. Phys. Lett., 1994, 224, 319–324 CrossRef CAS.
- G. Jeschke and H. W. Spiess, Chem. Phys. Lett., 1998, 293, 9–18 CrossRef CAS.
- N. Cox, W. Lubitz and A. Savitsky, Mol. Phys., 2013, 111, 2788–2808 CrossRef CAS.
- N. Cox, A. Nalepa, W. Lubitz and A. Savitsky, J. Magn. Reson., 2017, 280, 63–78 CrossRef CAS PubMed.
- D. Goldfarb, eMagRes, 2017, 6, 101–114 CAS.
- L. Rapatskiy, N. Cox, A. Savitsky, W. M. Ames, J. Sander, M. M. Nowaczyk, M. Rögner, A. Boussac, F. Neese, J. Messinger and W. Lubitz, J. Am. Chem. Soc., 2012, 134, 16619–16634 CrossRef CAS PubMed.
- A. Collauto, S. Mishra, A. Litvinov, H. S. Mchaourab and D. Goldfarb, Structure, 2017, 25, 1264–1274 CrossRef CAS PubMed.
- E. M. Bruch, M. T. Warner, S. Thomine, L. C. Tabares and S. Un, J. Phys. Chem. B, 2015, 119, 13515–13523 CrossRef CAS PubMed.
- M. Flores, A. G. Agrawal, M. Van Gastel, W. Gärtner and W. Lubitz, J. Am. Chem. Soc., 2008, 130, 2402–2403 CrossRef CAS PubMed.
- T. Hetzke, A. M. Bowen and T. F. Prisner, Appl. Magn. Reson., 2017, 48, 1375–1397 CrossRef.
- A. Aliabadi, R. Zaripov, K. Salikhov, V. Voronkova, E. Vavilova, M. A. Abdulmalic, T. Rüffer, B. Büchner and V. Kataev, J. Phys. Chem. B, 2015, 119, 13762–13770 CrossRef CAS PubMed.
- T. Hetzke, A. M. Bowen, M. Vogel, M. Gauger, B. Suess and T. F. Prisner, J. Magn. Reson., 2019, 303, 105–114 CrossRef CAS PubMed.
- C. Fan, C. M. Gorst, S. W. Ragsdale and B. M. Hoffman, Biochemistry, 1991, 30, 431–435 CrossRef CAS PubMed.
- R. J. Gurbiel, Y. C. Fann, K. K. Surerus, M. M. Werst, S. M. Musser, P. E. Doan, S. I. Chan, J. A. Fee and B. M. Hoffman, J. Am. Chem. Soc., 1993, 115, 10888–10894 CrossRef CAS.
- J. M. Peloquin, K. A. Campbell and R. D. Britt, J. Am. Chem. Soc., 1998, 120, 6840–6841 CrossRef CAS.
- J. Harmer, C. Finazzo, R. Piskorski, G. Bauer, B. Jaun, E. C. Duin, M. Goenrich, R. K. Thauer, S. Van Doorslaer and A. Schweiger, J. Am. Chem. Soc., 2005, 127, 17744–17755 CrossRef CAS PubMed.
- A. Silakov, E. J. Reijerse, S. P. J. Albracht, E. C. Hatchikian and W. Lubitz, J. Am. Chem. Soc., 2007, 129, 11447–11458 CrossRef CAS PubMed.
- L. V. Kulik, B. Epel, W. Lubitz and J. Messinger, J. Am. Chem. Soc., 2007, 129, 13421–13435 CrossRef CAS PubMed.
- S. M. Greer, J. McKay, K. M. Gramigna, C. M. Thomas, S. A. Stoian and S. Hill, Inorg. Chem., 2018, 57, 5870–5878 CrossRef CAS PubMed.
- I. Kaminker, T. D. Wilson, M. G. Savelieff, Y. Hovav, H. Zimmermann, Y. Lu and D. Goldfarb, J. Magn. Reson., 2014, 240, 77–89 CrossRef CAS PubMed.
- A. Potapov, B. Epel and D. Goldfarb, J. Chem. Phys., 2008, 128, 052320 CrossRef PubMed.
- N. Wili and G. Jeschke, J. Magn. Reson., 2018, 289, 26–34 CrossRef CAS PubMed.
- M. J. Crossley and P. L. Burn, J. Chem. Soc., Chem. Commun., 1991, 8, 1569 RSC.
- H. L. Anderson, Chem. Commun., 1999, 2323–2330 RSC.
- G. Kuang, S. Z. Chen, W. Wang, T. Lin, K. Chen, X. Shang, P. N. Liu and N. Lin, J. Am. Chem. Soc., 2016, 138, 11140–11143 CrossRef CAS PubMed.
- Z. Li, T. H. Park, J. Rawson, M. J. Therien and E. Borguet, Nano Lett., 2012, 12, 2722–2727 CrossRef CAS PubMed.
- T. Tanaka and A. Osuka, Chem. Soc. Rev., 2015, 44, 943–969 RSC.
- A. Tsuda and A. Osuka, Science, 2001, 293, 79–82 CrossRef CAS PubMed.
- A. Tsuda, H. Furuta and A. Osuka, Angew. Chem., Int. Ed., 2000, 39, 2549–2552 CrossRef CAS.
- T. Tanaka and A. Osuka, Chem – Eur. J., 2018, 17188–17200 CrossRef CAS PubMed.
- E. Leary, B. Limburg, A. Alanazy, S. Sangtarash, I. Grace, K. Swada, L. J. Esdaile, M. Noori, M. T. González, G. Rubio-Bollinger, H. Sadeghi, A. Hodgson, N. Agrat, S. J. Higgins, C. J. Lambert, H. L. Anderson and R. J. Nichols, J. Am. Chem. Soc., 2018, 140, 12877–12883 CrossRef CAS PubMed.
- N. Yoshida, T. Ishizuka, A. Osuka, D. H. Jeong, H. Cho, D. Kim, Y. Matsuzaki, A. Nogami and K. Tanaka, Chem – Eur. J., 2003, 9, 58–75 CrossRef CAS PubMed.
- F. C. Grozema, C. Houarner-Rassin, P. Prins, L. D. A. Siebbeles and H. L. Anderson, J. Am. Chem. Soc., 2007, 129, 13370–13371 CrossRef CAS PubMed.
- M. Rickhaus, A. Vargas Jentzsch, L. Tejerina, I. Grübner, M. Jirasek, T. D. Claridge and H. L. Anderson, J. Am. Chem. Soc., 2017, 139, 16502–16505 CrossRef CAS PubMed.
- T. Ikeue, K. Furukawa, H. Hata, N. Aratani, H. Shinokubo, T. Kato and A. Osuka, Angew. Chem., Int. Ed., 2005, 44, 6899–6901 CrossRef CAS PubMed.
- D. Khusnutdinova, B. L. Wadsworth, M. Flores, A. M. Beiler, E. A. Reyes Cruz, Y. Zenkov and G. F. Moore, ACS Catal., 2018, 8, 9888–9898 CrossRef CAS.
- M. Florent, I. Kaminker, V. Nagarajan and D. Goldfarb, J. Magn. Reson., 2011, 210, 192–199 CrossRef CAS PubMed.
- A. Leavesley, D. Shimon, T. A. Siaw, A. Feintuch, D. Goldfarb, S. Vega, I. Kaminker and S. Han, Phys. Chem. Chem. Phys., 2017, 19, 3596–3605 RSC.
- J. Haase, M. Conradi, C. Grey and A. Vega, J. Magn. Reson., Ser. A, 1994, 109, 90–97 CrossRef CAS.
- I. Kaminker, A. Potapov, A. Feintuch, S. Vega and D. Goldfarb, Phys. Chem. Chem. Phys., 2009, 11, 6799 RSC.
- A. Doll, M. Qi, S. Pribitzer, N. Wili, M. Yulikov, A. Godt and G. Jeschke, Phys. Chem. Chem. Phys., 2015, 17, 7334–7344 RSC.
- M. Ramirez Cohen, N. Mendelman, M. Radoul, T. D. Wilson, M. G. Savelieff, H. Zimmermann, I. Kaminker, A. Feintuch, Y. Lu and D. Goldfarb, Inorg. Chem., 2017, 56, 6163–6174 CrossRef CAS PubMed.
- S. Richert, I. Kuprov, M. D. Peeks, E. A. Suturina, J. Cremers, H. L. Anderson and C. R. Timmel, Phys. Chem. Chem. Phys., 2017, 19, 16057–16061 RSC.
- S. Stoll and D. Goldfarb, eMagRes, 2017, 6, 495–510 CAS.
- S. Stoll and A. Schweiger, J. Magn. Reson., 2006, 178, 42–55 CrossRef CAS PubMed.
- E. J. L. McInnes and D. Collison, eMagRes, 2016, 5, 1445–1458 CAS.
- R. L. Belford and D. C. Duan, J. Magn. Reson., 1978, 29, 293–307 CAS.
- L. K. White and R. Belford, Chem. Phys. Lett., 1976, 37, 553–555 CrossRef CAS.
- L. K. White and R. L. Belford, J. Am. Chem. Soc., 1976, 98, 4428–4438 CrossRef CAS.
- S. Kita, M. Hashimoto and M. Iwaizumi, J. Magn. Reson., 1982, 46, 361–373 CAS.
- S. S. Eaton, K. M. More, B. M. Sawant and G. R. Eaton, J. Am. Chem. Soc., 1983, 105, 6560–6567 CrossRef CAS.
- B. Bleaney and K. D. Bowers, Proc. R. Soc. A, 1952, 214, 451–465 CAS.
- P. A. S. Cruickshank, D. R. Bolton, D. A. Robertson, R. I. Hunter, R. J. Wylde and G. M. Smith, Rev. Sci. Instrum., 2009, 80, 103102 CrossRef PubMed.
- J. Soetbeer, P. Gast, J. J. Walish, Y. Zhao, C. George, C. Yang, T. M. Swager, R. G. Griffin and G. Mathies, Phys. Chem. Chem. Phys., 2018, 20, 25506–25517 RSC.
Footnotes |
| † Electronic supplementary information (ESI) available: Synthetic procedures, materials and methods, details on the simulation algorithm, additional experimental and simulated data. All raw data are also available under https://doi.org/10.3929/ethz-b-000323948. See DOI: 10.1039/c9cp01760g |
| ‡ Present address: Institut für Physikalische Chemie, Albert-Ludwigs-Universität Freiburg, Albertstr. 21, 79104 Freiburg, Germany. |
| This journal is © the Owner Societies 2019 |