Influence of the hydrophobic domain on the self-assembly and hydrogen bonding of hydroxy-amphiphiles

Abstract

The amphiphiles 1-octadecanol (octadecyl (stearyl) alcohol, ODA) and 1,2-dioleoylglycerol (DOG) were studied by IR spectroscopy and X-ray diffraction combined with multiscale theoretical modeling. The computations allowed us to rationalize the experimental findings and deduce the supramolecular structure of the formed assemblies while providing a fairly detailed insight into their hydrogen-bonding patterns. IR spectra revealed that the amphiphilic assemblies dramatically differ in structural order and hydrogen-bond strength, both being high in ODA and low in DOG. On the other hand, both compounds demonstrated common features, namely a splitting of the IR bands arising from O–H stretching vibrations (νOH) as well as complete hydrophobicity. However, the observed phenomena have different origins in the two amphiphiles. While the νOH split in ODA occurs due to a vibrational coupling along the string of inter-layer O–H⋯O hydrogen bonds, in DOG it arises from different types of hydrogen bonds (intra- and intermolecular). The hydrophobicity of ODA stems from the very tight O–H⋯O hydrogen bonding network connecting the opposite monolayers in a densely packed tilted crystalline phase (L_c′), whereas in DOG it occurs because the polar sites are locked inside reverted micellar-like assemblies. ODA and DOG illustrate that, in the assemblies of amphiphilic hydroxyl compounds, hydrogen bonds can be formed in a wide structural latitude, which is primarily governed by the chemical nature of apolar chains. Such a wide structural variability of OH-involving hydrogen bonds can be essential for the biological functioning of relevant molecules, such as glycolipids, acylglycerols, and, potentially, glycoproteins and carbohydrates.

---

1. Introduction

Amphiphilic molecules, composed of hydrophobic and hydrophilic parts, have been a focus of scientific interest for a long time. Understanding the functional implications of their structure is of great importance in the life sciences. Amphiphilic lipids are necessary components of biomembranes. While generally providing a membrane scaffold, they also often perform specific functions (e.g., act as cell-surface receptors for glycolipids (GLs)).^1,2 Moreover, amphiphiles have also been explored in material science owing to their wide-spread application as surfactants and additives in many technologies.^3,4

Due to the hydrophobic effect, amphiphilic molecules spontaneously assemble into higher-order structures. Polar groups affect this process. While the role of intra- and intermolecular binding in aggregation and assembling processes has been extensively studied and understood for phospholipids, the analogous studies of GLs are much less common. The binding potency of the latter is mainly governed by a number of hydroxyl groups forming complex O–H⋯O hydrogen-bonding networks in the polar region.⁵ Taking β-D-galactosyl-(2-D-hydroxyoctadecanoyl)-D-dihydrosphingosine as an example of a GL, altogether 14 different hydrogen bonds (H-bonds) of very different strength according to their r(O⋯O) distances between 2.63 and 3.02 Å were deduced using the crystal structure.⁶ Exploring such H-bonded systems, IR spectroscopy, as one of the ad hoc best suited physical methods,^7–10 is severely hampered by this complexity. Therefore, O–H⋯O hydrogen bonds are often not considered in GL studies.^2,9 Thus, for characterizing OH⋯OH hydrogen bonds in GLs by IR spectroscopy, it could be useful to consider simple model molecules first. As such, we have chosen 1-octadecyl (or stearyl) alcohol (ODA) and 1,2-dioleoylglycerol (or diolein) (DOG). They both contain one hydroxyl group and have hydrocarbon chains with the same length of 18 carbon atoms (Fig. 1). The potential complexity of H-bonds is enhanced from ODA to DOG, with the ability to form intramolecular H-bonds only in the latter case. These two amphiphiles were also selected since their apolar part covers an utterly large steric demand, with small and very high cross-section areas for ODA and DOG, respectively.

Fig. 1 Chemical structures of (a) 1-octadecanol (ODA) and (b) 1,2-dioleoylglycerol (DOG) with the relevant numbering of the oxygen atoms in DOG.

ODA and other long-chain aliphatic alcohols (n-alkanols) have found rather important practical applications. They served, e.g., as film coatings of metal surfaces,¹¹ wax models,¹² anti-evaporants and additives in cosmetics, and building blocks of other more complex lipids.¹³ Therefore, the structure of n-alkanols has been probed at different levels of aggregation and by using various methods. X-ray diffraction (XRD) and electron-diffraction revealed a complex polymorphism for crystallized fatty alcohols with chain lengths of 14 carbons and larger.^13–17 Two main forms, β and γ, were found at ambient temperatures, beside a pre-melting α form. While the γ-form is preferred in even-numbered fatty alkanols,^13–16 odd-numbered alkanols favorably adopt the β-form.^13,15,16 Tetra-, hexa- and octadecanol can exist in both β- and γ-forms.^16,17

Studies on crystals of n-heptadecanol (β-form), n-octadecanol (γ-form) and n-hexadecanol (γ-form) revealed a long chain of O–H⋯O hydrogen bonds connecting the opposing monolayers along the bilayer interface plane.^13–16 These findings were generally confirmed for powder samples¹⁸ and for multi-lamellar films¹⁹ (30–40 monolayers thick, similar to the samples in the present study).

In addition to the diffraction methods, vibrational, especially IR, spectroscopy has conveniently and frequently been used to characterize amphiphiles.^{2,5,10,20–22} IR spectroscopy is a fairly versatile and inexpensive method that has been proven to be extremely useful in exploring structural and binding (interaction) phenomena, especially in terms of H-bonds. Both IR^11,12,16,18 and Raman spectroscopies¹⁸ have been used mainly to monitor C–H vibrations of fatty alcohols. However, the polar head-group interactions have not been considered often. In an attempt to correlate IR spectra with crystal-XRD data for solid long-chain n-alkanols, the IR spectra were classified in two types, A and B, which correspond, respectively, to the crystallographic β- and γ-form.¹⁶ The spectral patterns for the A and B types are distinguished by well-defined features comprising both C–H (mainly) and O–H vibrational modes. For instance, a β-form alcohol typically has a single broad OH stretching (νOH) band at 3300 cm⁻¹, whereas a γ-form alcohol exhibits a split νOH band with sub-maxima at 3330 and 3250 cm⁻¹.¹⁶

ODA occurs rather rarely in nature (e.g., in an archaeon²³). By contrast, diacylglycerols, such as DOG, are abundant and very important in in vivo processes. They act as so-called lipid second messengers^24,25 and they are known to stimulate protein kinase C^24–26 as well as to induce or promote membrane fusion.^27,28 Moreover, more recently DOG has been increasingly used as an essential component of formulations for encapsulation of drugs or effectors.^29,30 As far as we are aware, there is only one IR-spectroscopic work devoted to diacylglycerol, but rather in complexes with phosphatidylethanolamine than as a pure compound.³¹

The present study is aimed to explore how ODA and DOG assemble in supramolecular phases and what is the role of H-bonds and the hydrophobic domain in this process. We applied IR spectroscopy and XRD to ODA for utilizing the particular synergism between these two methods,³² especially in order to probe whether the β- or γ-form is adopted under our experimental conditions. In experiments, DOG was studied only spectroscopically as its samples (non-oriented films in our case) did not provide any usable X-ray reflexes. Instead, molecular dynamics (MD) simulations were used to gain deeper insight into the supramolecular structure and dynamics of DOG assemblies. The MD approach was also extended to the ODA system. Since a clear and unambiguous interpretation of vibrational spectra is often difficult, quantum-mechanical (QM) calculations could be very useful in rationalizing spectroscopic features on a molecular scale. Thus, we developed simplified models accessible by QM methods. By using them, we could explain the spectral features found and verify the structural hypotheses derived from the IR and XRD experiments. Furthermore, to account for the conformational and dynamic effects in the flexible DOG system, we applied a recently developed multiscale MD/DFT computational approach.^33,34 The method is based on a combination of MD simulations and density functional theory (DFT) calculations of vibrational spectra. To achieve an adequate level of consideration, we have compiled an extensive data set arising from comprehensive IR studies of alcohols with different hydrocarbon chain lengths and aggregation numbers.

2. Materials and methods

2.1 Experimental

ODA and DOG were purchased from Sigma Co. (Munich) and used without further purification. Chemical structures involving the relevant atom numbering are shown in Fig. 1. Film preparation and IR measurements were carried out according to the protocols described in detail previously.¹⁰ The IR spectra of films cast from chloroform solutions of the amphiphiles onto ZnSe windows and treated by unidirectional stroking were recorded in situ by using an IFS-66 spectrometer (Bruker, Karlsruhe, Germany). The small-angle X-ray scattering (SAXS) and wide-angle X-ray scattering (WAXS) measurements were performed at the Deutsches Elektronen-Synchrotron (DESY) in Hamburg. The X33 double-focusing monochromator-mirror camera of the European Molecular Biology Laboratory (EMBL) on storage ring DORIS III was utilized. Films were prepared in the same way as in the spectroscopic investigations, but without stroking, and placed onto thin mica discs. For further details see our previous report,³² and the papers by M. Koch et al. cited therein.

2.2 Computations

MD and QM methods were used for calculations of more rigid ODA model systems. A multi-scale MD/DFT approach^33,34 accounting for the conformational and dynamic effects was applied to the flexible DOG system. Details on the computational procedures are provided in the ESI.†

3. Results and discussion

3.1 Experimental data

Fig. 2 displays the most instructive ranges of the IR spectra of ODA and DOG (panel (a), 3600–3100 cm⁻¹, panel (b), 3050–2750 cm⁻¹, and panel (c), 1800–1400 cm⁻¹), measured at 0% relative humidity. Table 1 lists the relevant absorption bands and their assignments. The main feature in panel (a) of Fig. 2 is that both amphiphiles show split νOH bands. However, these double bands differ markedly in peak wavenumbers and band shape. In Table S1 of the ESI,† the νOH wavenumbers of ODA and DOG are compared with related literature data (Batishcheva et al.,³⁵ Aldrich,³⁶ AIST³⁷ and Pohle et al.³⁸). Whenever alcohols are in a liquid state (due to the short length of the hydrocarbon chains (up to 12 carbon atoms), in unsaturated alcohols, and upon melting or dilution), they exhibit a single broad νOH band near 3340 cm⁻¹. The exact band position can range from 3366 cm⁻¹ for 2-methyl-2-propanol to 3322 cm⁻¹ for oleyl alcohol (see, e.g., the spectrum of dodecanol in Fig. 2a). Even-numbered analogs have somewhat higher νOH wavenumber values than the odd ones, and this is true also for secondary alcohols when compared to primary counterparts.

Fig. 2 Infrared spectra of ODA (red) and DOG (blue) obtained from films at 0% relative humidity in the OH stretching-vibration region (a) as well as a spectrum of dodecanol taken from NIST (with permission) for comparison (dashed line), the CH stretching-vibration region (b), and C=O stretching and CH₂ scissoring-vibration regions (c); the two vertical dotted lines at 2852 and 2922 cm⁻¹ for ν_sCH₂ and ν_aCH₂, respectively, in panel (b) indicate the boundaries between ordered and disordered phases, for explanation see the text.

Table 1 Wavenumbers (rounded to the next unity) for the most prominent IR bands of 1-octadecanol (ODA) and 1,2-dioleoylglycerol (DOG)

Wavenumber, cm^−1		Assignment
ODA	DOG
a Abbreviations: w – weak; vw – very weak; vvw – very very weak; m – medium; s – strong; vs – very strong; sh – shoulder; νa – antisymmetric stretch; νs – symmetric stretch; δ – bending (scissoring) vibration; ρ – rocking vibration. b A more detailed assignment and interpretation for each of the sub-component bands of the composite spectral contour will be given in the text below (in Sections 3.2–3.4) and in Table 4.
	∼3620 w sh^a	νOH free
	3515 s/3465 s	νOH H-bonded^b
3288 m sh/3227 s		νOH-H-bonded^b
	3005 w	νCH at C=C
2955 w(m)	2955 vw sh	ν aCH3
2918 vs	2926 vs	ν aCH2
2872 vvw	2871 vvw	ν sCH3
2850 vs	2855 vs	ν sCH2
	1744 s	νC=O free^b
	1726 m sh	νC=O H-bonded^b
	1653 vw	νC=C
1473 m(w)/1463 m	1466 m	δCH2
730 w(m)/720 m	723 m	ρCH2

---

As soon as long-chain alcohols (with 14 carbon atoms and longer) adopt a solid state (which happens at the ambient temperature, in neat films, nujol mulls and KBr discs), the νOH band splits and its wavenumber decreases to 3300 cm⁻¹ and below. Water-depleted bolalipid 22-hydroxybehenylphosphocholine, as the exception from that rule, exhibits only a single narrow band although being in solid state.³⁸ The νOH wavenumbers of all these alcohols are clearly below that for liquid water. According to the generally accepted correlation between H-bond strength and νOH wavenumber,^7,8,39,40 the O–H⋯O hydrogen bonds in alcohols are presumably stronger than those in water.

On the other hand, the νOH wavenumber of DOG is peculiar in dramatically surpassing all the other values listed in Table S1 (ESI†) including even water. This suggests that the H-bonds in DOG are exceptionally weak on the “O–H⋯O scale”. Moreover, DOG is extraordinary because its νOH absorption is split despite the fact that it is fluid. The half width of the overall νOH band for DOG (ca. 220 cm⁻¹) is significantly larger than that for ODA (ca. 160 cm⁻¹). This may indicate a considerably larger heterogeneity and/or flexibility of the H-bonds in DOG compared to those in ODA.

The νCH (3050–2750 cm⁻¹) and the 1800–1400 cm⁻¹ regions of the ODA and DOG spectra are displayed in panels (b) and (c) of Fig. 2, respectively. According to previous work, the boundary between ordered and disordered phases can be roughly drawn at 2852 cm⁻¹ for ν_sCH₂ and 2922 cm⁻¹ for ν_aCH₂ (indicated as dotted vertical lines in Fig. 2b).^10,20,22 In DOG and ODA, the wavenumbers of both ν_sCH₂ and ν_aCH₂ are located clearly above and below these phase-boundary values, respectively (Fig. 2b and Table 1). The much higher νCH₂ wavenumbers of DOG are accompanied by a considerable band broadening (Fig. 2b), which is characteristic for the transition from a solid to a liquid-crystalline phase in lipids.⁴¹ All these features prove the chain fluidity to be very high in DOG and very low in ODA.

These results are in accord with the features exhibited by the δCH₂ bands. While the scissoring (near 1470 cm⁻¹, Fig. 2c) as well as the rocking modes (near 720 cm⁻¹, Table 1) clearly appear as split bands for ODA, they are largely uniform in DOG. The doublet character of these δCH₂ bands was referred to a correlation-field splitting indicative of a dense packing of quasi-crystallized alkyl chains.^42,43 The νCC band progression at 1060 cm⁻¹ and below, emerging in our ODA spectra (data not shown), is also characteristic for frozen alkyl chains.¹⁶

X-ray diffraction data of ODA are shown in Fig. S1 (ESI†). The SAXS studies show equidistant reflexes revealing a lamellar phase with a spacing of 4.2 nm (resulting from a scattering vector of the first-order peak at 0.238 nm⁻¹). According to the molecular geometry of ODA, the total length of two H-bonded molecules in the bilayer arrangement is about 47 Å. Altogether, this provides a tilt angle of ∼25° (cos(25°) = 42/47), which is coincident with the results of the MD simulations shown below (see Section 3.2.2). The main feature in the WAXS pattern is a triplet typically indicating a crystalline or subgel phase.^44,45 This is in accord with the spectroscopic data, especially the pronounced splitting of the methylene deformation bands (cf.Fig. 2c and Table 1). Therefore, we can conclude that ODA has adopted a tilted lamellar crystalline phase (L_c′) under the conditions of our experiments.

The main peak of the νC=O band arising from the carbonyl groups of DOG at 1744 cm⁻¹ has a pronounced shoulder at about 1726 cm⁻¹ (Fig. 2c). Low-frequency components of the carbonyl absorption in lipid spectra were previously ascribed to carbonyl groups involved in H-bonding,^46,47 usually indicating an interaction with water. In water-depleted DOG, the presence of the low-wavenumber shoulder may suggest that some part of the carbonyl groups is involved in H-bonds with OH groups. At the same time, the wavenumber of the C=O peak maximum indicates a largely nonpolar surrounding of the major part of the carbonyls. This notion was indeed confirmed by the calculations (see Section 3.4.2 below).

In a further series of experiments, the amphiphile films were subjected to increasing relative humidity up to 100%. The experimental details for such hydration studies were described in detail previously.^10,32 Neither ODA nor DOG was able to imbibe any measurable amount of water. Consequently, the IR as well as the XRD spectra remained unchanged during these hydration attempts (data not shown). It should be noted that while most amphiphiles more or less readily hydrate,^48–50 such a pronounced hydrophobicity as found here for ODA and DOG is rather exceptional. The inability of water uptake is particularly surprising for DOG in view of its highly fluid acyl chains. Usually, unsaturated lipids exhibit a stronger hydrophilicity than their saturated counterparts (see, e.g., a comparison between distearyl- and dioleoylphosphatidylcholine^49,51). This circumstance has provided another motivation to select these two amphiphiles for the comprehensive theoretical consideration as described below. Furthermore, this allowed for the restriction onto H-bonds involving exclusively the OH groups of the amphiphile molecules, leaving aside any potentially interfering water molecules.

3.2 Octadecanol computations

3.2.1 Model systems. In order to understand and rationalize the experimentally observed spectral features of ODA supramolecular assemblies, we performed a detailed analysis of the spectroscopic response for a wide range of simplified models accessible for computational studies. The model systems were designed (i) with various numbers of molecules involved in the H-bonded chain (from 1 to 200) and (ii) with various lengths of the hydrocarbon tail (from 1 to 10 carbon atoms in the tail). This allowed us to devise general spectroscopic features of the studied systems and confidently assign them to the experimentally observed spectra of ODA.
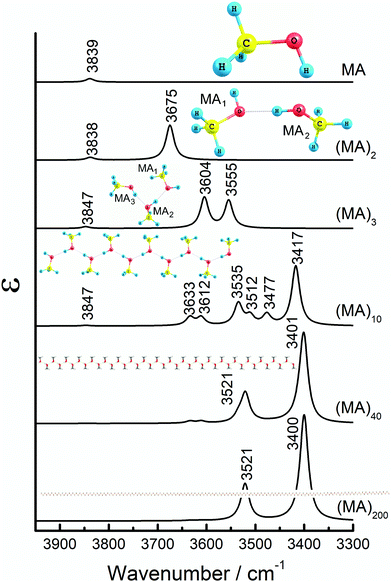
Methanol model (MA). The structures and corresponding IR spectra in the νOH region obtained from the QM and Cartesian coordinate transfer (CCT)^52,53 calculations of MA, (MA)₂, (MA)₃, (MA)₁₀, (MA)₄₀ and (MA)₂₀₀ models are shown in Fig. 3. The main geometrical parameters and band assignments are given in Table S2 (ESI†). Fig. S2 (ESI†) displays some of the νOH vibrational modes. A single MA molecule produces a νOH band at 3839 cm⁻¹. However, two H-bonded molecules have two distinct bands at 3838 and 3675 cm⁻¹, arising from non-H-bonded (free) and H-bonded OH groups of (MA)₂, respectively (Fig. S2, ESI†). As expected from H-bond theory, the free OH group vibrates at higher frequency and has notably lower intensity compared to the H-bonded group.^7–9 A similar observation was also reported for other alcohols.⁵⁴

Fig. 3 Calculated IR spectra in the νOH region, together with the optimized (B3LYP/6-31++G**) structures of different methanol models, (MA)_n; the spectra for (MA)₄₀ and (MA)₂₀₀ were calculated using the CCT method. Spectral intensity is expressed as a molar extinction coefficient (ε) normalized per one OH group.

If there are at least two H-bonded OH groups, as in (MA)₃, the νOH vibrations of the H-bonded groups couple and split into two bands at 3604 and 3555 cm⁻¹. Our calculations demonstrate that these bands arise from out-of-phase and in-phase coupling of OH vibrations, respectively (Fig. S2, ESI†). Fig. S3 (ESI†) gives a general scheme of in-phase and out-of-phase vibrational coupling in the three-molecule system. The resulting transition dipole moments for the two coupled vibrations in (MA)₃ are largely perpendicular to each other (Fig. S2, ESI†). The third band at 3847 cm⁻¹ emerges from the free OH group, the vibration of which is not coupled with any other vibrations.

If the number of H-bonded MA molecules increases further, the spectrum becomes more complex with several sub-types of out-of-phase and in-phase vibrations (Fig. 3). Such a splitting into multiple bands arises from the end effects and irregularities present in the structure. This results in a coupling of vibrations in one part of the system (e.g., at the more flexible ends) at a frequency slightly different from that in the other parts (e.g., in its more rigid middle part). Vibrational displacements for the most intense bands of (MA)₁₀ at 3535 and 3417 cm⁻¹ are plotted in Fig. S2 (ESI†).

This fine-splitting disappears with increased length of the MA string, when the contribution of end effects becomes more and more negligible and overall averaging of the vibrational modes occurs (Fig. 3 and Fig. S4, ESI†). In that case, the multiple peaks coalesce into two bands corresponding to overall out-of-phase and in-phase vibrations. Fig. S4 (ESI†) shows that this takes place for the length of 20 units (for (MA)₂₀) and larger. Thus, (MA)₄₀ and (MA)₂₀₀ produce only two major bands around 3521 and 3400 cm⁻¹, corresponding to the out-of-phase and in-phase coupled vibrations, respectively (Fig. 3). The dipole moment orientations for the out-of-phase and in-phase coupled modes are practically perpendicular to each other in all the models (Fig. S2, ESI†), in accord with the data obtained by polarization spectroscopy.^55,56

The integral intensity of the νOH bands arising from the H-bonded OH groups increases linearly with the number of the H-bonded monomeric units in the system (Fig. S5, ESI†). On the other hand, the intensity of the free OH stretch remains largely unchanged since the number of free OH groups does not increase with the elongation of the system. The same effect was also reported for ethanol assemblies of different size.⁵⁴

The magnitude of the static dipole moment is linearly correlated with the number of monomers (Fig. S6, ESI†); this suggests the absence of cooperative effects in the H-bond network formation. Hence, only the local H-bond interactions with the nearest neighbors are relevant. This is contradictory to the conclusions made by Sum and Sandler,⁵⁷ pointing at strong cooperative effects in the H-bonds occurring in the clusters of methanol and ethanol in vacuum. This discrepancy can be ascribed to the difference of the theoretical approach. Our systems have a strictly limited molecular mobility, which is due to the methodologically dictated pre-arrangement of long linear O–H⋯O chains mimicking crystal packing (which is, in turn, predetermined by the experimental finding of the L_c′ phase in ODA, see above). By contrast, the irregular systems studied in vacuo⁵⁷ generally have an unrestricted mobility of the molecules which have the ability to randomly clusterize.

Ethanol (EA), butanol (BA) and decanol (DA) models. The structures and corresponding IR spectra in the νOH region of EA, (EA)₂, (EA)₃, (EA)₁₀ and (EA)₄₀ are shown in Fig. 4. The main geometrical parameters and IR band assignments are given in Table 2. Selected νOH normal modes are displayed in Fig. S7 (ESI†).

Fig. 4 Calculated IR spectra in the νOH region and optimized (B3LYP/6-31++G**) structures for ethanol models, (EA)_n; the spectrum for (EA)₄₀ was calculated using the CCT method. Spectra for single EA are enlarged by a factor of 10 for better visualization. Dashed and solid lines in the spectrum for a single EA molecule correspond to trans (left structure) and gauche (right structure) conformers, respectively. Spectral intensity is expressed as a molar extinction coefficient (ε) normalized per one OH group.

Table 2 Main geometrical parameters for optimized (B3LYP/6-31++G**) ethanol models and their assignments in the νOH region; the individual molecules in (EA)₂ and (EA)₃ clusters are labeled with subscript indices as shown in Fig. 4; trans and gauche conformers are indicated using letters t and g, respectively

Fragment	Wavenumber, cm^−1	Assignment	C–O bond length, Å	C–C bond length, Å	O–C–C bond angle, °	O–H bond length, Å	O⋯O distance, Å	H-bond length, Å	O–H⋯O angle, °
a “(av)” stands for average. b This structure could not be optimized due to the large system size.
EA (t)	3837	Localized νOH	1.432	1.519	107.9	0.965	—	—	—
EA (g)	3819	Localized νOH	1.430	1.525	113.0	0.966	—	—	—
(EA)2 (tg)	3819w	Localized νOH of EA1g (free)	1.438 (EA1g)	1.523 (EA1g)	112.4 (EA1g)	0.967 (EA1g)
	3669	Localized νOH of EA2t (H-bonded)	1.424 (EA2t)	1.521 (EA2t)	108.5 (EA2t)	0.974 (EA2t)	2.874	1.903	175
(EA)3 (tgt)	3832 w	Localized νOH of EA3t (free)	1.447 (EA3t)	1.517 (EA3t)	108.6 (EA3t)	0.966 (EA3t)
	3592	Coupled νOH of EA1t and EA2g, out of phase	1.422 (EA1t)	1.521 (EA1t)	108.7 (EA1t)	0.979 (EA1t)	2.804 (EA1t⋯EA2g)	1.836 (EA1t⋯EA2g)	169 (EA1t⋯EA2g)
	3550	Coupled νOH of EA1t and EA2g, in phase	1.431 (EA2g)	1.525 (EA2g)	112.5 (EA2g)	0.979 (EA2g)	2.821 (EA2g⋯EA3t)	1.843 (EA2g⋯EA3t)	177 (EA2g⋯EA3t)
(EA)10 (tg)	3848 w	Localized νOH of the only free OH group	1.430 (av)^a	1.521 (av)	111.3 (av)	0.978 (av)	2.831 (av)	1.855 (av)	176 (av)
	3644 m, 3616 m, 3585	Coupled νOH, out of phase			109.2 (t)
	3508	Coupled νOH, in phase			113.3 (g)
(EA)40 (tg)^b	3848 w	Localized νOH of the only free OH group	—	—	—	—	—	—	—
	3586 m	Coupled νOH, out of phase
	3498	Coupled νOH, in phase

---

Depending on the position of the OH proton with respect to the alkyl chain, there can be two conformers for alcohols larger than methanol, namely trans and gauche (Fig. 4, two structures on top).^54,58–61 Following the abbreviations introduced by others, we will designate trans and gauche conformers with t and g, respectively, and trans–gauche (where the first conformer is an H-bond proton donor, and the second one is an acceptor) with tg. It should be pointed out that trans and gauche alcohol conformers denoting the position of the hydroxyl proton with respect to the hydrocarbon chain are completely unrelated to trans (C–C–C–C torsions are 180°) and gauche (C–C–C–C torsions are 60°) conformations of the hydrocarbon chain, not discussed here.

The trans and gauche ethanol conformers produce a single νOH band each, computed at 3837 cm⁻¹ and 3819 cm⁻¹, respectively (Fig. 4, top). The difference of the computed energies for the two conformers is below 1 kcal mol⁻¹. These values as well as the geometric parameters for both conformers (Table 2) agree well with previously reported data.^54,58–61 Otherwise, the IR spectra of the ethanol models in the νOH region are generally very similar to those of the related methanol ones and are further discussed in detail in the ESI.†

Since butanol (BA)_n and decanol (DA)_n models are too large to be optimized at the DFT level, the semi-empirical PM3 method was applied. Fortunately, in these cases the H-bond network could be adequately described at the semi-empirical level. In test calculations, the PM3 method provided qualitatively similar results with split νOH bands. However, semi-empirical data cannot be quantitatively compared with DFT results, since in the former case νOH wavenumbers are situated at systematically higher values. The spectra of (BA)₆, (BA)₁₀, (BA)₁₈, and (DA)₁₀ are shown in Fig. 5 together with the pertinent optimized structures. The studied butanol and decanol systems were optimized in tg conformation, which corresponds to monoclinic γ-form crystal structures.^14,62 The spectra of all the systems have two major peaks in the νOH region. The less intense band at higher frequency arises from the out-of-phase mode and the more intense one at lower frequency from the in-phase mode, similar as for respective MA and EA models. The fine-splitting of the bands observed for (BA)₆ and (BA)₁₀ is less pronounced. Hence, some bands emerge only as shoulders, and disappear if the length of the H-bond network increases (cf. (BA)₁₀ with (BA)₁₈), following the same trend as for methanol and ethanol.

Fig. 5 Calculated IR spectra in the νOH region and optimized (PM3) geometries for butanol (top three) and decanol (bottom) models in tg conformation; spectral intensity is expressed as a molar extinction coefficient (ε) normalized per one OH group.

3.2.2 MD simulations of the γ-form of ODA. The γ-form of ODA bilayers can occur either with trans conformers in one monolayer and gauche conformers in the other or with trans conformers in both monolayers. In the frame of our simulations, the overall arrangements will hereafter be denominated as the tg and tt models, respectively.

The starting structures for tg and tt models are shown at the top of Fig. 6 and 7, respectively, along with the pertinent structures resulting after 20 ns of MD simulations at the bottom. For better visualization of the overall structure of the systems, 9 periodic boundary condition (PBC) cells are shown for both the models in Fig. S8 (ESI†).

Fig. 6 Model of the ODA bilayer in the γ-form according to the tg model; top: front (xz) and side (yz) views of the starting structure for the MD simulation, bottom: front (xz) and side (yz) views of the structure resulting after 20 ns of MD simulation.

Fig. 7 Model of the ODA bilayer in the γ-form according to the tt model; top: front (xz) and side (yz) views of the starting structure for the MD simulation, bottom: front (xz) and side (yz) views of the structure resulting after 20 ns of MD simulation.

Several observations can be made from the MD results. The structures in both the models are highly regular and tightly packed (with a density of ca. 0.936 g cm⁻³). ODA molecules are arranged almost parallel to each other within a monolayer. The RMSD plot shows only minor (less than 0.5 Å) deviations of the structure from the starting geometry and minute variations (within 0.3 Å) in the course of MD simulations (Fig. S9, ESI†), which underlines the high rigidity and stability of the system.

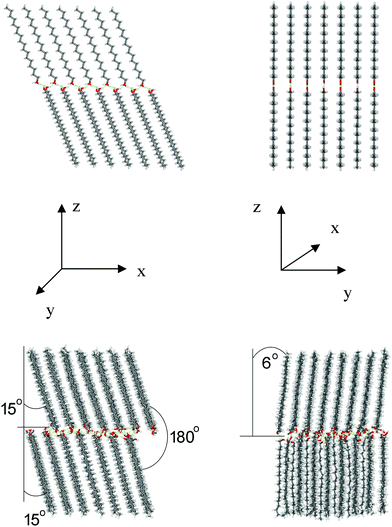
For the tg model, the initial parallel orientation of the molecules in the opposing monolayers in the xz plane (180° with respect to each other, Fig. 6) is preserved in the course of MD simulations. The two monolayers are equally tilted forming an angle of ca. 16° between the hydrocarbon-chain axis and the normal to the bilayer. In the yz plane, the molecules in the two monolayers form different tilts of ∼28° and ∼7° relative to the bilayer normal, resulting in an angle of about 145° with respect to each other (Fig. 6). The overall tilt of the chains in both planes can then be estimated at about 25° ((16° + 35°)/2), which fully agrees with the respective XRD finding based on the spacing of 4.2 nm found for ODA films (see Section 3.1 above).

Statistics on the H-bonds during the MD simulation of the tg model is shown in Fig. 8 (top row). From all the statistically relevant H-bonds (existing >1% of time, weighted according to the occupied time), 80% are inter-layer and 20% are intra-layer H-bonds. Most of the inter-layer H-bonds are relatively long-living (occupied between 30 and 60% of the time) and result in relatively uniform inter-layer O⋯O distances of 2.75–2.85 Å and H-bond angles between 160° and 167°. The distance values are in excellent agreement with the O⋯O distances for (EA)_n calculated by DFT, while the angle values deviate slightly from linearity more due to dynamics effects not considered in DFT calculations (Table 2). On the other hand, the intra-layer H-bonds are less numerous, very heterogeneous in length and H-bond angle, and they vary significantly in life-time.

Fig. 8 Statistics of the distance r(O⋯O) (left column) and the H-bond angle α(O–H⋯O) (right column) for inter- and intra-layer H-bonds obtained from the MD simulations of the ODA bilayer for the γ-form according to tg (top row) and tt (middle row) models, and for the β-form (bottom row); the occurrence of different H-bond types (in %, weighted according to the occupied time) is given in brackets.

According to the r(O⋯O) calibration curves,^39,40 the inter-layer O⋯O distances of 2.75–2.85 Å estimated in our MD simulations would result in νOH bands between 3100–3150 and 3350–3420 cm⁻¹ (Fig. S10, ESI†). This wavenumber range meets precisely the relatively high bandwidth of the νOH absorption with a maximum around 3250 cm⁻¹ measured in ODA films (Fig. 2a).

For the tt model, the molecules in opposing monolayers, initially oriented in parallel (at an angle of 180°), rearranged in the xz plane to form an angle of ca. 143° with respect to each other (Fig. 7). In contrast to tg, the monolayers show different tilts (∼30° and ∼7°). In the yz plane, the molecules in one monolayer remained oriented almost perpendicular to the bilayer plane, while they are tilted by 15°–20° to the bilayer normal in the opposing monolayer. The overall tilt of both planes can be estimated at about 27°. From all the statistically relevant H-bonds, 20% are inter-layer and 80% are intra-layer H-bonds (Fig. 8, middle row), which is exactly opposite to the tg model. The inter-layer H-bonds vary significantly in length, H-bond angle and life-time. On the other hand, the intra-layer H-bonds are relatively long-living (occupied 50–70% of the time, Fig. 8, middle row), have more uniform O⋯O distances (2.75–2.85 Å) and H-bond angles (around 165°). This should favor the stability of the individual monolayers rather than the stability of the bilayer.

Most of the XRD studies of even-numbered fatty alcohols have indicated the molecular arrangement according to the tg structure, which is in crystallography usually denoted as the monoclinic γ-form.^13,14,62 On the other hand, the tt structure was reported scarcely, e.g., for decanediol.⁶² Our data reveal a higher stability of the tg structure, confirming these findings. Although XRD data do not provide the definite location for protons, it was suggested that the position of the hydroxyl protons in the inter-layer H-bond network is rather disordered in solid alcohols.^14,62 This indicates that both OH conformers can be present in the H-bond network. Hydroxyl tautomerization was also proposed for such systems.⁵⁵

3.2.3 MD simulations of the β-form of ODA. In addition to the γ-form discussed above, where all the molecules in a monolayer adopt the same single configuration (either t or g, but not both), the β-form with alternating t and g molecules within the same monolayer should be considered.^16,17 Since it has not been extensively reported in the literature, we performed MD simulations for the sake of comparison with the γ-form. The starting structure of the β-form is shown in Fig. 9 at the top (with the t and g molecules alternating along the y-direction), and the structure resulting after 20 ns of MD simulations is presented at the bottom. Furthermore, the relevant 9 PBC cells are shown in Fig. S8c (ESI†).

Fig. 9 Model of the ODA bilayer in the β-form; top: front (xz) and side (yz) views of the starting structure for the MD simulation, bottom: front (xz) and side (yz) views of the structure resulting after 20 ns of MD simulation.

As can be seen from Fig. S8 (ESI†), the β-form is more tightly packed compared to both γ-form configurations since there are no voids between the layers, such as those present in the γ-form due to the protrusions of some of its individual molecules. This observation is confirmed by the density of the β-form, which is higher than that of the γ-forms (ca. 0.982 vs. ca. 0.936 g cm⁻³).

The initial parallel orientation of the molecules in the opposing monolayers in the xz plane (180° with respect to each other, Fig. 9) remains essentially unchanged during the MD simulations, similarly as in the tg model. Both monolayers are equally tilted forming an angle of ca. 15° between the hydrocarbon-chain axis and the normal to the bilayer. In the yz plane, one monolayer is tilted only slightly relative to the bilayer normal (∼6°), while the other one remains oriented almost perpendicular to the bilayer plane (Fig. 9). The overall tilt of the chains, estimated to be about 10°, is the smallest of all three structures. This should provide a bilayer thickness of ∼46 Å for the β-form. This value is significantly larger than the value of 42 Å found in our XRD measurements, testifying that the β-form is a less probable arrangement for the ODA samples used in the present study. This notion is supported by the H-bond analysis (Fig. 8, bottom row). From all the statistically relevant hydrogen bonds, 60% are inter-layer and 40% are intra-layer bonds. Shorter life-time of H-bonds (occupied 0 to 40% of the time), larger variety in the H-bond lengths and angles, and larger presence of intra-layer bonds (compared to the tg model) substantiate lower stability of the β-form, which may explain its rare detection in experiments and seldom reference in the literature.

3.2.4 MD simulation of ODA hydration. In order to test its ability for imbibing water, we performed MD simulations for ODA surrounded by a water shell. Fig. S11 (ESI†) exemplifies the starting geometries for the (ODA)₉₈ bilayer in the tg model with 1 and 10 water molecules per amphiphile (representing partial and full system hydration). Fig. 10a and b show the MD results for the partial hydration of the β-form and the tt model, respectively. The data reveal that, even at this low level of hydration (∼10% relative humidity), a substantial number of water molecules penetrate between the two monolayers in each case. This is mostly pronounced for the β-form (Fig. 10a). By contrast, in the tg model (Fig. 10c) most of the water molecules at this hydration level are accumulated at the edges of the ODA cell. Due to dynamical packing defects the two monolayers are shifted, thus exposing some of the OH groups to water. However, no water molecules are observed in the interface between the two monolayers.

Fig. 10 Snapshots after 20 ns of MD simulations of the hydration of the (ODA)₉₈ bilayer for different structures of the system: β-form (a), trans–trans conformation of the γ-form (b) and trans–gauche conformation of the γ-form (c and d); water molecules are illustrated by yellow balls. Panels (a–c) show the hydration by 1 water molecule per amphiphile, panel (d) shows the hydration by 10 water molecules per amphiphile (fully hydrated system). The starting structures for MD simulations were the same as shown in Fig. S11 (ESI†).

Furthermore, even upon increasing the relative humidity to 100% (corresponding to 10 water molecules per amphiphile) in the tg conformation (Fig. 10d), most of the water molecules are gathered outside the bilayer system, and only very few molecules penetrate inside the bilayer interface. Hence, the MD results demonstrate phase separation to occur in the ODA–water system. These data provide clear evidence that, among all the models considered here, only the tg model is compatible with the extensive hydrophobicity of ODA as observed in IR spectroscopy and XRD experiments.

3.3 Dioleoylglycerol computations

Due to the unavailability of XRD data for DOG, the structural arrangement of its molecules in the bulk phase is not known. In contrast to ODA, where structural data revealed by XRD can be used to build input geometries for QM calculations, other methods must be employed in order to obtain realistic conformations of DOG molecules. Therefore, we performed a combined MD/DFT computation, details of which are given in the ESI.† In this approach, the MD step delivered reasonable geometries and H-bond patterns for the DOG molecules in the assembly, which could be used as input structures for DFT optimization and spectra calculations. Since mainly the spectroscopic response of the polar DOG groups (OH and C=O) was the focus of this study, the hydrocarbon tails, less essential at this stage of computations, were truncated. The reduction of the molecular size allowed us to use high-level DFT methods, necessary for the correct spectra calculations. Furthermore, to simulate the experimental situation as realistically as possible, we performed a dynamical averaging to account for the different H-bond patterns and their dynamics in the system. The spectra obtained for all the H-bond patterns were statistically weighted according to the data retrieved from the MD trajectories as outlined in Fig. S12 and described in detail in the ESI.† An example of a resulting MD structure of (DOG)₁₀ at the lowest energy point is shown in Fig. 11a and b by two different representations. Analysis of the MD data reveals a largely spherical assembly with the polar regions of DOG molecules brought together and surrounded by apolar hydrocarbon tails (Fig. 11). Such structures strongly resembling inverted (or reversed) micelles were also obtained in our previous simulations with (DOG)₆ and (DOG)₆₀ systems with different initial arrangements of the individual molecules (ranging from random to bilayer and micellar arrangements).⁵¹ The RMSD plot in Fig. S9 (ESI†) shows that the structure of (DOG)₁₀ becomes relatively stable after a few nanoseconds of MD simulation. Examples of the fragments used in the DFT calculations are shown in Fig. 11c–f. The resulting MD-averaged and H-bond pattern-weighted spectrum of (DOG)₁₀ is compared with the simulated (EA)₄₀ spectrum as shown in Fig. 12.

Fig. 11 Top: MD snapshot of (DOG)₁₀ corresponding to the lowest-energy structure represented by sticks (a) and balls (b); red color indicates oxygen atoms. Middle and bottom: DOG fragments used for DFT computations with no H-bonds (free OH groups) (c) as well as with intramolecular (d) and intermolecular C=O⋯H–O (e) and H–O⋯H–O (f) H-bonds.

Fig. 12 IR spectra calculated for (EA)₄₀ (red) and (DOG)₁₀ (blue) in the νOH region (left) as well as for (DOG)₁₀ in the νC=O region (right); intensity of the calculated band for free OH in (EA)₄₀ is too low to be clearly visible in the scale of the figure.

When compared to ODA, the DOG structure is generally more irregular and much less tightly packed (cf.Fig. 6, 7 and 9 in context with Fig. 11). As demonstrated in Table 3, the headgroups of DOG molecules are involved in hydrogen bonding for about 73% of the time (ensemble-averaged). The configurations of individual molecules are quite different since the H-bond pattern ranges from intramolecular H-bonds between OH and closest C=O groups (the most abundant ones, Fig. 11d) to intermolecular H-bonds. The latter can be formed either between the OH group of one molecule and the carbonyl group of another one or between two OH groups of different molecules (Fig. 11e and f). There is also a small population of more extended H-bond networks involving three molecules connected with each other in a similar pattern (not shown). Relatively large flexibility of the DOG assembly can also be concluded from the deviations of the coordinates within about 2–3 Å in the RMSD plot as shown in Fig. S9 (ESI†) by contrast to only 0.3 Å deviations for ODA. The instability of the H-bonds due to their relatively large length and deviation from linearity, their short life-time (only about half of them are long-living and exist for more than 10% of the simulation time) and the mainly intramolecular nature of the long-living H-bonds (96% out of all) also testify an extraordinary flexibility of DOG (Table 3).

Table 3 Hydrogen-bond analysis of the 10 ns MD simulation of the (DOG)₁₀ ensemble; numbering of oxygen atoms is shown in Fig. 1. The wavenumbers of νOH_av (last column) were calculated using the weights of individual vibrations from column 3

Type of H-bonding		% of time H-bonds exist (ensemble-averaged)	% of all possible H-bonds (occupied-time – weighted)	% of long-living H-bonds (occupied-time – weighted)^a	O⋯O/O–H/H-bond lengths, Å	O–H⋯O angle, °	νOH, cm^−1	νOHav (weighted)
a Long-living H-bonds are those existing for more than 10% of the simulation time.
Intra-molecular	Total		61	96
	C=O3⋯H–O5		56.7		2.817/0.972/1.964	145	3720	3724
	O2⋯H–O5		2.5		2.857/0.968/2.090	135	3806
	C=O4⋯H–O5		0.5		—
	O1⋯H–O5		0.8		—
Inter-molecular	Total		39	4
	C=O3⋯H–O5		13.7		2.855/0.976/1.897	166	3637	3672
	O5⋯H–O5		10.9		2.888/0.973/1.925	170	3689
	C=O4⋯H–O5		12.5		2.873/0.973/1.914	168	3695
	O1⋯H–O5		1.5		—
	O2⋯H–O5		0.8		—
H-bonded DOG		73
Free DOG		27

---

Despite its high flexibility, DOG is not able to imbibe any measurable amount of water, just like ODA. The hydration pattern of (DOG)₆₀ obtained from the MD simulations of fully hydrated systems⁵¹ is compared with fully-hydrated (ODA)₉₈ as shown in Fig. S13 (ESI†). In both cases, there is a clear phase separation between amphiphiles and bulk water. In ODA the separation results from a tight rigid layered structure impermeable by water. On the other hand, the phase separation in DOG occurs because the molecules aggregate into an irregular assembly of micelles hiding their polar atoms inside and sticking together with their hydrophobic parts. Similar micelle-like structures with limiting hydration ability had also been suggested for different diacylglycerols (but not for pure DOG) by others previously.^63–66

The calculated IR spectra for (DOG)₁₀ and (EA)₄₀ in the νOH region (Fig. 12, left) can be directly compared to the experimental DOG and ODA spectra in the same region (Fig. 2a). The computed spectra correctly represent the high wavenumber of the νOH bands in DOG related to ODA. This corroborates the experimental finding that the H-bonding in DOG is much weaker than in ODA. Indeed, the computed length of the most abundant intramolecular H-bonds in DOG is 1.964 Å with the H-bond angle of 145° (Table 3), while in (EA)₁₀, for example, the length is 1.855 Å and the angle is 176° (Table 2). Fig. 2a demonstrates the absence of a free νOH band in the measured IR spectrum of ODA and the presence of a weak shoulder in the DOG spectrum around 3600 cm⁻¹. These findings suggest the involvement of by far the majority of the OH groups in H-bonding in ODA, but the presence of a certain fraction of free hydroxyls in DOG. This is confirmed by the calculations clearly unraveling two IR bands at 3845 and 3814 cm⁻¹ that arise from free OH groups existing in (DOG)₁₀ (Fig. 12). More specifically, according to the MD results, about a quarter of the OH groups in DOG are free (Table 3). The appearance of two distinct bands arising from free OH groups can be tentatively explained by different environments of hydroxyl groups situated either inside the micelle with ε = 0 (apolar neighborhood) or sticking outside and facing the implicit solvent with ε = 2. The larger half width of the νOH band in DOG with respect to ODA found experimentally is also correctly simulated. According to our computations, such a broad multi-component band occurs due to a large variety of H-bond patterns resulting in a wide range of H-bond lengths and angles in DOG (Table 3). This variety, in turn, can be ascribed to a large number of conformational sub-states in DOG due to the high degree of disorder.

The split of the νC=O band in measured IR spectra (Fig. 2c) is likewise reproduced correctly by the computations (Fig. 12, right). The weaker band at lower wavenumber (1773 cm⁻¹) in the computed spectrum corresponds to the C=O groups involved in H-bonding, while the more intense band at 1802 cm⁻¹ arises from free carbonyls. This strongly corroborates the assignment of the measured IR bands (see details in Section 3.4.2), namely the main νC=O peak to the free carbonyl groups and the low-wavenumber shoulder to the H-bonded ones (Fig. 2c and Table 1), in accord with the previous suggestions for phospholipids.^46,47

3.4 Origin of the νOH band splitting in octadecanol and dioleoylglycerol

3.4.1 Octadecanol. The doublet character of the νOH band observed in solid-state alcohols is an interesting feature. Two relevant explanations can be taken into account. First, two different types of O–H⋯O hydrogen bonds with alternating O⋯O distances may be formed in the polar region of ODA. This follows directly from XRD data.^14,15 These data demonstrate that the H-bond geometry significantly varies in the γ-form, with inter-layer distances being significantly shorter than the intra-layer ones.^13,14,16 On the other hand, in the β-form these distances are essentially the same.^15,16 The same feature could be realized by the static picture arising from our QM calculations of energetically optimized alcohol structures. In the dynamic picture, however, these distances become randomized, and are, hence, unable to rationalize the νOH split.

In the alternative explanation, the νOH band split is ascribed to coupling phenomena. This gives rise to two sub-bands originating from in-phase and out-of-phase coupled vibrations of adjacent O–H bonds along the O–H⋯O H-bond networks formed in alcohols⁵⁵ or phenols.⁶⁷ The present QM calculations support this notion, showing that indeed two bands arise from coupled in-phase and out-of-phase vibrational movements. The νOH band splitting occurs in all the model systems forming H-bond networks. Its nature is fairly conservative and does not change qualitatively with hydrocarbon chain length, or with the number of molecules involved in the H-bonding string after it reaches 20 monomers. At this length of the H-bond network the end effects become negligible and local fluctuations become averaged. As can be seen from the example of (EA)₃, the coupling concept is a fairly realistic interpretation for the observed νOH band split even when alternating O⋯O distances exist in static energy-minimized structures. Thus, (EA)₃ has two hydrogen bonds with slightly different O⋯O lengths of 2.804 and 2.821 Å (Table 2), but both its H-bonded O–H groups vibrate simultaneously with the in-phase and out-of-phase modes at 3550 and 3592 cm⁻¹, respectively (see Fig. 4, the third spectrum from above, and Fig. S7, ESI,† second row).

The spectral band shape computed for vibrational coupling is also in accord with the experiment: the low-frequency in-phase νOH band is generally more intense than the high-frequency out-of-phase band, as was also reported previously.⁵⁵ For the tested MA and EA systems, both bands undergo a wavenumber upshift with the increase of the hydrocarbon chain length (i.e., with increasing bulkiness of the apolar region of alcohols) for the systems with more than 10 monomeric units. Comparing (MA)₄₀ and (EA)₄₀ systems, the average shift is as high as about 80 cm⁻¹ (cf.Fig. 3 and 4). This can be tentatively explained by the presence of a steric clash between CH₂ and CH₃ groups in the EA system, which may induce a certain weakening of the pertinent H-bonds. The split between the out-of-phase and in-phase bands increases with the number of arrayed molecules (compare (MA)₃ with (MA)₁₀ in Fig. 3 and (EA)₃ with (EA)₁₀ in Fig. 4). This tendency is very sharp for fewer H-bonded molecules, but for networks with more than ten molecules the extent of splitting stabilizes. On the other hand, there is an opposite trend between split magnitude and alcohol-chain length. Thus, the largest split is computed for methanol (118 cm⁻¹ for (MA)₁₀), and it decreases to 77 cm⁻¹ for (EA)₁₀ (cf.Fig. 3 and 4). The same tendency is noted from the results of the PM3 computations (Fig. 5). Hence, the computed νOH-split values provide a correct trend towards the measured value of 61 cm⁻¹ representing the boundary value (quasi-infinite H-bond network in ODA) given by the experimental conditions. Therefore, our QM computations provide strong evidence that the νOH split can convincingly be explained by coupled out-of-phase and in-phase O–H vibrations proceeding along the H-bond strings formed in solid alcohols, which is outlined in Table 4.

Table 4 Specific assignments for the main sub-components of the split νOH bands observed in ODA and DOG as derived from the theoretical calculations; abbreviations are the same as in Table 1

Wavenumber, cm^−1		Assignment
ODA	DOG
	3515 s	νOH H-bonded intramolecular
	3465 s	νOH H-bonded intermolecular
3288 m sh		νOH coupled out-of-phase
3227 s		νOH coupled in-phase

---

It should be mentioned that the coupling of O–H vibrations seems to be a general feature of alcohol assemblies occurring as soon as a continuous network of equivalent consecutive H-bonds is formed. Consequently, this phenomenon is not bound to the solid state, but it can, in principle, emerge also in fluid systems, as it was experimentally revealed by Raman measurements of liquid alcohols.⁵⁶ Usually, the existence of such coupling effects in fluid or dissolved solid alcohols would be rather obscured by a strong heterogeneity, which is typical for such fluctuating systems with unfrozen structures, leading to a considerable variety of the H-bonds feasible therein.

A very instructive example demonstrating that a network of repetitive O–H⋯O hydrogen bonds is an essential factor for arising of vibrational coupling is provided by bipolar 22-hydroxybehenylphosphocholine. Instead of an expected doublet (since this bolaamphiphile is in a solid state), there is only a single νOH band near 3290 cm⁻¹ (see Table S1, ESI†).³⁸ This apparent contradiction can be resolved by considering the particular structure formed in the assemblies of 22-hydroxybehenylphosphocholine. They are composed of alternating and vice versa interdigitated molecules in monolayers with the OH group from one end of a molecule H-bonded to the phosphate group from the other end of the next molecule, and so on.³⁸ Such an alternation of OH and phosphate groups prevents the formation of a regular string of O–H⋯O hydrogen bonds and results in the impossibility of coupling and, consequently, in a single νOH band. Hence, this finding provides a further strong argument in favor of the coupling concept explaining the νOH band splitting observed in solid alcohols.

3.4.2 Dioleoylglycerol. As pointed out above, the experimental wavenumber of the νOH band of DOG is exceptionally high when compared with any of the alcohols or even with the νOH wavenumber of water occurring near 3400 cm⁻¹ (Table S1, ESI†). This proves an exorbitant weakness of the O–H⋯O hydrogen bonds in DOG. Correspondingly, the computed νOH wavenumbers as well as the O⋯H distances are relatively large. The H-bond weakness found in DOG stems mainly from the geometrical restraints of intramolecular H-bonds (e.g., a significant deviation of these H-bonds from linearity, see Fig. 11d and Table 3). Besides, intermolecular H-bonds are not abundant due to steric hindrance, as the bulky oleoyl chains may prevent a close approach of the H-bond donors and acceptors. Since the space available inside the DOG micelles might be scarce, even the formation of a per se energetically unfavorable 4-member ring geometry according to Holly and Sohar⁶⁸ can be taken into account. Altogether, our theoretical data reveal that DOG assemblies represent a very flexible system composed of multiple populations of molecules with different patterns of hydrogen bonding (see Section 3.3). Consequently, the bandwidth of the overall νOH absorption in DOG is considerably larger than in ODA, for both the experimental and the predicted spectra (Fig. 2 and 12, respectively). It is worth noting that, with respect to ODA and DOG, the νOH band of dodecanol has the highest half width (295 cm⁻¹), although its overall wavenumber is lower compared to DOG (Fig. 2a and Table S1, ESI†). These features appear to imply that the H-bonds in dodecanol are stronger but more heterogeneous than in DOG. Such a finding may emphasize once more the structurally determined restriction of the spatial diversity of H-bond formation facilities in DOG as discussed above.

In principle, the νOH split of DOG could again be evoked either by vibrational coupling or by a distinct heterogeneity of the O–H⋯O hydrogen bonds formed within two or more preferred structures. This question can be fairly unambiguously answered on the basis of the theoretical results obtained for (DOG)₁₀. The overall DOG structure comprising several species of H-bonds (OH⋯OH, OH⋯O=C; intra- and intermolecular) essentially rules out the presence of a continuous repetitive H-bond network, not to speak of a linear string as in fatty alcohols. Thus, the occurrence of vibrational coupling similar to that existing in ODA can also be ruled out. On the contrary, such an arrangement of DOG molecules is in favor of assuming the structural heterogeneity of the H-bonds as the cause for the νOH split.

As mentioned above, the intramolecular H-bonds in DOG deviate significantly from linearity (Fig. 11d and Table 3), which makes them weaker than the intermolecular H-bonds (and, apparently, even weaker than the H-bonds in bulk water). This results in a higher νOH wavenumber of the OH groups involved in intramolecular H-bonds. On the other hand, intermolecular H-bonds could be stronger due to their potential for a more linear geometry (Table 3) and, consequently, should appear at lower frequency. This is demonstrated in Fig. 12, where, indeed, all the νOH bands involved in intramolecular H-bonds arise at higher wavenumber, while all the bands evoked by intermolecular H-bonds appear at lower wavenumbers. These results are in agreement with earlier data for intramolecular H-bonds.⁶⁸ Thus, the experimental νOH doublet can be explained as a combination of νOH bands arising from OH groups involved in intramolecular and intermolecular H-bonds at higher and lower wavenumbers, respectively (Table 4). The large variations in strength of the intermolecular H-bonds arising from different H-bond patterns could also evoke the broad shoulder at the low-frequency side of the νOH band between ∼3450 and ∼3250 cm⁻¹ in the experimental spectrum (Fig. 2a). In contrast, the intramolecular H-bonds are limited in variety and produce a much narrower sub-band between 3600 and 3500 cm⁻¹ (Fig. 2a).

It should be noted that the intermolecular H-bonds in DOG are very short-living due to its high flexibility and fluidity. For example, the more stable long-living intermolecular bonds (existing for more than 10% of the simulation time) represent only 4% from all the bonds (Table 3). The high instability of these bonds elongates and weakens them. Thus, average values for the intermolecular H-bond length and angle in DOG are 1.91 Å and 168°, respectively, while in ODA the corresponding values are 1.855 Å and 176° (Tables 2 and 3). Such H-bond elongation and larger deviation from linearity shift the corresponding νOH bands in DOG to relatively high wavenumbers. This is depicted in Fig. 12, where they appear at much higher wavenumbers than the νOH absorption of ODA.

Hence, our results demonstrate that H-bond strength is generally governed by an interplay of the steric constraints and the flexibility of a system. Furthermore, both these factors (i.e., chain properties) determine the position of the νOH bands.

Another important point refers to the fact that only a minor part of the carbonyl groups is involved in the H-bond network formed in the DOG micelles. This is indicated by both the experimental (Fig. 2c) and the computed spectra (Fig. 12, right). A major portion of C=O groups freely vibrates in an apolar environment giving rise to an experimental IR peak near 1744 cm⁻¹ (calculated at 1802 cm⁻¹). Statistical analysis based on the MD results shows that only about 30% of all carbonyls participate in H-bonds (both intra- and intermolecular). This can be estimated as follows. As the number of carbonyls is twice as large as the number of hydroxyls, only 50% of C=O groups can be involved in H-bonds in the absence of any other H donors (e.g., water). From this half, about 84% are engaged in H-bonds according to the above mentioned statistics (Table 3 and Fig. S12, ESI;† only the H-bonds involving O3 and O4 carbonyl oxygens must be considered), which corresponds then to ∼42% of all C=O groups. Since 27% of all DOG molecules remain free of any H-bond (Table 3), altogether about 30% of C=O would be H-bonded after all (42% × 73%). This is in accord with the contour of both the experimental and the computed νC=O band. Correlations between νC=O wavenumbers and binding or environmental influences underlying these considerations have been widely discussed previously.^46,47

4. Conclusions

A combination of experimental methods (IR spectroscopy, X-ray diffraction and film hydration studies) with multiscale MD/DFT modeling was used to elucidate the structure and the IR-spectroscopic response for two amphiphiles, octadecanol and dioleoylglycerol. Despite a certain basic structural similarity (one OH group and hydrocarbon chains with 18 carbon atoms), they also offer some diversity in terms of their conformational disorder varying from very low (in ODA films) to extremely high (in fluid DOG). In spite of this difference, the two amphiphiles showed similar features, in particular a doublet structure of the νOH vibrational band and complete hydrophobicity. Theoretical calculations allowed us to rationalize these experimental findings. Furthermore, they provided a consistent picture of both the overall structure of the systems and fairly sophisticated details of the internal hydrogen-bonding patterns formed upon their supramolecular self-association.

For ODA, the experimental data from IR spectroscopy and XRD unravel the presence of a rigid lamellar phase (L_c′). This is characterized by a quasi-crystalline lattice of hydrocarbon chains forming a tilt of 25° with respect to the bilayer normal. The overall results for ODA match the trans–gauche conformation in the frame of the monoclinic γ-form very well. Other possible conformations suggested in the literature (trans–trans conformation of the γ-form, and the β-form) are not supported by our data. The individual chains in the bilayers adopting the trans–gauche conformation are densely packed, thus preventing the access of water molecules to the OH groups of ODA and explaining its hydrophobicity. Relatively low νOH wavenumbers indicate a considerable strength of the intermolecular O–H⋯O hydrogen bonds formed in the ODA assemblies. The νOH split observed in the IR spectra occurs due to in-phase and out-of-phase coupling of νOH vibrational modes, which takes place in the arrays of continuous repetitive hydrogen bonding networks.

By contrast, the hydrogen bonds formed in DOG films are exorbitantly weak, as indicated by high νOH wavenumbers. Nevertheless, and rather surprisingly, the DOG self-assemblies are also unable to take up any water. However, here this is the result of an inverse-micellar arrangement of the DOG molecules with the polar heads hidden inside the hydrophobic sphere and, hence, inaccessible for water. The heterogeneity of the hydrogen bonds, forming a rather loose network, is considerably larger than in ODA, and is responsible for an increased νOH bandwidth. Our computational results allow for a quantification of the different hydrogen bonding patterns occurring in DOG, which adequately reflects the experimental findings. In contrast to ODA, the split of the νOH band of DOG comes from the different strength of the intra- and intermolecular hydrogen bonds, leading to two separate peaks.

Ultimately, the combined experimental/theoretical approach enabled us to predict a fairly detailed higher-order structure of the amphiphile assemblies, which is not available by other techniques.

Regarding the practical point of view, ODA (and other long-chain saturated primary alkanols) may be one of the first choices whenever a stable, water-repelling layered coating is needed. On the other hand, the micellar-prone aggregation behavior of DOG emphasizes its potential application for encapsulating certain drugs or effectors. The reverted-micelle pattern could be advantageous for this, since the high concentration of polar binding sites (including free carbonyl groups) in the interior of the aggregates may favor the fixation of the molecules to be administered. At the same time, the apolar exterior of the micelles should promote their passage across largely apolar media (e.g., biological membranes). Besides, the low stability of DOG micelles, which is due to weak intermolecular H-bonding, should facilitate a desired easy resolvability of the complex after reaching its target. The fragility of the DOG assemblies could also be important in terms of the in vivo availability of single DOG molecules, making this particular amphiphile predetermined for its functioning as a second messenger.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

Czech Science Foundation (grant 16-04902S (VA)) and the Ministry of Education (grant CZ.02.1.01/0.0/0.0/16_019/0000729 (VA)) are acknowledged for the financial support of the computational part of this work. We thank D. Gauger for contributing to the experimental work and P. Bouř for the discussion and advice on some of the computations.

References

1. W. Curatolo, Biochim. Biophys. Acta, 1987, 906, 137–160.
2. K. Brandenburg and U. Seydel, in Handbook of Vibrational Spectroscopy, ed. J. M. Chalmers and P. R. Griffiths, John Wiley & Sons, Chichester, 2002, vol. 5, pp. 3481–3507.
3. J. Texter, Structure of Surfactant and Amphiphile Assemblies, Taylor & Francis, New York, 2007.
4. T. F. Tadros, Applied Surfactants: Principles and Applications, Wiley VCH, Weinheim, 2006.
5. D. A. Mannock, P. E. Harper, S. M. Gruner and R. N. McElhaney, Chem. Phys. Lipids, 2001, 111, 139–161.
6. I. Pascher and S. Sundell, Chem. Phys. Lipids, 1977, 20, 175–191.
7. G. C. Pimentel and A. L. McClellan, The Hydrogen Bond, W. H. Freeman & Co., San Francisco, 1960.
8. The Hydrogen Bond II. Structure and Spectroscopy, ed. P. Schuster, G. Zundel and C. Sandorfy, North-Holland Publishing Co., Amsterdam, 1976.
9. G. A. Jeffrey and W. Saenger, Hydrogen Bonding in Biological Structures, Springer-Verlag, Berlin/Heidelberg/New York, 1991.
10. W. Pohle, C. Selle, H. Fritzsche and H. Binder, Biospectroscopy, 1998, 4, 267–280.
11. I. Zawisza and J. Lipkowski, Langmuir, 2004, 20, 4579–4589.
12. L. Carreto, A. R. Almeida, A. C. Fernandes and W. L. C. Vaz, Biophys. J., 2002, 82, 530–540.
13. D. M. Small, The Physical Chemistry of Lipids, Plenum Press, New York, 1986.
14. S. Abrahamsson, G. Larsson and E. von Sydow, Acta Crystallogr., 1960, 13, 770–774.
15. T. Seto, Mem. Coll. Sci., Univ. Kyoto, Ser. A, 1962, 30, 89.
16. M. Tasumi, T. Shimanouchi, A. Watanabe and R. Goto, Spectrochim. Acta, 1964, 20, 629–666.
17. D. L. Dorset, Chem. Phys. Lipids, 1979, 23, 337–347.
18. L. Ventola, M. Ramirez, T. Calvet, X. Solans, M. A. Cuevas-Diarte, P. Negrier, D. Mondieig, J. C. van Miltenburg and H. A. J. Oonk, Chem. Mater., 2002, 14, 508–517.
19. C. L. Sutula and L. S. Bartell, J. Phys. Chem., 1962, 66, 1010–1014.
20. H. L. Casal and H. H. Mantsch, Biochim. Biophys. Acta, 1984, 779, 381–401.
21. H. H. Mantsch and R. N. McElhaney, Chem. Phys. Lipids, 1991, 57, 213–226.
22. R. N. A. H. Lewis and R. N. McElhaney, in Infrared Spectroscopy of Biomolecules, ed. H. H. Mantsch and D. Chapman, Wiley Liss, New York, Chichester, Brisbane, Toronto, Singapore, 1996, pp. 159–202.
23. M. Nishihara, S. Nagahama, M. Ohga and Y. Koga, Extremophiles, 2000, 4, 275–277.
24. Y. Nishizuka, Nature, 1984, 308, 693–698.
25. R. M. Bell and D. J. Burns, J. Biol. Chem., 1991, 266, 4661–4664.
26. M. Liscovitch and L. C. Cantley, Cell, 1994, 77, 329–334.
27. D. P. Siegel, J. Banschbach, D. Alford, H. Ellens, L. J. Lis, P. J. Quinn, P. L. Yeagle and J. Bentz, Biochemistry, 1989, 28, 3703–3709.
28. M. A. Churchward, T. Rogasevskaia, D. M. Brandman, H. Khosravani, P. Nava, J. K. Atkinson and J. R. Coorssen, Biophys. J., 2008, 94, 3976–3986.
29. M. L. Manca, M. Manconi, A. Nacher, C. Carbone, D. Valenti, A. M. Maccioni, C. Sinico and A. M. Fadda, Int. J. Pharm., 2014, 477, 176–186.
30. F. Tiberg, M. Johnsson, M. Jankunec and J. Barauskas, Chem. Lett., 2012, 41, 1090–1092.
31. S. Y. Chen and K. H. Cheng, Chem. Phys. Lipids, 1990, 56, 149–158.
32. W. Pohle, C. Selle, D. R. Gauger and K. Brandenburg, J. Biomol. Struct. Dyn., 2001, 19, 351–364.
33. V. Andrushchenko, L. Benda, O. Pav, M. Dračinsky and P. Bouř, J. Phys. Chem. B, 2015, 119, 10682–10692.
34. V. Andrushchenko, D. Tsankov, M. Krasteva, H. Wieser and P. Bouř, J. Am. Chem. Soc., 2011, 133, 15055–15064.
35. M. G. Batishcheva, Inzh.-Fiz. Zh., 1959, 2, 101–104.
36. C. J. Pouchert, The Aldrich Library of FT-IR Spectra, Aldrich Chem. Co., Inc., Milwaukee, 1st edn, 1985.
37. Spectral Database for Organic Compounds, SDBS, National Institute of Industrial Science and Technology, Japan.
38. W. Pohle, C. Selle, W. Rettig, U. Heiser, B. Dobner and S. Wartewig, Arch. Biochem. Biophys., 2001, 396, 151–161.
39. H. Ratajczak and W. J. Orville-Thomas, J. Mol. Struct., 1968, 1, 449–461.
40. K. Nakamoto, M. Margoshes and R. E. Rundle, J. Am. Chem. Soc., 1955, 77, 6480–6486.
41. C. Selle and W. Pohle, Biospectroscopy, 1998, 4, 281–294.
42. R. G. Snyder, J. Mol. Spectrosc., 1961, 7, 116–144.
43. R. G. Snyder, J. Chem. Phys., 1979, 71, 3229–3235.
44. D. Marsh, Chem. Phys. Lipids, 2012, 165, 59–76.
45. J. Katsaras, V. A. Raghunathan, E. J. Dufourc and J. Dufourcq, Biochemistry, 1995, 34, 4684–4688.
46. A. Blume, W. Hübner and G. Messner, Biochemistry, 1988, 27, 8239–8249.
47. R. N. A. H. Lewis, R. N. McElhaney, W. Pohle and H. H. Mantsch, Biophys. J., 1994, 67, 2367–2375.
48. J. H. Crowe and L. M. Crowe, in Biological Membranes, ed. D. Chapman, Academic Press, London, UK, 1984, vol. V, pp. 58–103.
49. T. J. McIntosh and A. D. Magid, in Phospholipids Handbook, ed. G. Cevc, Marcel Dekker, Inc., New York, US, 1993, pp. 553–578.
50. G. L. Jendrasiak, J. Nutr. Biochem., 1996, 7, 599–609.
51. D. R. Gauger, V. V. Andrushchenko, P. Bouř and W. Pohle, Anal. Bioanal. Chem., 2010, 398, 1109–1123.
52. P. Bouř, J. Sopková, L. Bednárová, P. Maloň and T. A. Keiderling, J. Comput. Chem., 1997, 18, 646–659.
53. V. Andrushchenko and P. Bouř, Chirality, 2010, 22, E96–E114.
54. P. Lalanne, J. M. Andanson, J. C. Soetens, T. Tassaing, Y. Danten and M. Besnard, J. Phys. Chem. A, 2004, 108, 3902–3909.
55. R. J. Jakobsen, Y. Mikawa and J. W. Brasch, Nature, 1967, 215, 1071–1072.
56. C. Perchard and J. P. Perchard, Chem. Phys. Lett., 1974, 27, 445–447.
57. A. K. Sum and S. I. Sandler, J. Phys. Chem. A, 2000, 104, 1121–1129.
58. R. A. Shaw, H. Wieser, R. Dutler and A. Rauk, J. Am. Chem. Soc., 1990, 112, 5401–5410.
59. M. L. Senent, Y. G. Smeyers, R. Dominguez-Gomez and M. Villa, J. Chem. Phys., 2000, 112, 5809–5819.
60. V. Dyczmons, J. Phys. Chem. A, 2004, 108, 2080–2086.
61. E. E. Fileti, M. A. Castro and S. Canuto, Chem. Phys. Lett., 2008, 452, 54–58.
62. J. L. Wang, F. Leveiller, D. Jacquemain, K. Kjaer, J. Alsnielsen, M. Lahav and L. Leiserowitz, J. Am. Chem. Soc., 1994, 116, 1192–1204.
63. D. Marsh, Biophys. J., 1997, 72, 2834–2836.
64. K. Schorn and D. Marsh, Biochemistry, 1996, 35, 3831–3836.
65. R. M. C. Dawson, R. F. Irvine, J. Bray and P. J. Quinn, Biochem. Biophys. Res. Commun., 1984, 125, 836–842.
66. J. M. Seddon, J. Robins, T. Gulik-Krzywicki and H. Delacroix, Phys. Chem. Chem. Phys., 2000, 2, 4485–4493.
67. J. J. Peron, C. Bourderon and C. Sandorfy, Chem. Phys. Lett., 1975, 33, 212–214.
68. S. Holly and P. Sohar, in Absorption Spectra in the Infrared Region, Theoretical and Technical Introduction, ed. L. Lang and W. H. Prichord, Akademiai Kiado, Budapest, 1975, p. 70.

---

Footnote

† Electronic supplementary information (ESI) available: Details on computational procedures, detailed analysis of the calculated IR spectra of ethanol models, supplementary tables and figures. See DOI: 10.1039/c9cp01475f

---