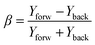Controlling intramolecular hydrogen migration by asymmetric laser fields: the water case

Abstract

Hydrogen and deuterium intramolecular migration in water's isotopomer dications has been found to depend on the wavelength of the laser used for the excitation. This is imprinted in H₂⁺ and D₂⁺ fragment ions’ observation in the mass spectra induced by single color fs laser irradiation with 800 nm ≤ λ ≤ 1570 nm. Based on these findings, experiments with ω/2ω asymmetric laser fields (1400/700 nm) have been performed. The dissociation channels of the dications exhibit different dependence on the phase between the ω and 2ω components of the field thus offering an ability for controlling the fragmentation. For the interpretation of these observations, a tunneling mechanism is invoked.

---

Introduction

Ultrashort laser pulses offer the ability to probe ultrafast processes on the time scale of molecular motions.¹ At the same time, the electric field of these pulses can be strong enough to modify the molecular potential energy surfaces which are crucial parameters as far as the fate of the molecular processes is concerned.^2,3 This close relation of the induced distortion of the molecular states and their evolution emerges the possibility to control molecular processes by changing the laser pulse characteristics. Among the techniques targeting this issue are those employing pulses of few-cycle duration, which are inherently asymmetric or two color (ω/2ω) fields of multi-cycle duration. In the first case, the spatial asymmetry varies as a function of the Carrier Envelope Phase (CEP),^4–6 while in the latter by changing the relative phase of the field components.^7–11 The two-color scheme was initially introduced by Brumer and Shapiro.^12,13 However, their methodology is conceptually different since it is based on the combined action of two monochromatic fields with commensurable frequencies and exploits the quantum interference of the two-associated pathways towards the common final state to exert control on its population.

Molecular isomerization,^14–16 and in particular intramolecular hydrogen migration,^17,18 is one of the molecular processes that can be affected under asymmetric laser irradiation. Due to the light mass of the H, its migration along the molecular skeleton can be fast and completed within a few fs¹⁹i.e. within the pulse duration. H-migration is of fundamental importance for a very broad variety of scientific areas such as astrophysics, chemistry and biology. Furthermore, H-liberation from molecules is regarded as one of the replacements for conventional energy sources.

Our group has extensively applied ω/2ω asymmetric laser fields in conjunction with a time-of-flight mass spectrometry technique in order to explore the ability to identify different molecular dissociation channels leading to fragments with the same mass and kinetic energy, the participation (or not) of metastable states in these processes, and the directional bond fragmentation and for probing the intramolecular H-migration.^10,11,20

In this work, we are focusing on the fragmentation of water molecules in the gas phase. Beyond the obvious significance of H₂O, this molecule is thought of as a prototype system for unimolecular fragmentation studies.

Especially, the dissociation from ionic states of H₂O leading to H₂⁺ ejection has attracted extensive experimental and theoretical effort. H₂⁺ formation has been reported as a result of H₂O ionization induced by fast electrons^21,22 or ion impact,²³ strong laser fields²⁴ and free electron lasers.²⁵ The formation of H₂⁺ prerequisites atomic rearrangement and by using ultrashort laser pulses, it is concluded that this process takes place within the pulse duration (<10 fs) from the doubly ionized parent molecule.²⁶ It has been established that the doubly ionized parent molecule fragments follow two dissociation routes:

H₂O²⁺ → H⁺ + OH⁺ (1)

→ H₂⁺ + O⁺ (2)

McCracken et al. reported that channel (2) was not detected in their experiments on D₂O conducted using 40 fs laser pulses at 800 nm and intensity within the 7 × 10¹⁴–2 × 10¹⁵ W cm⁻² range.²⁷ This observation is in agreement with the threshold intensity (2 × 10¹⁵ W cm⁻²) that Rajgara et al. have defined for the appearance of the H₂⁺ ionic signal.²⁴ More recently, Mathur et al.²⁶ have reported HD⁺ formation from HOD²⁺ fragmentation at lower laser intensities (1 × 10¹⁵ W cm⁻²) at 800 nm but with laser pulses of <10 fs duration, which are significantly shorter in time and at the same time broader in terms of spectral content with respect to the multi-cycle case.

Our aim in the present work is twofold. Firstly, to investigate if the lower intensity threshold reported for the shorter laser pulses reveals a dependence of H-migration on the spectral bandwidth which is expected to increase for shorter pulses. And secondly, to elucidate the possibility for preferential bond breaking by controlling the phase of a ω/2ω asymmetric laser field, which remains always a formidable challenge.

Therefore, the exploration of the ability to control the intramolecular H-migration and dissociation of the water molecule beyond the per se fundamental interest can reveal the potential of ω/2ω asymmetric laser fields as a useful experimental tool in chemical physics.

Experimental details

Two sets of experiments have been performed. Initially, the mass spectra of H₂O and D₂O induced by a single laser beam have been recorded by means of a Time-of-Flight (ToF) mass spectrometer. A 20 fs pulsed Ti:Sapphire laser with a 1 kHz repetition rate was used for the experiments at 800 nm. In order to produce tunable near-IR pulses, part of the 800 nm beam (3 mJ energy per pulse) is fed into an optical parametric amplifier (OPA). The tunable output beams have central wavelengths that range from 1220 nm to 1570 nm. The pulse duration was carefully determined for each wavelength used and varies from 32 fs to 60 fs. The pulse energy was measured just before the entrance window of the ToF mass spectrometer and the calibration of the laser intensity in the interaction region is based on multiple ionization of noble gases and especially the recorded ratio of the ionic signal corresponding to different charge states as a function of the energy per pulse.²⁸

The experiments with the asymmetric ω/2ω laser field were performed at 1400/700 nm. The electric field, in this case, is described by the equation: E(t) = E₀(t)[cos(ωt) + γ cos(2ωt + φ)], where E₀(t) is the pulse envelope, γ is the ratio of the electric field strengths and φ is the phase difference between the two colors. The pulse duration of the beam at 1400 nm was measured to be 40 fs. The 1400 nm beam propagates through a BBO crystal (200 μm thick) in order to produce its second harmonic which is initially separated in order to control the phase between the beams and then recomposed with the fundamental by passing through a set of dichroic mirrors. The phase control is achieved by rotating a calcite plate (1.6 mm thick, cut angle 55°) by intervals of 0.02° resulting in the phase steps of 30.5 ± 0.6°. Two neutral density filters can manipulate the intensity of each beam, ensuring control over the total intensity and the γ parameter. The two beams are then focused by a silver-coated spherical mirror of 7.5 cm focal distance located in the homemade Wiley–McLaren ToF-mass spectrometer. A detailed description is given elsewhere.²⁹ The resulting tunable total intensities range from 1–7 × 10¹⁴ W cm⁻² and the γ parameter from 0.3–1. The resulting ionic signal is measured by a Chevron-type micro-channel detector and recorded by an Ultrafast Multiscaler card (FASTComTec, Model TOF P7888) which has a 1 ns time resolution. The ambient pressure of the chamber was around 1.8 × 10⁻⁷ mbar, while the pressure was kept around 5 × 10⁻⁷ mbar during the experiments. The D₂O used was produced by Sigma-Aldrich (99.9% D atoms) and the substance flow was controlled via a needle valve with continuous flow.

Results and discussion

In Fig. 1(a) the part of the mass spectrum of H₂O corresponding to the H₂⁺ fragment ion recorded at λ = 800 nm is presented. As expected, the ion signal assigned to the H₂⁺ consists of many components which correspond to different dissociation channels and to ions ejected towards and backwards with respect to the ion detector. The kinetic energy of the fragments can be estimated by taking into account the temporal delay (Δt) between the backward and forward peak components:³⁰
where Δt is expressed in ns, F is the static electric field in the acceleration region of ToF in V cm⁻¹, n is the charge and m is the fragment mass in amu.

Fig. 1 Part of ToF spectra of water's isotopomers recorded at 800 nm. The areas corresponding to H₂⁺ (a) and to D₂⁺ (b) ions are depicted. The ionic signal axis in (b) is presented magnified (×1.5).

We, hereafter, focus on the molecular hydrogen (H₂⁺ and D₂⁺) mass spectra peak profiles, which are presented in Fig. 1(a) and (b) at two different laser intensities.

For the case of H₂⁺ at ∼3.5 × 10¹⁵ W cm⁻² high kinetic energy fragments (E_kin > 7.9 eV) are clearly observed and they can be attributed to a Coulomb explosion process of triply charged parent ions. This is in agreement with the study done by Hong et al.³¹ and the fact that the O²⁺ fragments of E_kin = 1.1 ± 0.2 eV are also recorded which is consistent with that predicted by momentum conservation for a two-body (H₂⁺, O²⁺) dissociation channel. The intensity threshold for the particular channel is found to be ∼1.3 ± 10¹⁵ W cm⁻² at 800 nm, while the corresponding ponderomotive energy (U_p (eV) = 9.33 × 10⁻¹⁴I (W cm⁻²) λ² (μm)) is evaluated to be ∼78 eV in accordance with the energy threshold determined by the electron impact experiments.³² It should be noted that there is no clear peak component with a kinetic energy around 4.8 eV, which is known to originate from the dissociation channel (2) even though the irradiation conditions are similar to the intensity threshold reported by Rajgara et al.²⁴ More strikingly, the peak components that could be assigned to the high kinetic D₂⁺ ions are absent from the D₂O mass spectra in contrast to the H₂O case.

Both of these observations seem to be in agreement with the recent work presented by McCracken et al.²⁷ where it was found that double ionization is significantly less probable than the triple ionization for the case of D₂O at similar irradiation conditions with the present work. Furthermore, as seen in Fig. 1(a) and (b), lower laser intensities do not reveal the second dissociative channel. However, the complete absence of high kinetic energy components from the D₂⁺ mass spectra peak profile originating from D₂O³⁺, contrary to the H₂⁺ case, highlights a strong isotopic effect in the production efficiency of the particular two-body dissociation channel.

In Fig. 2(a), the part of the H₂O mass spectra corresponding to the H₂⁺ ions recorded at different near-IR laser wavelengths (λ = 1220 nm, 1300 nm, 1400 nm, 1500 nm and 1570 nm) are presented. The H₂⁺ ions are produced with a remarkable kinetic energy meaning that their origin should be attributed to a fragmentation process within multiple charged parent ions, i.e. they are not molecules degassed from the water sample. In particular, H₂⁺ with 4.8 ± 0.2 eV kinetic energy are recorded and are expected to be released via channel (2). Moreover, their appearance seems to be aided by longer wavelengths, since the laser intensity needed for their observation decreases as the wavelength increases, whilst the working pressure was constant (P = 5 × 10⁻⁷ mbar). At first glance, the latter could be attributed to the dependence on λ² of the ponderomotive energy (U_p), but this is not the case since the estimated U_p also decreases. For instance, the estimated U_p values corresponding to the intensity thresholds at 1220 nm and 1570 nm are found to be 75 eV and 55 eV, respectively.

Fig. 2 ToF spectra recorded at different wavelengths of near-IR. (a) H₂⁺ spectrum, where the peaks corresponding to the dissociation of H₂O²⁺ and H₂O⁺ are noted. (b) D₂⁺ spectrum, magnified by 1.5 for scale. The peaks that are mentioned in (a) emerge using the near-IR pulses.

In Fig. 2(b), the same part of the mass spectrum of D₂O is depicted. It is impressive that highly kinetic energy D₂⁺ fragments (E_kin ∼ 4.3 ± 0.2 eV) are recorded for all the wavelengths used in the 1220–1570 nm range, while this was impossible for the 800 nm experiments, even though the maximum available intensity in the latter case is much higher. The E_kin = 4.3 eV value implies that these ions are produced through the dissociation route (2), since the total kinetic energy release (E_kinD₂⁺ and E_kinO⁺ ∼ 5.4 eV) is the same as the one measured for the H₂O case, within the experimental error. It is worth noting that the intensity thresholds for the observation of this fragmentation channel in D₂O are decreasing for longer laser wavelengths, and their values are almost identical to those recorded for the H₂O case.

As far as the production of O²⁺ ions from H₂O³⁺ and D₂O³⁺ is concerned, we found that although their intensity thresholds (I_thr) decrease at longer wavelengths (at λ = 800 nm the I_thr = 1.25 × 10¹⁵ W cm⁻², while at λ = 1570 nm I_thr = 3.3 × 10¹⁴ W cm⁻²) the corresponding ponderomotive energy remains constant within all the spectral regions studied. The estimated value is U_p = 75 eV, which is in absolute agreement with that determined by the electron impact technique.¹⁸ Therefore, it is reasonable to attribute the triple ionization of the parent molecules to an optical field ionization mechanism instead of a multiphoton ionization process.

From the above presented data, it is reasonable to conclude that: (i) the H-migration in H₂O takes place before the molecular fragmentation, (ii) D-migration is also a probable process in the D₂O²⁺ ions and (iii) these migration processes are dependent on laser wavelength; actually the abundance of the fragments released by channel (2) increases at the longer wavelengths used.

In order to further clarify the physical mechanism underlying the dissociation channel (2), we performed additional experiments using asymmetric laser fields at 1400/700 nm. At λ = 1400 nm, the available equipment ensures the production of the second harmonic beam with the required intensity. Moreover, for this ω/2ω field, we have recently performed experiments on CO molecules.²⁹ The CO molecule is considered a prototype case in the related field of research.^33,34 Therefore, it is used for the calibration of the Calcite plate's rotational angle in terms of the ω/2ω relative phase (30.6° per step, see Fig. 3). The advantage that the usage of the ω/2ω laser fields offers is the ability to interact selectively with molecules with the dipole moment aligned with the laser polarization vector and at the same time oriented with the laser electric field asymmetry. This facilitates the identification of the dissociation channels and often reveals information about the involved mechanisms.

Fig. 3 Asymmetry parameter (β) measurement and calibration of the calcite's plate rotation. The dotted line is used for eye-guiding purposes only. The C⁺ fragment is produced from the CO²⁺ dissociation recorded simultaneously with the H₂O mass spectra induced by a 1400/700 nm asymmetric laser field (I = 5 × 10¹⁴ W cm⁻² and γ = 0.76).

As mentioned above, the phase difference between the two laser beams (ω,2ω) was introduced by fine-tuning of a calcite plate. For the H₂O/D₂O experiments, the phase calibration is done by simultaneously introducing CO in the interaction region and measuring fragments from both the water target molecule and the CO reference one. The measured asymmetry parameter (β) is defined by the relation:

where Y_forw and Y_back refer to the total area yield of the forward and backward component of the specific ionic species.

The dependence of the asymmetry parameter (β) on the calcite plate angle for the C⁺ ions with E_kin = 2.6 eV released from the CO dissociation is presented (Fig. 3) along with that of the OH⁺ (E_kin = 0.3 eV) fragment of H₂O. This dependence allows the calibration of the calcite plate angle in terms of the phase difference in rad. In particular, for the phase difference zero (or nπ, where n an even number) the asymmetry of the C⁺ ion production increases which implies that the maximum of the intensity of the asymmetric field is pointed towards the O atom, i.e. the electronic cloud is removed in the C side of the oriented CO molecules.^33,34 Obviously, the situation is completely altered at the π (or at (n + 1) π) phase difference.

Having calibrated the induced phase difference between the two laser (1400/700 nm) beams, we recorded the phase dependence of the two dissociation channels of the doubly charged parent ions. In Fig. 4a, the phase dependence of the asymmetry for the component of the fragment ions H⁺ with E_kin = 4.8 eV and OH⁺ with E_kin = 0.3 eV is presented. These ions are released via channel (1) since the ratio of their kinetic energy is that expected by the aforementioned two-body dissociation. The same conclusion is further supported by the dependence of their asymmetry on the ω/2ω phase, presenting maximum values with a phase lag of π, which indicates that the specific fragments are released towards opposite directions. The analogous dependencies of the fragment components H₂⁺ with E_kin = 4.8 eV and O⁺ with E_kin = 0.6 eV that are generated from the dissociation route (2), are presented in Fig. 4b. Clearly, there is a phase dependence but the interesting point is that the amplitude for the asymmetry parameter β values is increased.

Fig. 4 Asymmetry parameter (β) measurements for the H₂O²⁺ fragment field (I = 5 × 10¹⁴ W cm⁻² and γ = 0.76). The lines are only used for eye-guiding purposes. (a) The fragments arising in accordance with channel (1) and (b) for those of channel (2).

In Fig. 5a, the asymmetry phase dependencies for the pairs of fragments OD⁺ (E_kin = 0.5 eV) and D⁺ (E_kin = 4.4 eV) (Fig. 5a) and for D₂⁺ (E_kin = 4.3 eV) and O⁺ (E_kin = 1.1 eV) (Fig. 5b) released from the dissociation of D₂O²⁺ are presented. It is obvious that the fragments exhibit the same dependence observed for the water molecule but the range within which the asymmetry parameter value varies is larger. It should be noted that the mass spectra of Fig. 4 and 5 were recorded under the same experimental conditions (I = 5 × 10¹⁴ W cm⁻², γ = 0.76).

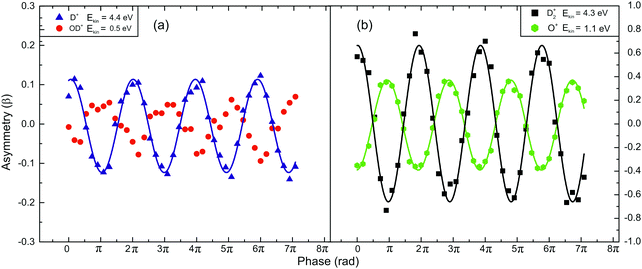Fig. 5 Asymmetry parameter (β) measurements of the fragments following D₂O²⁺ dissociation (I = 5 × 10¹⁴ W cm⁻² and γ = 0.76). The lines are used for eye-guiding purposes only: (a) the fragments of channel (1), and (b) the fragments of channel (2).

The fact that the fragments ejected via the dissociation channel (2) exhibit large variation of the β parameter values on the phase difference, implies that this channel is strongly dependent on the laser field asymmetry. Moreover, the larger variation of the β parameter values for the D₂O case reveals an isotopic effect.³⁵

Garg et al. made dynamic calculations for H₂O²⁺ and they focused on the dissociation channel that leads to the formation of H₂⁺ and O⁺.³⁶ Their study shows that for θ = 175° (the angle θ is in the Jacobi coordinate system and is illustrated in the inset of Fig. 6) there is a finite probability that within an interval up to 15 fs, the involved wavepacket evolution will emerge in two rectangular regions defined by the R and r coordinates. These two regions are related to the two dissociation channels of the dication. More specifically, the region of the potential energy surface (PES) where the r < 3.0a₀ and R > 2.0a₀ is expected to lead to H₂⁺ formation since the two hydrogen atoms are close enough to form a bond while the O⁺ ion is far from the H₂⁺ ion. Actually, from our data, it is easy to make an estimation of the distance (R) between the H₂⁺ and O⁺ just before the dissociation by using a simple formula which takes into account the total kinetic energy:³⁷

Fig. 6 Comparison of the asymmetry parameter (β) for the fragments arising from the two dissociation channels in D₂O²⁺ (I = 5 × 10¹⁴ W cm⁻² and γ = 0.76). The line is used for eye-guiding purposes only. On the right, an illustration of the Jacobi coordinates used is given.

Thus, the estimated value for both isotopomer dications is R = 2.7 Å. This value is quite big and R is longer than that predicted (R < 4a₀).³⁶ This observation is conceivable if the H-(D-) migration is taking place prior to the double ionization while the R is elongated to a critical value where the enhanced ionization mechanism³⁶ leads to the dication creation.

In Fig. 6, the asymmetry of the component of the D₂⁺ peak corresponding to the ions released with E_kin = 4.3 eV and the component of the OD⁺ fragments ejected with E_kin = 0.53 eV are presented. Taking into account the π phase lag between the asymmetry of the OD⁺ and D₂⁺ (and similarly the OH⁺ and H₂⁺) fragment, coming from the two competing dissociation channels, and the simultaneously measured asymmetries of the CO and D₂O molecules (Fig. 3), it is easy to conclude that the H₂⁺ and D₂⁺ ions are ejected preferentially towards the opposite direction with respect to the maximum composed electric field. Since the common dependence of the OD⁺ and OH⁺ ions on the field phase has been experimentally confirmed and by taking into account the discussion on Fig. 3, it is reasonable to conclude that the asymmetry of the D₂⁺ ion production – which is in close resemblance with that of the C⁺ fragment of the CO molecule – increases when the maximum intensity of the asymmetric ω/2ω field is pointed towards the O atom, i.e. the electronic cloud is removed in the D side of almost aligned (θ = 175°) D₂O molecules. Actually, this motion of the electronic cloud could visualize the D⁺ (or proton) migration in terms of electrostatic forces on the singly ionized molecule.

This motion of the electronic cloud implies the shape modification of the potential barriers. This is not surprising since for the laser beam intensity used (I = 5 × 10¹⁴ W cm⁻²) the corresponding electric field is ∼ 6 V Å⁻¹, i.e. of the same order of magnitude with the internal molecular field. Thus, within the pulse laser duration, the internal potential barriers can be suppressed and this lasts longer for laser beams at longer wavelengths. These two parameters (laser intensity and wavelength) obviously facilitate the tunneling process of the D⁺ (H⁺). The advantage of using the asymmetric laser fields is that this technique offers an experimental tool to shape the asymmetric electronic charge distribution and in that way the direction towards D⁺ (or proton) migration takes place. It is easily conceivable that for the sinusoidal symmetrical laser fields the expected value for the asymmetric parameter β is zero.

Finally, the observation that the amplitude of the asymmetry parameter which is almost 150% larger for the D₂⁺ compared to that of H₂⁺ (Fig. 4b and 5b), should be checked in terms of the above-suggested interpretation for the same experimental conditions (same laser intensity and γ value). Given that the laser intensity applied for the two water isotopomers is the same, this difference is attributed to the heavier mass of D⁺ and therefore D⁺-tunneling becomes probable for a smaller part of the intensity distribution of the asymmetric field, and in particular, to that corresponding only to higher intensity values. Therefore, the D⁺ migration process is feasible only for a narrow range of values around the (2n + 1)π electric field maxima. Due to the smaller mass of the H⁺ isotope, the restriction in terms of intensity and ω/2ω phase values is looser than the D⁺ case. Therefore, this interpretation suggests that the asymmetry observed for the H⁺ ejection should be smaller in amplitude than that of the D⁺ case, coming from the dissociation channel (2). In other words, the D⁺-migration has a stronger dependence on the laser field asymmetry and this is imprinted in the D₂⁺ ion production.

Conclusions

From the above work, it is concluded that H₂⁺ and D₂⁺ ionic fragments can be generated through the dissociation of doubly charged water isotopomers. The formation of these fragments follows an H-(D-) intramolecular migration which is enhanced for laser wavelengths longer than 800 nm. On the other hand, the migration is dependent on laser intensity too. These two characteristics imply that in the migration, a tunneling through internal barriers process is involved. The interaction of water isotopomers in the gas phase with a ω/2ω (1400/700 nm) asymmetric laser field indicates that the two dissociation routes of water dications have different dependencies on the phase of the asymmetric field. This difference offers a controlling ability over these two dissociation routes.

By the same set of experiments, it is firmly determined that the H- and D-migration is facilitated when the electronic cloud is removed by the asymmetric laser field in a direction opposite to the oxygen atom.

Our preliminary results, not presented here, indicate that the production of H₂⁺ and D₂⁺ water fragment ions is dependent not only on the laser intensity but also on the γ parameter, i.e. the degree of anisotropy of the ω/2ω field. A systematic work on this issue that is extended also to longer wavelengths will be presented in a forthcoming paper.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The experiments were performed in the Central Laser Facility of the University of Ioannina and we would like to express our thanks for the use of their facilities and their assistance. The authors also acknowledge the support of this work by the project “ELI – LASERLAB Europe Synergy, HiPER & IPERION-CH.gr” (MIS 5002735) which is implemented under the Action “Reinforcement of the Research and Innovation Infrastructure”, funded by the Operational Programme “Competitiveness, Entrepreneurship and Innovation” (NSRF 2014-2020) and co-financed by Greece and the European Union (European Regional Development Fund).

References

1. J. C. Polanyi and A. H. Zewail, Acc. Chem. Res., 1995, 28(3), 119–132.
2. P. Dietrich and P. B. Corkum, J. Chem. Phys., 1992, 97(5), 3187–3198.
3. M. E. Corrales, et al. , Nat. Chem., 2014, 6, 785–790.
4. G. Paulus, et al. , Nature, 2001, 414, 182–184.
5. S. Miura, et al. , Chem. Phys. Lett., 2014, 595–596, 61–66.
6. H. Li., et al. , Opt. Express, 2017, 25, 14192–14203.
7. H. Ohmura, T. Nakanaga and M. Tachiya, Phys. Rev. Lett., 2004, 92, 113002.
8. H. Ohmura and T. Nakanaga, J. Chem. Phys., 2004, 120, 5176–5180.
9. K. J. Betch, D. W. Pinkham and R. R. Jones, Phys. Rev. Lett., 2010, 105, 223002.
10. N. Kotsina, et al. , J. Chem. Phys., 2013, 139, 104313.
11. S. Kaziannis, N. Kotsina and C. Kosmidis, J. Chem. Phys., 2014, 141, 104319.
12. P. Brumer and M. Shapiro, Chem. Phys. Lett., 1986, 126, 541.
13. M. Shapiro and P. Brumer, Chem. Phys. Lett., 1988, 149, 451.
14. R. V. Ambartzumian, et al. , Opt. Commun., 1976, 18(3), 400–402.
15. H. Yazawa, et al. , J. Chem. Phys., 2007, 127, 124312.
16. A. Hishikawa, et al. , J. Chem. Phys., 2008, 128, 084302.
17. N. Kotsina, S. Kaziannis and C. Kosmidis, Chem. Phys. Lett., 2014, 604, 27–32.
18. N. Kotsina, S. Kaziannis and C. Kosmidis, Int. J. Mass Spectrom., 2015, 380, 34–39.
19. B. J. Rao and A. J. C. Varandas, J. Phys. Chem. A, 2015, 119(20), 4856–4863.
20. N. Kotsina, S. Kaziannis and C. Kosmidis, Chem. Phys. Lett., 2016, 651, 97–102.
21. H. C. Straub, B. G. Lindsay, K. A. Smith and R. F. Stebbings, J. Chem. Phys., 1998, 108(1), 109–116.
22. J. H. D. Elland, Chem. Phys., 2006, 323, 391–396.
23. I. Ben-Itzhak, et al. , Nucl. Instrum. Methods Phys. Res., Sect. B, 2005, 233(1–4), 56–61.
24. F. A. Rajgara, et al. , J. Chem. Phys., 2009, 130, 23.
25. H. B. Pedersen, et al. , Phys. Rev. A: At., Mol., Opt. Phys., 2013, 87, 013402.
26. D. Mathur, et al. , J. Phys. B: At., Mol. Opt. Phys., 2017, 50, 15.
27. G. A. McCracken, et al. , J. Chem. Phys., 2017, 147, 12.
28. E. F. Sistrunk, PhD thesis, The Ohio State University, 2011.
29. S. Kaziannis, S. Danakas, N. Kotsina and C. Kosmidis, Laser Phys. Lett., 2013, 13, 055301.
30. W. C. Wiley and I. H. McLaren, Rev. Sci. Instrum., 1955, 26, 1150.
31. L. Hong, et al. , Chin. Phys. Lett., 2006, 32, 6.
32. S. J. King and S. D. Price, Int. J. Mass Spectrom., 2008, 277(1–3), 84–90.
33. S. De, et al. , Phys. Rev. Lett., 2009, 103, 153002.
34. H. Li, et al. , Phys. Rev. A: At., Mol., Opt. Phys., 2011, 84, 043429.
35. A. M. Sayler, et al. , J. Phys. B: At., Mol. Opt. Phys., 2006, 39, 7.
36. M. Garg, A. K. Tiwari and D. Mathur, J. Chem. Phys., 2012, 136, 2.
37. P. Siozos, S. Kazianis and C. Kosmidis, Int. J. Mass Spectrom., 2003, 225, 249.

---