Shock wave and modelling study of the dissociation pathways of (C2F5)3N†
Received
26th February 2019
, Accepted 11th April 2019
First published on 11th April 2019
Abstract
The thermal decomposition of perfluorotriethylamine, (C2F5)3N, was investigated in shock waves by monitoring the formation of CF2. Experiments were performed over the temperature range of 1120–1450 K with reactant concentrations between 100 and 1000 ppm of (C2F5)3N in the bath gas Ar and with [Ar] in the range of (0.7–5.5) × 10−5 mol cm−3. The experiments were accompanied by quantum-chemical calculations of the energies of various dissociation paths and by rate calculations, in particular for the dissociation of C2F5via C2F5 → CF3 + CF2. The overall reaction can proceed in different ways, either by a sequence of successive C–N bond ruptures followed by fast C2F5 decompositions, or by a sequence of alternating C–C and C–N bond ruptures. A cross-over between the two pathways can also take place. At temperatures below about 1300 K, yields of less than one CF2 per (C2F5)3N decomposed were observed. On the other hand, at temperatures around 2000 K, when besides the parent molecule, CF3 also dissociates, yields of six CF2 per (C2F5)3N decomposed were measured. The rate-delaying steps of the dissociation mechanism at intermediate temperatures were suggested to be the processes (C2F5)NCF2 → (C2F5)N + CF2 and (CF2)N → N + CF2. The reduction of the CF2 yields at low temperatures was tentatively attributed to a branching of the mechanism at the level of (C2F5)2NCF2, from where the cyclic final product perfluoro-N-methylpyrrolidine, (C4F8)NCF3, is formed which was identified in earlier work from the literature.
1. Introduction
Perfluorotriethylamine, (C2F5)3N, has a number of interesting properties. On the one hand, it may serve as a benign liquid reaction medium for Lewis acid-catalyzed organic reactions1 and other preparative applications. On the other hand, its structure is remarkable, being characterized by a nearly planar C3N skeleton with CNC angles near to 120°.2 This skeleton is surrounded by an “inner shell” of CF2 groups and an “outer shell” of CF3 groups. The structure of (C2F5)3N has been discussed in relation to that of other fluorinated triamines such as (CF3)3N,3 (CH2CF3)3N,4 and (SF5)3N.5 Because of its favorable properties, (C2F5)3N has also been considered as an alternative to environmentally more harmful halons.6 In a study of the thermal decomposition of undiluted gaseous (C2F5)3N in a flow system, by employing gas chromatography (GC) and GC/mass spectrometry (MS) analyses of the final products, perfluoro-N-methylpyrrolidine, (C4F8)NCF3, was identified.6 In order to shed more light on the elementary steps of the pyrolysis, shock wave studies of the thermal decomposition of (C2F5)3N diluted in Ar appeared promising. As the decomposition may proceed through different pathways, however, the interpretation of the experiments had to be accompanied by quantum-chemical calculations of the energetics of the reactions involved. That is the subject of the present article.
At sufficiently high temperatures, an overall decomposition
| | 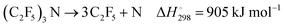 | (1) |
(with

from
ref. 7,

and

from
ref. 8; values for 298 K) would be accompanied by the dissociation of C
2F
5,
9,10| |  | (2) |
which then could be followed by CF
3 dissociation
11,12| |  | (3) |
and, finally, by CF
2 dissociation
| |  | (4) |
(unless stated differently, enthalpies in this work are from
ref. 8).
In more detail, the dissociation (1) could proceed by a sequence of C–N bond ruptures
| | | (C2F5)3N → (C2F5)2N + C2F5 | (5) |
| | | (C2F5)2N → (C2F5)N + C2F5 | (6) |
which would be followed by C
2F
5 dissociations
(2) (and, at a slower rate, by CF
3 dissociations
(3)). Because of the compact structure of (C
2F
5)
3N, also a dissociation sequence of alternating C–C and C–N bond ruptures
| | | (C2F5)3N → (C2F5)2NCF2 + CF3 | (8) |
| | | (C2F5)2NCF2 → (C2F5)2N + CF2 | (9) |
| | | (C2F5)2N → (C2F5)NCF2 + CF3 | (10) |
| | | (C2F5)NCF2 → (C2F5)N + CF2 | (11) |
| | | (C2F5)N → (CF2)N + CF3 | (12) |
appears possible. At the level of (C
2F
5)
2N and (C
2F
5)N a cross-over between the C–N and the C–C bond-breaking pathways would be possible.
(C2F5)3N has a low vapour pressure which, nevertheless, allows for the preparation of gaseous reactant/Ar mixtures suitable for shock wave experiments. The progress of the decomposition then can conveniently be followed by recording time-resolved UV absorption signals from CF2 near 248 nm (see ref. 13 and 14 for high-temperature absorption coefficients of CF2). Additional observations near 200 nm might be considered for the detection of CF3.15 At temperatures where CF2 becomes unstable, also absorption signals from CF might become observable.16 By analyzing absorption-time profiles, at first, the CF2 yields are of relevance. Second, the time dependence of the CF2 signals would be analyzed with respect to the sequence (5)–(7) followed by reactions (2) and (3) or the sequence (8)–(13) with the possibility of cross-over between the two pathways. Some speculations about the ultimate formation of (C4F8)NCF3 in the present work were also made. In high temperature experiments, finally, the kinetics of N/F/CF2 mixtures of known composition becomes accessible.
In the following, the description of experimental results is preceded by quantum-chemical calculations which facilitate the interpretation of the recorded CF2 yields and of the time dependence of the recorded concentration profiles of CF2. As the decomposition of C2F5viareaction (2) represents an important intermediate step of the mechanism and as only controversial information on its rate is available,9,10 a modelling of this rate also appeared desirable.
2. Quantum-chemical calculations of reaction energies
The enthalpies of reactions (2) and (5)–(13) (at 0 K) were determined by using a variety of DFT models, combined with a 6-311+G(3df) basis set, and using the Gaussian set of codes.17 In detail, B3LYP,18,19 M06-2X,20 BMK,21 and ωB97X-D22 models were used. The quality of the DFT results was tested for the dissociation of (C2F5)N in reactions (7) and (12) by also performing high-level ab initio CBS-QB3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 23 and G4
23 and G4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 24 calculations. As the agreement between the DFT and the ab initio calculations for the (C2F5)N dissociations appeared satisfactory, only DFT calculations were made for the dissociation of larger species. A comparison of the results obtained by using the various models is given in the ESI.†
24 calculations. As the agreement between the DFT and the ab initio calculations for the (C2F5)N dissociations appeared satisfactory, only DFT calculations were made for the dissociation of larger species. A comparison of the results obtained by using the various models is given in the ESI.†
ΔH00 values obtained by the ωB97X-D calculations are summarized in Table 1. Except for the dissociation of (C2F5)N → CF2N + CF3 where a barrier for the reverse reaction of about 20 kJ mol−1 was found, no barriers beyond ΔHo0 were observed for other reactions of the mechanism. The calculated value of ΔHo0 = 237 kJ mol−1 for the dissociation of C2F5 agreed satisfactorily with the literature value8 of 240.2 kJ mol−1. The resulting overall reaction enthalpy of ΔHo0 = 939 kJ mol−1 for reaction (1) (obtained from Table 1; calculated for 0 K) also appeared consistent with the estimate of ΔHo298 = 905 kJ mol−1 as given above (based on ref. 7 and 8 for 298 K). The results of Table 1 are illustrated in Fig. 1. They illustrate possibilities for cross-over between the C–N bond ruptures (5)–(7) accompanied by C2F5 dissociation (2) and the pathway of alternating C–C and C–N bond ruptures (8)–(13).
Table 1 Reaction enthalpies at 0 K in kJ mol−1 (obtained by calculations using the ωB97X-D model;22 results from other models are summarized in the ESI)
| Reaction |
|
ΔHo0 |
| (C2F5)3N → (C2F5)2N + C2F5 |
(5) |
327.2 |
| (C2F5)2N → (C2F5)N + C2F5 |
(6) |
320.9 |
| (C2F5)N → N + C2F5 |
(7) |
291.2 |
| C2F5 → CF3 + CF2 |
(2) |
237.2 |
| (C2F5)3N → (C2F5)2NCF2 + CF3 |
(8) |
345.6 |
| (C2F5)2NCF2 → (C2F5)2N + CF2 |
(9) |
218.0 |
| (C2F5)2N → (C2F5)NCF2 + CF3 |
(10) |
46.0 |
| (C2F5)NCF2 → (C2F5)N + CF2 |
(11) |
512.5 |
| (C2F5)N → CF2N + CF3 |
(12) |
103.8 |
| (TS12) |
|
123.4 |
| CF2N → N + CF2 |
(13) |
423.5 |
 |
| | Fig. 1 Energetics of dissociation pathways (reaction enthalpies at 0 K in kJ mol−1 obtained by ωB97X-D calculations of the present work, see the text and the ESI†). | |
A few pecularities in the sequence of reactions (8)–(13) should be noted: the alternation of high- and low-activation barrier steps in the sequence (8)–(13) indicates “bottle-necks” at reactions (11) and (13) which have particularly high barriers. Furthermore, while all other steps in the sequences (5)–(7) and (8)–(13) are of simple bond-fission character, reaction (12) involves a rigid activated complex. At least at intermediate temperatures this reduces the CF2 yield of the overall reaction. Only at sufficiently high temperatures, when all reactions are fast, one should obtain a yield of six CF2 per (C2F5)3N decomposed. This prediction could be controlled easily in experiments under conditions where reaction (4) does not consume CF2.
Apart from the energetics of steps (5)–(7) and (8)–(13), the rate of C2F5 decomposition (2) is of importance. We felt that an up-dated modelling of the falloff curves of reaction (2) was necessary.25,26 This was done with the formalism employed in our earlier work (see, e.g.ref. 13, 15 and 16; for more details, see the ESI†). The results are shown in Fig. 2. The calculation of individual rate constants for other reaction steps of the pathway was beyond the scope of the present work. Likewise, the complex rearrangement processes leading to the final cyclic product (C4F8)NCF3 were not further investigated here.
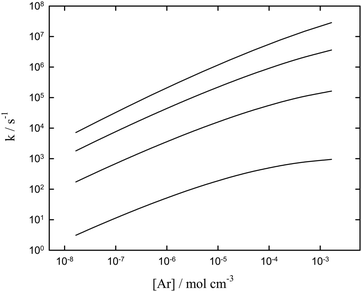 |
| | Fig. 2 Modelled falloff curves for the dissociation C2F5 → CF2 + CF3 (2) (pseudo-first order rate constans k; for details of the calculations, see the ESI†; T = 1000, 1250, 1500, and 1750 K, from bottom to top). | |
3. Experimental technique and results
Our shock wave technique has been described before (for details, see, e.g.ref. 12–16). Mixtures of (C2F5)3N (from Fluorochem, purity 96%) and Ar (from Air Liquide, purity 99.9999%) were prepared in mixing vessels outside the shock tube and then introduced into the tube. Usually, low-concentration mixtures of about 200 ppm of (C2F5)3N in Ar were used, but higher concentrations (up to about 1000 ppm (C2F5)3N) were also employed. The experimental conditions behind incident and reflected shock waves are included in Table 2 (and given in the figure captions). UV absorption signals were recorded at selected wavelengths over the range of 200–280 nm. The majority of the experiments were conducted at 248 nm where CF2 absorbs most strongly (CF2 absorption coefficients from eqn (5) of ref. 13 were used for the determination of absolute CF2 yields during (C2F5)3N decomposition).
Table 2 Apparent rate constants k of eqn (16), kin of eqn (19), and CF2 yields Y. (a) Experiments with Y = 1 and kin ≈ k; (b) experiments with Y < 1 and kin ≈ k; (c) experiments with Y < 1 and k > kin; see the text
|
T/K |
[Ar]/10−5 mol cm−3 |
k/s−1 |
k
in/s−1 |
Y
|
| (a) |
| 1451 |
4.1 |
1.4 × 105 |
|
|
| 1430 |
2.7 |
6.3 × 104 |
|
|
| 1371 |
0.71 |
2.6 × 104 |
|
|
| 1367 |
4.3 |
3.4 × 104 |
|
|
| 1347 |
4.3 |
3.6 × 104 |
|
|
| 1320 |
2.2 |
1.8 × 104 |
|
|
| 1297 |
0.76 |
1.1 × 104 |
|
|
|
|
| (b) |
| 1296 |
4.5 |
7.8 × 103 |
|
0.85 |
| 1246 |
4.8 |
4.9 × 103 |
|
0.53 |
| 1226 |
5.0 |
3.2 × 103 |
|
0.43 |
| 1211 |
4.9 |
2.8 × 103 |
|
0.39 |
| 1160 |
5.4 |
1.5 × 103 |
|
0.14 |
| 1133 |
5.5 |
1.1 × 103 |
|
0.09 |
| 1130 |
5.3 |
9.0 × 102 |
|
0.08 |
|
|
| (c) |
| 1246 |
4.8 |
|
1.8 × 103 |
|
| 1226 |
5.0 |
|
1.0 × 103 |
|
| 1196 |
5.3 |
|
1.2 × 102 |
|
| 1159 |
5.4 |
|
1.7 × 102 |
|
| 1132 |
5.3 |
|
6.3 × 101 |
|
| 1122 |
5.2 |
|
3.3 × 101 |
|
The recorded absorption-time profiles showed a number of interesting properties. Fig. 3 gives an example. The Schlieren peak at time zero indicates the arrival of the incident shock at the observation window. At the corresponding temperature of 1371 K, the concentration of CF2 increases up to a yield of Y(CF2) = [CF2]/[(C2F5)3N]t=0 = 1. Closer inspection of the signal near time zero indicates no absorption from the parent molecule. The nature of the absorbing species CF2 could uniquely be identified by the wavelength dependence of the signal. At the time of arrival of the reflected shock (at T = 2818 K), the absorption rises abruptly to a level corresponding to Y(CF2) = 6. This value of Y = 6 corresponds to a completion of reaction (1) followed by reactions (2)–(4) within less than 2 μs (the halflife of C2F5 here is about 0.025 μs, see Fig. 2, and the halflife of CF3 is about 1.8 μs, see ref. 12). The decrease in the absorption signal behind the reflected wave, on the one hand, reflects the dissociation of CF2 (halflife of about 700 μs, see ref. 12). On the other hand, there is evidence for a superimposed absorption which seems to arise from a species which has an even larger absorption coefficient than CF2. Tentatively we attribute this additional absorption to CF, being formed by the dissociation of CF2 in reaction (4) and/or a reaction
| |  | (14) |
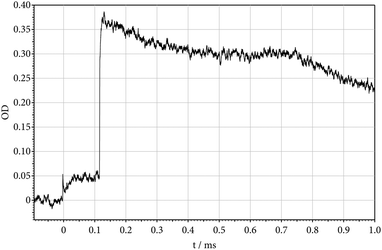 |
| | Fig. 3 Decomposition of (C2F5)3N behind the incident shock wave (absorption-time profile of formed CF2 at 248 nm; incident shock: T = 1371 K, [Ar] = 7.1 × 10−6 mol cm−3; reflected shock: T = 2818 K, [Ar] = 1.6 × 10−5 mol cm−3; 212 ppm (C2F5)3N in Ar; OD = ε·[CF2]·l with l = 9.4 cm and ε = 3.6 × 106 cm2 mol−1 for 1371 K and ε = 1.8 × 106 cm2 mol−1 for 2818 K; instantaneous dissociation of CF3 at the time of arrival of the reflected shock, followed by the slower dissociation (4) of CF2 with k = 103 s−1 and secondary reactions, see the text). | |
As information on further reactions like
| | 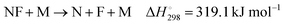 | (15) |
(M denotes the bath gas) and reactions of (CF
2)N is not available, an investigation of the superimposed absorption “humps” shown in
Fig. 3 did not appear warranted at the present time. Because the additional absorptions appeared only at temperatures above 2000 K, our study of (C
2F
5)
3N dissociation was not perturbed by this complication. The assumption of the presence of CF, however, did not appear improbable, because its absorption coefficient at 248 nm in
ref. 16 was found to be about 3 times that of CF
2.
The formation of CF2 was studied behind incident and reflected shock waves, as shown in Fig. 3 and 4. The temperature of the latter experiment (1347 K) and the rate of formation of CF2 (accounting for the compressed time scale, behind the incident wave) were close to that of Fig. 3, while the bath gas concentrations differed markedly ([Ar] = 7.1 × 10−6 mol cm−3 behind the incident shock as shown in Fig. 3 and [Ar] = 4.2 × 10−5 mol cm−3 behind the reflected shock as shown in Fig. 4). A pressure effect thus was not observed. The CF2 yields in both cases reached Y ≈ 1. This changed at lower temperatures. The CF2 concentration at 1246 K, as shown in Fig. 5, rose up to a yield of Y ≈ 0.6 only. As Fig. 4 and 5 were obtained with the same reaction mixture (209 ppm of (C2F5)3N in Ar), this observation could not have been produced by concentration uncertainties (with reaction mixtures above 1000 ppm, the small (C2F5)3N vapour pressure caused problems with accurate concentration determinations). Because of the limitation of the observation time behind the reflected shock to about 1 ms, the drop of Y with decreasing temperature could only be followed down to about T ≈ 1130 K.
 |
| | Fig. 4 Decomposition of (C2F5)3N behind the reflected shock wave (absorption-time profile of formed CF2 at 248 nm; T = 1347 K, [Ar] = 4.2 × 10−5 mol cm−3; 209 ppm (C2F5)3N in Ar). | |
 |
| | Fig. 5 The same as Fig. 4, but at lower temperature (T = 1246 K, [Ar] = 4.8 × 10−5 mol cm−3; 209 ppm (C2F5)3N in Ar; ε(1246 K)/ε(1347 K) ≈ 1.1513). | |
The recorded absorption-time profiles of CF2 were evaluated in two different ways. For the temperature range of 1130–1540 K, where a practically time-independent final CF2 yield Y(T) was reached within the observation time, an effective rate law
| | | [CF2]t/[(C2F5)3N]t=0 ≈ Y(T){1 − exp(−k(T)t)} | (16) |
appeared suitable. The resulting rate constants
k(
T) and yields
Y(
T) are summarized in
Table 2 and plotted in
Fig. 6 and 7, respectively. The Arrhenius representation of
k(
T) as shown in
Fig. 6 led to
| | k(T) ≈ 2.5 × 1013![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−213 kJ mol−1/RT)s−1 exp(−213 kJ mol−1/RT)s−1 | (17) |
while
Y(
T) in the form of
ref. 27 was approximated by
| | | Y(T) ≈ [1 − (T − Te)/(Te − Tm)][(T − T0)/(Te − T0)](Te−T0)/(Te−Tm) | (18) |
with the parameters
Te = 1351 K,
T0 = 1020 K, and fitted
Tm = 1295 K. Alternatively, the formation of CF
2 was characterized by its initial rate
| |  | (19) |
Values of
kin(
T) could also be derived for lower temperatures where a final stationary CF
2 level could not be attained within the observation time.
Fig. 6 and
Table 2 include values of
kin(
T). In Arrhenius form they are represented by
| | kin(T) ≈ 1.4 × 1017![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−339 kJ mol−1/RT)s−1 exp(−339 kJ mol−1/RT)s−1 | (20) |
when high-temperature limiting values of
k(
T) near 1500 K are combined with the measured points of
kin over the range of 1130–1250 K (one should note that the scatter of the values of
kin is due to some uncertainties of the (C
2F
5)
3N concentration in the reaction mixtures, see
eqn (19); this problem does not exist for the measurements of
k(
T); thus
eqn (20) is of qualitative importance only). The relation of the apparent
k(
T),
kin(
T), and
Y(
T) to the dissociation pathways illustrated in
Fig. 1 will be considered in Section 4.
 |
| | Fig. 7 Apparent final CF2 yields Y = [CF2]/[(C2F5)3N]t=0 over the range of 1130–1450 K (representation by eqn (18)). | |
It should be noted that experiments at higher temperatures (see Fig. 8), correspond to the dissociation of CF3 through reaction (3). The increase of the CF2 absorption behind the absorption step at the time of arrival of the reflected shock wave as shown in Fig. 8 (T = 1854 K) leads to a value of the rate constant for reaction (3) of k3 ≈ 3.5 × 103 s−1. This is in perfect agreement with the result obtained from the CF3 dissociation study of ref. 12. While this confirms the overall mechanism, it limits the study of the later stages of (C2F5)3N dissociation. One observes that the absorption step at the time of arrival of the reflected wave as shown in Fig. 8 corresponds to Y ≈ 2 while finally Y ≈ 3 is reached (as most clearly seen in the inset of Fig. 8). Apparently, CF3 dissociation and the slower steps of the (C2F5)3N dissociation here are superimposed and could not be separated in the present experiments. Monitoring CF3 near 200 nm did not help, as the strong CF2 absorption at high temperatures extends from 248 nm down to 200 nm and is then superimposed on the CF3 absorption. In any case, in the intermediate temperature range between 1500 and 2000 K a CF2 yield of Y = 6 was not reached. On the other hand, Y approached unity in the range of 1300–1500 K.
 |
| | Fig. 8 CF2 formation by the decomposition of CF3 produced during the decomposition of (C2F5)3N (reflected shock wave at 1854 K and [Ar] = 2.9 × 10−5 mol cm−3; [(C2F5)3N]t=0/[Ar]= 528 ppm; the inset resolves CF2 formation during the late stages of (C2F5)3N decomposition; for details see the text). | |
4. Discussion
Although only limited experimental and theoretical information about the reaction network of Fig. 1 became available, a number of important conclusions could be drawn. The following pathways appear possible: (i) (C2F5)3N dissociates in a sequence of C–N bond ruptures (5)–(7) followed by fast dissociation (2) of the product C2F5; (ii) (C2F5)3N dissociates in a sequence of C–C bond ruptures (8), (10), and (12), followed by C–N bond ruptures (9), (11), and (13); (iii) two pathways (i) and (ii) occur in parallel with the possibility of cross-over at the stages of formation of (C2F5)2N and (C2F5)N. At temperatures where the reactions of pathways (i)–(iii) are complete, and where CF3 dissociates through reaction (3) while reaction (4) is too slow to consume CF2, the overall CF2 yield Y(T) should be 6. This was indeed observed, but this does not allow one to distinguish between the pathways.
An exclusive mechanism (i) can be excluded for a number of reasons: although the enthalpies of the reaction steps slightly decrease from (5) to (7), rate constants k5, k6, and k7 should be of similar magnitude. With a fast dissociation of C2F5 this would then result in Y = 3. A modelling of the kinetics indicates that the effective rate constant k(T) in eqn (16) would correspond to about k(T) ≈ 2 k5. Furthermore, the derived value of k(T) should correspond to a simple bond fission process with a preexponential factor of the order of 1015–1017 s−1 while the activation energy should be of the order of the reaction enthalpy of reaction (5). These expectations are in disagreement with the experimental observations from Section 3.
Mechanism (ii) would have properties which are in closer agreement with the experiments. Particularly in its later stages, this mechanism would be governed by the alternation of low and high reaction barriers such that the reaction flux may “get stuck” at the level of (C2F5)N + 2CF3 + CF2. This would explain CF2 yields Y(T) near unity for experiments in the range of 1100–1500 K. However, the apparent rate constant k should again correspond to a simple bond fission and Y(T) should be close to unity even at the lowest temperatures of the present experiments. The latter two expectations are again in disagreement with the experimental observation.
It remains to inspect mechanism (iii) with the possibility of at least a partial cross-over between the two pathways (i) and (ii). The observation of a CF2 yield near unity over a wide temperature range suggests that the reaction gets stuck at the level of (C2F5)NCF2 + CF2 + 2 CF3, regardless of whether pathway (ii) or (i) with a cross-over at the level of (C2F5)2N precedes the approach of the bottle-neck of reaction (10). Unfortunately, CF2 formation beyond the bottle-neck at higher temperatures in our experiments could not be distinguished from CF2 formation by decomposition of CF3 (see Section 3). However all evidence is for a slow completion of the reaction after reaching the bottle-neck. Finally, the properties of the apparent rate constant k(T), kin(T), and the decrease of Y(T) to values below unity at low temperatures need to be rationalized. While the Arrhenius representation of k(T) by eqn (17) corresponds more to a rigid-activated complex process, kin(T) in eqn (19) would appear consistent with a loose-activated complex of bond-fission type, like that expected for k5 and/or k8 (from reactions (5) and (8)).
It appears more difficult to explain the decrease of Y(T) with decreasing temperature, while kin(T) corresponds to k5 and/or k8. An answer may come from speculations about the formation of the low-temperature final product (C4F8)NCF3. If there is a branching of the reaction flux at the level of (C2F5)2NCF2, i.e. beyond the low-temperature rate-determining step (8) of pathway (ii), then the rate constant kin(T) for CF2 formation would not be influenced while the CF2 yield would be. This branching by as yet unidentified rearrangement processes should involve rigid activated complexes with lower preexponential factors and activation energies than the competing bond fission (9). It would then win at lower temperatures and reduce here the CF2 yield of Y(T), and this was observed in our experiments. Obviously, more work would be necessary to validate the given interpretation which would be able to reconcile the present high-temperature observations with the earlier low-temperature measurements of final products from ref. 6.
5. Conclusions
The combination of quantum-chemical calculations and experiments monitoring the formation of product CF2 in (C2F5)3N decomposition provided evidence for a sequence of C–N and C–C bond ruptures taking place simultaneously. Apparently, dissociation steps in the inner CF2-shell and in the outer CF3-shell occur in parallel and proceed as simple bond fission processes. The alternation of bond energies for the C–C and C–N bond rupture sequence of reactions (8)–(13) deserves particular attention. At temperatures that are sufficiently high for reactions (5)–(13) to occur, but low enough to keep CF2 undissociated, the observed overall yield of 6 CF2 per consumed (C2F5)3N confirms the kinetic analysis.
Details of the mechanism would not have been understood without the quantum-chemical calculations. As the decomposition of C2F5 through reaction (2) forms an essential part of the mechanism and its rate was not well known before, the falloff curves of this important reaction also had to be modelled. Finally, the present experiments at temperatures above about 2000 K generate mixtures of N, F, and CF2 in a concentration ratio 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3
3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 6. Recording absorption-time profiles for this mixture suggests contributions from CF2 and CF, the latter not only arising from CF2 dissociation (4) but also from other, so far unidentified processes.
6. Recording absorption-time profiles for this mixture suggests contributions from CF2 and CF, the latter not only arising from CF2 dissociation (4) but also from other, so far unidentified processes.
Finally, a branching of the mechanism at the level of (C2F5)2NCF2, on the one hand, may provide an explanation for the low-temperature production of an end product like perfluoro-N-methylpyrrolidene, (C4F8)NCF3, such as was observed earlier in ref. 6; on the other hand, this detail may also be responsible for the properties of the CF2 yields observed at the low-temperature end of the present experiments.
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
Financial support from the Deutsche Forschungsgemeinschaft (Projekt TR69-20-3) is gratefully acknowledged. Open Access funding provided by the Max Planck Society.
References
- H. Nakano and T. Kitazume, Organic Reactions Without an Organic Medium, Utilization of Perfluorotriethylamine as a Reaction Medium, Green Chem., 1999, 1, 21–22 RSC.
- M. Gaensslen, U. Gross, H. Oberhammer and S. Rüdiger, Perfluorotriethylamine: An Amine with Unusual Structure and Reactivity, Angew. Chem., Int. Ed. Engl., 1992, 31, 1467–1468 CrossRef.
- H. Bürger, H. Niepel, G. Pawelke and H. Oberhammer, Vibrational Spectra and Normal Coordinate Analysis of CF3 Compounds: Part XXVII. Perfluorotrimethylamine. Reinvestigation of the Molecular Structure by Electron Diffraction, J. Mol. Struct., 1979, 54, 159–174 CrossRef.
- A. Dimitrov, H.-G. Mack, S. Rüdiger, K. Seppelt and H. Oberhammer, Structure and Conformation of Tris(2,2,2-trifluoroethyl)amine, N(CH2CF3)3, in the Gaseous and Solid State, J. Phys. Chem., 1994, 98, 11401–11405 CrossRef CAS.
- J. B. Nielsen, P. Zylka, M. Kronberg, X. Zeng, K. D. Robinson, S. G. Bott, H. Zhang, J. L. Atwood, H. Oberhammer, H. Willner and J. S. Thrasher, Solid- and Gas-Phase Structures and Spectroscopic and Chemical Properties of Tris(pentafluorosulfanyl)amine, N(SF5)3 and Bis(pentafluorosulfanyl)aminyl Radical, ˙N(SF5)2, J. Mol. Struct., 2017, 1132, 11–19 CrossRef CAS.
- T. Yamamoto, A. Yasuhara, F. Shiraishi, K. Kaya and T. Abe, Thermal Decomposition of Halon Alternatives, Chemosphere, 1997, 35(3), 643–654 CrossRef CAS.
- V. P. Kolesov and M. P. Kozina, Thermochemistry of Organic and Organohalogen Compounds, Russ. Chem. Rev., 1986, 55, 912–928 CrossRef.
-
E. Goos, A. Burcat and B. Ruscic, Extended Third Millenium Ideal Gas and Condensed Phase Thermochemical Data Base for Combustion with Updates from Active Thermochemical Tables <http://ftp.technion.ac.il/pub/supported/aetdd/thermodynamics> Jan 2015.
- K. Li, E. M. Kennedy and B. Z. Dlogogorski, Experimental and Computational Studies of the Pyrolysis of CBrF3, and the Reaction of CBrF3 with CH4, Chem. Eng. Sci., 2000, 55, 4067–4078 CrossRef CAS.
- A. F. Ainagos, Mechanism and Kinetics of Pyrolysis of Perfluorohexane, Kinet. Catal., 1991, 32, 720–725 Search PubMed.
- N. K. Srinivasan, M.-C. Su, J. V. Michael, A. W. Jasper, S. J. Klippenstein and L. B. Harding, Thermal Decomposition of CF3 and the Reaction of CF2 + OH → CF2O + H, J. Phys. Chem. A, 2008, 112, 31–37 CrossRef CAS PubMed.
- C. J. Cobos, A. E. Croce, K. Luther and J. Troe, Shock Wave Study of the Thermal Decomposition of CF3 and CF2 Radicals, J. Phys. Chem. A, 2010, 114, 4755–4761 CrossRef CAS PubMed.
- C. J. Cobos, A. E. Croce, K. Luther, L. Sölter, E. Tellbach and J. Troe, Experimental and Modeling Study of the Reaction C2F4 (+M) ↔ CF2 + CF2 (+M), J. Phys. Chem. A, 2013, 117, 11420–11429 CrossRef CAS PubMed.
- C. J. Cobos, G. Knight, L. Sölter, E. Tellbach and J. Troe, Kinetic and Spectroscopic Studies of the Reaction of CF2 with H2 in Shock Waves, J. Phys. Chem. A, 2017, 121, 7827–7834 CrossRef CAS PubMed.
- K. Glänzer, M. Maier and J. Troe, Shock-Wave Study of the High-Temperature UV Absorption and the Recombination of Trifluoromethyl Radicals, J. Phys. Chem., 1980, 84, 1681–1686 CrossRef.
- C. J. Cobos, G. Knight, L. Sölter, E. Tellbach and J. Troe, Experimental and Modeling Study of the Multichannel Thermal Dissociation of CH3F and CH2F, Phys. Chem. Chem. Phys., 2018, 20, 2627–2636 RSC.
-
M. J. Frisch, et al., Revision A.02, Gaussian Inc., Wallingford, CT, USA, 2009 Search PubMed.
- A. D. Becke, Densitiy-Functional Exchange-Energy Approximation with Correct Asymptotic Behavior, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 3098–3100 CrossRef CAS.
- C. Lee, W. Yang and R. G. Parr, Development of the Colle-Salvetti Correlation-Energy Formula into a Functional of the Electron Density, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789 CrossRef CAS.
- Y. Zhao and D. G. Truhlar, The M06 Suite of Density Functionals for Main Group Thermochemistry, Thermochemical Kinetics, Noncovalent Interactions, Excited States, and Transition Elements: Two New Functionals and Systematic Testing of Four M06-Class Functionals and 12 Other Functionals, Theor. Chem. Acc., 2008, 120, 215–241 Search PubMed.
- A. D. Boese and J. M. Martin, Development of Density Functionals for Thermochemical Kinetics, J. Chem. Phys., 2004, 121, 3405–3416 CrossRef CAS PubMed.
- J.-D. Chai and M. Head-Gordon, Long-Range Corrected Hybrid Density Functionals with Damped Atom-Atom Dispersion Corrections, Phys. Chem. Chem. Phys., 2008, 10, 6615–6620 RSC.
- J. A. Montgomery, M. J. Frisch, J. W. Ochterski and G. A. Petersson, A Complete Basis Set Model Chemistry. VI. Use of Density Functional Geometries and Frequencies, J. Chem. Phys., 1999, 110, 2822–2827 CrossRef CAS.
- L. A. Curtiss, P. C. Redfern and K. Raghavachari, Gaussian-4 Theory, J. Chem. Phys., 2007, 126, 084108 CrossRef PubMed.
- NIST Kinetics Database 17, Version 7.0 (Web Version), Release 1.6.8, Data Version 2015.09.
- Y. Li, X. Zhang, S. Xiao, Q. Chen, J. Tang, D. Chen and D. Wang, Decomposition Properties of C4F7N/N2 Gas Mixture: An Environmentally Friendly Gas to Replace SF6, Ind. Eng. Chem. Res., 2018, 57, 5173–5182 CrossRef CAS.
- X. Yin, J. Goudriaan, E. A. Latinga, J. Vos and H. J. Spiertz, A Flexible Sigmoid Function of Determinate Growth, Ann. Bot., 2003, 91, 361–371 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c9cp01142k |
|
| This journal is © the Owner Societies 2019 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article *cd
*cd
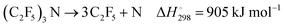
 from ref. 7,
from ref. 7,  and
and  from ref. 8; values for 298 K) would be accompanied by the dissociation of C2F5,9,10
from ref. 8; values for 298 K) would be accompanied by the dissociation of C2F5,9,10


![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 23 and G4
23 and G4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 24 calculations. As the agreement between the DFT and the ab initio calculations for the (C2F5)N dissociations appeared satisfactory, only DFT calculations were made for the dissociation of larger species. A comparison of the results obtained by using the various models is given in the ESI.†
24 calculations. As the agreement between the DFT and the ab initio calculations for the (C2F5)N dissociations appeared satisfactory, only DFT calculations were made for the dissociation of larger species. A comparison of the results obtained by using the various models is given in the ESI.†



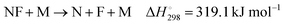


![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−213 kJ mol−1/RT)s−1
exp(−213 kJ mol−1/RT)s−1
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−339 kJ mol−1/RT)s−1
exp(−339 kJ mol−1/RT)s−1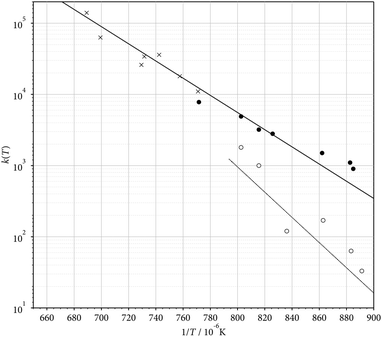

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3
3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 6. Recording absorption-time profiles for this mixture suggests contributions from CF2 and CF, the latter not only arising from CF2 dissociation (4) but also from other, so far unidentified processes.
6. Recording absorption-time profiles for this mixture suggests contributions from CF2 and CF, the latter not only arising from CF2 dissociation (4) but also from other, so far unidentified processes.

