Open Access Article
Open Access ArticleAtomistic characterization of collective protein–water–membrane dynamics†
Christopher
Päslack
a,
Lars V.
Schäfer
 *a and
Matthias
Heyden
*a and
Matthias
Heyden
 *b
*b
aCenter for Theoretical Chemistry, Faculty of Chemistry and Biochemistry, Ruhr-University Bochum, D-44780 Bochum, Germany. E-mail: lars.schaefer@ruhr-uni-bochum.de; Fax: +49 234 3214045; Tel: +49 234 3221582
bSchool of Molecular Sciences, Arizona State University, Tempe, AZ 85287-1604, USA. E-mail: heyden@asu.edu; Tel: +1 480 965-3980
First published on 15th April 2019
Abstract
Correlated vibrational motion on the sub-picosecond timescale and associated collective dynamics in a protein–membrane environment are characterized using molecular dynamics simulations. We specifically analyze correlated motion of a membrane-associated protein and a lipid bilayer for distinct separation distances. Correlated vibrations persist up to distances of 25 Å between both biomolecular surfaces. These correlations are mediated by separating layers of water molecules, whose collective properties are altered by the simultaneous presence of protein and lipid bilayer interfaces.
1 Introduction
Biomolecules in cells are tightly packed in the cytoplasm with molecular surfaces separated by distances on the order of 10 Å. This remaining space is filled by the aqueous solvent matrix in which many biomolecular processes take place.1 Recent experimental and theoretical studies focused on mechanisms that determine the structure and dynamics of proteins and reveal how protein and solvent dynamics affect each other.2–7 The structure and dynamics of water in the hydration shell of proteins differs from bulk water. Especially in the first hydration shell, diffusional and rotational dynamics of water molecules are slowed down, which is closely related to increased hydrogen bond (HB) lifetimes and shifted frequencies of intermolecular vibrations.8–13 Hydration water contributes to the stability of biomolecular structures and mediates interactions relevant for molecular recognition.14–16 Further, dewetting events are required to form intermolecular contacts and affect binding kinetics.17–19Collective motions in proteins cover a broad range of timescales. They were first investigated by normal mode analysis and linked to low-frequency modes in the density of states of proteins via incoherent neutron scattering.20,21 A study by Hong et al. revealed how specific, collective in-phase dynamic modes can facilitate access for substrates to the binding site of cytochrome P450cam.22 Further, simulations have characterized collective modes that propagate from the surface of a protein into its hydration shell.23–27 Despite this body of knowledge on protein solutions28–30 and the biological significance of membranes,31–33 collective protein–lipid dynamics – and how they are mediated by hydration water – have not yet been investigated.
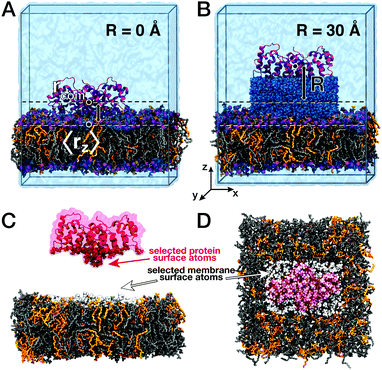
Here, we characterized correlated low-frequency vibrations between the membrane-associated protein annexin B12 (Anx) and a lipid bilayer consisting of a 7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 mixture of DOPC and DOPS lipids (Fig. 1). We further analyzed correlated vibrations of protein and lipid atoms with water separating both biomolecular surfaces. Atomic vibrations were sampled in all-atom molecular dynamics (MD) simulations and their correlations were analyzed for membrane-bound and unbound states. This analysis revealed the persistence of correlated vibrations between atoms of the Anx protein and membrane lipids up to 25 Å separation distances, which are mediated by the separating shell of hydration water. This finding is supported by the observation of simultaneous modifications of collective protein–water and lipid–water dynamics, which describe the propagation of collective modes from the protein and lipid bilayer surfaces into water layers separating both. A complementary analysis in the time-domain provides an estimate for the exchange of information with respect to the average thermal energy via the collective modes described here.
3 mixture of DOPC and DOPS lipids (Fig. 1). We further analyzed correlated vibrations of protein and lipid atoms with water separating both biomolecular surfaces. Atomic vibrations were sampled in all-atom molecular dynamics (MD) simulations and their correlations were analyzed for membrane-bound and unbound states. This analysis revealed the persistence of correlated vibrations between atoms of the Anx protein and membrane lipids up to 25 Å separation distances, which are mediated by the separating shell of hydration water. This finding is supported by the observation of simultaneous modifications of collective protein–water and lipid–water dynamics, which describe the propagation of collective modes from the protein and lipid bilayer surfaces into water layers separating both. A complementary analysis in the time-domain provides an estimate for the exchange of information with respect to the average thermal energy via the collective modes described here.
2 Methods
2.1 Simulation protocol
The peripheral membrane protein annexin B12 (Anx) was used as a model for a membrane-associating protein. For the membrane, we used a lipid bilayer consisting of a 7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 mixture of DOPC and DOPS lipids with a total of 512 lipids (256 lipids in each leaflet). We started from an X-ray crystal structure of Anx (PDB ID code 1DM5)34 and from a pre-equilibrated lipid bilayer.35 The simulated systems were prepared following a protocol described in previous work,11 where the initial position of the protein bound to the lipid bilayer was chosen according to experimental data.36
3 mixture of DOPC and DOPS lipids with a total of 512 lipids (256 lipids in each leaflet). We started from an X-ray crystal structure of Anx (PDB ID code 1DM5)34 and from a pre-equilibrated lipid bilayer.35 The simulated systems were prepared following a protocol described in previous work,11 where the initial position of the protein bound to the lipid bilayer was chosen according to experimental data.36
The protein and bilayer were placed in a rectangular box with a size of approximately 135 × 135 × 157 Å3 containing ca. 64![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 water molecules. The net charge of the system was neutralized with Na+ and Cl− ions. Periodic boundary conditions were applied in all three dimensions. The MD simulations were carried out using GROMACS 5.0.637 with the Amber ff99SB*-ILDNP force-field38–41 for Anx and the all-atom Slipids force-field35,42 for the lipids. The TIP4P/2005 model43 was used for water.
000 water molecules. The net charge of the system was neutralized with Na+ and Cl− ions. Periodic boundary conditions were applied in all three dimensions. The MD simulations were carried out using GROMACS 5.0.637 with the Amber ff99SB*-ILDNP force-field38–41 for Anx and the all-atom Slipids force-field35,42 for the lipids. The TIP4P/2005 model43 was used for water.
We employed the SETTLE and LINCS algorithms44,45 to constrain the internal degrees of freedom of water molecules and the bonds in other molecules, respectively, allowing to integrate the equations of motion with time steps of 2 fs. Short-range non-bonded Coulomb and Lennard-Jones 6,12 interactions were treated with a Verlet buffered pair list46 with potentials smoothly shifted to zero at a 10 Å cut-off. Long-range Coulomb interactions were treated using the smooth particle mesh Ewald (PME) scheme47,48 with a grid spacing of 1.2 Å and cubic spline interpolation. Analytical dispersion corrections were applied for energy and pressure to account for the truncation of the Lennard-Jones interactions.
After an initial energy minimization (500 steps steepest decent) of the Anx protein and the DOPC/DOPS bilayer, the protein and two bound Ca2+ ions were translated along the z-axis (i.e., the direction normal to the membrane) to generate configurations in which Anx is located at various distances R to the bilayer, covering an R-range from 0 to 32 Å. Each of the systems was then solvated with water. Sodium and chloride ions were included at physiological concentrations via substitution of randomly selected water molecules. Care was taken not to introduce water molecules in the hydrophobic part of the bilayer. After a second energy minimization (500 steps steepest decent), the systems were equilibrated for 5 ns in the isothermal–isobaric (NPT) ensemble with harmonic position restraining potentials applied to the heavy atoms of the protein (force constants 1000 kJ mol−1 nm−2). The temperature was kept at 298 K by a velocity-rescaling thermostat49 with a coupling time constant of 0.1 ps. For simulations at constant 1.0 bar pressure, a semi-isotropic Berendsen barostat50 with a coupling time constant of 0.5 ps and a compressibility of 4.5 × 10−5 bar−1 was applied, with lateral (xy) and normal (z) dimensions of the simulation box coupled separately.
For each configuration generated with a specific protein–membrane distance R, simulations of 100 ns were performed in the NPT ensemble. During the equilibrations (but not the production simulations, see below), two harmonic restraining potentials were applied to the angle between the z-axis and the connecting vectors between the Cα-atoms of (1) residues Ser35/Val195 and (2) residues Glu138/His254 (force constant 200 kJ mol−1 rad−2). This was required to avoid overall tumbling of the protein during the simulations. In addition, a harmonic umbrella potential with a force constant of 1500 kJ mol−1 nm−2 was applied in the z-direction between the centers of mass of Anx and selected phosphorus atoms in the lipid head groups of the upper leaflet. The phosphorus atoms were selected in a cylindrical geometry with an inner radius of r0 = 30 Å and an outer radius of r1 = 35 Å, where weighted contributions to the center of mass position were switched to 0 between r0 and r1. The harmonic restraint between the centers of mass of the protein and the phosphorus atoms in the defined cylindrical region kept the protein at the selected distance from the lipid bilayer.
After the 100 ns equilibrations, the NPT equilibrations were extended by another 5 ns for each distance with a stronger angle restraint (1000 kJ mol−1 rad−2) to enforce an ideal orientation of the protein, such that the bottom surface of Anx was parallel to the membrane surface (Fig. 1).
Finally, for selected distances (R = 0 to 30 Å, in 5 Å steps, and two additional distances of 28 Å and 32 Å), we carried out 20 independent 100 ps simulations in the NVE ensemble for analysis of collective motions. The starting structures for the NVE simulations were taken from the final 2 ns of the above NPT equilibrations, separated by 100 ps. Atom positions and velocities were recorded every 8 fs for vibrational analysis. The production simulations in the NVE ensemble were entirely unbiased, i.e., without umbrella potentials or angle restraints, to avoid artifacts in the time-correlation functions and their Fourier transforms due to the restraining potentials. The mass density profiles along the membrane normal (Fig. S1), as well as the analysis of the stability of protein orientation (Fig. S2) and position (Fig. S3 and S4) with respect to the bilayer are provided in the ESI.†
2.2 Velocity cross-correlation spectra
Collective vibrations in the protein–membrane system were analyzed using a generalized vibrational density of states (VDOS),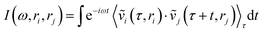 | (1) |
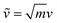 are weighted by the square-root of the atom mass yielding an expression for the average thermal energy for auto-correlations i = j. The brackets 〈…〉τ denote ensemble-averaged time-correlation functions with reference times τ. Eqn (1) allows for direct evaluation of correlated vibrational motion between protein and membrane surface atoms. Here, we restrict the analysis to non-hydrogen atoms, which dominate the vibrational spectra at far-infrared frequencies below 400 cm−1.
are weighted by the square-root of the atom mass yielding an expression for the average thermal energy for auto-correlations i = j. The brackets 〈…〉τ denote ensemble-averaged time-correlation functions with reference times τ. Eqn (1) allows for direct evaluation of correlated vibrational motion between protein and membrane surface atoms. Here, we restrict the analysis to non-hydrogen atoms, which dominate the vibrational spectra at far-infrared frequencies below 400 cm−1.
In addition to correlated protein–membrane vibrations, we analyzed protein–water and membrane–water correlated vibrations involving water molecules located in the space between Anx and the lipid bilayer. We computed cross-correlation spectra including water oxygens sampled at various distances to the protein or membrane surface, ranging from 2.5–10.0 Å with increments of 0.5 Å. Explicit atomic velocities were replaced by localized velocity densities,
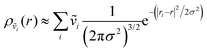 | (2) |
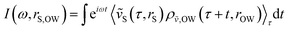 | (3) |
We visualize correlation spectra obtained as a function of the real-space distance using the inverse distance k = 2π/rS,OW, in analogy to coherent scattering data. We identify dispersive collective modes propagating with a wave velocity vmode = dω/dk. The k-resolved spectra, recorded for distinct protein–membrane separations R, are directly related to longitudinal density current spectra I‖J(k,ω) = (ω2/k2)S(k,ω), which describe correlated density fluctuations via the experimentally accessible dynamic structure factor S(k,ω).
3 Results and discussion
3.1 Collective protein–membrane vibrations
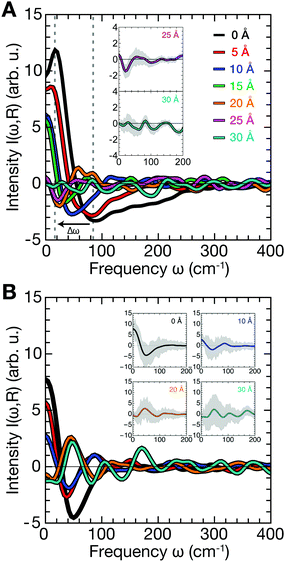
First, we assessed correlated motion between the protein and the lipid bilayer. We analyzed the evolution of the cross-correlation spectra I(ω,ri,rj) between non-hydrogen atoms of the protein (index i) and the lipids (index j), each selected at the corresponding interface (see Fig. 1C and D) with increasing protein–membrane distance R. For each separation distance R, we obtained I(ω,R) shown in Fig. 2A by averaging over individual pair-wise cross-correlations. Protein and membrane surface atoms were partitioned into slabs (Δx = 5 Å, Δy = 5 Å) within which the cross-correlations were analyzed to ensure alignment of the vectors rj − ri with the membrane normal. The most prominent feature in all spectra I(ω,R) is the positive-intensity peak at low frequencies ω < 25 cm−1, describing an in-phase oscillation of membrane and protein atoms along the connecting vector. As R increases, the peak is shifted toward zero frequencies. Additionally, a negative-intensity mode is observed at 30–120 cm−1, which describes anti-phase motion of protein and membrane atoms. This peak is broad at short distances and becomes narrow at larger distances. The amplitude of correlated vibrations of protein and lipid atoms remains detectable above the noise level for separation distances R of up to 25 Å (inset Fig. 2). For R ≥ 30 Å it is no longer possible to distinguish between correlated vibrations and statistical noise, demonstrating that correlations at smaller separation distances are not caused by finite-size effects. The negative-intensity mode is dispersive: its frequency decreases monotonically for increasing protein–membrane separations R resulting in a frequency shift of 67 cm−1 from 25 Å to 0 Å. For direct protein–membrane contact (R = 0 Å), the negative signal has a pronounced high-frequency tail, which we attribute to intermolecular vibrations between directly interacting protein and lipid groups.The results shown in Fig. 2A report on correlated vibrations between atoms of the protein and membrane surfaces. To investigate the propagation of collective modes, i.e., correlated vibrational motion between the lipid and protein surfaces analyzed in Fig. 2A into the interior of the protein, we repeated the analysis using mass-weighted atomic velocities of atoms selected within a hemisphere (oriented towards the membrane-facing protein surface) of 10 Å radius around the protein center of mass. The results are shown in Fig. 2B and indicate a decreased overall intensity of the correlations, as expected due to the increased separation distance between the membrane surface and the protein core in comparison to the separation between the binding interfaces. In addition, Fig. 2B shows that the correlation intensities decrease significantly faster with increasing R. Relative to the cross-correlation spectrum for R = 0 Å, both, the positive and negative peak intensities (apart from the dispersive shift in frequency) decrease to just 40% of their initial intensity for R = 10 Å in Fig. 2B. When intensities in the cross-correlation spectra are compared between membrane and protein surface atoms for R = 0 Å and R = 10 Å in Fig. 2A, the positive peak decreases only to approximately 50% of its original intensity, while the negative intensity even retains roughly 80%. Correlated vibrations between the protein core and the membrane surface are therefore more sensitive to the separation between both binding interfaces. Hence, collective modes that propagate through the HB network of water separating the protein and membrane surfaces seem to dissipate more efficiently within the protein.
3.2 Collective protein–water and membrane–water vibrations
Next, we analyzed protein–water and membrane–water correlations. As a reference, we first computed k-resolved protein–water and membrane–water cross-correlation spectra according to eqn (3) for simulations of Anx in water (no membrane) and the membrane in water (no protein) as shown in Fig. 3, which effectively represents an infinite protein–membrane separation distance R. The selection of surface atoms was the same as shown in Fig. 1C and D and velocity densities for water oxygens were sampled at distances to the selected protein or membrane surface atoms in the range from 2.5–10.0 Å. Compared to the protein, the overall correlation intensity is weaker for the membrane by approximately a factor of 2. Both systems have two distinct modes that dominate the spectra: (1) a dispersive high-frequency mode with negative intensity and (2) a low-frequency mode with positive intensity. In the high k/short distance (∼3 Å, first hydration layer) limit, the signals correspond to peaks found in the VDOS of water and exhibit their largest magnitude, describing intermolecular vibrations such as HB bending (<100 cm−1) and stretching modes (∼200 cm−1). The signals at smaller k/longer distances (>3 Å) correspond to collective modes that propagate through the water HB network. The dispersion relation dω/dk of the negative-intensity peak (Fig. 3, dashed lines) in the linear regime yields wave propagation velocities of 2313 ± 77 m s−1 for Anx and 1870 ± 128 m s−1 for the DOPC/DOPS bilayer.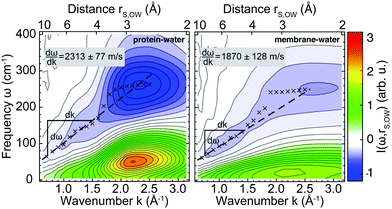 | ||
| Fig. 3 Cross-correlation spectra of mass-weighted atomic velocities and localized velocity densities (eqn (3)) for vibrations of non-hydrogen protein or membrane surface atoms with hydration water oxygen atoms as a function of reciprocal distance k = 2π/rS,OW. Shown are results for Anx in water (left panel; without a lipid bilayer) and for a DOPC/DOPS bilayer (right panel; without a protein). Crosses trace the peak-intensity of the negative-intensity modes for which linear dispersion curves (dashed lines) were determined. | ||
3.3 Distance-dependence of wave velocities
Analogous to the analysis in Fig. 3, longitudinal collective protein–water and membrane–water vibrations were also analyzed from k-resolved cross-correlation spectra obtained from simulations including both the protein and the membrane at varying separation distances R. As shown in Fig. 1B, the water molecules considered here are located in between the protein and membrane. Applying the dispersion relation for the protein–membrane systems, we obtain wave propagation velocities from protein–water and membrane–water cross-correlation spectra at varying protein–membrane distances as shown in Fig. 4. Notably, the observed propagation velocities of the analyzed collective modes vmode are increased significantly in both cases for separation distances R < 25 Å between protein and membrane. While this increase only amounts to 10% in case of the protein–water collective modes, the propagation velocities are increased by 40% for collective membrane–water modes. The data in Fig. 4 demonstrate a sharp modulation of the mode velocities in a narrow distance range (between R = 25–28 Å) corresponding to the thickness of a single hydration shell. Reassuringly, the mode velocities for the largest studied separation distances converge to the values at infinite separation distance as reported in Fig. 3.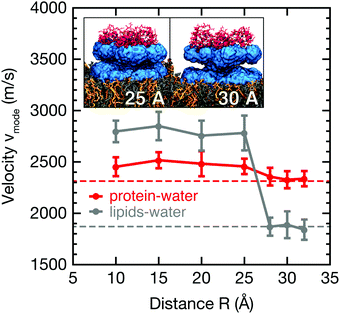 | ||
| Fig. 4 Wave propagation velocities of longitudinal, collective protein–water (red) and membrane–water (gray) modes for distinct protein–membrane separation distances R (see Fig. S6 in the ESI† for corresponding cross-correlation spectra). Error bars show standard errors of the mean from 20 individual simulations. Dashed lines indicate reference values for Anx in water (no membrane) and the lipid bilayer in water (no protein); insets visualize the onset of overlapping protein and membrane hydration layers of 10 Å thickness. | ||
The maximum change Δvmode is about +927 m s−1 for the lipid bilayer and +307 m s−1 for Anx. The propagation of collective modes involving the lipid bilayer and its hydration water becomes similar to fast sound in bulk water (≈3000 m s−1).52,53 However, we do not observe a strictly monotonous trend for neither protein nor lipid bilayer besides the increase for distances R < 25 Å, which coincides with the gradually increasing overlap of the protein and membrane hydration shells. The inset of Fig. 4 shows that the protein surface is not planar and its hydration shell has a conical shape. Assuming a 10 Å thickness of the hydration layer, there is almost no overlap of the protein and membrane hydration shells at a separation distance of R = 30 Å. However, at 25 Å distance the hydration shells begin to partially overlap. When the protein binds to the membrane, i.e., for short distances, the protein and lipids share one single hydration shell. Single particle dynamics, such as water self-diffusion and rotational relaxation, are slowed down in the hydration shell and the hydrogen bond network becomes effectively more rigid.6,11,54,55 This is correlated to changes in local thermodynamic properties as observed in our previous work,11 but the effects are short-ranged and mainly affect a single hydration layer within distances of 3–5 Å. However, here we analyze collective modes involving protein and membrane surface atoms and surrounding water molecules, which tend to extend over distances of at least 10 Å as observed in Fig. 3 and in previous studies on protein–water systems.24,26
In addition to these previous observations, we observe that the presence of two biomolecular surfaces with separation distances of 25 Å or less modifies collective protein–water and membrane–water dynamics and results in the onset of correlated motion of protein and lipid atoms. Our observations can be compared to abrupt dynamical transitions in water hydrogen bond network dynamics for crowded protein solutions observed experimentally for protein–protein distances of 30–40 Å and 20–25 Å in accompanying simulations.56 Indeed, the increased propagation velocity of protein–water and membrane–water collective modes for separation distances R < 25 Å may serve as a sensitive indicator of long-lived water hydrogen bond networks connecting both biomolecular surfaces, which are likely to feature collective properties similar to low-temperature water or ice.57,58
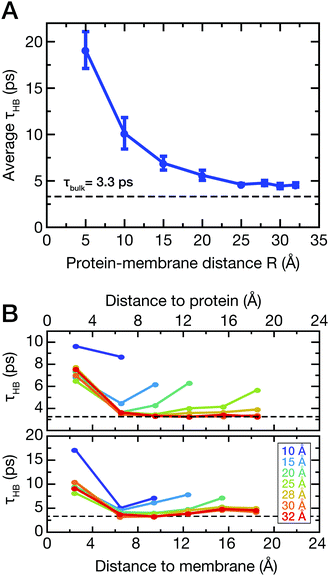
To support this assumption, the lifetimes of water–water hydrogen bonds involving the water molecules between the protein and the membrane (see Fig. 1B, dark blue) were analyzed. As described in the ESI,† we computed the hydrogen bond correlation functions CHB(t) and estimated the HB lifetimes τHB as CHB(τHB) = 1/e. The average lifetimes for all water molecules between the protein and the membrane are shown in Fig. 5A.
For short protein–membrane distances R ≤ 10 Å, the average lifetimes deviate strongly from the bulk lifetime of about 3 ps. Water molecules are confined and H-bonds persist on average up to almost 20 ps, i.e., almost one order of magnitude longer than in bulk. For increasing distances R, the correlation times drop to almost the bulk lifetime, however, not reaching the bulk value since water molecules in the first hydration shells are still included in the average. These findings agree with previous results from two-dimensional infrared spectroscopy and MD simulations,56 where a dynamic transition of HB lifetimes of water molecules between proteins in crowded solutions occurred for comparable separation distances between protein surfaces. In addition, we analyzed the average HB lifetimes involving water molecules selected as a function of distance from either the protein or membrane surface (Fig. 5B, top and bottom panels, respectively); these analyses were carried out for simulations with varying protein–membrane distances R. Notably, only at protein–membrane distances of R ≥ 25 Å, i.e., in the center between protein and membrane, the dynamics of water become similar to bulk, marking the onset of overlapping solvation shells. These results corroborate the interpretation of shifted mode velocities vmode (Fig. 4) due to hydration shell overlap. Notably, collective modes with a propagation velocity of 2500 m s−1 traverse a 25 Å separation distance between the protein and the membrane in just 1 ps.
The observation that correlated vibrations between the protein and membrane persist up to 25 Å separation distance may have important implications for crowded environments such as the cytoplasm. The wave velocities of protein–water and membrane–water collective modes are affected by the combined influence of both biomolecular surfaces. Importantly, the presence of a protein substantially increases the propagation velocities obtained from membrane–water cross-correlation spectra, in this respect resembling fast sound-like dynamics as observed in solid forms of water with slow structural relaxation times. However, the propagation velocities of protein–water collective vibrations are enhanced to a much smaller extent upon hydration shell overlap. While the protein–water collective vibrations propagate inherently faster than the membrane–water vibrations in the infinite dilution limit, membrane–water collective vibrations exhibit faster propagation velocities for protein-membrane separation distances R < 25.
3.4 Time-domain analysis of correlated motions
To complement our analysis of correlated vibrational motion vs. frequency shown in Fig. 2 and 3, we provide the corresponding time-resolved cross-correlations in Fig. 6. The latter are normalized by the corresponding average auto-correlations of protein or lipid atoms at zero correlation time, which correspond to the product of the particle mass and the squared velocity component along the vector separating the cross-correlated atoms. This normalization allows one to interpret cross-correlation intensities in terms of fractions of the average thermal energy per degree of freedom exchanged between particles.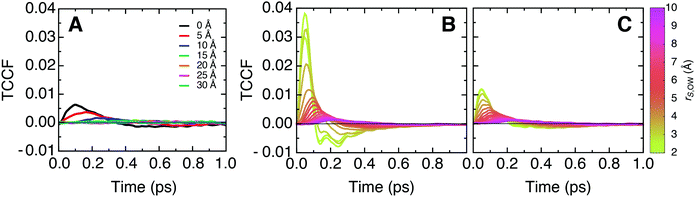 | ||
| Fig. 6 Time domain representation of the longitudinal mass-weighted velocity cross-correlation functions (TCCF) between (A) protein–membrane, (B) protein–water, and (C) membrane–water atoms for distinct separation distances. The data correspond to the inverse Fourier transform of the frequency spectra shown in Fig. 2A and 3. The cross-correlation functions are normalized by the value of the corresponding mass-weighted velocity time auto-correlation function at t = 0, which describes the thermal energy per degree of freedom at the simulation temperature. | ||
The peak intensities of the cross-correlation functions indicate that, in this single degree of freedom, correlated particles exchange between 0.25% and 1% of their energy with each other on a 50 fs timescale. Since our simulations are carried out under equilibrium conditions, no net flow of energy takes place. However, the amount of exchanged energy can be interpreted in terms of dynamic information relative to the thermal fluctuations.
Further, we follow the peak intensities of the time-resolved cross-correlation functions for distinct separation distances in Fig. 7, which describe the spatial dissipation of this dynamic information. While the maximum peak intensities observed at the shortest correlation distances, i.e., for particles in direct contact with each other, are only about 1% of the thermal energy, we note that the exchange of dynamic information and its propagation to larger distances is very fast (ca. 10–100 fs), as seen from the position of the peaks in Fig. 6. Therefore, the amount of energy exchanged between particles quickly accumulates on picosecond timescales.
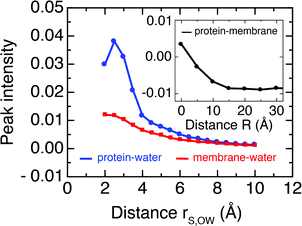 | ||
| Fig. 7 Peak intensity of mass-weighted velocity time cross correlation functions between protein–membrane atoms (black, inset) and protein–water (blue) and membrane–water atoms (red) as a function of separation distance. Numerical values are equivalent to the y-axis scales in Fig. 6 and describe fractions of the average thermal energy per degree of freedom. | ||
4 Conclusions
The correlated vibrational motion of Anx, the lipid bilayer and the separating layers of hydration water may affect the kinetics of binding of the protein to the membrane surface. The expulsion of the last separating hydration water layers between binding interfaces is observed as a collective dewetting transition in simplified hydrophobic model systems17 and creates a kinetic barrier, which can be characterized as a peak in the friction profile along the binding coordinate. While the models, for which this behavior has been studied in detail, lack the chemical heterogeneity and flexibility of a realistic biomolecular surface, enhanced water density fluctuations and transient dewetting can be observed for hydrophobic protein surface patches in more realistic simulation models.59 We speculate that collective dewetting transitions may be influenced by the correlated vibrations between atoms in both binding interfaces, mediated through the separating water molecules as observed in this study. The intensities of membrane–water correlated vibrations are weaker than those for the protein and water. A reason may be that a lipid bilayer possesses a large variety of collective dynamics spanning timescales from 10−4–10−10 s, where a large number of vibrational modes fall into the ns-regime of peristaltic and undulatory oscillations.60 Finally, our results corroborate the idea of hydration water-mediated collective motion between biomolecular interfaces over length scales of >10 Å. This may be of key importance in crowded cellular environments, where average distances between neighboring biomolecular surfaces are frequently on the order of ∼10 Å. Changes in single-particle dynamics such as self-diffusion and rotational reorientation of water molecules are typically restricted to the first hydration shell, while collective protein–water dynamics persist up to ∼10 Å. Our findings provide evidence for the mediation of correlated motion between biomolecular surfaces by a dynamic hydration shell, which features modified characteristics of membrane–water and protein–water correlated vibrations.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The Steinbuch Centre for Computing (SCC), Karlsruhe/Germany, is acknowledged for providing computational resources. This work was funded by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) under Germany's Excellence Strategy – EXC-2033 – project number 390677874 and an Emmy-Noether grant (SCHA 1574/3-1) to L. V. S.References
- P. Ball, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, 13327–13335 CrossRef CAS PubMed
.
- Y. Levy and J. N. Onuchic, Annu. Rev. Biophys. Biomol. Struct., 2006, 35, 389–415 CrossRef CAS PubMed
.
- S. Ebbinghaus, S. J. Kim, M. Heyden, X. Yu, U. Heugen, M. Gruebele, D. M. Leitner and M. Havenith, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 20749–20752 CrossRef CAS PubMed
.
- L. Hong, X. Cheng, D. C. Glass and J. C. Smith, Phys. Rev. Lett., 2012, 108, 238102 CrossRef PubMed
.
- V. Conti Nibali and M. Havenith, J. Am. Chem. Soc., 2014, 136, 12800–12807 CrossRef CAS PubMed
.
- A. C. Fogarty and D. Laage, J. Phys. Chem. B, 2014, 118, 7715–7729 CrossRef CAS PubMed
.
- G. Schirò, Y. Fichou, F.-X. Gallat, K. Wood, F. Gabel, M. Moulin, M. Härtlein, M. Heyden, J.-P. Colletier, A. Orecchini, A. Paciaroni, J. Wuttke, D. J. Tobias and M. Weik, Nat. Commun., 2015, 6, 6490 CrossRef PubMed
.
- B. Bagchi, Chem. Rev., 2005, 105, 3197–3219 CrossRef CAS PubMed
.
- A. R. Bizzarri and S. Cannistraro, J. Phys. Chem. B, 2002, 106, 6617–6633 CrossRef CAS
.
- M. Heyden and M. Havenith, Methods, 2010, 52, 74–83 CrossRef CAS PubMed
.
- O. Fisette, C. Päslack, R. Barnes, J. M. Isas, R. Langen, M. Heyden, S. Han and L. V. Schäfer, J. Am. Chem. Soc., 2016, 138, 11526–11535 CrossRef CAS PubMed
.
- A. Debnath, B. Mukherjee, K. Ayappa, P. K. Maiti and S.-T. Lin, J. Chem. Phys., 2010, 133, 174704 CrossRef PubMed
.
- R. A. X. Persson, V. Pattni, A. Singh, S. M. Kast and M. Heyden, J. Chem. Theory Comput., 2017, 13, 4467–4481 CrossRef CAS PubMed
.
- M. Chaplin, Nat. Rev. Mol. Cell Biol., 2006, 7, 861–866 CrossRef CAS PubMed
.
- M.-C. Bellissent-Funel, A. Hassanali, M. Havenith, R. Henchman, P. Pohl, F. Sterpone, D. van der Spoel, Y. Xu and A. E. Garcia, Chem. Rev., 2016, 116, 7673–7697 CrossRef CAS PubMed
.
- D. Laage, T. Elsaesser and J. T. Hynes, Chem. Rev., 2017, 117, 10694–10725 CrossRef CAS PubMed
.
- P. Setny, R. Baron, P. M. Kekenes-Huskey, J. A. McCammon and J. Dzubiella, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 1197–1202 CrossRef CAS PubMed
.
- R. Godawat, S. N. Jamadagni and S. Garde, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 15119–15124 CrossRef CAS PubMed
.
- R. Baron, P. Setny and J. A. McCammon, J. Am. Chem. Soc., 2010, 132, 12091–12097 CrossRef CAS PubMed
.
- J. C. Smith, S. Cusack, U. Pezzeca, B. Brooks and M. Karplus, J. Chem. Phys., 1986, 85, 3636–3654 CrossRef CAS
.
- T. Ichiye and M. Karplus, Proteins, 1991, 11, 205–217 CrossRef CAS PubMed
.
- L. Hong, N. Jain, X. Cheng, A. Bernal, M. Tyagi and J. C. Smith, Sci. Adv., 2016, 2, e1600886 CrossRef PubMed
.
- A. Orecchini, A. Paciaroni, A. D. Francesco, C. Petrillo and F. Sacchetti, J. Am. Chem. Soc., 2009, 131, 4664–4669 CrossRef CAS PubMed
.
- M. Heyden and D. J. Tobias, Phys. Rev. Lett., 2013, 111, 218101 CrossRef PubMed
.
- V. Conti Nibali, G. D'Angelo, A. Paciaroni, D. J. Tobias and M. Tarek, J. Phys. Chem. Lett., 2014, 5, 1181–1186 CrossRef CAS PubMed
.
- M. Heyden, J. Chem. Phys., 2014, 141, 22D509 CrossRef PubMed
.
- L. U. L. Brinkmann and J. S. Hub, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, 10565–10570 CrossRef CAS PubMed
.
- K. Moritsugu, A. Kidera and J. C. Smith, J. Phys. Chem. B, 2014, 118, 8559–8565 CrossRef CAS PubMed
.
- T. R. M. Barends, L. Foucar, A. Ardevol, K. Nass, A. Aquila, S. Botha, R. B. Doak, K. Falahati, E. Hartmann, M. Hilpert, M. Heinz, M. C. Hoffmann, J. Köfinger, J. E. Koglin, G. Kovacsova, M. Liang, D. Milathianaki, H. T. Lemke, J. Reinstein, C. M. Roome, R. L. Shoeman, G. J. Williams, I. Burghardt, G. Hummer, S. Boutet and I. Schlichting, Science, 2015, 350, 445–450 CrossRef CAS PubMed
.
- D. Russo, A. Laloni, A. Filabozzi and M. Heyden, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, 11410–11415 CrossRef CAS PubMed
.
- S. H. Chen, C. Y. Liao, H. W. Huang, T. M. Weiss, M. C. Bellisent-Funel and F. Sette, Phys. Rev. Lett., 2001, 86, 740–743 CrossRef CAS PubMed
.
- M. C. Rheinstädter, C. Ollinger, G. Fragneto, F. Demmel and T. Salditt, Phys. Rev. Lett., 2004, 93, 108107 CrossRef PubMed
.
- M. C. Rheinstädter, T. Seydel and T. Salditt, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2007, 75, 011907 CrossRef PubMed
.
- J.-P. Cartailler, H. Haigler and H. Luecke, Biochemistry, 2000, 39, 2475–2483 CrossRef CAS
.
- J. P. M. Jämbeck and A. P. Lyubartsev, J. Chem. Theory Comput., 2012, 8, 2938–2948 CrossRef PubMed
.
- C.-Y. Cheng, J. Varkey, M. R. Ambroso, R. Langen and S. Han, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 16838–16843 CrossRef CAS PubMed
.
- M. J. Abraham, T. Murtola, R. Schulz, S. Páll, J. C. Smith, B. Hess and E. Lindahl, SoftwareX, 2015, 1, 19–25 CrossRef
.
- V. Hornak, R. Abel, A. Okur, B. Strockbine, A. Roitberg and C. Simmerling, Proteins: Struct., Funct., Bioinf., 2006, 65, 712–725 CrossRef CAS PubMed
.
- R. B. Best and G. Hummer, J. Phys. Chem. B, 2009, 113, 9004–9015 CrossRef CAS PubMed
.
- K. Lindorff-Larsen, S. Piana, K. Palmo, P. Maragakis, J. L. Klepeis, R. O. Dror and D. E. Shaw, Proteins, 2010, 78, 1950–1958 CAS
.
- A. E. Aliev, M. Kulke, H. S. Khaneja, V. Chudasama, T. D. Sheppard and R. M. Lanigan, Proteins, 2014, 82, 195–215 CrossRef CAS PubMed
.
- J. P. M. Jämbeck and A. P. Lyubartsev, J. Phys. Chem. B, 2012, 116, 3164–3179 CrossRef PubMed
.
- J. L. Abascal and C. Vega, J. Chem. Phys., 2005, 123, 234505 CrossRef CAS PubMed
.
- S. Miyamoto and P. A. Kollman, J. Comput. Chem., 1992, 13, 952–962 CrossRef CAS
.
- B. Hess, J. Chem. Theory Comput., 2008, 4, 116–122 CrossRef CAS PubMed
.
- S. Páll and B. Hess, Comput. Phys. Commun., 2013, 184, 2641–2650 CrossRef
.
- T. Darden, D. York and L. Pedersen, J. Chem. Phys., 1993, 98, 10089–10092 CrossRef CAS
.
- U. Essmann, L. Perera, M. L. Berkowitz, T. Darden, H. Lee and L. G. Pedersen, J. Chem. Phys., 1995, 103, 8577–8593 CrossRef CAS
.
- G. Bussi, D. Donadio and M. Parrinello, J. Chem. Phys., 2007, 126, 014101 CrossRef PubMed
.
- H. Berendsen, J. Postma, W. van Gunsteren, A. DiNola and J. Haak, J. Chem. Phys., 1984, 81, 3684–3690 CrossRef CAS
.
- M. Heyden, J. Sun, S. Funkner, G. Mathias, H. Forbert, M. Havenith and D. Marx, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 12068–12073 CrossRef CAS PubMed
.
- A. Rahman and F. H. Stillinger, Phys. Rev. A: At., Mol., Opt. Phys., 1974, 10, 368 CrossRef CAS
.
- F. Sciortino and S. Sastry, J. Chem. Phys., 1994, 100, 3881–3893 CrossRef CAS
.
- M. Tarek and D. J. Tobias, Phys. Rev. Lett., 2002, 88, 138101 CrossRef CAS PubMed
.
- F. Sterpone, G. Stirnemann and D. Laage, J. Am. Chem. Soc., 2012, 134, 4116–4119 CrossRef CAS PubMed
.
- J. T. King, E. J. Arthur, C. L. Brooks and K. J. Kubarych, J. Am. Chem. Soc., 2014, 136, 188–194 CrossRef CAS PubMed
.
- F. Sette, G. Ruocco, M. Krisch, C. Masciovecchio, R. Verbeni and U. Bergmann, Phys. Rev. Lett., 1996, 77, 83–86 CrossRef CAS PubMed
.
- S. Saito and B. Bagchi, J. Chem. Phys., 2019, 150, 054502 CrossRef PubMed
.
- S. N. Jamadagni, R. Godawat and S. Garde, Annu. Rev. Chem. Biomol. Eng., 2011, 2, 147–171 CrossRef CAS PubMed
.
- E. Lindahl and O. Edholm, Biophys. J., 2000, 79, 426–433 CrossRef CAS PubMed
.
Footnote |
| † Electronic supplementary information (ESI) available: Simulation protocol, details on analysis of correlated motions. See DOI: 10.1039/c9cp00725c |
| This journal is © the Owner Societies 2019 |