Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Substitutional disorder: structure and ion dynamics of the argyrodites Li6PS5Cl, Li6PS5Br and Li6PS5I†
I.
Hanghofer
*a,
M.
Brinek
a,
S. L.
Eisbacher
a,
B.
Bitschnau
b,
M.
Volck
c,
V.
Hennige
c,
I.
Hanzu
 ad,
D.
Rettenwander
ad,
D.
Rettenwander
 a and
H. M. R.
Wilkening
a and
H. M. R.
Wilkening
 *ad
*ad
aChristian Doppler Laboratory for Lithium Batteries and Institute for Chemistry and Technology of Materials, Graz University of Technology (NAWI Graz), Stremayrgasse 9, 8010 Graz, Austria. E-mail: isabel.hanghofer@tugraz.at; wilkening@tugraz.at; Fax: +43 316 873 32332; Tel: +43 316 873 32330
bInstitute of Physical and Theoretical Chemistry, Graz University of Technology, Stremayrgasse 9, 8010 Graz, Austria
cAVL List GmbH, 8020 Graz, Austria
dAlistore-ERI European Research Institute, 33 rue Saint Leu, 80039 Amiens, France
First published on 27th March 2019
Abstract
For the development of safe and long-lasting lithium-ion batteries we need electrolytes with excellent ionic transport properties. Argyrodite-type Li6PS5X (X: Cl, Br, I) belongs to a family of such a class of materials offering ionic conductivities, at least if Li6PS5Br and Li6PS5Cl are considered, in the mS cm−1 range at room temperature. Although already tested as ceramic electrolytes in battery cells, a comprehensive picture about the ion dynamics is still missing. While Li6PS5Br and Li6PS5Cl show an exceptionally high Li ion conductivity, that of Li6PS5I with its polarizable I anions is by some orders of magnitude lower. This astonishing effect has not been satisfactorily understood so far. Studying the ion dynamics over a broad time and length scale is expected to help shed light on this aspect. Here, we used broadband impedance spectroscopy and 7Li NMR relaxation measurements and show that very fast local Li ion exchange processes are taking place in all three compounds. Most importantly, the diffusion-induced NMR spin–lattice relaxation in Li6PS5I is almost identical to that of its relatives. Considering the substitutional disorder effects in Li6PS5X (X = Br, Cl), we conclude that in structurally ordered Li6PS5I the important inter-cage jump processes are switched off, hindering the ions from taking part in long-range ion transport.
1 Introduction
Energy from renewable sources can be stored in various ways. Considering electrochemical storage, Li-based batteries offer high energy densities combined with a high degree of design flexibility.1–3 In particular, batteries using Li+ as an ionic charge carrier are an emerging option to power electric vehicles.1–7 Such batteries may, however, suffer from flammable fluorinated liquid electrolytes conventionally used in these energy storage systems. Next-generation Li batteries with, e.g., metallic Li anodes and equipped with solid electrolytes have aroused great interest.8–12 Devices with non-flammable ceramic electrolytes are anticipated to benefit from increased safety as they easily withstand higher temperatures. Thus, such systems are less sensitive to thermal runaway.To take full advantage of all-solid-state Li (or Na) batteries, electrolytes with exceptionally high ionic conductivities are needed.8–15 In the past, only a few ceramics were available fulfilling this requirement.16,17 This lack of suitable materials prevented any commercialization on a large scale.18,19 Ideal candidates should (i) show room-temperature ionic conductivities with values comparable to those of liquids, (ii) be chemically stable over a sufficiently wide temperature range and (iii) possess a sufficiently high electrochemical stability over a large potential window.10,11 For battery applications, the conductivity of a ceramic material should reach a value of 10−3 S cm−1 at room temperature.10,14
Over the last years several classes of materials have been presented whose members show very high conductivities. These materials include sulfides, such as Li7P3S11 and Li10GeP2S12, oxides including garnets, such as Li7La3Zr2O12, or phosphates based on the NASICON structure.8–15,20–26 Although the ionic bulk conductivities of oxides and phosphates can reach very high values, the materials may suffer from high grain boundary (g.b.) resistances.27 For the softer sulfides the difference between the bulk and g.b. conductivities28 is expected to be much lower. Of course, Li-bearing sulfides or thiophosphates are sensitive to air and moisture, thus requiring careful handling and adequate processing. As an example, the Ge-containing thiophosphate Li10GeP2S12 (LGPS),13 which initiated the renaissance to consider sulfide-based systems as candidates for solid electrolytes, is characterised by an ionic conductivity of 12 mS cm−1. Meanwhile the expensive element Ge has been replaced by cheaper and naturally abundant materials.29 The electrochemical stability of LGPS-based systems needs, however, to be improved.30
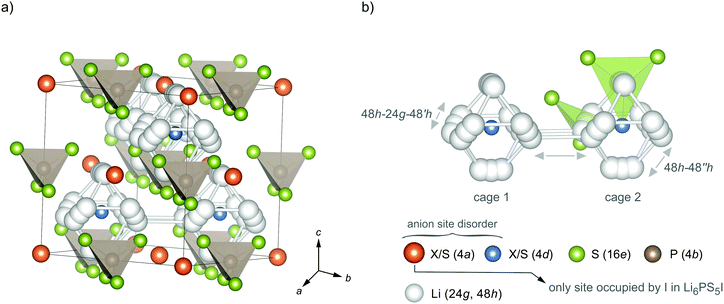
Besides LGPS, Deiseroth and co-workers introduced Li-containing argyrodite-type Li6PS5X (X = Cl, Br, I).31 The crystal structure is shown in Fig. 1; the possible Li exchange processes are illustrated as well. As an example, the ionic conductivity of Li6PS5Br and Li6PS5Cl is reported to range from 10−3 S cm−1 to 10−2 S cm−1 depending on the preparation technique, which influences the type and number of defects as well as the overall morphology.32,33 Thus, the ionic conductivity of Li-argyrodites is only slightly smaller than that of the LGPS family. Lower costs make this family of electrolytes highly attractive for application in all-solid-state batteries.31,34
In 2008 Deiseroth et al. reported the solid-state synthesis of Li6PS5X (X = Cl, Br, I) and characterised the local and long-range structure by X-ray diffraction and NMR.31 Three years later Rao et al. discussed the synthesis of the lithium argyrodite via ball milling.35 Rayavarapu et al. showed that the disorder in both the lithium distribution over the available cation sites and the disorder in the S2−/Cl− and S2−/Br− sublattices promotes lithium ion conductivity.36 This view has further been supported by bond-valence calculations.37
Over the last years a number of studies have been carried out to measure the ionic conductivities of the Li6PS5X family by using standard impedance measurements.31–40 The overall goal, not only for Li6PS5X, is to relate macroscopic application relevant properties to crystal chemical and morphological properties. So far, the results reported have rarely been related to the length-scale specific properties of the measuring technique applied. The ionic conductivities for Li6PS5X vary from 10−7 S cm−1 to 10−2 S cm−1, while the highest values are found for X = Cl, Br. The corresponding activation energies reported, either experimentally probed or calculated, take values from 0.11 eV to 0.57 eV.31–40 Astonishingly, the I-compound Li6PS5I shows the lowest conductivity. According to the strategy of substitutional disorder, size mismatch and polarizability of the halogen anion one could have expected the opposite trend. Replacing S by a larger and more polarizable anion such as I, as compared to the small and unpolarizable Li cation, is expected to cause lattice distortions which on their part lead to a broader distribution of slightly inequivalent Li sites in the Li sublattice. Without any strong site preference of the Li ions they are expected to jump quickly between the local minima of such a heterogeneous, i.e., non-uniformly shaped, potential landscape. Such a situation, sometimes also connected to geometric frustration, is very similar to F diffusion in the recently investigated system (Ba,Ca)F2,41,42 Li diffusion in Li7La3Zr2O12 oxides43 and Na diffusion in some closo-borates.44 While this situation might be the origin for the high conductivity in Li6PS5Br and Li6PS5Cl, for the I analogue it seems to incompletely describe the real situation as for Li6PS5I relatively low ion conductivities are reported.
In an elegant way, Kraft et al.34 tried to establish a connection between the stiffness (or polarizability) of the anion sublattice in Li6PS5X and the macroscopic ionic transport properties. They used impedance spectroscopy and ultrasonic speed of sound measurements to collect information on activation energies and the pre-factors governing the underlying Arrhenius equation. They reported that soft lattices, as is the case for Li6PS5I, lead to smaller Arrhenius pre-factors than obtained for Li6PS5Cl and Li6PS5Br. This decrease in pre-factor, which might originate from a change of the migration entropy or attempt frequencies, has been used to explain the low (overall) ion conductivity in Li6PS5I.
Here, we employed impedance and NMR spectroscopy to shed more light on the effect seen for Li6PS5I. The important structural differences between the three argyrodites have to be taken into account to explain the significant changes in ionic conductivities, pre-factors and activation energies. For this purpose we have not only looked at the monosubstituted compounds like Li6PS5X, but also at samples with two or three different anions such as Li6PS5Cl0.5Br0.5 or Li6PS5Cl1/3Br1/3I1/3. The non-substituted compound Li7PS6 served as a reference material. Importantly, complementary techniques which are sensitive to ion dynamics on different length-scales and time-scales are used to fully characterise the transport properties. We will show that, on a short-range length scale, the Li ions in Li6PS5I are as rapid as in the Br and Cl analogues. Obviously, the ordered S2−/I− sublattice, as compared to the disordered situation for Li6PS5Cl and Li6PS5Br, is responsible for a more regular potential landscape with a higher degree of site preference for the Li ions. As a consequence, we assume that intercage jump processes in Li6PS5I occur less frequently. These processes are, however, needed to establish rapid long-range ion dynamics in the iodide.
2 Experimental
2.1 Sample preparation through a solid state reaction
The Li argyrodites Li6PS5X, with the compositions shown in Fig. 2b, have been prepared by mixing stoichiometric amounts of Li2S (Sigma-Aldrich ≥99.98%), P2S5 (Honeywell Fluka ≤99%) and LiCl (Sigma-Aldrich, anhydrous, 99%), LiBr (Sigma-Aldrich, anhydrous, 99.98%) and LiI (Sigma-Aldrich, 99.9%). The starting compounds were mechanically milled using a high-energy planetary ball mill (Fritsch Pulverisette 7 Premium line) at a rotation speed of 400 rpm for 4 hours (15 min milling; 15 min pause). Milling was carried out using ZrO2 beakers (45 ml) filled with 180 balls (ZrO2, 5 mm in diameter). Afterwards the mixtures were uniaxially pressed (0.4 tons) into pellets with a diameter of 5 mm, filled into quartz ampoules and sealed under a vacuum. The ampules were preheated at 573 K under a dynamic vacuum to remove traces of water. The reaction was carried out at 823 K (heating rate: 5 K min−1, duration 7 days; cooling rate 10 K min−1). All preparation steps were strictly carried out in an Ar gas atmosphere (H2O < 1 ppm, O2 < 1 ppm).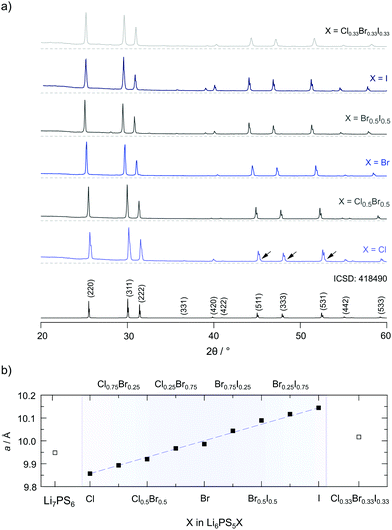 | ||
| Fig. 2 (a) X-ray powder diffraction patterns of the Li6PS5X series investigated within this study (X = Cl, Cl0.5Br0.5, Br, Br0.5I0.5, I and Cl0.33Br0.33I0.33). The XRPD patterns were recorded after the final annealing step at room temperature. In some cases, little, almost negligible, amounts of Li3PO4 and LiX are visible; the amount of LiX does not exceed 1.5 wt%. Only for Li6PS5Cl ca. 3.3 wt% Li3PO4 is seen, see the arrows; in all other cases its amount is negligible or less than 1.5 wt%, see the ESI† for Rietveld refinements (Fig. S1 and S2). (b) Lattice parameter of Li6PS5X obtained from Rietveld refinements of the patterns shown in (a). The lattice parameter increases continuously with the radius of X. | ||
2.2 X-ray powder diffraction (XRPD)
The samples were analyzed by X-ray diffraction using a Bruker D8 Advance diffractometer (Bragg Brentano geometry, Cu Kα radiation). The patterns, shown in Fig. 2, were recorded with a step size of 0.02° (measuring time 2 s) in the 2θ-range 20° to 100°. Rietveld refinement, see Fig. 3 and the ESI† (Fig. S1 and S2), was carried out by using X'PertHighScorePlus (Panalytical).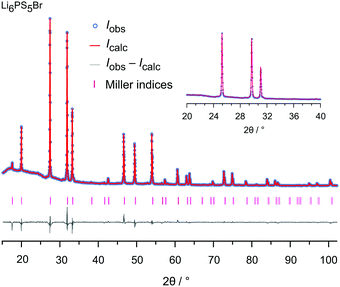 | ||
| Fig. 3 Rietveld analysis of the XRPD pattern of Li6PS5Br recorded at 293 K (RBragg = 4.633%). In this plot the Bragg positions as well as calculated and observed profiles are depicted. The analysis reveals a phase pure sample. The Rw profile is 10.84% and the GoF amounts to 4.82; see the ESI† for further explanations. | ||
2.3 Impedance spectroscopy
To measure the impedance responses of the pellets, Au electrodes were applied. We used a LEICA EM SCD 050 sputter coater to equip the samples with a thin Au layer of 100 nm thickness. Impedance spectra were recorded with a Novocontrol Concept 80 broadband dielectric spectrometer; the frequency range covered ranged from ν = 10 mHz to 10 MHz. The temperature T was varied from 173 K to 453 K in steps of 20 K; the temperature in the sample holder was controlled by a QUATRO cryosystem (Novocontrol) that uses freshly evaporated nitrogen and a heater to adjust the temperature with an accuracy of ±0.5 K. The measurements were carried out in a dry nitrogen atmosphere to avoid any contamination with water and oxygen.2.4 7Li static NMR measurements
For the time-domain NMR measurements the samples Li6PS5Cl, Li6PS5Br and Li6PS5I were sealed in Duran© glass tubes (ca. 4 cm in length and 3 mm in diameter). They were kept under a vacuum to protect them from any reaction with humidity or traces of oxygen. We used 7Li NMR line shape measurements and spin–lattice relaxation (SLR) experiments to collect information about Li activation energies and jump rates. Longitudinal NMR SLR rates (1/T1) as well as spin-lock rates (1/T1ρ) were measured by employing a Bruker Avance III spectrometer connected to a shimmed cryomagnet with a nominal magnetic field of 7 T. This field corresponds to a 7Li Larmor frequency of ω0/2π = 116 MHz. For the measurements at temperatures T ranging from 173 K to 433 K a ceramic high-temperature probe (Bruker Biospin) was used. At a power level of 200 W the π/2 pulse length ranged from 2.7 to 3.2 μs slightly depending on temperature. A Eurotherm temperature controller in combination with a type T thermocouple was used to control and to monitor the temperature in the sample chamber. Low temperature measurements down to T = 124 K were performed with a cryo probe (Bruker) that uses freshly evaporated nitrogen to reach temperatures below ambient. The π/2 pulse length of the cryo probe ranged from 3.0 to 4.3 μs at a power level of 95 W. It is equipped with a LakeShore 331 element equipped with two Cernox temperature sensors.7Li NMR SLR rates 1/T1 ≡ R1 in the laboratory frame were acquired with the well-known saturation recovery pulse sequence.45,46 This sequence uses a comb of closely spaced π/2 pulses to destroy any longitudinal magnetization Mz. The subsequent recovery of Mz was detected as a function of waiting time td with a π/2 reading pulse: 10 × π/2 − td − π/2 − acquisition.15 To construct the magnetization transients Mz(td), we plotted the area under the free induction decays (FIDs) vs. td. Up to 16 FIDs were accumulated for each waiting time.
The transients Mz(td) were parameterised with stretched exponentials, Mz(td) ∝ 1 − exp(−(td/T1)γ), to extract the SLR rates R1. Additionally, rotating-frame 7Li NMR SLRρ rates 1/T1ρ ≡ R1 were measured by means of the spin-lock technique: π/2 − plock acquisition. We used a locking frequency ω1/2π of 20 kHz.47,48 The duration tlock of the locking pulse plock was varied between 22 μs and 460 ms. To ensure full longitudinal relaxation between each spin-lock scan the recycle delay was set to at least 5 × T1. Again, the R1ρ rates were obtained by analysing the resulting transients Mρ(tlock) with stretched exponentials of the form Mρ(tlock) ∝ exp(−(tlock/T1ρ)κ). While the stretching exponents γ varied from 1 to 0.9, the exponents κ range from 0.4 to 1, depending on the temperature. Some of the T1ρ transients showed bi-exponential behaviour and were analyzed with a sum of two stretched exponential functions.
2.5 Magic angle spinning (MAS) NMR
6Li (73.6 MHz), 31P (202.4 MHz), 127I (100.1 MHz), 79Br (125.3 MHz) and 35Cl (49.0 MHz) NMR spectra under magic angle spinning (MAS) conditions were recorded with a 500 MHz Avance spectrometer (Bruker). The high-resolution MAS NMR spectra were measured at a rotation speed of 25 kHz using 2.5 mm rotors with an ambient bearing gas temperature. Spectra were recorded with a single pulse sequence. We accumulated up to 128 scans for one spectrum. LiCl, KBr, LiI and 85% H3PO4 served as ref. 31 to determine chemical shifts δiso. In order to detect also very slow diffusion processes and to obtain quantitative MAS NMR spectra we varied the recycle delay from 1 s to 180 s. Sufficiently long relaxation delays guarantee full longitudinal relaxation of all spectral components. Further information on pulse lengths, temperature effects and delay times are given in the ESI,† see Table S1.3 Results and characterization
3.1 Sample characterization by X-ray powder diffraction
To study the ion dynamics in argyrodite-type Li6PS5X we used a solid-state synthesis approach to prepare samples with the following compositions: X = Cl, Cl0.75Br0.25, Cl0.5Br0.5, Cl0.25Br0.75, Br, Br0.75I0.25, Br0.5I0.5, Br0.25I0.75, I and X = Cl0.33Br0.33I0.33, respectively. Through replacing S2− with X− we change the average lattice constant of the crystal structure, the polarisability of the anion lattice and the degree of anion disorder. The relative density of our samples, estimated from the sintered pellets used for impedance spectroscopy, reached values ranging from 92% to 98%. Argyrodite-type Li6PS5X is expected to crystallise with cubic F4![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m face centered (fc) symmetry; the crystal structure is depicted in Fig. 1.
m face centered (fc) symmetry; the crystal structure is depicted in Fig. 1.
In Fig. 2a the XRPD patterns of all samples are shown including a reference pattern taken from the literature (entry no. 418490 in the inorganic crystal structure database (ICSD)). The positions and intensities of the reflections obtained for the different patterns of Li6PS5X including Li7PS6 match very well with what is expected from the literature. Humps at low diffraction angles originate from the mercapto foil used to protect the samples from reaction with air during the measurements.
To characterise the samples in detail, Rietveld refinements were carried out. As an example, the result of the analysis is shown for Li6PS5Br in Fig. 3. The Li6PS5Br sample is phase pure and crystallises with cubic symmetry (space group F4![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m); the lattice parameter turned out to be a = 9.986 Å. The same symmetry is found for the other samples; the amount of side phases or impurities turned out to be extremely low, see the ESI.† When going from Li6PS5Cl to Li6PS5I the lattice parameter a increases from a = 9.857 Å to a = 10.145 Å. Lattice expansion of the unit cell is expected because the radius r of the anion increases in the order rCl < rBr < rI. Here, an increasing unit cell volume stabilises the lithium ions in the transition state 24g; the change in lattice constant a seems to also affect the Li occupancies in the Li6PS5X series as has been shown by neutron diffraction.34
m); the lattice parameter turned out to be a = 9.986 Å. The same symmetry is found for the other samples; the amount of side phases or impurities turned out to be extremely low, see the ESI.† When going from Li6PS5Cl to Li6PS5I the lattice parameter a increases from a = 9.857 Å to a = 10.145 Å. Lattice expansion of the unit cell is expected because the radius r of the anion increases in the order rCl < rBr < rI. Here, an increasing unit cell volume stabilises the lithium ions in the transition state 24g; the change in lattice constant a seems to also affect the Li occupancies in the Li6PS5X series as has been shown by neutron diffraction.34
Recent neutron and X-ray synchrotron diffraction studies have shown that in fc cubic argyrodite-type Li6PS5Cl and Li6PS5Br the S2− and X anions can occupy three different crystallographic positions. Whereas the 16e site is fully occupied by S2− anions, the sites 4a and 4d are shared by the S2− and X anions. For Li6PS5Cl Kraft et al. found that 38.5% of the 4a site and 61.5% of the 4d site is occupied by Cl−.34 The rest is filled by S2− anions; Li+ only occupies the 48h sites. For Li6PS5Br Rietveld analysis yielded occupancies of 77.9% (4a) and 22.1% (4d) with Li+ distributed over the 48h (44.1%) and 24g (11.9%) sites. Thus, the highest degree of anion disorder is found for Li6PS5Cl, while cation disorder for the samples rich in Br. This finding is in contrast to what Rietveld refinement resulted in for Li6PS5I. While Li disorder is also present for the split-site (48h (39.1%) and 24g (21.9%)), in Li6PS5I the I anions solely occupy the 4a sites. The 4d sites are fully occupied by S2−. Deiseroth and co-workers also reported on the same order/disorder effects earlier.31,40,49
The larger difference in ionic radii between I− and S2− (rI− = 216 pm vs. rS2− = 184 pm, as compared to rCl− = 181 pm and rBr− = 195 pm) might lead to this site preference for the anions. The anion sublattice in Li6PS5I is, thus, structurally ordered as compared to Li6PS5Cl (and Li6PS5Br); simultaneously, cation disorder shows up for Li6PS5Br and Li6PS5I.36,37,50 The compounds with mixed halogen compositions agree well with the trend in S2−/X occupancy and cation disorder.34 As will be discussed below, anion ordering seems to have an important impact on long-range ion diffusion in the I compound.
The 24g site represents an intermediate state used by the Li ions on 48h to diffuse through. As a result of these two lithium positions three different jump processes can occur; they are explicitly shown in Fig. 1b. (i) A strongly localised process is given by 48h–24h–48h′ jumps. Intracage jumps are possible within the octahedral cage when the Li ions jump between the 48h sites: (ii) 48h–48h′′. (iii) Long-range ion dynamics needs 48h1–48h2 intercage jump processes between two different cages 1 and 2. The latter jump process is expected to be strongly affected by the anion site disorder of X and S2−. We expect that a high degree of substitutional disorder will have a significant impact on the associated jump rate, which characterises exchange processes between the cages.
3.2 Magic angle spinning NMR
To investigate local structures of the argyrodites, we recorded 31P (spin-quantum number I = 1/2) MAS NMR spectra of Li6PS5X (X = Cl, Br, I) at a spinning speed of 25 kHz. The spectra are shown in Fig. 4a. In line with the report of Deiseroth and co-workers,31 the 31P MAS NMR resonance of Li6PS5I shows a very sharp line centered at δiso = 96.3 ppm pointing to an ordered anion framework with the I anions non-randomly occupying selected crystal sites. Small shoulders near the main signal might point to defect sites in Li6PS5I.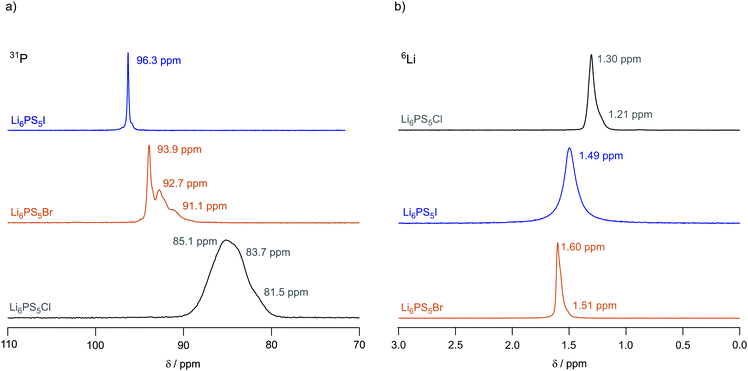 | ||
| Fig. 4 (a) 31P MAS NMR spectra of Li6PS5I, Li6PS5Br and Li6PS5Cl recorded at 202.4 MHz and a spinning frequency of 25 kHz. The spectra have been referenced to 85% H3PO4 and were recorded at an ambient bearing gas temperature.31 (b) 6Li MAS NMR spectra of Li6PS5Cl, Li6PS5Br and Li6PS5I recorded at 73.6 MHz and a spinning speed of 25 kHz. All spectra have been referenced to solid LiCH3COO. Values given in ppm indicate the isotropic chemical shifts. | ||
The 31P MAS NMR spectrum of Li6PS5I is in stark contrast to the situation that is met for Li6PS5Cl, for which we expect the influence of strong S/Cl disorder on the line shape, see above. Indeed, its very broad line, which can hardly be resolved, reveals a wide distribution of chemical shifts and strong spin–spin interactions. Chemical shifts of lines constituting the overall line range from 85 to 81 ppm. Therefore, 31P MAS NMR clearly reveals anion disorder in Li6PS5Cl. The 31P MAS NMR line of Li6PS5Br takes an intermediate position. It is composed of narrower lines than those seen for Li6PS5Cl; nevertheless, line broadening, as compared to Li6PS5I, reveals disorder in the S/Br sublattice. At least the spectrum is composed of three distinct lines located at 93.9 ppm, 92.7 ppm and 91.1 ppm, respectively. The same increase in substitutional disorder might be seen if we consider the corresponding 127I, 79Br and 35Cl MAS NMR spectra of the three compounds; the corresponding spectra of the three quadrupole nuclei are shown in the ESI,† Fig. S3. Clearly, because of the large quadrupole moment of I (|Q(127I)| = 0.721b) the full spectrum including its spinning side bands is rather broad. The isotropic signal, however, is much smaller than that for Li6PS5Cl and Li6PS5Br with |Q(35Cl)| = 0.855b and |Q(79Cl)| = 0.330b. Although exposed to less second order quadrupole effects, the line of Li6PS5Cl is as broad as that of the Br compound. Site disorder in Li6PS5Cl might explain this additional broadening.
The ordered anion framework seen for Li6PS5I by 31P MAS NMR, synchrotron X-ray diffraction and neutron diffraction34 is fully consistent with results from 7Li SLR NMR on the ion dynamics in the I compound. As we will show and discuss below, an almost symmetric diffusion-induced 7Li NMR rate peak describes longitudinal spin–lattice relaxation in Li6PS5I; Li+ disorder on the split-site does not influence this symmetry. This observation mainly points to the absence of pronounced site disorder in the anion sublattice. Structural anion disorder is, thus, expected to have a significant impact on both the Li ion diffusion and ionic conductivity in Li6PS5X.
For the sake of completeness, we also recorded 6Li (I = 1) MAS NMR spectra at an ambient bearing gas temperature, these spectra are shown in Fig. 4b. They have been referenced to LiCH3COO. For Li6PS5Br and Li6PS5Cl we observe a slightly asymmetric line with chemical shifts of δiso = 1.6 ppm and δiso = 1.3 ppm, respectively. The line of Li6PS5I turned out to be more symmetric in shape and is broader than the other lines. As Li6PS5Br and Li6PS5Cl show rapid Li ion long-range translational dynamics their lines represent already coalesced spectra at the measurement temperature of 307 K, see the ESI.† This observation is in perfect agreement with 7Li NMR motional line narrowing (see below), which has reached its extreme limit already well below ambient temperature.
In contrast, complete line narrowing of the static 7Li NMR line of Li6PS5I is shifted toward much higher temperature, revealing significantly slower long-range ion dynamics (vide infra). In addition, the absence of effective Li ion dynamics in Li6PS5I, which would be able to also average (small) second order quadrupolar interactions that the spin-1 nucleus 6Li is exposed to, might further increase the width of the NMR line of Li6PS5I as compared to the samples with X = Cl or Br. The increased anisotropy seen for Li6PS5Cl is in line with the degree of site disorder in Li6PS5Cl and Li6PS5Br.
Interestingly, according to the halogen anion introduced into the argyrodite struture the isotropic chemical shift values δiso of the 6Li MAS NMR spectra increase from Li6PS5Br to Li6PS5I and further to Li6PS5Cl. Thus, the paramagnetic component of the NMR line decreases; obviously, the different halogen anions change the electron density distribution in the direct neighborhood of the Li spins with Li6PS5Br having the highest density.
3.3 Ion dynamics as seen by conductivity spectroscopy
We used broadband impedance spectroscopy51–53 covering frequencies from the mHz to the MHz region to study the ion dynamics in Li6PS5X to see the change in the overall ionic transport properties with the X substitution. As an example, in Fig. 5a the real part σ′ of the complex conductivity![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e111.gif) of Li6PS5Br is plotted vs. the frequency ν.
of Li6PS5Br is plotted vs. the frequency ν.
At low frequencies and high temperatures T the isotherms σ′(ν) reveal electrode polarization, which results from the accumulation of ions at the surface of the ion blocking electrodes applied.52–54 Towards higher frequencies or at sufficiently low T, distinct direct current (DC) plateaus show up, which reflect long-range ion transport. The corresponding σDC value is governed by both bulk and grain boundary contributions. For the bromide sample, Li6PS5Br, log10(σDC)T follows Arrhenius behaviour
σDCT = σ0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−Ea,DC/(kBT)) exp(−Ea,DC/(kBT)) | (1) |
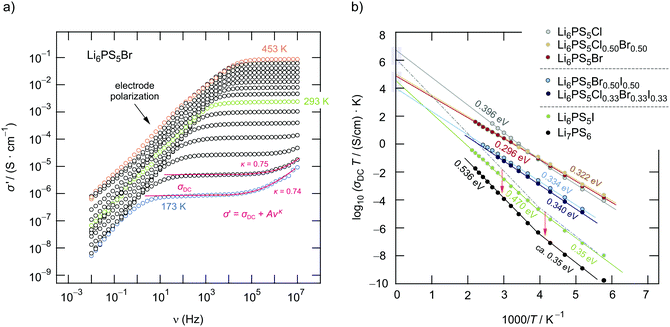
For comparison, in Fig. 5b the temperature dependence of log10(σDC)T of the other samples is presented. Li6PS5I and Li7PS6 are characterised by the lowest conductivities and the highest activation energies Ea,DC of 0.47 eV and 0.37 eV. At approximately 250 K we notice a slight deviation from the Arrhenius line determining log10(σDC)T at higher T. This behaviour cannot be related to the phase transition of Li6PS5I;31,39,40,49 the I compound transforms into a low-T phase at T ≈ 160 K, see below. Such a slight deviation is also seen for Li6PS5Cl.
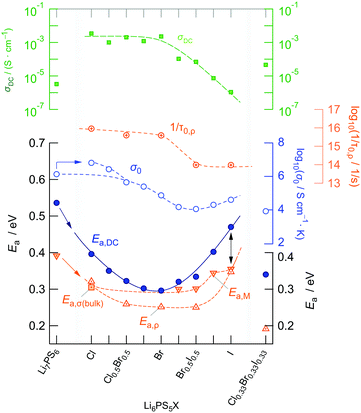
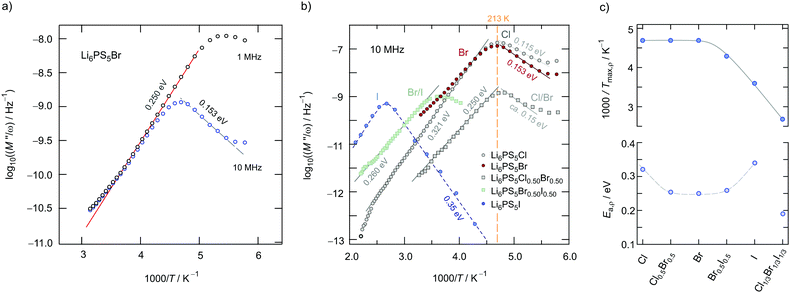
In Fig. 6a the changes in activation energies, ionic conductivities and Arrhenius pre-factors (σ0, see eqn (1)) are illustrated. In all cases, the replacement of sulfur anions in Li7PS6 by heavier halide anions leads to a decrease in activation energies. Except for Li6PS5Cl and Li6PS5Cl0.75Br0.25 the Arrhenius pre-factor σ0 also decreases. This feature, which is seen when Li6PS5Br is compared with Li7PS6 (or Li6PS5Cl), has been interpreted in terms of the Meyer–Neldel56 rule and related to a reduction in Debye frequencies for soft lattices created by substitution of Br and I for S.34 If we compare our results for Li6PS5Cl with respect to the conductivity behaviour of Li7PS6 we witness both a decrease in Ea,DC from 0.536 eV to 0.396 eV and an increase in σ0 by one order of magnitude. This favorable combination of Ea,DC and σ0 results in a room temperature ionic conductivity of σDC = 3.8 mS cm−1. For Li6PS5Br, with its more polarisable anions on the other hand, the low activation energy is compensated by a pre-factor two orders of magnitude lower than that for Li6PS5Cl. Considering high temperatures this feature causes σDC to adopt values lower than those of Li6PS5Cl.
Interestingly, the ionic conductivity of ordered Li6PS5I is even lower than that of the non-substituted compound Li7PS6; this decrease, despite the higher activation energy found for Li7PS6, can also be explained by the relatively low value for σ0. The pre-factor is proportional to the attempt frequencies νa, the number of effective charge carriers nLi and an entropy term.42 Besides the effect of νa, trapping effects in Li6PS5I, because of a very low intercage jump rate, might reduce N for this sample. If we assume similar νa values for Li6PS5Cl and Li6PS5Br, entropy effects could serve as an explanation for the change in σ0. Especially for the highly disordered Li6PS5Cl sample50 the migration entropy might take a decisive role in influencing the ion dynamics. For the ordered Li6PS5I compound this contribution might be absent.
When going from Li6PS5Br to Li6PS5I we see that, despite the introduction of polarisable iodine anions, the pre-factor remains almost the same, A = log(σ0/(S cm−1 K)) = 4.9 for Li6PS5Br and A = 4.6 for Li6PS5I, but Ea,DC increases from 0.296 eV to 0.47 eV. From this point of view, although the lattice gets softer in the case of I, Kraft et al. mentioned34 that Meyer Neldel seems to be not fully applicable to describe the situation in Li6PS5I. One could have expected the more polarisable I anions to allow the Li ions to squeeze through smaller voids.50 Obviously, this concept does not work for Li6PS5Br and Li6PS5I, at least if we regard the (overall) averaged long-range ion transport process as probed by σDC measurements.
The ionic conductivities of the mixed compounds containing I anions, viz. Li6PS5Br0.5I0.5 and Li6PS5Cl1/3Br1/3I1/3, do not vary much. Obviously, the introduction of I plays the crucial role to lower σDC. The Cl anions do not affect the ionic transport in these high-entropy compounds in a positive way, at least for compounds containing two anions greatly differing in ionic radius (181 pm vs. 216 pm). To take a closer look at the exceptional behaviour of Li6PS5Cl with its high degree of anion disorder we tried to separate the bulk and grain boundary contributions of this sample. Moreover, we used complex resistivity measurements to further characterise the ion dynamics.
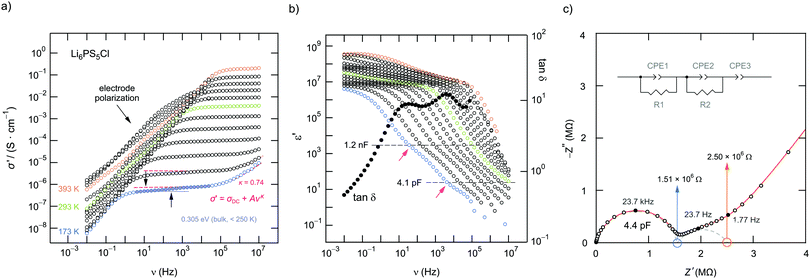
The σ′(ν) isotherms of Li6PS5Cl are shown in Fig. 7a. A careful look at the DC plateau region shows that it contains a small step. Thus, it is composed of actually two plateaus. Below 250 K, the corresponding activation energies turned out to be 0.310 eV and 0.305 eV, see Fig. 7b. The two-step behaviour of the σ′(ν) isotherms of Li6PS5Cl are also seen if we plot the real part ε′ of the complex permittivity vs. ν (Fig. 7b). We used the equation for a parallel-plate capacitor to estimate the corresponding capacitance C of the two steps:
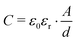 | (2) |
For comparison, the two contributions in the electrical relaxation of Li6PS5Cl are also seen in the loss factor tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ = ε′′/ε′ when plotted as a function of frequency ν (see also Fig. 7b). The maxima in tan
δ = ε′′/ε′ when plotted as a function of frequency ν (see also Fig. 7b). The maxima in tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ, showing up at 15.36 Hz (g.b.) and 4.21 kHz (bulk), correspond to the plateaus or inflection points of ε′ν, see also Fig. 8. According to
δ, showing up at 15.36 Hz (g.b.) and 4.21 kHz (bulk), correspond to the plateaus or inflection points of ε′ν, see also Fig. 8. According to ![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e111.gif) = iωε0
= iωε0![[small epsilon, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e107.gif) = iωε0ε′ + ωε0ε′′ the maxima in tan
= iωε0ε′ + ωε0ε′′ the maxima in tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ produce two minima if the frequency dependence of the imaginary part σ′′(∝ε′) is analyzed (Fig. 8).
δ produce two minima if the frequency dependence of the imaginary part σ′′(∝ε′) is analyzed (Fig. 8).
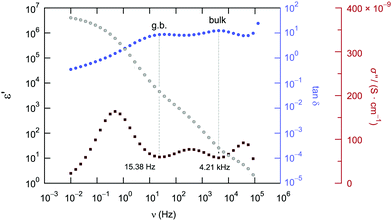 | ||
Fig. 8 Comparison of the frequency dependence of tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ, ε′ and σ′′ of Li6PS5Cl measured at 173 K. Plateaus (or inflection points) in ε′ result in minima in σ′′ and maxima in tan δ, ε′ and σ′′ of Li6PS5Cl measured at 173 K. Plateaus (or inflection points) in ε′ result in minima in σ′′ and maxima in tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ, respectively. δ, respectively. | ||
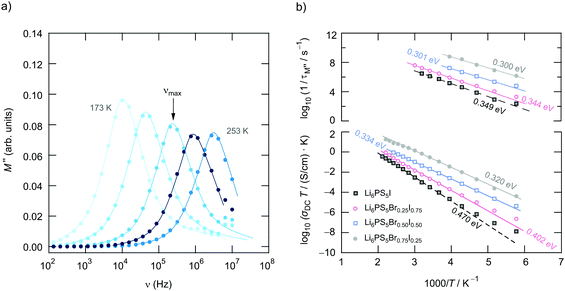
To further characterise ion hopping in Li6PS5X, especially if we consider samples with lower conductivity than Li6PS5Cl and Li6PS5Br, we used the electric modulus representation58,59 to take a look at electrical relaxation frequencies τM′′−1 = νmax. As an example, in Fig. 9 for Li6PS5Br0.5I0.5 the imaginary part M′′ of the complex modulus is plotted vs. ν. Since the amplitude of M′′ is proportional to 1/C, bulk processes are mainly seen. For samples with very high conductivities, such as Li6PS5Cl, the peaks are shifted to too high frequencies and are, thus, no longer fully visible. Activation energies Ea,M′′ from our M′′(ν) analysis are also included in Fig. 6. For comparison, the bulk activation energy deduced from Fig. 7 is included, too. They reveal that the activation energies, which we ascribe to bulk properties, do not change much if we consider compounds up to the composition Li6PS5Br0.5I0.5. This behaviour changes if we increase the I concentration. Importantly, for the compounds rich in I, especially if we consider Li6PS5I, the observation Ea,M′′ < Ea,DC suggests that the charge carrier concentration increases with temperature. For Li6PS5I the difference Ea,DC − Ea,M′′ turned out to be relatively high, viz. 0.121 eV (see the vertical arrow in Fig. 6).
Additionally, after we took a look at the overall and bulk ion dynamics in Li6PS5X we used complex resistivity measurements, ![[small rho, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b7.gif) = 1/
= 1/![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e111.gif) =
= ![[M with combining circumflex]](https://www.rsc.org/images/entities/i_char_004d_0302.gif) /(iωε0), carried out at constant frequency but varying temperature, to answer the question of how the bulk ion dynamics depends on the time-scale and length-scale that the technique applied is sensitive to. In Fig. 10a the temperature dependence of the real part ρ′ = M′′/ω of the complex resistivity
/(iωε0), carried out at constant frequency but varying temperature, to answer the question of how the bulk ion dynamics depends on the time-scale and length-scale that the technique applied is sensitive to. In Fig. 10a the temperature dependence of the real part ρ′ = M′′/ω of the complex resistivity ![[small rho, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b7.gif) is shown for Li6PS5Br. The peaks in Fig. 10a have been recorded for two different frequencies viz. 1 MHz and 10 MHz.
is shown for Li6PS5Br. The peaks in Fig. 10a have been recorded for two different frequencies viz. 1 MHz and 10 MHz.
ρ′ is given by a Lorentzian-shaped function containing the electrical relaxation time τρ:60
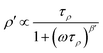 | (3) |
We cannot see any strong variation in Ea,ρ when comparing the response of Li6PS5Br0.5I0.5 with that of Li6PS5Br. Ea,ρ values have also been included in Fig. 6; for the sake of clarity, they are separately shown in Fig. 10c. Obviously, a lower pre-factor of the underlying Arrhenius relation is responsible for this shift. The same effect is seen for Li6PS5I. Although the lattice is expected to be much softer in the case of Li6PS5I as compared to the situation in Li6PS5Cl, ρ(ω) tells us that the activation energies Ea,ρ of the two compounds are very similar (0.32 eV vs. 0.35 eV). However, the peak ρ′(ω) of Li6PS5I is clearly shifted toward higher T and shows up at 385 K; the origin of this difference has to be looked for in the bulk ion dynamics, g.b. resistances cannot explain it. As compared to the peak of Li6PS5Cl the peak of the I compound is symmetric in shape (β ≈ 1.95) and points to an ordered structure.
Obviously, as in the case of Ea,DC the reason for the lower conductivity and, thus, the slower bulk electrical relaxation in Li6PS5I (and in Li6PS5Br0.5I0.5) has been looked for in the prefactor of the underlying Arrhenius relationships. Most likely, the anion site disorder in Li6PS5Cl is responsible for this behaviour. Indeed, if we approximate the ρ′(ν) peaks with eqn (3) we can extract pre-factor τ0,ρ−1 assuming τρ−1 to be depending on temperature according to Arrhenius. τ0,ρ−1 values are also included in Fig. 6; indeed, they clearly reveal lower pre-factors for Li6PS5I by approximately two orders of magnitude. If we assume that the attempt frequencies are similar for Li6PS5Cl and Li6PS5I a significant change in migration entropy, as mentioned above, might explain the prominent change seen. To check whether this phenomenon is also apparent in SLR NMR, which is in general sensitive to both short-range and long-range ion dynamics, we carried out 7Li NMR measurements in both the laboratory and rotating-frame of reference.64,65 Line shape measurements carried out at temperatures down to the cryogenic region complement our investigation.
3.4 7Li NMR relaxometry to probe the bulk ion dynamics
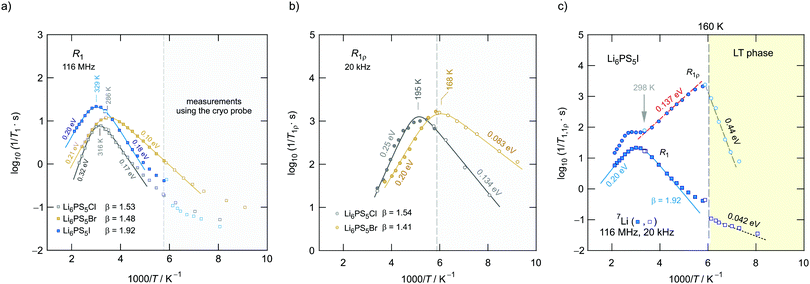
In Fig. 11 an overview of the 7Li NMR spin–lattice relaxation rates 1/T1 ≡ R1 and 1/T1ρ ≡ R1ρ measured over a wide temperature range is given. To identify the thermally activated regions the rates of Li6PS5X, with X = Cl, Br, and I, were plotted using an Arrhenius representation, i.e., log(1/T1) is plotted vs. 1000/T. The rates have been recorded at a Larmor frequency of ω0/2π = 116 MHz; for the locking frequency we used a magnetic B1 field corresponding to ω1/2π = 20 kHz. At very low temperatures (T < 160 K) the R1 rates shown in Fig. 11a reveal a non-diffusive background; in this T range longitudinal relaxation is primarily induced by lattice vibrations or coupling of the Li spins (I = 3/2) with paramagnetic impurities.61,65–67At higher T we expect spin–lattice relaxation to be increasingly induced by Li self-diffusion.61 Indeed, the rates sharply increase with temperature and characteristic diffusion-induced rate peaks show up. We recognise that R1 passes through well-defined maxima as has been found by some of us in an earlier study on the ion dynamics in Li6PS5Br.15 At the temperature Tmax, where R1 reaches its maximum value, the motional correlation rate 1/τc is given by τcω0 ≈ 1. 1/τc is identical within a factor of two to the Li jump rate 1/τ.61,65 The same holds for R1ρ, for which the maximum condition is ω1τ ≈ 0.5.61,65 As ω0 and ω1 differ by more than three orders of magnitude, the SLR NMR experiments, when taken together, are able to sense motional processes covering a large time scale.67,68
We notice that the rate peak of Li6PS5Br shows up at Tmax = 286 K. The peak is asymmetric and we used a Lorentzian-type (BPP-type)62,69 spectral density function J(ω0) ∝ R1 of the form70
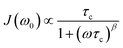 | (4) |
Here, the analysis of the rate peak of Li6PS5Br with eqn (4) yields an activation energy Ea,NMR of 0.213 eV, which is in perfect agreement with earlier findings for this compound.15,50 As mentioned above, the parameter β describes the deviation from symmetric behaviour (β = 2). β turned out to be β ≈ 1.5,65 which gives rise to a much lower activation energy Ea,low on the low-T side of the peak. In this regime, characterised by τcω0 ≪ 1, short-range or localised ion dynamics in double-well potentials, including also highly correlated forward–backward jumps, are sensed by R1.61 The activation energy of the low-T flank is given by 0.10 eV, which is in very good agreement with that seen by ρ′(ω). Localised intracage jump processes involving the 48h and 24g sites in Li6PS5Br could be mainly responsible for spin–lattice relaxation in this region, as has been precisely calculated (0.11 eV) by De Klerk et al.50 The higher activation energy Ea,high(=Ea,NMR) seen in the limit τcω0 ≪ 1 might, however, additionally be affected by 48h–48h jumps. Usually in this regime, in which many jump processes occur during one Larmor precession of the spin, Ea,NMR should be comparable with Ea,DC (0.296 eV) or Ea,ρ (0.250 eV).61Ea,DC could be influenced by g.b. effects; here, Ea,NMR < Ea,ρ shows that the number of jump events sensed by NMR, which should not necessarily include all types of jumps needed for long-range diffusion, is sufficient to generate a full R1 peak.
A very similar behaviour is found for Li6PS5Cl. The corresponding rate peak is shifted toward higher temperature revealing that faster ion dynamics is present in Li6PS5Br. In agreement with conductivity spectroscopy and our ρ′(ω) analysis, for Li6PS5Cl higher activation energies (Ea,high = 0.32 eV, Ea,low = 0.17 eV) than those seen for the Br analogue were found. Although Ea,high = 0.32 eV perfectly agrees with Ea,ρ, see Fig. 10, and calculated values,35 it is higher than expected from R1ρ NMR in the limit τcω1 ≪ 1 (0.248 eV). Furthermore, the shapes of the R1(1/T) peaks of the two compounds are very similar. Obviously, similar (local) jump processes influence the NMR rates. In Table 1 an overview of the parameters is given obtained from the analysis with individual BBP-type spectral densities for each peak.
| Li6PS5Cla | Li6PS5Bra | Li6PS5Ib | |
|---|---|---|---|
| a The best R1ρ fit is obtained if we replace ω1/2π = 20 kHz by a slightly higher effective locking frequency ωeff that also takes into account local magnetic fields. For Li6PS5Cl several runs of the global fit procedure yields ωeff = 1.68 × ω1; for Li6PS5Br ωeff is given by ωeff = 1.41 × ω1. b Li6PS5I undergoes a phase transition at 160 K; thus, no βρ can be observed. The symmetric rate peak (β ≈ 2) agrees with the ordered anion sublattice as suggested by XRPD, see above. | |||
| β | 1.53(2) | 1.48(2) | 1.92(1) |
| E a | 0.320(1) eV | 0.213(1) eV | 0.198(1) eV |
| E a,low | 0.170(4) eV | 0.102(5) eV | 0.182(5) eV |
| τ 0 | 1.3(5) × 10−14 s | 2.3(5) × 10−13 s | 8.2(5) × 10−13 s |
| β ρ | 1.54 | 1.41 | — |
| E a,ρ | 0.248(9) eV | 0.201(9) eV | 0.137(3) eV |
| E a,low | 0.134(1) eV | 0.083(1) eV | — |
| τ 0,ρ | 9.5(5) × 10−13 s | 3.3(1) × 10−12 s | — |
Exactly the same trend is seen when we look at the R1ρ(1/T) peaks of the two compounds, which are shown in Fig. 11b. These have been, independently of the R1 experiments, also parameterised with Lorentzian-shaped spectral density functions. The activation energies of the peak of Li6PS5Br (0.201 eV, 0.083 eV) match with those reported earlier15 also including calculated values.50 They also agree with those from the R1 peak. Here, R1ρ(1/T) of Li6PS5Br turned out to be much smaller that that reported by Yu et al.;77 most likely, the difference has to be looked for in the preparation conditions such as milling steps and annealing procedures.
In Fig. 12 so-called joint fits65 of the two types of NMR experiments, R1 and R1ρ, are shown. For the joint fits the parameters Ea,NMR and τ0−1, which is the pre-factor of the Arrhenius equation of τc−1, have been linked to each other. The best fit is obtained if we use two independent values for β and if we replace ω1 by effective frequencies ω1,eff, also taking into account local magnetic fields.73 To estimate the latter, we did not fix ω1 and looked at how the quality of the fit changes if it is a free parameter. Only a slight change of ω1 was necessary giving rise to ωeff ≈ 1.5 × ω1. A successful joint fit shows that the same overall diffusion processes govern the peaks R1 and R1ρ. The results of our joint fits are shown in Table 2. The activation energies Ea,NMR (=Ea,high) obtained fulfill the relationship
| Ea,low = (β(ρ) − 1)Ea,high. | (5) |
 | ||
| Fig. 12 Arrhenius plot of the 7Li NMR relaxation rates R1 and R1ρ of (a) Li6PS5Cl and (b) Li6PS5Br measured in the laboratory frame of reference (116 MHz) and in the rotating frame of reference (20 kHz, nominal locking frequency). The solid lines represent the global fit based on a modified BPP model that takes into account peak asymmetries by the parameter β(ρ). The fastest Li diffusion is found for Li6PS5Br with the peak maxima showing up at 286 K and 168 K, respectively. The second R1ρ relaxation process, most likely also influenced by spin–spin relaxation to a certain degree, is indicated, too. As mentioned before (see Fig. 11), the open symbols represent rates that were measured with an NMR probe designed for experiments at cryogenic temperatures; the filled symbols show rates which were acquired with the standard probe. | ||
| E a,NMR | C | β (ρ) | τ 0 | |
|---|---|---|---|---|
| a The best global fits are obtained if we replace ω1 by the effective locking frequencies ωeff = 1.68 × ω1 (Li6PS5Cl) and ωeff = 1.41 × ω1 (Li6PS5Br). The coupling constant C, which is the amplitude of the rate peak, J(ω0) = Cτc/(1 + (ωτc)β), turns out to be on the order of 109 to 1010 s−2. | ||||
| Li6PS5Cl | ||||
| R 1 | 0.273(5) eV | 3.5(5) × 109 s−2 | 1.60(1) | 4.9(4) × 10−14 s |
| R 1ρ | 3.1(5) × 1010 s−2 | 1.47(1) | ||
| Li6PS5Br | ||||
| R 1 | 0.218(1) eV | 5.6(7) × 109 s−2 | 1.48(1) | 2.0(2) × 10−13 s |
| R 1ρ | 3.3(9) × 1010 s−2 | 1.47(1) | ||
| Li6PS5Ia | ||||
| R 1 | 0.198(1) eV | 1.1(4) × 1010 s−2 | 1.92(1) | 8.2(9) ×10−13 s |
| R 1ρ | 0.137(3) eV | — | — | — |
Considering the overall constants C obtained from the joint fits, they reveal that both dipolar and electric quadrupolar interactions govern the diffusion-induced SLR NMR rates. Estimating Cdipolar with the help of the rigid lattice line width for Li6PS5Br and Li6PS5Cl would underestimate C to be on the order of 1010 s−2.46 As we will discuss below, for Li6PS5Br quadrupolar interactions have been identified to greatly influence longitudinal relaxation.15
Interestingly, a very close look at the R1ρ magnetization transients revealed that they contain a minor magnetization component that leads to activation energies of 0.484 eV (Li6PS5Cl) and 0.298 eV (Li6PS5Br); the corresponding R1ρ rates are included in Fig. 12. We cannot exclude that these rates are to a certain degree also influenced by spin–spin relaxation. Obviously, the rates sense long-range Li jump processes characterised by higher activation energies. The intercage jumps might contribute to this type of magnetic relaxation, too.
For X = Cl and Br, if we consider activation energies, Tmax, β and βρ, the 7Li SLR NMR data reveal the same trend for the ion dynamics as seen by the conductivity and ρ′(ω). Li6PS5Br shows fast ion dynamics and the lowest activation energies. For Li6PS5Cl we witness slightly higher activation energies; simultaneously, the peaks shift toward higher temperature. For Li6PS5I, on the other hand, significant differences show up (see the next section).
The NMR rate peaks of Li6PS5I, remembering its low σDC conductivity of 10−6 S cm−1 at ambient temperature, are expected to show up at temperatures much higher than 320 K. We would expect much higher activation energies, at least similar to or higher than those found for Li6PS5Cl. Surprisingly, the R1 rate peak of Li6PS5I shows up at a temperature highly comparable to that of Li6PS5Cl viz. at Tmax = 329 K, see Fig. 11a. In stark contrast to our expectation, NMR does not point to slower Li+ diffusion. Hence, in Li6PS5I the same fast (local) jump processes are present as in their parent compounds.35,40,50 Here, we anticipate that the Li ions in Li6PS5I, with its ordered anion sublattice, have access to the same rapid intracage jump processes. According to NMR the barriers have to be characterised by an activation energy of 0.2 eV. Obviously, only intracage jump processes in Li6PS5I are sufficient to produce a full R1(1/T) peak, see the discussion above.
As expected for a material with an ordered anion lattice such as Li6PS5I and without severe influences of motional correlation effects, an almost symmetric rate peak R1(1/T) (β = 1.92(≈β′)) is obtained for Li6PS5I. The same shape was seen in ρ′(ω). Interestingly, an even lower activation energy determines R1ρ(1/T), see Fig. 11c: in the limit τcω1 ≪ 1 the rates follow an Arrhenius line whose activation energy Ea,high is given by only 0.137 eV. This value is remarkably similar to a cage-like local pathway studied by Rao and Adams (0.15 eV) who used a bond valence approach to investigate the Li ion dynamics in Li6PS5I. Our experimental value also coincides with that of Pecher et al.40 (0.14 eV) who studied the local ion dynamics by molecular dynamics simulations.
The amplitude (R1)max of the R1(1/T) rate of Li6PS5I turned out to be higher that that of the peaks belonging to Li6PS5Cl and Li6PS5Br. This could be because of stronger heteronuclear Li–X interactions and the fact that Li ions on the distorted 24g sites give rise to stronger dipolar and electric quadrupolar couplings constants. These are lowest for the Li6PS5Cl compound. In general, (R1)max is proportional to the square of the magnetic dipolar or electric quadrupolar coupling constant.75,78,79 If we use an electric quadrupole constant of at least 50 kHz, as has been estimated for Li7PS6,46 we obtain (R1)max ≈ 2 s−1 yielding log10((R1)max/s) ≈ 0.3, showing that for Li6PS5Cl both dipolar and electric quadrupolar interactions play a role in determining the relaxation mechanism. For Li6PS5Br we showed via comparative 7Li and 6Li SLR NMR measurements that quadrupole fluctuations greatly affect the overall spin–lattice relaxation.15
Coming back to the temperature dependence of the SLR NMR rates of Li6PS5I, we see that at higher temperatures than ambient the rates R1ρ are increasingly governed by R1, which produces an apparent maximum at ca. 330 K. Unfortunately, the peak maximum of R1ρ(1/T) cannot be detected as Li6PS5I undergoes a phase transition at 160 K;31,39,40,49 see the abrupt change in R1ρ in Fig. 11c. The ion dynamics in the low-T (LT) phase is characterised by a much higher activation energy of 0.44 eV. Below 160 K the rates R1 are no longer induced by diffusive Li jump processes.
To explain the evident differences between the results from conductivity measurements and nuclear spin relaxation in Li6PS5I we anticipate that the fast diffusion Li processes in the I compound are not interconnected to give rise to long-range, through-going ion transport. As has been pointed out in detail by Wagemaker and co-workers, and first mentioned by Rao and Adams,35 the jump probability between two rings in Li6PS5I is very low.50 Intercage jump processes with higher activation energies lead to poor ion transport in Li6PS5I. On a shorter length scale, however, the same structural motifs in Li6PS5X cause very similar NMR rate peaks. Anion disorder, taking advantage of anions with radii that do not differ much to that of S2−, switches on the intercage exchange processes, making Li6PS5Br a fast ion conductor. This design principle causes the overall activation energy to increase in the following order: Li6PS5Br < Li6PS5Cl < Li6PS5I.
To verify whether some intragrain translational processes needed for long-range diffusion in Li6PS5I are indeed missing or governed by higher activation energies we carefully looked at the R1ρ transients and recorded 7Li NMR line shapes over a broad temperature range (Fig. 13). Interestingly, the above-mentioned slow magnetization component seen for Li6PS5Cl and Li6PS5Br (Fig. 12) is missing for the I compound. Furthermore, the intercage jumps are expected to contribute to the averaging of homonuclear (Li–Li) dipole–dipole interactions. If missing at low temperatures, for Li6PS5I the change in line width Δν should occur in two steps. Full averaging is expected at temperatures for which the intercage exchange rate reaches sufficiently high values on the order of some kHz. Indeed, whereas for Li6PS5Br and Li6PS5Cl the 7Li NMR line width continuously decreases with temperature revealing typical narrowing curves (Fig. 13a), that of Li6PS5I is different.
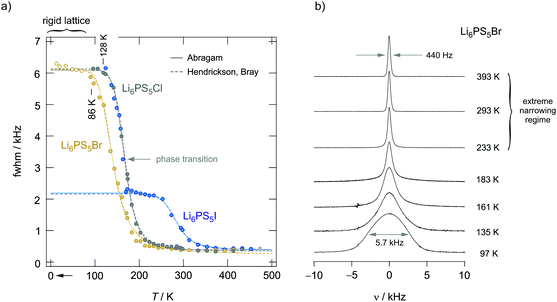 | ||
| Fig. 13 (a) Temperature dependence of the 7Li NMR line widths (FWHM = full width at half maximum) of the aryrodites Li6PS5X (X: Cl, Br and I). Some of the data points referring to Li6PS5Br and measured at temperatures lower than 80 K were taken from Epp et al.;15 they perfectly complement the results of the sample studied here. Line widths Δνr(T) of Li6PS5Br start to narrow at temperatures as low as 86 K indicating ultrafast hopping processes that average homonuclear dipole–dipole interactions being responsible for the rigid lattice line width Δνr ≈ 6.1 kHz. Li diffusion in the compound with Cl is slightly slower as the onset of line narrowing is shifted toward higher T. The line of Δνr(T) of Li6PS5I narrows in steps of two. At T < 160 kHz it indicates dipole averaging in the low-T phase. Because inter-ring jump processes are absent, the line does not reach its extreme value at a temperature comparable to that of Li6PS5Br and Li6PS5Cl. Higher temperatures are necessary to obtain a fully narrowed 7NMR line. Lines represent fits according to the models of Hendrickson and Bray (dashed lines) and Abragam (solid lines). (b) 7NMR line shapes of Li6PS5Br recorded at the temperatures indicated; the line transforms from a Gaussian shape at low T to a Lorentzian one at elevated temperatures. | ||
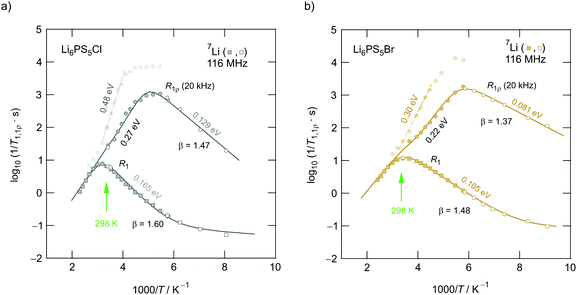
For Li6PS5Br and Li6PS5Cl the extreme narrowing regime is already reached at 250 K (ν∞ ≈ 300 Hz); the final line width is caused by external field inhomogeneities. In contrast to the situation observed for Li6PS5Br and Li6PS5Cl, at 250 K the 7Li NMR line of Li6PS5I is still relatively broad and shows a width of ν = 2.2 kHz. At 350 K it finally reaches ν∞. Thus, for Li6PS5I full averaging of the NMR line width is shifted by ΔT = 100 K toward higher T. Most likely, the latter step corresponds to intercage ion dynamics which are governed by a larger activation barrier. Hence, it is clear from NMR motional narrowing data that in Li6PS5I a much slower process kicks in only at higher T. The fact that Δν of Li6PS5I and Li6PS5Cl is very similar, at least at temperatures just above the phase transition, shows that mainly fast intracage jump processes are responsible for the narrowing seen in this T range. Differences show up, however, if we consider the rotating-frame spin–lattice relaxation rates, see above. The activation energies of the two samples differ by ca. 0.11 eV. Interestingly, the R1ρ(1/T) peak of Li6PS5I is expected at a similar temperature to that of Li6PS5Br (0.20 eV), again pointing to very fast intracage jump processes in the iodide compound. Most likely, so-called doublet-jump processes50 have to be considered to explain this feature, see below.
Unfortunately, we cannot probe the rigid-lattice line width ν0 of the Li6PS5I compound because of the phase transition that occurs at 160 K.31,39,40,49 For both Li6PS5Br and Li6PS5Cl the value of ν0 is very similar; ν0 turned out to be ca. 6.1 kHz. Therefore, the magnetic dipolar Li–Li interactions, which are determined by the Li–Li distances, are almost the same in the two compounds. The inflexion point of the motional narrowing curve of Li6PS5Br is located at T = 150 K (Fig. 13a). R1ρ(1/T) tells us that at this temperature the motional correlation rate τc−1 (≈2ω1) should be on the order of 2.51 × 105 s−1. This value clearly exceeds ν0 and causes full averaging of the spin–spin interactions in this T range. The changes of the corresponding 7Li NMR lines are shown in Fig. 13b. Li6PS5Br shows one of the lowest onset temperatures seen by NMR motional line narrowing; already at 86 K the shape of the NMR line starts to change as a result of rapid Li+ self-diffusion.15 This observation excellently agrees with results from density functional theory molecular dynamics simulations.50
Extracting quantitative information from NMR motional line narrowing is always fraught with difficulties.80 Abragam81 and Hendrickson and Bray82,83 introduced models to use the change in line widths to deduce activation energies for the hopping process behind. There is still debate over whether these models are accurate enough for this purpose. Hence, we should not overinterpret the results but regard them as estimates. The dashed lines in Fig. 13 refer to the following relationships82
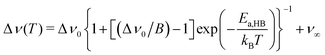 | (6) |
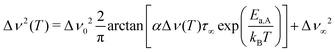 | (7) |
| E a,A (eV) | E a,HB (eV) | E a (low-T flank) (eV) | |
|---|---|---|---|
| Li6PS5Cl | 0.11(1) | 0.18(2) | 0.17(4) |
| Li6PS5Br | 0.06(1) | 0.09(1) | 0.10(4) |
| Li6PS5I | 0.23(1) | 0.38(2) | 0.18(5) |
Finally, we will quantitatively compare jump rates τ−1 from NMR with electrical relaxation rates from impedance and conductivity spectroscopy. Using the Nernst–Einstein equation84 we can convert σ′ into diffusion coefficients and, thus, jump rates. The easiest way, being also independent of any relaxation model, is to determine jump rates τ−1 at the temperatures where the NMR relaxation rate peaks show up. With the conditions τcω1(ρ) = 1(0.5), valid at Tmax, and the jump distances ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) obtained from XRD we estimated diffusion coefficients according to the Einstein–Smoluchowski relation84 for 3D diffusion
obtained from XRD we estimated diffusion coefficients according to the Einstein–Smoluchowski relation84 for 3D diffusion
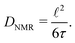 | (8) |
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) we used the jump distance of the 48h–48h jump process, which is assumed to be the slowest one. The results are listed in Table 4. At Tmax the jump rate turned out to be on the order of 1.36 × 10−9 s−1. As an example, the mean residence time of the Li ions in Li6PS5Br at 286 K is on the order of 1 ns only. Such a short residence time, which is already reached below room temperature, corresponds to ionic conductivities on the order of 10−3 to 10−2 S cm−1.
we used the jump distance of the 48h–48h jump process, which is assumed to be the slowest one. The results are listed in Table 4. At Tmax the jump rate turned out to be on the order of 1.36 × 10−9 s−1. As an example, the mean residence time of the Li ions in Li6PS5Br at 286 K is on the order of 1 ns only. Such a short residence time, which is already reached below room temperature, corresponds to ionic conductivities on the order of 10−3 to 10−2 S cm−1.
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) /Å /Å |
T max(R1)/K | D NMR/cm2 s−1 | n Li/m−3 | |
|---|---|---|---|---|
For ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) we used the 48h–48h distance, which is the longest jump distance in Li6PS5Br, when we consider cation hopping processes near the regularly occupied Li sites. we used the 48h–48h distance, which is the longest jump distance in Li6PS5Br, when we consider cation hopping processes near the regularly occupied Li sites. |
||||
| Li6PS5Cl | 2.34 | 316 | 6.7 × 10−8 | 6.3 × 1027 |
| Li6PS5Br | 2.41 | 286 | 7.1 × 10−8 | 6.0 × 1027 |
| Li6PS5I | 2.66 | 329 | 8.6 × 10−8 | 5.8 × 1027 |
Using structural data from our Rietveld analysis we also estimated the charge carrier density nLi in Li6PS5Br. nLi, which is on the order of 1027 m−3, is needed to convert DNMR into conductivities expected at or near Tmax. Disregarding any correlation effects for our estimation of σNMR, the following relation holds11
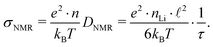 | (9) |
| σ NMR/mS cm−1 | σ DC/mS cm−1 | |
|---|---|---|
| Li6PS5Cl | 2.46 (316 K) | 9.00 (313 K) |
| Li6PS5Br | 2.78 (286 K) | 2.20 (293 K) |
| Li6PS5I | 2.80 (329 K) | 8.60 × 10−3 (333 K) |
While good agreement is seen for σNMR and σDC of Li6PS5Br, we have to notice a somewhat larger difference for the Cl compound. In general, conductivities indirectly deduced from NMR should be regarded as estimates because relaxation NMR and conductivity spectroscopy sense different kinds of motional correlation functions. Agreement over a large temperature is only obtained if both techniques are sensitive to the same diffusion process and the same correlation function.51
As expected, for Li6PS5I the values listed in Table 5 differ by three orders of magnitude. Whereas σDC is mainly governed by successful jump processes resulting in long-range ion transport, σNMR reflects short-range ion dynamics. The difference can easily be explained by the fact that in Li6PS5I the intercage jump processes are less probable; these processes hinder the ions in long-range diffusion. Note that the comparison in Table 5 only refers to T ≈ Tmax at which the NMR peaks show up. Comparing dynamic parameters over the full temperature range will show deviations between nuclear spin relaxation and conductivity spectroscopy as the techniques deliver different activation energies in the present case. Such a comparison is presented in Fig. 14. Squares represent jump rates obtained at the NMR rate peaks; at T → 0 we have indicated the pre-factors of the Arrhenius lines.
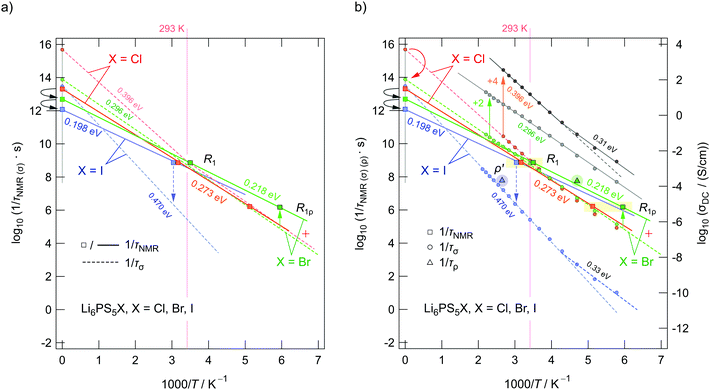 | ||
| Fig. 14 Arrhenius plot of the jump rates deduced from the 7Li NMR rate peaks shown in Fig. 11c, 12a and (b). (a) Squares represent either pre-factors or jump rates at the maxima of the peaks. Solid lines represent the Arrhenius lines according to the joint fits. Dashed lines indicate the position of τσ−1, i.e., estimated from σDC. (b) The same data points as in (a) but with τDC−1 included as data points. The lines referring to Li6PS5Cl and Li6PS5Br have been shifted by a factor of +4 (+2) (on the log scale) to illustrate the kink seen in τDC−1(1/T) for Li6PS5Cl. It is absent for Li6PS5Br. Electrical relaxation rates τρ−1 from our ρ′(1/T) analyses have been included as well. The vertical arrow drawn with a dashed line indicates the large difference in jump rates seen for Li6PS5I. The arrows near the ordinate illustrate the change in pre-factors. See the text for further explanation. | ||
In Fig. 14aτNMR−1 as deduced from the joint fits of Li6PS5Cl and Li6PS5Br are shown. The line belonging to Li6PS5I refers to the R1 rates only. First of all, we notice a correlation between Ea,NMR and the pre-factor τ0−1 (see also Table 2). The decrease in Ea,NMR, which changes from 0.273 eV to 0.218 eV and further to 0.198 eV (R1 of Li6PS5I), is accompanied by a decrease in τ0−1. The attempt frequency τ0−1 decreases by a factor of 80 when going from Li6PS5Cl to Li6PS5I. This small variation either reflects a decrease in phonon frequencies or a change in migration entropy ΔS of the ions as τ0−1 = νp,0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(ΔS/kB). Phonon frequencies, to which νp,0 is proportional, usually take values on the order of 1012 to 1015 s−1. As discussed above, for Li6PS5I a decrease in migration entropy is reasonable because of the ordered anion sublattice. The decrease in Ea,NMR reflects the increase in anion polarizability (I > Br > Cl), which should, apart from effects due to disorder, also lead to lower hopping barriers. This trend for Ea,NMR is at least valid for the elementary Li+ jumps seen by NMR. If we include τσ−1 values obtained by transforming σDC into hopping rates after eqn (9), we notice that good agreement is only seen at temperatures around Tmax, see Fig. 14a and b. Clearly, the fact that Ea,NMR ≠ Ea,DC leads to deviations at temperatures T ≶ Tmax. For comparison, in Fig. 14b hopping rates from ρ′(T) have also been included.
exp(ΔS/kB). Phonon frequencies, to which νp,0 is proportional, usually take values on the order of 1012 to 1015 s−1. As discussed above, for Li6PS5I a decrease in migration entropy is reasonable because of the ordered anion sublattice. The decrease in Ea,NMR reflects the increase in anion polarizability (I > Br > Cl), which should, apart from effects due to disorder, also lead to lower hopping barriers. This trend for Ea,NMR is at least valid for the elementary Li+ jumps seen by NMR. If we include τσ−1 values obtained by transforming σDC into hopping rates after eqn (9), we notice that good agreement is only seen at temperatures around Tmax, see Fig. 14a and b. Clearly, the fact that Ea,NMR ≠ Ea,DC leads to deviations at temperatures T ≶ Tmax. For comparison, in Fig. 14b hopping rates from ρ′(T) have also been included.
The pre-factors of the Arrhenius lines referring to τσ−1 estimated from σDC also vary with X. While we cannot see any large difference between τ0,σ−1 from Li6PS5I and Li6PS5Br as mentioned above, we see that τ0,σ−1 of the Cl-compound is much higher than expected. This increase is caused by a change in slope of σDC at a temperature slightly below 400 K; it is also seen for Li6PS5I. Below 400 K the ionic conductivity σDC (as well as τσ−1) follows an Arrhenius law with an activation energy very similar to that of Li6PS5Br (0.273 eV). As σDC of Li6PS5Br and Li6PS5Cl almost coincide in this T range, also the corresponding pre-factors τ0,σ−1 would be the same. Here, the fact that τ0,σ−1 of Li6PS5Cl is larger than that of Li6PS5Br originates the kink in the Arrhenius line causing σDCT(1/T) to be characterised by an activation energy (0.396 eV) much larger than that in the low-T range. Obviously, another Li+ diffusion process, being characterised by an activation energy larger than 0.3 eV, contributes to τσ−1 of Li6PS5Cl.
Such an additional process, which we assume could stem from an ordered Li sublattice in Li6PS5Cl, has been seen by R1ρ, see Fig. 12. The R1ρ magnetization transients of Li6PS5Cl are characterised by a second decay process that is thermally activated by 0.48 eV. The same feature is also seen for Li6PS5Br with both a disordered anion structure and Li+ sublattice. The corresponding activation energy of 0.30 eV (see Fig. 12) is, however, very similar to that of σDCT(1/T). This similarity thus gives rise to no increase in σDCT above T ≈ 400 K.
The pre-factors seen by conductivity spectroscopy, especially those of Li6PS5Cl, clearly represent mean values. In materials with several diffusion processes taking place in parallel, each process needs to be characterised by its individual pre-factor. In the case of 7Li NMR, which is primarily sensitive to the elementary jump processes between 24g and 48h, we see a slight increase in the pre-factor when going from X = I to X = Cl (see above). The change in τ0−1 is, however, small as compared to the drastic decrease in σDCT(1/T) seen for Li6PS5I. Hence, the increase in overall migration enthalpy for Li6PS5I, for which the intercage diffusion process is characterised by a high hopping barrier, turned out to be mainly responsible for its poor ionic conductivity. On shorter length scales, Li ion hopping in Li6PS5I, with its ordered anion sublattice, is as fast as in Li6PS5Br. This result is in perfect agreement with the pioneering calculations by Rao and Adams as well as the in-depth study presented by De Klerk et al.50 They already pointed out, as mentioned above, that for Li6PS5I the intercage jump processes are interrupted and fast localized motions with very low activation energies are present. By 7Li NMR relaxometry their observation is now fully supported. The calculations by Pecher et al. point in the same direction.40 As an example, De Klerk et al. report an activation energy as low as 0.05 eV for the doublet jump process in Li6PS5I.50
Besides these peculiarities for Li6PS5Cl and Li6PS5I, the complex ion dynamics in Li-bearing argyrodites with anion disorder is reflected in the distribution of activation energies. Table 6 summarises the activation energies obtained by the different methods applied. Depending on the length-scale and time-scale to which the specific method is sensitive quite different activation energies can be probed. Such a result is typical for ionic conductors whose charge carriers are exposed to an irregularly shaped energy landscape that gives rise to highly correlated forward and backward motions or fast (local) dynamics on the angstrom length scale.
| Li6PS5Cl (eV) | Li6PS5Br (eV) | Li6PS5I (eV) | |
|---|---|---|---|
| a The values referring either to the high-T or to the low-T flank were obtained by a line fit. b Results from the global fit analysis are obtained by linking Ea and τ0−1 of the individual relaxation rate peaks. Values in brackets refer to the low-T flanks of the global fit. | |||
| σ DC | 0.396(3) | 0.296(2) | 0.470(5) |
| ρ′, high-T flanka | 0.321(3) | 0.250(3) | 0.347(7) |
| ρ′, low-T flanka | 0.153(2) | 0.115(9) | 0.305(2) |
| M′′ | — | — | 0.349(5) |
| R 1, high-T flanka | 0.320(1) | 0.213(1) | 0.198(1) |
| R 1, low-T flanka | 0.170(4) | 0.102(4) | 0.182(5) |
| R 1ρ, high-T flanka | 0.248(9) | 0.201(9) | 0.137(3) |
| R 1ρ, low-T flanka | 0.134(1) | 0.083(1) | — |
| R 1 (global fit)b | 0.273(5) | 0.218(1) | — |
| (0.165(8)) | (0.105(4)) | — | |
| R 1ρ (global fit)b | 0.273(5) | 0.218(1) | — |
| (0.129(7)) | (0.081(4)) | — | |
4 Summary and conclusion
We studied the Li ion dynamics in argyrodite-type Li6PS5X (X: Cl, Br, I) by a wide range of complementary techniques with a special focus on conductivity spectroscopy and nuclear magnetic relaxation. The latter technique is able to probe short-range as well as long-range bulk ion dynamics. The analysis of electric modulus data also helped us to shed light on the bulk ion dynamics. In all compounds, even in those where two different halogen atoms were used to replace a sulfur anion per formula unit, complex ion dynamics is found. Heterogenous Li ion transport is traced back to the fact of an irregularly shaped potential landscape that the ions are exposed to during diffusion. The vacancy-rich Li sublattice offers a range of hopping barriers between the Li sites involved in the overall ionic transport. Depending on the method applied to study the hopping processes, Li ion translational motions on quite different time scales and lengths scales are probed. This circumstance results in activation energies ranging from 0.08 eV to values as high as 0.48 eV.Anion disorder in Li6PS5Br and Li6PS5Cl, as verified by X-ray powder diffraction measurements, boosts the ion dynamics as compared to the parent compound Li7PS6. The halogen anions are clearly distributed over the crystallographic sites 4a and 4d. Li6PS5Br reveals the lowest activation energies and the bulk ion conductivities follow a single Arrhenius line. Deviations from this behaviour are seen for Li6PS5Cl and Li6PS5I. For Li6PS5Cl an additional dynamic process shows up at higher T, which is also seen in 7Li spin-lock NMR spectroscopy. This process leads to a relatively high mean activation energy in σDC characterising the overall ion transport.
Most importantly, also for the poor ionic conductor Li6PS5I our NMR relaxation measurements reveal very fast Li ion dynamics on a local to medium-range length scale. Obviously, the ions have access to the same, rapid exchange processes as in Li6PS5Br but long-range transport is switched off. In the spirit of De Klerk and co-workers we think that the ordered anion sublattice, combined with the larger lattice constant, is responsible for this peculiarity. It leads to a heterogeneous potential landscape with low and high hopping barriers. High activation barriers seem to characterize the intercage jumps; these jump processes are, however, necessary to transport the ions over long distances.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
Financial support by the Deutsche Forschungsgemeinschaft (DFG Research Unit 1277, grant no. WI3600/2-1(4-1) (FOR1277)) as well as by the Austrian Federal Ministry of Science, Research and Economy, and the Austrian National Foundation for Research, Technology and Development (Christian Doppler Laboratory of Lithium Batteries: Ageing Effects, Technology and New Materials) is greatly appreciated. Furthermore, we thank the FFG in the frame of the K project safe battery.References
- M. S. Whittingham, Chem. Rev., 2004, 104, 4271 CrossRef CAS.
- J. B. Goodenough and Y. Kim, Chem. Mater., 2010, 22, 587 CrossRef CAS.
- Lithium Ion Batteries, ed. M. Wakihara and O. Yamamoto, Wiley-VCH, Weinheim, 1998 Search PubMed.
- A. S. Aricó, P. Bruce, B. Scrosati, J.-M. Tarascon and W. V. Schalkwijc, Nat. Mater., 2005, 4, 366 CrossRef PubMed.
- P. G. Bruce, B. Scrosati and J.-M. Tarascon, Angew. Chem., Int. Ed., 2008, 47, 2930 CrossRef CAS PubMed.
- B. L. Ellis and L. F. Nazar, Curr. Opin. Solid State Mater. Sci., 2012, 16, 168 CrossRef CAS.
- V. Etacheri, R. Marom, R. Elazari, G. Salitra and D. Aurbach, Energy Environ. Sci., 2011, 4, 3243–3262 RSC.
- V. Thangadurai, S. Narayanan and D. Pinzaru, Chem. Soc. Rev., 2014, 43, 4714–4727 RSC.
- J. C. Bachman, S. Muy, A. Grimaud, H.-H. Chang, N. Pour, S. F. Lux, O. Paschos, F. Maglia, S. Lupart, P. Lamp, L. Giordano and Y. Shao-Horn, Chem. Rev., 2016, 116, 140–162 CrossRef CAS PubMed.
- Z. Zhang, Y. Shao, B. Lotsch, Y.-S. Hu, H. Li, J. Janek, L. F. Nazar, C.-W. Nan, J. Maier, M. Armand and L. Chen, Energy Environ. Sci., 2018, 11, 1945–1976 RSC.
- M. Uitz, V. Epp, P. Bottke and M. Wilkening, J. Electroceram., 2017, 38, 142–156 CrossRef CAS.
- A. Hayashi and M. Tatsumisago, Electron. Mater. Lett., 2012, 8, 199 CrossRef CAS.
- N. Kamaya, K. Homma, Y. Yamakawa, M. Hirayama, R. Kanno, M. Yonemura, T. Kamiyama, Y. Kato, S. Hama, K. Kawamoto and A. Mitsui, Nat. Mater., 2011, 10, 682–686 CrossRef CAS PubMed.
- S. Hori, T. Saito, K. Suzuki, M. Hirayama, A. Mitsui, M. Yonemura, H. Iba and R. Kanno, Nat. Energy, 2016, 1, 16303 Search PubMed.
- V. Epp, O. Gün, H.-J. Deiseroth and M. Wilkening, J. Phys. Chem. Lett., 2013, 4, 2118–2123 CrossRef CAS.
- D. Brinkmann, Prog. Nucl. Magn. Reson. Spectrosc., 1992, 24, 527 CrossRef CAS.
- P. Knauth, Solid State Ionics, 2009, 180, 911 CrossRef CAS.
- J. Fergus, J. Power Sources, 2010, 195, 4554–4569 CrossRef CAS.
- C. Julien and G. A. Nazri, Solid State Batteries: Materials, Design and Optimization, Kluwer Academic, Boston, 1994 Search PubMed.
- S. Jacke, J. Song, L. Dimesso, J. Brötz, D. Becker and W. Jägermann, J. Power Sources, 2011, 196, 6911–6914 CrossRef CAS.
- S. Wang, L. Ben, H. Li and L. Chen, Solid State Ionics, 2014, 268, 110–116 CrossRef CAS.
- R. Murugan, V. Thangadurai and W. Weppner, Angew. Chem., Int. Ed., 2007, 46, 7778 CrossRef CAS PubMed.
- S. Narayanan, V. Epp, M. Wilkening and V. Thangadurai, RSC Adv., 2012, 2, 2553 RSC.
- V. Epp, Q. Ma, E.-M. Hammer, F. Tietz and M. Wilkening, Phys. Chem. Chem. Phys., 2015, 17, 32115–32121 RSC.
- H. Buschmann, J. Dölle, S. Berendts, A. Kuhn, P. Bottke, M. Wilkening, P. Heitjans, A. Senyshyn, H. Ehrenberg, A. Lotnyk, V. Duppel, L. Kienle and J. Janek, Phys. Chem. Chem. Phys., 2011, 13, 19378 RSC.
- B. Stanje, D. Rettenwander, S. Breuer, M. Uitz, S. Berendts, M. Lerch, R. Uecker, G. Redhammer, I. Hanzu and M. Wilkening, Ann. Phys., 2017, 529, 1700140 CrossRef.
- S. Breuer, D. Prutsch, Q. Ma, V. Epp, F. Preishuber-Pflügl, F. Tietz and M. Wilkening, J. Mater. Chem. A, 2015, 3, 21343–21350 RSC.
- S. Lunghammer, Q. Ma, D. Rettenwander, I. Hanzu, F. Tietz and H. Wilkening, Chem. Phys. Lett., 2018, 701, 147–150 CrossRef CAS.
- P. Bron, S. Johansson, K. Zick, J. Schmedt auf der Günne, S. Dehnen and B. Roling, J. Am. Chem. Soc., 2013, 135, 15694–15697 CrossRef CAS.
- S. Wenzel, S. Randau, T. Leichtweiß, D. A. Weber, J. Sann, W. G. Zeier and J. Janek, Chem. Mater., 2016, 28, 2400–2407 CrossRef CAS.
- H.-J. Deiseroth, S.-T. Kong, H. Eckert, J. Vannahme, C. Reiner, T. Zaiss and M. Schlosser, Angew. Chem., Int. Ed., 2008, 47, 755–758 CrossRef CAS PubMed.
- S. Boulineau, M. Courty, J.-M. Tarascon and V. Viallet, Solid State Ionics, 2012, 221, 1–5 CrossRef CAS.
- S. Boulineau, J.-M. Tarascon, J.-B. Leriche and V. Viallet, Solid State Ionics, 2013, 242, 45–48 CrossRef CAS.
- M. A. Kraft, S. P. Culver, M. Calderon, F. Böcher, T. Krauskopf, A. Senyshyn, C. Dietrich, A. Zevalkink, J. Janek and W. G. Zeier, J. Am. Chem. Soc., 2017, 139, 10909–10918 CrossRef CAS PubMed.
- R. P. Rao and S. Adams, Phys. Status Solidi, 2011, 208, 1804–1807 CrossRef CAS.
- P. R. Rayavarapu, N. Sharma, V. K. Peterson and S. Adams, J. Solid State Electrochem., 2012, 16, 1807–1813 CrossRef CAS.
- H. M. Chen, C. Maohua and S. Adams, Phys. Chem. Chem. Phys., 2015, 17, 16494–16506 RSC.
- R. P. Rao, N. Sharma, V. Peterson and S. Adams, Solid State Ionics, 2013, 230, 72–76 CrossRef CAS.
- H.-J. Deiseroth, J. Maier, K. Weichert, V. Nickel, S.-T. Kong and C. Reiner, Z. Anorg. Allg. Chem., 2011, 637, 1287–1294 CrossRef CAS.
- O. Pecher, S.-T. Kong, T. Göbel, V. Nickel, K. Weichert, C. Reiner, H.-J. Deiseroth, J. Maier, F. Haarmann and D. Zahn, Chem. – Eur. J., 2010, 16, 8347–8354 CrossRef CAS PubMed.
- A. Düvel, B. Ruprecht, P. Heitjans and M. Wilkening, J. Phys. Chem. C, 2011, 115, 23784–23789 CrossRef.
- S. Breuer and M. Wilkening, Dalton Trans., 2018, 47, 4105–4117 RSC.
- B. Kozinsky, S. A. Akhade, P. Hirel, A. Hashibon, C. Elsässer, P. Mehta, A. Logeat and U. Eisele, Phys. Rev. Lett., 2016, 116, 055901 CrossRef PubMed.
- K. E. Kweon, J. B. Varley, P. Shea, N. Adelstein, P. Mehta, T. W. Heo, T. J. Udovic, V. Stavila and B. C. Wood, Chem. Mater., 2017, 29, 9142–9153 CrossRef CAS.
- E. Fukushima and S. Roeder, Experimental Pulse NMR, Addison-Wesley, Reading, 1981 Search PubMed.
- V. Epp, O. Gün, H.-J. Deiseroth and M. Wilkening, Phys. Chem. Chem. Phys., 2013, 15, 7123–7132 RSC.
- D. C. Look and I. J. Lowe, J. Chem. Phys., 1966, 44, 2995 CrossRef CAS.
- D. C. Ailion and C. P. Slichter, Phys. Rev., 1965, 137, A235 CrossRef.
- S.-T. Kong, H.-J. Deiseroth, C. Reiner, Z. Gün, E. Neumann, C. Ritter and D. Zahn, Chem. – Eur. J., 2010, 16, 2198–2206 CrossRef CAS PubMed.
- N. J. J. de Klerk, I. Roslon and M. Wagemaker, Chem. Mater., 2016, 28, 7955–7963 CrossRef CAS.
- F. Preishuber-Pflügl, P. Bottke, V. Pregartner, B. Bitschnau and M. Wilkening, Phys. Chem. Chem. Phys., 2014, 16, 9580–9590 RSC.
- F. Preishuber-Pflügl and M. Wilkening, Dalton Trans., 2016, 45, 8675–8687 RSC.
- F. Preishuber-Pflügl and M. Wilkening, Dalton Trans., 2014, 43, 9901–9908 RSC.
- M. Wilkening, A. Düvel, F. Preishuber-Pflügl, K. Silva, S. Breuer, V. Šepelák and P. Heitjans, Z. Kristallogr. - Cryst. Mater., 2016, 232, 107–127 Search PubMed.
- D. L. Sidebottom, Rev. Mod. Phys., 2009, 81, 999 CrossRef.
- R. Metselaar and G. Oversluizen, J. Solid State Chem., 1984, 55, 320–326 CrossRef CAS.
- J. T. S. Irvine, D. C. Sinclair and A. R. West, Adv. Mater., 1990, 2, 132–138 CrossRef CAS.
- K. L. Ngai, Relaxation and Diffusion in Complex Systems, Springer, New York, 2011 Search PubMed.
- K. L. Ngai, G. N. Greaves and C. T. Moynihan, Phys. Rev. Lett., 1998, 80, 1018 CrossRef CAS.
- R. Winter, K. Siegmund and P. Heitjans, J. Non-Cryst. Solids, 1997, 212, 215–224 CrossRef CAS.
- M. Wilkening and P. Heitjans, Chem. Phys. Chem., 2012, 13, 53–65 CrossRef CAS PubMed.
- P. Heitjans, A. Schirmer and S. Indris, in Diffusion in Condensed Matter, ed. P. Heitjans and J. Kärger, Springer, 2005, ch. 9, p. 367 Search PubMed.
- V. Epp, C. Brüning, M. Binnewies, P. Heitjans and M. Wilkening, Z. Phys. Chem., 2012, 226, 513 CrossRef CAS.
- M. Wilkening, A. Kuhn and P. Heitjans, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 054303 CrossRef.
- A. Kuhn, S. Narayanan, L. Spencer, G. Goward, V. Thangadurai and M. Wilkening, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 094302 CrossRef.
- P. Heitjans and M. Wilkening, Defect Diffus. Forum, 2009, 283–286, 705 CAS.
- M. Wilkening and P. Heitjans, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 024311 CrossRef.
- M. Wilkening, W. Küchler and P. Heitjans, Phys. Rev. Lett., 2006, 97, 065901 CrossRef CAS PubMed.
- N. Bloembergen, E. M. Purcell and R. V. Pound, Phys. Rev., 1948, 73, 679–712 CrossRef CAS.
- W. Küchler, P. Heitjans, A. Payer and R. Schöllhorn, Solid State Ionics, 1994, 70/71, 434 CrossRef.
- M. Meyer, P. Maass and A. Bunde, Phys. Rev. Lett., 1993, 71, 573–576 CrossRef CAS PubMed.
- A. Kuhn, P. Sreeraj, R. Pöttgen, H.-D. Wiemhöfer, M. Wilkening and P. Heitjans, J. Am. Chem. Soc., 2011, 133, 11018–11021 CrossRef CAS PubMed.
- A. Kuhn, S. Narayanan, L. Spencer, G. Goward, V. Thangadurai and M. Wilkening, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 094302 CrossRef.
- T. M. Kirschgen, M. D. Zeidler, B. Geil and F. Fujara, Phys. Chem. Chem. Phys., 2003, 5, 5243–5246 RSC.
- R. Bertermann and W. Müller-Warmuth, Z. Naturforsch., A: Phys. Sci., 1998, 53, 863–873 CAS.
- E. Göbel, W. Müller-Warmuth, H. Olyschläger and H. Dutz, J. Magn. Reson., 1979, 36, 371–387 Search PubMed.
- C. Yu, S. Ganapathy, E. R. H. van Eck, L. van Eijck, S. Basak, Y. Liu, L. Zhang, H. Zandbergen and M. Wagemaker, J. Mater. Chem. A, 2017, 5, 21178–21188 RSC.
- K. Hayamizu, S. Tsuzuki and S. Seki, Magn. Reson. Chem., 2011, 49, 6–8 CrossRef CAS PubMed.
- M. Grüne, H. Meierkord, W. Müller-Warmuth, P. Z. Hebel, B. Krebs and M. Wulff, Ber. Busenges. Phys. Chem., 1989, 93, 1313–1317 CrossRef.
- M. Wilkening, D. Bork, S. Indris and P. Heitjans, Phys. Chem. Chem. Phys., 2002, 4, 3246–3251 RSC.
- A. Abragam, The principles of nuclear magnetism, Oxford University Press, 1999 Search PubMed.
- J. R. Hendrickson and P. J. Bray, J. Magn. Reson., 1973, 9, 341–357 CAS.
- J. R. Hendrickson and P. J. Bray, J. Chem. Phys., 1974, 61, 2754–2764 CrossRef CAS.
- H. Mehrer, Diffusion in Solids: Fundamentals, Methods, Materials, Diffusion-Controlled Processes, Springer, Berlin, 2007 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Rietveld refinements and structural data, further NMR data. See DOI: 10.1039/c9cp00664h |
| This journal is © the Owner Societies 2019 |