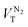Nanoscale dynamics of water confined in ordered mesoporous carbon†
Received
17th December 2018
, Accepted 22nd March 2019
First published on 8th April 2019
Abstract
The single particle dynamics of water confined within two ordered mesoporous carbon matrices was investigated in the temperature range from 290 K to 170 K by quasielastic neutron scattering using three high resolution neutron spectrometers. Thus, it was possible to investigate the mobility of water confined in model hydrophobic cavities at the nanoscale. Models developed for the nanoscale dynamics of supercooled water and water confined within hydrophilic matrices were able to describe the collected data but remarkable differences with analogous silica confined matrices were observed in these carbon samples. A significant fraction of the water molecules was immobile on the nanosecond timescale, even at room temperature. As the temperature was lowered, the mobility of the water molecules slowed down, but the strongly non-Arrhenius behavior observed in bulk water and for fully hydrated hydrophilic confinement was absent, which indicates frustration of the hydrogen bond network formation. The obtained results were relevant for applications of mesoporous carbon materials.
1. Introduction
The properties of water in micropores and mesopores (defined according to the International Union of Pure and Applied Chemistry (IUPAC) convention as pores smaller than 2 nm and in the range between 2 nm and 50 nm, respectively) attract a lot of interest due to their relevance in various fields such as biology, catalysis, electrochemistry, and mining, as well as for their scientific relevance.2,3 For example, water confined in pores smaller than ≈20 Å does not crystallize even below the homogeneous nucleation temperature, and therefore, nanoconfined water has been used4,5 as a proxy to investigate the properties of water in the supercooled regime.5 Though there has been some criticism, the results have pointed in particular to ascertain the existence of a possible second critical point of water.6 Confinement within model hydrophilic pores has been initially widely investigated; however, confinement within hydrophobic pores and in carbon based matrices has recently drawn significant interest.7 In fact, the water properties on a hydrophobic surface might lead to anomalous behavior, such as forming a depletion layer,8,9 but also have relevance to biological systems.10–12 Porous carbon based materials in particular are attracting increasing attention due to their applications in gas separation, water purification, catalysis and electrochemistry.13 These materials are usually considered hydrophobic and have also been widely regarded as paradigms for non-polar interfaces and to study water dynamics. However, there is evidence that carbon based surfaces, such as graphene, may also display hydrophilic behavior.14 Empirically, the presence of adsorption sites, defects, etc. are also factors which affect the wettability of carbon surfaces.15
Confinement of water in nonpolar pores is characterized by the coexistence of filled and empty spaces and strong interaction between the water molecules. However, the size of the confinement and the molecular topography of the surface, as well as the details of the interaction between water and the confined surface are all relevant parameters which should ideally be controlled; this is possible by computer simulations16,17 but much harder experimentally. In this regard, the availability of the recently synthesized Ordered Mesoporous Carbon (OMC) offers a unique model system.18 The synthesis of OMC via a soft template method, which provides a more simplified assembly process than hard template ones,18 has been developed. OMC is characterized by uniform mesopores arranged in a hexagonal geometry, in a way comparable to the nanoporous silica matrix MCM-41.19 Its high surface area, large pore volume, chemical inertness, and the narrow distribution of mesopore sizes make this material very attractive for investigating the physico-chemical properties of water in hydrophobic pores. Moreover, OMC is a promising candidate for a variety of applications such as electrode materials for batteries, fuel cells, and supercapacitors, as sorbents for separation processes and gas storage, and as supports for catalytic processes.20 For the development of such applications, it is crucial to understand the behavior of water confined in carbon materials.
The properties of water in confinement were investigated using several experimental and computational techniques. For the study of its dynamic properties at the molecular level Quasielastic Neutron Scattering21 (QENS) affords unique capabilities. Because the incoherent scattering cross section of hydrogen atoms is much larger than the scattering cross-section of essentially any other atom, the QENS data can be rather straightforwardly related to the single particle dynamics of the hydrogen atoms in the system. Moreover, this technique provides both spatial and temporal information on relaxation processes with characteristic time in the range between a picosecond to several nanoseconds over length scales from an angstrom to a few angstroms. Because of these characteristics QENS was used to study the dynamics of water confined in cylindrical mesoporous silica, MCM-41.22–24 More recently, hydrophobic confined materials have been investigated as well.15,25–27
In this work, we compare the dynamics of water in two kinds of ordered mesoporous carbon samples differing in the morphology of their mesopores. We find that in both cases water is confined mostly in the micropores which have a size of ≈8 Å. We studied the mobility of the confined water molecule as a function of temperature. The results indicate the presence of a fraction of water immobile on the nanosecond timescale and a suppression of the hydrogen bond network which results, at low temperature, in an increased mobility of the confined water molecules with respect to the bulk. The paper is organized as follows. In Section 2, we describe the sample preparation and characterization. Section 3 reports the details of the QENS experiments. The obtained results are presented in Section 4 along with relevant discussion. Section 5 is devoted to a concise summary.
2. Materials
Ordered mesoporous carbons (OMCs) with channel structures were synthesized according to the method of Tanaka et al.18 High resolution transmission electron microscopy images of the two samples showing ordered structures are shown in the ESI† (Fig. S1). In brief, they were synthesized by using an organic–organic interaction between a thermosetting polymer and a thermally decomposable surfactant to form a periodic ordered nanocomposite. The thermosetting polymer is carbonized by heating under Ar, after which it retains a carbonaceous pore wall. In order to minimize the presence of residual hydrophilic sites the samples were calcined at 900 °C for at least 3 hours. The nitrogen adsorption isotherms were measured at 77 K using an automatic gas adsorption apparatus, BELSORP-max (Microtrac BEL Corp.), as shown in Fig. 1. Both the OMC samples exhibited a large amount of adsorption at the initial stage due to micropores. OMC-1 showed a type H4 loop which is indicative of narrow slit-shaped pores and OMC-2 showed a hysteresis loop of type H1 typical of relatively narrow distributions of mesoporous materials.28 The pore size distribution was estimated from nitrogen adsorption using a non-local density functional theory (NLDFT) slit pore model, as shown in the inset of Fig. 1. Both samples showed a large population of micropores, which have been modeled as slits. OMC-1 has a narrow distribution of micropores centered at ≈8 Å, and a small fraction of mesopores. OMC-2 has a similar micropore distribution, albeit slightly broader, to OMC-1 and has a broad distribution of mesopores. The micropore volumes, VGCMCmicro, and the total pore volumes, VGCMCT, were calculated by Grand Canonical Monte Carlo (GCMC) simulations. Software developed by Microtrac BEL Japan (BEL Master ver. 6.3.1.0) was used to calculate the distributions. Simulations were conducted using the data of the adsorption branch based on the assumption that carbons have slit-shaped pores. The GCMC method is believed to yield a more precise value for the micropore volume. The characteristic properties of the OMC samples are summarized in Table 1. The main difference between the two samples is that the micropores occupy 85% of the OMC-1 and 26% of the OMC-2 spaces, as calculated by GCMC simulations.
 |
| | Fig. 1 The adsorption/desorption isotherms of nitrogen at 77 K and pore size distribution (inset) for the two OMC samples investigated, OMC-1: grey; OMC-2: red. | |
Table 1 Structural properties of the OMC samples from N2 and H2O adsorption/desorption isotherms
2.1 Sample hydration
OMC powder in a cell was placed in a vacuum chamber and evacuated for one day with a turbo molecular pump and then exposed to water vapor (relative pressure P/P0 = 0.6 to 0.7) at 298 K to achieve the capillary condensation of water. For quasi-elastic neutron scattering experiments the water hydration degree of the samples was 0.13 and 0.08 (weight of water/total weight), corresponding to volumes VH2O of 0.15 cm3 g−1 and 0.10 cm3 g−1, for the OMC-1 and OMC-2 sample, respectively. These values indicate that ≈70% of the micropore volume (as estimated by GCMC) is filled with water. In agreement with previous reports,29–32 the adsorption–desorption isotherms of H2O for OMC-1 and OMC-2, measured gravimetrically at 298 K using a BELSORP-max (Microtrac BEL Corp.) (ESI† Fig. S2), show that water is adsorbed in the micropores. Water was of Milli-Q purity grade (18.3 MΩ cm) and produced using a deionization apparatus (Milli-Q Direct 8) from EMD Millipore Corp. DSC measurements were performed at a scanning rate of 2 K min−1 in the range from 298 K to 163 K, using a Pyris 1 (PerkinElmer Inc.) apparatus equipped with a liquid nitrogen cooling system. The obtained data showed no peaks due to crystallization indicating that water confined in both of OMCs remains in the liquid state within this temperature range. The samples were packed in aluminum cells.
3. Experiments
Introduction to quasielastic neutron scattering.
In a QENS experiment the relevant measured quantity is the double differential scattering cross section,  , which can be directly related to the dynamic structure factor, S(Q,E), representing the probability that a neutron is scattered by the sample exchanging a momentum ħQ = ħ(kf − ki) and energy E = Ef − Ei; kf and ki and Ef and Ei are the final and initial neutron wavevector and energy respectively. For isotropic samples,
, which can be directly related to the dynamic structure factor, S(Q,E), representing the probability that a neutron is scattered by the sample exchanging a momentum ħQ = ħ(kf − ki) and energy E = Ef − Ei; kf and ki and Ef and Ei are the final and initial neutron wavevector and energy respectively. For isotropic samples, 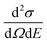 only depends on the modulus of the exchanged wavevector Q = |Q|. The neutrons are scattered by the nuclei and, because of the way the neutron scattering probability depends on the nuclear spin and isotopic state of the nucleus, the scattering signal is divided into the sum of a coherent contribution, which carries information on the relative position and motion of the atoms, and an incoherent term which relays information on the motion of the individual atom only. At low Q, the coherent small angle scattering from the structure of the OMC matrix is the dominant contribution. At the same time, the incoherent scattering cross section of hydrogen is much larger than that of any other element in our sample. Thus, the incoherent scattering signal, Sinc(Q,E), is equal to the hydrogen single particle dynamic structure factor, Sinc(Q,E) = SsH(Q,E) which is the Fourier transform of the hydrogen single particle Intermediate Scattering Function (ISF), IsH(Q,t) = Iinc(Q,t):
only depends on the modulus of the exchanged wavevector Q = |Q|. The neutrons are scattered by the nuclei and, because of the way the neutron scattering probability depends on the nuclear spin and isotopic state of the nucleus, the scattering signal is divided into the sum of a coherent contribution, which carries information on the relative position and motion of the atoms, and an incoherent term which relays information on the motion of the individual atom only. At low Q, the coherent small angle scattering from the structure of the OMC matrix is the dominant contribution. At the same time, the incoherent scattering cross section of hydrogen is much larger than that of any other element in our sample. Thus, the incoherent scattering signal, Sinc(Q,E), is equal to the hydrogen single particle dynamic structure factor, Sinc(Q,E) = SsH(Q,E) which is the Fourier transform of the hydrogen single particle Intermediate Scattering Function (ISF), IsH(Q,t) = Iinc(Q,t):| | | SsH(Q,E) = FT{IsH(Q,t)} = FT{〈exp[−QrH(t) + QrH(0)]〉} | (1) |
where FT{![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) } indicates a Fourier transformation in time, 〈
} indicates a Fourier transformation in time, 〈![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 〉 represents an ensemble average and rH(t) is the position of a hydrogen atom at time t.
〉 represents an ensemble average and rH(t) is the position of a hydrogen atom at time t.
3.1 Modeling of the data
The single particle dynamics of the hydrogen atoms in the water molecules can be modeled assuming an ISF in the form of a stretched exponential decay:| |  | (2) |
where IimmH(T) represents the temperature dependent fraction of hydrogens immobile over the accessible time window. Such a fraction is zero in bulk water but it could be non-negligible in confinement in the presence of the strong interfacial interaction between water and the confined surface. In the QENS literature, the fraction of immobile scattering is often referred to as the Elastic Incoherent Structure Factor (EISF).21 However, this term more appropriately refers to the spatial Fourier transform of the space explored by the incoherent scatterer in its motion with respect to an (immobile) point of reference, e.g. the center of mass of a molecule, and the center of a confined cavity; in these cases, the EISF is Q dependent. Within the picture outlined above, for the hydrated OMC samples, the elastic contribution is only related to the fraction of immobile hydrogen atoms and as such Q is independent. The description of the single particle ISF of water with a stretched exponential function, with both the characteristic time, τ, and the stretching exponent, β, dependent on both Q and temperature, was originally proposed on the basis of strong coupling between density fluctuation and single particle dynamics in the extensively hydrogen bonded supercooled water.33 This approach was successfully extended to confined34 and interfacial water.35 More recently, it has been shown that a sum of two exponential decays is suitable for the dynamics of bulk water and other liquids.36,37 However, in the case of confined water it is still reasonable to expect a distribution of relaxation times originating from the different local environments experienced by the confined water molecules. A stretched exponential decay is a common phenomenological approach to describe such a distribution of relaxation processes without employing further assumptions in the model. In the limit of β equals 1, the stretched exponential reverts to a simple exponential decay indicating the absence of a distribution of relaxation time. Under these conditions, introducing an additional relaxation process to account for localized dynamics or rotations would be beyond what can be reliably extracted from the data. Moreover, from the extensive Molecular Dynamics work on the SPC/E model of water, it has been shown that at Q values smaller than ≈1 Å−1,38 a stretched exponential decay within 10% is a good approximation for the single particle dynamics of the hydrogen atoms in the water molecules, where most of the dynamics can be associated with the center of mass motion of the water molecules.
As far as the coherent scattering contribution from the matrix is concerned, it can be assumed immobile on the length scales and time scales probed, Icoh(Q).
3.2 Instrumentation
The QENS experiments were carried out at the National Institute of Standards and Technology (NIST) Center for Neutron Research using disk chopper time-of-flight (DCS),39 High-Flux Backscattering (HFBS),40 and neutron spin-echo (NSE) spectrometers.41 The DCS is a time-of-flight direct geometry spectrometer. It was operated in its low-resolution configuration using 5 Å and 9 Å incoming wavelengths. In the former case, the instrumental resolution was ≈100 μeV whereas in the latter it was ≈20 μeV as measured using a run of the same sample at a temperature of ≈20 K. The use of two different wavelengths allowed the study of dynamical processes in a wider time range from ≈2 ps to 100 ps. A measurement on a standard vanadium sample was used for detector efficiency normalization. After subtraction of the empty can scattering, the data were reduced to spectra at constant Q using the Mslice routine in DAVE.42 The so obtained dynamic structure factors were Fourier transformed to the time domain after deconvolution of the instrumental energy resolution using DAVE software. The obtained I(Q,t) data from the different wavelengths used could thus be merged together in a range of Qs between ≈0.4 Å−1 and ≈1.1 Å−1. If this would not have been done, a complex global fitting procedure should have been implemented. HFBS is an inverse geometry spectrometry technique where the final energy of the scattered neutron is fixed by the Si 111 reflection of the analyzer crystals. The incoming neutron wavelength is varied by Doppler shifting the energies of the neutrons reflected by a moving a monochromator with Si 111 crystals. The Doppler was operated at a frequency that allowed data collection in a ±10 μeV energy window with an instrumental energy resolution of ≈0.8 μeV. A measurement on a standard vanadium sample was used for detector efficiency normalization. The data were reduced to S(Q,E) spectra using routines available in DAVE, and Fourier transform of the data was not necessary. The Neutron Spin Echo spectrometer measures the loss of polarization of a beam processing through two identical magnets located before and after the sample, which can be related to the Fourier transform of the dynamics structure factor, i.e. the intermediate scattering function. Thus, the NSE spectrometer works in the time domain and the instrumental resolution effect can be eliminated during the reduction process. Because the coherent scattering process does not change the neutron spin state whereas the incoherent scattering has a 2/3 probability of flipping it, the NSE results are a combination, not the simple sum as for DCS and HFBS, of the coherent and incoherent ISFs:| |  | (3) |
A measurement of the beam polarization when effectively the precession field is off amounts to a static (t = 0), polarized diffraction experiment which provides information on the total, as well as on the ratio of the coherent and incoherent, scattering as a function of Q.43
Using the NSE spectrometer, the experiments were performed using an incoming wavelength of λ = 5 Å (for OMC-1) and λ = 6 Å (for OMC-2) with Δλ/λ ≈ 20%, at a Q value of 0.70 Å−1. The data were collected in the time range from 40 ps to 10 ns for the OMC-1 sample and from 40 ps to 17.5 ns for the OMC-2 sample. In all cases, the samples were contained in an annular aluminum can with a thickness less than 1 mm in order to ensure transmission greater than ≈90%, thus minimizing multiple scattering contributions. The sample temperature was controlled using a closed cycle refrigerator with an accuracy of ≈0.5 K. The data were collected at different temperatures using the three instruments, matching the sample dynamics at a specific temperature to the instrumental accessible time window. In all cases a measurement of the same sample at temperatures <20 K was used to determine the instrumental resolution.
4. Results and discussion
Fig. 2 shows the results of polarized diffraction measurements performed using a NSE spectrometer. Although the Q resolution of the instrument is relatively poor, ≈20%, the NSE spectrometer allows the separation of the coherent and incoherent contributions and investigation of a relatively wide Q range, extending to Q values as low as 0.1 Å−1. The comparison between the hydrated and dry samples confirms, as expected, that a significant incoherent contribution is only present in the hydrated samples, originating from the hydrogens in the water. The coherent contribution originates mostly from the carbon matrix scattering and extends to Q as high as 1 Å−1, likely because of the presence of micropores whose small sizes induce scattering at Q values larger than usually accessible on small angle scattering instruments. The results also indicate that the Q dependence of the coherent scattering depends on the hydration of the sample, which can be rationalized in terms of the different contrast induced by the water molecules over different length scales depending on which pores (micropores or mesopores) are hydrated. In the OMC samples most of the water is believed to hydrate the micropores,29–32 and hence the scattered intensity related to these structures changes whereas that related to the mesopores is affected less. This occurrence precludes the possibility to reliably subtract the contribution of the matrix using a measurement of the dry sample. For this reason, the analyzed spectra will contain scattering originating from both the incoherent scattering of the water molecules and the coherent scattering of the matrix; the latter is however expected to be static, as mentioned in Section 3.2.
 |
| | Fig. 2 Polarized diffraction measurements performed using the NSE spectrometer on the two investigated samples, in the dry and hydrated form. | |
Fig. 3 shows the intermediate scattering functions as obtained using the NSE spectrometer for the two samples at different temperatures. The unusual shape of the experimental data, which normally decay from 1 at short times to zero at longer times, is due to the non-negligible presence of both coherent and incoherent contributions. The data were analyzed using the following equation:
| |  | (4) |
 |
| | Fig. 3 NSE data together with the fitting results according to eqn (4) where the stretching exponent value has been fixed. | |
A preliminary analysis of the data using eqn (4) (see the ESI† Fig. S3 and Table S1) yields a value of the stretching exponent, β, independent of temperature within experimental uncertainties (β = 0.67 ± 0.04 for OMC-1 and β = 0.58 ± 0.4 for OMC-2, ESI† Fig. S4). Thus, the data were again analyzed by keeping β fixed to its average value. Eqn (4) can be derived from eqn (2) and (3) within the model described above:
| |  | (5) |
Eqn (4) and (5) imply the following identities:
| |  | (6) |
and
| |  | (7) |
From the polarized diffraction measurements, the ratio between the coherent and incoherent intensities can be determined. In particular, 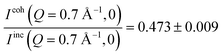 for OMC-1 and
for OMC-1 and  for OMC-2. Note that the
for OMC-2. Note that the  ratio is temperature independent as the structure of the sample did not change. Thus, the temperature dependent immobile water fraction values, IimmH(T), could be determined using eqn (7) from the A(Q = 0.7 Å−1,T) fitting results from the NSE data. A similar analysis could be performed for the DCS data as follows. As mentioned above, the DCS data were analyzed in the time domain after Fourier transformation of the spectra and normalization by the data collected at 20 K, representing the instrumental energy resolution, Res(Q,t), multiplied by the sample static structure factor at T = 20 K:
ratio is temperature independent as the structure of the sample did not change. Thus, the temperature dependent immobile water fraction values, IimmH(T), could be determined using eqn (7) from the A(Q = 0.7 Å−1,T) fitting results from the NSE data. A similar analysis could be performed for the DCS data as follows. As mentioned above, the DCS data were analyzed in the time domain after Fourier transformation of the spectra and normalization by the data collected at 20 K, representing the instrumental energy resolution, Res(Q,t), multiplied by the sample static structure factor at T = 20 K:
| | 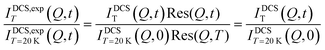 | (7a) |
It should be mentioned that the DCS data in the time domain are normalized to the total intensity of the resolution sample, IDCST=20K(Q,t). Here,  represents the total scattering intensity at a specific Q value. It is worth noticing that the NSE data are normalized by INSE(Q) which is obtained by a static measurement, i.e. no analysis of the energy of the scattered neutrons is performed; on the other hand, for DCS, the total scattered intensity is calculated by an integral in the experimental energy window. In summary, however, an equation similar to that used to analyze the NSE data can be adopted for the fitting of the DCS spectra (see the ESI† Fig. S5):
represents the total scattering intensity at a specific Q value. It is worth noticing that the NSE data are normalized by INSE(Q) which is obtained by a static measurement, i.e. no analysis of the energy of the scattered neutrons is performed; on the other hand, for DCS, the total scattered intensity is calculated by an integral in the experimental energy window. In summary, however, an equation similar to that used to analyze the NSE data can be adopted for the fitting of the DCS spectra (see the ESI† Fig. S5):
| |  | (8) |
Fig. 4 shows the DCS data for T = 290 K at different Q values. In this case, as opposed to the NSE case, the data decrease with increasing t because the spectra are the sum of the coherent and incoherent contributions. It can be seen that  is smaller than 1, which could be explained by the presence of fast dynamics outside the DCS energy window or to the loss of total spectral intensity due to atomic vibrations, i.e. the Debye–Waller factor.21 This latter phenomenon seems to be dominant, in fact the values of
is smaller than 1, which could be explained by the presence of fast dynamics outside the DCS energy window or to the loss of total spectral intensity due to atomic vibrations, i.e. the Debye–Waller factor.21 This latter phenomenon seems to be dominant, in fact the values of  obtained from the fitting could be well analyzed using an expression for the Debye–Waller factor:
obtained from the fitting could be well analyzed using an expression for the Debye–Waller factor:
| |  | (9) |
where 〈
u2〉 represents the mean square displacement. The values obtained for 〈
u2〉, of the order of 0.2 Å
2, are in agreement with previous reports from the literature (ESI
† Fig. S6). At 290 K, the long time plateau component,
p(
Q,
T = 290 K), was determined from the fitting of the data according to
eqn (8). Its
Q dependence has been modeled, purely phenomenologically, with a simple decay function (ESI
† Fig. S7):
| | 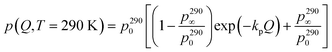 | (10) |
where
kp is temperature independent because the
Q decay originates from the coherent scattering of the matrix which does not change with
T. The instrumental
Q resolution and experimental uncertainty do not warrant more insightful analysis than the phenomenological
eqn (10). The obtained values for the parameters
p2900,
kp, and
p290∞ are reported in
Table 2 for both samples.
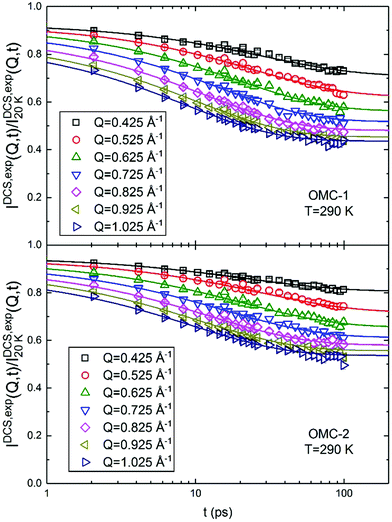 |
| | Fig. 4 Fourier transform DCS data at T = 290 K. The continuous lines are the result of the fits according to eqn (7) with p values fixed according to the parametrization of Table 2 and the stretching exponent β fixed to its Q averaged value. | |
Table 2 Parameters for the parametrization of p(Q) as obtained from the fitting of the DCS data at 290 K
|
|
p
2900
|
k
p (Å−1) |
p
290∞
|
| OMC-1 |
1.95 ± 0.45 |
3.93 ± 0.64 |
0.49 ± 0.01 |
| OMC-2 |
2.07 ± 0.31 |
4.10 ± 0.51 |
0.59 ± 0.01 |
p(Q,T) can be related to the immobile fraction of the hydrogen atoms and the coherent scattering contribution through the following equations:
| |  | (11) |
which implies:
| |  | (12) |
Based on the assumption that the Debye–Waller factor is mostly responsible for the reduction of the total spectral intensity within the DCS energy window, the following approximation is valid:
| |  | (13) |
So that
eqn (10) can be inverted to determine the immobile water fraction from the DCS results and the polarized diffraction measurements:
| |  | (14) |
Thus, combining the results from the polarized diffraction measurement for  with the parametric expression of p(Q), the estimated values of IimmH(T = 290 K) are obtained from eqn (14) and shown in Fig. 5. As expected, within experimental uncertainties the obtained values of IimmH do not depend on Q, yielding an average value of 0.36 ± 0.01 for OMC-1 and 0.46 ± 0.02 for OMC-2, as shown in Fig. 5.
with the parametric expression of p(Q), the estimated values of IimmH(T = 290 K) are obtained from eqn (14) and shown in Fig. 5. As expected, within experimental uncertainties the obtained values of IimmH do not depend on Q, yielding an average value of 0.36 ± 0.01 for OMC-1 and 0.46 ± 0.02 for OMC-2, as shown in Fig. 5.
 |
| | Fig. 5 (a and b) Immobile hydrogen fraction as obtained from the parametrized expression of p(Q) and the polarized diffraction data using eqn (14). The data are consistent, within error bars, with a Q independent value of IimmH, which is indicated by the dashed red lines, as obtained by the weighted average of the data points shown. (c and d) Temperature dependence of the immobile hydrogen fraction. | |
The temperature dependence of IimmH(T) was determined combining the results obtained from NSE with those from DCS, calculated using eqn (7) and (14), respectively. Panels (c) and (d) of Fig. 5 show an increase of IimmH by about 40% with decreasing temperatures from 290 K to 190 K, which within the probed range can be described with a linear parametrization:
| | | IimmH(T) = 0IimmH + slopeIimmH × T | (15) |
where the obtained parameters are reported in
Table 3. The obtained results suggest a slightly larger immobile water fraction in OMC-2 though it is not outside the experimental uncertainty. The increase of
IimmH(
T) with decreasing temperature is most likely due to the reduced thermal energy which does not allow the water molecules to escape the local landscape traps.
Table 3 Parameters for the parametrization of IimmH(T) as obtained from the fitting of the NSE and DCS results. Notice that 0IimmH is larger than 1 for OMC-1, which indicates that the linear parametrization cannot be extended below the temperature range probed
|
|
0
I
immH
|
slope
I
immH
|
| OMC-1 |
1.17 ± 0.08 |
−0.0028 ± 0.0003 |
| OMC-2 |
1.00 ± 0.06 |
−0.0019 ± 0.0003 |
Interestingly, no discernible immobile fraction was present for water confined in MCM-41, especially at room temperature.23 Within hydrophilic substrates, the immobile water fraction is explained as water molecules adsorbed on the confined surfaces. In the hydrophobic OMC samples here, such an explanation seems counter intuitive. Therefore, this result seems to point to the relevance of the pore size, which is smaller in the OMC slit micropores than in MCM-41, to form a population of water molecules immobile on the nanosecond timescale. In the following sections of this paper, the results reported are obtained by analyzing the data fixing the fraction of immobile water, as well as the derived parameter p(Q,T) (for DCS and HFBS) and A(Q = 0.7 Å−1,T) (for the NSE data), to the values obtained using eqn (15). A(Q = 0.7 Å−1,T) was obtained using eqn (6) from the values of IimmH(T) and  . For HFBS and DCS, p(Q,T) was obtained assuming that the Q dependence of p does not change with temperature so that:
. For HFBS and DCS, p(Q,T) was obtained assuming that the Q dependence of p does not change with temperature so that:
| | 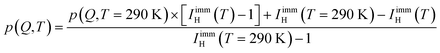 | (16) |
We can now turn our focus to the timescale of the water dynamics as a function of the probed length scale, Q, and temperature.
In the fit of the DCS data, the stretching exponent does not show any Q dependence (ESI† Fig. S8) and it has been fixed to its averaged Q value in a second iteration of the analysis.
The analysis of the HFBS data was carried out in the energy domain using as a fitting function the Fourier transform of the expression reported in eqn (7):
| |  | (17) |
where Res(
Q,
E) is the experimentally determined instrumental energy resolution function and BKG(
Q) is a background which also takes into account fast dynamical processes outside the HFBS energy window.
Initially the data were analyzed allowing the value of β to vary as a function of Q and T. However, as shown in the ESI,† within experimental uncertainties, β does not vary with Q and was later fixed to its average value (ESI† Fig. S8). The obtained values fluctuate between ≈0.5 and ≈0.7. Typical fits are shown in Fig. 6. It should be kept in mind that the value of β is strongly coupled with τ and the instrumental resolution, so that the real uncertainty is larger than the error bar determined from the fit. Previous studies on confined water have often indicated that the value of the stretching exponent can be considered Q and T independent. In the past a value of β = 0.5 has been successfully employed.23 The current data yield Q averaged values of beta, 〈β〉Q, generally larger than 0.6 with no clear temperature dependence (ESI† Fig. S8 and S9). This finding indicates that the dynamics of the mobile water molecules in OMC-1 and OMC-2 is slightly more homogeneous or Debye-like than in other hydrophilic confining mediums. This result has to be qualified considering that a significant fraction of the hydrating water molecules, the immobile water fraction, was not sampled here. The results reported in the following refer to the analysis of the data using 〈β〉Q for the analysis. As the relaxation time depends on the values of the stretching exponent, to quantify the water mobility for different stretching exponents, an average relaxation time can be calculated:
| |  | (18) |
 |
| | Fig. 6 Typical spectra collected on HFBS together with the fits according to eqn (7). | |
The obtained results for 〈τ〉 are shown in Fig. 7. Several models have been proposed and applied for the Q dependence of the QENS spectra from water. For a heterogeneous diffusion process, in which all the scatterers exhibit a diffusive motion with a distribution of diffusion coefficients, a stretched exponential decay of the ISF would be observed, as mentioned above, and the relaxation time would scale with the square of Q, i.e. τ ∼ Q−2, as for a simple diffusion process.44 In bulk water, the Q dependence of the inverse of the characteristic relaxation time is analyzed in terms of a random jump diffusion model which yields a Q−2 dependence (diffusive behavior) at low Q and a Q-independent behavior (localized motion) at high Q.45 Some studies have analyzed the QENS spectra from water in nanoconfinement according to the Volino and Dianoux model; such a theory predicts a Q-independent behavior of the inverse of the characteristic relaxation time at Q values smaller than the inverse of the pore sizes and a Q2 dependence at higher Q.46 For supercooled water, the hydrogen bonding caging effects introduce stretching in the relaxation behavior of the water molecules and according to the Relaxing Cage Model (RCM)33 the average relaxation time is fitted to a power law:
 |
| | Fig. 7 The Q dependence of the average relaxation time as obtained from the DCS (a and b) and HFBS (c and d) data. The straight lines are fits to a power law, eqn (19). | |
This expression reduces to the heterogeneous diffusion expression when γ = 2/β. However, for supercooled bulk water, it is assumed that in the hydrodynamics limit, i.e. for Q small enough, β → 1 and γ → 2; this limit is however not attainable in QENS measurements. Eqn (19) and the RCM have been successfully applied to analyze data from water confined within different nanoscopic pores22 and on the surface of various hydrated biological and inorganic materials.35,47 In these cases, of course, both heterogeneities in the microstructure and intrinsically non-Debye relaxation behavior can result in QENS spectra with non-Lorentzian line shapes.
In the present work, the obtained 〈τ〉 was analyzed according to the RCM, using eqn (19), as no clear plateauing of the data can be consistently discerned at low or high Q, as shown in Fig. 7. Fig. 8 shows the temperature dependence of the parameters of eqn (19). Panels (a) and (c) of Fig. 8 show that the results for A〈τ〉 from HFBS and DCS are not in agreement within the experimental error bars, especially in the case of the OMC-1 sample. This occurrence is not unusual and can ultimately be traced back to an imperfect modeling of the data, which is necessarily a simplification, resulting in these types of inconsistencies when instruments with different experimental resolutions and dynamic windows are employed in conjunction. These problems notwithstanding, the obtained agreement is sufficient to estimate the time scale of water dynamics and its temperature dependence. The Q dependence of τ, shown in panels (c) and (d) of Fig. 8, provides information regarding the geometry of the motion. In the investigated Q range, the product βγ takes values smaller than 0 and larger than −2. This finding indicates that for the length scale of relevance here, from  to
to  the dynamics is not localized as this would imply a Q independent 〈τ〉.
the dynamics is not localized as this would imply a Q independent 〈τ〉.
 |
| | Fig. 8 Temperature dependence of the parameters describing the behavior of 〈τ〉 according to eqn (19). | |
At the same time, within a certain approximation, a heterogeneous diffusion scenario seems to apply. Within this picture, the non-exponentiality of the observed ISF is ought to be a distribution of diffusive processes, likely connected to a distribution of microscopic environment; βγ would be expected to take values close to −1, for β ≈ 0.5, as observed here. The homogeneous scenario assumes instead that the dynamics of all the probed scatterers is the same and non-exponential in character, which would result in βγ values of ≈−2. The heterogeneous scenario was found to apply for water confined in hydrophilic and partially hydrophobic mesoporous silica matrices, MCM-41.48 In this context, the above mentioned larger values of 〈β〉Q obtained here with respect to the stretching exponent values reported for water in hydrophilic nanoconfinement indicate a narrower distribution of diffusivities and in turn a more homogenous microscopic landscape experienced by the water molecules. In this regard, therefore, the dynamics of water confined in the hydrophobic OMC matrices is similar to that observed in hydrophilic nanopores. It is worth noticing that as temperature is lowered the values of βγ tend to increase, signalling a slight tendency to more localized dynamics. This trend was also observed in hydrophilic nanopores but in a much more pronounced manner with a sharp reduction in the absolute values of βγ below 230 K. Fig. 9 shows an Arrhenius plot of the temperature dependence on the relaxation time at Q ≈ 0.7 Å−1, for simplicity. Almost no difference can be discerned between the behaviour of water in OMC-1 and OMC-2. This could be understood considering that in both cases water is believed29–32 to be confined in the micropores of the samples, which had similar sizes. These results would confirm that the characteristic of the mesopores in the samples is not relevant and only a negligible amount, if any, of water is confined in these larger pores. Fig. 9 also shows the comparison between our results and those of bulk water as well as those for water confined in other nanoscopic matrices, both hydrophilic and hydrophobic. Around room temperature, the dynamics in the micropores of the OMC matrices is slower than that of bulk water. As the temperature is lowered we observe only a slight tendency of non-Arrhenius behavior. This is qualitatively different from what has been observed in bulk water and in hydrophilic confinement where the Vogel–Fulcher–Tammann law23 was used to describe the slowing down of the dynamics. Below 250 K (where there are no available data for bulk water), the characteristic relaxation times lie in between those measured in hydrophilic, MCM-41,49 or partially hydrophobic, MCM-41-SM,48 confinement and in Single Wall NanoTube (SWNT) and Double Wall NanoTube (DWNT).50 No evidence of a fragile-to-strong (FTS) crossover, which has been observed for the dynamics of water in other confined matrices, could be observed here in the investigated temperature range. The results shown in Fig. 9 indicate that the hydrogen bonding network of water confined in the micropores of OMC is strongly frustrated and it is not allowed to develop as temperature decreases. This effect could be related to the size of the pores, but it could also be due to the hydrophobic nature of the confined surfaces. This can be confirmed by a comparison between the results obtained for water confined in the hydrophilic MCM-41, partially hydrophobic MCM-41-SM, and water in OMC. The timescale of motions for water confined in these matrices at room temperature is similar; however, as temperature decreases the non-Arrhenius behavior is less pronounced as the degree of the hydrophobicity of the matrix is increased. Moreover, the FTS crossover is not observed in the partially hydrophobic MCM as well as in the OMC. These occurrences are explained by a lack of an extensive tetrahedral hydrogen bond network in the system.51,52
 |
| | Fig. 9 The temperature dependence of 〈τ〉 at Q = 0.70 Å−1 as measured using the three spectrometers. The results are compared with the behavior of bulk water as well as that of water confined in other nanoscopic matrices, both hydrophilic and hydrophobic.1 | |
5. Conclusion
Two hydrophobic OMC matrices were used in this study to investigate the dynamics of water in extreme hydrophobic confinement. Models developed to describe the dynamics of water in hydrophilic nanoporous confinement are able to describe the dynamics observed here as well. A significant fraction of water (≈40%), immobile on the investigated time scales was observed, which slowly increases with reducing temperature. The mobile fraction of water has heterogeneous diffusive dynamics ought to be the distribution of the microscopic environments experienced. As the temperature was lowered, the time scale of motion was faster than that observed in hydrophilic and partially hydrophobic confinement, with only a slight non-Arrhenius behavior; these findings, together with the absence of a FTS crossover, indicate that the hydrogen bond network of water is not developed in the hydrophobic confinement. However this occurrence due to the size (the micropores of ≈8 Å) or the hydrophobic nature of the confining wall could not be ascertained. Finally, the two samples investigated, differing only in the pore size distribution and the presence or absence of nanopores, only show a minor difference in the fraction of immobile water. This finding suggests, in agreement with previous reports,29–32 that in these OMCs the hydration water is confined mainly within the micropores. A better understanding of the water dynamical properties in OMCs at the nanoscale is a necessary component for a rational design of future applications of these systems in electrochemistry, catalysis, and purification systems.
Note
Throughout the paper uncertainties and error bars represent one standard deviation.
Disclaimer
Certain commercial equipment, instruments, or materials (or suppliers, or software, etc.) have been identified in this paper to foster understanding. Such identification does not imply recommendation or endorsement by the National Institute of Standards and Technology, nor does it imply that the materials or equipment identified are necessarily the best available for the purpose. Throughout the paper uncertainties and error bars represent one standard deviation.
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
The authors thank Professor Syunsuke Tanaka of Kansai University for providing authentic samples of OMC. The research by K. Ito and S.H. Chen at MIT related to this work during 2014–16 was supported by DOE grant DE-FG02-90ER45429. Access to the Neutron Spin Echo and the HFBS spectrometers was provided by the Center for High Resolution Neutron Scattering, a partnership between the National Institute of Standards and Technology and the National Science Foundation under Agreement No. DMR-1508249.
References
- In panel (b), the data taken on NSE at the two lowest temperature should be taken with some scrutiny as the observed relaxation time is much longer than the probed time window. The data have been included though considering that with the other fitting parameters having been fixed the error bars would provide a reliable confidence range.
-
N. Giovambattista, P. J. Rossky and P. G. Debenedetti, in Annual Review of Physical Chemistry, ed. M. A. Johnson and T. J. Martinez, Annual Reviews, Palo Alto, 2012, vol. 63, pp. 179–200 Search PubMed.
-
S. H. Chen and M. C. Bellissentfunel, in Hydrogen Bond Networks, ed. M. C. BellissentFunel and J. C. Dore, Kluwer Academic Publ, Dordrecht, 1994, vol. 435, pp. 307–336 Search PubMed.
- Y. Zhang, A. Faraone, W. A. Kamitakahara, K. H. Liu, C. Y. Mou, J. B. Leao, S. Chang and S. H. Chen, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 12206–12211 CrossRef CAS PubMed.
- S. Cerveny, F. Mallamace, J. Swenson, M. Vogel and L. Xu, Chem. Rev., 2016, 116, 7608–7625 CrossRef CAS.
- P. H. Poole, F. Sciortino, U. Essmann and H. E. Stanley, Nature, 1992, 360, 324–328 CrossRef CAS.
- J. C. Rasaiah, S. Garde and G. Hummer, Annu. Rev. Phys. Chem., 2008, 59, 713–740 CrossRef CAS PubMed.
- A. Wallqvist and B. J. Berne, J. Phys. Chem., 1995, 99, 2893–2899 CrossRef CAS.
- K. Lum, D. Chandler and J. D. Weeks, J. Phys. Chem. B, 1999, 103, 4570–4577 CrossRef CAS.
- N. Choudhury, J. Phys. Chem. B, 2008, 112, 6296–6300 CrossRef CAS PubMed.
- J. Mittal and G. Hummer, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 20130–20135 CrossRef CAS PubMed.
- A. J. Patel, P. Varilly and D. Chandler, J. Phys. Chem. B, 2010, 114, 1632–1637 CrossRef CAS PubMed.
- A. Eftekhari and Z. Fan, Mater. Chem. Front., 2017, 1, 1001–1027 RSC.
- S. R. Accordino, J. M. M. d. Oca, J. A. R. Fris and G. A. Appignanesi, J. Chem. Phys., 2015, 143, 154704 CrossRef PubMed.
- E. Mamontov, Y. Yue, J. Bahadur, J. Guo, C. I. Contescu, N. C. Gallego and Y. B. Melnichenko, Carbon, 2017, 111, 705–712 CrossRef CAS.
- P. J. Rossky, Faraday Discuss., 2010, 146, 13–18 RSC.
- T. G. Lombardo, N. Giovambattista and P. G. Debenedetti, Faraday Discuss., 2009, 141, 359–376 RSC.
- S. Tanaka, A. Doi, N. Nakatani, Y. Katayama and Y. Miyake, Carbon, 2009, 47, 2688–2698 CrossRef CAS.
- J. S. Beck, J. C. Vartuli, W. J. Roth, M. E. Leonowicz, C. T. Kresge, K. D. Schmitt, C. T. W. Chu, D. H. Olson, E. W. Sheppard, S. B. McCullen, J. B. Higgins and J. L. Schlenker, J. Am. Chem. Soc., 1992, 114, 10834–10843 CrossRef CAS.
-
N. N. A. S. Tanaka, in Nanoporous Materials Synthesis and Applications, ed. Q. Xu, CRC Press, Boca Raton, FL 33487-2742, 2013, ch. 4, p. 99 Search PubMed.
-
M. Bée, Quasielastic neutron scattering: principles and applications in solid state chemistry, biology and materials science, A. Hilger, Bristol, Philadelphia, 1988 Search PubMed.
- A. Faraone, L. Liu, C. Y. Mou, P. C. Shih, J. R. D. Copley and S. H. Chen, J. Chem. Phys., 2003, 119, 3963–3971 CrossRef CAS.
- A. Faraone, L. Liu, C. Y. Mou, C. W. Yen and S. H. Chen, J.
Chem. Phys., 2004, 121, 10843–10846 CrossRef CAS PubMed.
- K. Yoshida, T. Yamaguchi, S. Kittaka, M. C. Bellissent-Funel and P. Fouquet, J. Chem. Phys., 2008, 129, 11 Search PubMed.
- X. Q. Chu, A. I. Kolesnikov, A. P. Moravsky, V. Garcia-Sakai and S. H. Chen, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2007, 76, 6 CrossRef PubMed.
- X. Q. Chu, K. H. Liu, M. S. Tyagi, C. Y. Mou and S. H. Chen, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2010, 82, 4 CrossRef PubMed.
- S. M. Chathoth, E. Mamontov, A. I. Kolesnikov, Y. Gogotsi and D. J. Wesolowski, EPL, 2011, 95, 6 Search PubMed.
- K. S. W. Sing, Colloids Surf., 1989, 38, 113–124 CrossRef CAS.
- Y. Hanzawa and K. Kaneko, Langmuir, 1997, 13, 5802–5804 CrossRef CAS.
- T. Horikawa, N. Sakao and D. D. Do, Carbon, 2013, 56, 183–192 CrossRef CAS.
- D. D. Do, S. Junpirom and H. D. Do, Carbon, 2009, 47, 1466–1473 CrossRef CAS.
- D. D. Do and H. D. Do, Carbon, 2000, 38, 767–773 CrossRef CAS.
- S. H. Chen, C. Liao, F. Sciortino, P. Gallo and P. Tartaglia, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1999, 59, 6708–6714 CrossRef CAS.
- J. M. Zanotti, M. C. Bellissent-Funel and S. H. Chen, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1999, 59, 3084–3093 CrossRef CAS.
- E. Fratini, S. H. Chen, P. Baglioni and M. C. Bellissent-Funel, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2001, 64, 4 CrossRef.
- J. Qvist, H. Schober and B. Halle, J. Chem. Phys., 2011, 134, 20 CrossRef PubMed.
- E. Mamontov, Chem. Phys. Lett., 2012, 530, 55–60 CrossRef CAS.
- S. H. Chen, P. Gallo, F. Sciortino and P. Tartaglia, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1997, 56, 4231–4243 CrossRef CAS.
- J. R. D. Copley and J. C. Cook, Chem. Phys., 2003, 292, 477–485 CrossRef CAS.
- A. Meyer, R. M. Dimeo, P. M. Gehring and D. A. Neumann, Rev. Sci. Instrum., 2003, 74, 2759–2777 CrossRef CAS.
-
N. Rosov, S. Rathgeber and M. Monkenbusch, in Scattering from Polymers: Characterization by X-Rays, Neutrons, and Light, ed. P. Cebe, B. S. Hsiao and D. J. Lohse, 2000, vol. 739, pp. 103–116 Search PubMed.
- R. T. Azuah, L. R. Kneller, Y. M. Qiu, P. L. W. Tregenna-Piggott, C. M. Brown, J. R. D. Copley and R. M. Dimeo, J. Res. Natl. Inst. Stand. Technol., 2009, 114, 341–358 CrossRef CAS.
- A. M. Gaspar, S. Busch, M. S. Appavou, W. Haeussler, R. Georgii, Y. X. Su and W. Doster, Biochim. Biophys. Acta, Proteins Proteomics, 2010, 1804, 76–82 CrossRef CAS PubMed.
- A. Arbe, J. Colmenero, M. Monkenbusch and D. Richter, Phys. Rev. Lett., 1998, 81, 590–593 CrossRef CAS.
- J. Teixeira, M. C. Bellissent-Funel, S. H. Chen and A. J. Dianoux, Phys. Rev. A: At., Mol., Opt. Phys., 1985, 31, 1913–1917 CrossRef CAS.
- M. C. Bellissent-Funel, S. H. Chen and J. M. Zanotti, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1995, 51, 4558–4569 CrossRef CAS.
- E. Fratini, S. H. Chen, P. Baglioni and M. C. Bellissent-Funel, J. Phys. Chem. B, 2002, 106, 158–166 CrossRef CAS.
- A. Faraone, K.-H. Liu, C.-Y. Mou, Y. Zhang and S.-H. Chen, J. Chem. Phys., 2009, 130, 134512 CrossRef PubMed.
- Z. Wang, P. Le, K. Ito, J. B. Leão, M. Tyagi and S.-H. Chen, J. Chem. Phys., 2015, 143, 114508 CrossRef PubMed.
- E. Mamontov, C. J. Burnham, S.-H. Chen, A. P. Moravsky, C.-K. Loong, N. R. d. Souza and A. I. Kolesnikov, J. Chem. Phys., 2006, 124, 194703 CrossRef CAS.
- C. E. Bertrand, Y. Zhang and S.-H. Chen, Phys. Chem. Chem. Phys., 2013, 15, 721–745 RSC.
- C. E. Bertrand, K. H. Liu, E. Mamontov and S. H. Chen, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2013, 87, 042312 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c8cp07704e |
| ‡ Present address: Material Measurement Laboratory, Material Science and Engineering Division, National Institute of Standards and Technology, 100 Bureau Drive, Gaithersburg, MD 20899, USA. |
|
| This journal is © the Owner Societies 2019 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article a,
Antonio
Faraone
b,
Madhusudan
Tyagi
bc,
Toshio
Yamaguchi
a,
Antonio
Faraone
b,
Madhusudan
Tyagi
bc,
Toshio
Yamaguchi
 *d and
Sow-Hsin
Chen
*a
*d and
Sow-Hsin
Chen
*a

 , which can be directly related to the dynamic structure factor, S(Q,E), representing the probability that a neutron is scattered by the sample exchanging a momentum ħQ = ħ(kf − ki) and energy E = Ef − Ei; kf and ki and Ef and Ei are the final and initial neutron wavevector and energy respectively. For isotropic samples,
, which can be directly related to the dynamic structure factor, S(Q,E), representing the probability that a neutron is scattered by the sample exchanging a momentum ħQ = ħ(kf − ki) and energy E = Ef − Ei; kf and ki and Ef and Ei are the final and initial neutron wavevector and energy respectively. For isotropic samples, 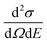 only depends on the modulus of the exchanged wavevector Q = |Q|. The neutrons are scattered by the nuclei and, because of the way the neutron scattering probability depends on the nuclear spin and isotopic state of the nucleus, the scattering signal is divided into the sum of a coherent contribution, which carries information on the relative position and motion of the atoms, and an incoherent term which relays information on the motion of the individual atom only. At low Q, the coherent small angle scattering from the structure of the OMC matrix is the dominant contribution. At the same time, the incoherent scattering cross section of hydrogen is much larger than that of any other element in our sample. Thus, the incoherent scattering signal, Sinc(Q,E), is equal to the hydrogen single particle dynamic structure factor, Sinc(Q,E) = SsH(Q,E) which is the Fourier transform of the hydrogen single particle Intermediate Scattering Function (ISF), IsH(Q,t) = Iinc(Q,t):
only depends on the modulus of the exchanged wavevector Q = |Q|. The neutrons are scattered by the nuclei and, because of the way the neutron scattering probability depends on the nuclear spin and isotopic state of the nucleus, the scattering signal is divided into the sum of a coherent contribution, which carries information on the relative position and motion of the atoms, and an incoherent term which relays information on the motion of the individual atom only. At low Q, the coherent small angle scattering from the structure of the OMC matrix is the dominant contribution. At the same time, the incoherent scattering cross section of hydrogen is much larger than that of any other element in our sample. Thus, the incoherent scattering signal, Sinc(Q,E), is equal to the hydrogen single particle dynamic structure factor, Sinc(Q,E) = SsH(Q,E) which is the Fourier transform of the hydrogen single particle Intermediate Scattering Function (ISF), IsH(Q,t) = Iinc(Q,t):![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) } indicates a Fourier transformation in time, 〈
} indicates a Fourier transformation in time, 〈![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 〉 represents an ensemble average and rH(t) is the position of a hydrogen atom at time t.
〉 represents an ensemble average and rH(t) is the position of a hydrogen atom at time t.








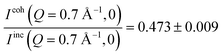 for OMC-1 and
for OMC-1 and  for OMC-2. Note that the
for OMC-2. Note that the  ratio is temperature independent as the structure of the sample did not change. Thus, the temperature dependent immobile water fraction values, IimmH(T), could be determined using eqn (7) from the A(Q = 0.7 Å−1,T) fitting results from the NSE data. A similar analysis could be performed for the DCS data as follows. As mentioned above, the DCS data were analyzed in the time domain after Fourier transformation of the spectra and normalization by the data collected at 20 K, representing the instrumental energy resolution, Res(Q,t), multiplied by the sample static structure factor at T = 20 K:
ratio is temperature independent as the structure of the sample did not change. Thus, the temperature dependent immobile water fraction values, IimmH(T), could be determined using eqn (7) from the A(Q = 0.7 Å−1,T) fitting results from the NSE data. A similar analysis could be performed for the DCS data as follows. As mentioned above, the DCS data were analyzed in the time domain after Fourier transformation of the spectra and normalization by the data collected at 20 K, representing the instrumental energy resolution, Res(Q,t), multiplied by the sample static structure factor at T = 20 K: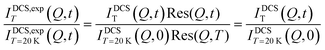
 represents the total scattering intensity at a specific Q value. It is worth noticing that the NSE data are normalized by INSE(Q) which is obtained by a static measurement, i.e. no analysis of the energy of the scattered neutrons is performed; on the other hand, for DCS, the total scattered intensity is calculated by an integral in the experimental energy window. In summary, however, an equation similar to that used to analyze the NSE data can be adopted for the fitting of the DCS spectra (see the ESI† Fig. S5):
represents the total scattering intensity at a specific Q value. It is worth noticing that the NSE data are normalized by INSE(Q) which is obtained by a static measurement, i.e. no analysis of the energy of the scattered neutrons is performed; on the other hand, for DCS, the total scattered intensity is calculated by an integral in the experimental energy window. In summary, however, an equation similar to that used to analyze the NSE data can be adopted for the fitting of the DCS spectra (see the ESI† Fig. S5):
 is smaller than 1, which could be explained by the presence of fast dynamics outside the DCS energy window or to the loss of total spectral intensity due to atomic vibrations, i.e. the Debye–Waller factor.21 This latter phenomenon seems to be dominant, in fact the values of
is smaller than 1, which could be explained by the presence of fast dynamics outside the DCS energy window or to the loss of total spectral intensity due to atomic vibrations, i.e. the Debye–Waller factor.21 This latter phenomenon seems to be dominant, in fact the values of  obtained from the fitting could be well analyzed using an expression for the Debye–Waller factor:
obtained from the fitting could be well analyzed using an expression for the Debye–Waller factor:
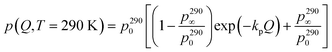





 with the parametric expression of p(Q), the estimated values of IimmH(T = 290 K) are obtained from eqn (14) and shown in Fig. 5. As expected, within experimental uncertainties the obtained values of IimmH do not depend on Q, yielding an average value of 0.36 ± 0.01 for OMC-1 and 0.46 ± 0.02 for OMC-2, as shown in Fig. 5.
with the parametric expression of p(Q), the estimated values of IimmH(T = 290 K) are obtained from eqn (14) and shown in Fig. 5. As expected, within experimental uncertainties the obtained values of IimmH do not depend on Q, yielding an average value of 0.36 ± 0.01 for OMC-1 and 0.46 ± 0.02 for OMC-2, as shown in Fig. 5.
 . For HFBS and DCS, p(Q,T) was obtained assuming that the Q dependence of p does not change with temperature so that:
. For HFBS and DCS, p(Q,T) was obtained assuming that the Q dependence of p does not change with temperature so that: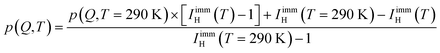




 to
to  the dynamics is not localized as this would imply a Q independent 〈τ〉.
the dynamics is not localized as this would imply a Q independent 〈τ〉.