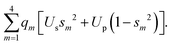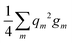Open Access Article
Open Access ArticleRelative stability of diamond and graphite as seen through bonds and hybridizations
Ilya V.
Popov
ab,
Arno L.
Görne
c,
Andrei L.
Tchougréeff
 *abc and
Richard
Dronskowski
*abc and
Richard
Dronskowski
 *cd
*cd
aA.N. Frumkin Institute of Physical Chemistry and Electrochemistry of the Russian Academy of Science, Moscow, Russia
bIndependent University of Moscow, Moscow, Russia
cChair of Solid State and Quantum Chemistry, RWTH Aachen University, 52056 Aachen, Germany. E-mail: andrei.tchougreeff@ac.rwth-aachen.de; drons@HAL9000.ac.rwth-aachen.de
dJülich–Aachen Research Alliance, JARA-HPC, RWTH Aachen University, 52056 Aachen, Germany
First published on 20th May 2019
Abstract
The relative stability of the two most important forms of elemental carbon, diamond and graphite, is readdressed from a newly developed perspective as derived from historically well-known roots. Unlike other theoretical studies mostly relying on numerical methods, we consider an analytical model to gain fundamental insight into the reasons for the quasi-degeneracy of diamond and graphite despite their extremely different covalent bonding patterns. We derive the allotropes’ relative energies and provide a qualitative picture predicting a quasi-degenerate electronic ground state for graphite (graphene) and diamond at zero temperature. Our approach also gives numerical estimates of the energy difference and interatomic separations in good agreement with experimental data and recent results of hybrid DFT modeling, although obtained with a much smaller numerical but highly transparent effort. An attempt to extend this treatment to the lowest energy allotropes of silicon proves to be successful as well.
Introduction
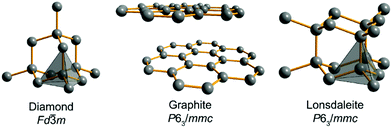
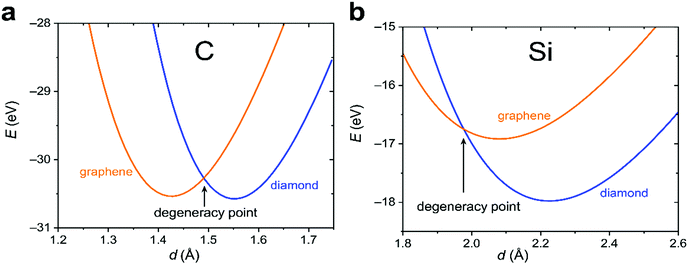
Carbon allotropes are a hot topic with a plethora of newly proposed ones, predicted to have fascinating physical properties. To navigate this large zoo of allotropes, we recommend a comprehensive and timely database,1 a survey2 and two recent articles dealing with the bonding of these carbon allotropes3 and sp-mixing triangle maps from first principles.4 The experimentally available allotropes are by far less numerous but of interest in different areas: graphene and fullerenes are popular materials in material sciences and electrochemistry,5,6 and modified nanotubes have been found to be efficient catalytic systems.7 Despite the impressive diversity of novel carbons, the well-known diamond and graphite (Fig. 1, as well as hexagonal diamond dubbed lonsdaleite) form the centerpiece of the entire carbon story. These two allotropes have been known to humans for thousands of years, being the only crystalline forms present in nature rather than prepared artificially. Also, they are the most studied carbons and prototypical for other allotropes variously combining sp3- and sp2-hybridized C atoms.2,11–13 Remarkably, diamond itself can exist in two forms, the usual cubic diamond and hexagonal lonsdaleite10 featuring the same local arrangements of C–C bonds but differing by the hexagonal ABAB stacking as compared to the cubic ABCABC one (Fig. 1).The most intriguing fact about diamond and graphite is their relative stability. Experimentally, graphite is thermodynamically more stable at 1 atm and 298 K, but only barely (ca. 2 kJ mol−1, that is, they are degenerate within a chemical accuracy of 1 kcal mol−1). Any attempt to find a rigorous explanation of this quasi-degeneracy stumbles upon the problem that diamond and graphite are just too different from the point of view of, say, topology, which is accepted as a basis of allotrope classification in ref. 1. Indeed, diamond and graphite adopt different space-group symmetry, different unit cells, different band structures and extremely different physical properties, so why should they have (almost) equal energies? We recall that solid-state chemistry would portray diamond and graphite as species featuring different hybridization patterns (sp3vs. sp2), different localization, and different covalent bonding types. Thus, it might look easier to explain if graphite were significantly more stable since the delocalized π-system might also decrease graphite's total energy as habitually evoked in organic chemistry. Vice versa, if diamond were significantly more stable, one might argue in terms of the larger number of strong covalent bonds per atom. A recent, comprehensive DFT study of the relative stability of diamond and graphite14 provides valuable numerical information on the exact allotropic energy difference under different conditions, but in our contribution, we try to understand how diamond and graphite can come so close on the energy scale in terms of an analytical model.
Experimental situation
First, we specify the quantity to be reproduced. Under standard conditions, the difference in Gibbs energies ΔG° between diamond and graphite falls in the range of 2.87–2.90 kJ mol−1, graphite being lower,15 but this quantity is contaminated by the lattice contribution. Since the crystal structures and elasticity modules and, thus, the phonon spectra are rather different, one cannot a priori exclude changes in the order of electronic energies. We therefore extrapolated the difference in Gibbs energies to zero temperature; the standard experimental data (NIST) of entropy and heat capacities for graphite (see Appendix A)16 are fit to the Debye–Sommerfeld model, Cp = γT + αT3. For diamond, this yields γ = 0 (nonmetallic and no other degrees of freedom yielding a linear term) but graphite features so called flexural vibrations (Fig. 2),17 whose dispersion law produces a T2 contribution to the low-temperature heat capacity, as predicted quite long ago19 and documented experimentally.20 Even with accounting for the flexural modes, graphite is still more stable than diamond at 0 K, but the difference in Gibbs energies is even smaller (1.39–1.55 kJ mol−1) than at room temperature. Taking into account the ZPEs (as estimated in ref. 14) of either allotrope yields a difference of electronic energies in the range of 0.14–0.78 kJ mol−1 in favor of graphite. | ||
| Fig. 2 A snapshot of a flexural vibration of an individual graphite sheet yielding the T2 contribution to the heat capacity.18 | ||
Another uncertainty is the weak interaction between the graphene layers forming graphite. To avoid this overwhelmingly complex problem (in particular when relying on DFT approaches), we notice that adding the recently21 determined exfoliation energy of graphite (about 3 kJ per mole of carbon atoms) puts the electronic energy of an individual graphene sheet ca. 2.5–3 kJ mol−1 above diamond. This suggests that, within chemical accuracy, diamond and graphene (and graphite, too) are almost degenerate states of carbon. Thus, we use graphene in our considerations for reasons of simplicity.
Model
Now, we turn to constructing an analytical model of the electronic structures for both carbon allotropes, relying upon fundamental chemical concepts such as bonding, hybridization etc. Like in the Molecular Mechanics or Force Field22–27 approaches, we represent the energy of each allotrope as a sum of energies of the bonds formed by differently hybridized orbitals, complemented by the energies of atoms in the respective hybridization states and by the energy of repulsion of the atomic “cores”, that is, the atoms bereft of their valence electrons.† Instead of a priori inferring the form of the bond energies, we use expressions stemming from a general quantum-mechanical theory of the molecular electronic structure, the formal background being the group-function formalism.28–30 The diamond energy per atom is that of the sp3 hybridized carbon atom supplied by the energies of two σ-bonds formed by these hybrids (four σ-bonds counted 50% per atom) and the structure-dependent repulsion energy. Likewise, graphene contains 3/2 σ-bonds formed by sp2 hybrids per atom, but their energy must be augmented by that of a delocalized π-electron per atom. Thus, we write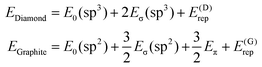 | (1) |
Clearly, the carbon atoms in the allotropes have different hybridizations. Normally, the one-center energies E0(h) strongly depend on hybridization,31–33 but the allotropes of the group IV elements represent a remarkable exception.31 For them, the populations of all atomic hybrid orbitals are equal to unity, and the one-center terms are equal in graphene and diamond (see proof in Appendix B), so we can exclude them from now on.
The repulsion energies E(D)rep and E(G)rep come from the general formula for the repulsion of the atomic charge distribution if one takes into account the differences between interactions of the core point charges and of the electron distributions with a spatial extent.30,32 Hence, repulsive interactions between electroneutral atoms acquire a quasi-Yukawa form Y(d), that is, d−1 multiplied by exponentials assuring a faster decay at longer distances d, and we may write
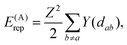 | (2) |
In quantum chemistry, the bond energies may be expressed through quantum-mechanical quantities such as the Coulson bond order P.35 For the energy of the bonding interactions between two equivalent orbitals of hybridization h, one has
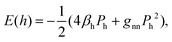 | (3) |
In the delocalized π-system of graphene, the nearest-neighbor Coulson bond order derives from the band (equivalent to Hückel) approximation. Its solution for the graphene π-system40 yields Pπ ≈ 0.525 (see, for example, ref. 59). Just like for the σ-bonds, it is parameter- and distance-independent, defined exclusively by the “topology” of the graphene lattice. Since the graphene lattice divides into two sublattices, so that sites of one sublattice have neighbors only in another one, the alternation theorem41 holds for graphene's π-bond orders. According to this, all bond orders between orbitals from the same sublattice – that is, the second-nearest ones – vanish. Therefore, despite the delocalization, we may retain only the nearest-neighbor interactions in the π-system. Further neighbors fall out due to the exponential decay of the hopping (resonance) interactions.
That being said, the energies of diamond and graphene are just two different functions of the interatomic separation, comprising Coulomb repulsion gnn, core–core repulsion Y, and orbital–orbital hopping elements βμν for which all quantum-mechanical electronic-structure variables (hybridizations and bond orders) are fixed by the symmetry. The only remaining variable, the interatomic separation d, enters through the exponentially decaying terms
EG,D(d) ≍ −BG,D![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−ξd) + DG,D exp(−ξd) + DG,D![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−αd) exp(−αd) | (4) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 42 The difference of the allotropes’ energies as a function of d has a similar form
42 The difference of the allotropes’ energies as a function of d has a similar formΔDGE(d) ≍ −ΔDGB![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−ξd) + ΔDGD exp(−ξd) + ΔDGD![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−αd), exp(−αd), | (5) |
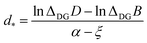 | (6) |
This result is remarkable since it shows that the (quasi-)degeneracy of diamond and graphene is not accidental, but rather predetermined by the structure of the respective energy functions. Near the degeneracy point, the energies of the two allotropes expand up to the second power in (d − d*), as shown below. The energy difference between them is that of the stabilization energies at their respective equilibrium bond lengths, dG< d*< dD:
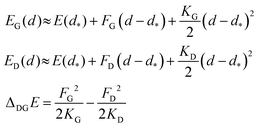 | (7) |
Implementation and results
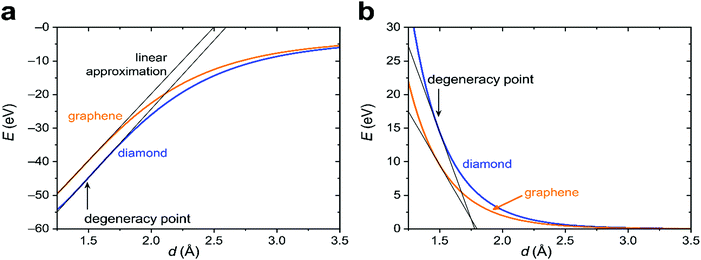
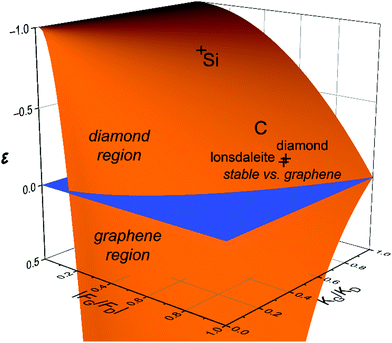
To proceed further, we need to specify the resonance integrals βμν (μ, ν = s, p, π) and the quasi-Yukawa potential Y. For the former, we extracted their distance dependence from density-functional calculations on graphite as projected on local atomic orbitals with the LOBSTER package43–45 (see Appendix C). The results of this extraction fit fairly well to the traditional semi-empirical (MNDO) form of the resonance integrals βμν= β0μνSμν, where Sμν are the overlap integrals of the Slater orbitals μν, and β0μν are the scaling factors specific for the orbital type (s, p, π) and the chemical element.48 In view of the good agreement of the form of βμν, it is reasonable to take them, as well as the quasi-Yukawa core repulsion Y, as given in the MNDO-based method46,47 using the local bonds formed by the strictly local hybrids. This setting agrees with the asymptotic form of either allotrope energy (eqn (4)), assuring the existence of a degeneracy point.The bonding energy contributions are depicted in Fig. 3a. Their slopes (= forces) are almost equal at the degeneracy point of d* = 1.490 Å, differing by less than 3%. Interestingly, the attractive force in graphene is smaller than in diamond as is the graphene attraction energy. The total force is the sum of the attractive and repulsive contributions partially compensating each other. For graphene, the repulsive force is always weaker than for diamond (Fig. 3b). At the degeneracy point, the total force is attractive for graphene (contracting the bond relative to d*), but repulsive for diamond (stretching the bond relative to d*). This ultimately leads to the energy profiles for carbon in the diamond and graphene structures shown in Fig. 4a, which qualitatively agree with the experiments. More numerical results are given in Table 1.
 | ||
| Fig. 4 Total-energy profiles (sums of the contributions from Fig. 3a and b) near the “degeneracy point” for the graphene and diamond structures of carbon (a) and silicon (b). | ||
| C | Si | ||||
|---|---|---|---|---|---|
| Calc. | Exp. | Calc.52 | Exp. | ||
| a This value is obtained in the present work (Appendix A) from the recommended value of ΔDGG° and experimental data for the heat capacities.16 b The same including the exfoliation energy21 and the ZPE corrections.14 c result of a DFT calculation.55 d Lonsdaleite is the closest analogue of usual diamond featuring the same local environment, differing either by stacking (see the Introduction) or alternatively formulated by the conformation taken by the atoms adjacent to a given bond: eclipsed (lonsdaleite) vs. staggered (diamond). Although, there are some doubts70 as to whether lonsdaleite indeed exists in nature (at least in meteoritic craters, as originally conjectured10), for the purpose of the present paper, it is enough that the corresponding structure appears as a local energy minimum from a reasonable solid-state calculation, e.g.ref. 71 and 72. | |||||
| Bond lengths (Å) | D | 1.551 | 1.54449 | 2.226 | 2.35253 |
| G | 1.426 | 1.41951 | 2.080 | 2.226c![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 55 55 |
|
| L | 1.552 | 1.54550 | 2.226 | 2.37554 | |
| ΔE (kJ mol−1) | D vs. G | −3.61 | 1.39–1.55a | −102.47 | −57.957 |
| −2.5 to −3b | |||||
| D vs. L | −2.76 | −0.60 | −0.9656 | ||
According to our analysis, the observed relative energies of the allotropes (eqn (7)) appear due to a paradoxical interplay of factors: the weaker attractive force in diamond is compensated by a stronger repulsive force, producing a total repulsive force larger by its absolute value than the total attractive force in graphene. The difference in favor of the repulsive force is so large that when squared (numerator in the second term of the third row of eqn (7)), it still produces a stronger stabilizing effect despite the larger rigidity (corresponding denominator) of diamond. Comparing this to lonsdaleite, we find a slightly larger repulsive contribution of the 3rd and farther neighbors in the latter, which leads to a slightly larger energy of this allotrope and to a minor increase of the equilibrium interatomic separations as compared to cubic diamond.
One of the key elements leading to the energetic quasi-degeneracy of the graphene and diamond structures in the carbon case is the independence of the atomic energy on hybridization, as shown in Appendix B. The reasoning given there applies to all group IV atoms. Thus, we also looked at the heavier homologue, silicon. Like for carbon, we first performed a DFT calculation on the Si crystal and extracted the resonance integrals (Appendix C), which also showed fair proportionality to the overlap integrals as expressed within MNDO theory. By using these parameters, the components of the attractive and repulsive forces as well as the rigidities were calculated for silicon at the degeneracy point, which is d* = 1.977 Å. We then find that the bonding forces in silicon are smaller than in carbon by an order of magnitude, and the trend for silicon is opposite to carbon: the diamond structure has a smaller bonding force as compared to graphene (4.12 vs. 6.47 eV Å−1). Attractive forces are overcome by the repulsive ones, so that the overall forces in the case of either silicon allotrope turn out to be repulsive at the degeneracy point. For this very reason, the degeneracy point corresponds to a smaller interatomic separation than either of the equilibrium ones for silicon, unlike for the carbon case. Finally, the larger repulsive force characteristic of the diamond structure results in a stronger stabilization of the diamond structure (Table 1 and Fig. 4b) and sheds new light on the unavailability of silicene (silicon in the graphene structure).
Remarkably, the negative sign of the force acting on silicene at the degeneracy point corroborates with its instability towards corrugation.55 Indeed, given constant hybridization, the only effect of small corrugation is the replacement of the nearest-neighbor interatomic separations d by d/cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) α in all distance-dependent functions.§ For small values of α, it produces the energy correction FGα2/2, which for negative FG (silicene), leads to an immediate instability of the planar structure, whereas in the case of carbon, the positive sign of FG guarantees that the planar structure remains stable with respect to corrugation.
α in all distance-dependent functions.§ For small values of α, it produces the energy correction FGα2/2, which for negative FG (silicene), leads to an immediate instability of the planar structure, whereas in the case of carbon, the positive sign of FG guarantees that the planar structure remains stable with respect to corrugation.
Another way of plotting the astonishing difference in energetics of the carbon and silicon allotropes is presented in Fig. 5, in which the horizontal axes are given by the relative forces and rigidities for diamond and graphene at the degeneracy point. In the blue plane, the intersecting line corresponds to the phase diagram with the above coordinates. Above the blue plane, diamond is preferred; below the blue plane, graphene is preferred. The energies of diamond and lonsdaleite relative to graphene are shown by crosses. Similarly, the energies of the diamond and lonsdaleite structures of Si relative to its graphene form (silicene) are shown; they coincide on this scale.
Conclusions
To summarize, we have performed a theoretical analysis of the relative stabilities of the lowest-energy carbon allotropes occurring in nature: graphite (graphene), diamond and lonsdaleite. Within our approach, we first excluded large and potentially imprecise contributions and then established the existence of an analytically given degeneracy point: the interatomic separation at which the energies of the allotropes coincide despite the drastic differences in their topology, spatial and electronic structures. This allowed us to shift the focus to the quantity of interest, that is, the difference of the allotropes’ energies. In this setting, the sought energy difference comprises about 10% of the corrections to the energy at the degeneracy point.Admittedly, one might think that the significant simplifications make our approach more qualitative than quantitative and do not permit us to arrive at an exact estimate of the relative energy of the lowest-energy allotropes of carbon and silicon. Quite to the contrary, it is puzzling to note the rather correct relative positioning on the energy scale almost arriving at “chemical accuracy” accessed by very simple means. Similarly, rather good numerical data for the interatomic separations (with an error smaller than 0.5% for carbon), comparable to high-level DFT calculations,¶ have been achieved. All this was reached by making use of the empirical information about the general construction of the electronic wave functions of the respective allotropes (that is, form and character of the local and delocalized bonds) and a far smaller numerical effort than in hard-core numerical approaches (see, for example, ref. 13, 15 and 57). Clearly, the use of the bonding paradigm is important because, as mentioned,58 it allows one to keep track of chemical similarities not easily accessible otherwise. At the same time, the almost precise compensation of counteracting factors (that is, different hybridization, bonding pattern, and as well global and local structure) could also be reproduced in the case of graphene/diamond if based on bonds and hybridizations.
We hope that our qualitative analysis might be helpful, providing a refreshing view on the carbon allotropy, complementary to other numerical and experimental approaches.
Conflicts of interest
There are no conflicts to declare.Theoretical appendix
A. Overview of experimental data on the relative energies of allotropes. Which one is more stable at zero temperature?
The difference between the zero-point enthalpies of two ideal crystalline allotropes is given as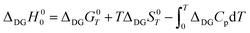 | (A1) |
By substituting the experimental relative standard Gibbs energy and entropy at 300 K,60 we get
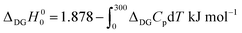 | (A2) |
To arrive at the zero-temperature relative energy, the integral needs to be evaluated. This was done16 using experimental heat capacities of diamond and graphite, extrapolated to the zero temperature by the Debye–Sommerfeld relation: Cp = γT + αT3. The difference of zero temperature enthalpies ΔDGH00 obtained by this procedure amounts to 1.39–1.42 kJ mol−1.
In graphite, one must also take into account flexural vibrational modes (Fig. 2), yielding a quadratic term in the heat capacity.19,20 Thus, the formula Cp = βT2 + αT3 must be used to extrapolate the heat capacity to zero temperature. Several sets of experimental points, recommended by NIST,61 were handled within this setting, and we found that the temperature correction to the enthalpy (sum of the entropic and the integral terms in eqn (A1)) of graphite lies in the range of 1.15–1.20 kJ mol−1, which yields ΔDGH00 = 1.48–1.55 kJ mol−1 for the difference of the zero-temperature enthalpies. Thus, the value of the zero-temperature enthalpy difference obtained, taking into account the flexural modes in graphite, is slightly larger than that evaluated from the data of ref. 16. However, the difference is insignificant (0.1 kJ mol−1). Thus, it is reasonable to expect that ΔDGH00 lies in the range of 1.39–1.55 kJ mol−1. Finally, the difference of ZPE between diamond and graphite was estimated in ref. 14 to be in the range of 0.77–1.15 kJ mol−1 in favor of graphite. This reduces the difference of their electronic energies to the range of 0.14–0.78 kJ mol−1 still in favor of graphite.
B. Hybridization (in)dependence of one-center energies for group IV atoms with nonpolar bonds
The weights of the s-AOs in the system of hybrids are subject to the normalization condition:
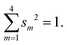 | (B1) |
Inserting qm = 1 (no polar bonds) and using eqn (B1), we get the constant one-center attraction: Us + 3Up. Thus, in group IV atoms with nonpolar bonds, the one-center attraction energy does not depend on hybridization.
| gkm = C4 + C5[sm2 + sk2] + C3sm2sk2. |
Here, Ci are, as well, known combinations of the atomic Slater–Condon parameters31 whose explicit forms are not required. Inserting the populations of the hybrids qm = 1 and performing the summation with the use of the normalization condition eqn (B1), we get:
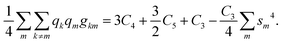 | (B2) |
Now, we complement the Coulomb interaction between different hybrids in eqn (B2) with the interaction of electrons within hybrids:
The intrahybrid Coulomb matrix elements gm are, as well, known:31
| gm = C1 + C2sm2 + C3sm4. |
Inserting qm = 1, performing summation and using again the normalization condition from eqn (B1), we see that the terms quadratic in sm sum up to a constant C2/4, whereas the sum of terms quartic in sm exactly cancels the corresponding term in the interhybrid interaction energy in eqn (B2). Thus, we arrive at the main conclusion of this Appendix: the energy of a group IV atom forming no polar bonds is hybridization-independent.
C. Parameter extraction by LOBSTER
In order to clarify the key parameters of this study, the resonance integrals for carbon and silicon atoms, we first performed DFT calculations by employing the Vienna Ab initio Simulation Package (VASP)62–65 using the PBE exchange–correlation functional66 and PAW pseudo-potentials.67,68 A convergence criterion of at least 10−5 eV was used, and the atomic positions were optimized until the Hellmann–Feynman forces fell below 5 × 10−3 eV Å−1.We then utilized the LOBSTER package to project the DFT results onto a local basis of contracted Slater-type orbitals using primitive unit cells.43–45 The processing yields the values of the resonance integrals between the atomic orbitals at the interatomic separations available in the respective crystals (Fig. 6 and 7).
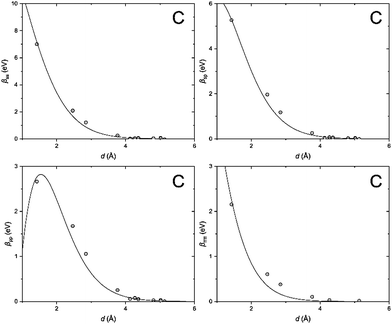 | ||
| Fig. 6 Distance dependence of the resonance integrals for carbon as obtained by LOBSTER and fitted as being proportional to the overlap integrals. | ||
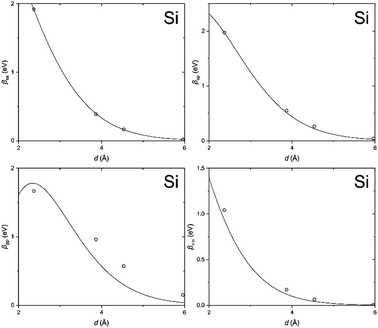 | ||
| Fig. 7 Same as Fig. 6, but for silicon. | ||
The DFT-derived hopping matrix elements were fitted as products of the energy scales β0μν and the overlap integrals Sμν of the Slater-type orbitals (Table 2) with the orbital exponents taken from the standard MNDO parametrization.48,69 The results of the numerical fit reproduce characteristic features of the MNDO system of parameters. For carbon, there is a strong dependence of the scaling factors on the orbital type (a factor of about two between the ss and pp energy scales) as well as the MNDO specific combination rule: 2β0sp= β0ss + β0pp; for silicon, by contrast, there is only a weak dependence of the scales on the orbital type.
Acknowledgements
This work is supported by the Volkswagenstiftung (grant no. 151110) “Deductive Quantum Molecular Mechanics of Carbon Allotropes” in the frame of a trilateral project between scholars and scientists from the Ukraine, Russia, and Germany. The authors are thankful to Prof. R. Hoffmann (Cornell) for valuable discussion on lonsdaleite and to Prof. Dr W. H. E. Schwarz (Siegen, Bejing) for discussion on the importance of repulsion terms. Dr A. Tokmachev (Moscow) is acknowledged for drawing ALT's attention to the problem of corrugation in silicene. The authors are also thankful to the Referees for valuable comments, which helped to improve the final version of this paper.Notes and references
- SACADA Database http://sacada.sctms.ru/.
- R. Hoffmann, A. A. Kabanov, A. A. Golov and D. M. Proserpio, Angew. Chem., Int. Ed., 2016, 55, 10962–10976 CrossRef CAS PubMed.
- M. Esser, A. A. Esser, D. M. Proserpio and R. Dronskowski, Carbon, 2017, 121, 154–162 CrossRef CAS.
- M. Esser and R. Dronskowski, Carbon, 2017, 123, 708–716 CrossRef CAS.
- E. P. Randviir, D. A. C. Brownson and C. E. Banks, Mater. Today, 2014, 17, 426–432 CrossRef CAS.
- S. F. A. Acquaha, A. V. Penkova, D. A. Markelov, A. S. Semisalova, B. E. Leonhardt and J. M. Magi, ECS J. Solid State Sci. Technol., 2017, 6, M3155–M3162 CrossRef.
- W. Jun Lee, U. Narayan Maiti, J. Min Lee, J. Lim, T. H. Han and S. O. Kim, Chem. Commun., 2014, 50, 6818 RSC.
- T. Hom, W. Kiszenikand and B. Post, J. Appl. Crystallogr., 1975, 8, 457–458 CrossRef.
- P. Trucano and R. Cheb, Nature, 1975, 258, 136–137 CrossRef CAS.
- F. P. Bundy and J. S. Kasper, J. Chem. Phys., 1967, 46, 3437–3446 CrossRef CAS.
- X.-L. Sheng, Q.-B. Yan, F. Ye, Q.-R. Zheng and G. Su, Phys. Rev. Lett., 2011, 106, 155703 CrossRef PubMed ; and reference therein.
- H. W. Kroto, J. R. Heath, S. C. Obrien, R. F. Curl and R. E. Smaliey, Nature, 1985, 318, 162 CrossRef CAS; S. Iijima, Nature, 1991, 354, 56 CrossRef; Y. Liu, G. Wang, Q. Huang, L. Guo and X. Chen, Phys. Rev. Lett., 2012, 108, 225505 CrossRef PubMed.
- I. A. Baburin, D. M. Proserpio, V. A. Saleev and A. V. Shipilova, Phys. Chem. Chem. Phys., 2015, 17, 1332–1338 RSC.
- W. Grochala, Angew. Chem., Int. Ed., 2014, 53, 3680–3683 CrossRef CAS PubMed.
- H. W. Day, Am. Mineral., 2012, 97, 52–62 CrossRef CAS.
- R. J. Corruccini and J. J. Gniewek, Natl. Bur. Stand., Monogr., 1960, 21 Search PubMed.
- J.-W. Jiang, B.-S. Wang, J.-S. Wang and H. S. Park, J. Phys.: Condens. Matter, 2015, 27, 083001 CrossRef PubMed.
- Picture by J. Hedberg licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 3.0 Unported License, http://www.jameshedberg.com/scienceGraphics.php?sort=all&id=graphene-sheet-atoms.
- V. V. Tarasov, DAN SSSR, 1945, 46, 22 CAS; V. V. Tarasov, Zh. Fiz. Khim., 1950, 24, 111 Search PubMed.
- W. DeSorbo and W. W. Tyler, J. Chem. Phys., 1953, 21, 1660–1663 CrossRef CAS; E. Pop, V. Varshney and A. K. Roy, MRS Bull, 2012, 37, 1273 CrossRef.
- W. Wang, S. Dai, X. Li, J. Yang, D. J. Srolovitz and Q. Zheng, Nat. Commun., 2015, 6, 7853 CrossRef CAS PubMed.
- N. L. Allinger and U. Burkert, Molecular Mechanics, An American Chemical Society Publication, 1982 Search PubMed.
- A. Leach, Molecular Modelling: Principles and Applications, 2nd edn, Prentice Hall, Harlow, 2001 Search PubMed.
- The ‘quantum’ MM schemes25–27 represent, in fact, tedious interpolations of the multiple energy contributions while for the quantum mechanical quantities, some ad hoc expressions are used.
- J. Che, T. Çağın and W. A. Goddard III, Theor. Chem. Acc., 1999, 102, 346 Search PubMed.
- D. W. Brenner, Phys. Rev. B: Condens. Matter Mater. Phys., 1990, 42, 9458 CrossRef CAS.
- V. G. S. Box, J. Mol. Model., 1997, 3, 124–141 CrossRef CAS.
- R. McWeeny and B. T. Sutcliffe, Methods of molecular quantum mechanics, AP, London, 1969 Search PubMed; R. McWeeny, Methods of Molecular Quantum Mechanics, AP, London, 1992 Search PubMed.
- A. L. Tchougréeff, J. Struct. Chem., 2007, 48, S39–S62 Search PubMed [in Russian]; A. L. Tchougréeff, J. Struct. Chem., 2007, 48, S32–S54 CrossRef [in English].
- A. L. Tchougréeff, Hybrid Methods of Molecular Modeling, Springer, 2008 Search PubMed.
- A. L. Tchougréeff, THEOCHEM, 2003, 630, 243–263 CrossRef; A. L. Tchougréeff and A. M. Tokmachev, Int. J. Quantum Chem., 2004, 96, 175–184 CrossRef.
- A. L. Tchougréeff and R. Dronskowski, Mol. Phys., 2016, 1423–1444 CrossRef.
- A. L. Tchougréeff, AIP Conf. Proc., 2017, 1906, UNSP 030004 CrossRef; A. L. Tchougréeff, Theor. Chem. Acc., 2018, 137, 138 Search PubMed.
- It is not always realized but the hardness – rigidity – of a body or material is a consequence not of “bonding” contributions because these are largely concave functions of inter-atomic separations, providing negative (i.e., softening) contribution to the elastic moduli. Rather, the core repulsion terms preventing nuclei to come too close together and therefore produce large convex contribution (positive second derivative). Thus, one should not be surprised that diamond with a larger coefficient at the repulsion term in the total energy is harder than graphite.
- J. Pople and D. Beveridge, Approximate Molecular Orbital Theory, McGraw–Hill, 1970 Search PubMed; I. Levine, Quantum Chemistry, Prentice Hall, 4th edn, 1991 Search PubMed; C. J. Cramer, Essentials of Computational Chemistry, Wiley, Chichester, 2002 Search PubMed; A. Szabo, N. S. Oslund, Modern Quantum Chemistry: Introduction to Advanced Electronic Structure Theory, Dover, 1996 Search PubMed.
- A. L. Tchougréeff and A. M. Tokmachev, Int. J. Quantum Chem., 2006, 106, 571–587 CrossRef.
- A. M. Tokmachev and A. L. Tchougréeff, J. Comput. Chem., 2001, 22, 752–764 CrossRef CAS.
- A. M. Tokmachev and A. L. Tchougréeff, Int. J. Quantum Chem., 2002, 88, 403–413 CrossRef CAS.
- A. M. Tokmachev and A. L. Tchougréeff, J. Comput. Chem., 2005, 26, 491–505 CrossRef CAS PubMed.
- P. R. Wallace, Phys. Rev., 1947, 71, 622 CrossRef CAS.
- C. A. Coulson and H. C. Longuet-Higgins, Proc. Roy. Soc. Lond. A, 1947, 191, 16–32 Search PubMed; C. A. Coulson and A. Golebiewski, Proc. Phys. Soc., 1961, 78, 1310 CrossRef CAS.
- G. C. Abell, Phys. Rev. B: Condens. Matter Mater. Phys., 1985, 31, 6184–6196 CrossRef CAS.
- V. L. Deringer, A. L. Tchougréeff and R. Dronskowski, J. Phys. Chem. A, 2011, 115, 5461–5466 CrossRef CAS PubMed.
- S. Maintz, V. L. Deringer, A. L. Tchougréeff and R. Dronskowski, J. Comput. Chem., 2013, 34, 2557–2567 CrossRef CAS PubMed.
- S. Maintz, V. L. Deringer, A. L. Tchougréeff and R. Dronskowski, J. Comput. Chem., 2016, 37, 1030–1035 CrossRef CAS PubMed.
- A. M. Tokmachev and A. L. Tchougréeff, J. Phys. Chem. A, 2005, 109, 7613–7620 CrossRef CAS PubMed.
- A. L. Tchougréeff, A. M. Tokmachev and R. Dronskowski, J. Phys. Chem. A, 2009, 113, 11406–11415 CrossRef PubMed.
- M. J. S. Dewar and W. Thiel, J. Am. Chem. Soc., 1977, 99, 4899–4907 CrossRef CAS.
- R. A. Andrievski, Int. J. Refract. Met. Hard Mater., 2001, 19, 447 CrossRef CAS.
- F. P. Bundy and J. S. Kasper, J. Chem. Phys., 1967, 46, 3437–3446 CrossRef CAS.
- C. Kittel, Introduction to Solid State Physics, Wiley, 1996 Search PubMed.
- It is well known that the MNDO parameterization usually underestimates the Si–Si bond lengths. For example, in the original work69 the calculated value of the Si–Si bond length in H3Si–SiH3 equals 2.284 Å, while the experimental value is 2.352 Å. It is also discussed in R. Hull, Properties of Crystalline Silicon, IET, 1999 that both MNDO parameterizations for silicon fail to reproduce the experimental structure of silicon correctly.
- A. D. Elliott, Acta Crystallogr., Sect. B: Struct. Sci., 2010, 66, 271–279 CrossRef PubMed.
- R. H. Wentorf and J. S. Kasper, Science, 1963, 338–339 CrossRef CAS.
- K. Takeda and K. Shiraishi, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 14916 CrossRef CAS.
- B. Haberl, T. A. Strobel and J. E. Bradby, Appl. Phys. Rev., 2016, 3, 040808 Search PubMed.
- L. C. Lew Yan Voon, J. Zhu and U. Schwingenschlögl, Appl. Phys. Rev., 2016, 3, 040802 Search PubMed; E. Durgun, S. Tongay and S. Ciraci, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 075420 CrossRef.
- A. Tchougréeff, Abstracts ACS, 2017, 254, 209.
- A. Zunger, Phys. Rev. B: Condens. Matter Mater. Phys., 1978, 17, 626–642 CrossRef.
- Knovel database, http://why.knovel.com/accessed Oct 2013.
- NIST database, https://webbook.nist.gov/cgi/formula?ID=C7782425&Mask=2.
- G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558–561 CrossRef CAS.
- G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 14251–14269 CrossRef CAS.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS.
- G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775 CrossRef CAS.
- M. J. S. Dewar, M. L. McKee and H. S. Rzepa, J. Am. Chem. Soc., 1978, 100, 3607 CrossRef CAS.
- P. Németh, L. A. J. Garvie, T. Aoki, N. Dubrovinskaia, L. Dubrovinsky and R. Buseck, Nat. Commun., 2014, 5, 5447 CrossRef PubMed.
- Z. Pan, H. Sun, Y. Zhang and C. Chen, Phys. Rev. Lett., 2009, 102, 055503 CrossRef PubMed.
- L. Quingkun, S. Yi, L. Zhiyuan and Z. Yu, Scr. Mater., 2011, 65, 229–232 CrossRef.
- T. Gruber, K. Liao, T. Tsatsoulis, F. Hummel and A. Grüneis, Phys. Rev. X, 2018, 8, 021043 CAS.
Footnotes |
| † For the carbon atom, the effective core charge arrives at +4 because there is an electronic configuration of 1s22s22p2 from which the 2s22p2 valence electrons are separated, leaving the core containing the +6 atomic nucleus plus the 1s2 electrons together charged as +4. |
| ‡ We remind the reader that in the true Morse potential, we have α = 2ξ. |
| § The corrugation angle α is the one between the graphene C–C bond and the graphene plane. |
| ¶ Even more, our numerical result agrees with the most recent coupled cluster calculation,73 also positioning diamond below graphite on the energy scale. |
| This journal is © the Owner Societies 2019 |