A study of the reactions of Al+ ions with O3, N2, O2, CO2 and H2O: influence on Al+ chemistry in planetary ionospheres
Abstract
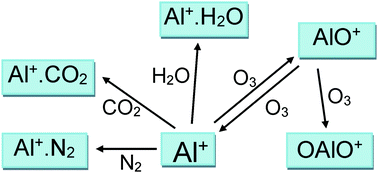
The reactions between Al+(31S) and O3, O2, N2, CO2 and H2O were studied using the pulsed laser ablation at 532 nm of an aluminium metal target in a fast flow tube, with mass spectrometric detection of Al+ and AlO+. The rate coefficient for the reaction of Al+ with O3 is k(293 K) = (1.4 ± 0.1) × 10−9 cm3 molecule−1 s−1; the reaction proceeds at the ion–dipole enhanced Langevin capture frequency with a predicted T−0.16 dependence. For the recombination reactions, electronic structure theory calculations were combined with Rice–Ramsperger–Kassel–Markus theory to extrapolate the measured rate coefficients to the temperature and pressure conditions of planetary ionospheres. The following low-pressure limiting rate coefficients were obtained for T = 120–400 K and He bath gas (in cm6 molecule−2 s−1, uncertainty ±σ at 180 K): log10(k, Al+ + N2) = −27.9739 + 0.05036 log10(T) − 0.60987(log10(T))2, σ = 12%; log10(k, Al+ + CO2) = −33.6387 + 7.0522 log10(T) − 2.1467(log10(T))2, σ =13%; log10(k, Al+ + H2O) = −24.7835 + 0.018833 log10(T) − 0.6436(log10(T))2, σ = 27%. The Al+ + O2 reaction was not observed, consistent with a D°(Al+–O2) bond strength of only 12 kJ mol−1. Two reactions of AlO+ were also studied: k(AlO+ + O3, 293 K) = (1.3 ± 0.6) × 10−9 cm3 molecule−1 s−1, with (63 ± 9)% forming Al+ as opposed to OAlO+; and k(AlO+ + H2O, 293 K) = (9 ± 4) × 10−10 cm3 molecule−1 s−1. The chemistry of Al+ in the ionospheres of Earth and Mars is then discussed.
- This article is part of the themed collections: 2019 PCCP HOT Articles and Photodissociation and reaction dynamics


 Please wait while we load your content...
Please wait while we load your content...