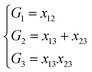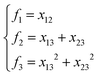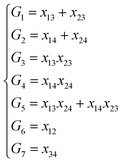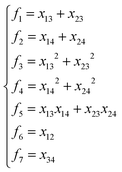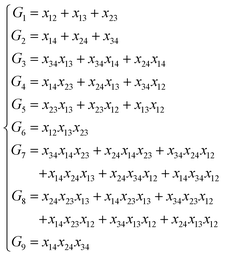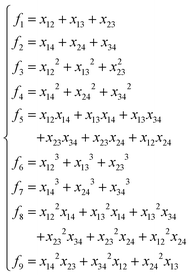Open Access Article
Open Access ArticleA critical comparison of neural network potentials for molecular reaction dynamics with exact permutation symmetry
Jun
Li
 *ab,
Kaisheng
Song
a and
Jörg
Behler
*ab,
Kaisheng
Song
a and
Jörg
Behler
 *b
*b
aSchool of Chemistry and Chemical Engineering, Chongqing University, Chongqing 401331, China. E-mail: jli15@cqu.edu.cn
bUniversität Göttingen, Institut für Physikalische Chemie, Theoretische Chemie, Tammannstr. 6, 37077 Göttingen, Germany. E-mail: joerg.behler@uni-goettingen.de
First published on 11th January 2019
Abstract
The availability of accurate full-dimensional potential energy surfaces (PESs) is a mandatory condition for efficient computer simulations of molecular systems. Much effort has been devoted to developing reliable PESs with physically sound properties, such as the invariance of the energy with respect to the permutation of chemically identical atoms. In this work, we compare the performance of four neural network (NN)-based approaches with a rigorous permutation symmetry for fitting five typical reaction systems: OH + CO, H + H2S, H + NH3, H + CH4 and OH + CH4. The methods can be grouped into two categories, invariant polynomial based NNs and high-dimensional NN potentials (HD-NNPs). For the invariant polynomial based NNs, three types of polynomials, permutation invariant polynomials (PIPs), non-redundant PIPs (NRPIPs) and fundamental invariants (FIs), are used in the input layer of the NN. In HD-NNPs, the total energy is the sum of atomic contributions, each of which is given by an individual atomic NN with input vectors consisting of sets of atom-centered symmetry functions. Our results show that all methods exhibit a similar level of accuracy for the energies with respect to ab initio data obtained at the explicitly correlated coupled cluster level of theory (CCSD(T)-F12a). The HD-NNP method allows study of systems with larger numbers of atoms, making it more generally applicable than invariant polynomial based approaches, which in turn are computationally more efficient for smaller systems. To illustrate the applicability of the obtained potentials, quasi-classical trajectory calculations have been performed for the OH + CH4 → H2O + CH3 reaction to reveal its complicated mode specificity.
I. Introduction
Within the Born–Oppenheimer realm, any reactive or non-reactive process can be considered to take place on an adiabatic potential energy surface (PES). Once the PES has been determined, various dynamical properties of the nuclei can be simulated according to either classical or quantum mechanical (QM) theory. Consequently, the performance of a simulation is largely determined by the accuracy of the underlying PESs. Therefore, developing accurate PESs is of great significance in the field of theoretical/computational chemistry. While the accuracy of empirical potentials relying on physical approximations is often limited, numerous approaches have been developed to represent PESs based on very flexible and purely mathematical functional forms, which can be grouped into two categories: (1) interpolation methods, which provide error-free energies for the available reference data but interpolate in between, such as cubic splines, reproducing kernel Hilbert space (RKHS),1 interpolating moving least square (IMLS)2 and modified Shepard interpolation (MSI) methods;3 and (2) fitting methods relying on specific functional forms such as polynomials within the many body expansion regime,4,5 sum-of-product forms6,7 and permutation invariant polynomials (PIPs).8–10In spite of all these methods, the accurate description of global PESs has remained a formidable challenge even for comparably small polyatomic systems, because they often exhibit a complex topology with several reactants and products, saddle points and intermediates, and in general it is impossible to derive suitable functional forms based on physical considerations. A new promising class of PESs relies on machine learning (ML) techniques.11,12 While the first ML potentials employed artificial neural networks (NNs),13–15 in recent years many other methods have been proposed.12,16–18 NNs are “universal approximators”, as they are in principle able to approximate any unknown multidimensional function with arbitrary accuracy by “learning” from a large set of known function values.19 Recently, NNs have become a powerful tool to develop PESs for various systems with excellent fitting performance.14,15,20–27
One important property of any PES is that the potential energy values must be invariant under permutations of like atoms.28,29 Thus, a key issue is how to incorporate this permutation symmetry into PESs, which not only is important for constructing physically correct PESs, but also influences the efficiency of the sampling and the performance of the fitting process. For NN potentials, the first attempts to construct PESs with permutation symmetry have been made for electrolyte models of an ion interacting with fixed-geometry water monomers30 and for molecule surface scattering employing frozen surfaces to reduce the dimensionality of the PES,20,31 but all these early attempts suffered from a very limited applicability.
The first NN potential with exact permutation symmetry for arbitrarily high-dimensional systems has been proposed by Behler and Parrinello in 2007.32 In these high-dimensional NN potentials (HD-NNPs), the total energy of the system is expressed as the sum of atomic energy contributions, which depend on the local atomic chemical environments that are described by many-body atom-centered symmetry functions.33 For each element in the system there is a specific NN architecture with its associated weight parameters, making the resulting PES fully permutationally invariant.11,15,19,33–35 Although the method is based on atomic energy contributions, only total energies, not the individual atomic energies, are needed to optimize the parameters of NNs. The most important advantage of HD-NNPs is that this method is highly scalable for large systems of up to thousands of atoms with all their degrees of freedom considered explicitly. HD-NNPs have been constructed for a variety of mainly condensed systems with very different types of interactions from covalent bonds to metallic bonding and dispersion interactions.35 In 2016, Guo and coworkers applied HD-NNPs to three prototypically reactive molecular systems, H + H2, H + H2O and H + CH4, with a Monte Carlo based method for efficiently selecting mapping functions. It should be noted that in their work, the points of the three systems have been sampled from pre-existing well-behaved analytical PESs, not from ab initio data sets.36 In addition, Lu et al. employed the HD-NNP approach to fit the PES of the H2 + SH reaction based on ab initio calculated points, and the quantum dynamical results of the HD-NNP and PIP-NN PESs have been found to be essentially the same.37
Building on the extensive work of Bowman and coworkers on molecular PESs based on permutation invariant polynomials (PIPs),10,29 in 2013, Guo and co-workers proposed to use PIPs in the input layer of a NN to obtain another type of NN potential with exact permutation invariance.24,25 In practice, all PIPs of Bowman and co-workers,8,9 truncated at a specified total degree, are used in the input layer of the NN. For a given system, the total degree of truncation is at least the highest degree of the primary and secondary invariants of the PIPs, and can be determined using Molien's series based on symmetry operations of the corresponding complete nuclear permutation and inversion (CNPI) group.38,39 If the degree is not sufficiently high, some primary or secondary invariants might be missing, and some additional “artificial” symmetry properties could be present in the PES. This approach is called PIP-NN, and combines the advantages of both the NN and PIP methods: the fitting performance is guaranteed by the NN with rigorous permutation invariance incorporated by the PIPs.
However, the number of PIPs increases quickly with the number of degrees of freedom in the system. Therefore, it is hard to apply it directly to complicated systems, for instance, with more than approximately ten like atoms, as too many PIPs have to be used in the NN input layer. For instance, 1331 PIPs are used as the input layer of the NN for fitting the OH + CH4 PES.40 As many of the input PIPs are redundant, it is possible to express PIPs as functions of only the non-redundant terms corresponding to the primary and secondary invariant polynomials. Indeed, Xie and Bowman developed an algorithm to speed up the evaluation of the PIPs based on a straightforward symmetrization of a primitive monomial basis and the fact that any high-degree invariant polynomial constructed by using a monomial symmetrization approach can be decomposed into a product of two low-degree polynomials with a remainder invariant polynomial of the same degree.41 However, some redundant polynomials cannot be decomposed further by this approach for more complicated polyatomic systems. Nonetheless, one can use only the non-redundant terms of PIPs as the input layer of NNs for the fitting process. In 2016, for the H + H2S (A3B) system, only 9 non-redundant PIPs have been used in the NN PES (NRPIP-NN), resulting in a root mean squared error (RMSE) of 6.9 meV, which is comparable to 3.9 meV by 4th-order PIPs (50 terms) and 3.0 meV by 3rd-order PIPs (22 terms), respectively.42 One can see that the number of the non-redundant terms is extremely small, especially for complicated systems.
Unfortunately, when the system becomes more complicated, the decomposition is hard to achieve completely. Consequently, some redundancy remains in the non-redundant PIPs, although redundancy is generally not a problem for NNs. It is known that all polynomials invariant under a given symmetry group can be represented as polynomials in a finite generating set of invariant polynomials, whose degree bound can also be determined. There exists a complete set of generating invariants for a given system, although their form is not unique. The complete set of the generating invariants for a given system can be determined according to King's algorithm, which has been implemented in software like MAGMA43 and SINGULAR.44 In 2013, Opalka and Domcke employed 31 generating invariant polynomials in their linear fitting of multi-sheeted PESs for A4B molecules.45 In 2016, Zhang and co-workers proposed to use the complete set of generating invariants of the system in the input layer of NNs.27 Since generating invariants can generate all the invariant polynomials for a given symmetry group, they call them fundamental invariants (FIs) and the resulting fitting approach is called FI-NN. Because the number of the FIs increases mildly with the degree, as in the NRPIP mentioned above, the architecture of the FI-NN is more flexible resulting in a faster evaluation of the energy, in particular, for complicated systems, than for PIP-NNs.46
All methods, PIP-NN, NRPIP-NN and FI-NN, employ invariant polynomials as the input layer of the NN. As systems become more and more complicated, it is harder and harder, and even impractical for high-dimensional systems beyond approximately 10 like atoms, to employ these NN approaches due to the vast increase in the number of the polynomials, and it is difficult to determine the least order of the PIPs. In the HD-NNP method, on the other hand, such systems can directly be addressed with the same rigorous inclusion of the permutation invariance, although, with a few exceptions,46–51 to date it has been mainly applied to condensed systems.
In this work, the HD-NNP approach as implemented in the RuNNer code52 is examined for five prototypical reactions, OH + CO, H + H2S, H + NH3, H + CH4 and OH + CH4, whose PIP-NN PESs have been developed based on large numbers of high level ab initio data points.40,42,53–55 Note that to date HD-NNPs have been mainly applied to condensed systems with very high-dimensionality but a rather homogeneous spatial distribution of the atoms. On the other hand, for the reactive systems here, some inter-nuclear distances change within a large range while the number of atoms is rather small. NRPIP-NN and FI-NN approaches have been also examined and compared. The remainder of this publication is organized as follows. In section II, the relevant theory of the NN-based fitting methods is summarized. Then section III presents the comparison and discussion of these methods on fitting these five systems mentioned above. It has been shown that both PIP-NN PES and HD-NNP for the H + H2S system yield essentially the same dynamical results by accurate quantum mechanical calculations. It is expected that the resulting different PESs of the same system should yield the same dynamical outcomes thanks to the high fidelity representation of the NN. As an application, the mode specificity in the OH + CH4 reaction is studied by the quasi-classical trajectory (QCT) method based on the PIP-NN PES due to its much faster speed in evaluation, and relevant results and discussions are given in section IV. The conclusions and summary are presented in section V.
II. Theory
II-A. Invariant polynomial based NN
For constructing PESs, NNs serve as a non-linear fitting tool that converts signals, here the input vector G = {Gi} describing the atomic positions, to a scalar output E, the potential energy, via one or more hidden layers of the interconnected neurons. In most cases, a standard feed-forward NN with two hidden layers is sufficient for fitting PESs and its explicit form is,56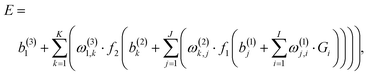 | (1) |
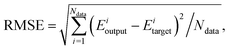 | (2) |
The input layer of the NN in general contains a set of functions of the atomic positions defining the molecular geometry. In the PIP-NN approach, PIPs of Morse-like variables of internuclear distances, Rij, are used as the input layer of the NN: 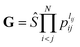 , where pij = exp(−αRij), and Ŝ is the symmetrization operator, which consists of all the permutation operations between atoms of the same element in the system.10 In practice, all PIPs up to a specific maximum order are included in the input layer. As discussed above, many PIPs are redundant. Therefore, we can also use only the non-redundant PIPs as the input layer, which can be determined in a straightforward fashion by the algorithm of Xie and Bowman.41 However, some redundancies might remain due to the possible incomplete decomposition of the algorithm in some practical systems. To overcome this possible problem, FI-NNs can be used with the input layer FIs containing only the smallest possible number of generating invariants.45,46
, where pij = exp(−αRij), and Ŝ is the symmetrization operator, which consists of all the permutation operations between atoms of the same element in the system.10 In practice, all PIPs up to a specific maximum order are included in the input layer. As discussed above, many PIPs are redundant. Therefore, we can also use only the non-redundant PIPs as the input layer, which can be determined in a straightforward fashion by the algorithm of Xie and Bowman.41 However, some redundancies might remain due to the possible incomplete decomposition of the algorithm in some practical systems. To overcome this possible problem, FI-NNs can be used with the input layer FIs containing only the smallest possible number of generating invariants.45,46
For the PIP-NN, NRPIP-NN and FI-NN fitting methods, several different NN architectures with two or three hidden layers have been tested. For each architecture, 50–200 different NNs have been optimized differing in the initial randomly assigned fitting parameters. To avoid overfitting, the “early stopping” algorithm21 is used with the data divided randomly into three parts, i.e., the training (90%), validation (5%) and test (5%) sets for each NN fitting. To minimize false extrapolation due to possible edge points in the randomly selected validation and test sets, only fits with similar RMSEs for all three sets are accepted as the final PES. Besides, the maximum deviation is a good criterion for choosing the final PIP-NN PES.
II-B. HD-NNPs
In the HD-NNP approach, the total energy E of a molecular system is expressed as the sum of atomic energy contributions Ei,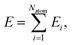 | (3) |
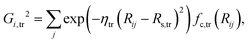 | (4) |
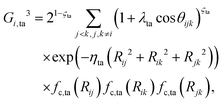 | (5) |
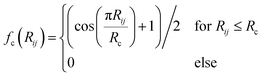 | (6) |
In the invariant polynomial based NN approaches, the permutation symmetry is explicitly guaranteed by the symmetrization operators. It is worth presenting how the permutation symmetry is implemented in the HD-NNP approach explicitly. With A2BC (like OH + CO) as an example, we label the atoms in the following order A(1)A(2)B(3)C(4). Then the components of the sum in eqn (4) and (5) read explicitly as,
| Gij,tr2 = exp(−ηtr(Rij − Rs,tr)2)fc,tr(Rij), | (7) |
Gijk,ta3 = 21−ςta(1 + λta![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θijk)ςta θijk)ςta![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−ηta(Rij2 + Rik2 + Rjk2))fc,ta(Rij)fc,ta(Rik)fc,ta(Rjk), exp(−ηta(Rij2 + Rik2 + Rjk2))fc,ta(Rij)fc,ta(Rik)fc,ta(Rjk), | (8) |
 | (9) |
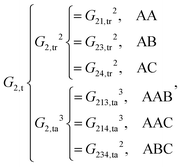 | (10) |
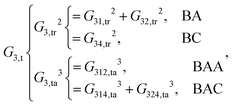 | (11) |
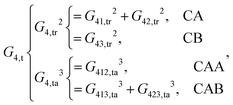 | (12) |
As shown, for each central atom, the radial and the angular functions are grouped together according to their interaction types. If the central atom is A, there are three types of radial interactions, AA, AB and AC, and three types of angular interactions, AAB, AAC and ABC. For the central atom being B, there are only two types of radial interactions, BA and BC, and two types of angular interactions, BAA and BAC. The same situation holds for the central atom being C. According to eqn (3), the entire energy is expressed as follows:
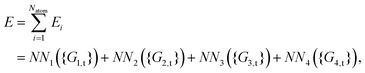 | (13) |
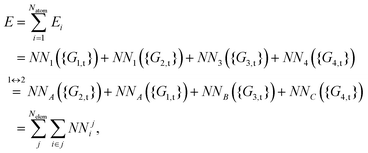 | (14) |
It is also worth pointing out explicitly the significance of inclusion of the angular symmetry functions, eqn (5), for the correct description of the chemical environment of the central atom. If only radial symmetry functions are included, i.e., only eqn (4) is used, eqn (9)–(12) would only have Gi,tr2 (i = 1–4) left. One can easily find that the resulting fingerprints include additional “false symmetry” properties with respect to the permutations of the bond pair, either (r13, r23) or (r14, r24), while the correct symmetry property for any A2BC system is invariant with respect to the only permutation of two like atoms 1 and 2, which corresponds to two exchanges of (r13, r23) and (r14, r24) simultaneously. Hence, these radial symmetry functions Gi,tr2 (i = 1–4) alone are insufficient to distinguish between these molecular configurations. Actually, similar situations have been pointed out and discussed in the PIP-NN approach.25 Some additional cross terms, corresponding to the secondary invariants, have to be included to distinguish molecular configurations that have the same primary invariants.28 The angular functions in the HD-NNP approach seem to function, to some extent, like the secondary invariants in the polynomial based NN approaches, PIP-NN, NRPP-NN and FI-NN.
III. Comparison of the fitting approaches
The five prototypical reactions OH + CO, H + H2S, H + NH3, H + CH4 and OH + CH4 have been studied extensively due to their fundamental significance in the field of quantum reaction dynamics. Full-dimensional accurate PESs have been fitted with the PIP-NN approach for these systems based on large numbers of ab initio points calculated at the level of the explicitly correlated coupled cluster singles, doubles and perturbative triples with the augmented correlation corrected valence triple-zeta basis set (CCSD(T)-F12a/AVTZ).40,42,53–55 About 74![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000, 34
000, 34![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000, 100
000, 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000, 63
000, 63![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 and 135
000 and 135![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 points were calculated at the CCSD(T)-F12a/AVTZ level for the aforementioned systems, respectively. Their distributions are shown in Fig. 1–5(a). It can be seen that, most sampling points are of low to medium energies, albeit with some in the high energy regions, which is necessary for quantum dynamical calculations. First, the HD-NNP approach is used to fit these PESs. For each system, different NN architectures with two or three hidden layers with different sets of atom-centered symmetry functions have been carefully tested to identify the best fitting with its final total RMSE comparable to that by the PIP-NN approach. Although different NN architectures are in principle allowed for different elements in the HD-NNP approach, we found that using different numbers of layers or neurons per layer does not significantly improve the fitting performance. Hence, we choose to use the same NN architectures for all the elements in this work. Therefore, for each system, its entire NN structure can be specified as nA/nB/nC–n1–n2–1: n1 and n2 denote the number of neurons in the first and second hidden layers, respectively; 1 corresponds to the output neuron, the energy; and nA/nB/nC are the number of atom-centered symmetry functions for elements A, B and C, constituting the input neurons. In this work, these systems are labeled as O2CH, H3S, H4N, H5C and H5CO, respectively. Consequently, the number of the fitting parameters are given as ntA/ntB/ntC for elements A, B and C respectively. Table 1 shows the structures, number of fitting parameters (ntot) and total RMSEs (meV) of the HD-NNP approach for these five systems above.
000 points were calculated at the CCSD(T)-F12a/AVTZ level for the aforementioned systems, respectively. Their distributions are shown in Fig. 1–5(a). It can be seen that, most sampling points are of low to medium energies, albeit with some in the high energy regions, which is necessary for quantum dynamical calculations. First, the HD-NNP approach is used to fit these PESs. For each system, different NN architectures with two or three hidden layers with different sets of atom-centered symmetry functions have been carefully tested to identify the best fitting with its final total RMSE comparable to that by the PIP-NN approach. Although different NN architectures are in principle allowed for different elements in the HD-NNP approach, we found that using different numbers of layers or neurons per layer does not significantly improve the fitting performance. Hence, we choose to use the same NN architectures for all the elements in this work. Therefore, for each system, its entire NN structure can be specified as nA/nB/nC–n1–n2–1: n1 and n2 denote the number of neurons in the first and second hidden layers, respectively; 1 corresponds to the output neuron, the energy; and nA/nB/nC are the number of atom-centered symmetry functions for elements A, B and C, constituting the input neurons. In this work, these systems are labeled as O2CH, H3S, H4N, H5C and H5CO, respectively. Consequently, the number of the fitting parameters are given as ntA/ntB/ntC for elements A, B and C respectively. Table 1 shows the structures, number of fitting parameters (ntot) and total RMSEs (meV) of the HD-NNP approach for these five systems above.
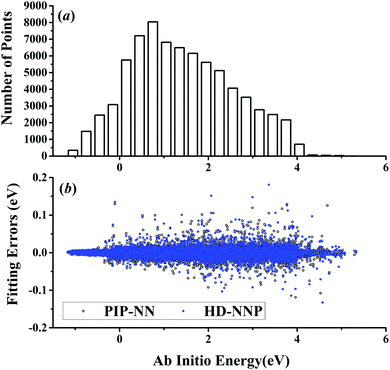 | ||
| Fig. 1 (a) The distribution of the sampled points, and (b) PIP-NN and HD-NNP fitting errors (eV) as a function of the ab initio energy (eV) relative to the reactant asymptote for the OH + CO system. | ||
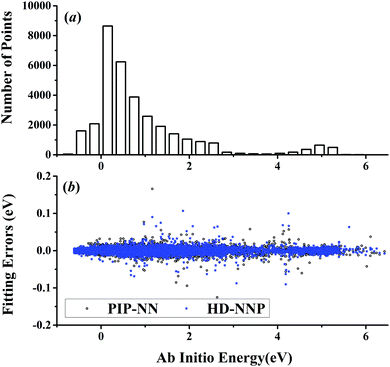 | ||
| Fig. 2 (a) The distribution of the sampled points, and (b) PIP-NN and HD-NNP fitting errors (eV) as a function of the ab initio energy (eV) relative to the reactant asymptote for the H + H2S system. | ||
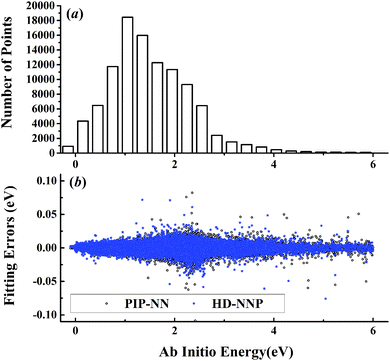 | ||
| Fig. 3 (a) The distribution of the sampled points, and (b) PIP-NN and HD-NNP fitting errors (eV) as a function of the ab initio energy (eV) relative to the reactant asymptote for the H + NH3 system. | ||
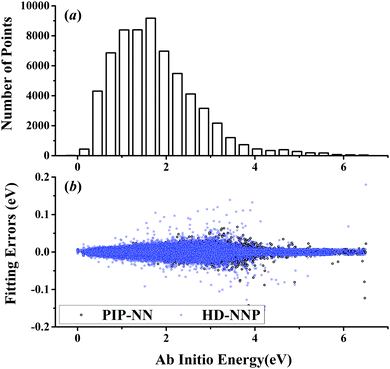 | ||
| Fig. 4 (a) The distribution of the sampled points, and (b) PIP-NN and HD-NNP fitting errors (eV) as a function of the ab initio energy (eV) relative to the reactant asymptote for the H + CH4 system. | ||
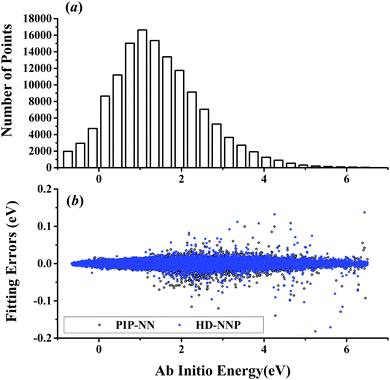 | ||
| Fig. 5 (a) The distribution of the sampled points, and (b) PIP-NN and HD-NNP fitting errors (eV) as a function of the ab initio energy (eV) relative to the reactant asymptote for the OH + CH4 system. | ||
| Systems | Items | HD-NNP | PIP-NN | NRPIP-NN | FI-NN |
|---|---|---|---|---|---|
| O2CH | Structure | 48/32/32–60–60–1 | 17–50–80–1 | 7–50–90–1 | 7–50–80–1 |
| n tot | 6661/5701/5701 | 5061 | 5081 | 4561 | |
| RMSE | 5.8 | 5.5 | 6.8 | 6.7 | |
| H3S | Structure | 28/14–20–80–1 | 22–20–60–1 | 9–40–50–1 | 9–30–60–1 |
| n tot | 2341/2061 | 1781 | 2501 | 2221 | |
| RMSE | 5.0 | 3.0 | 6.9 | 5.6 | |
| H4N | Structure | 28/14–60–60–1 | 81–20–80–1 | 38–30–70–1 | 31–30–60–1 |
| n tot | 5461/4621 | 3421 | 3411 | 2881 | |
| RMSE | 3.8 | 3.4 | 3.6 | 4.7 | |
| H5C | Structure | 28/14–60–60–1 | 848–4–100–1 | 203–15–45–1 | |
| n tot | 5461/4621 | 3997 | 3826 | ||
| RMSE | 8.0 | 5.1 | 6.3 | ||
| H5CO | Structure | 50/28/28–60–60–1 | 1331–4–100–1 | ||
| n tot | 6781/5461/5461 | 5929 | |||
| RMSE | 4.7 | 3.9 |
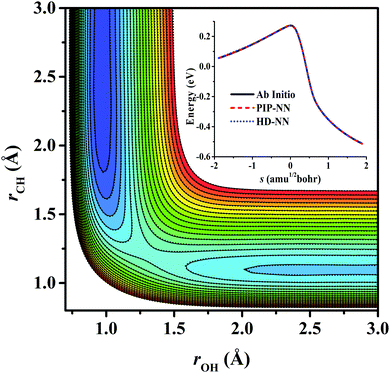
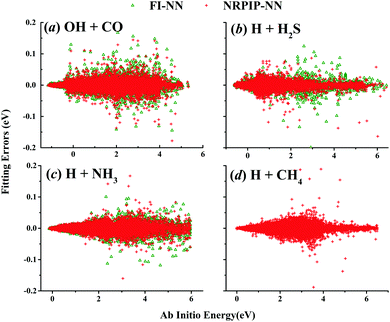
For OH + CO, the atomic environments of oxygen, carbon and hydrogen, have been described by 48, 32 and 32 atom-centered symmetry functions, respectively. Each of the two hidden layers possesses 60 neurons, resulting in 6661, 5701 and 5701 fitting parameters for oxygen, carbon and hydrogen, respectively. The total RMSE is 5.8 meV, compared to 5.5 meV of the total RMSE in the PIP-NN PES. However, the PIP-NN PES consists of only one NN, 17–50–80–1, with 5061 fitting parameters. Therefore, HD-NNP is slower than the PIP-NN PES. The HD-NNP RMSEs for H3S, H4N, H5C and H5CO are 5.0, 3.8, 8.0 and 4.7 meV, respectively, which are all comparable to those fitted by the PIP-NN approach, albeit with more fitting parameters. Unlike one NN used for the entire system in the invariant polynomial based NN approaches, there are as many NNs as the number of atoms in HD-NNPs. Therefore, the HD-NNP is roughly the number of atoms slower in evaluation than the PIP-NN PES but more general. We note that in contrast to other HD-NNP applications reported in the literature, for which energy errors normalized per atom are given, the present RMSEs refer to energies of the entire system. Fig. 1–5(b) present the HD-NNP fitting errors along with the ab initio energy relative to the respective reactant asymptotes of the five systems. The PIP-NN fitting errors are also included for comparison. As shown clearly, both fitting approaches show similar fitting performance for these reactions: the small errors are evenly distributed within the energy range for each system. Therefore, the PESs from either the HD-NNP or PIP-NN are expected to give the same dynamical results, as has been demonstrated for the reaction H2 + HS.37 Furthermore, Fig. 6 presents the comparison of the contour plots of the HD-NNP and PIP-NN PESs along the two reaction coordinates, rOH and rCH, for the abstraction reaction OH + CH4 → H2O + CH3. They are essentially identical. In the inset of the same figure, the minimum energy paths of the PIP-NN and HD-NNP PESs and by the ab initio calculation are also indistinguishable from each other, confirming the equivalence of the two fitting approaches.
NRPIP-NN and FI-NN are then compared by fitting PESs for OH + CO, H + H2S and H + NH3, whose FIs are available.46 As has been mentioned above, the form of the invariant polynomials is not unique. Taking A2B, A(1)A(2)B(3), as an example, FIs and NRPIPs are given explicitly in Table 2. For A2B systems, NRPIPs are essentially the same as FIs, as G3 = (f22−f3)/2. However, the evaluation of G3 is faster than that of f3 due to more evaluations of the polynomials involved in f3. Similar situations hold for A2BC and A3B: the evaluation of NRPIPs is 10% faster than that of FIs, as shown also in Table 2. Indeed, for O2CH and H3S, NRPIPs and FIs are essentially the same as each other, as they can be converted to each other with the same number of terms. For NH4, the number of NRPIPs is larger than that of FIs due to the incomplete decomposition of the algorithm. Nonetheless, the resulting fitting errors of the OH + CO, H + H2S and H + NH3 systems with the two fitting approaches resemble each other, as shown in Fig. 7(a–c). As shown in Table 1, the percentages of the FIs or NRPIPs become smaller with the molecular size: for O2CH and H3S, it is 7/17 and 9/22 for both methods; for H + NH3, it is 35/81 for NRPIP-NN and 31/81 for FI-NN. Finally, the H + CH4 system is fitted by the NRPIP-NN approach, resulting in a total RMSE of 6.3 meV with 203 NRPIPs from 848 PIPs. One can see that for complicated systems, the number of the NRPIPs is still quite large. The fitting errors in Fig. 7(d) resemble those by PIP-NN and HD-NN, as shown in Fig. 4.
IV. Mode specificity of OH + CH4
Mode specificity is defined by the differences in reactivity due to excitations in various reactant modes. It is an important and interesting non-statistical phenomenon in reaction dynamics, and related to the laser control of reactions. In this work, the mode specificity in the vibrational modes of the reactants for the OH (vOH) + CH4 (vu, vrock, vss, vas) → H2O + CH3 reaction is studied by the QCT implemented in the VENUS chemical dynamics program.58 There are four types of vibrational modes in the CH4 reactant, namely, umbrella, rock, symmetric stretch and asymmetric stretch modes. The HD-NNP and PIP-NN PESs are expected to yield the same dynamical results, as has been demonstrated in our previous work.36,37 However, the PIP-NN PES is much faster with relatively smaller RMSEs. Therefore, the PIP-NN PES is used in the subsequent computations. At the collision energies of 4.0, 10.0, 15.0, 20.0, 25.0 and 30.0 kcal mol−1 (1 eV = 23.06 kcal mol−1), 7–15 × 104 trajectories are calculated with initial reactants being at the ro-vibrational ground states (v = 0), or with one vibrational mode excited by one quantum (v = 1). For each different initial condition, the maximum impact parameter (bmax) is determined using small batches of trajectories with trial values. Then the impact parameter b for each trajectory is sampled according to b = bmaxRN1/2, where RN is a random number between 0 and 1. The initial separation between the reactants and the termination criteria for non-reactive and reactive processes are both set as 8.0 Å. The scattering parameters including the spatial orientation of the initial reactants, vibrational phases and the impact parameter, are determined according to the Monte Carlo approach as implemented in VENUS.58 The propagation time step is selected to be 0.05 fs and the gradients of the PES with respect to atomic coordinates are calculated numerically. The combined fourth-order Runge–Kutta and sixth-order Adams–Moulton algorithms are used for the integration of the trajectories. Almost all trajectories conserve energy within a chosen criterion (10−4 kcal mol−1). The reactive integral cross section (ICS) is calculated according to the following formula:| σr(Ec) = πbmax2(Ec)Pr(Ec), | (15) |
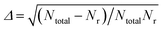 . In this work, the statistical errors are all less than 4.0% except for Ec = 4.0 kcal mol−1, at which the statistical error is less than 8%.
. In this work, the statistical errors are all less than 4.0% except for Ec = 4.0 kcal mol−1, at which the statistical error is less than 8%.
Fig. 8(a) presents the corresponding ICSs along the collision energy. At the ground state (v = 0) of the reactants, the reactivity at 4.0 kcal mol−1 is very small, which is consistent with the zero point energy (ZPE) corrected barrier height of 4.6 kcal mol−1.40 Then the reactive ICS increases monotonically with the collision energy, which is common for activated reactions. When one of the vibrational modes in the reactants is excited by one quantum, all the resulting ICSs still go up monotonically with the collision energy. However, their effects on the reactivity are different. In order to see their effects clearly and directly, scaled ICSs are defined as ICS(vi = 1, Ec)/ICS(v = 0, Ec), and are plotted in Fig. 9. As shown clearly, the OH vibrational mode is essentially a spectator within the range of the collision energy, as expected since OH is not involved in the bond forming or breaking during the chemical reaction. On the other hand, all the vibrational modes of the CH4 reactant enhance the reaction significantly, especially at low collision energy. For instance, at Ec = 4 kcal mol−1, the scaled ICSs are 3.74, 5.22, 1.65 and 1.49, for vas = 1, vss = 1, vrock = 1 and vu = 1, respectively. At this low collision energy, their effects are significantly different. Along with the collision energy, initially, the scaled ICSs of all the vibrational modes of the CH4 reactant drop down drastically, then decrease gradually, and finally tend to become flat eventually. Besides, the effects of the symmetric and asymmetric stretching modes are always larger, compared to the umbrella and rock modes within the energy range. At Ec = 30 kcal mol−1, the scaled ICSs read 1.26, 1.25, 1.16 and 1.11, for vas = 1, vss = 1, vrock = 1 and vu = 1, respectively. The promoting effect by the excitation of the C–H stretch mode was also found in the OH + CHD3 → H2O + CD3 reaction by reduced-dimensional quantum dynamical (QD) and full-dimensional QCT calculations.59 However, the excitation of the umbrella mode was found to be a spectator in that work.59
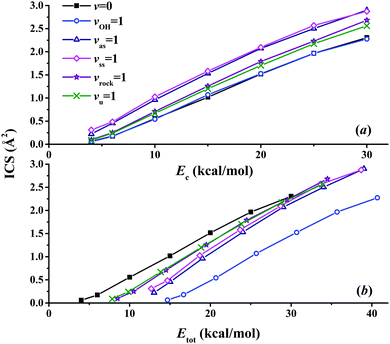 | ||
| Fig. 8 The calculated integral cross sections (ICSs) for the OH (vOH) + CH4 (vu, vrock, vss, vas) → H2O + CH3 reaction as a function of (a) the collision energy and (b) the total energy. | ||
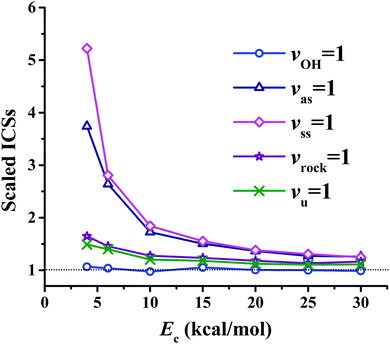 | ||
| Fig. 9 The scaled ICSs for the OH (vOH) + CH4 (vu, vrock, vss, vas) → H2O + CH3 reaction as a function of the collision energy. | ||
In order to compare the relative efficacies of the reactant modes and the collision energy in promoting the reaction, the ICSs are also plotted in Fig. 8(b) as a function of the total energy, which is defined as the sum of the initial ro-vibrational energy relative to the ZPE corrected reactant asymptote and the collision energy. As shown clearly, all the energy thresholds are shifted to higher energies for the reactants in the vibrationally excited states (v = 1), indicating that not all vibrational energies are used to surmount the potential barrier. The efficacy of the OH vibrational mode is never higher than the collision energy due to its spectator nature. For vibrational modes of the CH4 reactant, the situation is complicated. With the total energy up to ca. 30 kcal mol−1, the collision energy is more effective in promoting the reaction than all vibrational modes of CH4. This is consistent with the prediction according to the Polanyi rules for this early-barrier reaction. With even higher total energy, it seems that the efficacies of all the vibrational modes of CH4 become comparable to that of the collision energy. On the other hand, the different efficacies of the vibrational modes cannot be explained simply. These findings are also significantly different from those in the OH + CHD3 → H2O + CD3 reaction: the reactivity was found to be largely enhanced by the excitation of the C–H stretch mode at high total energies larger than ca. 14 kcal mol−1.59
Based on the assumption of the sudden approximation, namely, the intramolecular vibrational relaxation (IVR) of the reactants is much slower than the collision time scale, the recently proposed sudden vector projection model (SVP) attributes the efficacy of the specified reactant mode in promoting the reaction to its coupling with the reaction coordinate at the transition state.60–63 In particular, it is quantified approximately by the overlap between the reactant normal mode vector and the reaction coordinate vector. For the OH + CH4 reaction, the calculated SVP values are 0.31, 0.42, 0.02, 0.09, 0.01 and 0.43, respectively, for the asymmetric stretch, symmetric stretch, rock and umbrella modes of CH4, the OH vibrational mode and the collision motion.62 The spectator nature of the OH vibrational mode is consistent with the near-zero SVP value. On the other hand, SVP predicts that symmetric and asymmetric stretch modes are much more effective than the rock and umbrella modes in promoting the reactivity. In addition, the rock and umbrella modes should have small efficacies. The collision motion is the most effective in promoting the reaction compared to the vibrational modes of the reactants. However, Fig. 8(b) shows that: at low total energies, the rock and umbrella modes are more effective than the stretch modes, and the efficacies of all the vibrational modes of CH4 become similar to each other along with the total energy eventually. Although the QCT results resemble the QD results for activated reactions generally, one should bear in mind that QCT cannot describe QM effects, such as ZPE conservation, tunneling and resonance. Besides, the time scale of IVR might be comparable to that of the collision time for complicated molecular systems. Therefore, it is highly desirable to perform accurate QM calculations, albeit too demanding for the 15-dimensional system currently. Nonetheless, the complicated mode specificity of this reaction dynamics cannot be understood in a simple way.
We note in passing that several investigations have been reported on the SVP model in predicting the mode specificity of H/F/Cl + CH4/CHD3 reactions.59,62,64–67 The SVP predictions are generally in good agreement with QCT or QD computations. For instance, in the H + CHD3 → H2 + CD3 reaction, it has been found that all excitations in the C–H stretch, and the CD3 umbrella motions enhance the reactivity significantly with the collision energy of up to 36.9 kcal mol−1,68 consistent with the SVP values, 0.98 and 0.21.62 However, the SVP value for the CH bending motion is 0.0, in contradiction to the evident enhancement at high total energies calculated by QD.68 In the F + CHD3 reaction, the C–H stretch excitation enhances the reactivity for the product channel HF + CD3, and has no effect on the other product channel DF + CHD2. These QCT calculations are consistent with the SVP values: 0.14 and 0.01.65 However, the SVP model may not be appropriate due to the existence of the pre-reaction well for this reaction with a low barrier height, as pointed out earlier.62 In Cl + CHD3 → HCl + CD3 reaction, the C–H stretch excitation was found to promote the reactivity significantly,69 consistent again with the large SVP value: 0.93.62 Interested readers are also referred to those references for further detailed discussions on the SVP predictions.
V. Conclusions
Recently, fitting global PESs for molecular systems with NNs has attracted much attention, primarily due to its efficiency and high fidelity. Any PES must be invariant with respect to nuclear permutation and the inversion group. This is not only because the molecular Hamiltonian commutes with the symmetry operators of the system, but also because a PES without permutation and inversion symmetries might yield false spectroscopic and reaction dynamics outcomes. In this study, several different symmetry strategies in the NN approach, including HD-NNP, PIP-NN, NRPIP-NN and FI-NN, have been compared in fitting several prototypical reaction systems, OH + CO, H + H2S, H + NH3, H + CH4 and OH + CH4. For each NN, it takes several hours to days to get the optimal fitting. The fitting results demonstrate that the three invariant polynomial based approaches are effectively equivalent, consistently exhibiting similar energy errors in representing the five reaction systems. The form of the invariant polynomials is not unique and the comparison between NRPIP and FI shows that evaluation of NRPIPs is faster than that of FIs.For very high dimensional systems with several tens and even up to thousands of atoms, it is impractical to determine their invariant polynomials. This issue is addressed by the HD-NNP, which also include full permutation invariance and in which the total energy is expressed as the sum of atomic contributions. HD-NNP is highly scalable, and has been applied successfully in fitting various practical systems. In this work, it is found that the HD-NNP works well in fitting the small systems mentioned above, but typically relies on more fitting parameters.
The mode specificity of the OH + CH4 → H2O + CH3 reaction has been studied using the QCT approach on the globally accurate PIP-NN PES. It has been found that resulting mode specificity is rather complicated. All the vibrational modes of CH4 can enhance the reaction, especially at low collision energies. The OH mode is essentially a spectator. Compared to the collision energy, all the vibrational modes of CH4 are less effective in promoting the reaction with total energies less than ca. 30 kcal mol−1. This is consistent with the prediction according to the Polanyi rules for this early barrier reaction. For the total energies larger than 30 kcal mol−1, the efficacies of the CH4 vibrational modes are comparable to that of the collision energy. The results are partially consistent with the SVP predictions for the stretching modes, the collision motion, and the OH vibrational mode, while the efficacies of the low frequency modes, rock and umbrella modes of CH4, are underestimated significantly by the SVP model. Both the intrinsic flaw of QCT and the possible slow IVR in the complicated CH4 system could be the cause to yield such results.
Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
This work was financially supported by National Natural Science Foundation of China (Contract No. 21573027 to J. L.) and by the Alexander von Humboldt Foundation (Humboldt Fellowship for Experienced Researchers for JL). JB acknowledges the DFG for a Heisenberg Professorship (Be3264/11-2).References
- T. Hollebeek, T.-S. Ho and H. Rabitz, Annu. Rev. Phys. Chem., 1999, 50, 537–570 CrossRef CAS.
- M. Majumder, S. A. Ndengue and R. Dawes, Mol. Phys., 2016, 114, 1–18 CrossRef CAS.
- M. A. Collins, Theor. Chem. Acc., 2002, 108, 313–324 Search PubMed.
- J. N. Murrell, S. Carter, S. C. Farantos, P. Huxley and A. J. C. Varandas, Molecular Potential Energy Functions, Wiley, Chichester, 1984 Search PubMed.
- A. J. C. Varandas, Adv. Chem. Phys., 1988, 74, 255–338 CAS.
- A. Jackle and H.-D. Meyer, J. Chem. Phys., 1996, 104, 7974 CrossRef.
- A. Jackle and H.-D. Meyer, J. Chem. Phys., 1998, 109, 3772 CrossRef CAS.
- B. J. Braams and J. M. Bowman, Int. Rev. Phys. Chem., 2009, 28, 577–606 Search PubMed.
- J. M. Bowman, G. Czakó and B. Fu, Phys. Chem. Chem. Phys., 2011, 13, 8094–8111 RSC.
- C. Qu, Q. Yu and J. M. Bowman, Annu. Rev. Phys. Chem., 2018, 69, 151–175 CrossRef CAS PubMed.
- J. Behler, J. Chem. Phys., 2016, 145, 170901 CrossRef PubMed.
- V. Botu, R. Batra, J. Chapman and R. Ramprasad, J. Phys. Chem. C, 2017, 121, 511–522 CrossRef CAS.
- T. B. Blank, S. D. Brown, A. W. Calhoun and D. J. Doren, J. Chem. Phys., 1995, 103, 4129–4137 CrossRef CAS.
- C. M. Handley and P. L. A. Popelier, J. Phys. Chem. A, 2010, 114, 3371–3383 CrossRef CAS PubMed.
- J. Behler, Phys. Chem. Chem. Phys., 2011, 13, 17930–17955 RSC.
- A. P. Bartók, M. C. Payne, R. Kondor and G. Csányi, Phys. Rev. Lett., 2010, 104, 136403 CrossRef PubMed.
- M. Rupp, A. Tkatchenko, K.-R. Müller and O. A. von Lilienfeld, Phys. Rev. Lett., 2012, 108, 058301 CrossRef PubMed.
- E. V. Podryabinkin and A. V. Shapeev, Comput. Mater. Sci., 2017, 140, 171–180 CrossRef CAS.
- J. Behler, Int. J. Quantum Chem., 2015, 115, 1032–1050 CrossRef CAS.
- S. Lorenz, A. Groß and M. Scheffler, Chem. Phys. Lett., 2004, 395, 210–215 CrossRef CAS.
- L. M. Raff, R. Komanduri, M. Hagan and S. T. S. Bukkapatnam, Neural Networks in Chemical Reaction Dynamics, Oxford University Press, Oxford, 2012 Search PubMed.
- J. Chen, X. Xu, X. Xu and D. H. Zhang, J. Chem. Phys., 2013, 138, 221104 CrossRef PubMed.
- J. Chen, X. Xu and D. H. Zhang, J. Chem. Phys., 2013, 138, 154301 CrossRef PubMed.
- B. Jiang and H. Guo, J. Chem. Phys., 2013, 139, 054112 CrossRef PubMed.
- J. Li, B. Jiang and H. Guo, J. Chem. Phys., 2013, 139, 204103 CrossRef PubMed.
- S. Manzhos, R. Dawes and T. Carrington, Int. J. Quantum Chem., 2015, 115, 1012–1020 CrossRef CAS.
- K. Shao, J. Chen, Z. Zhao and D. H. Zhang, J. Chem. Phys., 2016, 145, 071101 CrossRef PubMed.
- J. Ischtwan and M. A. Collins, J. Chem. Phys., 1991, 94, 7084–7097 CrossRef CAS.
- A. Brown, B. J. Braams, K. Christoffel, Z. Jin and J. M. Bowman, J. Chem. Phys., 2003, 119, 8790–8793 CrossRef CAS.
- H. Gassner, M. Probst, A. Lauenstein and K. Hermansson, J. Phys. Chem. A, 1998, 102, 4596–4605 CrossRef CAS.
- J. Behler, S. Lorenz and K. Reuter, J. Chem. Phys., 2007, 127, 014705 CrossRef PubMed.
- J. Behler and M. Parrinello, Phys. Rev. Lett., 2007, 98, 146401 CrossRef PubMed.
- J. Behler, J. Chem. Phys., 2011, 134, 074106 CrossRef PubMed.
- J. Behler, J. Phys.: Condens. Matter, 2014, 26, 183001 CrossRef CAS PubMed.
- J. Behler, Angew. Chem., Int. Ed., 2017, 56, 12828–12840 CrossRef CAS PubMed.
- B. Kolb, B. Zhao, J. Li, B. Jiang and H. Guo, J. Chem. Phys., 2016, 144, 224103 CrossRef.
- D. Lu, J. Qi, M. Yang, J. Behler, H. Song and J. Li, Phys. Chem. Chem. Phys., 2016, 18, 29113–29121 RSC.
- J. Ischtwan and M. A. Collins, J. Chem. Phys., 1994, 100, 8080–8088 CrossRef CAS.
- A. Schmelzer and J. N. Murrell, Int. J. Quantum Chem., 1985, 28, 287–295 CrossRef CAS.
- J. Li and H. Guo, J. Chem. Phys., 2015, 143, 221103 CrossRef PubMed.
- Z. Xie and J. M. Bowman, J. Chem. Theory Comput., 2010, 6, 26–34 CrossRef CAS PubMed.
- D. Lu and J. Li, J. Chem. Phys., 2016, 145, 014303 CrossRef PubMed.
- W. Bosma, J. Cannon and C. Playoust, J. Symb. Comput., 1997, 24, 235–265 CrossRef.
- G.-M. Greuel, G. Pfister and H. Schönemann, SINGULAR 3.0.4—A computer algebra system for polynomial computations, 2007, see http://www.singular.uni-kl.de.
- D. Opalka and W. Domcke, J. Chem. Phys., 2013, 138, 224103 CrossRef PubMed.
- B. Fu and D. H. Zhang, J. Chem. Theory Comput., 2018, 14, 2289–2303 CrossRef CAS.
- K. V. J. Jose, N. Artrith and J. Behler, J. Chem. Phys., 2012, 136, 194111 CrossRef PubMed.
- M. Gastegger and P. Marquetand, J. Chem. Theory Comput., 2015, 11, 2187–2198 CrossRef CAS.
- M. Gastegger, C. Kauffmann, J. Behler and P. Marquetand, J. Chem. Phys., 2016, 144, 194110 CrossRef PubMed.
- B. Jiang, J. Li and H. Guo, Int. Rev. Phys. Chem., 2016, 35, 479–506 Search PubMed.
- J. S. Smith, O. Isayev and A. E. Roitberg, Chem. Sci., 2017, 8, 3192–3203 RSC.
- J. Behler, RuNNer-A code for constructing high-dimensional neural network potentials, Georg-August-Universtität, 2018 Search PubMed.
- J. Li, J. Chen, D. H. Zhang and H. Guo, J. Chem. Phys., 2014, 140, 044327 CrossRef PubMed.
- J. Li and H. Guo, Phys. Chem. Chem. Phys., 2014, 16, 6753–6763 RSC.
- J. Li, J. Chen, Z. Zhao, D. Xie, D. H. Zhang and H. Guo, J. Chem. Phys., 2015, 142, 204302 CrossRef PubMed.
- C. M. Bishop, Neural Networks for Pattern Recognition, Oxford University Press, Inc., New York, NY, USA, 1995, ISBN:0198538642 Search PubMed.
- G. Imbalzano, A. Anelli, D. Giofré, S. Klees, J. Behler and M. Ceriotti, J. Chem. Phys., 2018, 148, 241730 CrossRef PubMed.
- X. Hu, W. L. Hase and T. Pirraglia, J. Comput. Chem., 1991, 12, 1014–1024 CrossRef CAS.
- H. Song, Y. Lu, J. Li, M. Yang and H. Guo, J. Chem. Phys., 2016, 144, 164303 CrossRef.
- B. Jiang and H. Guo, J. Chem. Phys., 2013, 138, 234104 CrossRef.
- B. Jiang and H. Guo, J. Am. Chem. Soc., 2013, 135, 15251–15256 CrossRef CAS.
- B. Jiang and H. Guo, J. Chin. Chem. Soc., 2014, 61, 841–959 CrossRef.
- H. Guo and B. Jiang, Acc. Chem. Res., 2014, 47, 3679–3685 CrossRef CAS.
- R. Welsch and U. Manthe, J. Chem. Phys., 2014, 141, 051102 CrossRef.
- C. Xie, B. Jiang, M. Yang and H. Guo, J. Phys. Chem. A, 2016, 120, 6521–6528 CrossRef CAS.
- R. Ellerbrock and U. Manthe, J. Chem. Phys., 2017, 147, 241104 CrossRef.
- R. Ellerbrock and U. Manthe, J. Chem. Phys., 2018, 148, 224303 CrossRef PubMed.
- Z. Zhang, J. Chen, S. Liu and D. H. Zhang, J. Chem. Phys., 2014, 140, 224304 CrossRef PubMed.
- Z. Zhang, Y. Zhou, D. H. Zhang, G. Czakó and J. M. Bowman, J. Phys. Chem. Lett., 2012, 3, 3416–3419 CrossRef CAS PubMed.
| This journal is © the Owner Societies 2019 |