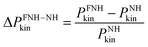Fast Nosé–Hoover thermostat: molecular dynamics in quasi-thermodynamic equilibrium†
Received
1st November 2018
, Accepted 16th February 2019
First published on 18th February 2019
Abstract
An extension of the Nosé–Hoover thermostat equation for molecular dynamics (MD) simulation is introduced, which perturbs fast degrees of freedom out of canonical equilibrium, while preserving the average temperature of the system. Based on the generalised Liouville equation, it is shown that the newly introduced fast Nosé–Hoover (FNH) equations give rise to a dynamical system with a well-defined non-equilibrium probability distribution. Corresponding thermostat parameters are identified, which in principle allow to sample arbitrarily close to canonical equilibrium. Results show that the dynamic system properties (e.g. self-diffusion, shear viscosity, dielectric permittivity and rotational relaxation times) are only moderately perturbed for typical FNH setups. However, the non-equilibrium FNH equations modify the occurrence of rare events substantially and thus offer a novel approach for enhanced sampling in MD. In particular, it is shown that the FNH thermostat increased significantly the frequency of the folding and unfolding process of short β-peptides. The efficiency of the phase-space exploration solely depends on the additionally imposed quasi-equilibrium conditions, i.e. it does not rely on any modification of the potential-energy surface.
1 Introduction
Molecular dynamics (MD) simulations are typically performed under canonical (NVT) or isothermal–isobaric (NPT) conditions in order to compare simulated and experimental properties and to study temperature-dependent processes explicitly.1 For this purpose, many different thermostat methods have been developed over the past decades to simulate canonical equilibrium2–6 or closely related conditions.7,8 A thorough overview of different thermostat approaches can for example be found in ref. 1 and 9.
Significant research effort has been aimed in the past years to develop thermostats that do not only generate a canonical ensemble but also damp numerical artefacts. This offers new ways to accelerate simulations. In particular, performance-wise it is tempting to partition a dynamical systems into multiple subproblems with different time scales in order to treat them using different time steps. However, such multi time-step integration (MTS) setups can lead to significant numerical artefacts.10–12 A possible remedy for this issue is the use of specially designed thermostats, which stabilise large time-step integration. Typically, they reduce energy drifts and they disrupt high frequency modes from resonating with lower frequencies.13 The most common choice is to couple (damp) each atom to a white noise Langevin bath,13–15 or by imposing isokinetic constraints on each degree of freedom.16–18 However, the gain in performance obtained by using large time steps may be substantially reduced due to the disruption of the slow modes, thus greatly hindering diffusive and orientational motion.13,19 As recently shown, this undesired side-effect can be mitigated with coloured-noise thermostats,19–21 which couple fast modes strongly and slow modes weakly to the bath.
In this study, a contrary thermostat approach is developed, which has similarities to an idea originally proposed by Barth et al.22 Instead of using MTS integration, they obtained a substantial sampling enhancement by modifying the Nosé–Hoover (NH) equation3,4,23 to generate a non-canonical equilibrium distribution with increased tail probabilities.22 In principle, this setup allows to accelerate the phase-space exploration without increasing the integration time steps or modifying the potential-energy surfaces. Hence, it would avoid the occurrence of undesired MTS resonance artefacts by construction. However, a priori it remains unclear if such a non-canonical equilibrium approach would not lead to significantly different dynamic properties, even for small perturbations compared to the canonical equilibrium.
Here, a novel perturbation of the fast degrees of freedom is introduced for the canonical NH equations. The resulting equations of motion are termed fast Nosé–Hoover (FNH) equations. In the Theory section, it is shown that the FNH equations give rise to a well-defined non-equilibrium probability distribution, which can be tuned arbitrarily close to the canonical equilibrium. In the Method section, simulation details and analysis tools are described, which were used to validate the theoretical derivations. The Results and discussion section is split into two parts. First, relevant thermostat parameters and dynamic properties are discussed for a homogeneous water system using classical MD simulations. Second, the efficiency of the phase space exploration for non-equilibrium perturbations is investigated with respect to the occurrence of rare events. For this purpose, the folding/unfolding equilibrium of two β-peptides in methanol is analysed. The folding process of these β-peptides has been extensively studied in the past,24–32 since it occurs on a relatively fast time scale. In the Conclusion section, relevant scientific findings are summarised and future research directions are discussed.
2 Theory
2.1 Nosé–Hoover equations of motion
Let a physical system be described by a classical Hamiltonian H = Ekin(p) + V(q) on a 2N-dimensional phase space Γ = (p,q). This implies that the dynamic system is conservative, i.e. the total energy is conserved, but not the temperature. Experimental measurements are, however, often performed under constant temperature (and constant pressure) conditions. In order to emulate these additional constraints, Nosé3 and Hoover4 developed the following non-Hamiltonian equations of motions,| |  | (1) |
| |  | (2) |
| |  | (3) |
which are defined on an extended phase space ΓNH′ = (p,q,qξ,ξ). The thermostat mass is labelled by Q1 and particle masses of phase-space coordinates (pi,qi) are termed mi. ξ is the Nosé–Hoover (NH) control variable and qξ is defined according to eqn (6). T0 corresponds to the desired reference temperature of the system and Ndf to the number of degrees of freedom. The Boltzmann constant is indicated by kB.
The key property of the NH eqn (1)–(3) is related to their ability to sample from a canonical equilibrium distribution,
| | 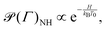 | (4) |
provided that some requirements of
H on
Γ are fulfilled. For example, there should be no additional conserved quantities in the system apart from a generalised energy,
3,4,23,33| | 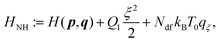 | (5) |
with
| |  | (6) |
Typically this can be ensured by the removal of the centre of mass (COM) motion in order to avoid any impact of Newton's third law

on the distribution
![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif)
(
Γ)
NH in the absence of other external forces. Additionally, the system should be “simple” enough such that the different time scales present in the system are well-behaved with regard to the chosen thermostat parameters. In practise, this often requires different NH thermostats for solvents and solutes.
1
2.2 Fast Nosé–Hoover equations of motion
In the following, we introduce an extension of the NH eqn (1)–(3), which imposes an additional constraint on the fast degrees of freedom. Let the dynamical system be described by the following deterministic, non-Hamiltonian equations of motions,| |  | (7) |
| |  | (8) |
| |  | (9) |
| |  | (10) |
defined on the extended phase space Γ′ = (p,q,qξ,qζ,ξ,ζ).
The mathematical form of the fast Nosé–Hoover (FNH) eqn (7)–(10) resembles earlier work from Barth et al.22 as well as from Bulgac and Kusnezov,34–36 who introduced a generalised form of the NH thermostat equations. T0 corresponds to the desired reference temperature of the system, controlled by the ordinary NH variable ξ in eqn (8) and (9).3,4,23 In addition, the auxiliary thermostat variable ζ is introduced, which perturbs fast motions according to eqn (10). For this purpose, a Heaviside step function is defined as,
| |  | (11) |
where
![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif)
≥ 0 corresponds to the temperature beyond which
pi is additionally controlled by
ζ,
i.e. for
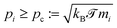
.
Note that the definition of an instantaneous temperature  in eqn (9) follows from the equipartition theorem in the canonical equilibrium. Likewise, the auxiliary constraint set in eqn (10) can be related to the second order equipartition theorem, i.e. by integration by parts (I.P.) one can show that,
in eqn (9) follows from the equipartition theorem in the canonical equilibrium. Likewise, the auxiliary constraint set in eqn (10) can be related to the second order equipartition theorem, i.e. by integration by parts (I.P.) one can show that,
| | 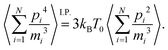 | (12) |
Consequently, the FNH equations defined by
eqn (7)–(10) do not only allow to control the desired average temperature
T of a system
H on
Γ, but also the “variance”-like expression of the velocities according to
eqn (10)i.e. based on
(12). The parameter
α defines the degree of perturbation acting on the fast motions according to
eqn (8) (a more thorough discussion is given below). By increasing the probabilities in the tails of the velocity distributions using
ζ, rare events (
e.g. crossing of high-energy barriers) should become more probable within short simulation time,
22 while statistically averaged properties should not be affected substantially for small perturbations.
Q1,
Q2 correspond to the usual thermostat masses, which determine how fast the thermostat variables (

) respond to a change in the system. Note that the proposed definition for

given in
eqn (10) has the advantage that

, as it is the case for
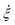
. Hence, typical numerical integration time-steps of MD simulations (
e.g. 2 fs) should still be applicable with the FNH equations. This may not be the case anymore for smaller system sizes when the auxiliary thermostatting control variable is related directly to the instantaneous variance of the momenta,
e.g. by imposing
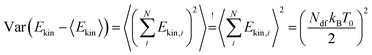
, which would result in

.
A priori there is no reason to assume that the proposed FNH eqn (7)–(10) sample a probability distribution close to canonical equilibrium. Therefore, in order to study the behaviour of the extended system dynamics on Γ′, one has to rely on the generalised non-Hamiltonian Liouville equation,
| | 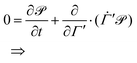 | (13) |
| |  | (14) |
which describes the time evolution of the probability density
![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif)
(
Γ′,
t) of the dynamic system
Γ′. Note that if an equilibrium solution
![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif) 0
0 exists, it could be constructed by interpreting

as a product of a distribution function
f with nontrivial metric
g associated to the curved phase space
Γ′.
33,37,38 The equilibrium
![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif) 0
0 then follows immediately from all conservation laws of the extended system.
33,37,38 However, for the following derivation of
![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif)
(
Γ′,
t) for the FNH equations, we follow an alternative pathway described by Nosé in
ref. 23.
Let the generalised FNH energy be defined as,
| |  | (15) |
| | 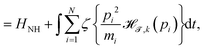 | (16) |
where the continuous logistic function

is used as an approximation of the Heaviside step function with lim
k→∞![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif)
![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) ,k
,k(
pi) =
![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif)
![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif)
(
pi). It is straightforward to show that
HFNH is conserved as,
| |  | (17) |
From this conservation law, a solution for the generalised Liouville
eqn (14) of the non-Hamiltonian system dynamics described by the FNH
eqn (7)–(10) is obtained using,
| | 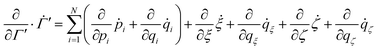 | (18) |
| |  | (19) |
| |  | (20) |
where a reduced
Ndf is considered in the last step due to additionally imposed constraints (
e.g. rigid molecular bonds) and

. It can be shown that the resulting non-equilibrium probability density obeying
eqn (14) can be written as,
| |  | (21) |
| | 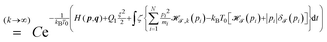 | (22) |
| |  | (23) |
where in the last step,
| |  | (24) |
was introduced for the ease of notation.
From eqn (23), it follows that the non-equilibrium FNH probabilities are modified with respect to the canonical NH probabilities in eqn (4) based on the following mapping,
| |  | (25) |
Note that the non-equilibrium perturbations are discontinuous in the chosen setup with (
k → ∞), which is expected to disrupt the smooth motion compared to the canonical equilibrium. In addition, if
![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif)
>
T0 the following property holds,
| |  | (26) |
Based on aforementioned theoretical considerations it is possible to discuss several practical aspects of the proposed FNH equations:
(1) A canonical equilibrium probability distribution for Γ can only be obtained if 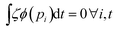 . For arbitrary initial conditions, this is only possible for limQ2→∞ζ = 0 or lim
. For arbitrary initial conditions, this is only possible for limQ2→∞ζ = 0 or lim![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) →∞ϕ(pi) = 0 due to eqn (26), which means the normal NH eqn (1)–(3) are recovered.
→∞ϕ(pi) = 0 due to eqn (26), which means the normal NH eqn (1)–(3) are recovered.
(2) Condition (1) automatically implies that  with a canonical equilibrium solution of the Liouville equation. This result is in agreement with the properties obtained in ref. 39 for multi-temperature dynamics. Therefore, the proposed FNH equations can at best approximate a (canonical) equilibrium distribution for finite
with a canonical equilibrium solution of the Liouville equation. This result is in agreement with the properties obtained in ref. 39 for multi-temperature dynamics. Therefore, the proposed FNH equations can at best approximate a (canonical) equilibrium distribution for finite ![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) , Q2.
, Q2.
(3) For practical purposes, one needs to ensure that the tail perturbations of the FNH equations remain small with respect to the canonical equilibrium, i.e. ![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif) (Γ,t)FNH ≈
(Γ,t)FNH ≈ ![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif) (Γ)NH. The requirement of such a quasi equilibrium distribution leads to the following conditions for the thermostat parameters and the simulated systems:
(Γ)NH. The requirement of such a quasi equilibrium distribution leads to the following conditions for the thermostat parameters and the simulated systems:
(a) ![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) ≫ T0 restricts perturbations to the tails of the kinetic-energy distribution.
≫ T0 restricts perturbations to the tails of the kinetic-energy distribution.
(b) N ≫ 1 ensures that ∃pi with  , which can be efficiently controlled by ζ at every time-step.
, which can be efficiently controlled by ζ at every time-step.
(c) To limit the non-equilibrium perturbations to a small value, one can define a “quasi” canonical equilibrium at αexact0 as follows,
| |  | (27) |
which is non-trivial to solve. In practice,
αexact0 can be estimated based on
eqn (10),
| |  | (28) |
by setting
Q2 ≫
Q1 and
α = 0. This approximation relies on condition (1), for which the FNH equations approximate a canonical equilibrium distribution. Any coupling effects between
ξ and
ζ, which may occur for finite
Q2, are neglected. Typically these effects should be small for systems with a high number of degrees of freedom. Thus, the accuracy of the estimated
α0 depends on
Ndf as well as on the particular system studied. For well-behaved systems, a small perturbation
δα of
α0 is expected to drive the system gently out of quasi-canonical equilibrium.
(4) In order to obtain a rough estimate for reasonable choices of the thermostat mass Qi, one can investigate the dynamics of the extended system variables ξ, ζ for linearised FNH equations assuming  and α = 1. For simplicity, we additionally assume that the dynamics of ξ and ζ are completely decoupled by setting ṗ(ξ)i := −ξpi and ṗ(ζ)i := −ζpi. For a rough estimate, this is a reasonable assumption if one considers that ζ only controls the tails, whereas ξ mainly controls the mean of
and α = 1. For simplicity, we additionally assume that the dynamics of ξ and ζ are completely decoupled by setting ṗ(ξ)i := −ξpi and ṗ(ζ)i := −ζpi. For a rough estimate, this is a reasonable assumption if one considers that ζ only controls the tails, whereas ξ mainly controls the mean of ![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif) . These assumptions lead to the following two decoupled ordinary differential equations (see Appendix A),
. These assumptions lead to the following two decoupled ordinary differential equations (see Appendix A),
| |  | (29) |
| |  | (30) |
with an implied thermostat times scale, which can be defined as,
| |  | (31) |
| | 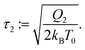 | (32) |
In classical MD, typically
τ1 ≈ 0.1 ps is chosen with NH. For the FNH extension, we recommend
τ1 <
τ2 ≈ 1 ps as a default, in order to reduce instabilities in case condition (3b) is violated.
(5) To anticipate the preservation of hydrodynamic properties by the FNH equations, one can apply a similar argument for Ndf → ∞ as given in ref. 40. In order to ensure efficient equilibration, above-mentioned implied thermostat time scales τ1 and τ2 should remain fixed independently of Ndf. Using eqn (29), it follows Q1 → ∞ if Ndf → ∞, which automatically implies 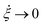 according to eqn (9). Therefore, one can show that in canonical equilibrium
according to eqn (9). Therefore, one can show that in canonical equilibrium  for NH equations, which in turn leads to ξ → 0.40 Consequently, the NH equations reduce to Newtonian equations if the system size is increased. Therefore, hydrodynamic properties are preserved for large systems. In contrast, since τ2 is independent of Ndf for a FNH thermostat,
for NH equations, which in turn leads to ξ → 0.40 Consequently, the NH equations reduce to Newtonian equations if the system size is increased. Therefore, hydrodynamic properties are preserved for large systems. In contrast, since τ2 is independent of Ndf for a FNH thermostat, 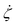 is not necessarily 0, ∀t. For this reason, the FNH equations do not strictly converge to Newtonian equations of motion for Ndf → ∞, which means that hydrodynamic properties remain affected also for larger system sizes. The underlying reason for Q2 not depending on Ndf is related to the fractional definition of
is not necessarily 0, ∀t. For this reason, the FNH equations do not strictly converge to Newtonian equations of motion for Ndf → ∞, which means that hydrodynamic properties remain affected also for larger system sizes. The underlying reason for Q2 not depending on Ndf is related to the fractional definition of  given in eqn (10), which ensures numerical stability for typical integration time steps and intermediate Ndf values based on the
given in eqn (10), which ensures numerical stability for typical integration time steps and intermediate Ndf values based on the ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) (pi2)-scaling. However, hydrodynamic properties of the FNH thermostat remain mostly preserved in practice for typical simulation setups, as will be shown in the Results & discussion section.
(pi2)-scaling. However, hydrodynamic properties of the FNH thermostat remain mostly preserved in practice for typical simulation setups, as will be shown in the Results & discussion section.
(6) Note that the computational complexity of the FNH equations remains unaffected by the additional control variable and constraint in eqn (8) and (10). The number of operations for the force calculation in eqn (10) is, however, slightly increased for every degree of freedom due to the additional control term. Practically more relevant is the evaluation of a global expression for  and
and  , which involves global communication across processors. Similar to NH, this is a disadvantage with respect to an efficient parallel implementation.40 However, the additional control term ζ, which acts on the forces, should not affect the speed of the computation significantly compared to a normal NH thermostat. As mentioned earlier, the auxiliary constraint is also designed such that the integration time step does not have to be adjusted, which ensures an efficient numerical integration.
, which involves global communication across processors. Similar to NH, this is a disadvantage with respect to an efficient parallel implementation.40 However, the additional control term ζ, which acts on the forces, should not affect the speed of the computation significantly compared to a normal NH thermostat. As mentioned earlier, the auxiliary constraint is also designed such that the integration time step does not have to be adjusted, which ensures an efficient numerical integration.
(7) Note that it should be straightforward to replace the NH thermostat within the FNH equations by a NH chain thermostat5 in order to the control the dynamics of ξ.
3 Methods
3.1 Simulation details
Two different types of systems were used for the investigation of the FNH properties: homogeneous systems (liquids) and short β-peptides. First, a cubic box of 1000 SPC water molecules41 was simulated using different thermostat parameters. In addition, auxiliary systems consisting of a cubic box with 1000 chloroform molecules42 and two boxes with 1000 and 5000 argon atoms were used to investigate the impact of different system properties onto the estimated quasi-equilibrium parameter α0.
Second, two β-peptides (Fig. 1) solvated in methanol were studied (1096 and 1123 molecules, respectively).31,32 Their topology and initial coordinates were taken from ref. 32. For peptide 1, a left-handed 314 helical fold was used as starting structure, and for peptide 2 a right-handed 2.710/12 helical fold.32 The β-peptides offer an ideal test system as they fold on a time scale of nanoseconds in methanol, which is easily accessible with classical MD.24 However, the folding events are rare with respect to other implied time scales of the dynamical system (e.g. rotational relaxation times τ or thermostat times τ1 and τ2). Therefore, the effect of the perturbed FNH tail distributions onto rare events can be investigated using these β-peptides.
 |
| | Fig. 1 Amino acid sequence of two β-peptides: (a) peptide 1: H2+-β3-HVal-β3-HAla-β3-HLeu-(S,S)-β3-HAla(αMe)-β3-HVal-β3-HAla-β3-HLeu-OH; (b) peptide 2: H2+-β2-HVal-β3-HAla-β2-HLeu-β3-HVal-β2-HAla-β3-HLeu-OH. | |
For all simulations, a modified version of the GROMOS software package43,44 was used in combination with the GROMOS 54A7β force field.45,46 Periodic boundary conditions were imposed for all systems and all simulations were performed under NVT conditions. The water and chloroform systems were simulated at 300 K, the argon system at 80 K, and the β-peptides at 340 K. As a canonical reference system, the NH thermostat was used with a relaxation time of 0.1 ps.3,4 Newton's equations of motion were integrated using the leapfrog scheme47 with a time step of 2 fs using a single cutoff at 1.4 nm with a pairlist update every 10 fs.12 The centre of mass (COM) motion was stopped every 1 ps. Bond lengths were constrained using the SHAKE algorithm.48 Long-range electrostatic interactions were described using a homogeneous RF approach,49 with a charge-group based cutoff R = 1.4 nm.50 For all simulations involving SPC, a dielectric permittivity of 78.4 (experimental value of water51) was used. For methanol 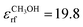 (calculated value from ref. 52) and for chloroform
(calculated value from ref. 52) and for chloroform  (experimental value from ref. 53) were chosen. For argon no long-range electrostatics have to be considered. The water systems were simulated for 50 ns, the auxiliary systems for 1.5 ns, and the β-peptides for 350 ns. Coordinates, velocities and energies were written out every 1 ps, unless stated otherwise. The quasi canonical equilibrium parameter α0 was obtained from eqn (28) by setting τ2 = 1000 μs and by taking the ensemble average from 1 ns trajectories after 0.5 ns equilibration. In all FNH simulations,
(experimental value from ref. 53) were chosen. For argon no long-range electrostatics have to be considered. The water systems were simulated for 50 ns, the auxiliary systems for 1.5 ns, and the β-peptides for 350 ns. Coordinates, velocities and energies were written out every 1 ps, unless stated otherwise. The quasi canonical equilibrium parameter α0 was obtained from eqn (28) by setting τ2 = 1000 μs and by taking the ensemble average from 1 ns trajectories after 0.5 ns equilibration. In all FNH simulations, ![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) = 7T0 was used, which was considered a reasonable value to restrict the non-canonical perturbations of
= 7T0 was used, which was considered a reasonable value to restrict the non-canonical perturbations of ![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif) to the tails.
to the tails.
3.2 Analysis
Different statistical quantities were extracted from the simulation trajectories and averaged using the GROMOS++ analysis tools.54 Self-diffusion coefficients D were obtained according to the Einstein relation55,56 using the  program. For this purpose, 12 short simulations of 1.5 ns length (after 2 ns equilibration) were performed with different initial setups. The uncertainty of the self-diffusion was quantified by calculating the standard deviation of the 12 different values. Similarly, shear viscosities ηshear were extracted from the off-diagonal elements of the pressure tensor using a modified version of the
program. For this purpose, 12 short simulations of 1.5 ns length (after 2 ns equilibration) were performed with different initial setups. The uncertainty of the self-diffusion was quantified by calculating the standard deviation of the 12 different values. Similarly, shear viscosities ηshear were extracted from the off-diagonal elements of the pressure tensor using a modified version of the  program.56,57 For this purpose, the slope of a linear least-square fit of the squared pressure tensor integrals was evaluated between 0 and 10 ps. The data for the pressure tensor integrals was gathered from 1 ns of simulation with a time resolution of 2 fs. The uncertainty of the shear viscosity was quantified based on the standard deviation of the fitted slope. The rotational relaxation time τ was calculated from fitting an exponential decaying function Ce−t/τ to the first-order autocorrelation functions, which were calculated for vectors pointing along different directions (e.g. H–H-bond) of the molecular reference frame. The autocorrelation function was obtained using the
program.56,57 For this purpose, the slope of a linear least-square fit of the squared pressure tensor integrals was evaluated between 0 and 10 ps. The data for the pressure tensor integrals was gathered from 1 ns of simulation with a time resolution of 2 fs. The uncertainty of the shear viscosity was quantified based on the standard deviation of the fitted slope. The rotational relaxation time τ was calculated from fitting an exponential decaying function Ce−t/τ to the first-order autocorrelation functions, which were calculated for vectors pointing along different directions (e.g. H–H-bond) of the molecular reference frame. The autocorrelation function was obtained using the  program. For this analysis, the coordinates were written out every 2 fs over 10 ps of simulation time, after an equilibration time of 25 ns. The dielectric permittivity ε was calculated from 50 ns trajectories (discarding the first 1 ns as equilibration) by solving a Kirkwood–Fröhlich-type equation,58 implemented in the
program. For this analysis, the coordinates were written out every 2 fs over 10 ps of simulation time, after an equilibration time of 25 ns. The dielectric permittivity ε was calculated from 50 ns trajectories (discarding the first 1 ns as equilibration) by solving a Kirkwood–Fröhlich-type equation,58 implemented in the  program. Note that this approach involves the dielectric permittivity of the reaction field as an input parameter. In order to quantify the uncertainty of the dielectric permittivity estimate, the standard deviation was calculated from 10 simulations with identical starting coordinates but different initial velocities. In order to measure the folding and unfolding of the β-peptides, the atom-positional root-mean-square deviation (RMSD) of the backbone atoms between residues 2–6 (peptide 1) and residues 2–5 (peptide 2) were calculated using the
program. Note that this approach involves the dielectric permittivity of the reaction field as an input parameter. In order to quantify the uncertainty of the dielectric permittivity estimate, the standard deviation was calculated from 10 simulations with identical starting coordinates but different initial velocities. In order to measure the folding and unfolding of the β-peptides, the atom-positional root-mean-square deviation (RMSD) of the backbone atoms between residues 2–6 (peptide 1) and residues 2–5 (peptide 2) were calculated using the  program.
program.
4 Results & discussion
4.1 Homogeneous systems
In a first step, the quasi-equilibrium parameter α0 was determined according to eqn (28) for all simulated systems. As can be seen in Table 1, α0 = 1 for the argon simulation. This is an expected result in the absence of any constraints (apart from the COM removal) due to the generalised equipartition theorem given in eqn (12). However, in the presence of constraints (i.e. bonds with fixed length) the estimated α0 parameters depend on the system studied and cannot be anticipated without preparatory simulations. This becomes apparent if one compares 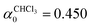 and
and  , which were both obtained for systems containing 1000 molecules with an equally number of degrees of freedom
, which were both obtained for systems containing 1000 molecules with an equally number of degrees of freedom  (both solvent models are fully constrained, i.e. without internal degrees of freedom).
(both solvent models are fully constrained, i.e. without internal degrees of freedom).
Table 1 Comparison of estimated α0 with corresponding standard deviations Δα0 for different systems. For the homogeneous systems, α0 values were estimated from 1 ns simulation trajectories after equilibration for 0.5 ns. For the β-peptides, 1 ns equilibration and 2 ns production run were performed. In all cases, the following parameters were set during the estimation run: τQ1 = 0.1 ps, τQ2 = 1 ms (!) and α = 0. Note that the removal of the COM is considered in the calculation of Ndf
| System |
Argon |
Argon |
Water |
Chloroform |
Peptide 1 |
Peptide 2 |
|
N
atoms
|
1000 |
5000 |
3000 |
5000 |
3352 |
3425 |
|
N
df
|
2997 |
14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 997 997 |
5997 |
5997 |
6702 |
6848 |
|
α
0 ± Δα0 |
0.998 ± 0.050 |
0.999 ± 0.036 |
0.658 ± 0.044 |
0.450 ± 0.031 |
0.637 ± 0.034 |
0.637 ± 0.036 |
The effect of the quasi equilibrium arising from ζ onto the probability distribution ![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif) with respect to different perturbations δα of α0 was investigated in detail for the water box (Fig. 2 and Table 2). For this system, α0 = 0.658 was estimated using eqn (28).
with respect to different perturbations δα of α0 was investigated in detail for the water box (Fig. 2 and Table 2). For this system, α0 = 0.658 was estimated using eqn (28).
 |
| | Fig. 2 Impact of different α-parameters on the time-averaged temperature T and dynamic system properties of water (self-diffusion D, shear viscosity ηshear, rotational relaxation time τ and dielectric permittivity ε). The data with α = α0 is shown in red. Canonical equilibrium values from NH simulation are indicated as a horizontal black line. If displayed, dotted black lines correspond to error bars of the NH reference. For all simulations, the following thermostat parameters were chosen: τQ1 = 0.1 ps, τQ2 = 1.0 ps, ![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) = 2100 K, T0 = 300 K. = 2100 K, T0 = 300 K. | |
Table 2 Impact of the choice of the α-parameter on the time-averaged static temperature T and dynamic system properties (self-diffusion D, shear viscosity ηshear, rotational relaxation time τ, dielectric permittivity ε). Canonical equilibrium values from NH simulation are given in the last column as reference. For all simulations, the following thermostating parameters were chosen: τQ1 = 0.1 ps, τQ2 = 1.0 ps, ![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) = 2100 K, T0 = 300 K
= 2100 K, T0 = 300 K
|
α
|
0.614 |
0.640 |
0.650 |
0.654 |
0.658 |
0.662 |
0.666 |
0.676 |
0.702 |
Nosé–Hoover |
| 〈T〉 [K] |
299.94 ± 4.73 |
300.04 ± 4.90 |
299.98 ± 4.99 |
300.06 ± 5.15 |
300.04 ± 5.29 |
299.99 ± 6.67 |
299.89 ± 6.73 |
299.87 ± 7.09 |
299.91 ± 9.06 |
300.06 ± 5.46 |
| 〈D〉 [10−9 m2 s−1] |
4.94 ± 0.11 |
4.36 ± 0.11 |
4.26 ± 0.12 |
4.23 ± 0.12 |
4.26 ± 0.09 |
4.68 ± 0.12 |
5.13 ± 0.36 |
5.26 ± 0.31 |
5.36 ± 0.33 |
4.31 ± 0.09 |
|
η
shear [cP] |
0.48 ± 0.03 |
0.53 ± 0.02 |
0.52 ± 0.02 |
0.51 ± 0.02 |
0.48 ± 0.01 |
0.51 ± 0.03 |
0.52 ± 0.03 |
0.53 ± 0.03 |
0.57 ± 0.05 |
0.53 ± 0.03 |
|
τ
HH [ps] |
2.553 ± 0.016 |
2.816 ± 0.017 |
2.749 ± 0.016 |
2.920 ± 0.021 |
2.874 ± 0.019 |
2.576 ± 0.021 |
2.811 ± 0.018 |
2.796 ± 0.016 |
2.667 ± 0.019 |
2.824 ± 0.018 |
|
τ
OH [ps] |
2.588 ± 0.017 |
2.875 ± 0.020 |
2.790 ± 0.017 |
2.947 ± 0.022 |
2.912 ± 0.022 |
2.646 ± 0.039 |
2.876 ± 0.018 |
2.871 ± 0.018 |
2.688 ± 0.018 |
2.895 ± 0.020 |
|
τ
⊥ [ps] |
1.711 ± 0.016 |
1.879 ± 0.018 |
1.852 ± 0.017 |
1.984 ± 0.022 |
1.924 ± 0.019 |
1.761 ± 0.020 |
1.811 ± 0.019 |
1.903 ± 0.018 |
1.918 ± 0.018 |
1.918 ± 0.019 |
|
ε
|
65.7 ± 0.55 |
65.00 ± 0.87 |
64.35 ± 0.78 |
64.05 ± 0.40 |
64.62 ± 0.51 |
63.76 ± 0.64 |
63.48 ± 0.64 |
63.69 ± 0.55 |
63.94 ± 0.58 |
64.27 ± 0.49 |
All setups have in common that the average system temperature corresponds to the desired system temperature (T ≈ T0). However, depending on the chosen FNH perturbation, the standard deviation of the system's temperature is decreased for α < α0 or increased for α > α0. This is an expected behaviour since the fluctuations in kinetic energy ΔEkin (i.e. temperature) can be used to probe the canonicity of a thermostat.59 For finite systems of size N without constraints (e.g. without rigid bonds) in canonical equilibrium, the deviation of the average kinetic energy can be written as  .59 Any non-canonical equilibrium distribution of the velocities will result in deviations regarding the observed temperature fluctuations for finite systems. Therefore, the non-equilibrium property of the FNH equation leads to α-dependent temperature fluctuations as observed in Fig. 2.
.59 Any non-canonical equilibrium distribution of the velocities will result in deviations regarding the observed temperature fluctuations for finite systems. Therefore, the non-equilibrium property of the FNH equation leads to α-dependent temperature fluctuations as observed in Fig. 2.
The analysis of the self-diffusion coefficient D shows a relatively small sigmoid-like increase for α > α0. Thus, significant deviations from canonical equilibrium values were already observed for very small perturbations δα = ±0.004, which are well within the standard deviation Δα0 = 0.044 of the estimated α0. For example, a reduction of α = α0 − 0.004 leads to a slightly slower diffusion and vice versa for an increased α (Fig. 2). However, overall, the self-diffusion remains relatively well preserved over the entire α-parameter range. In particular, all values are well within the range of computed values, which were obtained from different simulation studies of SPC water.57,60–67
Interestingly, the second calculated transport property, i.e. the shear viscosity ηshear seems to be almost unaffected by the non-equilibrium perturbation of the fast motions, except for the most extrem α-values. Similarly to the diffusivity, all obtained shear viscosities agree well with computational values from literature.57,60,61,67,68 The FNH thermostat seems to be capable of calculating shear viscosity relatively accurately for reasonable thermostatting parameter choices, despite its inability to preserve momentum exactly for Ndf → ∞ as it is the case for the normal NH equations. For the accurate calculation of transport properties, often NVE simulations that start from a well initialised temperature and pressure level are performed in practice, which preserve hydrodynamic properties.56,69 If the NVE simulations are short enough, the temperature and pressure remains approximately constant. However, in the vicinity of a critical point (i.e. close to a phase transition) long simulation runs are required due to critical slowing down, causing a problem with such NVE simulations.69,70 Therefore, often simulations with NH or dissipative particle dynamics (DPD) thermostats are employed instead.40,69,71 For NH, it is known that self-diffusion and shear viscosity are adequately derived. With DPD, also accurate bulk viscosities are accessible, despite the reduced capability of DPD thermostats to control temperature.69 Note that transport properties can alternatively also be derived from non-equilibrium MD simulations (see e.g.ref. 71). Based on these considerations and the results displayed in Fig. 2, one can conclude that the FNH equations preserve the known NH capabilities with respect to the calculation of transport properties (diffusivity and shear viscosity) for α close to α0, i.e. for small non-equilibrium perturbations. Results for rotational correlation times and dielectric permittivities are shown in Fig. 2 and Table 2. All values are mostly preserved over the entire range of α-values. Especially the dielectric permittivity shows nearly no dependence on α.
Overall, these results show that the dynamic properties of the system studied remain close to the respective canonical equilibrium values for FNH setups with small perturbation. The deviations are on the same order of magnitude as observed for a coloured-noise thermostat applied to suppress MTS integration errors,13 and substantially lower than for other MTS-optimised thermostats.13,19 In particular, the quasi-canonical equilibrium solution α0 corresponds closely to the canonical NH solution for every observed quantity as expected from theory. This observation indicates that eqn (28) provides indeed a reasonable estimator for α0.
In order to quantify the effect of the perturbed probability density function ![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif) further, the corresponding probability distribution functions of the molecular kinetic energies Pkin were compared for the water box (Fig. 3a). A plot of the relative probability differences
further, the corresponding probability distribution functions of the molecular kinetic energies Pkin were compared for the water box (Fig. 3a). A plot of the relative probability differences  with respect to canonical equilibrium is given in Fig. 3b. Both plots nicely illustrate that the FNH equations indeed generate kinetic energy distributions close to canonical equilibrium, but with substantially perturbed tails of the distribution. This result was theoretically predicted from
with respect to canonical equilibrium is given in Fig. 3b. Both plots nicely illustrate that the FNH equations indeed generate kinetic energy distributions close to canonical equilibrium, but with substantially perturbed tails of the distribution. This result was theoretically predicted from ![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif) (Γ′,t) given in eqn (23), and for small perturbations in eqn (25). Surprisingly, the highest positive perturbation Δα0 = 0.044 has a weaker impact on the tail probabilities (dark red line) than smaller positive perturbations α > α0. The reason for that becomes evident if one investigates the time evolution of the thermostat control variables ξ and ζ with respect to α (Fig. 4). For α = α0 + 0.044 = 0.702, these do not converge to a quasi-equilibrium with constant sign as it is the case for smaller perturbations. Therefore, according to eqn (25), the perturbations of the fast motions are not always negative for this case. This results in a reduced increase of the time-averaged tail probabilities (Fig. 3b) and larger temperature fluctuations (Fig. 2).
(Γ′,t) given in eqn (23), and for small perturbations in eqn (25). Surprisingly, the highest positive perturbation Δα0 = 0.044 has a weaker impact on the tail probabilities (dark red line) than smaller positive perturbations α > α0. The reason for that becomes evident if one investigates the time evolution of the thermostat control variables ξ and ζ with respect to α (Fig. 4). For α = α0 + 0.044 = 0.702, these do not converge to a quasi-equilibrium with constant sign as it is the case for smaller perturbations. Therefore, according to eqn (25), the perturbations of the fast motions are not always negative for this case. This results in a reduced increase of the time-averaged tail probabilities (Fig. 3b) and larger temperature fluctuations (Fig. 2).
 |
| | Fig. 3 (a) Probability density of the molecular kinetic energy Pkin of water for different FNH thermostat parameters α at 300 K. The reference Nosé–Hoover (NH) distribution is shown in black. The dotted vertical line denotes 〈Ekin〉 = 3kBT. (b) Corresponding relative differences of the tail probabilities with respect to the canonical equilibrium values, by calculating 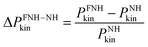 . . | |
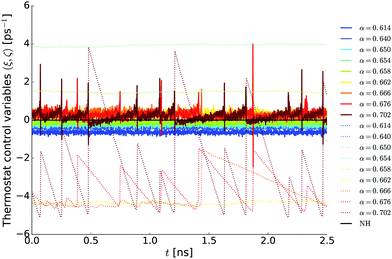 |
| | Fig. 4 Time evolution of the thermostat control variables ξ (solid lines) and ζ (dotted lines) with respect to different fast Nosé–Hoover (FNH) perturbations α for a test system of 1000 water molecules. The estimated α0 = 0.658 (green lines). The Nosé–Hoover (NH) reference value for canonical equilibrium is shown in black. Note that some doted lines are outside the chosen scale for the y-axis (e.g. 〈ζFNH(α = 0.614)〉 = 31.99). | |
In addition, Fig. 4 reveals four more interesting properties of the FNH equations. First, the FNH thermostat is very sensitive regarding the choice of α, since substantial deviations of 〈ζ〉 from its quasi canonical equilibrium value 〈ζ(αexact0)〉 = 0 can already occur for very small deviations of α. In particular, the simulations showed that αexact0 ∈ (0.658, 0.662) for the water box. Second, the control variables ξ and ζ are substantially more noisy for all FNH setups compared to ξ of the NH thermostat (black line in Fig. 4), as one would expect from the discontinuities introduced by the Heaviside function. Third, imposing the additional constraint for the fast degrees of freedom in the FNH eqn (10) is an asymmetric and nonlinear problem. This becomes evident for symmetric perturbations ±Δα0, which lead to a relatively stable solution for 〈ζ(α0 − 0.044)〉 ≈ 32 ps−1, but cause oscillations for 〈ζ(α0 + 0.044)〉 ∈ (−5, 0) ps−1. Fourth, the FNH equations remain relatively close to canonical equilibrium for the estimated α0 values (green lines in Fig. 4), i.e. 〈ξ(α0)〉 ≈ 〈ξNH〉 but with slightly reduced tail probabilities since ζ(α0) > 0∀t.
4.2 β-Peptides in methanol
Having analysed the effect of the FNH equations on dynamic properties of homogeneous systems, we investigated the effect of a perturbed tail distribution on the efficiency of phase-space exploration in a next step. The focus was thereby on the variation in the probability distribution of rare events. A good example of such rare events are transitions between folded and unfolded states of peptides, which occur relatively infrequently during typical simulation times. For peptide 1 (Fig. 1), the time evolution of the backbone atom-positional RMSD is shown in Fig. 5a with corresponding probability distributions for the canonical equilibrium and for estimated α0, α0 ± Δα0.
 |
| | Fig. 5 Results of the simulations of β-peptides 1 and 2 in methanol at 340 K using the canonical Nosé–Hoover (NH) or the fast Nosé–Hoover (FNH) thermostat with different perturbations. (a) Time series (left) and distribution (right) of the atom-positional backbone RMSD with respect to the left-handed 314-helical fold of peptide 1. Residues 2–6 were used for the RMSD calculation. (b) Time evolution (left) and distribution (right) of the atom-positional backbone RMSD with respect to a right-handed 2.710/12-helical fold (black line) and left-handed 314-helical fold (grey line) of peptide 2. Residues 2–5 were used for the RMSD calculation. | |
The increase of the tail probability of the velocity distributions was found to have a substantial impact on the number of transitions between the folded and unfolded states of peptide 1, which indicates a faster exploration of the phase space. A similar observation was made for peptide 2 (Fig. 5b). In addition, when suppressing the fast motions using α = α0 − Δα0, peptide 2 remained often trapped in either the left-handed 314-helical fold (grey line) or the initial right-handed 2.710/12 helical fold state (black line). By increasing α, a more balanced distribution of the RMSD values was obtained. These results are in line with ref. 72, where faster folding was observed for the folding of a 16-residue helical peptide when non-canonical modifications of the potential-energy surface according to Tsallis73,74 were introduced. Time-averages of the thermostat control variables are given in Table 3, with the related time series in Fig. S1 and S2 of the ESI.†
Table 3 Time averages of the thermostat control variables ξ, ζ with respect to different perturbations α for the two β-peptides in methanol. The sign (±) of 〈ζ〉 indicates whether the probability of fast motions is increased (−) or decreased (+) with respect to the canonical equilibrium
|
|
α = α0 − Δα0 = 0.597 |
α = α0 = 0.637 |
α = α0 + Δα0 = 0.677 |
Nosé–Hoover |
| Peptide 1 |
〈ξ〉 [ps−1] |
−0.168 ± 0.075 |
−0.012 ± 0.084 |
0.028 ± 0.113 |
0.002 ± 0.121 |
| 〈ζ〉 [ps−1] |
10.402 ± 0.073 |
0.381 ± 0.131 |
−0.384 ± 1.267 |
— |
|
|
| Peptide 2 |
〈ξ〉 [ps−1] |
−0.161 ± 0.075 |
−0.008 ± 0.084 |
0.021 ± 0.104 |
0.0014 ± 0.1202 |
| 〈ζ〉 [ps−1] |
10.047 ± 0.072 |
0.267 ± 0.108 |
−0.301 ± 1.053 |
— |
All findings are in agreement with the results of the water system. In particular, for a positive perturbation α = α0 + Δα0, sgn(〈ζ〉) = −1 which indicates an increased probability of the fast degrees of freedom, leading to faster transitions. However, for the estimated quasi-equilibrium α0, the results are ambiguous. For peptide 1, it appears that the tail probabilities are reduced on the chosen simulation timescale, whereas the opposite was observed for peptide 2, i.e. significantly more transitions occurred than in canonical equilibrium. This highlights that it is difficult to determine the quasi-equilibrium αexact0, which solves eqn (27) exactly, and thus small deviations may already have a significant impact on the dynamics of the system.
5 Conclusion
In this work, a modification of the Nosé–Hoover thermostat equations was introduced, which allows to gently force the system out of canonical equilibrium. Rigorous mathematical properties of the FNH equations were derived, showing that the dynamics of the non-equilibrium system remains close to the canonical equilibrium for reasonable thermostat parameters and a sufficiently high number of degrees of freedom in the system. In more detail, a quasi-equilibrium parameter α was identified, which determines whether tail probabilities are increased or decreased with respect to canonical equilibrium, while the time-averaged temperature is preserved. Simulations showed that it is easily possible to determine an approximative value α0, which is close to quasi-canonical equilibrium. However, it was found to be non-trivial to control the exact strength of the perturbation, since the tail distributions are highly sensitive to perturbations of α. The effect of the FNH equations for relevant test systems showed that slightly increased tail probabilities substantially effect the occurrence of rare events (i.e. folding and unfolding of helical β-peptides). Interestingly, averaged transport properties (e.g. self-diffusion and shear-viscosity of water) were mostly preserved for the tested FNH setups. This observation in combination with the well-defined perturbation of the canonical equilibrium points to interesting future applications of the FNH thermostat. In particular, the well preserved shear viscosity potentially offers the opportunity to reduce critical slowing down in the vicinity of critical points by perturbations of the tail probabilities. Moreover, it should also be possible to obtain canonical ensemble averages from FNH simulations by using appropriate ensemble reweighting techniques. Hence, equilibrium simulations could be accelerated by using the non-equilibrium FNH thermostat. In the future, we plan to investigate corresponding reweighting techniques and applications on interesting chemical systems.
Conflicts of interest
There are no conflicts to declare.
Appendix: Thermostat masses Q1, Q2
By using the assumptions for the thermostat masses stated in Section 2, one can decouple and simplify the FNH equations as follows:| |  | (33) |
and| |  | (34) |
which leads to the simple expressions given in eqn (29) and (30).
Acknowledgements
The authors thank Gregor Weiss and Philippe Hünenberger for helpful discussions. The fruitful comments of the reviewers are highly appreciated. Financial support by the Swiss National Science Foundation (Grant Number 200021-178762) and by ETH Zürich (ETH-34 17-2) is gratefully acknowledged.
References
-
P. H. Hünenberger, Adv. Comp. Sim., Springer, 2005, pp. 105–149 Search PubMed.
- H. C. Andersen, J. Chem. Phys., 1980, 72, 2384–2393 CrossRef CAS.
- S. Nosé, J. Chem. Phys., 1984, 81, 511–519 CrossRef.
- W. G. Hoover, Phys. Rev. A: At., Mol., Opt. Phys., 1985, 31, 1695 CrossRef.
- G. J. Martyna, M. L. Klein and M. E. Tuckerman, J. Chem. Phys., 1992, 97, 2635–2643 CrossRef.
- G. Bussi, D. Donadio and M. Parrinello, J. Chem. Phys., 2007, 126, 014101 CrossRef PubMed.
- H. J. Berendsen, J. v. Postma, W. F. van Gunsteren, A. DiNola and J. Haak, J. Chem. Phys., 1984, 81, 3684–3690 CrossRef CAS.
- P. Minary, G. J. Martyna and M. E. Tuckerman, J. Chem. Phys., 2003, 118, 2510–2526 CrossRef CAS.
-
B. Leimkuhler and C. Matthews, Molecular Dynamics, Springer, 2016 Search PubMed.
- J. J. Biesiadecki and R. D. Skeel, J. Comput. Phys., 1993, 109, 318–328 CrossRef.
- Q. Ma, J. A. Izaguirre and R. D. Skeel, SIAM J. Sci. Comput., 2003, 24, 1951–1973 CrossRef.
- D. Sidler, M. Lehner, S. Frasch, M. Cristófol-Clough and S. Riniker, F1000Research, 2019, 7, 1745 Search PubMed.
- J. A. Morrone, T. E. Markland, M. Ceriotti and B. J. Berne, J. Chem. Phys., 2011, 134, 014103 CrossRef PubMed.
- E. Barth and T. Schlick, J. Chem. Phys., 1998, 109, 1617–1632 CrossRef CAS.
- X. Qian and T. Schlick, J. Chem. Phys., 2002, 116, 5971–5983 CrossRef CAS.
- P. Minary, M. E. Tuckerman and G. J. Martyna, Phys. Rev. Lett., 2004, 93, 150201 CrossRef CAS PubMed.
- B. Leimkuhler, D. T. Margul and M. E. Tuckerman, Mol. Phys., 2013, 111, 3579–3594 CrossRef CAS.
- D. T. Margul and M. E. Tuckerman, J. Chem. Theory Comput., 2016, 12, 2170–2180 CrossRef CAS PubMed.
- J. A. Izaguirre, D. P. Catarello, J. M. Wozniak and R. D. Skeel, J. Chem. Phys., 2001, 114, 2090–2098 CrossRef CAS.
- M. Ceriotti, G. Bussi and M. Parrinello, Phys. Rev. Lett., 2009, 102, 020601 CrossRef PubMed.
- M. Ceriotti, G. Bussi and M. Parrinello, J. Chem. Theory Comput., 2010, 6, 1170–1180 CrossRef CAS.
- E. J. Barth, B. B. Laird and B. J. Leimkuhler, J. Chem. Phys., 2003, 118, 5759–5768 CrossRef CAS.
- N. Shuichi, Prog. Theor. Phys. Suppl., 1991, 103, 1–46 CrossRef.
- X. Daura, W. F. van Gunsteren and A. E. Mark, Proteins, 1999, 34, 269–280 CrossRef CAS.
- X. Daura, K. Gademann, B. Jaun, D. Seebach, W. F. van Gunsteren and A. E. Mark, Angew. Chem., Int. Ed., 1999, 38, 236–240 CrossRef CAS.
- X. Daura, K. Gademann, H. Schäfer, B. Jaun, D. Seebach and W. F. van Gunsteren, J. Am. Chem. Soc., 2001, 123, 2393–2404 CrossRef CAS PubMed.
- W. F. van Gunsteren, R. Bürgi, C. Peter and X. Daura, Angew. Chem., Int. Ed., 2001, 40, 351–355 CrossRef PubMed.
- X. Daura, A. Glättli, P. Gee, C. Peter and W. F. Van Gunsteren, Adv. Protein Chem., 2002, 62, 341–360 CrossRef CAS PubMed.
-
W. F. van Gunsteren and Z. Gattin, in Foldamers: Structure, Properties and Application ed. S. Hecht and I. Huc, 2007, pp. 173–192 Search PubMed.
- Z. Lin, N. Schmid and W. F. van Gunsteren, Mol. Phys., 2011, 109, 493–506 CrossRef CAS.
- W. Huang, Z. Lin and W. F. van Gunsteren, J. Chem. Theory Comput., 2011, 7, 1237–1243 CrossRef CAS PubMed.
- W. Huang, S. Riniker and W. F. van Gunsteren, J. Chem. Theory Comput., 2014, 10, 2213–2223 CrossRef CAS PubMed.
-
M. Tuckerman, Statistical mechanics: Theory and molecular simulation, Oxford University Press, 2010 Search PubMed.
- A. Bulgac and D. Kusnezov, Phys. Rev. A: At., Mol., Opt. Phys., 1990, 42, 5045 CrossRef CAS.
- D. Kusnezov, A. Bulgac and W. Bauer, Ann. Phys., 1990, 204, 155–185 CAS.
- B. Leimkuhler, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2010, 81, 026703 CrossRef PubMed.
- M. E. Tuckerman, C. J. Mundy and G. J. Martyna, EPL, 1999, 45, 149 CrossRef CAS.
- M. E. Tuckerman, Y. Liu, G. Ciccotti and G. J. Martyna, J. Chem. Phys., 2001, 115, 1678–1702 CrossRef CAS.
- Z. Jia and B. Leimkuhler, ESAIM: Math. Modell. Numer. Anal., 2007, 41, 333–350 CrossRef.
- T. Soddemann, B. Dünweg and K. Kremer, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2003, 68, 046702 CrossRef PubMed.
-
H. J. Berendsen, J. P. Postma, W. F. van Gunsteren and J. Hermans, Intermolecular forces, Springer, 1981, pp. 331–342 Search PubMed.
- I. G. Tironi and W. F. van Gunsteren, Mol. Phys., 1994, 83, 381–403 CrossRef CAS.
- N. Schmid, C. D. Christ, M. Christen, A. P. Eichenberger and W. F. van Gunsteren, Comput. Phys. Commun., 2012, 183, 890–903 CrossRef CAS.
- S. Riniker, C. D. Christ, H. S. Hansen, P. H. Hünenberger, C. Oostenbrink, D. Steiner and W. F. van Gunsteren, J. Phys. Chem. B, 2011, 115, 13570–13577 CrossRef CAS PubMed.
- N. Schmid, A. P. Eichenberger, A. Choutko, S. Riniker, M. Winger, A. E. Mark and W. F. van Gunsteren, Eur. Biophys. J., 2011, 40, 843 CrossRef CAS PubMed.
- Z. Lin and W. F. van Gunsteren, J. Comput. Chem., 2013, 34, 2796–2805 CrossRef CAS PubMed.
-
R. W. Hockney, Potential calculation and some applications, Langley research center, hampton, va. technical report, 1970.
- J.-P. Ryckaert, G. Ciccotti and H. J. Berendsen, J. Comput. Phys., 1977, 23, 327–341 CrossRef CAS.
- I. G. Tironi, R. Sperb, P. E. Smith and W. F. van Gunsteren, J. Chem. Phys., 1995, 102, 5451–5459 CrossRef CAS.
- W. R. Scott, P. H. Hünenberger, I. G. Tironi, A. E. Mark, S. R. Billeter, J. Fennen, A. E. Torda, T. Huber, P. Krüger and W. F. van Gunsteren, J. Phys. Chem. A, 1999, 103, 3596–3607 CrossRef CAS.
-
W. M. Haynes, CRC Handbook of Chemistry and Physics, 2016 Search PubMed.
- R. Walser, A. E. Mark, W. F. van Gunsteren, M. Lauterbach and G. Wipff, J. Chem. Phys., 2000, 112, 10450–10459 CrossRef CAS.
-
D. R. Lide, Handbook of Chemistry and Physics, CRC Press/Taylor & Francis, Boca Raton, FL, 88th edn, 2007–2008 Search PubMed.
- A. P. Eichenberger, J. R. Allison, J. Dolenc, D. P. Geerke, B. A. Horta, K. Meier, C. Oostenbrink, N. Schmid, D. Steiner, D. Wang and W. F. van Gunsteren, J. Chem. Theory Comput., 2011, 7, 3379–3390 CrossRef CAS PubMed.
-
M. P. Allen and D. J. Tildesley, Computer simulation of liquids, Oxford University Press, 2017 Search PubMed.
- E. J. Maginn, R. A. Messerly, D. J. Carlson, D. R. Roe and J. R. Elliott, Living J. Comput. Mol. Sci., 2019, 1, 6324 Search PubMed.
- P. E. Smith and W. F. van Gunsteren, Chem. Phys. Lett., 1993, 215, 315–318 CrossRef CAS.
- M. Neumann, Mol. Phys., 1983, 50, 841–858 CrossRef CAS.
- R. Dimelow and A. Masters, Mol. Simul., 2007, 33, 1165–1166 CrossRef CAS.
- Y. Wu, H. L. Tepper and G. A. Voth, J. Chem. Phys., 2006, 124, 024503 CrossRef PubMed.
- A. Glättli, X. Daura and W. F. van Gunsteren, J. Chem. Phys., 2002, 116, 9811–9828 CrossRef.
- D. van der Spoel, P. J. van Maaren and H. J. C. Berendseni, J. Chem. Phys., 1998, 108, 10220–10230 CrossRef CAS.
- D. Van Der Spoel and P. J. van Maaren, J. Chem. Theory Comput., 2006, 2, 1–11 CrossRef CAS PubMed.
- K. Watanabe and M. L. Klein, Chem. Phys., 1989, 131, 157–167 CrossRef CAS.
- P. Mark and L. Nilsson, J. Phys. Chem. A, 2001, 105, 9954–9960 CrossRef CAS.
- M. W. Mahoney and W. L. Jorgensen, J. Chem. Phys., 2001, 114, 363–366 CrossRef CAS.
- G. Guevara-Carrion, J. Vrabec and H. Hasse, J. Chem. Phys., 2011, 134, 074508 CrossRef PubMed.
- B. Hess, J. Chem. Phys., 2002, 116, 209–217 CrossRef CAS.
- S. Roy and S. K. Das, Eur. Phys. J. E: Soft Matter Biol. Phys., 2015, 38, 132 CrossRef PubMed.
- S. Roy and S. K. Das, Europhys. Lett., 2011, 94, 36001 CrossRef.
- G. Jung and F. Schmid, J. Chem. Phys., 2016, 144, 204104 CrossRef PubMed.
- Y. Pak and S. Wang, J. Chem. Phys., 1999, 111, 4359–4361 CrossRef CAS.
- C. Tsallis, J. Stat. Phys., 1988, 52, 479–487 CrossRef.
- E. M. Curado and C. Tsallis, J. Phys. A: Gen. Phys., 1991, 24, L69 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available: Time evolutions of FNH thermostat control variables for β-peptides in methanol. See DOI: 10.1039/c8cp06800c |
|
| This journal is © the Owner Societies 2019 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article *
*



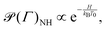
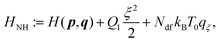

 on the distribution
on the distribution ![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif) (Γ)NH in the absence of other external forces. Additionally, the system should be “simple” enough such that the different time scales present in the system are well-behaved with regard to the chosen thermostat parameters. In practise, this often requires different NH thermostats for solvents and solutes.1
(Γ)NH in the absence of other external forces. Additionally, the system should be “simple” enough such that the different time scales present in the system are well-behaved with regard to the chosen thermostat parameters. In practise, this often requires different NH thermostats for solvents and solutes.1





![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) ≥ 0 corresponds to the temperature beyond which pi is additionally controlled by ζ, i.e. for
≥ 0 corresponds to the temperature beyond which pi is additionally controlled by ζ, i.e. for 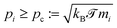 .
.
 in eqn (9) follows from the equipartition theorem in the canonical equilibrium. Likewise, the auxiliary constraint set in eqn (10) can be related to the second order equipartition theorem, i.e. by integration by parts (I.P.) one can show that,
in eqn (9) follows from the equipartition theorem in the canonical equilibrium. Likewise, the auxiliary constraint set in eqn (10) can be related to the second order equipartition theorem, i.e. by integration by parts (I.P.) one can show that,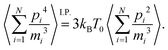
 ) respond to a change in the system. Note that the proposed definition for
) respond to a change in the system. Note that the proposed definition for  given in eqn (10) has the advantage that
given in eqn (10) has the advantage that  , as it is the case for
, as it is the case for 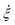 . Hence, typical numerical integration time-steps of MD simulations (e.g. 2 fs) should still be applicable with the FNH equations. This may not be the case anymore for smaller system sizes when the auxiliary thermostatting control variable is related directly to the instantaneous variance of the momenta, e.g. by imposing
. Hence, typical numerical integration time-steps of MD simulations (e.g. 2 fs) should still be applicable with the FNH equations. This may not be the case anymore for smaller system sizes when the auxiliary thermostatting control variable is related directly to the instantaneous variance of the momenta, e.g. by imposing 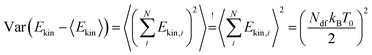 , which would result in
, which would result in  .
.
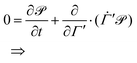

![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif) (Γ′,t) of the dynamic system Γ′. Note that if an equilibrium solution
(Γ′,t) of the dynamic system Γ′. Note that if an equilibrium solution ![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif) 0 exists, it could be constructed by interpreting
0 exists, it could be constructed by interpreting  as a product of a distribution function f with nontrivial metric g associated to the curved phase space Γ′.33,37,38 The equilibrium
as a product of a distribution function f with nontrivial metric g associated to the curved phase space Γ′.33,37,38 The equilibrium ![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif) 0 then follows immediately from all conservation laws of the extended system.33,37,38 However, for the following derivation of
0 then follows immediately from all conservation laws of the extended system.33,37,38 However, for the following derivation of ![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif) (Γ′,t) for the FNH equations, we follow an alternative pathway described by Nosé in ref. 23.
(Γ′,t) for the FNH equations, we follow an alternative pathway described by Nosé in ref. 23.

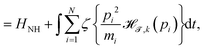
 is used as an approximation of the Heaviside step function with limk→∞
is used as an approximation of the Heaviside step function with limk→∞![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif)
![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) ,k(pi) =
,k(pi) = ![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif)
![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) (pi). It is straightforward to show that HFNH is conserved as,
(pi). It is straightforward to show that HFNH is conserved as,
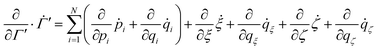


 . It can be shown that the resulting non-equilibrium probability density obeying eqn (14) can be written as,
. It can be shown that the resulting non-equilibrium probability density obeying eqn (14) can be written as,
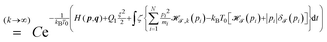



![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) > T0 the following property holds,
> T0 the following property holds,
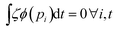 . For arbitrary initial conditions, this is only possible for limQ2→∞ζ = 0 or lim
. For arbitrary initial conditions, this is only possible for limQ2→∞ζ = 0 or lim![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) →∞ϕ(pi) = 0 due to eqn (26), which means the normal NH eqn (1)–(3) are recovered.
→∞ϕ(pi) = 0 due to eqn (26), which means the normal NH eqn (1)–(3) are recovered. with a canonical equilibrium solution of the Liouville equation. This result is in agreement with the properties obtained in ref. 39 for multi-temperature dynamics. Therefore, the proposed FNH equations can at best approximate a (canonical) equilibrium distribution for finite
with a canonical equilibrium solution of the Liouville equation. This result is in agreement with the properties obtained in ref. 39 for multi-temperature dynamics. Therefore, the proposed FNH equations can at best approximate a (canonical) equilibrium distribution for finite ![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) , Q2.
, Q2.![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif) (Γ,t)FNH ≈
(Γ,t)FNH ≈ ![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif) (Γ)NH. The requirement of such a quasi equilibrium distribution leads to the following conditions for the thermostat parameters and the simulated systems:
(Γ)NH. The requirement of such a quasi equilibrium distribution leads to the following conditions for the thermostat parameters and the simulated systems:![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) ≫ T0 restricts perturbations to the tails of the kinetic-energy distribution.
≫ T0 restricts perturbations to the tails of the kinetic-energy distribution. , which can be efficiently controlled by ζ at every time-step.
, which can be efficiently controlled by ζ at every time-step.

 and α = 1. For simplicity, we additionally assume that the dynamics of ξ and ζ are completely decoupled by setting ṗ(ξ)i := −ξpi and ṗ(ζ)i := −ζpi. For a rough estimate, this is a reasonable assumption if one considers that ζ only controls the tails, whereas ξ mainly controls the mean of
and α = 1. For simplicity, we additionally assume that the dynamics of ξ and ζ are completely decoupled by setting ṗ(ξ)i := −ξpi and ṗ(ζ)i := −ζpi. For a rough estimate, this is a reasonable assumption if one considers that ζ only controls the tails, whereas ξ mainly controls the mean of ![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif) . These assumptions lead to the following two decoupled ordinary differential equations (see Appendix A),
. These assumptions lead to the following two decoupled ordinary differential equations (see Appendix A),


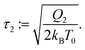
 according to eqn (9). Therefore, one can show that in canonical equilibrium
according to eqn (9). Therefore, one can show that in canonical equilibrium  for NH equations, which in turn leads to ξ → 0.40 Consequently, the NH equations reduce to Newtonian equations if the system size is increased. Therefore, hydrodynamic properties are preserved for large systems. In contrast, since τ2 is independent of Ndf for a FNH thermostat,
for NH equations, which in turn leads to ξ → 0.40 Consequently, the NH equations reduce to Newtonian equations if the system size is increased. Therefore, hydrodynamic properties are preserved for large systems. In contrast, since τ2 is independent of Ndf for a FNH thermostat, 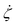 is not necessarily 0, ∀t. For this reason, the FNH equations do not strictly converge to Newtonian equations of motion for Ndf → ∞, which means that hydrodynamic properties remain affected also for larger system sizes. The underlying reason for Q2 not depending on Ndf is related to the fractional definition of
is not necessarily 0, ∀t. For this reason, the FNH equations do not strictly converge to Newtonian equations of motion for Ndf → ∞, which means that hydrodynamic properties remain affected also for larger system sizes. The underlying reason for Q2 not depending on Ndf is related to the fractional definition of  given in eqn (10), which ensures numerical stability for typical integration time steps and intermediate Ndf values based on the
given in eqn (10), which ensures numerical stability for typical integration time steps and intermediate Ndf values based on the ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) (pi2)-scaling. However, hydrodynamic properties of the FNH thermostat remain mostly preserved in practice for typical simulation setups, as will be shown in the Results & discussion section.
(pi2)-scaling. However, hydrodynamic properties of the FNH thermostat remain mostly preserved in practice for typical simulation setups, as will be shown in the Results & discussion section. and
and  , which involves global communication across processors. Similar to NH, this is a disadvantage with respect to an efficient parallel implementation.40 However, the additional control term ζ, which acts on the forces, should not affect the speed of the computation significantly compared to a normal NH thermostat. As mentioned earlier, the auxiliary constraint is also designed such that the integration time step does not have to be adjusted, which ensures an efficient numerical integration.
, which involves global communication across processors. Similar to NH, this is a disadvantage with respect to an efficient parallel implementation.40 However, the additional control term ζ, which acts on the forces, should not affect the speed of the computation significantly compared to a normal NH thermostat. As mentioned earlier, the auxiliary constraint is also designed such that the integration time step does not have to be adjusted, which ensures an efficient numerical integration.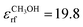 (calculated value from ref. 52) and for chloroform
(calculated value from ref. 52) and for chloroform  (experimental value from ref. 53) were chosen. For argon no long-range electrostatics have to be considered. The water systems were simulated for 50 ns, the auxiliary systems for 1.5 ns, and the β-peptides for 350 ns. Coordinates, velocities and energies were written out every 1 ps, unless stated otherwise. The quasi canonical equilibrium parameter α0 was obtained from eqn (28) by setting τ2 = 1000 μs and by taking the ensemble average from 1 ns trajectories after 0.5 ns equilibration. In all FNH simulations,
(experimental value from ref. 53) were chosen. For argon no long-range electrostatics have to be considered. The water systems were simulated for 50 ns, the auxiliary systems for 1.5 ns, and the β-peptides for 350 ns. Coordinates, velocities and energies were written out every 1 ps, unless stated otherwise. The quasi canonical equilibrium parameter α0 was obtained from eqn (28) by setting τ2 = 1000 μs and by taking the ensemble average from 1 ns trajectories after 0.5 ns equilibration. In all FNH simulations, ![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) = 7T0 was used, which was considered a reasonable value to restrict the non-canonical perturbations of
= 7T0 was used, which was considered a reasonable value to restrict the non-canonical perturbations of ![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif) to the tails.
to the tails. program. For this purpose, 12 short simulations of 1.5 ns length (after 2 ns equilibration) were performed with different initial setups. The uncertainty of the self-diffusion was quantified by calculating the standard deviation of the 12 different values. Similarly, shear viscosities ηshear were extracted from the off-diagonal elements of the pressure tensor using a modified version of the
program. For this purpose, 12 short simulations of 1.5 ns length (after 2 ns equilibration) were performed with different initial setups. The uncertainty of the self-diffusion was quantified by calculating the standard deviation of the 12 different values. Similarly, shear viscosities ηshear were extracted from the off-diagonal elements of the pressure tensor using a modified version of the  program.56,57 For this purpose, the slope of a linear least-square fit of the squared pressure tensor integrals was evaluated between 0 and 10 ps. The data for the pressure tensor integrals was gathered from 1 ns of simulation with a time resolution of 2 fs. The uncertainty of the shear viscosity was quantified based on the standard deviation of the fitted slope. The rotational relaxation time τ was calculated from fitting an exponential decaying function Ce−t/τ to the first-order autocorrelation functions, which were calculated for vectors pointing along different directions (e.g. H–H-bond) of the molecular reference frame. The autocorrelation function was obtained using the
program.56,57 For this purpose, the slope of a linear least-square fit of the squared pressure tensor integrals was evaluated between 0 and 10 ps. The data for the pressure tensor integrals was gathered from 1 ns of simulation with a time resolution of 2 fs. The uncertainty of the shear viscosity was quantified based on the standard deviation of the fitted slope. The rotational relaxation time τ was calculated from fitting an exponential decaying function Ce−t/τ to the first-order autocorrelation functions, which were calculated for vectors pointing along different directions (e.g. H–H-bond) of the molecular reference frame. The autocorrelation function was obtained using the  program. For this analysis, the coordinates were written out every 2 fs over 10 ps of simulation time, after an equilibration time of 25 ns. The dielectric permittivity ε was calculated from 50 ns trajectories (discarding the first 1 ns as equilibration) by solving a Kirkwood–Fröhlich-type equation,58 implemented in the
program. For this analysis, the coordinates were written out every 2 fs over 10 ps of simulation time, after an equilibration time of 25 ns. The dielectric permittivity ε was calculated from 50 ns trajectories (discarding the first 1 ns as equilibration) by solving a Kirkwood–Fröhlich-type equation,58 implemented in the  program. Note that this approach involves the dielectric permittivity of the reaction field as an input parameter. In order to quantify the uncertainty of the dielectric permittivity estimate, the standard deviation was calculated from 10 simulations with identical starting coordinates but different initial velocities. In order to measure the folding and unfolding of the β-peptides, the atom-positional root-mean-square deviation (RMSD) of the backbone atoms between residues 2–6 (peptide 1) and residues 2–5 (peptide 2) were calculated using the
program. Note that this approach involves the dielectric permittivity of the reaction field as an input parameter. In order to quantify the uncertainty of the dielectric permittivity estimate, the standard deviation was calculated from 10 simulations with identical starting coordinates but different initial velocities. In order to measure the folding and unfolding of the β-peptides, the atom-positional root-mean-square deviation (RMSD) of the backbone atoms between residues 2–6 (peptide 1) and residues 2–5 (peptide 2) were calculated using the  program.
program.
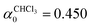 and
and  , which were both obtained for systems containing 1000 molecules with an equally number of degrees of freedom
, which were both obtained for systems containing 1000 molecules with an equally number of degrees of freedom  (both solvent models are fully constrained, i.e. without internal degrees of freedom).
(both solvent models are fully constrained, i.e. without internal degrees of freedom).
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 997
997![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif) with respect to different perturbations δα of α0 was investigated in detail for the water box (Fig. 2 and Table 2). For this system, α0 = 0.658 was estimated using eqn (28).
with respect to different perturbations δα of α0 was investigated in detail for the water box (Fig. 2 and Table 2). For this system, α0 = 0.658 was estimated using eqn (28).![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) = 2100 K, T0 = 300 K
= 2100 K, T0 = 300 K
 .59 Any non-canonical equilibrium distribution of the velocities will result in deviations regarding the observed temperature fluctuations for finite systems. Therefore, the non-equilibrium property of the FNH equation leads to α-dependent temperature fluctuations as observed in Fig. 2.
.59 Any non-canonical equilibrium distribution of the velocities will result in deviations regarding the observed temperature fluctuations for finite systems. Therefore, the non-equilibrium property of the FNH equation leads to α-dependent temperature fluctuations as observed in Fig. 2.![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif) further, the corresponding probability distribution functions of the molecular kinetic energies Pkin were compared for the water box (Fig. 3a). A plot of the relative probability differences
further, the corresponding probability distribution functions of the molecular kinetic energies Pkin were compared for the water box (Fig. 3a). A plot of the relative probability differences  with respect to canonical equilibrium is given in Fig. 3b. Both plots nicely illustrate that the FNH equations indeed generate kinetic energy distributions close to canonical equilibrium, but with substantially perturbed tails of the distribution. This result was theoretically predicted from
with respect to canonical equilibrium is given in Fig. 3b. Both plots nicely illustrate that the FNH equations indeed generate kinetic energy distributions close to canonical equilibrium, but with substantially perturbed tails of the distribution. This result was theoretically predicted from ![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif) (Γ′,t) given in eqn (23), and for small perturbations in eqn (25). Surprisingly, the highest positive perturbation Δα0 = 0.044 has a weaker impact on the tail probabilities (dark red line) than smaller positive perturbations α > α0. The reason for that becomes evident if one investigates the time evolution of the thermostat control variables ξ and ζ with respect to α (Fig. 4). For α = α0 + 0.044 = 0.702, these do not converge to a quasi-equilibrium with constant sign as it is the case for smaller perturbations. Therefore, according to eqn (25), the perturbations of the fast motions are not always negative for this case. This results in a reduced increase of the time-averaged tail probabilities (Fig. 3b) and larger temperature fluctuations (Fig. 2).
(Γ′,t) given in eqn (23), and for small perturbations in eqn (25). Surprisingly, the highest positive perturbation Δα0 = 0.044 has a weaker impact on the tail probabilities (dark red line) than smaller positive perturbations α > α0. The reason for that becomes evident if one investigates the time evolution of the thermostat control variables ξ and ζ with respect to α (Fig. 4). For α = α0 + 0.044 = 0.702, these do not converge to a quasi-equilibrium with constant sign as it is the case for smaller perturbations. Therefore, according to eqn (25), the perturbations of the fast motions are not always negative for this case. This results in a reduced increase of the time-averaged tail probabilities (Fig. 3b) and larger temperature fluctuations (Fig. 2).