Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Detailed benchmark ab initio mapping of the potential energy surfaces of the X + C2H6 [X = F, Cl, Br, I] reactions
Dóra
Papp
 *,
Balázs
Gruber
and
Gábor
Czakó
*,
Balázs
Gruber
and
Gábor
Czakó
 *
*
Interdisciplinary Excellence Centre and Department of Physical Chemistry and Materials Science, Institute of Chemistry, University of Szeged, Rerrich Béla tér 1, Szeged H-6720, Hungary. E-mail: dorapapp@chem.u-szeged.hu; gczako@chem.u-szeged.hu
First published on 3rd December 2018
Abstract
We investigate three reaction pathways of the X + C2H6 [X = F, Cl, Br, I] reactions: H-abstraction, methyl-substitution, and H-substitution, with the latter two proceeding via either Walden-inversion or front-side-attack mechanisms. We report classical and adiabatic relative energies of unprecedented accuracy for the corresponding stationary points of the reaction potential energy surfaces (PESs) by augmenting the CCSD(T)-F12b/aug-cc-pVQZ energies by core-correlation, post-CCSD(T) and spin–orbit corrections. Taking these correction terms into account turns out to be essential to reach subchemical, i.e. <0.5 kcal mol−1, accuracy. Our new benchmark 0 K reaction enthalpies show excellent agreement with experimental data. Spin–orbit coupling in these open-shell systems is also monitored throughout the reaction paths and found to be non-negligible even in some transition-state geometries. Barrier heights corresponding to the different channels of the title reactions appear in the same order with increasing energy: H-abstraction, Walden-inversion methyl-substitution, Walden-inversion H-substitution, front-side-attack H-substitution and front-side-attack methyl-substitution, except for X = I where the latter two come in reverse order. Similarly, product channels follow the energy order of the corresponding barrier heights in all four cases. We find strongly reactant-like transition-state structures for the exothermic F + C2H6 reaction paths, while more and more product-like transition states are observed along with increasing endothermicity as going from Cl to I. Several entrance and exit channel minima are also identified for the studied reactions with significant spin–orbit effects for the formers.
Introduction
Reactions of atoms (X) with methane1–6 and ions (X−) with methyl-halides (CH3Y)7–10 have become benchmark systems to study the dynamics and mechanisms of polyatomic chemical reactions. The main reaction channel of the former systems is hydrogen-abstraction leading to HX + CH3, and for the latter bimolecular nucleophilic substitution (SN2) resulting in Y− + CH3X. Recent studies, however, revealed that these reactions are not so simple and several other reaction channels may become available at higher collision energies.3,7,8,11 For X + methane reactions substitution leads to H + CH3X products via different stereospecific reaction pathways involving configuration inversion or retention around the carbon center.11 In the case of the X− + CH3Y systems the SN2 reaction can proceed with Walden-inversion, front-side-attack, double-inversion,12 roundabout,10etc. mechanisms and proton transfer leading to HX + CH2Y− may occur at higher collision energies. Furthermore, as we replace CH3Y with CH3CH2Y a new channel, called bimolecular elimination (E2), leading to Y− + HX + C2H4 becomes possible. Recently we reported a benchmark ab initio characterization of the F− + CH3CH2Cl reaction.13 In the present work we plan to extend our previous work1,11 on X + methane reactions by replacing methane with the ethane (C2H6) molecule. Halogen + ethane reactions represent a more complex system with more of degrees of freedom and new possible reaction mechanisms. Besides the main H-abstraction reaction path and the higher-energy H-substitution studied also for halogen + methane reactions, in the X + C2H6 [F, Cl, Br, I] reactive system methyl-substitution appears as a new mechanism and is expected to occur at lower energies then H-substitution. For these reactions so far only the H-abstraction channel (X = F, Cl)14–33 or its reverse reaction (X = Br, I)34–41 have been investigated.Stationary points for the F + C2H6 → HF + C2H5 reaction were identified in 2007 using the CCSD(T)/cc-pVDZ method along with energy computations at the CCSD(T)/cc-pVQZ level of theory,14 proposing an early-barrier transition state (TS) for the highly exothermic reaction. Later state-to-state scattering experiments also proposed an early-barrier TS from the mostly vibrationally excited HF products, however, a significant amount of vibrationally non-excited HF molecules implied energy transfer from HF to the ethyl unit during the H-abstraction reaction.15 Direct dynamics simulations were performed by Troya and co-workers using a reparametrized semiempirical Hamiltonian, based on MP2/aug-cc-pVDZ geometry optimization and CCSD(T)/aug-cc-pVDZ energy computation on the stationary points, for the reactions of fluorine with small alkanes including ethane, where the effect of the length of the alkane chain on the dynamics was studied.16 Espinosa-Garcia et al. have very recently reported the first analytical valence-bond – force-field-based PES of the F + C2H6 → HF + C2H5 reaction based on CCSD(T)/triple-zeta ab initio data and depending on 63 adjustable parameters.17
The hydrogen-abstraction reaction between Cl and ethane has been studied more extensively both experimentally and theoretically. In the late ‘90s Zare and coworkers investigated this reaction by the state-selective detection of the HCl18,19 or the ethyl radical product.20 They proposed a loose transition state and claimed that the ethyl unit was a spectator during the slightly exothermic reaction. Later crossed molecular beam experiments detecting HCl product states indicated significant internal excitation of the ethyl radical, which contradicts its spectator character.21,23,24 Crossed-beam scattering experiments of Suits and coworkers also strengthened the considerable ethyl internal excitation.31,32 In parallel, stationary points of the Cl + C2H6 → HCl + C2H5 reaction were theoretically characterized using the MP2 method with correlation-consistent basis sets combined with CCSD(T) energy computations suggesting a loose TS and a post-TS minimum.25 The reaction was also studied by direct dynamics simulations using semiempirical Hamiltonians.22,25 The joint experimental and theoretical investigations of Orr-Ewing and coworkers concerning the reactions of Cl with alkanes, including ethane, and functionalized small organic molecules revealed that rotational distribution of the HCl product is cold in the case of alkanes, whereas significant rotational excitation for HCl is observed in case of functionalized molecules due to dipole–dipole interaction between HCl and polar radical products in the post-TS region.26–30 In a recent paper Rangel and Espinosa-Garcia have published an analytical PES including valence-bond and molecular-mechanic terms for this abstraction reaction.33 They also characterized the stationary points using the CCSD(T) method with different basis sets and implied that high-level quantum chemical computations are needed to determine the exact energetics of the reaction.
In the case of X = Br and I mainly the reverse, i.e. the HX + C2H5 → X + C2H6 reactions have been the subject of both theoretical and experimental investigations due to their supposedly non-Arrhenius behavior.34–41 For the HBr + C2H5 → Br + C2H6 reaction theoretical studies using the CCSD(T)/cc-pVTZ method as highest level of theory revealed a loosely-bound adduct in the entrance channel and a tightly-bound TS very close in energy and both being below the reactant asymptote.35,38,39 The HI + C2H5 → I + C2H6 reaction has also been studied both by experimental34,40 and theoretical40,41 techniques. Leplat et al. reported CCSD/cc-pVDZ structures along with spin–orbit corrections for the stationary points of this reaction.41
In the present study we extend the investigations of the halogen + ethane reactions towards new, so far unstudied mechanisms, such as H-substitution and methyl-substitution. We also consider the Walden-inversion and front-side-attack pathways for both substitution channels. We identify the corresponding stationary points using the explicitly-correlated CCSD(T)-F12b/aug-cc-pVTZ level of theory, and provide the corresponding classical and adiabatic relative energies with unprecedented accuracy, i.e. CCSD(T)-F12b/aug-cc-pVQZ energies corrected by core-valence, post-CCSD(T), and spin–orbit effects. Spin–orbit coupling throughout the reaction paths along with structural changes are also thoroughly analyzed. This work is meant to be a first step towards developing global analytical ab initio potential energy surfaces thereby making possible to study the multi-channel dynamics of the title reactions in detail.
Computational details
In this work three different channels of the X + C2H6 [F, Cl, Br, I] reactions are studied: hydrogen-abstraction (HA), hydrogen-substitution (HS), and methyl-substitution (MS) leading to C2H5 + HX, C2H5X + H, and CH3X + CH3, respectively. HS and MS can proceed via a Walden-inversion (W) transition state (TS) or via a front-side-attack (FS) TS. This nomenclature is used throughout the paper. In the case of HA post-TS minima, referred to as HA postmin, are also found.The stationary-point geometries of the potential energy surfaces of the X + C2H6 [F, Cl, Br, I] reactions are pre-optimized using the restricted open-shell second-order Møller–Plesset perturbation theory42 (RMP2) using the correlation-consistent aug-cc-pVDZ basis set.43 A few geometries (HS FS TS for F + C2H6, and HA TS and postmin for Br + C2H6) could only be identified with the unrestricted MP2 (UMP2) method, in these cases we use the UMP2 energies of the reactant halogen atom to determine relative energies. Then the restricted open-shell Hartree–Fock-based unrestricted explicitly-correlated coupled cluster singles, doubles, and perturbative triples method, ROHF-UCCSD(T)-F12b,44 with the aug-cc-pVDZ basis set is applied for geometry optimization and harmonic frequency computations. Geometry optimizations are then also performed at the ROHF-UCCSD(T)-F12b/aug-cc-pVTZ43 level of theory for all stationary points. To obtain benchmark relative energies further single-point energy computations are carried out at the most accurate ROHF-UCCSD(T)-F12b/aug-cc-pVTZ geometries: ROHF-UCCSD(T)-F12b/aug-cc-pVQZ,43 UHF-UCCSD(T),45 UHF-UCCSDT,46 and UHF-UCCSDT(Q)47 with the cc-pVDZ basis set, and ROHF-UCCSD(T)/aug-cc-pwCVTZ48 with both frozen-core (FC) and all-electron (AE) approaches. For the Br and I atoms small-core relativistic effective core potentials (ECPs)49 are used with the corresponding cc-pVDZ-PP, aug-cc-pVDZ-PP, aug-cc-pVTZ-PP, aug-cc-pVQZ-PP, and aug-cc-pwCVTZ-PP basis sets.50 ECPs replace the inner-core 1s22s22p6 electrons of Br and the 1s22s22p63s23p63d10 electrons of I. In all cases the frozen-core approach is applied correlating the valence electrons only, except in AE computations, where the following electrons are also correlated: 1s2 for C and F, 2s22p6 for Cl, 3s23p63d10 for Br, and 4s24p64d10 for I.
For spin–orbit (SO) computations a corrected multireference configuration interaction [MRCI+Q] method51,52 is applied, within the frozen-core approach. The Davidson correction (+Q)53 estimates higher-order correlation energy effects. In the multireference computations a minimal active space of 5 electrons in the 3 spatial np-like orbitals, where n = 2, 3, 4, and 5 for F, Cl, Br, and I, respectively, is used. The SO computations are based on the Breit–Pauli operator in the interacting-states approach.54 The SO eigenstates are obtained by diagonalizing a 6 × 6 SO matrix, whose diagonal elements are replaced by the Davidson-corrected MRCI energies. SO computations have been carried out scanning the entrance channel of the X + C2H6 [F, Cl, Br, I] reactions, representing three different directions of the halogen atom approaching the ethane molecule: (1) X approaching ethane from one of the methyl-groups maintaining a C3v point-group symmetry, (2) X approaching one H atom of ethane (3) X approaching perpendicularly the C–C bond of ethane. The ethane molecule is kept fixed at its CCSD(T)-F12b/aug-cc-pVTZ equilibrium geometry while changing the separation distance of X. SO computations are also performed at the CCSD(T)-F12b/aug-cc-pVTZ geometries of the TSs, postmins and products, where the products are separated by 15 Å. The ΔSO corrections to the TS, postmin and product relative energies are determined by subtracting the difference of the computed SO and non-SO ground-state energies from the 1/3 of the experimental SO splittings (ε) of the halogen atoms, which splittings are the following: ε = 1.16(F), 2.52(Cl), 10.54(Br), and 21.74(I) kcal mol−1.
All ab initio computations are carried out with the Molpro program package,55 except the UHF-UCCSD(T), UHF-UCCSDT, and UHF-UCCSDT(Q) computations, which are performed using the MRCC program56 interfaced to Molpro.
The benchmark classical relative energies at the UCCSD(T)-F12b/aug-cc-pVTZ geometries of the stationary points are calculated as follows:
| ΔE(UCCSD(T)-F12b/aug-cc-pVQZ) + δ[UCCSDT] + δ[UCCSDT(Q)] + Δcore + ΔSO, | (1) |
| δ[UCCSDT] = ΔE(UCCSDT/cc-pVDZ) − ΔE(UCCSD(T)/cc-pVDZ), | (2) |
| δ[UCCSDT(Q)] = ΔE(UCCSDT(Q)/cc-pVDZ) − ΔE(UCCSDT/cc-pVDZ), | (3) |
| Δcore = ΔE(AE-UCCSD(T)/aug-cc-pwCVTZ) − ΔE(FC-UCCSD(T)/aug-cc-pwCVTZ). | (4) |
The benchmark adiabatic relative energies are determined as follows:
| ΔE(UCCSD(T)-F12b/aug-cc-pVQZ) + δ[UCCSDT] + δ[UCCSDT(Q)] + Δcore + ΔSO + ΔZPE, | (5) |
In determining the relative energies of the stationary points a few issues have emerged: (1) the HA TS of the F + C2H6 reaction could not be identified by optimizing the geometry at the UCCSD(T)-F12b/aug-cc-pVDZ level of theory, probably due to the flatness of the entrance channel of the corresponding potential energy surface and/or the large multireference character of this TS, thus, instead, an UCCSD(T)-F12b/aug-cc-pVDZ single point energy computation is performed on the RMP2/aug-cc-pVDZ geometry and for ZPE correction the RMP2/aug-cc-pVDZ harmonic frequencies are used. Due probably also to the larger multireference character, at the UCCSD(T)-F12b/aug-cc-pVTZ geometry of this HA TS neither the RHF, nor the UHF computation have converged during the correction-term computations. (2) Since in the I + C2H6 HA reaction the TS and postmin geometries could only be identified at the CCSD/cc-pVDZ-PP level of theory, reproducing previous results,41 UCCSD(T)-F12b/aug-cc-pVDZ-PP, UCCSD(T)-F12b/aug-cc-pVTZ-PP single point energies and all the above defined correction terms are computed for these structures (and also for ethane in these cases) at the UCCSD/cc-pVDZ-PP geometries. To calculate the ZPE correction for these TS and postmin the CCSD/cc-pVDZ-PP harmonic frequencies are used. Attempts to optimize these geometries have been made at the following levels of theory: RMP2/aug-cc-pVDZ-PP, UMP2/aug-cc-pVDZ-PP, UCCSD-F12b/aug-cc-pVDZ-PP, UCCSD(T)-F12b/aug-cc-pVDZ-PP, UCCSD(T)-F12b/aug-cc-pVTZ-PP, using different geometry optimization algorithms available in Molpro.
Results and discussion
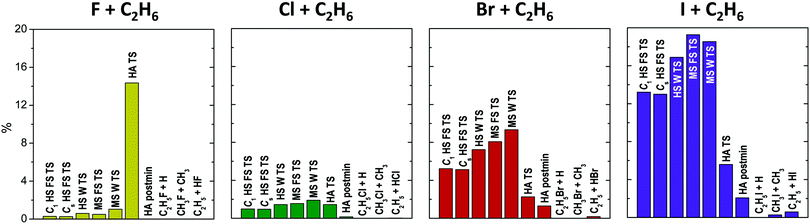
The schematic representation of the potential energy surfaces (PESs) and different pathways of the X + C2H6 [F, Cl, Br, I] reactions are shown in Fig. 1, with the benchmark classical (adiabatic) energies of the stationary points relative to the reactants, obtained from eqn (1) (eqn (5)). The relative energies determined at different ab initio levels of theory (RMP2/aug-cc-pVDZ and UCCSD(T)-F12b with aug-cc-pVDZ, aug-cc-pVTZ, and aug-cc-pVQZ bases) and the post-CCSD(T), core-correlation, spin–orbit and ZPE corrections are presented in Table 1.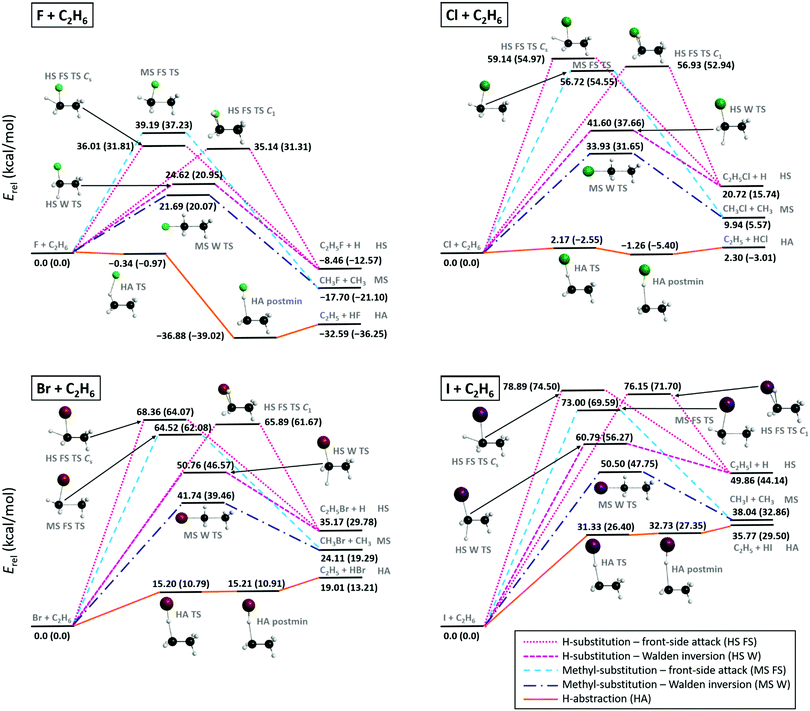 | ||
| Fig. 1 Schematic energetics and different reaction mechanisms of the X + C2H6 [X = F, Cl, Br, I] reactions showing benchmark classical (adiabatic) relative energies in kcal mol−1 of the stationary points, see Table 1, obtained from eqn (1) (eqn (5)). | ||
| Stationary points | MP2/DZa | MP2 ΔZPEb | CC/DZc | CC/TZd | ΔCC/QZe | Δcoref | δTg | δ(Q)h | ΔSOi | Classicalj | CC ΔZPEk | Adiabaticl |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| a ROHF-RMP2/aug-cc-pVDZ. b ΔZPE (ROHF-RMP2/aug-cc-pVDZ). c ROHF-UCCSD(T)-F12b/aug-cc-pVDZ. d ROHF-UCCSD(T)-F12b/aug-cc-pVTZ. e ROHF-UCCSD(T)-F12b/aug-cc-pVQZ − ROHF-UCCSD(T)-F12b/aug-cc-pVTZ. f ΔE(AE-ROHF-UCCSD(T)/aug-cc-pwCVTZ) − ΔE(FC-ROHF-UCCSD(T)/aug-cc-pwCVTZ). g UHF-UCCSDT/cc-pVDZ − UHF-UCCSD(T)/cc-pVDZ. h UHF-UCCSDT(Q)/cc-pVDZ − UHF-UCCSDT/cc-pVDZ. i Difference between the spin–orbit (SO) and non-SO ground states (FC-MRCI+Q(5,3)/aug-cc-pVDZ and experimental SO splittings of the halogens). j QZ + δT + δ(Q) + Δcore + ΔSO. k ΔZPE (ROHF-UCCSD(T)-F12b/aug-cc-pVDZ). l QZ + δT + δ(Q) + Δcore + ΔSO + CC ΔZPE. m UHF-UMP2/aug-cc-pVDZ. n ROHF-UCCSD(T)-F12b/aug-cc-pVDZ energy is obtained at the ROHF-RMP2/aug-cc-pVDZ geometry. o Neither ROHF, nor UHF converges at the ROHF-UCCSD(T)-F12b/aug-cc-pVTZ geometry. p ROHF-RMP2/aug-cc-pVDZ ZPE was used to calculate the ΔZPE correction to the relative energy. q In the first two columns ROHF-UCCSD/cc-pVDZ data are shown. All other relative energies are computed at the ROHF-UCCSD/cc-pVDZ geometry. For the ΔZPE corrections the ROHF-UCCSD/cc-pVDZ level of theory is used. | ||||||||||||
| F | ||||||||||||
| HS FS TS C1 | 33.82m | −3.94m | 35.45 | 35.42 | −0.01 | 0.20 | −0.42 | −0.44 | 0.39 | 35.14 | −3.83 | 31.31 |
| HS FS TS Cs | 32.87 | −3.30 | 36.36 | 36.31 | −0.04 | 0.22 | −0.42 | −0.44 | 0.39 | 36.01 | −4.21 | 31.81 |
| HS W TS | 21.90 | −3.76 | 25.13 | 24.83 | −0.03 | 0.16 | −0.32 | −0.41 | 0.39 | 24.62 | −3.67 | 20.95 |
| MS FS TS | 35.44 | −3.48 | 39.93 | 39.49 | −0.03 | 0.37 | −0.56 | −0.47 | 0.39 | 39.19 | −1.96 | 37.23 |
| MS W TS | 21.37 | −0.59 | 22.64 | 21.86 | −0.06 | 0.34 | −0.40 | −0.43 | 0.39 | 21.69 | −1.63 | 20.07 |
| HA TS | 2.45 | −0.63 | −3.27n | −0.68 | —o | —o | —o | —o | 0.33 | −0.34 | −0.63p | −0.97 |
| HA POSTMIN | −39.15 | −1.94 | −37.11 | −36.88 | −0.07 | −0.07 | −0.07 | −0.17 | 0.39 | −36.88 | −2.14 | −39.02 |
| C2H5F + H | −13.99 | −4.23 | −9.20 | −8.61 | −0.06 | 0.01 | 0.01 | −0.20 | 0.39 | −8.46 | −4.12 | −12.57 |
| CH3F + CH3 | −18.00 | −3.33 | −17.90 | −17.90 | −0.15 | 0.17 | −0.09 | −0.12 | 0.39 | −17.70 | −3.40 | −21.10 |
| C2H5 + HF | −34.50 | −3.67 | −32.39 | −32.44 | −0.26 | −0.06 | −0.06 | −0.16 | 0.39 | −32.59 | −3.66 | −36.25 |
| Cl | ||||||||||||
| HS FS TS C1 | 58.86 | −4.28 | 56.17 | 56.79 | −0.06 | 0.06 | −0.38 | −0.31 | 0.83 | 56.93 | −3.99 | 52.94 |
| HS FS TS Cs | 61.25 | −3.96 | 58.27 | 59.02 | −0.07 | 0.09 | −0.41 | −0.33 | 0.83 | 59.14 | −4.16 | 54.97 |
| HS W TS | 43.48 | −3.65 | 40.86 | 41.32 | −0.07 | 0.06 | −0.26 | −0.28 | 0.83 | 41.60 | −3.94 | 37.66 |
| MS FS TS | 60.90 | −1.26 | 56.42 | 56.67 | 0.00 | 0.27 | −0.69 | −0.35 | 0.83 | 56.72 | −2.17 | 54.55 |
| MS W TS | 38.84 | −0.67 | 33.81 | 33.67 | −0.09 | 0.27 | −0.46 | −0.29 | 0.82 | 33.93 | −2.29 | 31.65 |
| HA TS | 1.60 | −4.18 | 1.26 | 1.83 | −0.10 | −0.12 | −0.13 | −0.14 | 0.83 | 2.17 | −4.72 | −2.55 |
| HA PM | −0.60 | −3.69 | −2.78 | −1.76 | −0.06 | −0.13 | −0.08 | −0.06 | 0.84 | −1.26 | −4.14 | −5.40 |
| C2H5Cl + H | 17.45 | −5.09 | 18.84 | 20.19 | −0.10 | −0.12 | 0.07 | −0.16 | 0.84 | 20.72 | −4.98 | 15.74 |
| CH3Cl + CH3 | 12.72 | −4.30 | 8.64 | 9.33 | −0.14 | 0.03 | −0.06 | −0.06 | 0.84 | 9.94 | −4.37 | 5.57 |
| C2H5 + HCl | 3.83 | −5.18 | 0.99 | 1.76 | −0.10 | −0.09 | −0.07 | −0.04 | 0.84 | 2.30 | −5.31 | −3.01 |
| Br | ||||||||||||
| HS FS TS C1 | 65.83 | −3.94 | 63.20 | 63.64 | 0.07 | −0.38 | −0.47 | −0.30 | 3.33 | 65.89 | −4.22 | 61.67 |
| HS FS TS Cs | 68.57 | −3.77 | 65.70 | 66.15 | 0.07 | −0.37 | −0.50 | −0.32 | 3.33 | 68.36 | −4.30 | 64.07 |
| HS W TS | 50.48 | −4.02 | 47.89 | 48.32 | 0.08 | −0.36 | −0.27 | −0.26 | 3.26 | 50.76 | −4.19 | 46.57 |
| MS FS TS | 67.23 | −1.62 | 62.45 | 62.47 | 0.12 | −0.11 | −0.84 | −0.34 | 3.23 | 64.52 | −2.45 | 62.08 |
| MS W TS | 44.78 | −1.63 | 39.42 | 39.34 | 0.05 | −0.08 | −0.50 | −0.26 | 3.18 | 41.74 | −2.28 | 39.46 |
| HA TS | 13.43m | −4.21m | 11.85 | 12.55 | 0.02 | −0.58 | −0.13 | −0.09 | 3.43 | 15.20 | −4.41 | 10.79 |
| HA PM | 13.36m | −4.06m | 11.71 | 12.48 | 0.02 | −0.57 | −0.11 | −0.06 | 3.46 | 15.21 | −4.30 | 10.91 |
| C2H5Br + H | 28.49 | −5.47 | 31.22 | 32.30 | 0.05 | −0.59 | 0.06 | −0.16 | 3.51 | 35.17 | −5.39 | 29.78 |
| CH3Br + CH3 | 23.67 | −4.71 | 20.76 | 21.09 | −0.02 | −0.35 | −0.07 | −0.05 | 3.51 | 24.11 | −4.82 | 19.29 |
| C2H5 + HBr | 17.69 | −5.64 | 15.52 | 16.12 | −0.05 | −0.45 | −0.09 | −0.02 | 3.50 | 19.01 | −5.80 | 13.21 |
| I | ||||||||||||
| HS FS TS C1 | 73.87 | −4.40 | 70.82 | 71.56 | 0.17 | −0.96 | −0.60 | −0.32 | 6.29 | 76.15 | −4.45 | 71.70 |
| HS FS TS Cs | 77.00 | −4.54 | 73.59 | 74.31 | 0.20 | −0.94 | −0.65 | −0.34 | 6.31 | 78.89 | −4.39 | 74.50 |
| HS W TS | 58.16 | −4.72 | 55.36 | 56.16 | 0.19 | −1.02 | −0.31 | −0.26 | 6.03 | 60.79 | −4.52 | 56.27 |
| MS FS TS | 74.08 | −2.16 | 68.59 | 68.97 | 0.21 | −0.63 | −1.04 | −0.36 | 5.85 | 73.00 | −3.41 | 69.59 |
| MS W TS | 51.23 | −2.67 | 45.64 | 45.94 | 0.14 | −0.66 | −0.56 | −0.25 | 5.91 | 50.50 | −2.76 | 47.75 |
| HA TSq | 30.63 | −4.92 | 24.73 | 25.67 | 0.12 | −1.08 | −0.15 | −0.08 | 6.84 | 31.33 | −4.92 | 26.40 |
| HA PMq | 30.10 | −5.38 | 25.70 | 26.68 | 0.09 | −0.98 | −0.12 | −0.04 | 7.10 | 32.73 | −5.38 | 27.35 |
| C2H5I + H | 39.87 | −5.81 | 42.49 | 43.83 | 0.17 | −1.27 | 0.06 | −0.18 | 7.25 | 49.86 | −5.72 | 44.14 |
| CH3I + CH3 | 34.45 | −5.09 | 31.26 | 31.79 | 0.08 | −0.91 | −0.09 | −0.06 | 7.23 | 38.04 | −5.18 | 32.86 |
| C2H5 + HI | 31.63 | −6.10 | 28.74 | 29.46 | 0.01 | −0.79 | −0.11 | −0.01 | 7.21 | 35.77 | –6.27 | 29.50 |
For all four X + C2H6 reactions the 0 K reaction enthalpies of the different reaction channels follow the same order: H-abstraction (HA), H-substitution (HS), and methyl-substitution (MS) with increasing relative energies. The energy difference between the products of HS and MS is around 10 kcal mol−1 in all cases, whereas, as the atomic number of the halogen increases the energy gap between the MS and the HA product channels decrease significantly. The different reaction paths become more and more endothermic from X = F to X = I, along with increasing barrier heights, which usually also follow the same energy order regarding all four reactions. The lowest-barriers appear for HA, the main reaction path at low collision energies, followed by the higher-energy TSs of the Walden-inversion pathway of MS and then that of HS. At high energies first the front-side-attack (FS) mechanism of HS becomes available and finally the FS MS channel features higher barriers, except for X = I, where FS HS has higher barrier than FS MS. Thus, with increasing collision energy, first the HA, then the MS and finally the HS channels open. For X = F and Cl the global minima of the PESs correspond to the HA postmin geometries, whereas for X = Br and I the lowest energy stationary points are located in the entrance channel, see discussion below.
In the F + C2H6 reaction all channels are exothermic with 0 K reaction enthalpies −36.3, −21.1 and −12.6 kcal mol−1, for HA, MS, and HS, respectively. For the Cl + C2H6 reaction only HA has negative 0 K reaction enthalpy (−3.0 kcal mol−1), however, if ZPE correction is not taken into account, HA is an endothermic (2.3 kcal mol−1) reaction path. For X = Br and I all reaction channels are endothermic, even the main HA channel has 10.8 and 26.4 kcal mol−1 barrier heights, respectively, with the highest channel-opening at 71.7 kcal mol−1 for the front-side I + C2H6 → C2H5I + H substitution reaction. Endothermicity and the corresponding barrier heights increase significantly, with 16–33 kcal mol−1 by changing F with Cl (except for HA TS), and somewhat more moderately (with 8–17 kcal mol−1) from X = Cl to Br, or from X = Br to I. Regarding H-abstraction, between the TS and postmin geometries an energy gain of 38.1 kcal mol−1 occurs for X = F, which decreases to 2.8 kcal mol−1 for X = Cl, and almost vanishes in the case of X = Br and I, where the close relative energies of the TS and the postmin indicate a flat potential energy surface region and make hard to identify these stationary points. (Note that the relative energies at the optimized postmin geometries without corrections are lower than at the optimized TS geometries both for X = Br and I). H-abstraction is a barrierless channel for the F + C2H6 reaction and also for Cl + C2H6 when the adiabatic energies are considered. Interestingly, the reverse HA reactions for Br and I, i.e. the widely-studied34–41 HX + C2H5 [X = Br, I] reactions also have submerged barriers, thus can occur spontaneously. The higher-energy HS and MS reactions proceed either via Walden or front-side TSs, where the FS mechanism has about 11–17 kcal mol−1 (17–23 kcal mol−1) higher barriers than Walden inversion in the case of H-substitution (methyl-substitution) for all four reactions. Two HS FS TSs are found close in energy (with 0.5–2.8 kcal mol−1 differences) in all four cases, one with Cs and the other with C1 (having always the lower relative energy) point-group symmetry.
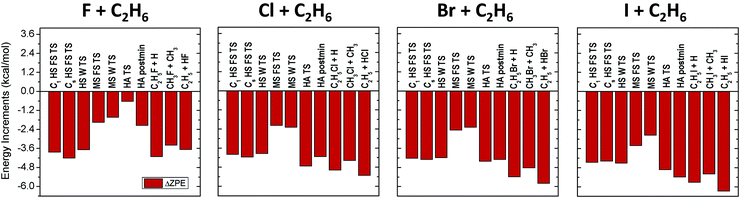
All ZPE corrections to the relative energies, as shown in Fig. 2, turn out to be negative covering the 0.5–6 kcal mol−1 energy range, so these terms always lower the barrier heights and reaction energies. The smallest corrections (excluding the very reactant-like HA TS of the F + C2H6 reaction) correspond to methyl-substitution TSs, and product channels, where the breaking C–C bonds are replaced by newly forming C–X bonds, resulting in similar harmonic vibrational frequencies, however, the number of vibrational degrees of freedom (dofs) decreases by 3 during product formation, which causes the negative ZPE correction. Larger corrections appear for the HS TSs and products, due to the formation of C–X bonds instead of the breaking C–H bonds, where C–X bonds have smaller vibrational frequencies. Slightly larger ZPE corrections are observed for the HA TSs and products, where the C–H bonds are replaced by H–X bonds, resulting in smaller vibrational frequencies along with the reduction of dofs by 2. As the C–X and H–X frequencies decrease from X = F to I, in Fig. 2 an increase in the magnitude of ZPE corrections can be observed for the corresponding stationary points from left to right.
In Table 1 the MP2/aug-cc-pVDZ (MP2/DZ) relative energies and ZPE corrections are also listed. This level of theory provides relative energies far from chemical accuracy, with average deviations of 2.8 kcal mol−1 (with a maximum value of 5.4 kcal mol−1) from the CCSD(T)-F12b/aug-cc-pVTZ energies. MP2/DZ energies are even poorer when compared to the benchmark classical values, with an average difference of 3.2 kcal mol−1 and a maximum deviation of 6.9 kcal mol−1. The harmonic ZPE corrections obtained at the MP2/DZ level are of better quality, reproducing the CCSD(T)-F12b/aug-cc-pVDZ ZPE contributions with an average deviation of 0.37 kcal mol−1 (the maximum difference is 1.62 kcal mol−1). Therefore, despite being widely used, the MP2/aug-cc-pVDZ level of theory is not recommended for studying such systems if chemical accuracy is desired.
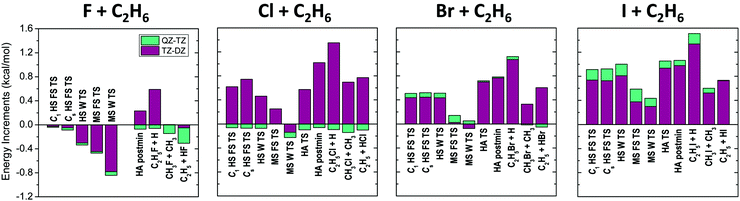
The different correction terms summarized in Table 1 and presented graphically in Fig. 3 and 4 allow estimating the accuracy of the new benchmark relative energies. The remarkably fast basis set convergence of the UCCSD(T)-F12b relative energies is highlighted in Fig. 3. The aug-cc-pVTZ (TZ) and the aug-cc-pVQZ (QZ) energies are of similar quality, with an average deviation of only 0.1 kcal mol−1, and with the largest deviations observed for the X = I TSs. The TZ-DZ increments show an average magnitude of 0.6 kcal mol−1, which, together with the small QZ-TZ corrections, indicates that even the DZ energies are within chemical accuracy for most of the stationary points.
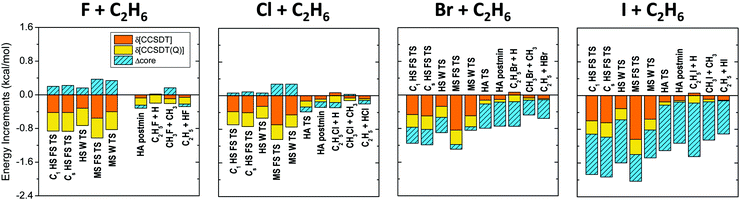 | ||
| Fig. 4 Post-CCSD(T), eqn (2) and (3), and core, eqn (4), correlation energy effects for the different stationary points of the X + C2H6 [X = F, Cl, Br, I] reactions. In the case of the HA TS of the F + C2H6 reaction neither ROHF, nor UHF converged at the UCCSD(T)-F12b/aug-cc-pVTZ geometry. | ||
As shown in Table 1 and Fig. 4 the post-CCSD(T) and core-valence corrections are usually in the same order of magnitude or even larger than the basis set convergence errors, especially for X = I. The core-correlation terms have an average value of 0.4 kcal mol−1, and are usually positive and relatively small (average: 0.2 kcal mol−1) for X = F and Cl. For X = Br and I, this effect becomes more significant (average: 0.7 kcal mol−1) and always lowers the barrier heights and reaction energies. For the C2H5I + H products this correction reaches even −1.3 kcal mol−1. δ[CCSDT] and δ[CCSDT(Q)] increments also represent a significant contribution to the relative energies and cannot be neglected if chemical accuracy is desired. These corrections are larger for the TSs than the products, and are almost always negative, thus for X = F and Cl they can be partially cancelled by the positive core-valence terms, as seen previously for several other systems.57–59 However, unexpectedly for X = Br and I both the core-valence and post-CCSD(T) corrections are negative, thus the cancelling effect does not occur. δ[CCSDT] corrections are larger in magnitude than the δ[CCSDT(Q)] terms, with average values of 0.3 and 0.2 kcal mol−1, respectively.
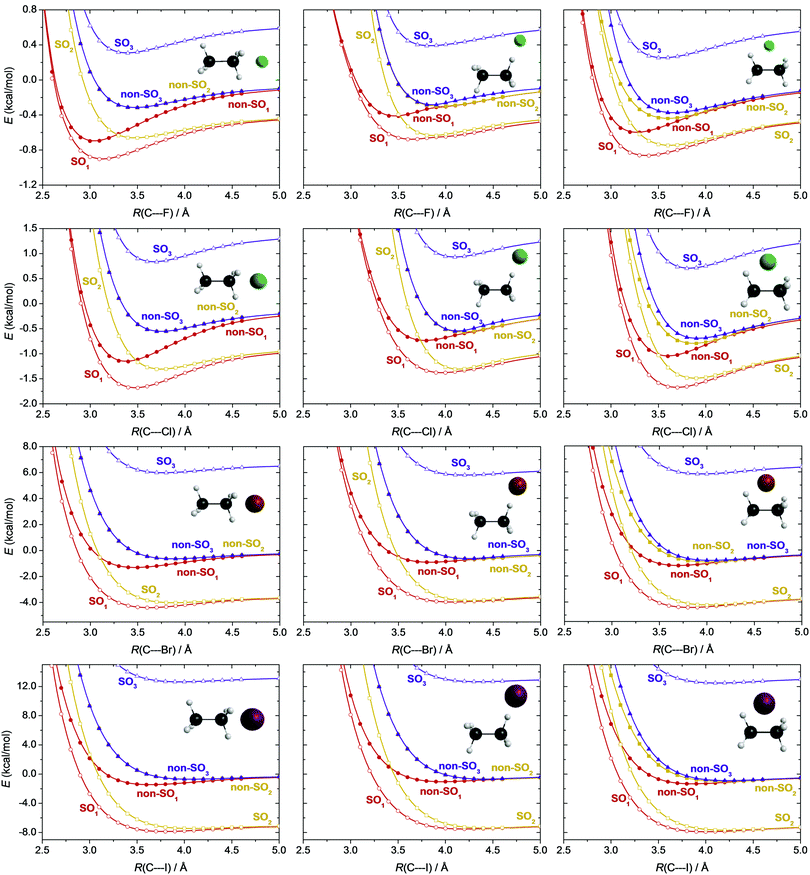
In such open-shell systems the energy lowering due to the relativistic spin–orbit (SO) interaction in the halogen atoms should also be taken into account. The non-relativistic ground state of a halogen atom is 2P, which splits into two energy levels, 2PJ=3/2 and 2PJ=1/2, due to spin–orbit coupling, where J is the total angular momentum quantum number. Because of the (2J + 1)-fold degeneracy of the SO states, the ground 2P3/2 state is lower in energy by 1/3 of the SO-splitting, while the excited 2P1/2 state is higher by 2/3 of the splitting energy with respect to the non-SO 2P state. In Fig. 5, where all the data are shown relative to the ground non-SO 2P asymptotic limit, we monitored what happens if the isolated halogen atom approaches the ethane molecule. As seen in Fig. 5 the interaction with the ethane molecule splits the fourfold degenerate 2P3/2 state into a twofold degenerate SO ground state (SO1) and an (also twofold degenerate) excited (SO2) state. The higher-energy 2P1/2 state (SO3) is not further split. The sixfold degenerate non-relativistic 2P state is also split due to the interaction into a non-SO ground state (non-SO1), and two non-SO excited states (non-SO2 and non-SO3), all three states having twofold degeneracy. Among these only the SO1 and non-SO1 ground states are reactive within the Born–Oppenheimer approximation and therefore of interest concerning the title reactions. We consider three different directions of the halogen atom (X) nearing to the C2H6 unit: (1) X approaching one of the methyl-groups of ethane maintaining a C3v point-group symmetry, (2) X approaching one H atom of ethane, and (3) X approaching perpendicularly the C–C bond of ethane. In the first case, the C3v symmetry causes an exact degeneracy of the non-SO2 and non-SO3 states, as can be seen in the first column of Fig. 5. In our MRCI+(Q)(5,3)/aug-cc-pVDZ(-PP) (PPs for Br and I) computations the experimental atomic splittings, which are 1.16(F), 2.52(Cl), 10.54(Br), and 21.74(I) kcal mol−1, are reproduced qualitatively well, within a few 0.1 kcal mol−1, calculated as the difference between the asymptotic limits of the SO potential energy curves of Fig. 5. As seen from the energy scales of Fig. 5 and the experimental splitting values, spin–orbit coupling has a significant energy-lowering effect in the entrance channel of the title reactions, especially when the reactants are far from each other. This effect is around a few 0.1 kcal mol−1 for X = F, almost 1 kcal mol−1 for X = Cl, a few kcal mol−1 for Br, and can exceed 7 kcal mol−1 for X = I. The reactive non-SO1 and SO1 potentials feature van der Waals (vdW) minima along the C⋯X coordinate, that is entrance-channel valleys of the PESs of the X + C2H6 reactions, which may play an important role in their dynamics. In the case of X = Br and I these minima turn out to be the global minima of the corresponding PESs.
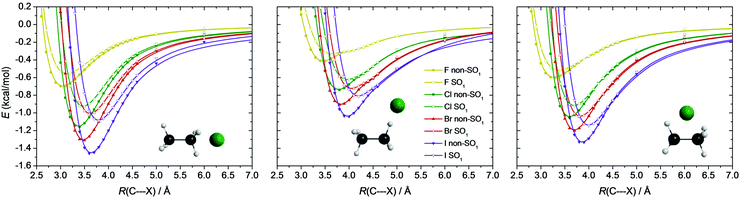
To visualize the relative depths of these vdW valleys, in Fig. 6 scaled non-SO1 and SO1 potential energy curves are shown with the SO1 curves shifted by their asymptotic limits and all data being relative to the non-SO1 potential energy asymptote of the corresponding halogen. From X = F to I the entrance channel minima become deeper and deeper, and the energy gap between the non-SO1 and the less deep SO1 minima increases. These minima are the deepest in the C3v-symmetry case, when the halogen approaches one methyl-group (0.5–1.5 kcal mol−1), and are slightly shallower when the halogen atom comes perpendicularly (0.5–1.3 kcal mol−1). The smallest depths, 0.3–1.1 kcal mol−1, appear when the halogen accesses one of the H-atoms, similar to the X + CH4 systems.1 It is also seen that the C⋯X distance corresponding to the minima of both the non-SO1 and the SO1 potentials is shifted towards larger values as one goes from F to I, and the SO1 minima always appear at larger C⋯X distances than the non-SO1 ones. The C⋯X distances corresponding to the minimum values of the potentials are the smallest (3.0–3.7 Å) in the C3v-symmetry case, whereas in the other two cases they are considerably larger (3.5–4.3 Å). Such entrance-channel minima may play a crucial role in the reactivity of the low-barrier HA pathways of the F and Cl + C2H6 reactions.
SO-coupling is usually considered to play a role only in the entrance channel of the reactions of halogen atoms, where the halogen is “far” from its reaction partner. Nonetheless, we carried out SO computations at the TS and even at the product geometries to check the validity of this assumption. It turned out that if the TS is reactant-like (which is mostly the case for X = F, see discussion below) or if the SO splitting is large (thus especially for X = I), the lowering of relative energies due to SO coupling at the TS geometries can reach even the 20% of the SO corrections of the corresponding halogen atoms, as shown in Fig. 7. For X = F, the HA TS has a strongly reactant-like structure with the F atom being 1.94 Å from the H atom of ethane, which gives rise to considerable SO-effect (0.06 kcal mol−1, 15% of the SO correction of F). In the case of X = Cl SO-coupling is not very significant (0.01–0.02 kcal mol−1) for the TSs, while for X = Br even a 0.3 kcal mol−1 (9% for MS W TS) energy lowering can be observed. The largest effect, both in the change in relative energy and in percent, emerges for X = I, where most of the TSs feature 15–20% SO corrections compared to that of the I atom, with a maximum value of 1.4 kcal mol−1 in the case of MS FS TS. It is apparent that if subchemical accuracy is aimed, the SO-coupling cannot be neglected in determining the relative energies of the TSs of the title reactions. In the case of the product geometries SO coupling is not significant, however, for X = I it has a −0.02 and −0.04 kcal mol−1 contribution to the MS and HA reaction energies.
Scalar relativistic effects are taken into account for Br and I through the effective core potentials used in our computations. For all other atoms the scalar relativistic corrections are expected to be small (10–50% of the core correlation effects),59 thus these are neglected in this study.
The above determined corrections make possible to estimate the uncertainty of our computed benchmark relative energies of the stationary points of the X + C2H6 [X = F, Cl, Br, I] reactions. Due to the fast basis-set convergence of the explicitly correlated CCSD(T)-F12b method, the basis-set error might only contribute to the overall uncertainty with about 0.1 kcal mol−1. Somewhat larger uncertainties may come from the post-CCSD(T) corrections, whose error could reach 50% of the correction value, giving rise for a 0.3-0.4 kcal mol−1 uncertainty. The harmonic ZPE corrections are supposed to account for approximately the 95% of the anharmonic correction resulting in about a 0.2 kcal mol−1 uncertainty. Taken together, the total uncertainty of our computed data is estimated to be within 0.5 kcal mol−1, far superseding chemical accuracy.
In Table 2 we compare the benchmark 0 K reaction enthalpies determined in this work to those obtained from the Active Thermochemical Tables (ATcT) along with their uncertainties. A very good agreement is observed as the differences of the best available experimental and our new theoretical data are between 0.05–0.65 kcal mol−1 regarding all the twelve cases. As expected, these small deviations are mostly within the predicted uncertainty of our new benchmark relative energies.
| This worka | Experimentb | |
|---|---|---|
| a Benchmark theoretical reaction enthalpies obtained by eqn (5). b Data obtained from the latest version (1.122) of the Active Thermochemical Tables (ATcT). Uncertainties are derived from the uncertainties of each 0 K enthalpy of formation given in ATcT using the Gaussian error-propagation law. | ||
| F | ||
| C2H5F + H | −12.57 | −12.01 ± 0.10 |
| CH3F + CH3 | −21.10 | −20.78 ± 0.07 |
| C2H5 + HF | −36.25 | −36.02 ± 0.08 |
| Cl | ||
| C2H5Cl + H | 15.74 | 16.24 ± 0.06 |
| CH3Cl + CH3 | 5.57 | 5.79 ± 0.07 |
| C2H5 + HCl | −3.01 | −2.96 ± 0.07 |
| Br | ||
| C2H5Br + H | 29.78 | 29.94 ± 0.07 |
| CH3Br + CH3 | 19.29 | 19.07 ± 0.08 |
| C2H5 + HBr | 13.21 | 12.78 ± 0.09 |
| I | ||
| C2H5I + H | 44.14 | 44.43 ± 0.12 |
| CH3I + CH3 | 32.86 | 32.36 ± 0.06 |
| C2H5 + HI | 29.50 | 28.85 ± 0.08 |
Comparing our new benchmark data to previous results14,16,17,22,25,28–30,33,35,37–41 of the literature, where only the main H-abstraction channel was investigated for the X + C2H6 [X = F, Cl, Br, I] reactions, we find considerable inaccuracies regarding the barrier heights, even their signs for X = F and Cl. Deviations from a few tenth to even 3 kcal mol−1 can be observed between previously published relative energies and ours, with small differences found mostly when authors carried out some kind of extrapolation of low-level energies. Note that, as these barrier heights (for X = Br and I provided for the reverse reactions in the literature) have small absolute values, the above deviations can mean very large relative errors with respect to the accurate energies.
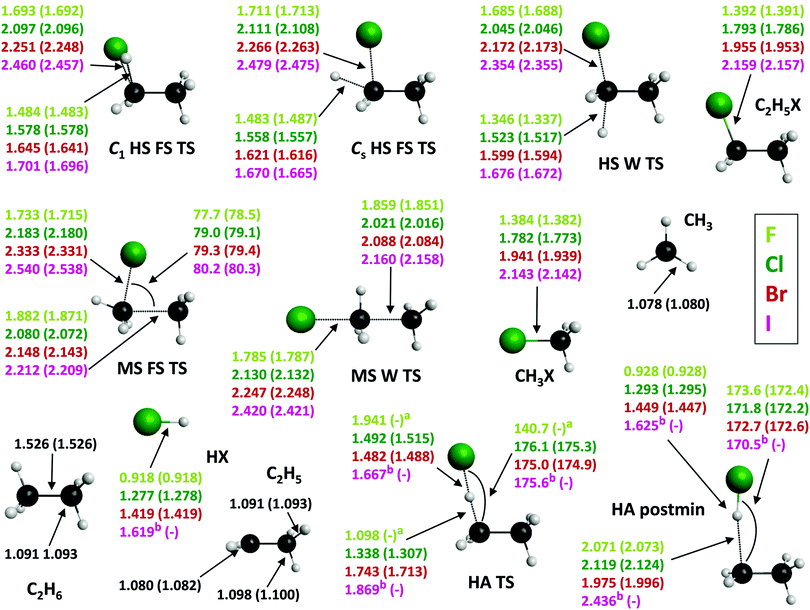
The three possible mechanisms of the title reactions are also studied in terms of structural changes; the corresponding data are shown Fig. 8. Together with energetics, the structural parameters of the stationary points allow for making predictions concerning the dynamics of the title reactions and the validity of the Polanyi rules,60 which were established for the dynamics of the simple A + BC reactions. As seen in Fig. 8, the UCCSD(T)-F12b geometries obtained with the aug-cc-pVDZ and with the aug-cc-pVTZ basis sets are basically the same usually within a few 0.001 Å in bond lengths and a few 0.1 degrees in bond angles, confirming the very fast basis set convergence observed for the relative energies (Table 1 and Fig. 3). For the H-substitution channel in all three TS geometries both the breaking C–H and the forming C–X bond lengths increase as going from F to I, with the largest increments between X = F and Cl. These C–H and C–X bonds are usually the shortest in the Walden-inversion TS, as it is the sterically most favorable mechanism due to back-side attack. The breaking C–H bond lengths in the FS as well as in the W TSs show increasing differences (26 to 35% for FS TSs and 20 to 35% for W TS) from the C–H bond in ethane, accompanied by the increasing resemblance of the C–X bond lengths of the TSs (19 to 13% for FS TSs and 17 to 8% for W TS) to those observed in the corresponding ethyl-halides as the atomic number of the halogen increases, thus one can talk about more and more product-like TSs.
In the case of methyl-substitution both the C–C and the C–X distances increase in the TS geometries from X = F to I with the C–C bond lengths being slightly shorter and the C–X bond lengths changing in a narrower scale in W TS. For the MS FS TS structures also the jump in the bond-length values between the X = F (1.882 Å for C–C and 1.733 Å for C–F) and Cl (2.080 Å for C–C 2.183 Å for C–Cl) cases is the largest. The X–C–C bond angles rise slightly from X = F to I as the size of the halogen atom increases. The C–C bond lengths in the TS structures increase (with 18–32% for both FS and W TSs) compared to ethane from X = F to I, while the C–X bond lengths are more and more similar, with differences decreasing by 20–16% for FS TS and by 22–11% for W TS to those observed in the methyl-halides, indicating more and more product-like TSs.
As to H-abstraction, in the TS geometry the breaking C–H bond lengths increase from F to I, whereas the X–H distances decrease significantly from the extremely large value for X = F (1.941 Å). (Note that, for X = I the HA TS and postmin geometries are obtained at the less accurate CCSD/cc-pVDZ level of theory.) The X–H–C bond angle is also unusually bent for X = F (140.7°), whereas for the other halogens it is around 175° indicating a nearly collinear TS. In the postmin structure the H–X bonds are shorter (in the case of X = F by 50%) and the breaking C–H bonds are much longer compared to those of the TS geometries. H–X bond lengths in the HA TSs differ less and less from those of the HX products, by 53(F), 14(Cl), 4(Br), and 3(I)%, whereas in the postmin geometries these differences are only between 0–2% for all four cases. The breaking C–H bond in the TS geometries is getting more and more elongated from X = F to I (1–42%), while a 45–55% increase of the breaking C–H bond lengths can be observed in the postmin structures compared to ethane. Accordingly, for the HA channel the TS and postmin structures are more and more product-like, with a very reactant-like TS in the case of X = F, similar to the X + CH4 reactions.1
Our findings regarding the geometrical changes during the title reactions are in accord with their energetics (Fig. 1) and thus with Hammond's postulate61 stating that in exothermic(endothermic) reactions the TS has a geometry similar to the reactants(products). Knowing the position of the TSs along the reaction coordinate also allows for making some wary predictions regarding the dynamical behavior of the title reactions based on the Polanyi rules.60 According to these basic rules, one may expect for the early-barrier F + C2H6 reaction paths that translational energy will be the most efficient in promoting the reaction, while e.g. the late-barrier I + C2H6 reactions will require strong vibrational excitation in order to increase reactivity. However, only dynamics simulations on accurate PESs can reveal the real effect of the complexity of these 9-atomic systems and the role of e.g. the entrance-channel van der Waals minima in these reactions.
Summary and conclusions
In this study we have thoroughly mapped the complex potential energy surfaces of the X + C2H6 [F, Cl, Br, I] reactions using the explicitly-correlated UCCSD(T)-F12b method with different basis sets, concerning three possible reaction mechanisms: the already studied main H-abstraction, which is the only available path at low collision energies, and the so far uninvestigated higher-energy H-substitution and methyl-substitution reaction paths. For the substitution channels both the Walden-inversion and the front-side-attack mechanisms have been under consideration. We have identified the corresponding stationary points and report their benchmark-quality classical and adiabatic relative energies, including core-valence, post-CCSD(T) and spin–orbit corrections to the highly accurate UCCSD(T)-F12b/aug-cc-pVQZ energies. It turns out, that methyl-substitution is the next available channel above the main H-abstraction pathway for all the title reactions, and at somewhat higher energies H-substitution also opens. Therefore, at high collision energies all the three reactions can occur, which could be experimentally investigated as was done in the high-energy crossed-beam study of the O(3P) + CH4 multi-channel reaction.62 For both of the substitution channels the Walden-inversion pathway features lower barrier heights then front-side attack. Transition states follow the same order in energy for all four halogens (HA TS, MS W TS, HS W TS, HS FS TS, MS FS TS), except the X = I case, where the barrier of the front-side-attack pathway of H-substitution is higher than that of methyl-substitution. Product channels are also in the same increasing energy order in all four cases: H-abstraction, methyl-substitution and H-substitution. Our new benchmark 0 K reaction enthalpies are in excellent agreement with the best available experimental results. We have compared the relative energies obtained at the MP2/aug-cc-pVDZ level of theory, which is widely used for similar-sized systems, to the benchmark relative energies and we find MP2 results being far from chemical accuracy, with errors of several kcal mol−1. Our results show that if subchemical accuracy, i.e. <0.5 kcal mol−1, is desired for such chemical systems, one needs to take all of the above correction terms into account. Spin–orbit couplings have also been studied throughout the reaction paths revealing a non-negligible effect even in the transition-state structures. We have also identified several minima in the entrance and exit channels along the different reaction paths, which may have a significant effect on the dynamics of the title reactions. We further investigated the structural changes during the course of the reactions and find fully reactant-like transition states for the X = F case, whereas more and more product-like TS geometries along with increasing endothermicity can be observed as the atomic number of the halogen increases, in accord with Hammond's postulate. Based on the basic dynamical rules proposed by Polanyi, the location of the TS along the reaction coordinate can give us hints concerning the effect of translational or vibrational excitation on reactivity, however, only accurate dynamics simulations can reveal the validity of these rules in systems of such complexity. In line with that, this study is a first step towards developing global analytical ab initio PESs, which provide opportunity to investigate the dynamics of the different channels of the title reactions in detail. Such a PES for the Cl + C2H6 reaction is already being developed in our group.Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
We thank the National Research, Development and Innovation Office – NKFIH, K-125317 and the Ministry of Human Capacities, Hungary grant 20391-3/2018/FEKUSTRAT for financial support. We acknowledge KIFÜ for awarding us access to resource based in Hungary at Szeged.References
- G. Czakó and J. M. Bowman, J. Phys. Chem. A, 2014, 118, 2839 CrossRef PubMed.
- C. Rangel, M. Navarrete, J. C. Corchado and J. Espinosa-García, J. Chem. Phys., 2006, 124, 124306 CrossRef PubMed.
- J. Chen, X. Xu, S. Liu and D. H. Zhang, Phys. Chem. Chem. Phys., 2018, 20, 9090 RSC.
- F. Meng, W. Yan and D. Y. Wang, Phys. Chem. Chem. Phys., 2012, 14, 13656 RSC.
- K. Liu, J. Chem. Phys., 2015, 142, 080901 CrossRef PubMed.
- J. Qi, H. Song, M. Yang, J. Palma, U. Manthe and H. Guo, J. Chem. Phys., 2016, 144, 171101 CrossRef PubMed.
- J. Xie and W. L. Hase, Science, 2016, 352, 32 CrossRef CAS PubMed.
- I. Szabó and G. Czakó, J. Phys. Chem. A, 2017, 121, 9005 CrossRef PubMed.
- J. Xie, R. Otto, J. Mikosch, J. Zhang, R. Wester and W. L. Hase, Acc. Chem. Res., 2014, 47, 2960 CrossRef CAS PubMed.
- J. Mikosch, S. Trippel, C. Eichhorn, R. Otto, U. Louderaj, J.-X. Zhang, W. L. Hase, M. Weidemüller and R. Wester, Science, 2008, 319, 183 CrossRef CAS PubMed.
- L. Krotos and G. Czakó, J. Phys. Chem. A, 2017, 121, 9415 CrossRef CAS PubMed.
- I. Szabó and G. Czakó, Nat. Commun., 2015, 6, 5972 CrossRef PubMed.
- V. Tajti and G. Czakó, J. Phys. Chem. A, 2017, 121, 2847 CrossRef PubMed.
- O. Roberto-Neto and F. B. C. Machado, Chem. Phys. Lett., 2007, 449, 67 CrossRef CAS.
- E. S. Whitney, A. M. Zolot, A. B. McCoy, J. S. Francisco and D. J. Nesbitt, J. Chem. Phys., 2005, 122, 124310 CrossRef PubMed.
- J. P. Layfield, A. F. Sweeney and D. Troya, J. Phys. Chem. A, 2009, 113, 4294 CrossRef CAS PubMed.
- J. Espinosa-Garcia, J. C. Corchado, M. Garcia-Chamorro and C. Rangel, Phys. Chem. Chem. Phys., 2018, 20, 19860 RSC.
- S. A. Kandel, T. P. Rakitzis, T. Lev-On and R. N. Zare, J. Chem. Phys., 1996, 105, 7550 CrossRef CAS.
- S. A. Kandel, T. P. Rakitzis, T. Lev-On and R. N. Zare, Chem. Phys. Lett., 1997, 265, 121 CrossRef CAS.
- S. A. Kandel, T. P. Rakitzis, T. Lev-On and R. N. Zare, J. Phys. Chem. A, 1998, 102, 2270 CrossRef CAS.
- P. C. Samartzis, D. J. Smith, T. P. Rakitzis and T. N. Kitsopoulos, Chem. Phys. Lett., 2000, 324, 337 CrossRef CAS.
- O. Roberto-Neto and F. B. C. Machado, Theor. Chem. Acc., 2001, 107, 15 Search PubMed.
- M. J. Bass, M. Brouard, C. Vallance, T. N. Kitsopoulos, P. C. Samartzis and R. L. Toomes, J. Chem. Phys., 2003, 119, 7168 CrossRef CAS.
- R. L. Toomes and T. N. Kitsopoulos, Phys. Chem. Chem. Phys., 2003, 5, 2481 RSC.
- A. Fernandez-Ramos, E. Martinez-Nunez, J. M. C. Marques and S. A. Vazquez, J. Chem. Phys., 2003, 118, 6280 CrossRef CAS.
- C. Murray and A. J. Orr-Ewing, Int. Rev. Phys. Chem., 2004, 23, 435 Search PubMed.
- S. Rudic, C. Murray, J. N. Harvey and A. J. Orr-Ewing, J. Chem. Phys., 2004, 120, 186 CrossRef CAS PubMed.
- C. Murray, J. K. Pearce, S. Rudic, B. Retail and A. J. Orr-Ewing, J. Phys. Chem. A, 2005, 109, 11093 CrossRef CAS PubMed.
- S. J. Greaves, J. Kim, A. J. Orr-Ewing and D. Troya, Chem. Phys. Lett., 2007, 441, 171 CrossRef CAS.
- S. J. Greaves, A. J. Orr-Ewing and D. Troya, J. Phys. Chem. A, 2008, 112, 9387 CrossRef CAS PubMed.
- C. S. Huang, W. Li and A. G. Suits, J. Chem. Phys., 2006, 125, 133107 CrossRef PubMed.
- W. Li, C. S. Huang, M. Patel, D. Wilson and A. Suits, J. Chem. Phys., 2006, 124, 011102 CrossRef PubMed.
- C. Rangel and J. Espinosa-Garcia, Phys. Chem. Chem. Phys., 2018, 20, 3925 RSC.
- J. A. Seetula, J. J. Russell and D. Gutman, J. Am. Chem. Soc., 1990, 112, 1347 CrossRef CAS.
- Y. H. Chen and E. Tschuikow-Roux, J. Phys. Chem., 1993, 97, 3742 CrossRef CAS.
- J. A. Seetula, J. Chem. Soc., Faraday Trans., 1998, 94, 891 RSC.
- J. A. Seetula, Phys. Chem. Chem. Phys., 2000, 2, 3807 RSC.
- L. Sheng, Z. S. Li, J. Y. Liu, J. F. Xiao and C. C. Sun, J. Comput. Chem., 2004, 25, 423 CrossRef CAS PubMed.
- D. M. Golden, J. P. Peng, A. Goumri, J. Yuan and P. Marshall, J. Phys. Chem. A, 2012, 116, 5847 CrossRef CAS PubMed.
- N. Leplat, A. Wokaun and M. J. Rossi, J. Phys. Chem. A, 2013, 117, 11383 CrossRef CAS PubMed.
- N. Leplat, J. Federic, K. Sulkova, M. Sudolska, F. Louis, I. Cernusak and M. J. Rossi, Z. Phys. Chem., 2015, 229, 1475 CAS.
- C. Møller and M. S. Plesset, Phys. Rev., 1934, 46, 618 CrossRef.
- T. H. Dunning Jr., J. Chem. Phys., 1989, 90, 1007 CrossRef.
- T. B. Adler, G. Knizia and H.-J. Werner, J. Chem. Phys., 2007, 127, 221106 CrossRef PubMed.
- K. Raghavachari, G. W. Trucks, J. A. Pople and M. Head-Gordon, Chem. Phys. Lett., 1989, 157, 479 CrossRef CAS.
- J. Noga and R. J. Bartlett, J. Chem. Phys., 1987, 86, 7041 CrossRef CAS.
- M. Kállay and J. Gauss, J. Chem. Phys., 2005, 123, 214105 CrossRef PubMed.
- K. A. Peterson and T. H. Dunning Jr., J. Chem. Phys., 2002, 117, 10548 CrossRef CAS.
- K. A. Peterson, D. Figgen, E. Goll, H. Stoll and M. Dolg, J. Chem. Phys., 2003, 119, 11113 CrossRef CAS.
- K. A. Peterson and K. E. Yousaf, J. Chem. Phys., 2003, 133, 174116 CrossRef PubMed.
- H.-J. Werner and P. J. Knowles, J. Chem. Phys., 1988, 89, 5803 CrossRef CAS.
- P. J. Knowles and H.-J. Werner, Chem. Phys. Lett., 1988, 145, 514 CrossRef CAS.
- S. R. Langhoff and E. R. Davidson, Int. J. Quantum Chem., 1974, 8, 61 CrossRef CAS.
- A. Berning, M. Schweizer, H.-J. Werner, P. J. Knowles and P. Palmieri, Mol. Phys., 2000, 98, 1823 CrossRef CAS.
- H.-J. Werner, P. J. Knowles, G. Knizia, F. R. Manby, M. Schütz, et al., Molpro, version 2015.1, a package of ab initio programs, see http://www.molpro.net Search PubMed.
- MRCC, a quantum chemical program suite written by M. Kállay, Z. Rolik, I. Ladjánszki, L. Szegedy, B. Ladóczki, J. Csontos and B. Kornis, See also Z. Rolik and M. Kállay, J. Chem. Phys., 2011, 135, 104111 CrossRef PubMed , as well as: http://www.mrcc.hu.
- I. Szabó and G. Czakó, J. Phys. Chem. A, 2017, 121, 5748 CrossRef PubMed.
- D. A. Tasi, Z. Fábián and G. Czakó, J. Phys. Chem. A, 2018, 122, 5773 CrossRef CAS PubMed.
- G. Czakó, I. Szabó and H. Telekes, J. Phys. Chem. A, 2014, 118, 646 CrossRef PubMed.
- J. C. Polanyi, Science, 1987, 236, 680 CrossRef CAS PubMed.
- G. S. Hammond, J. Am. Chem. Soc., 1955, 77, 334 CrossRef CAS.
- D. Troya, G. C. Schatz, D. J. Garton, A. L. Brunsvold and T. K. Minton, J. Chem. Phys., 2004, 120, 731 CrossRef CAS PubMed.
| This journal is © the Owner Societies 2019 |