 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
A density functional theory study of the hydrogenation and reduction of the thio-spinel Fe3S4{111} surface†
Alberto
Roldan
 *a and
Nora H.
de Leeuw
*a and
Nora H.
de Leeuw
 ab
ab
aSchool of Chemistry, Cardiff University, Main Building, Park Place, Cardiff, CF10 3AT, UK. E-mail: roldanmartineza@cardiff.ac.uk
bDepartment of Earth Sciences, Utrecht University, Princetonplein 8A, 3584 CC, Utrecht, The Netherlands
First published on 17th January 2019
Abstract
The mineral greigite, Fe3S4, shows promising electro-reduction activity, especially towards carbon dioxide conversion to small organic molecules. We have employed density functional theory calculations with correction for the long-range dispersion forces to investigate the behavior of hydrogen on the greigite{111} surface. We have studied the adsorption, diffusion, surface reduction and associative (i.e. Volmer–Tafel mechanism) and molecular desorption of hydrogen as a function of its coverage. We found that (i) the H ad-atoms adsorb on S sites far from metallic centres in the topmost surface layer; (ii) the reduction of greigite by hydrogen is energetically unfavorable at any surface coverage; and (iii) molecular hydrogen evolution has a transition state at ∼0.5 eV above the energy of the reactants on Fe3S4{111}, which is very similar to the barrier found experimentally on Pt{111}. We have also determined the electrode potential under room conditions at which the H2 evolution reaction becomes energetically barrierless.
1. Introduction
Sulfides of iron, the most abundant transition metal element in the Earth's crust, frequently contain Fe and S in different oxidation states, yielding various types of natural iron sulfides. Among them, greigite is isomorphic with magnetite (Fe3O4)1 and has been associated as a catalyst in a number of biochemical reactions, for example those associated with the “iron–sulfur world” hypothesis for the origin of life.2–5 Thio-spinel crystal structures, such as greigite, resemble the reactive cubane structures (Fe4S4) found in enzymes but linked through terminal sulfides.6–8 Although most biomimetic catalysts lack the protection and long-range interactions of the protein backbone, they show interesting catalytic activity.9 Fe3S4 also has promising applications in spintronic devices,10 electrodes for lithium-ion batteries,11 drug delivery and hydrogen storage,12–14 and it has been used as a catalyst in electro-reductive experiments.15 Understanding the redox properties of this material is therefore crucial for optimising its performance, while mitigating, for example, its corrosion. The early oxidation stages of the Fe3S4 surface indicate the formation of oxide shell structures (Fe3O4), although the inner material remains a sulfide (Fe3S4).16,17 Nevertheless, the behaviour of the greigite surface under anodic potentials remains unreported. Generally, transition metal sulfides (TMS) have gained scientific interest as catalysts, in part due to their similitude to important enzymatic catalytic centres, e.g. in the H2–CO2 reaction couple.18–20 TMS such as MoS2, NiSx, RuS2 and spinel-type Mo3S4 have been tested, concluding that the TMS redox character depends on the nature of the metal atom and the sulfur coordination environment.21–26 More sophisticated catalysts such as chalcogels enhance the evolution of H2 but at very low turnover, even when doping the inorganic structure with other metals such as Ni, Co or Mo.27Accurate simulations of electrochemical processes, however, are a challenging task due to the presence of a solid–solvent interface, and multiple species dynamically interacting with the surface, e.g. ions, solvent, reactive species and the flow of electrons.28 We have therefore followed a simple approximation in which the reaction energies are plotted as a function of the variation in the work-function under a fixed external potential.29 Thus, the electronic structure calculations are related to the surface potential by the variations of the dipole.30
Based on previous research and the fact that H binds on top of low-coordinated S atoms on TMS surfaces,31–33 we have used density functional theory with a correction for the long-range dispersion forces to focus on the Fe3S4{111} surface, which has been shown to be exposed in Fe3S4 crystallites. In particular, we have analysed the H ad-atom migration, the surface reduction by either H-incorporation or by H2S formation, and the catalytic activity towards the hydrogen evolution reaction (HER) via the Tafel reaction.34
2. Computational methods
Periodic plane-wave DFT-D calculations were carried out to study the hydrogen interaction and reactivity on the greigite Fe3S4{111} surface. All calculations were performed using the Vienna Ab initio Simulation Package (VASP)35,36 with the computational details that accurately describe greigite, in full agreement with recent synchrotron radiation measurements and catalytic experiments.15,37 Hence, the ion–electron interactions were represented by the projector-augmented wave (PAW) method38 within the generalized gradient approximation (GGA) with the Perdew–Wang 91 functional39 and employing the spin interpolation formula of Vosko et al.40 All calculations included the D2 long-range dispersion correction approach by Grimme (s6 = 0.75),41 as this correction has been shown to reproduce well the interaction of the sulfides with molecules.32,33,42,43 The PBE functional and D3 long-range dispersion showed no difference with the setup used here.44 The Kohn–Sham valence states were expanded in a plane-wave basis set with a cut off at 600 eV for the kinetic energy.45 This high cut off energy ensured that no Pulay stresses occurred within the cell during relaxations. Calculations were carried out with Monkhorst–Pack46 grids of 5 × 5 × 1 K-points, which ensured electronic and ionic convergence. The geometries of all stationary points were found by the conjugate-gradient algorithm and were considered converged when the force on each ion dropped below 0.03 eV Å−1, whereas the energy threshold defining self-consistency of the electron density was set to 10−5 eV. To improve the convergence of the Brillouin-zone integrations, the partial occupancies were determined using the tetrahedron method with Blöchl correction smearing, with a set width for all calculations of 0.02 eV.The initial magnetic moment with high spin distribution describes the FeA(FeB)2S4 spinel structure with both types of Fe, i.e. octahedral (B) and tetrahedral (A), in a ferrimagnetic orientation, as reported previously.37,47 For an accurate treatment of the electron correlation in the localised d-Fe orbital, we have used the U approximation,48,49 which improves the description of local states in highly correlated systems where standard LDA and GGA functionals fail.50 A problem with this approximation is the rather empirical character of the choice of U parameter, a feature which also appears when using hybrid functionals, since the amount of Fock exchange is system-dependent.51–53 Here, we have used Ueff = 1 eV for greigite, based on the lattice parameters and the band gap as compared with the available experimental data.10,47,54
2.1 Slab model
After a full relaxation of the bulk, we prepared the Fe3S4 surfaces by cutting the bulk structure and creating slab models using the METADISE code.55 These models consider periodicity and provide the different atomic layer stacking resulting in a null dipole moment perpendicular to the surface plane.32,56 The slabs contain 56 atoms (24 Fe and 32 S) per unit cell where the atoms are placed in four layers of two Fe3S4 units. We added a vacuum width of 12 Å between periodic slabs, which is big enough to avoid interactions between the slab and its periodic images, leading to a surface area at each end of the slab of 81.0 Å2. The slab is thick enough to relax the two uppermost layers (four Fe3S4 units) keeping the bottom layers frozen to model the bulk structure. To obtain the properties of the isolated molecules, we placed them in the centre of a 15 × 16 × 17 Å3 box to avoid lateral interactions and using the same convergence criteria as in the iron sulfide systems.The calculations of the different minima provide the necessary information to estimate the thermodynamics of the reaction. A saddle point (TS) in the potential energy surface links these minima and determines the kinetics of the process. We have identified these particular points by means of the dimer method.57,58 We further confirmed the TS by a vibrational frequency analysis, where only one imaginary frequency was obtained corresponding to the reaction coordinate. Afterwards, the dimer images were relaxed to the neighbouring local minima, where in a successful search, one of the images will minimise into the initial state, and the other will become the final state.
We have calculated the binding energies of the adsorbates (EB) per number of ½ H2 molecules on the Fe3S4 surface from eqn (1),
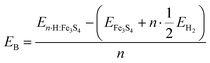 | (1) |
We carried out charge analyses using AIMS,59,60 as implemented in the Henkelman algorithm.61 Within this approach, the electron (and spin) density associated with each atom is integrated over the Bader volume of the atom in question. We can use this method to monitor changes in charges, for example as an effect of surface adsorption.
3. Results and discussion
Synthetic greigite particles mainly express the {001} and {111} surfaces,15,62 which contain two types of terminal Fe atoms derived from the tetrahedral (FeA) and the octahedral (FeB) bulk positions.63 Upon relaxation of these surfaces, cations tend to move inwards into the bulk and anions outwards, i.e. the top FeA and FeB move underneath the sulfur layer.32 Here, we have focused on the {111} surface as it has shown interesting redox properties towards the reduction of CO2.15,42,64 This surface exposes in the uppermost atomic layer an FeB and two FeA surrounded by eight S atoms per unit cell. At the surface, both FeA and FeB atoms have a formal charge of 3+.3.1 Hydrogen adsorption and diffusion on Fe3S4{111}
We have approached a single H atom on non-equivalent adsorption sites on the Fe3S4{111} surface to study its binding characteristics and found that H prefers to adsorb on S far from any surface FeB. Although the S–H distances are very similar on the different adsorption sites (dS–H ∼ 1.36 Å), the most exothermic location (EB = −0.4 eV) corresponds to sites 3 and 4 in Fig. 1, whereas site 1 on top of FeB leads to the least favourable adsorption. There, the distance FeB–H is 0.14 Å longer than the main dS–H, and its EB is endothermic by +0.7 eV. We did not find any minimum for H adsorbed on top of FeA. The S sites directly connected to FeA, i.e. 3 and 4, present a stronger basic character than the average, which is due to the distortion created by the FeA reconstruction upon relaxation of the naked surface that slightly modifies the local electronic structure. In fact, the H binding energy has a linear relation with the S electronic structure, see Fig. S2 (ESI†). Hence, the surface basicity is associated with the external electrons of the S-bands, and the more negatively charged is S, the weaker is the bond with the H atoms. | ||
| Fig. 1 Top-view representation of non-equivalent H adsorption sites on the Fe3S4{111} surface. Grey balls and sticks denote Fe cations, dark-yellow S anions and white H atoms. Numbers and arrows indicate the H position and migration direction in Table 1. | ||
We have analysed the S–H bond by charge analysis and charge density difference flux. The latter, depicted in Fig. S3 (ESI†), shows charge density accumulation between S and H, where H couples its lone electron with one from sulfur leading to a bond with covalent character. This result agrees with the charge analysis, which indicates paired electrons with no spin density and a charge transfer of 0.6 e from the sulfur to the bond. In contrast, the low stability of the FeB–H interaction is characterised by a charge transfer of 0.4 e to the H, i.e. half the charge of the FeB.
We have investigated the migration of a single H ad-atom over the Fe3S4{111} surface using both thermodynamic and kinetic arguments. Although the H position on top of the S atoms is the energetically most favourable configuration, we have also considered the FeB site to provide a more general picture. The arrows in Fig. 1 schematically represent the H migration path over the surface for the processes summarised in Table 1. The reaction energies in this table show that H migrates easily to a position far from the FeB. Although at low temperatures process A is more likely than B due to its lower energy barrier (by 0.12 eV), B leads to a more stable configuration (by 0.16 eV), which may drive the diffusion process. Once on the S sites, H can migrate to another S by overcoming an average energy barrier of 0.7 eV via a transition state on top of a sub-surface FeB.
| Process | Initial site | Final site | E A (eV) | E R (eV) | E B (eV) | D (cm2 s−1) | |
|---|---|---|---|---|---|---|---|
| A | 1 | → | 2 | 0.01 | −0.80 | −0.07 | 3.29· × 10−3 |
| B | 1 | → | 5 | 0.13 | −0.96 | −0.23 | 1.41 × 10−5 |
| C | 2 | → | 3 | 0.83 | −0.32 | −0.39 | 4.41 × 10−17 |
| D | 2 | → | 7 | 0.39 | 0.14 | 0.07 | 2.58 × 10−10 |
| E | 3 | → | 4 | 0.93 | −0.02 | −0.41 | 8.87 × 10−19 |
| F | 3 | → | 7 | 0.78 | 0.46 | 0.07 | 2.16 × 10−16 |
| G | 5 | → | 6 | 0.54 | 0.29 | 0.05 | 1.67 × 10−12 |
We have derived the H diffusion coefficient (D) on the Fe3S4{111} surface by evaluating the changes in the vibrational contribution to the energies within the limits of validity of the transition state theory.65 We used eqn (2) considering that a single displacement occurred when an H atom moved from one site to the next.
 | (2) |
The resulting diffusion coefficients indicate a hindered movement of the H ad-atom in comparison to values on transition metals,67e.g. the diffusion coefficients range from 3.35 × 10−4 to 2.2 × 10−3 cm2 s−1 on body cubic centered Fe at 233 K.68 Nevertheless, our values are in the range of diffusion on oxide surfaces with variations in acid–base character,69,70 showing the localization of the electron and the varying character of the sulfur sites according to their local electronic structure.
3.2 Hydrogen coverage on Fe3S4{111}
Actual surfaces are dynamic systems whose properties and processes depend on the concentration and types of adsorbents. The H coverage (θH) is, therefore, a factor to consider when developing a general picture of the surface character. We defined θH as the number of H atoms per S site on the surface but note that H may also adsorb on FeB only under strong conditions, i.e. high hydrogen chemical potentials. We increased θH by adding pairs of H atoms on the surface and compared the energies with a reference system: the naked slab and a number of isolated H2 molecules in the gas phase. Fig. 2 represents the EB per atom as a function of θH starting from 1 up to 8 H atoms per cell, i.e. θH = 0.125 to 1 ML. We tested the effect of increasing up to 10 H by placing the extra H on FeA and FeB, but this resulted in an endothermic step by 0.44 eV. A similar energy increment was found at θH > 1 ML on Pt{111}, which has been interpreted as a strong and repulsive interaction between H ad-atoms.70 While neighbouring H ad-atoms are interacting by less than 0.1 eV on Fe3S4{111}, we related this step of 0.44 eV with the surface electronic structure. The increment of θH polarises the surface, shown by the average sulfur charge on the surface, see Fig. S4 (ESI†), which shows how the S sites become electron-deficient at high θH, while decreasing the overall stability of the system. Hence, at high θH, the S charge density localises along the S–H bonds generating a dipole perpendicular to the surface which drives some reconstruction.56 | ||
| Fig. 2 Binding energies per atom (EB) as a function of H coverage (θH) on Fe3S4{111}. Solid line represents the logarithmic regression: EB = −0.096 + 0.4623·ln(θH + 0.3902), R = 0.99. | ||
As the number of H ad-atoms increases, the number of available adsorption sites decreases and the lateral interaction between hydrogens could become considerable. However, we have calculated the H–H interaction to be very weak (<0.1 eV), which is in good agreement with experimental values in another catalyst.71 In general, we have noted that the presence of –SH groups modifies the surface electronic structure in a way that enhances the basicity of nearby sulfur sites. The presence of polar adsorbates and solvents changes their orientation according to the generated dipole, i.e. creating a double layer model.28,32,72
3.3 Hydrogen evolution on Fe3S4{111}
As the hydrogen coverage increases on the surface, so does the probability of their recombination into molecular hydrogen. We have studied the H2 associative and molecular desorption processes from ad-atoms on S, FeA and FeB. In the first mode, the two H ad-atoms recombine as they leave the surface – the inverse process to dissociative adsorption. Commonly, H2 is adsorbed dissociatively, and its desorption may follow a similar trajectory.73 In the latter, the H2 molecule is formed on the surface prior to desorption – the inverse process to molecular adsorption and dissociation. We have summarised in Table 2, and schematically represented in Fig. S5 (ESI†), the H2 formation on the surface before desorption, i.e. molecular desorption, and the association of both H ad-atoms along the desorption process, i.e. associative desorption.| Process | Site | E A (eV) | E R (eV) | |
|---|---|---|---|---|
| 1 | MD | FeB | 0.09 | −0.79 |
| 2 | AD | FeB–S | 1.36 | −0.63 |
| 3 | AD | FeA–S | 0.17 | −0.98 |
| 4 | AD | S–S′ | 1.52 | 0.17 |
| 5 | AD | S–S′ | 0.46 | −0.48 |
| 6 | AD | S–S′ | 1.41 | 0.63 |
| 7 | AD | S–S′ | 2.09 | 0.63 |
Molecular desorption takes place only when both H atoms are adsorbed on FeB, e.g. process 1 in Table 2, which is very unlikely due to the instability of H adsorption on FeB. Examples of thermodynamically favorable associative desorption are: (i) two hydrogens on S and FeA and (ii) two hydrogens on neighbouring sulfurs, listed as processes 3 and 5 in Table 2, respectively. This latter process is exothermic by 0.48 eV, and its energy barrier (EA) is only 0.5 eV, which is similar to the barrier found experimentally on Pt{111}.74 We will focus on system 5, as it has the lowest activation barrier for the association of two H sited on the preferred S sites.
Under low H chemical potentials, i.e. low coverages, the H ad-atoms are located on top of S sites surrounding FeA, i.e. 3 and 4 in Fig. 1. While the hydrogen associative desorption on these sites is endothermic by 0.63 eV (process 7 in Table 2) an increase in the hydrogen coverage (θH) may lead to the more feasible process 5 (see Fig. S5, ESI†).
We have approximated our DFT energies (E) to the Gibbs free energies (G) by adding the zero-point energy (ZPE) and including the energy contribution from the configurational (Sconf in eqn (3)) and the vibrational (Svib in eqn (4)) entropies. The differential configurational entropy, dSconf/dθH, has been found to compare well with Monte Carlo simulations on hexagonal surfaces, such as the S site distributions,75–77 whereas the vibrational entropy is commonly described by a Boltzmann distribution.78 For the gas phase product (H2), we have introduced the energy variation with temperature using the specific heat (Cp) and the rotational, translational, and vibrational energy contributions from the entropy (S) derived from the DFT partition functions. We have considered the electronic partition function as the ground state. This approach led to a relative error between the resulting H2 free energy (G) and the thermochemistry data from ref. 79, which is smaller than 0.09% in a range of temperatures from 250 to 700 K, see Fig. S6 (ESI†).
| Sconf = −kB(θH·ln(θH) + (1 − θH)·ln(1 − θH)) | (3) |
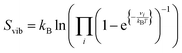 | (4) |
As described in the hydrogen coverage section, an increment of θH polarises the surface, which affects the surface work function (ϕ)–the minimum work required to extract an electron from the top of the valence band of the uncharged surface and place it in a vacuum. We have related the changes in the work function upon evolution of H2 (final states) to an electrode potential at zero-charge (U = ϕ − ϕNHE) relative to a normal hydrogen electrode (NHE) of 4.5 V,28,30 which is within the range found in the literature, 4.4–4.9 V.78 We have derived a Tafel transfer coefficient of 0.62, which expresses the fraction of the overpotential that helps to lower the activation energy of the homolytic H2 formation and the potential affecting the current density. Fig. 3B indicates how the H ad-atoms on the Fe3S4{111} surface accumulate under cathodic potentials–solid line in Fig. 3. Although the H2 evolution becomes thermodynamically favourable below 0.35 V (vs. NHE)–the H2 evolution is lower in energy than adsorption–, it is kinetically hindered–big difference between ΔGTS and ΔGB–until U = −0.4 V (vs. NHE), where the process becomes barrierless. Indeed, bubbling has been observed at potentials of 0.6 V (vs. NHE) at room pressure and temperature.15
3.4 Fe3S4{111} surface reduction
4. Conclusions
We have performed a systematic study of common processes involving hydrogen on greigite. We have used DFT-based calculations with the PW91 exchange–correlation potential, including dispersion through the Grimme's D2 approach and the on-site Hubbard correction (Ueff), to evaluate H adsorption and diffusion, H2 evolution by ad-atoms recombination, and reduction of the surface by either H-incorporation or H2S formation on the Fe3S4{111}. We found that H adsorbs preferentially on surface S-sites far from the top surface FeB, which distorts the nearby electronic structure, making the S-sites more acidic. Thus, the H ad-atoms diffuse across the {111} surface along paths that avoid low-coordinated FeB. On the Fe3S4{111} surface, the strongest mono-atomic binding energy is −0.4 eV, which becomes weaker with coverage, following a logarithmic trend up to a θH of 1 ML; above this coverage, there is a trend discontinuity, not only due to the H–H interaction (<0.1 eV) but because of changes in the surface polarisation. The reduction of the Fe3S4{111} surface by incorporation of H into the thio-spinel structure is an endothermic process by more than 0.8 eV. H2S formation is in thermodynamic equilibrium with two contiguous HS, but the process is kinetically prevented between 0.25 and 1 ML (EA ∼ 2 eV). The H2 evolution reaction takes place via associative desorption from distinctive sites, and both the barrier and the reaction energies decrease with increasing H-coverage: the reaction becomes thermodynamically favourable at coverage higher than 0.35 ML. We have also related the θH with the electrode potential via the work function and found that at bias of 0.4 V vs. NHE the H2 evolution becomes thermodynamically favourable but kinetically controlled. At potentials lower than −0.45 V, the activation energy becomes negligible and the Tafel process becomes very fast and exothermic.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We acknowledge the Engineering & Physical Sciences Research Council (grants EP/K035355/1 and EP/K035355/2) for funding. This work made use of the ARCHER facilities, the UK's national high-performance computing service, which is provided by UoE HPCx Ltd at the University of Edinburgh, Cray Inc. and NAG Ltd, funded by the Office of Science and Technology through EPSRC's High-End Computing Programme and provided via our membership of the HPC Materials Chemistry Consortium (EPSRC EP/L000202). The authors also acknowledge the use of the UCL Legion High-Performance Computing Facility and the Advanced Research Computing@Cardiff (ARCCA) at Cardiff University, and associated support services, in the completion of this work. All data created during this research are openly available from the University of Cardiff Research Portal at http://doi.org/10.17035/d.2018.0053780764.References
- A. Roldan, D. Santos-Carballal and N. H. de Leeuw, A comparative DFT study of the mechanical and electronic properties of greigite Fe3S4 and magnetite Fe3O4, J. Chem. Phys., 2013, 138, 204712 CrossRef CAS PubMed.
- S. Mann, N. H. C. Sparks, R. B. Frankel, D. A. Bazylinski, H. W. Jannasch, D. A. Bazylinski and H. W. Jannasch, Biomineralization of ferrimagnetic greigite (Fe3S4) and iron pyrite (FeS2) in a magnetotactic bacterium, Nature, 1990, 343, 258–261 CrossRef CAS.
- T. Kasama, M. Posfai, R. K. K. Chong, A. P. Finlayson, P. R. Buseck, R. B. Frankel and R. E. Dunin-Borkowski, Magnetic properties, microstructure, composition, and morphology of greigite nanocrystals in magnetotactic bacteria from electron holography and tomography, Am. Mineral., 2006, 91, 1216–1229 CrossRef CAS.
- M. Posfai, P. R. Buseck, D. A. Bazylinski and R. B. Frankel, Iron sulfides from magnetotactic bacteria: structure, composition, and phase transitions, Am. Mineral., 1998, 83, 1469–1481 CrossRef CAS.
- M. Posfai, P. R. Buseck, D. A. Bazylinski and R. B. Frankel, Reaction sequence of iron sulfide minerals in bacteria and their use as biomarkers, Science, 1998, 280, 880–883 CrossRef CAS PubMed.
- H. Dobbek, V. Svetlitchnyi, L. Gremer, R. Huber and O. Meyer, Crystal structure of a carbon monoxide dehydrogenase reveals a Ni-4Fe-5S cluster, Science, 2001, 293, 1281–1285 CrossRef CAS PubMed.
- M. Dorr, J. Kassbohrer, R. Grunert, G. Kreisel, W. A. Brand, R. A. Werner, H. Geilmann, C. Apfel, C. Robl and W. Weigand, A possible prebiotic formation of ammonia from dinitrogen on iron sulfide surfaces, Angew. Chem., Int. Ed., 2003, 42, 1540–1543 CrossRef CAS PubMed.
- U. P. Apfel and W. Weigand, Efficient activation of the greenhouse gas CO2, Angew. Chem., Int. Ed., 2011, 50, 4262–4264 CrossRef CAS PubMed.
- B. D. Yuhas, C. Prasittichai, J. T. Hupp and M. G. Kanatzidis, Enhanced Electrocatalytic Reduction of CO2 with Ternary Ni-Fe4S4 and Co-Fe4S4-Based Biomimetic Chalcogels, J. Am. Chem. Soc., 2011, 133, 15854–15857 CrossRef CAS PubMed.
- B. Zhang, G. A. de Wijs and R. A. de Groot, Switchable Fermi surface sheets in greigite, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 20404–20406 CrossRef.
- X. Jia, Z. Chen, X. Cui, Y. Peng, X. Wang, G. Wang, F. Wei and Y. Lu, Building robust architectures of carbon and metal oxide nanocrystals toward high-performance anodes for lithium-ion batteries, ACS Nano, 2012, 6, 9911–9919 CrossRef CAS PubMed.
- F. Cao, W. Hu, L. Zhou, W. Shi, S. Song, Y. Lei, S. Wang and H. Zhang, 3D Fe3S4 flower-like microspheres: high-yield synthesis via a biomolecule-assisted solution approach, their electrical, magnetic and electrochemical hydrogen storage properties, Dalton Trans., 2009, 9246–9252 RSC.
- Y.-S. Chang, S. Savitha, S. Sadhasivam, C.-K. Hsu and F.-H. Lin, Fabrication, characterization, and application of greigite nanoparticles for cancer hyperthermia, J. Colloid Interface Sci., 2011, 363, 314–319 CrossRef CAS PubMed.
- M. Feng, Y. Lu, Y. Yang, M. Zhang, Y.-J. Xu, H.-L. Gao, L. Dong, W.-P. Xu and S.-H. Yu, Bioinspired greigite magnetic nanocrystals: chemical synthesis and biomedicine applications, Sci. Rep., 2013, 3, 2994 CrossRef PubMed.
- A. Roldan, N. Hollingsworth, A. Roffey, H.-U. Islam, J. B. M. Goodall, C. R. A. Catlow, J. A. Darr, W. Bras, G. Sankar, K. B. Holt, G. Hogarth and N. H. de Leeuw, Bio-inspired CO2 conversion by iron sulfide catalysts under sustainable conditions, Chem. Commun., 2015, 51, 7501–7504 RSC.
- S. N. A. Zakaria, N. Hollingsworth, H. U. Islam, A. Roffey, D. Santos-Carballal, A. Roldan, W. Bras, G. Sankar, G. Hogarth, K. B. Holt and N. H. de Leeuw, Insight into the Nature of Iron Sulfide Surfaces During the Electrochemical Hydrogen Evolution and CO2 Reduction Reactions, ACS Appl. Mater. Interfaces, 2018, 10, 32078–32085 CrossRef CAS PubMed.
- D. Santos-Carballal, A. Roldan and N. H. de Leeuw, Early Oxidation Processes on the Greigite Fe3S4 (001) Surface by Water: A Density Functional Theory Study, J. Phys. Chem. C, 2016, 120, 8616–8629 CrossRef CAS.
- Y. Nicolet, P. Amara, J. M. Mouesca and J. C. Fontecilla-Camps, Unexpected electron transfer mechanism upon AdoMet cleavage in radical SAM proteins, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 14867–14871 CrossRef CAS PubMed.
- T. Hayashi and A. A. Stuchebrukhov, Electron tunneling in respiratory complex I, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 19157–19162 CrossRef CAS PubMed.
- H. Seino and M. Hidai, Catalytic functions of cubane-type M4S4 clusters, Chem. Sci., 2011, 2, 847–857 RSC.
- M. Neurock and R. A. Vansanten, Theory of Carbon–Sulfur Bond Activation by Small Metal Sulfide Particles, J. Am. Chem. Soc., 1994, 116, 4427–4439 CrossRef CAS.
- F. Frechard and P. Sautet, Chemisorption of H-2 and H2S on the (100) surface of RuS2: an ab initio theoretical study, Surf. Sci., 1997, 389, 131–146 CrossRef CAS.
- A. Travert, H. Nakamura, R. A. van Santen, S. Cristol, J. F. Paul and E. Payen, Hydrogen activation on Mo-based sulfide catalysts, a periodic DFT study, J. Am. Chem. Soc., 2002, 124, 7084–7095 CrossRef CAS PubMed.
- X. D. Wen, T. Zeng, B. T. Teng, F. Q. Zhang, Y. W. Li, H. G. Wang and H. J. Jiao, Hydrogen adsorption on a Mo(27)S(54)cluster: a density functional theory study, J. Mol. Catal. A: Chem., 2006, 249, 191–200 CrossRef CAS.
- M. V. Bollinger, K. W. Jacobsen and J. K. Nørskov, Atomic and electronic structure of MoS2 nanoparticles, Phys. Rev. B, 2003, 67, 085410 CrossRef.
- Y. D. Hou, B. L. Abrams, P. C. K. Vesborg, M. E. Bjorketun, K. Herbst, L. Bech, A. M. Setti, C. D. Damsgaard, T. Pedersen, O. Hansen, J. Rossmeisl, S. Dahl, J. K. Norskov and I. Chorkendorff, Bioinspired molecular co-catalysts bonded to a silicon photocathode for solar hydrogen evolution, Nat. Mater., 2011, 10, 434–438 CrossRef CAS PubMed.
- B. D. Yuhas, A. L. Smeigh, A. P. Douvalis, M. R. Wasielewski and M. G. Kanatzidis, Photocatalytic Hydrogen Evolution from FeMoS-Based Biomimetic Chalcogels, J. Am. Chem. Soc., 2012, 134, 10353–10356 CrossRef CAS PubMed.
- A. Roldan, Frontiers in first principles modelling of electrochemical simulations, Curr. Opin. Electrochem., 2018, 10, 1–6 CrossRef CAS.
- J. Rossmeisl, E. Skúlason, M. E. Björketun, V. Tripkovic and J. K. Nørskov, Modeling the electrified solid–liquid interface, Chem. Phys. Lett., 2008, 466, 68–71 CrossRef CAS.
- S. Trasatti, Structure of the Metal Electrolyte Solution Interface – New Data for Theory, Electrochim. Acta, 1991, 36, 1657–1658 CrossRef.
- S. Haider, A. Roldan and N. H. de Leeuw, Catalytic Dissociation of Water on the (001), (011), and (111) Surfaces of Violarite, FeNi2S4: A DFT-D2 Study, J. Phys. Chem. C, 2014, 118, 1958–1967 CrossRef CAS.
- A. Roldan and N. H. de Leeuw, A kinetic model of water adsorption, clustering and dissociation on the Fe3S4{001} surface, Phys. Chem. Chem. Phys., 2017, 19, 12045–12055 RSC.
- A. Roldan and N. H. de Leeuw, Catalytic water dissociation by greigite Fe3S4 surfaces: density functional theory study, Proc. R. Soc. A, 2016, 472, 20160080 CrossRef CAS PubMed.
- J. Tafel, Polarization in cathodic hydrogen evolution, Z. Phys. Chem., 1905, 50, 641–712 CAS.
- G. Kresse and J. Furthmüller, Efficiency of ab initio total energy calculations for metals and semiconductors using a plane-wave basis set, Comput. Mater. Sci., 1996, 6, 15 CrossRef CAS.
- G. Kresse and J. Hafner, Ab initio molecular dynamics for liquid metals, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558 CrossRef CAS.
- D. Santos-Carballal, A. Roldan, R. Grau-Crespo and N. H. de Leeuw, First-principles study of the inversion thermodynamics and electronic structure of FeM2X4 (thio)spinels (M = Cr, Mn, Co, Ni; X = O,S), Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 195106 CrossRef.
- G. Kresse and D. Joubert, From ultrasoft pseudopotentials to the projector augmented-wave method, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758 CrossRef CAS.
- J. P. Perdew, J. Chevary, S. Vosko, K. A. Jackson, M. R. Pederson, D. J. Singh and C. Fiolhais, Erratum: atoms, molecules, solids, and surfaces: Applications of the generalized gradient approximation for exchange and correlation, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 48, 4978 CrossRef.
- S. H. Vosko, L. Wilk and M. Nusair, Accurate spin-dependent electron liquid correlation energies for local spin-density calculations – A critical analysis, Can. J. Phys., 1980, 58, 1200–1211 CrossRef CAS.
- S. Grimme, Semiempirical GGA-type density functional constructed with a long-range dispersion correction, J. Comput. Chem., 2006, 27, 1787–1799 CrossRef CAS PubMed.
- A. Roldan and N. H. de Leeuw, Selective hydrogenation of CO on Fe3S4{111}: a computational study, Faraday Discuss., 2017, 197, 325–336 RSC.
- A. Roldan and N. H. de Leeuw, Methanol formation from CO2 catalyzed by Fe3S4{111}: formate versus hydrocarboxyl pathways, Faraday Discuss., 2016, 188, 161–180 RSC.
- S. Posada-Pérez, D. Santos-Carballal, U. Terranova, A. Roldan, F. Illas and N. H. de Leeuw, CO2 interaction with violarite (FeNi2S4) surfaces: a dispersion-corrected DFT study, Phys. Chem. Chem. Phys., 2018, 20, 20439–20446 RSC.
- N. D. Mermin, Thermal Properties of the Inhomogeneous Electron Gas, Phys. Rev., 1965, 137, A1441–A1443 CrossRef.
- H. J. Monkhorst and J. D. Pack, Special Points for Brillouin-Zone Integrations, Phys. Rev. B: Condens. Matter Mater. Phys., 1976, 13, 5188–5192 CrossRef.
- A. J. Devey, R. Grau-Crespo and N. H. de Leeuw, Electronic and magnetic structure of Fe3S4: GGA+U investigation, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 195126 CrossRef.
- V. I. Anisimov, M. A. Korotin, J. Zaanen and O. K. Andersen, Spin Bags, Polarons, and Impurity Potentials in La2-Xsrxcuo4 from 1st Principles, Phys. Rev. Lett., 1992, 68, 345–348 CrossRef CAS PubMed.
- S. L. Dudarev, G. A. Botton, S. Y. Savrasov, C. J. Humphreys and A. P. Sutton, Electron-energy-loss spectra and the structural stability of nickel oxide: an LSDA+U study, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 57, 1505–1509 CrossRef CAS.
- I. D. R. Moreira, F. Illas and R. L. Martin, Effect of Fock exchange on the electronic structure and magnetic coupling in NiO, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 65, 155102 CrossRef.
- I. Ciofini, F. Illas and C. Adamo, Performance of the tau-dependent functionals in predicting the magnetic coupling of ionic antiferromagnetic insulators, J. Chem. Phys., 2004, 120, 3811–3816 CrossRef CAS PubMed.
- F. Illas and R. L. Martin, Magnetic coupling in ionic solids studied by density functional theory, J. Chem. Phys., 1998, 108, 2519–2527 CrossRef CAS.
- D. Munoz, N. M. Harrison and F. Illas, Electronic and magnetic structure of LaMnO3 from hybrid periodic density-functional theory, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 69, 85115–85124 CrossRef.
- J. Wang, S. H. Cao, W. Wu and G. M. Zhao, The Curie temperature and magnetic exchange energy in half-metallic greigite Fe3S4, Phys. Scr., 2011, 83, 45702–45705 CrossRef.
- G. W. Watson, E. T. Kelsey, N. H. de Leeuw, D. J. Harris and S. C. Parker, Atomistic simulation of dislocations, surfaces and interfaces in MgO, J. Chem. Soc., Faraday Trans., 1996, 92, 433 RSC.
- P. W. Tasker, The stability of ionic crystal surfaces, J. Phys. C: Solid State Phys., 1979, 12, 4977–4984 CrossRef CAS.
- G. Henkelman and H. Jonsson, A dimer method for finding saddle points on high dimensional potential surfaces using only first derivatives, J. Chem. Phys., 1999, 111, 7010–7022 CrossRef CAS.
- A. Heyden, A. T. Bell and F. J. Keil, Efficient methods for finding transition states in chemical reactions: comparison of improved dimer method and partitioned rational function optimization method, J. Chem. Phys., 2005, 123, 224101 CrossRef PubMed.
- E. Sanville, S. D. Kenny, R. Smith and G. Henkelman, Improved grid-based algorithm for Bader charge allocation, J. Comput. Chem., 2007, 28, 899–908 CrossRef CAS PubMed.
- R. F. W. Bader, Atoms in molecules, Acc. Chem. Res., 1985, 18, 9–15 CrossRef CAS.
- G. Henkelman, A. Arnaldsson and H. Jonsson, A fast and robust algorithm for Bader decomposition of charge density, Comput. Mater. Sci., 2006, 36, 354–360 CrossRef.
- L. Chang, A. P. Roberts, Y. Tang, B. D. Rainford, A. R. Muxworthy and Q. Chen, Fundamental magnetic parameters from pure synthetic greigite (Fe3S4), J. Geophys. Res., 2008, 113, 1–16 CrossRef.
- D. Santos-Carballal, A. Roldan, R. Grau-Crespo and N. H. de Leeuw, A DFT study of the structures, stabilities and redox behaviour of the major surfaces of magnetite Fe3O4, Phys. Chem. Chem. Phys., 2014, 16, 21082–21097 RSC.
- A. Roldan and N. H. de Leeuw, Methanol formation from CO2 catalyzed by Fe3S4{111}: formate versus hydrocarboxyl pathways, Faraday Discuss., 2016, 188, 161–180 RSC.
- H. Eyring, The Activated Complex and the Absolute Rate of Chemical Reactions, Chem. Rev., 1935, 17, 65–77 CrossRef CAS.
- A. Einstein and R. Fürth, Investigations on the Theory of the Brownian Movement, Dover Publications, 1956 Search PubMed.
- L. Kristinsdóttir and E. Skúlason, A systematic DFT study of hydrogen diffusion on transition metal surfaces, Surf. Sci., 2012, 606, 1400–1404 CrossRef.
- X. Shen, J. Chen, Y. M. Sun and T. Liang, Hydrogen diffusion on Fe surface and into subsurface from first principles, Surf. Sci., 2016, 654, 48–55 CrossRef CAS.
- A. B. Belonoshko, A. Rosengren, Q. Dong, G. Hultquist and C. Leygraf, First-principles study of hydrogen diffusion in α-Al2O3 and liquid alumina, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 69, 024302 CrossRef.
- C. Chen, H. Yu and S. Zheng, First-principles study of hydrogen diffusion mechanism in Cr2O3, Sci. China: Technol. Sci., 2011, 54, 88–94 CrossRef CAS.
- G. Jerkiewicz, Hydrogen sorption at/in electrodes, Prog. Surf. Sci., 1998, 57, 137–186 CrossRef CAS.
- W. Schmickler and R. Guidelli, Ionic adsorption and the surface dipole potential, J. Electroanal. Chem. Interfacial Electrochem., 1987, 235, 387–392 CrossRef CAS.
- IUPAC Compendium of Chemical Terminology, ed. M. Nič, J. Jirát, B. Košata, A. Jenkins and A. McNaught, IUPAC, Research Triangle Park, NC, 2009 Search PubMed.
- G. S. Karlberg, T. F. Jaramillo, E. Skúlason, J. Rossmeisl, T. Bligaard and J. K. Nørskov, Cyclic Voltammograms for H on Pt(111) and Pt(100) from First Principles, Phys. Rev. Lett., 2007, 99, 126101 CrossRef CAS PubMed.
- G. S. Karlberg, T. F. Jaramillo, E. Skúlason, J. Rossmeisl, T. Bligaard and J. K. Nørskov, Cyclic Voltammograms for H on Pt(111) and Pt(100) from First Principles, Phys. Rev. Lett., 2007, 99, 126101 CrossRef CAS PubMed.
- E. Skúlason, G. S. Karlberg, J. Rossmeisl, T. Bligaard, J. Greeley, H. Jónsson and J. K. Nørskov, Density functional theory calculations for the hydrogen evolution reaction in an electrochemical double layer on the Pt(111) electrode, Phys. Chem. Chem. Phys., 2007, 9, 3241–3250 RSC.
- E. Skúlason, V. Tripkovic, M. E. Björketun, S. Gudmundsdóttir, G. Karlberg, J. Rossmeisl, T. Bligaard, H. Jónsson and J. K. Nørskov, Modeling the Electrochemical Hydrogen Oxidation and Evolution Reactions on the Basis of Density Functional Theory Calculations, J. Phys. Chem. C, 2010, 114, 18182–18197 CrossRef.
- I. Chorkendorff and J. W. Niemantsverdriet, Concepts of Modern Catalysis and Kinetics, Wiley-VCH, Weinheim, FRG, 2003 Search PubMed.
- M. W. J. Chase, Journal of Physical and Chemical Reference Data. Monograph No. 9. NIST-JANAF Thermochemical Tables, 1998, p. 1951.
Footnote |
| † Electronic supplementary information (ESI) available: Details of the model used in this paper, the schematic representation of the pathways, the relation between S-band and EB, H-coverage vs. local charge of sulfur in the pristine surface, as well as the effect on the derived potential at a neutral charge. See DOI: 10.1039/c8cp06371k |
| This journal is © the Owner Societies 2019 |


