Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Interfacial premelting of ice in nano composite materials†
Hailong
Li
 a,
Markus
Bier
a,
Markus
Bier
 bcg,
Julian
Mars
bcg,
Julian
Mars
 ad,
Henning
Weiss
a,
Ann-Christin
Dippel
ad,
Henning
Weiss
a,
Ann-Christin
Dippel
 e,
Olof
Gutowski
e,
Veijo
Honkimäki
f and
Markus
Mezger
e,
Olof
Gutowski
e,
Veijo
Honkimäki
f and
Markus
Mezger
 *ad
*ad
aMax Planck Institute for Polymer Research, Ackermannweg 10, 55128 Mainz, Germany. E-mail: mezger@mpip-mainz.mpg.de
bMax Planck Institute for Intelligent Systems, Heisenbergstr. 3, 70569 Stuttgart, Germany
cInstitute for Theoretical Physics IV, University of Stuttgart, Pfaffenwaldring 57, 70569 Stuttgart, Germany
dInstitute of Physics, Johannes Gutenberg University Mainz, Staudingerweg 10, 55128 Mainz, Germany
eDeutsches Elektronen-Synchrotron DESY, Notkestr. 85, 22607 Hamburg, Germany
fESRF-The European Synchrotron, Avenue des Martyrs 71, 38043 Grenoble Cedex 9, France
gFaculty of Applied Natural Sciences and Humanities, University of Applied Sciences Würzburg-Schweinfurt, Ignaz-Schön-Straße 11, 97421 Schweinfurt, Germany
First published on 7th November 2018
Abstract
The interfacial premelting in ice/clay nano composites was studied by high energy X-ray diffraction. Below the melting point of bulk water, the formation of liquid water was observed for the ice/vermiculite and ice/kaolin systems. The liquid fraction is gradually increasing with temperature. For both minerals, similar effective premelting layer thicknesses of 2–3 nm are reached 3 K below the bulk melting point. For the quantitative description of the molten water fraction in wet clay minerals we developed a continuum model for short range interactions and arbitrary pore size distributions. This model quantitatively describes the experimental data over the entire temperature range. Model parameters were obtained by fitting using a maximum entropy (MaxEnt) approach. Pronounced differences in the deviation from Antonow's rule relating interfacial free energy between ice, water, and clay are observed for the charged vermiculite and uncharged kaolin minerals. The resultant parameters are discussed in terms of their ice nucleation efficiency. Using well defined and characterized ice/clay nano composite samples, this work bridges the gap between studies on single crystalline ice/solid model interfaces and naturally occurring soils and permafrost.
1 Introduction
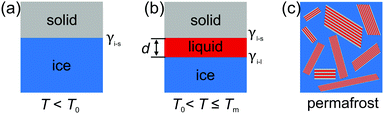
Interface induced premelting of ice has important implications for environmental and technical processes. The formation of this liquid water layer at ice/solid interfaces contributes to the low friction observed on ice surfaces.1 In addition, most of the fresh water on earth is contained in ground ice and permafrost soil. The material properties of these composites strongly depend on the ice/solid interfacial properties.2 Already in 1859, Faraday proposed the existence of a liquid-like layer at ice surfaces.3 However, despite its importance and the amount of research devoted to the understanding of the surface and interfacial premelting of ice, the formation mechanism of this liquid layer is still under debate.4–6As of today, different physical effects contributing to the interfacial premelting phenomenon have been identified.5,7 In ice composites, the most relevant ones are the intrinsic interfacial melting, impurities, confinement, and geometry effects (Fig. 1). For non-planar interfaces such as in ice nano-crystals,8 nano-pores,9 and spherical nano-powders10 the geometry of the ice/water phase boundary plays an important role. Here, the Gibbs–Thomson effect leads to a melting point depression proportional to the mean curvature of the phase boundary.7 Confinement leads to a hysteresis in the freezing and melting process.11,12 Most impurities such as ions have a lower solubility in ice compared to liquid water. These impurities will be expelled from the ice phase. Their concentration in the remaining liquid phase will therefore gradually lower its melting point.13 Finally, the intrinsic interfacial premelting and the grain boundary melting of a material are governed by the thickness dependent balance between the ice/liquid and the liquid/solid interfacial tension.14
Since the first observations by Faraday, several experimental techniques have been employed to disentangle these contributions to the premelting mechanism for different ice interfaces. Well defined, planar, single crystalline ice surfaces and ice/solid interfaces were investigated by glancing angle X-ray scattering,15 X-ray reflectivity,16–18 X-ray photoemission spectroscopy,19 sum frequency generation spectroscopy,20 and molecular dynamics simulations.21,22 Premelting in nanosized ice/solid composites was studied by thermodynamic measurements,23,24 X-ray25 and neutron diffraction,26 quasi elastic neutron scattering,27 NMR,28 and time-domain reflectometry.29 However, the liquid layer thicknesses obtained by the different experimental techniques and computer simulations differ by almost two orders of magnitude.5,6 In particular, for the class of ice composites, most studies focused on the premelting in naturally occurring samples from permafrost regions with complex composition and morphology.30,31 In general, this precludes a quantitative discussion of the intrinsic premelting mechanisms in terms of physical models. This led to the development of semi-empirical descriptions24 rather than unifying theories as discovered for premelting at free surfaces.32 Thus, experimental results on well defined model systems are essential to advance the physical understanding of interfacial premelting at buried interfaces and inside slit pore confinement.
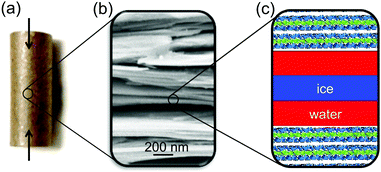
Here, we present a high energy X-ray diffraction (XRD) study of the interfacial melting in ice/vermiculite and ice/kaolin composites. Vermiculite and kaolin are phyllosilicate clay minerals, forming planar platelets with a large aspect ratio and a large specific surface area (Fig. 2). The paper is structured as follows: In Section 2 we introduce a premelting model for water and ice inside slit pores with specified size distributions. In Section 3 we report the preparation and characterization of the nano composite materials. Well defined vermiculite samples of high purity were obtained by chemical processing of the natural mineral. This suppresses geometry and impurity driven effects. The high energy X-ray diffraction experiments and data processing are described in Sections 3.2 and 4.1. The growth law of the effective premelting layer thickness vs. temperature, ![[d with combining macron]](https://www.rsc.org/images/entities/i_char_0064_0304.gif) (T), is calculated from the scattering data and clay powder properties. The quantitative analysis of the experimentally obtained growth law using the maximum entropy (MaxEnt) approach is described in Section 4.2. In Section 5 we discuss the parameters extracted from the experimental data. From comparison between the results obtained for charged vermiculite and uncharged kaolin clays we extract information on the relevant molecular interactions governing the intrinsic interfacial melting mechanism.
(T), is calculated from the scattering data and clay powder properties. The quantitative analysis of the experimentally obtained growth law using the maximum entropy (MaxEnt) approach is described in Section 4.2. In Section 5 we discuss the parameters extracted from the experimental data. From comparison between the results obtained for charged vermiculite and uncharged kaolin clays we extract information on the relevant molecular interactions governing the intrinsic interfacial melting mechanism.
2 Premelting in slit pore structures
2.1 Premelting at semi-infinite planar interfaces
Near interfaces, intermolecular interactions differ from bulk. Locally, these differences can induce phase transitions such as surface melting and surface freezing. The thermodynamics of these interface induced phase transitions can be described within the framework of classical wetting theory.33,34 In the special case of interfacial premelting adjacent to a solid (s), a liquid layer (l) is wetting its crystalline ice phase (i). The growth law of the premelting layer thickness d(T) is determined by the balance between the effective thickness-dependent interfacial free energy γ(d) and the entropy of the liquid relative to the crystalline ice.5,33–36 For short-range forces the interfacial free energy γ(d) exhibits an exponential asymptotic decay, which can be approximated by the following empirical form:| γ(d) = γi−s + φ(d)Δγ, | (1) |
| φ(d) = 1 − e−d/λ. | (2) |
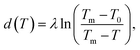 | (3a) |
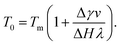 | (3b) |
2.2 Decay length and bulk correlations
Based on a Landau–Ginzburg model for a non-ordering surface phase transition, Lipowsky proposed that in the generic case the decay length λ of the surface free energy γ(d) and the bulk correlation length ξ of the liquid are identical.37,38 In eqn (2) the coupling between the (i–l) and (l–s) interfaces over the distance d leading to the gradual change in the interfacial free energy γ(d) is mediated via the correlations in the interfacial liquid layer. Given an effective intermolecular potential of finite range, the envelope of the two point correlation function in a bulk liquid asymptotically decays with r−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−r/ξ) as r → ∞.39,40
exp(−r/ξ) as r → ∞.39,40
At surfaces and buried interfaces, as is expressed by the Yvon equation,40 these correlations drive an interfacial profile that decays with exp(−r/ξ).41 Hence, the decay length λ in the growth given by eqn (3) is linked to the bulk correlation length ξ of the liquid.
Information on ξ is contained in the liquid structure factor. It can be determined from MD simulations, or from X-ray or neutron scattering. From high precision scattering data42–45 we extract λ = ξ = 2.42 Å for the bulk correlation length introduced in eqn (2) (Section A, ESI†). Temperature changes lead to slight variation in the X-ray scattering patterns,46 mainly affecting the periodicity.
2.3 Premelting in slit pores
In contrast to semi-infinite ice/solid interfaces (Fig. 1b) premelting in clay minerals occurs in slit pores (Fig. 2). In order to model premelting in such geometries, we first consider a single pore of width D in between two parallel planar solid substrates filled with water at the reduced temperature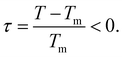 | (4) |
Two different premelting configurations are conceivable. Firstly, the slit pore can be partially molten. In this case, layers of liquid water of thickness d ∈ [0, 1/2D) cover each solid substrate (Fig. 3a). The free energy of the liquid layers F(d) per substrate area A is obtained from eqn (1) and (2):
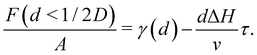 | (5) |
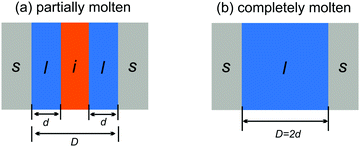 | ||
| Fig. 3 Partially (a) and completely (b) molten case of liquid water (l) and ice (i) confined in a slit pore made of two solids (s) spaced by a distance D. | ||
The first term on the right-hand side of eqn (5) accounts for the free energy of the liquid/solid and the ice/liquid interfaces. The second term describes the free energy increase due to the premelting layers of bulk metastable liquid water being formed instead of bulk stable ice.
In the second case, the slit pore is completely molten i.e. d = 1/2D. Here, liquid water fills the entire pore such that no ice/liquid interfaces are present (Fig. 3b). Then the free energy per interfacial area is given by
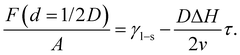 | (6) |
For reduced temperatures τ < 0, the equilibrium layer thickness
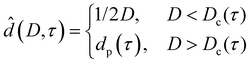 | (7) |
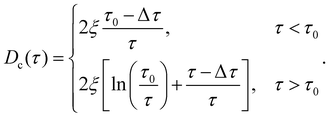 | (8) |
In the case of partial premelting, an equilibrium water layer thickness
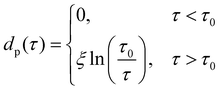 | (9) |
In analogy to eqn (3b), the reduced onset temperature
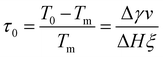 | (10) |
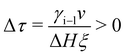 | (11) |
To include interface coupling via long-range van der Waals forces,47–50eqn (2) is modified. However, the procedure described here for interactions dominated by exponentially decaying effective short-range forces can be followed in an analog way.
2.4 Pore size distribution
For slit- or wedge-shaped pores with size distribution P(D) the effective growth law![[d with combining macron]](https://www.rsc.org/images/entities/i_char_0064_0304.gif) (T) of the liquid water layer thickness with temperature is expected to differ from the semi-infinite case discussed in Section 2.1. This particularly holds true for the premelting in clay minerals determined by X-ray scattering reported in Section 4.
(T) of the liquid water layer thickness with temperature is expected to differ from the semi-infinite case discussed in Section 2.1. This particularly holds true for the premelting in clay minerals determined by X-ray scattering reported in Section 4.
Let P(D) denote the probability density of a surface element of the substrate walls to belong to a pore of width D. Using eqn (7), the effective layer thickness ![[d with combining macron]](https://www.rsc.org/images/entities/i_char_0064_0304.gif) (T) at temperature T can be expressed as
(T) at temperature T can be expressed as
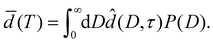 | (12) |
In Section 4.2 this relation is inverted to obtain the pore size distribution P(D) from expermimetally determined effective water layer thicknesses ![[d with combining macron]](https://www.rsc.org/images/entities/i_char_0064_0304.gif) (T) by a MaxEnt approach.
(T) by a MaxEnt approach.
3 Experimental
3.1 Sample preparation
Charged vermiculite nano-platelets were prepared from thermally exfoliated natural vermiculite (Sigma Aldrich) by a physiochemical process. Gross impurities were removed by iteratively dispersing the raw material in deionized water and removing dense minerals by sedimentation. A slurry of 5 wt% vermiculite in H2O2 solution (15 wt%) was stirred at 50 °C for one hour to promote exfoliation.51 Motivated by the RCA standard cleaning procedure,52 the H2O2 slurry was then sonicated for 30 min in an alkaline environment (2 wt% NH3), followed by stirring in an acidic solution (5 wt% HCl). The alkaline treatment further increases the surface area by zeta potential induced exfoliation of the vermiculite sheets and effectively reduces organic contaminants. The acidic treatment removes Fe2 + and Mg2 + ions from the surface. Cations at the vermiculite surface were exchanged with K+ by repeated dispersion in 1 mol L−1 KCl solution to limit swelling.53 Excess ions were removed by multiple subsequent dispersion in deionized water and filtering. Kaolin powder (Acros Organics) with neutral surface charge was used as received (ID31 sample) or purified by dispersion/filtering cycles (P07 sample). Properties of the different samples are summarized in Table 1.![[D with combining macron]](https://www.rsc.org/images/entities/i_char_0044_0304.gif) sa, and surface free ion concentration cs
sa, and surface free ion concentration cs
| BL | Vermiculite | Kaolin | |
|---|---|---|---|
| ρ | 2.63 g cm−3 | 2.70 g cm−3 | |
| s | 36.4 m2 g−1 | 10.9 m2g−1 | |
| L | 20.9 nm | 68.0 nm | |
| w m | ID31 | 27 wt% | 20 wt% |
| P07 | — | 12 wt% | |
![[D with combining macron]](https://www.rsc.org/images/entities/i_char_0044_0304.gif) sa
sa
|
ID31 | 20.3 nm | 45.9 nm |
| P07 | — | 25.0 nm | |
| c s | ID31 | 0.40 μmol m−2 | 0.35 μmol m−2 |
| P07 | — | 0.04 μmol m−2 |
3.2 High energy X-ray diffraction
The ice content in partially frozen clay composites was studied by high energy X-ray diffraction at beamlines ID31, ESRF and P07, PETRAIII. Experimental details are summarized in Table S2 (ESI†). As an internal XRD calibration standard, 1 wt% CeO2 was added to the clays. Cylindrical pellets (6 mm diameter, 15 mm length) were prepared by uniaxially compacting the water soaked materials at approx. 100 bar (Fig. 2a). The resultant total water mass content wm of the pellets was determined in retrospect by thermogravimetric analysis (TGA/DSC 3+, Mettler Toledo) after the XRD experiments. Measurements result in 27 wt%, 20 wt%, and 12 wt% for the vermiculite, ID31 and P07 kaolin samples, respectively. The pellets were placed inside a temperature controlled titanium cell with stability better than ±0.005 °C. To increase thermal contact and to avoid water evaporation during the measurements, the cell was filled with 2,2,4-trimethylpentane. Scattered intensities were recorded on area detectors. For each temperature, at least two series of 117 independent 2D-scattering patterns were collected by rotating and translating the sample along the cylinder axes. This procedure allowed the collection of representative and reproducible XRD averages. After rapidly cooling the sample below −60 °C and equilibration for 40 min, XRD measurements were made while stepwise increasing the temperature until complete melting was observed.4 Analysis and results
4.1 High energy X-ray diffraction
The 2D-XRD scattering patterns from kaolin and vermiculite samples measured at different sample positions were normalized by their integrated CeO2(111) Bragg intensities and averaged (Fig. S6, ESI†). Pronounced textures are observed in the clay Bragg reflections. For the vermiculite (002), kaolin (001), and kaolin (002) reflections, maxima are observed in the vertical direction, i.e. parallel to the apex of the cylindrical pellet. This is explained by the parallel alignment of the platelets during the pellet preparation by uniaxial compression (Fig. 2). No singular intense Bragg spots were observed in the 2D-XRD patterns from ice. This indicates the absence of large ice single crystals after rapid freezing of the composite samples. Therefore, the integrated intensity of the Bragg reflections provides a quantitative measure of the ice content.After azimuthal integration, high temperature scattering patterns of the molten samples were subtracted from each temperature set (Fig. 4, Section G, ESI†). This procedure efficiently eliminates most of the scattering signal from the clay minerals, CeO2 reference, and sample container. Thermal expansion leads to S-shaped curves in the difference patterns in the region around the kaolin (002) and (111), vermiculite (021), and CeO2 (111) Bragg reflections.
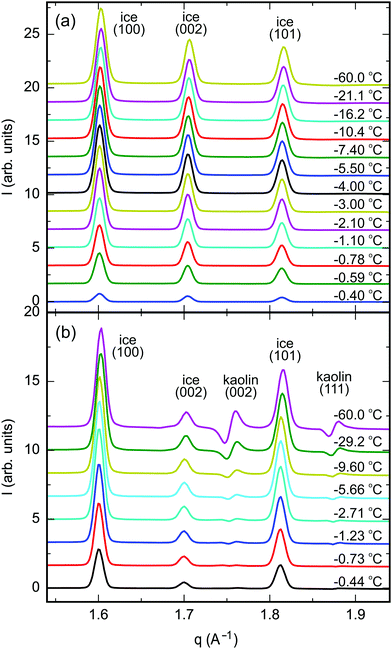 | ||
| Fig. 4 Azimuthally integrated XRD difference patterns between partially frozen samples at −60 °C < T − Tm < 0 °C and the molten samples above Tm; (a) vermiculite, (b) kaolin (ID31, ESRF). | ||
Integrated Bragg intensities of ice Ih were determined from simultaneously fitting three Gaussian peaks for the ice (100), (002), and (101) Bragg reflections to the corrected azimuthally integrated XRD difference patterns (Tables S3–S5, ESI†). The positions of the Bragg reflections agree well with literature values for the ice lattice spacings and thermal expansion.54 The peaks’ FWHM are limited by the angular resolution of the experimental setup using large pellet samples of 6 mm diameter. Therefore, details in the line shape of the Bragg reflections are concealed.
Below the bulk melting point Tm, the intensities I(T) of the (100), (002), and (101) ice Ih Bragg reflections rapidly increase (Fig. 4). This corresponds to a decreasing liquid water fraction (Fig. S8, ESI†) that is related to the effective premelting layer thickness ![[d with combining macron]](https://www.rsc.org/images/entities/i_char_0064_0304.gif) (Section G, ESI†). Fig. 5 shows
(Section G, ESI†). Fig. 5 shows ![[d with combining macron]](https://www.rsc.org/images/entities/i_char_0064_0304.gif) vs. temperature below melting, Tm − T. Upon cooling, a rapid decrease of
vs. temperature below melting, Tm − T. Upon cooling, a rapid decrease of ![[d with combining macron]](https://www.rsc.org/images/entities/i_char_0064_0304.gif) is observed for all samples.
is observed for all samples.
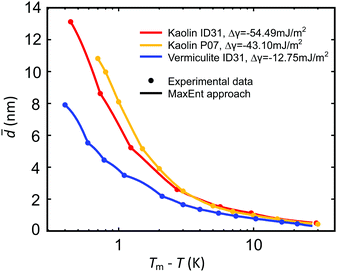 | ||
Fig. 5 Effective premelting layer thickness ![[d with combining macron]](https://www.rsc.org/images/entities/i_char_0064_0304.gif) vs. temperature below melting, Tm − T, for vermiculite (blue) and kaolin (ID31: red; P07: orange) composite samples extracted from the intensity of the ice (100), (002), (101) Bragg reflections (dots). Solid curves are calculated by eqn (2) with pore size distributions P(D) obtained from a MaxEnt analysis (Section 4.2 and Fig. 6). vs. temperature below melting, Tm − T, for vermiculite (blue) and kaolin (ID31: red; P07: orange) composite samples extracted from the intensity of the ice (100), (002), (101) Bragg reflections (dots). Solid curves are calculated by eqn (2) with pore size distributions P(D) obtained from a MaxEnt analysis (Section 4.2 and Fig. 6). | ||
4.2 MaxEnt analysis
In this section, we estimate the pore size distribution P(D) of a sample from a set of liquid water layer thicknesses![[d with combining macron]](https://www.rsc.org/images/entities/i_char_0064_0304.gif) i =
i = ![[d with combining macron]](https://www.rsc.org/images/entities/i_char_0064_0304.gif) (Ti), i ∈ {1,…,n}, measured at n temperatures Ti (Section 4.1).
(Ti), i ∈ {1,…,n}, measured at n temperatures Ti (Section 4.1).
The functional form of the pore size distribution P(D) is constrained by the normalization condition
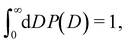 | (13) |
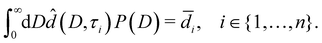 | (14) |
Note that ![[d with combining circumflex]](https://www.rsc.org/images/entities/i_char_0064_0302.gif) (D,τ) in eqn (7) additionally depends on the a priori unknown reduced onset temperature τ0.
(D,τ) in eqn (7) additionally depends on the a priori unknown reduced onset temperature τ0.
The MaxEnt method yields the least biased distribution P(D) compatible with the boundary conditions eqn (13) and (14) by constrained maximization of a certain entropy functional H[![[P with combining tilde]](https://www.rsc.org/images/entities/i_char_0050_0303.gif) ] on the set of all distributions
] on the set of all distributions ![[P with combining tilde]](https://www.rsc.org/images/entities/i_char_0050_0303.gif) (D).55,56 For the present case of linear constraints, the relevant functional is given by57
(D).55,56 For the present case of linear constraints, the relevant functional is given by57
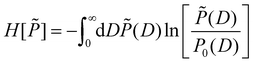 | (15) |
![[d with combining macron]](https://www.rsc.org/images/entities/i_char_0064_0304.gif) i, i ∈ {1,…,n} into account. Here P0(D) is the uniform distribution in the range D ∈ [0, Dmax]
i, i ∈ {1,…,n} into account. Here P0(D) is the uniform distribution in the range D ∈ [0, Dmax]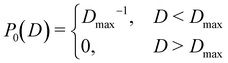 | (16) |
The entropy functional H[![[P with combining tilde]](https://www.rsc.org/images/entities/i_char_0050_0303.gif) ] was maximized under the constraints eqn (13) and (14) with respect to
] was maximized under the constraints eqn (13) and (14) with respect to ![[P with combining tilde]](https://www.rsc.org/images/entities/i_char_0050_0303.gif) (D) and τ0 using the method of Lagrange multipliers. For all samples, the effective premelting layer thicknesses
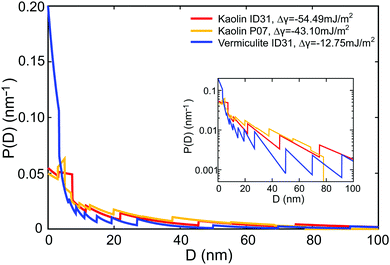
(D) and τ0 using the method of Lagrange multipliers. For all samples, the effective premelting layer thicknesses ![[d with combining macron]](https://www.rsc.org/images/entities/i_char_0064_0304.gif) (T) (Fig. 5, solid lines) calculated from the resultant pore size distributions P(D) (Fig. 6) reproduce the experimentally observed values (Fig. 5, symbols). The value of Δγ for each individual sample is calculated from τ0viaeqn (10). Parameters for the reduced onset temperature τ0, the deviation from Antonow's rule Δγ, and the average pore size
(T) (Fig. 5, solid lines) calculated from the resultant pore size distributions P(D) (Fig. 6) reproduce the experimentally observed values (Fig. 5, symbols). The value of Δγ for each individual sample is calculated from τ0viaeqn (10). Parameters for the reduced onset temperature τ0, the deviation from Antonow's rule Δγ, and the average pore size ![[D with combining macron]](https://www.rsc.org/images/entities/i_char_0044_0304.gif) psd are summarized in Table 2.
psd are summarized in Table 2.
![[D with combining macron]](https://www.rsc.org/images/entities/i_char_0044_0304.gif) psd obtained for a cut-off width Dmax within the MaxEnt approach of Section 4.2 for the three clay nano composite samples characterized in Table 1
psd obtained for a cut-off width Dmax within the MaxEnt approach of Section 4.2 for the three clay nano composite samples characterized in Table 1
| Sample | τ 0 | Δγ (mJ m−2) |
![[D with combining macron]](https://www.rsc.org/images/entities/i_char_0044_0304.gif) psd (nm)
psd (nm) |
D max (nm) |
|---|---|---|---|---|
| Vermiculite | −0.158 | −12.8 | 15.8 | 134 |
| Kaolin (ID31) | −0.675 | −54.5 | 26.2 | 123 |
| Kaolin (P07) | −0.534 | −43.1 | 21.6 | 87 |
5 Discussion and conclusions
In Section. 4.1, we experimentally determined the interfacial premelting of ice in two well characterized ice-nanocomposite model systems comprised of a charged and an uncharged clay. The growth of the effective premelting layer thickness![[d with combining macron]](https://www.rsc.org/images/entities/i_char_0064_0304.gif) vs. temperature below melting Tm − T is shown in Fig. 5. Close to the bulk melting point, layer thicknesses approach values corresponding to half the average slit pore widths
vs. temperature below melting Tm − T is shown in Fig. 5. Close to the bulk melting point, layer thicknesses approach values corresponding to half the average slit pore widths ![[D with combining macron]](https://www.rsc.org/images/entities/i_char_0044_0304.gif) psd. In the low temperature region, liquid water is still detected below −20 °C. For both kaolin samples we find consistently larger
psd. In the low temperature region, liquid water is still detected below −20 °C. For both kaolin samples we find consistently larger ![[d with combining macron]](https://www.rsc.org/images/entities/i_char_0064_0304.gif) values compared to vermiculite at the same temperature. At Tm − T = 1.0 K the liquid fractions f(Tm – T) lie in between 0.2 and 0.4. This corresponds to premelting layer thicknesses of 3.5 nm for vermiculite and 7.5 nm for kaolin samples. The former value is similar to the premelting layer thicknesses of 2 nm to 4 nm observed by X-ray reflectivity at the interface between single crystalline ice and amorphous SiO2
values compared to vermiculite at the same temperature. At Tm − T = 1.0 K the liquid fractions f(Tm – T) lie in between 0.2 and 0.4. This corresponds to premelting layer thicknesses of 3.5 nm for vermiculite and 7.5 nm for kaolin samples. The former value is similar to the premelting layer thicknesses of 2 nm to 4 nm observed by X-ray reflectivity at the interface between single crystalline ice and amorphous SiO2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 16 and quartz.18 For graphitized carbon black and talc powders Maruyama extracted frozen fractions by quasi elastic neutron scattering.27 At Tm − T = 1.0 K, the more hydrophobic carbon black (f ∼ 0.4) shows significantly larger liquid fractions compared to the sheet silicate talc (f ∼ 0.09). For the free ice surface even thicker premelting layers from 30 nm to 50 nm were reported by Lied15 and Döppenschmidt.58 Thus, phenomenological comparison of our results for the effective premelting layer thickness
16 and quartz.18 For graphitized carbon black and talc powders Maruyama extracted frozen fractions by quasi elastic neutron scattering.27 At Tm − T = 1.0 K, the more hydrophobic carbon black (f ∼ 0.4) shows significantly larger liquid fractions compared to the sheet silicate talc (f ∼ 0.09). For the free ice surface even thicker premelting layers from 30 nm to 50 nm were reported by Lied15 and Döppenschmidt.58 Thus, phenomenological comparison of our results for the effective premelting layer thickness ![[d with combining macron]](https://www.rsc.org/images/entities/i_char_0064_0304.gif) with the literature provides a first hint for a presumably general tendency: for ice, the premelting layer thickness gets larger at more hydrophobic interfaces.
with the literature provides a first hint for a presumably general tendency: for ice, the premelting layer thickness gets larger at more hydrophobic interfaces.
However, for a quantitative analysis and interpretation the interactions with the solid substrate governing Δγ and the pore size distribution P(D) have to be taken into account. A slit pore premelting model (Section 2) in conjunction with a MaxEnt method (Section 4.2) allows for a full quantitative analysis of experimentally determined growth laws ![[d with combining macron]](https://www.rsc.org/images/entities/i_char_0064_0304.gif) (T). Fig. 5 demonstrates that this continuum model adequately describes the experimental premelting data over the entire measured temperature range.
(T). Fig. 5 demonstrates that this continuum model adequately describes the experimental premelting data over the entire measured temperature range.
The pore size distribution P(D), extracted by the MaxEnt analysis (Fig. 6), is an important parameter of the model. Its functional dependency exhibits a fast decay for larger D values. For all clay nano composite samples, the average slit pore widths ![[D with combining macron]](https://www.rsc.org/images/entities/i_char_0044_0304.gif) psd calculated from P(D) (Table 2) are consistent with the
psd calculated from P(D) (Table 2) are consistent with the ![[D with combining macron]](https://www.rsc.org/images/entities/i_char_0044_0304.gif) sa values determined from the gas adsorption isotherms (Table 1). The systematically smaller values obtained for the dry powders (
sa values determined from the gas adsorption isotherms (Table 1). The systematically smaller values obtained for the dry powders (![[D with combining macron]](https://www.rsc.org/images/entities/i_char_0044_0304.gif) sa) compared to the pressed clay/water pellets (
sa) compared to the pressed clay/water pellets (![[D with combining macron]](https://www.rsc.org/images/entities/i_char_0044_0304.gif) psd) are explained by their different preparation states.
psd) are explained by their different preparation states.
For the effective coupling between the solid/liquid and liquid/ice interface we assume effective short-range forces, generating an exponentially decaying interfacial free energy γ(d) in eqn (2). Their decay length λ equals the bulk correlation length ξ in the liquid phase.37 From bulk X-ray scattering data of liquid water, we extract λ = ξ = 2.42 Å. Indeed, our experimental premelting data is perfectly reproduced using this bulk value for all samples independent of the contained clay mineral. Thus, our results are in agreement with the standard theory of interface phase transitions. Likewise, Smit et al. found that the characteristic spectroscopic response from the ice premelting layer and supercooled bulk water is indistinguishable by sum-frequency generation spectroscopy.59 However, changes in the water structure have been observed for water confined in nano-pores.60 Scattering experiments indicate that confined water exhibits a higher order compared to bulk.61–64 Likewise, the increase in premelting liquid layer density adjacent to hydrophilic SiO2 by 20% compared to bulk water16 and surface spectroscopy experiments20,65 indicate different properties. Such huge density changes would require structural changes that are much larger compared to the temperature variations observed for supercooled water.46 The interpolation of the interfacial free energy γ(d) between d = 0 and d → ∞ given in eqn (1) and (2) obeys the thermodynamically correct exponential asymptotic decay on the scale of the bulk correlation length λ = ξ. However, from the results discussed above it is expected that the structural properties of confined water lead to deviations from this simple form. Hence, deviations from eqn (9) may occur for small water layer thicknesses dp at low temperatures. The present work highlights the importance of the pore size distribution P(D) for the premelting behavior in nano composite materials such as sheet silicates. In consequence, the specific small-thickness features of the interfacial free energy γ(d) are expected to become relevant only for samples with a large fraction of very small pores.
The third parameter affecting premelting in slit pore confinement is the deviation from Antonow's rule Δγ. This quantity, related to the spreading coefficient S = −Δγ of liquid water on the solid compared to ice, depends on the balance of the interactions between the three components. Both clays studied in this work form planar hydrophilic sheets (Fig. S4 and S5, ESI†). While vermiculite surfaces are charged by 1.2–1.8 unit charges per unit cell, polar kaolin surfaces are neutral.66 Therefore, different Δγ values are expected to result in different premelting curves for vermiculite and kaolin based ice/clay composites. Indeed, about four times larger negative Δγ values were extracted for kaolin compared to vermiculite by MaxEnt analysis (Table 2).
For vermiculite, we find Δγ = −12.8 mJ m−2. For comparison, for single crystal ice/SiO2 interfaces Δγ = −5.03 mJ m−2 is obtained from Tm − T0 = 17 K reported by Engemann et al.16 A common property of vermiculite and SiO2 surfaces is their negative charge.
For the two kaolin samples, Δγ values agree well, despite their different preparation protocols leading to different ion and water concentrations. This confirms the robustness of the MaxEnt analysis method. It also indicates that the differences in the observed growth law for kaolin and vermiculite are primarily related to the surface properties and the pore size distribution of the clay minerals rather than impurities. Bare kaolin surfaces have a surface tension of 171 mN m−1 with a ratio of 40% dispersive and 60% nondispersive interactions.67 The positive spreading coefficient S = 76 mN m−1 of liquid water vs. its vapor, calculated by the Fowkes method,68 reflects the strong hydrophilic nature of the bare kaolin surface. With about 50 mJ m−2 the spreading coefficient of liquid water vs. ice found in this work is on the same order of magnitude.
For the free ice surface, an even larger negative Δγ value of −384 mJ m−2 is reported in the literature.58 Consistently, a large dangling hydrogen bond density was detected at the free ice surface by SFG spectroscopy.20,69 In contrast to ice, in liquid water the hydrogen bonding network adjacent to interfaces can rearrange. Therefore, the formation of a liquid premelting layer at ice surfaces is energetically favorable. This is reflected in a large negative Δγ value.
Generally, larger negative Δγ values indicate that the ice structure at an interface is less compatible with the opposing medium. Therefore, these media tend to be less efficient ice nucleators and vice versa. Murray et al. studied heterogeneous ice nucleation by kaolin particles in suspensions.70 Compared to other minerals, kaolin is a rather inefficient ice nucleator.71 Accordingly, we observe large premelting layer thicknesses caused by Δγ values around −50 mJ m−2. On the other hand, at quartz with a smaller absolute Δγ = −5.03 mJ m−2, ice nucleates with a significantly higher activity.71 Likewise, ice/vermiculite interfaces with Δγ = −12.8 mJ m−2, exhibit thinner premelting layer thicknesses.
Premelting layer formation at ice/solid interfaces has important implications in atmospheric physics72 and geophysics.2 Our experiments on well defined ice/clay nano composite samples bridge the gap between studies on single crystalline ice/solid model interfaces16 and naturally occurring soils.30,31 Compared to naturally occurring soils, the ion concentration in the sample was reduced to investigate the influence of the surface properties of the adjacent solid. For ice/clay nano composites, in addition to the deviation from Antonow's rule the pore size distribution is a decisive parameter determining the liquid water fraction vs. temperature. The experimental premelting data is quantitatively reproduced over the entire temperature range by a theoretical continuum model including effective short-range interactions. Thorough material characterization allows for the comparison of parameters extracted by a MaxEnt analysis with independent experimental observations.
Future theoretical and experimental work focusing on the dynamics of the water molecules in the premelting layer of ice/clay nano composites might provide complementary information on the nature of the interfacial premelting layer.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank Thomas Buslaps (ESRF), Roberto Verbeni (ESRF), and Uta Rütt (PETRA III) for their assistance during our synchrotron experiments at beamlines ID15 and ID31, ESRF-The European Synchrotron, Grenoble and at P07, PETRA III, DESY, Hamburg, a member of the Helmholtz Association (HGF), Maren Müller (MPI-P) for SEM, Helma Burg (MPI-P) and Rüdiger Berger (MPI-P) for AFM measurements, Alexei Kiselev (KIT Karlsruhe) and Hans-Jürgen Butt (MPI-P) for helpful discussions. J. M. and M. M. acknowledge the MAINZ Graduate School of Excellence, funded through the Excellence Initiative (DFG/GSC 266). H. L. was supported by the China Scholarship Council. Open Access funding provided by the Max Planck Society.References
- A.-M. Kietzig, S. G. Hatzikiriakos and P. Englezos, J. Appl. Phys., 2010, 107, 081101 CrossRef.
- P. J. Williams, in The Freezing of Soils: Ice in a Porous Medium and Its Environmental Significance, ed. J. S. Wettlaufer, J. G. Dash and N. Untersteiner, Springer, Heidelberg, 1999, pp. 219–239 Search PubMed.
- M. Faraday, Philos. Mag., 1859, 17, 162–169 Search PubMed.
- R. Rosenberg, Phys. Today, 2005, 58, 50–55 CrossRef CAS.
- J. G. Dash, A. W. Rempel and J. S. Wettlaufer, Rev. Mod. Phys., 2006, 78, 695–741 CrossRef CAS.
- Y. Li and G. A. Somorjai, J. Phys. Chem. C, 2007, 111, 9631–9637 CrossRef CAS.
- H. Hansen-Goos and J. S. Wettlaufer, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2010, 81, 031604 CrossRef.
- D. Pan, L.-M. Liu, B. Slater, A. Michaelides and E. Wang, ACS Nano, 2011, 5, 4562–4569 CrossRef CAS.
- Y. Suzuki, H. Duran, M. Steinhart, M. Kappl, H.-J. Butt and G. Floudas, Nano Lett., 2015, 15, 1987–1992 CrossRef CAS.
- J. W. Cahn, J. G. Dash and H. Fu, J. Cryst. Growth, 1992, 123, 101–108 CrossRef CAS.
- K. Morishige and K. Kawano, J. Chem. Phys., 1999, 110, 4867–4872 CrossRef CAS.
- G. H. Findenegg, S. Jähnert, D. Akcakayiran and A. Schreiber, ChemPhysChem, 2008, 9, 2651–2659 CrossRef CAS.
- J. S. Wettlaufer, Phys. Rev. Lett., 1999, 82, 2516–2519 CrossRef CAS.
- Y. Yang, M. Asta and B. B. Laird, Phys. Rev. Lett., 2013, 110, 096102 CrossRef.
- A. Lied, H. Dosch and J. H. Bilgram, Phys. Rev. Lett., 1994, 72, 3554–3557 CrossRef CAS.
- S. Engemann, H. Reichert, H. Dosch, J. Bilgram, V. Honkimäki and A. Snigirev, Phys. Rev. Lett., 2004, 92, 205701 CrossRef CAS.
- M. Mezger, S. Schöder, H. Reichert, H. Schröder, J. Okasinski, V. Honkimäki, J. Ralston, J. Bilgram, R. Roth and H. Dosch, J. Chem. Phys., 2008, 128, 244705 CrossRef.
- S. Schöder, H. Reichert, H. Schröder, M. Mezger, J. S. Okasinski, V. Honkimäki, J. Bilgram and H. Dosch, Phys. Rev. Lett., 2009, 103, 095502 CrossRef.
- H. Bluhm, D. F. Ogletree, S. F. Charles, H. Zahid and S. Miquel, J. Phys.: Condens. Matter, 2002, 14, L227–L233 CrossRef CAS.
- X. Wei, P. B. Miranda and Y. R. Shen, Phys. Rev. Lett., 2001, 86, 1554–1557 CrossRef CAS.
- M. M. Conde, C. Vega and A. Patrykiejew, J. Chem. Phys., 2008, 129, 014702 CrossRef CAS.
- D. T. Limmer and D. Chandler, J. Chem. Phys., 2014, 141, 18C505 CrossRef.
- T. Kozlowski, Cold Reg. Sci. Technol., 2004, 38, 93–101 CrossRef.
- T. Kozlowski, Cold Reg. Sci. Technol., 2007, 49, 226–236 CrossRef.
- D. M. Anderson and P. Hoekstra, Science, 1965, 149, 318–319 CrossRef CAS PubMed.
- J. M. Gay, J. Suzanne, J. G. Dash and H. Fu, J. Cryst. Growth, 1992, 125, 33–41 CrossRef CAS.
- M. Maruyama, M. Bienfait, J. G. Dash and G. Coddens, J. Cryst. Growth, 1992, 118, 33–40 CrossRef.
- T. Ishizaki, M. Maruyama, Y. Furukawa and J. G. Dash, J. Cryst. Growth, 1996, 163, 455–460 CrossRef CAS.
- K. Watanabe and T. Wake, Cold Reg. Sci. Technol., 2009, 59, 34–41 CrossRef.
- A. R. Tice, D. M. Anderson and K. F. Sterrett, Eng. Geol., 1981, 18, 135–146 CrossRef.
- A. R. Tice, P. B. Black and R. L. Berg, Cold Reg. Sci. Technol., 1989, 17, 103–111 CrossRef.
- B. F. Henson and J. M. Robinson, Phys. Rev. Lett., 2004, 92, 246107 CrossRef CAS.
- S. Dietrich, in Wetting Phenomena in Phase Transitions and Critical Phenomena, ed. C. Domb and J. Lebowitz, Academic Press, London, 1988, pp. 1–218 Search PubMed.
- M. Schick, in Introduction toWetting Phenomena, ed. J. Charvolin, J. F. Joanny and J. Zinn-JustinNorth-Holland, Amsterdam, 1990, pp. 415–497 Search PubMed.
- R. Lipowsky, Phys. Rev. Lett., 1982, 49, 1575–1578 CrossRef CAS.
- J. G. Dash, F. Haiying and J. S. Wettlaufer, Rep. Prog. Phys., 1995, 58, 115–167 CrossRef CAS.
- R. Lipowsky, U. Breuer, K. C. Prince and H. P. Bonzel, Phys. Rev. Lett., 1989, 62, 913–916 CrossRef CAS.
- J. F. van der Veen, Surf. Sci., 1999, 433, 1–11 CrossRef.
- G. A. Martynov, Fundamental Theory of Liquids, Hilger, Bristol, 1992 Search PubMed.
- J.-P. Hansen and I. R. McDonald, Theory of Simple Liquids: With Applications to Soft Matter, Academic Press, Oxford, 2013 Search PubMed.
- M. Mezger, R. Roth, H. Schröder, P. Reichert, D. Pontoni and H. Reichert, J. Chem. Phys., 2015, 142, 164707 CrossRef.
- G. Hura, J. M. Sorenson, R. M. Glaeser and T. Head-Gordon, J. Chem. Phys., 2000, 113, 9140–9148 CrossRef CAS.
- A. Soper, Chem. Phys., 2000, 258, 121–137 CrossRef CAS.
- T. Head-Gordon and G. Hura, Chem. Rev., 2002, 102, 2651–2670 CrossRef CAS.
- A. Soper, J. Phys.: Condens. Matter, 2007, 19, 335206 CrossRef CAS.
- L. B. Skinner, C. Benmore, J. C. Neuefeind and J. B. Parise, J. Chem. Phys., 2014, 141, 214507 CrossRef CAS.
- D.-M. Zhu and J. Dash, Phys. Rev. Lett., 1988, 60, 432–435 CrossRef CAS.
- B. Pluis, T. Taylor, D. Frenkel and J. Van der Veen, Phys. Rev. B: Condens. Matter Mater. Phys., 1989, 40, 1353–1356 CrossRef.
- H. Löwen, T. Beier and H. Wagner, EPL, 1989, 9, 791–796 CrossRef.
- L. A. Wilen, J. S. Wettlaufer, M. Elbaum and M. Schick, Phys. Rev. B: Condens. Matter Mater. Phys., 1995, 52, 12426–12433 CrossRef CAS.
- C. Marcos and I. Rodríguez, Appl. Clay Sci., 2014, 87, 219–227 CrossRef CAS.
- W. Kern, J. Electrochem. Soc., 1990, 137, 1887–1892 CrossRef CAS.
- O. Gjems, Clay Miner. Bull., 1963, 5, 183–193 CrossRef.
- K. Röttger, A. Endriss, J. Ihringer, S. Doyle and W. Kuhs, Acta Crystallogr., Sect. B: Struct. Sci., 2012, 68, 91 CrossRef.
- E. T. Jaynes, Probability Theory: The Logic of Science, Cambridge University Press, 2003 Search PubMed.
- D. Sivia and J. Skilling, Data Analysis: A Bayesian Tutorial, Oxford University Press, Oxford, 2006 Search PubMed.
- J. Shore and R. Johnson, IEEE Trans. Inf. Theory, 1980, 26, 26–37 CrossRef.
- A. Döppenschmidt and H.-J. Butt, Langmuir, 2000, 16, 6709–6714 CrossRef.
- W. J. Smit and H. J. Bakker, Angew. Chem., 2017, 129, 15746–15750 CrossRef.
- M. Erko, G. Findenegg, N. Cade, A. Michette and O. Paris, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 104205 CrossRef.
- J. Dore, Chem. Phys., 2000, 258, 327–347 CrossRef CAS.
- M. Ricci, F. Bruni, P. Gallo, M. Rovere and A. Soper, J. Phys.: Condens. Matter, 2000, 12, A345–A350 CrossRef CAS.
- M. Bellissent-Funel, J. Phys.: Condens. Matter, 2001, 13, 9165 CrossRef CAS.
- T. Yamaguchi, H. Hashi and S. Kittaka, J. Mol. Struct., 2006, 129, 57–62 CAS.
- M. A. Sánchez, T. Kling, T. Ishiyama, M.-J. van Zadel, P. J. Bisson, M. Mezger, M. N. Jochum, J. D. Cyran, W. J. Smit and H. J. Bakker, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, 227–232 CrossRef.
- I. Bihannic, A. Delville, B. Demé, M. Plazanet, F. Villiéras and L. J. Michot, in Clay Swelling: New Insights from Neutron-Based Techniques, ed. L. Liang, R. Rinaldi and H. Schober, Springer, New York, 2009, pp. 521–546 Search PubMed.
- E. Chibowski and P. Staszczuk, Clays Clay Miner., 1988, 36, 455–461 CrossRef CAS.
- F. M. Fowkes, Ind. Eng. Chem., 1964, 56, 40–52 CrossRef CAS.
- X. Wei, P. B. Miranda, C. Zhang and Y. Shen, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 66, 085401 CrossRef.
- B. Murray, S. Broadley, T. Wilson, J. Atkinson and R. Wills, Atmos. Chem. Phys., 2011, 11, 4191–4207 CrossRef CAS.
- J. D. Atkinson, B. J. Murray, M. T. Woodhouse, T. F. Whale, K. J. Baustian, K. S. Carslaw, S. Dobbie, D. OSullivan and T. L. Malkin, Nature, 2013, 498, 355–358 CrossRef CAS.
- T. Peter, Annu. Rev. Phys. Chem., 1997, 48, 785–822 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Sample characterization, experimental details and data processing. See DOI: 10.1039/c8cp05604h |
| This journal is © the Owner Societies 2019 |