Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Three-dimensional image based modelling of transport parameters in lithium–sulfur batteries†
Chun
Tan
 ,
Matthew D. R.
Kok
,
Sohrab R.
Daemi
,
Daniel J. L.
Brett
,
Matthew D. R.
Kok
,
Sohrab R.
Daemi
,
Daniel J. L.
Brett
 and
Paul R.
Shearing
and
Paul R.
Shearing
 *
*
Electrochemical Innovation Lab, Department of Chemical Engineering, University College London, London, WC1E 7JE, UK. E-mail: p.shearing@ucl.ac.uk
First published on 2nd October 2018
Abstract
An elemental sulfur electrode was imaged with X-ray micro and nano computed tomography and segmented into its constituent phases. Morphological parameters including phase fractions and pore and particle size distributions were calculated directly from labelled image data, and flux based simulations were performed to determine the effective molecular diffusivity of the pore phase and electrical conductivity of the conductive carbon and binder phase, Deff and σeff, that can be used as an input for Li–S battery modelling. In addition to its crucial role in providing electrical conductivity within the sulfur electrode, the intrinsic porosity of the carbon binder domain was found to significantly influence Li-ion transport within the electrode. Neglecting this intrinsic porosity results in an overestimation of the electrical conductivity within the sulfur electrode, and an underestimation of the tortuosity of the Li-ion conducting phase by ca. 56%. The derivation of effective transport parameters directly from image data may aid in the development of more realistic models of Li–S battery systems by reducing the reliance on empirical correlations, and the uncertainties arising from assumptions made in these correlations.
Introduction
Lithium–sulfur (Li–S) batteries are rapidly emerging as a viable successor to Li-ion technology, and have garnered significant interest particularly in automotive and aerospace applications, due to their higher gravimetric energy density (ca. 2567 W h kg−1) compared to transition metal oxide based cathodes (ca. 387 W h kg−1).1 However, the practical implementation and commercialisation of Li–S batteries has been plagued by a multitude of factors that have been discussed in detail by various authors2–4 – namely, poor electrical conductivity of elemental S8 and the discharge product Li2S; complex multi-step reaction mechanisms involving solid–liquid–solid phase transitions; the polysulfide shuttle effect stemming from soluble polysulfides in the electrolyte phase; and lithium metal anode degradation.The need to develop a better mechanistic understanding of the electrochemical reactions occurring within the Li–S battery has driven increased interest in the application of continuum modelling techniques commonly used in Li-ion battery research. One of the first mathematical descriptions of the Li–S battery system was pioneered by Mikhaylik and Akridge,5 based on a purely thermodynamic representation of the reaction mechanisms to describe the polysulfide shuttle phenomenon, and the fitting of an empirical shuttle constant to experimental data as a function of electrolyte salt concentration, charge, and discharge currents. This was followed by a 1D Newman-type continuum model presented by Kumaresan et al.,6 that considered the physics of multi-component transport phenomena, modified with an empirical parameter to account for the variation in electrode porosity induced by the dissolution and precipitation of S and Li2S into and out of the electrolyte phase as discharge progresses, and the reverse that occurs during charge. Danner et al. proposed a 1 + 1D model by defining a particle model that considered the transport of sulfur species radially from a perfectly spherical particle, in addition to a macroscopic cell-level model.7 Subsequently, Thangavel et al.8 reported a microstructurally resolved multi-scale model of a Li–S battery, where the cathode was assumed to be packed with uniformly sized spherical mesoporous sulfur/carbon composite particles. The sulfur-filled mesopores of the carbon particles were themselves assumed to be spherical with a uniform size distribution.
All the continuum models presented by these authors utilize some form of empirical or theoretical correlation to estimate the volume averaged effective diffusivity or conductivity from the porosity of the phase of interest. The fundamental basis of continuum modelling techniques is the assumption that a heterogeneous material can be viewed as a continuum on the microscopic scale with effective properties assigned to it because the average domain size is much larger than the molecular dimensions.9 However, Li–S battery modelling is complicated by the inherent heterogeneity in cathode architecture and the fundamentally different reaction mechanisms occurring with the active material between conversion- and intercalation-type cathodes respectively.
Furthermore, porosity-tortuosity factor correlations commonly used in continuum models, such as the Bruggeman correlation, may not be valid due to the heterogeneous cathode microstructure, high volume fractions (of insulating material), and the non-spherical nature of the insulating phase.10 In particular, the dissolution and re-crystallization of elemental sulfur during cycling results in a wide range of porosities as a function of state of charge, and this must be taken into account when applying theoretical and empirical correlations relating tortuosity factor to porosity. According to Tjaden et al., tortuosity factors predicted from porosities by theoretical and empirical correlations fall within a narrow band for typical electrode porosities of 30–70%, and may not exhibit a true correlation with measured tortuosity factors.10
The emergence of X-ray computed tomography (CT) and other advanced imaging techniques in energy storage materials research over the past decade has permitted the visualization of the microstructure of battery materials in three dimensions at a range of length scales.11 These materials can be studied in a host of different experimental or real conditions; these range from post-mortem analysis of degradation or failure mechanisms,12–15 to mechanistic studies through in situ and operando measurements.16–19 Valuable metrics such as porosity, pore and particle size distributions, and tortuosity can be extracted directly from the volumetric image data, serving as a diagnostic tool that offers a deeper insight into performance limitations and degradation pathways leading to failure. More recently, the availability of greater computing power has facilitated the use of actual image data to build more realistic models of battery systems. One area of interest is the calculation of effective conductivity values directly from actual microstructural data in a range of electrochemical devices, thereby accounting for inhomogeneities and geometric variations within the porous electrodes contained within almost all of these devices.20–22
In Li–S battery modelling, Dysart et al. were the first to use image data in their continuum model, by stochastically reconstructing a virtual 3D electrode microstructure from 2D SEM images to derive the effective ionic conductivity of their cathode material.23 In this paper, we propose a workflow involving the derivation of effective conductivity values directly from binarized volumetric CT image data of actual Li–S cathodes. The advantage of the image-based workflow compared to existing approaches in Li–S battery modelling lies in the elimination of the reliance on empirical parameterizations to describe transport parameters. By considering the relationship between electrode morphology and conductivity of ionic and electronic species,24 this approach has the potential to bridge the gap between computer simulations and physical electrochemical characterization.
Methods
Electrode preparation
Elemental sulfur (325 mesh, Alfa Aesar), conductive carbon black (Super C65, Timcal), Ketjenblack (EC600-JD, Akzo Nobel) and polyvinylidene fluoride binder (Solef 5130, Solvay) were combined in a 75![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 12
12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3
3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10 weight ratio and homogenized in N-methyl-2pyrrolidinone (NMP, Sigma Aldrich) by a high shear laboratory mixer (L5M, Silverson) to form an ink with 20% total solids content. The ink was cast onto 15 μm thick aluminium foil (MTI Corp.) using a micrometre adjustable film applicator with a 400 μm blade gap, and dried overnight in a vacuum oven to remove residual NMP.
10 weight ratio and homogenized in N-methyl-2pyrrolidinone (NMP, Sigma Aldrich) by a high shear laboratory mixer (L5M, Silverson) to form an ink with 20% total solids content. The ink was cast onto 15 μm thick aluminium foil (MTI Corp.) using a micrometre adjustable film applicator with a 400 μm blade gap, and dried overnight in a vacuum oven to remove residual NMP.
X-ray micro-computed tomography
X-ray micro-CT was performed on the sulfur electrode mounted onto a stainless steel pin with quick setting epoxy. A lab-based micro-CT instrument (Zeiss Xradia Versa 520, Carl Zeiss Inc.) was used, containing a polychromatic micro-focus sealed source set to an accelerating voltage of 80 kV on a tungsten target at a maximum power of 7 W. The scintillator was coupled to a 40X objective lens and 2048 × 2048 pixel CCD detector with a pixel binning of 1, resulting in a pixel size of 233.6 nm and field of view of ca. 460 μm. There was no significant geometric magnification as the sample was set close to the detector to reduce the effects of penumbra blurring arising from the cone beam nature of the source. The sample was rotated through 360° with radiographs collected at discrete angular intervals amounting to a total of 3201 projections. The radiographic projections were then reconstructed with proprietary reconstruction software (XMReconstructor, Carl Zeiss Inc.) using a modified Feldkamp–David–Kress (FDK) algorithm for cone beam geometry.X-ray nano-computed tomography
X-ray nano-CT was performed on the carbon binder domain of the sulfur electrode that was laser milled to a pillar ca. 100 μm in diameter. A lab-based nano-CT instrument (Zeiss Xradia Ultra 810, Carl Zeiss Inc.) was used, containing a rotating Cr anode source set to an accelerating voltage of 35 kV. The beam was quasi-monochromatized at the Cr-Kα emission line of 5.4 keV by a capillary condenser, illuminating the sample with a hollow cone beam focused on the sample, with a Fresnel zone plate as the objective element creating a magnified image on a 1024 × 1024 pixel CCD detector.25 The insertion of a Au phase ring in the back focal plane of the objective shifts the un-diffracted component of the beam, resulting in negative Zernike phase contrast. Large field of view mode with a pixel binning of 1 was used, resulting in a pixel size of ca. 63 nm and a field of view of ca. 65 μm. The sample was rotated through 180° with radiographs collected at discrete angular intervals amounting to 1601 projections. The radiographic projections were then reconstructed with proprietary reconstruction software (XMReconstructor, Carl Zeiss Inc.) using a parallel beam reconstruction algorithm.Image post-processing, segmentation and analysis
The micro-CT dataset was imported into Avizo (Visualization Sciences Group, FEI Company) and a sub-volume of 1350 × 1179 × 705 voxels was extracted for processing. An edge-preserving de-noising bilateral filter was applied followed by a rough threshold segmentation based on grayscale values to generate the markers used as seeds for the watershed segmentation algorithm. The electrode was then segmented into 5 phases consisting of the exterior, aluminium foil, sulfur, carbon binder domain and pores through a combination of manual and watershed segmentation. An island filter was used to remove small spots and holes, and dilation via a disc structuring element with a size of 3 pixels was performed on the carbon binder domain label field to remove pixels between the sulfur phase and pore phase that were falsely identified during segmentation as carbon binder domain due to the partial volume effect. Morphological parameters were extracted through voxel counting of the label field in Avizo, and continuous pore size distributions were carried out on binary TIFF stacks exported to ImageJ.26 The sulfur phase was quantified by separating the sulfur label field into individual particles in Avizo, and label analysis was then performed on the separated particles, from which metrics such as particle size distribution and average particle size were calculated from particle volumes. The largest sub-volume fully internal to the cathode (i.e. containing only the sulfur, CBD and pore phase) of 1179 × 1350 × 380 voxels, was then extracted for simulation in Avizo and TauFactor.For the nano-CT dataset, a sub-volume of 340 × 447 × 60 voxels was extracted for processing. A non-local means filter was applied for image de-noising, followed by watershed segmentation with the same method used for the micro-CT dataset. The carbon binder domain was segmented into two phases, a solid carbon binder phase and a pore phase, and the resulting binary dataset was used for simulation in Avizo and TauFactor.
Results and discussion
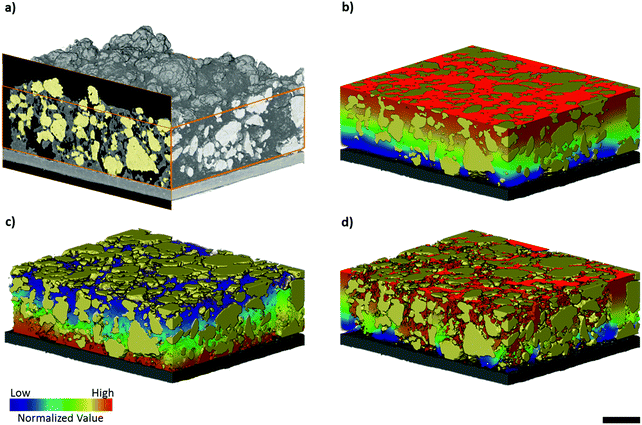
The elemental sulfur electrode used in this work was imaged with micro-CT, producing a tomographic volume that forms the basis of the analysis carried out in later sections. A cross-sectional slice of the electrode volume is presented in Fig. 1(a), and three separate phases can be distinguished from the difference in absorption contrast between sulfur particles (highest contrast values), carbon binder domain (CBD) and the bulk pore phase (lowest contrast values). To elucidate more information about the pore structure in the carbon binder domain below the spatial resolution of micro-CT, complementary nano-CT was performed on a laser milled pillar of the same electrode,27 selected to include only the CBD. The nano-CT volume was segmented into carbon binder and pore phases, and the micro-CT volume was segmented into CBD, bulk pore and sulfur phases. A distinction is made between the bulk pores identified in the micro-CT volume and the porosity within the CBD imaged by nano-CT – the latter are not visible within the micro-CT volume due to resolution limitations.Morphological parameters of sulfur electrode
Morphological parameters, including the volume fractions of all phases identified within the sulfur electrode are presented in Table 1, and were obtained by label analysis of the segmented micro-CT volume as shown in Fig. 1(b). The sulfur mass loading of the electrode was found to be ca. 9.05 mg cm−2 based on a density of 2.06 g cm−3, in close agreement with a sulfur loading of ca. 9.12 mg cm−2 calculated directly from the mass of the electrode.| Parameter | Measured from CT data | Calculated |
|---|---|---|
| a Values were calculated from electrode thickness measured from CT data. b Effective density of the CBD phase was calculated based on this volume fraction from CT data. | ||
| Sulfur areal volume loading (cm3 cm−2) | 0.00439 | — |
| Sulfur areal mass loading (mg cm−2) | 9.05 | 9.12 |
| Sulfur volume fraction | 0.411 | 0.414a |
| CBD volume fraction | 0.385 | 0.376a,b |
| Bulk pore volume fraction | 0.204 | 0.210a |
| CBD nano-porosity (nano-CT) | 0.324 | 0.439 |
The nano-porosity of the CBD phase was calculated to be 0.439 compared to a porosity of 0.324 measured by the segmentation of the nano-CT data. Nano-porosity was calculated from the weighed mass of the electrode, known mass fraction of the CBD and the volume fraction of the carbon binder domain obtained from the micro-CT data. It is hypothesized that the discrepancy in nano-porosity results from the presence of nano-scopic pores that fall below the spatial resolution of nano-CT. This is to be expected because the mesoporous carbon used in the electrode would naturally have an inherent porosity smaller than the primary particle size of ca. 100 nm.
Particle size distribution and sphericity
The volumes of each sulfur particle in the micro-CT dataset were converted to equivalent spherical diameters for the purpose of determining the particle size distribution, presented in Fig. 2(a). The particle size distribution is in close agreement with the specifications of the 325 mesh size (ca. 44 μm) sulfur used in the electrode, whilst the presence of sparse, larger particles may be explained by the formation of sulfur agglomerates that were not broken up during electrode ink mixing. As discussed by Chung et al., electrodes with a polydisperse particle size distribution exhibit variations in lithium concentration accumulation resulting in different electrochemical states within the electrode.28 The resulting electrical field across the electrode is therefore spatially inhomogeneous, adding a degree of uncertainty to the use of continuum modelling techniques on Li–S battery systems.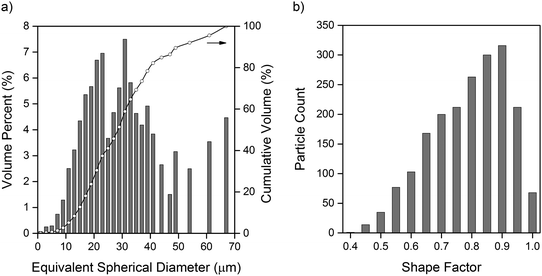 | ||
| Fig. 2 (a) Particle size distribution of sulfur particles, with equivalent spherical diameter converted from volume of individual particles. (b) Shape factor distribution of sulfur particles. | ||
In the wider context of cell performance, Chung et al. have found that whilst the power density of electrodes with a monodisperse particle size distribution outperform those of a polydisperse particle size distribution, polydispersity may improve energy density at lower C-rates due to the faster reaction kinetics contributed by smaller particles. Despite the fundamentally different reaction mechanisms between the LiMn2O4 electrodes used in that study, and conversion-type sulfur electrodes, similar inhomogeneities are invariably present within Li–S electrodes.
To better understand the suitability of applying the Bruggeman correlation to estimate the effective transport parameters in Li–S electrode materials, the shape factor of each sulfur particle was calculated by the method outlined by Haibel et al.,29 where a value of 1 represents perfect sphericity. Particles smaller than 2 μm in equivalent spherical diameter were excluded due to artefacts introduced by the cubic nature of voxels, however, this represented less than 0.1% of the total volume of particles in the dataset. It is clear from the shape factor distribution presented in Fig. 2(b) that the sulfur particles deviate significantly from perfect sphericity, with an average shape factor of 0.74. As one of the key assumptions in the derivation of the Bruggeman correlation is perfect sphericity of particles comprising the solid phase,10 this demonstrates the potential value of applying image-based simulation methods to calculate effective transport parameters.
Continuous pore size distribution
Continuous pore size distributions (PSDs) were calculated from the two- and three-phase label fields of the micro-CT dataset through the method outlined by Münch et al.26 and provided in the ImageJ plugin XLib. The pore radii range was selected to be between 0 and 200 μm in steps of 0.1168 μm, a reasonable bound as the diameter of the largest pore will not exceed the largest dimension of the volume. For the two-phase segmentation, the PSD was performed on the combined carbon binder domain and bulk pore phases, shown in black and grey in Fig. 1(b), while for the three-phase segmentation, the PSD was performed on only the bulk pore phase, shown in black in Fig. 1(b). The PSD on the two-phase segmentation highlights the importance of correctly evaluating the influence of the CBD phase on transport, which may be overlooked in favour of just evaluating the active material distribution especially when there is poor contrast between the CBD and pore phases.The macroscopic porosity of the electrode arising from the bulk pore phase exhibits a narrow distribution of pore sizes clustered around ca. 1 to 4 μm in radius as presented in Fig. 3(a). It is hypothesized that these pores arise from micro cracks forming during the evaporation of solvent from the electrode ink and are therefore highly dependent on processing conditions. Whilst the CBD is in itself highly porous and percolated with electrolyte, the porosity inherent to the CBD falls below the spatial resolution achievable in micro-CT. Therefore, a continuous pore size distribution, presented in Fig. 3(b), was performed on the two-phase segmentation, capturing all the electrolyte percolated non-sulfur phase within the electrode. A much broader pore size distribution was observed compared to Fig. 3(a), clustered around ca. 4 to 8 μm in radius. Interestingly, a jump in the pore size distribution is observed at the smallest pore radii of 0.1168 μm, most likely an artefact of image processing and application of the CPSD algorithm; however this is negligible as it only accounts for less than ca. 1% of the total pore volume.
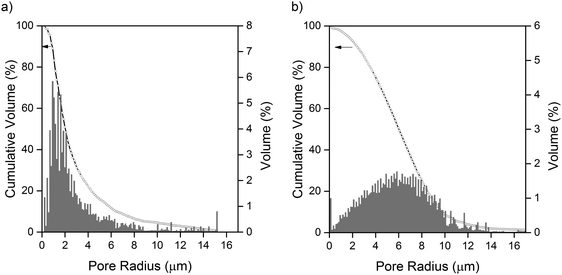 | ||
| Fig. 3 (a) Continuous pore size distribution of the bulk pore phase. (b) Continuous pore size distribution of the combined bulk pore phase and carbon binder phase (assumed to be completely porous). | ||
Unlike Li-ion cathode materials that exhibit little volume change during cycling, it is typical for sulfur and other conversion-type electrode materials to evolve dynamically as a function of state of charge and cycle life. Pore size distributions on the electrolyte percolated phase may serve as a good approximation of the evolution of the general electrode microstructure as a function of these variables.
Molecular diffusivity and electrical conductivity simulations
Two flux-based simulation approaches will be used to determine the tortuosity factor of the phase of interest, from which effective conductivity or diffusivity can be derived from a known porosity and bulk conductivity. The first approach, Avizo XLab, uses a finite volume discretization to solve Ohm's law of electrical conduction or Fick's law of diffusion, forming a system of linear equations that are directly resolved through matrix inversion. The second approach, the MATLAB application TauFactor, uses a finite difference-type discretization to solve Fick's law of diffusion, with an iterative over-relaxation method to resolve the system of linear equations.22 By comparison of the flux through the porous phase to the flux through a fully dense control volume of the same dimensions, tortuosity factor can then be obtained.30 All the Li–S battery models discussed above consider mass transport to be diffusive in nature, an assumption typical in models of closed battery cells.31,32 However, as some natural convection may stem from the soluble polysulfide intermediates produced in the conversion reactions occurring, absolute permeability simulations were performed for completeness and are presented in ESI.†Due to the mathematically analogous nature of the Laplacian equations for Fick's law of diffusion, Ohm's law of electronic conduction, and Fourier's law of heat transfer, the effective conductivity/diffusivity values for one parameter can be simulated interchangeably by any of these.22 The effective electrical conductivity of the electrode can therefore be calculated by performing the diffusive flux based simulations on the carbon binder domain.
All simulations were carried out on a cropped sub-volume internal to the micro-CT dataset, or on a volume fully containing the carbon binder domain in the nano-CT dataset. Two boundary conditions consisting of arbitrary input and output initial concentrations were applied on two opposite faces orthogonal to the direction of transport within the electrode. The bulk diffusivity or conductivity value was set to an arbitrary value in Avizo XLab, and assumes a default value of 1 m2 s−1 in TauFactor. For the purposes of the transport simulations, it was assumed that no reaction takes place within the solid phase, and all mass transport is diffusive in nature.
Tortuosity factor, τ, is a metric for describing resistance to diffusive flow through porous media due to convoluted flow paths22 and its use can be analogously extended to describe resistance to electron flow in the solid phase of porous media, or the electrical tortuosity. It is defined as:
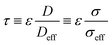 | (1) |
The effective diffusivity values in the through-plane direction were converted to tortuosity factors and are presented in Table 2 for ease of comparison.
| Tortuosity factors of the ion-conducting phase | ||
|---|---|---|
| Phase | Avizo XLab | TauFactor |
| Pore (nano-CT) | 4.89 | 4.92 |
| Lumped pore and CBD (micro-CT, two-phase segmentation) | 1.43 | 1.45 |
| Bulk pore phase (micro-CT, three-phase segmentation) | 4.08 | 4.12 |
| Combined pore phase (micro- and nano-CT) | — | 2.26 |
Effective molecular diffusivity of the carbon and binder phase
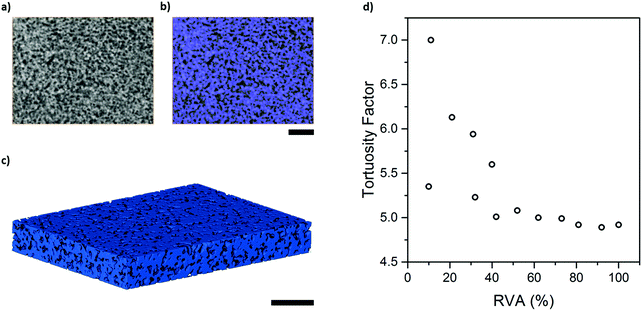
In order to determine the effective diffusivity intrinsic to the carbon binder domain, effective molecular diffusivity simulations were performed in Avizo XLab and TauFactor on the pore phase of the binary nano-CT label field as shown in Fig. 5(a–c), with an estimated volume fraction of ca. 32.4%. Tortuosity factor was determined to be 4.89 in Avizo XLab, in close agreement with 4.92 calculated in TauFactor. As discussed earlier, the effective diffusivity in the CBD will be underestimated to some degree as the nano porosities of the porous carbon were excluded because they remain below the spatial resolution capabilities of the instrument.Due to the small volume of the nano-CT dataset used for simulation in TauFactor, representative volume element analysis (RVE) was conducted: as illustrated in Fig. 5(d), representativeness was attained when the volume element examined exceeded 40% of the original volume, where tortuosity factor oscillated within a narrow band centred about ca. 4.9. The effective diffusivity of 0.0658 m2 s−1 from a bulk diffusivity of 1 m2 s−1, corresponding to this tortuosity factor, will be used in a later section to determine the mean diffusivity of the combined pore phase.
Effective molecular diffusivity of the Li–S cathode
Contrast resolution in absorption X-ray imaging is highly material dependent and in imaging battery electrode materials with lab-based XCT, numerous authors have reported difficulty in distinguishing between the carbon binder domain and pore phase due to similar X-ray absorption coefficients.33–35 Thus, many have resorted to a two-phase segmentation consisting of an active material phase and lumped carbon binder and pore phase.Flux-based simulations of effective transport properties on tomography data may underestimate tortuosity arising from the intrinsic porosity of the carbon binder domain, as found by Landesfeind et al. in the context of Li-ion electrodes,36 especially in the presence of highly tortuous pore networks within the CBD. In order to overcome these limitations, various approaches have been suggested in the literature, and these include correlative imaging with FIB-SEM, imposing a statistically relevant virtual microstructure,35,37,38 or through phase contrast enhancement. The latter technique is usually performed at specialist synchrotron facilities with advanced X-ray optics: for example, Chen-Wiegart et al. have successfully identified the carbon binder domain of LCO and NMC electrodes using synchrotron nano-CT with Zernike phase contrast.39 Whilst a three-phase segmentation (sulfur, bulk pore and CBD phase) was possible from the absorption contrast micro-CT data, lab-based Zernike phase contrast nano-CT was used here to examine the intrinsic porosity of the CBD with an enhanced pixel and contrast resolution, to reduce the degree of underestimation inherent to image-based simulations.
Effective diffusivity simulations were carried out on the lumped bulk pore and CBD phase (equivalent to the two-phase segmentation discussed previously), and the bulk pore phase of the three-phase segmentation. Both simulations represent extremes in that the former assumes a fully porous CBD phase through which there is no obstruction to ion transport by the solid conductive carbon and binder, whilst the latter assumes a fully solid CBD phase through which no ion transport occurs. To account for the resistance of the conductive carbon structure to Li-ion flow, the mean diffusivity across the bulk pore and CBD phases was simulated in TauFactor by inscribing a separate Deff value for the CBD calculated from the nano-CT dataset in TauFactor. The tortuosity factors presented in Table 2 were all found to be in close agreement between Avizo XLab and TauFactor. A mean tortuosity factor of 2.26 across both the pore and the carbon binder phase was determined, demonstrating that the lumped pore and carbon binder phase of a two-phase segmentation results in an underestimated tortuosity factor of only 1.45. Whilst it is acknowledged that the meso- and micro-pores of the carbon binder phase remain below the spatial resolution achievable in nano- and micro-CT, these pores only contribute to an estimated 10% of total porosity of the carbon binder phase as calculated earlier.
Design and optimisation of electrode architectures for Li–S systems is inherently more complex than for Li-ion counterparts: in addition to the promotion of fast lithium ion transport to maximize power density, there is an additional requirement to minimize polysulfide diffusion from the sulfur electrode in order to prolong cycle life in Li–S batteries. A multifaceted approach is required to balance these diametrically opposed goals, consisting of not only research into electrolyte formulations but also careful engineering of electrode microstructures.7 For instance, such engineered electrode microstructures may have variable porosities, tortuosities or sulfur loading as a function of electrode thickness. In this respect, image-based modelling serves as a powerful and convenient tool for the exploration of these engineering approaches, as these variations can easily be imposed on an original microstructure by direct modification of the labelled volumetric dataset. The aim of the modelling workflow presented in this paper is to provide a more informed approach to electrode structuring and intelligent electrode design.
Effective electrical conductivity of the sulfur electrode
To determine the effective electrical conductivity of the sulfur electrode, flux based simulations were performed using Avizo XLab and TauFactor on both the micro- and nano-CT dataset. The normalized voltage profile across the electrode in the through-plane direction can be visualized in Fig. 4(c), and effective conductivity values are presented in Table 3.| Effective electrical conductivity | ||
|---|---|---|
| Phase | Avizo XLab | TauFactor |
| CBD (nano-CT) | 0.45 | 0.46 |
| Sulfur electrode (micro-CT, uncorrected for effective conductivity of the CBD phase) | 0.16 | 0.16 |
| Sulfur electrode (micro-CT, corrected for effective conductivity of the CBD phase obtained from nano-CT) | 0.073 | 0.073 |
Simulations were first performed on the electrically conductive carbon and binder phase of the nano-CT dataset in order to determine the resistance to electron flow imposed by the intrinsic porosity inherent to the CBD. Both simulations were found to yield the same effective electrical conductivity, of ca. 0.45 S m−1 from an initial arbitrary bulk conductivity value of 1.00 S m−1 with a carbon and binder phase fraction of 67.6% in the CBD.
The effective conductivity of the CBD obtained from the first simulation was then used as input for simulations on the whole sulfur electrode performed on the micro-CT dataset, revealing the effective electrical conductivity across the sulfur electrode in the through-plane direction to be 0.073 S m−1 based on the initial bulk conductivity of 1.00 S m−1 used earlier. For the purposes of comparison, simulations were also performed on the sulfur electrode neglecting the intrinsic porosity of the CBD phase. In this case, an initial bulk conductivity value of 1.00 S m−1 was imposed directly on the CBD phase, with the effective electrical conductivity calculated to be 0.16 S m−1. From this, it is clear that neglecting the intrinsic porosity of the CBD phase results in a significant overestimation of the effective electrical conductivity of the electrode as a whole.
When compared to the use of empirical correlations to determine effective electrical conductivity in Li–S battery models, the image-based approach we have presented to measure effective electrical conductivity based on the actual microstructure of the sulfur electrode can be used to generate more realistic models for the design and optimization of sulfur electrodes when combined with experimental measurements of bulk conductivity.40
Optimization of parameters for battery performance
Computational techniques can be used for the optimisation of material morphologies, with the obvious benefits of in silico approaches compared with laborious, and often incremental, empirical approaches. For example, minor variations in electrode parameters such as active material particle size distribution, porosity and tortuosity can be readily imposed in simulations to investigate their influence on electrochemical performance and degradation pathways. A sensitivity analysis performed by Ghaznavi et al.32,41,42 evaluated the influence of parameters including charge and discharge rates, transport properties and reaction kinetics, on an earlier mathematical model developed by Kumaresan et al.6The optimisation of transport parameters is important in Li–S battery systems due to the pivotal role that dissolved polysulfide species play in contributing to capacity fade and poor Coulombic efficiency.7 The CBD microstructure influences conductivity and is central to electrochemical performance because of the electronically and ionically insulating nature of S and Li2S. The applications of this image-based workflow are not limited to evaluating transport properties as presented here. Instead, an opportunity is presented for a paradigm shift in the evaluation of other important battery parameters including C-rate, temperature and kinetics. The use of actual image data as a starting point ensures a faithful representation of the actual microstructure of the sulfur cathode upon which electrochemical models can be built. For instance, different conductive carbon additives and binders have been extensively explored in the literature, but the resulting morphologies of the formed electrodes remain poorly understood. The image-based workflow presented here will enable direct quantification of the influence that these resulting structures have on battery performance. To conclude, battery modelling can be a powerful tool to identify optimal Li–S electrode and cell designs, and validate theory with experimental results.43
Conclusions
The performance of the sulfur electrode is intimately linked with the conductivity of the carbon binder domain, as it not only acts as the sole electrically conductive framework for the transport of electrons from the current collector to connected sulfur particles, but also as a reaction surface on which the reduction of polysulfide species occurs, and where the final discharge product, Li2S, is formed at the lower voltage plateau. The sulfur phase itself is highly electronically and ionically insulating, and the electrochemical reaction front evolves as a function of state of charge due to the solubility of intermediate polysulfide species. At the fully charged state, reduction of sulfur predominantly occurs at the three phase boundary between a sulfur particle, the carbon binder phase and the electrolyte phase. This is further complicated by the solubility of sulfur in certain organic electrolytes that results in some proportion of the dissolved sulfur being reduced throughout the conductive carbon phase. Rational design of high performance electrodes should take account of the influence of the CBD on the electrical and ionic conductivity in the composite electrode structure, and therefore these tools are valuable for microstructure optimisation.One of the more compelling advantages of X-ray tomography compared to other techniques such as FIB-SEM is the non-destructive nature of the imaging process, which allows in situ and operando characterization to be carried out in specialized cells as previously reported by our group.44 In particular for sulfur electrodes, tortuosity and effective electrical conductivity are a strong function of state of charge and cycle life. Cycling data for the elemental sulfur electrode has been included in ESI,† that we propose can be validated in future work with cell simulation models, such as those presented by Danner et al.7 and Thangavel et al.,8 with the inclusion of the image-based workflow presented here. Furthermore, studies conducted as a function of cycle life may be used as an input for degradation modelling of Li–S batteries, providing an insight into the phenomenological origins of degradation mechanisms arising from microstructural heterogeneity. When full electrode imaging by micro-CT is combined with nano-CT information, a multi length-scale map of the electrode microstructure and morphology can be generated, facilitating the application of three dimensional modelling techniques such as Lattice Boltzmann modelling of pore-scale species distribution directly on volumetric image data.45 Given the importance of the CBD in determining the performance of sulfur electrodes, X-ray tomography is a powerful tool that provides unparalleled access to actual microstructural characteristics of the electrodes.
Author contributions
C. T., M. D. R. K. and S. R. D. contributed equally to the electrode fabrication, imaging and simulations in the work. D. J. L. B. and P. R. S. directed research. All authors discussed the results and contributed to the manuscript.Conflicts of interest
The authors declare no competing financial interests.Acknowledgements
The authors acknowledge financial support from the EPSRC under grants EP/M009394/1, EP/R020973/1, EP/N032888/1 and EP/K005030/1 and UCL. P. R. S. acknowledges funding from the Royal Academy of Engineering and M. D. R. K. acknowledges funding from the STFC Global Challenge Network in Batteries and Electrochemical Energy Devices.References
- P. G. Bruce, S. A. Freunberger, L. J. Hardwick and J. M. Tarascon, Nat. Mater., 2012, 11, 19–29 CrossRef CAS PubMed.
- L. F. Nazar, M. Cuisinier and Q. Pang, MRS Bull., 2014, 39, 436–442 CrossRef CAS.
- M. Barghamadi, A. Kapoor and C. Wen, J. Electrochem. Soc., 2013, 160, A1256–A1263 CrossRef CAS.
- M. A. Pope and I. A. Aksay, Adv. Energy Mater., 2015, 5, 1500124 CrossRef.
- Y. V. Mikhaylik and J. R. Akridge, J. Electrochem. Soc., 2004, 151, A1969 CrossRef CAS.
- K. Kumaresan, Y. Mikhaylik and R. E. White, J. Electrochem. Soc., 2008, 155, A576 CrossRef CAS.
- T. Danner, G. Zhu, A. F. Hofmann and A. Latz, Electrochim. Acta, 2015, 184, 124–133 CrossRef CAS.
- V. Thangavel, K.-H. Xue, Y. Mammeri, M. Quiroga, A. Mastouri, C. Guéry, P. Johansson, M. Morcrette and A. A. Franco, J. Electrochem. Soc., 2016, 163, A2817–A2829 CrossRef CAS.
- S. Torquato, Random Heterogeneous Materials, Springer-Verlag New York, New York, 1st edn, 2002 Search PubMed.
- B. Tjaden, S. J. Cooper, D. J. L. Brett, D. Kramer and P. R. Shearing, Curr. Opin. Chem. Eng., 2016, 12, 44–51 CrossRef.
- P. Pietsch and V. Wood, Annu. Rev. Mater. Res., 2017, 47, 451–479 CrossRef CAS.
- Z. Liu, J. Scott Cronin, Y.-C. K. Chen-Wiegart, J. R. Wilson, K. J. Yakal-Kremski, J. Wang, K. T. Faber and S. A. Barnett, J. Power Sources, 2013, 227, 267–274 CrossRef CAS.
- Y.-C. K. Chen-Wiegart, P. Shearing, Q. Yuan, A. Tkachuk and J. Wang, Electrochem. Commun., 2012, 21, 58–61 CrossRef CAS.
- D. P. Finegan, M. Scheel, J. B. Robinson, B. Tjaden, M. Di Michiel, G. Hinds, D. J. Brett and P. R. Shearing, Phys. Chem. Chem. Phys., 2016, 18, 30912–30919 RSC.
- D. P. Finegan, E. Darcy, M. Keyser, B. Tjaden, T. M. M. Heenan, R. Jervis, J. J. Bailey, R. Malik, N. T. Vo, O. V. Magdysyuk, R. Atwood, M. Drakopoulos, M. DiMichiel, A. Rack, G. Hinds, D. J. L. Brett and P. R. Shearing, Energy Environ. Sci., 2017, 10, 1377–1388 RSC.
- O. O. Taiwo, J. M. Paz-García, S. A. Hall, T. M. M. Heenan, D. P. Finegan, R. Mokso, P. Villanueva-Pérez, A. Patera, D. J. L. Brett and P. R. Shearing, J. Power Sources, 2017, 342, 904–912 CrossRef CAS.
- D. Schröder, C. L. Bender, T. Arlt, M. Osenberg, A. Hilger, S. Risse, M. Ballauff, I. Manke and J. Janek, J. Phys. D: Appl. Phys., 2016, 49, 404001 CrossRef.
- G. Tonin, G. Vaughan, R. Bouchet, F. Alloin, M. Di Michiel, L. Boutafa, J. F. Colin and C. Barchasz, Sci. Rep., 2017, 7, 2755 CrossRef.
- S.-H. Yu, X. Huang, K. Schwarz, R. Huang, T. A. Arias, J. D. Brock and H. D. Abruña, Energy Environ. Sci., 2018, 11, 202–210 RSC.
- D. Kehrwald, P. R. Shearing, N. P. Brandon, P. K. Sinha and S. J. Harris, J. Electrochem. Soc., 2011, 158, A1393 CrossRef CAS.
- K. Rhazaoui, Q. Cai, C. S. Adjiman and N. P. Brandon, Chem. Eng. Sci., 2013, 99, 161–170 CrossRef CAS.
- S. J. Cooper, A. Bertei, P. R. Shearing, J. A. Kilner and N. P. Brandon, SoftwareX, 2016, 5, 203–210 CrossRef.
- A. D. Dysart, J. C. Burgos, A. Mistry, C.-F. Chen, Z. Liu, C. N. Hong, P. B. Balbuena, P. P. Mukherjee and V. G. Pol, J. Electrochem. Soc., 2016, 163, A730–A741 CrossRef CAS.
- T. Zhang, M. Marinescu, S. Walus and G. J. Offer, Electrochim. Acta, 2016, 219, 502–508 CrossRef CAS.
- A. Tkachuk, F. Duewer, H. Cui, M. Feser, S. Wang and W. Yun, Z. Kristallogr. – Cryst. Mater., 2007, 222, 650–655 CAS.
- B. Münch and L. Holzer, J. Am. Ceram. Soc., 2008, 91, 4059–4067 CrossRef.
- J. J. Bailey, T. M. M. Heenan, D. P. Finegan, X. Lu, S. R. Daemi, F. Iacoviello, N. R. Backeberg, O. O. Taiwo, D. J. L. Brett, A. Atkinson and P. R. Shearing, J. Microsc., 2017, 267, 384–396 CrossRef CAS.
- D. W. Chung, P. R. Shearing, N. P. Brandon, S. J. Harris and R. E. Garcia, J. Electrochem. Soc., 2014, 161, A422–A430 CrossRef CAS.
- A. Haibel, I. Manke, A. Melzer and J. Banhart, J. Electrochem. Soc., 2010, 157, A387 CrossRef CAS.
- B. Tjaden, D. P. Finegan, J. Lane, D. J. L. Brett and P. R. Shearing, Chem. Eng. Sci., 2017, 166, 235–245 CrossRef CAS.
- B. Horstmann, T. Danner and W. G. Bessler, Energy Environ. Sci., 2013, 6, 1299 RSC.
- M. Ghaznavi and P. Chen, Electrochim. Acta, 2014, 137, 575–585 CrossRef CAS.
- B. Yan, C. Lim, L. Yin and L. Zhu, J. Electrochem. Soc., 2012, 159, A1604–A1614 CrossRef CAS.
- M. Ebner, F. Geldmacher, F. Marone, M. Stampanoni and V. Wood, Adv. Energy Mater., 2013, 3, 845–850 CrossRef CAS.
- L. Zielke, T. Hutzenlaub, D. R. Wheeler, C.-W. Chao, I. Manke, A. Hilger, N. Paust, R. Zengerle and S. Thiele, Adv. Energy Mater., 2015, 5, 1401612 CrossRef.
- J. Landesfeind, M. Ebner, A. Eldiven, V. Wood and H. A. Gasteiger, J. Electrochem. Soc., 2018, 165, A469–A476 CrossRef CAS.
- S. Vierrath, L. Zielke, R. Moroni, A. Mondon, D. R. Wheeler, R. Zengerle and S. Thiele, Electrochem. Commun., 2015, 60, 176–179 CrossRef CAS.
- T. Prill, D. Jeulin, F. Willot, J. Balach and F. Soldera, Transp. Porous Media, 2017, 120, 141–165 CrossRef CAS.
- Y.-c. K. Chen-Wiegart, Z. Liu, K. T. Faber, S. A. Barnett and J. Wang, Electrochem. Commun., 2013, 28, 127–130 CrossRef CAS.
- M. Park, X. Zhang, M. Chung, G. B. Less and A. M. Sastry, J. Power Sources, 2010, 195, 7904–7929 CrossRef CAS.
- M. Ghaznavi and P. Chen, J. Power Sources, 2014, 257, 394–401 CrossRef CAS.
- M. Ghaznavi and P. Chen, J. Power Sources, 2014, 257, 402–411 CrossRef CAS.
- A. A. Franco, M. L. Doublet and W. G. Bessler, Physical Multiscale Modeling and Numerical Simulation of Electrochemical Devices for Energy Converrsion and Storage, Springer, 2015 Search PubMed.
- A. Yermukhambetova, C. Tan, S. R. Daemi, Z. Bakenov, J. A. Darr, D. J. Brett and P. R. Shearing, Sci. Rep., 2016, 6, 35291 CrossRef CAS.
- J. R. Izzo, A. S. Joshi, K. N. Grew, W. K. S. Chiu, A. Tkachuk, S. H. Wang and W. Yun, J. Electrochem. Soc., 2008, 155, B504 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c8cp04763d |
| This journal is © the Owner Societies 2019 |