General existence of flexural mode doublets in nanowires targeting vectorial sensing applications

Abstract

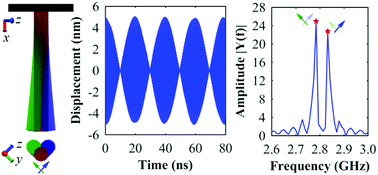
Nanowires (NWs) are one of the fundamental building blocks for nanoscale devices, and have been frequently utilized as mechanical resonators. Earlier studies show that ultra-sensitive vectorial sensing toolkits can be fabricated by changing the flexural mode of NWs to oscillation doublets along two orthogonal directions. Based on in silico studies and the Timoshenko beam theory, this work finds that the dual orthogonal flexural mode of NWs can be effectively controlled through the proper selection of their growth direction. It is found that metallic NWs with a directional-independent shear modulus possess a single flexural mode. However, NWs with a directional-dependent shear modulus naturally exhibit flexural mode doublets, which do not disappear even with increasing slenderness ratio. Further studies show that such a feature generally exists in other NWs, such as Si NWs. Mimicking a pendulum configuration as used in NW-based scanning force microscopy, the cantilevered 〈110〉 Si NW demonstrates zeptogram mass resolution and a force sensitivity down to the order of 10⁻²⁴ N Hz^−1/2 (yN Hz^−1/2) in both transverse directions. The findings in this work open up a new and facile avenue to fabricate 2D vectorial force sensors, which could enable ultra-sensitive and novel detection devices/systems for 2D effects, such as the anisotropy strength of atomic bonds.