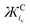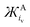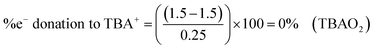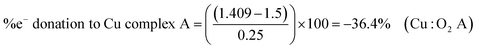Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Evaluating chemical bonding in dioxides for the development of metal–oxygen batteries: vibrational spectroscopic trends of dioxygenyls, dioxygen, superoxides and peroxides†
Petar M.
Radjenovic
and
Laurence J.
Hardwick
 *
*
Stephenson Institute for Renewable Energy, Department of Chemistry, University of Liverpool, L69 7ZF, UK. E-mail: hardwick@liverpool.ac.uk
First published on 8th January 2019
Abstract
Dioxides (dioxygenyl (O2+), dioxygen (O2), superoxide (O2˙−) and peroxide (O22−)) are of immense biological, chemical and environmental importance. The ability to accurately detect and measure the changing strength of their chemical bonding and coordination in situ or operando is extremely beneficial in order to evaluate their chemical properties, this has been particularly important recently in the field of metal–oxygen batteries, where understanding the reactivity of the O2˙− intermediate is crucial in the development of more stable electrolytes. Meta-analysis of the collated vibrational Raman and IR spectral bands of numerous (>200) dioxygen species was used to interpret the effect that the immediate chemical environment has on the O–O bond. Subsequently, the dioxide vibrational spectral bands were empirically related directly with the bond electron density and other fundamental bond properties, with surprisingly high accuracy, allowing each property to be estimated, simply, from experimental spectroscopic observations. Important chemical information about the strength of secondary interactions between reduced oxygen species and its chemical environment can be also elucidated which provides a convenient method for determining the attractive strength an ion exerts over neighbouring counter ions.
1. Introduction
Oxygen (O) is a reactive and abundant element of immense chemical, biological, and environmental importance, warranting classification as a field of study in its own right similar to organic (carbon) and inorganic (transitional metal) chemistries.1,2 Gaseous dioxygen (O2), composed of two covalently bonded homonuclear atoms, constitutes 20.95% of Earth's atmosphere, providing an oxidising environment and thermodynamic driving force for many biological processes. Crucially, the controlled reaction of O2 in the oxidation of glucose during aerobic respiration allows life on Earth to thrive. However, living organisms must also possess kinetic barriers to slow oxidation reactions with O2 to survive. The gradual decay of these kinetic barriers to oxidation in the body is responsible for ageing. In humans, reactive oxide species (ROSs): O2˙−, O22−, O2−, HO2, H2O2 and OH˙ are produced as by-products of normal cell processes and are used in the immune response of white blood cells. However, excessive production of ROSs adds oxidative stress to cells causing cell and DNA damage (specifically mitochondrial DNA) which is linked to the formation of cancer cells.3–5Metal–oxygen (M–O2) batteries have to deal with many of the same problems faced by biological systems, such as controlling the production and side reaction rate of ROSs. In addition, dioxide ligands are prevalent in organometallic and catalysis chemistry. Therefore, the chemistry of dioxide species’ (O2x, where x = −2, −1, 0 or +1) has warranted detailed scientific study in multiple fields.1,2,6
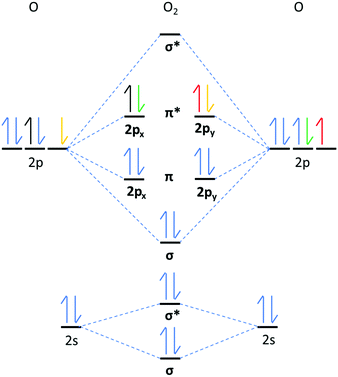
O2x are homonuclear molecules that possess covalent O–O bonds and their characteristic symmetric stretching vibrations (νO–O) are visible spectroscopically. Examining the νO–O spectral band can provide valuable information about the chemical nature of the O2x. The oxidation state and reactivity of O2x, depends on the number of electrons occupying the highest occupied molecular orbital (HOMO), which are the π*(2pxy) valence antibonding orbitals (Fig. 1), their spin state(s) and the O–O bond order (BO, defined as the number of covalent bonds, see eqn (1)). O2+ cations possess one electron in the π*(2px) antibonding orbital and have a BO of 2.5. O–O bonding electrons in O2+ cations experience high effective nuclear charge from the O nuclei, so have a short O–O bond length (BL, 1.12 Å) and a high wavenumber νO–O (1876 cm−1) value.7,8 From O2+ to O22−, the BO decreases by 0.5 for each electron added into the π*(2pxy) orbital. As an electron is added to the π*(2pxy) orbital, increased antibonding and Coulombic repulsion between bonding electrons cause the O–O BL to increase and the νO–O to red-shift. O22− possesses a BO of 1 and has the longest O–O bond (1.49 Å) of the homonuclear dioxides with the lowest νO–O value (∼743 cm−1).9 In addition to O–O bond lengthening and the characteristic red shifts in νO–O spectra, each electron transferred to O2x causes a decrease in the bond force constant (Bk) and a drop in the bond dissociation enthalpy (BH) of the O–O bond, discussed in more detail later.
 | (1) |
Neutral O2 contains two electrons in the π*(2pxy) orbital(s) that can occupy three different spin states (Fig. 1); high-energy singlet (1Σ+g), singlet (1Δg) and triplet (3Σ−g). Unlike many common diatoms and organic molecules, which favour the 1Δg state, the 3Σ−g state is the lowest energy ground state of O2 with two electrons in degenerate orbitals with the same spin. The 3Σ−g O2 orbital structure complicates coupling with other molecules in the 1Δg state, which adds to the chemical stability of 3Σ−g O2. It is the: one-electron, two-electron or four-electron transition from 3Σ−g O2 to: O2˙−, O22− or O2−, respectively, and back again, that underpins the oxygen reduction and evolution reactions (ORR/OERs). For non-aqueous lithium oxygen (Li–O2) batteries, in situ surface enhanced Raman spectroscopic (SERS) studies of νO–O have been instrumental in showing a O2˙− intermediary reaction mechanism and the existence of lithium peroxide (Li2O2) as the primary battery discharge product.10–12
Johnson et al.11 in particular highlighted the effect of solvent choice in the determination of the ORR pathway via either surface or solution route. Using SERS they showed that low-donor number solvents, such as acetonitrile, lead to a surface reaction resulting in thin, insulating Li2O2 film growth. In contrast, in high-donor number solvents, such dimethyl sulfoxide resulted in preferential Li2O2 particle growth in solution. High donor number solvents are thereby preferable in the context of Li–O2 batteries as Li2O2 solution growth leads to higher capacities.
Creighton et al. first reported the νO–O stretch of O2˙− with Raman spectroscopy of KO2 and contaminated Na2O2 in 1964.13 This was corroborated and expanded upon with other group-1 alkali-metal cation complexes ([M+⋯O2˙−], where M = Li, Na, K, Rb or Cs) in the following decade at a variety of different temperatures.14–21 Sawyer et al. synthesised and spectroscopically characterised the first O2˙− salt with an organic cation, in 1983, by substituting K+ with tetramethylammonium (TMA+).22 [TMA+⋯O2˙−] had a spectrum analogous to KO2, though slightly red shifted (∼22 cm−1).22 Since then, the νO–O of many O2˙− complexes [C+⋯O2˙−] have been detected in a variety of systems and phases. Such as: solid salts,13,22 doped into other salts,23 as an organometallic complex,6 dissolved in organic solvents24 or generated electrochemically at a SERS active electrode–electrolyte interface.10,11,25,26
Understanding the reactivity and bonding environment of the O2˙− intermediate is crucial in the development of more stable M–O2 battery electrolytes and in particular, ambiguity around the existence and chemical character of the lithium superoxide (LiO2) intermediary remains.27,28 Thus, a detailed look at the νO–O spectra of species produced during ORR/OERs is warranted to better understand in the reaction mechanisms in non-aqueous electrolytes in order to assist in the fundamental understanding of lithium–oxygen and in more general other M–O2 batteries.
2. Experimental
2.1. Calculation of ion properties
Ionic volumes, ionic surface area, charge distributions and electrostatic potential surface distributions for a number of molecular ions were determined using a simple density functional theory (DFT, B3LYP functional, 6-31G* basis set) in Spartan 16. Ionic volumes and surface areas for atomic cations were calculated using a simple pace-filling calotte (CPK) model.3. Results and discussion
3.1. Meta-analysis of superoxide's Raman spectra
To investigate possible trends of O2˙− bonding, relevant literature reports of >50 species were collated and examined.10,11,13–18,25,26,29–60 See Table S1 (ESI†) for a catalogue of reported [C+⋯O2˙−] complexes.Raman spectral band positions reflect molecular energy levels in a vibrating bond and are well known to be influenced by (1) the mass of the atoms in the bond, (2) the bond force constant and (3) lattice/symmetry effects. For [C+⋯O2˙−], counter cations (or strongly coordinating solvents) attract O–O bond electron density at different rates which also influences the force constant of the vibration, resulting in νO–O band shifts, explained further below.61
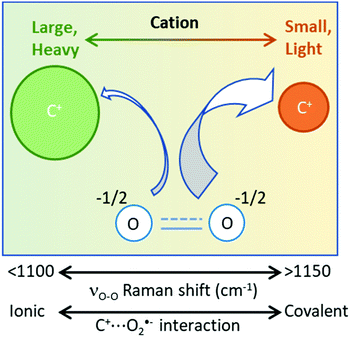
The molecular mass-to-charge ratio (MrQ−1, units: mol g−1 C−1) of an ion can dictate its Columbic attractive strength towards counter-ions. Generally, ions with low MrQ−1 values are stronger Coulombic attractors than ions with high values. In a [C+⋯O2˙−] complex, where interactions between O2˙− and the counter-cation (C+) are weak: electron density is more concentrated on the O2˙− anion, the effective nuclear charge experienced by O–O valence bonding electrons is lower and the bond is longer than when O2˙− is strongly coordinated. This effect is visible spectroscopically, with weakly coordinated O2˙− complexes having lower wavenumber νO–O values (e.g. tetrabutylammonium [TBA+⋯O2˙−]: <1115 cm−1)10,11,25,26,60 and strongly coordinated O2˙− complexes having higher νO–O values (e.g. [Na+⋯O2˙−]: ≥1155 cm−1).15,17,47–52,62 The strength of the attraction between the coordinating cation and O2˙− effects valence bond electron density and the O–O bond force constant, causing the observed difference in νO–O wavenumbers.
For monovalent [C+⋯O2˙−] complexes (independent of phase), plotting reported νO–O values against the MrQ−1 value of the coordinating cation (Fig. 2) shows an inverse trend (R2 = 0.757). In Fig. 2, two further sub-trends are apparent for: (1) single atom cations (shown in blue) and (2) molecular cations (shown in red). Single atom cations such as Rb+ (85.5 mol g−1 C−1) and Cs+ (132.9 mol g−1 C−1) have similar Mr values as TMA+ (74 mol g−1 C−1) and tetraethylammonium (TEA+) (130.0 mol g−1 C−1), respectively, but have higher wavenumber νO–O spectral bands (>15 cm−1). This difference in the νO–O spectral bands can be accounted for by considering the size difference in these cations. Single atom alkali-metal cations are spatially smaller allowing them interact more closely with O2˙− valence bond electron density than large molecular organic cations. Therefore, as a general rule: strong O2˙− coordination has a higher wavenumber νO–O spectral band.
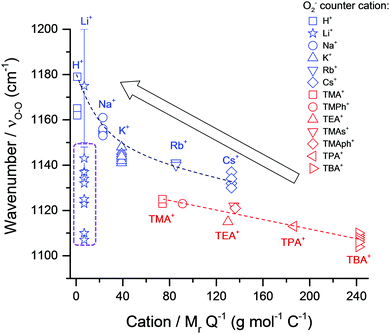 | ||
| Fig. 2 ν O–O Raman bands for [C+⋯O2˙−] complexes plotted against the MrQ−1 value of the coordinating cation (listed data in Table S1, ESI†). An inverse trend is visible with heavier coordinating cations having lower wavenumber νO–O bands indicating a less energetic O2˙− bond vibration and a ‘freer’ more Lewis basic species. A general fit produced R2 values of 0.757 for the overall trend. Two sub-trends are apparent: (1) single atom and (2) molecular coordinating-cations. Lines of best fit for both trends (dashed lines) had R2 values of 0.850 and 0.867 for single atom (blue) and molecular (red) coordinating cations, respectively. Circled bands (purple dashed line) are reports of LiO2 related species. These do not match the expected trend for Li+, discussed later. Error bar refers to broad band between 1150–1200 cm−1 reported as LiO2 by Xia et al.36 | ||
3.2. Ionic charge dispersion
The immediate coordinating environments ability to interact with O2˙− also provides interesting information about the reactivity and basicity of O2˙− in the complex which is reflected in the νO–O value. From Fig. 2, [C+⋯O2˙−] containing high Mr cations (e.g. TBA+) have low νO–O values indicative of a more ionic ‘freer’ O2˙− species. In these complexes, O2˙− is a stronger Lewis base and can be expected to more readily donate electron density. Inversely, low Mr cation containing [C+⋯O2˙−] complexes such as (H+) have stronger C+-to-O2˙− interactions with slight covalent character, resulting in higher wavenumber νO–O bands indicative of a weaker Lewis base O2˙− species. It was found that for cations coordinating O2x species, the: size, mass and charge influence the strength of coordination and in turn the O–O bond force constant which causes detectable changes in νO-O. Thus, the physical parameters of one ion can indirectly influence the bond force constant and wavenumber of bonds present in the counter-ion. These values for ions can be simply quantified in terms of the Mr, ionic volume (iv) and the charge on the ion (z). In O2x complexes; changes in the Mr and iv of the coordinating counter-ions were found to be inversely proportional to changes in νO–O whilst changes in the charge of the counter-ion were proportional quantified by the term. Considering the effect the size of the cation has on the νO–O of O2˙− complexes, this can be quantified by either the ionic volume (iv) or the available ionic surface area (is.a.), measured in Å3 and Å2, respectively. iv and is.a. values are known for most alkali-metal cations and can be calculated computationally using simple CPK or DFT models for larger molecular cations.The νO–O of a [C+⋯O2˙−] complex changes proportionally with the charge (q) on the cation and inversely proportionally with the molecular mass (Mr) and iv (and is.a.) of the coordinating cation (eqn (2)). Assuming a uniform charge distribution over the ion: multiplying the MrQ−1 and a spatial component (iv or is.a.) gives a parameter (eqn (3)), hereon named the ‘ionic charge dispersion’ (Ж).
 | (2) |
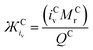 | (3) |
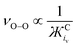 | (4) |
The Ж value can be used to estimate the Coulombic attractive strength of an ion and the effect it will have on counter-ions. The Cyrillic symbol for Ž (Ж) is used for ionic charge dispersion, subscripts iv and is.a. denote the use of ionic volume or ionic surface area, respectively, and superscripts A and C denote anion and cation, respectively. Ж is an analogue of the charge density of an ion (MrQ−1iv−1). However, charge density does not account for the proportional relationship between: Mr, iv and the Columbic attractive strength of the ion. Thus, Ж has been derived as a simple value to describe these ionic properties. Ж is a measure the ‘bulkiness’ of the counter-ion, where, the higher the Ж value the bulkier the ion is.
Excluding outliers, plotting the reported νO–O values of [C+⋯O2˙−] complexes from Table 1 against the calculated 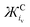 (units: mol g−1 Å3 C−1) or
(units: mol g−1 Å3 C−1) or  (units: mol g−1 Å2 C−1) of each coordinating cation shows a clear inverse exponential relationship (Fig. 3 and Fig. S1, respectively, ESI†). Ж provides a much better fit than using the MCr or iCv of the coordinating cation alone. The spatial components iCv or iCs.a. are used to calculate Ж but it appears to be unimportant which is used as they both change proportionally with one another between different cations. However, iCv gives a slightly better fit with a higher R2 value of 0.952 (given the larger number of independent reports using different phases, systems and detection equipment spanning over >50 years this is a fairly good fit) compared with 0.942 using iCs.a. (Fig. S1, ESI†). Plotting on a logarithmic scale shows this correlation more clearly (Fig. 3). All reports of LiO2 except for one36 were excluded, this is discussed in Section 3.6.
(units: mol g−1 Å2 C−1) of each coordinating cation shows a clear inverse exponential relationship (Fig. 3 and Fig. S1, respectively, ESI†). Ж provides a much better fit than using the MCr or iCv of the coordinating cation alone. The spatial components iCv or iCs.a. are used to calculate Ж but it appears to be unimportant which is used as they both change proportionally with one another between different cations. However, iCv gives a slightly better fit with a higher R2 value of 0.952 (given the larger number of independent reports using different phases, systems and detection equipment spanning over >50 years this is a fairly good fit) compared with 0.942 using iCs.a. (Fig. S1, ESI†). Plotting on a logarithmic scale shows this correlation more clearly (Fig. 3). All reports of LiO2 except for one36 were excluded, this is discussed in Section 3.6.
 and
and  values for some common cations and IL cations. Cations with smaller Ж values are expected to be stronger Lewis acids
values for some common cations and IL cations. Cations with smaller Ж values are expected to be stronger Lewis acids
| Cation | M r (g mol−1) | i Cv (Å3) | i Cs.a. (Å2) | Q (C) | (g mol−1 Å3 C−1) | (g mol−1 Å2 C−1) |
|---|---|---|---|---|---|---|
| H+ | 1.0 | 7.2 | 18.1 | 1 | 7 | 18 |
| Li+ | 6.9 | 5.6 | 10.2 | 1 | 39 | 71 |
| Na+ | 23.0 | 10.1 | 19.3 | 1 | 233 | 443 |
| Ca2+ | 40.1 | 15.0 | 29.4 | 2 | 301 | 589 |
| K+ | 39.1 | 21.1 | 37.0 | 1 | 827 | 1446 |
| Bi3+ | 209.0 | 31.85 | 48.60 | 3 | 2219 | 3386 |
| Rb+ | 85.5 | 26.6 | 43.1 | 1 | 2272 | 3681 |
| Cs+ | 132.9 | 35.2 | 51.9 | 1 | 4678 | 6903 |
| TMA+ | 74.1 | 105.2 | 128.4 | 1 | 7799 | 9523 |
| TMP+ | 91.1 | 115.2 | 141.8 | 1 | 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 497 497 |
12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 923 923 |
| TES+ | 119.3 | 148.5 | 109.8 | 1 | 17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 704 704 |
13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 093 093 |
| TEA+ | 130.3 | 195.4 | 177.5 | 1 | 25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 451 451 |
23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 115 115 |
| Pyr14+ | 142.3 | 183.2 | 129.4 | 1 | 26![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 060 060 |
18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 408 408 |
| TPA+ | 186.4 | 250.4 | 273.8 | 1 | 46![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 662 662 |
51![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 030 030 |
| Di-Im2+ | 296.4 | 358.0 | 338.4 | 2 | 53![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 062 062 |
50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 154 154 |
| TBA+ | 242.5 | 324.0 | 355.0 | 1 | 78![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 566 566 |
86![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 065 065 |
| N1888+ | 368.7 | 489.0 | 540.1 | 1 | 180![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 316 316 |
199![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 128 128 |
 | ||
Fig. 3
ν
O–O Raman band positions for [C+⋯O2˙−] complexes plotted versus the calculated  (see Table S1, ESI†) of the coordinating cation. Empirically derived equations for the lines of best fit and R2 values for the fits are shown in bottom left-hand corner. ЖC was calculated using iCv which provides a better fit than using iCs.a.. iCv and iCs.a.. Ionic volumes and surface areas were calculated in Spartan 15 using a CPK model for single atom cations (blue) and DFT (B3LYP, 6-31G*) for molecular cations (red). A single reference36 of LiO2 (νO–O) has been considered due to the wide variation in wavenumber position reported, as discussed within the main text. (see Table S1, ESI†) of the coordinating cation. Empirically derived equations for the lines of best fit and R2 values for the fits are shown in bottom left-hand corner. ЖC was calculated using iCv which provides a better fit than using iCs.a.. iCv and iCs.a.. Ionic volumes and surface areas were calculated in Spartan 15 using a CPK model for single atom cations (blue) and DFT (B3LYP, 6-31G*) for molecular cations (red). A single reference36 of LiO2 (νO–O) has been considered due to the wide variation in wavenumber position reported, as discussed within the main text. | ||
When detecting the νO–O of O2˙−, the derived equation for the line of best-fit (eqn (5)) from Fig. 3 can be used to help estimate its ionic character and the coordination strength of the environment in terms of  . With this knowledge, O2˙− can be used as a diagnostic molecule to probe ion and even electrolyte interactions spectroscopically in environments where the coordination strength is unknown (e.g. novel electrolytes). This relationship between νO–O and
. With this knowledge, O2˙− can be used as a diagnostic molecule to probe ion and even electrolyte interactions spectroscopically in environments where the coordination strength is unknown (e.g. novel electrolytes). This relationship between νO–O and  in Fig. 3 was found to hold in most cases. However, it can be manipulated by changing the symmetry, steric hindrance and charge of the coordinating cation, as well as the solvents Gutmann acceptor/donor numbers63 and the potential at an electrode surface, where O2˙− is generated electrochemically (to be discussed elsewhere).
in Fig. 3 was found to hold in most cases. However, it can be manipulated by changing the symmetry, steric hindrance and charge of the coordinating cation, as well as the solvents Gutmann acceptor/donor numbers63 and the potential at an electrode surface, where O2˙− is generated electrochemically (to be discussed elsewhere).
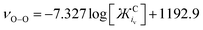 | (5) |
3.3. Ionic charge dispersion of other ions
The Ж value estimates the dispersion of a formal charge on an ion by assuming the charge is delocalised (i.e. dispersed uniformly across the volume and molecular mass of the ion). Ж is a simple value that can be calculated for any ion to approximate its coordination strength and/or propensity to interact with oppositely charged ions. Small Ж values indicate ions that are strong: coordinators or Lewis acid/bases, whilst large values represent weak: coordinators or Lewis acid/bases. This can be further explained in terms of hard–soft acid–base (HSAB) theory. Hard acids interact better with hard bases and soft acids with soft bases.64 Ions with low Ж values can be consider hard Lewis acid/bases and ions with high Ж values can be considered soft Lewis acid/bases.
Tables 1 and 2 list calculated Ж values for some common cations and anions, respectively. The Ж value is a clear simplification of the charge on an ion, excluding many important contributions to inter-ion interactions such as: steric hindrance, charge density, the component molecules oxidation states and symmetry etc. However, as discussed, Ж values give a good approximation for the influence of the cation on the νO–O of O2˙− and are likely applicable to other systems too. Furthermore, additional quantifiable values for other ion properties (such as: symmetry etc.) could be added to refine the Ж parameter further in future. When selecting ions for their attractive strength Ж parameters (and possibly ЖC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ЖA ratios) could be used to quickly screen some of the near infinite number of ions and combinations that can be selected. Also, Ж parameters give a quick and cheap starting point when designing and tailoring novel IL electrolytes or salts. This is a good starting point compared with more precise computational or experimental techniques which are expensive, time consuming and would necessarily come later after first narrowing the field of search. Based on the
ЖA ratios) could be used to quickly screen some of the near infinite number of ions and combinations that can be selected. Also, Ж parameters give a quick and cheap starting point when designing and tailoring novel IL electrolytes or salts. This is a good starting point compared with more precise computational or experimental techniques which are expensive, time consuming and would necessarily come later after first narrowing the field of search. Based on the 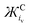 value, the calculated Coulombic attractive strength of cations on anions is suggested to be similar for: Na+ and Ca2+ (233 and 301 g mol−1 Å3 C−1), Rb+ and Bi3+ (2272 and 2219 g mol−1 Å3 C−1) and TEA+ and Pyr14+ (25
value, the calculated Coulombic attractive strength of cations on anions is suggested to be similar for: Na+ and Ca2+ (233 and 301 g mol−1 Å3 C−1), Rb+ and Bi3+ (2272 and 2219 g mol−1 Å3 C−1) and TEA+ and Pyr14+ (25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 451 and 26
451 and 26![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 060 g mol−1 Å3 C−1, respectively).
060 g mol−1 Å3 C−1, respectively).
 and
and  values for common anions and IL anions. Anions with smaller values are expected to be stronger Lewis bases
values for common anions and IL anions. Anions with smaller values are expected to be stronger Lewis bases
| Anion | M r (g mol−1) | i v (Å3) | i sa (Å2) | Q (C) | (g mol−1 Å3 C−1) | (g mol−1 Å3 C−1) |
|---|---|---|---|---|---|---|
| O2− | 16.0 | 14.7 | 29.0 | 2 | −118 | −232 |
| F− | 19.0 | 14.5 | 28.8 | 1 | −276 | −547 |
| OH− | 17.0 | 17.1 | 32.8 | 1 | −291 | −558 |
| O22− | 32.0 | 25.1 | 44.1 | 2 | −402 | −705 |
| O2˙− | 32.0 | 23.1 | 40.7 | 1 | −738 | −1302 |
| Cl− | 35.5 | 23.7 | 39.9 | 1 | −840 | −1415 |
| Br− | 79.9 | 28.0 | 44.7 | 1 | −2239 | −3569 |
| NO3− | 62.0 | 41.2 | 61.6 | 1 | −2552 | −3817 |
| SO42− | 96.1 | 55.0 | 73.7 | 2 | −2642 | −3538 |
| I− | 126.9 | 34.8 | 51.5 | 1 | −4414 | −6539 |
| DiCN− | 66.0 | 65.0 | 88.7 | 1 | −4295 | −5859 |
| ClO4− | 99.4 | 54.1 | 70.2 | 1 | −5384 | −6981 |
| OTf− | 149.1 | 83.6 | 81.4 | 1 | −12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 455 455 |
−12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 127 127 |
| TFSI− | 280.1 | 153.5 | 115.2 | 1 | −43![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 014 014 |
−32![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 262 262 |
Similarly, for the  of anions, the Coulombic attractive strength of anions on cations is suggested to be similar for: F− and OH− (−276 and −296 g mol−1 Å3, respectively), Cl− and O2˙− (−840 and 738 g mol−1 Å3, respectively), whilst I− is comparable with dicyanamide (DiCN−) and ClO4− (−4414, −4295 and −5384 g mol−1 Å3, respectively).
of anions, the Coulombic attractive strength of anions on cations is suggested to be similar for: F− and OH− (−276 and −296 g mol−1 Å3, respectively), Cl− and O2˙− (−840 and 738 g mol−1 Å3, respectively), whilst I− is comparable with dicyanamide (DiCN−) and ClO4− (−4414, −4295 and −5384 g mol−1 Å3, respectively).
3.4. Dioxygen spectra and important bond parameters
It is of great practical value to relate physical bond parameters with spectral measurements so they can be derived with ease experimentally. To that end, several efforts have been made, however, these methods remain empirical.65 Key O2x bond parameters such as the bond order (BO), bond dissociation enthalpy (BH), bond force constant (Bk) and bond length (BL) require various experimental procedures to derive, like X-ray crystallography (XRC). Bond parameter values for most O2x species exist and can be correlated well with empirically measured νO–O values. Table 3 lists these bond parameters for different O2x species. Correlating these O–O bond parameters allows for variations in each bond parameter to be estimated by only measuring the νO–O of the O2x species.| O–O bond parameters | O22− | O2•− | O2 | O2+ | Ref. |
|---|---|---|---|---|---|
| Where: a = νO–O of (weakly coordinated) Cs2O2 salt, b = νO–O of TBAO2 generated in dimethyl sulfoxide (DMSO), c = νO–O of gaseous dioxides. | |||||
| π*(2pxy) MO outer valence structure | ↿⇂ ↿⇂ | ↿⇂ ↿ | ↿ ↿ | ↿ | — |
| Bond length/BL (Å) | 1.49 | 1.34 | 1.24 | 1.12 | 68 |
| Bond enthalpy/BH (kJ mol−1) | 149 | 360 | 498 | 644 | 68 |
| Bond force constant/Bk (mdyn Å−1) | 2.56 | 6.18 | 11.4 | 16.3 | 8, 13 and 69 |
| ν O–O x | 743a | 1108b | 1556c | 1876c | 9, 15, 53, 58 and 70–72 |
| Bond order/BO | 1 | 1.5 | 2 | 2.5 | — |
| ν O–O x /νperoxideO–O | 1 | 1.49 | 2.10 | 2.53 | — |
Considering the relationship between νO–O and the coordinating cation discussed in the previous section: [C+⋯O2˙−] complexes with strong coordinating cations can be considered to have partial-covalent character, i.e. the coordinating cation abstracts some amount of the O2˙− valence bond electron density. This bond electron density abstraction interaction between the dioxide ion and its coordinator is here on referred to as secondary covalency. For different O2˙− species, the amount of electron density abstracted by the cation can be estimated by considering the BO of other O2x species. A change of 0.5 in the BO corresponds to an electron being added or removed from the O–O bond. By assuming the BO is variable, then a change of 0.25 indicates a valence bond electron being shared with the coordination environment, discussed later. A fully dissociated O22− species has a BO of 1 and there is an approximately linear relationship between the BO and the bond force constant.66,67 As the bond force constant dictates the wavenumber of the νO–O, therefore, calculating the ratio between the νO–O of various O2x species and the νO–O of O22− (νO–Ox/νperoxideO–O) generates values that match well with the actual O–O BO (Table 3) as observed by Livneh et al.9
Due to their high  values; Cs+ (4678 g mol−1 Å3 C−1) and TBA+ (78
values; Cs+ (4678 g mol−1 Å3 C−1) and TBA+ (78![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 656 g mol−1 Å3 C−1) are weak coordinating cations. Therefore, the BO of Cs2O29,15,53 and [TBA+⋯O2˙−]25,26 can be assumed to be 1 and 1.5 and their Raman spectra used as νO–O values for dissociated O22− and O2˙−, respectively. In reality, both oxides will have some slight covalent character, however, even without considering this, and also the contributions from anharmonicity in the O–O bond vibration (which are relatively small and decrease in magnitude from O2+ to O22−),9 we see good agreement between the BO and νO–Ox/νperoxideO–O ratios in Table 3. Fitting bond parameters in Fig. 5 with respect to known BO values allows simple fits (eqn (6) and Table S2, ESI†) for estimating O2x bond parameters to be derived. The trends are approximately linear, however, more accurate cubic fits where used. Therefore, provided the νO–O of a O2x is know, it is suggested that all other bond parameters can be estimated.
656 g mol−1 Å3 C−1) are weak coordinating cations. Therefore, the BO of Cs2O29,15,53 and [TBA+⋯O2˙−]25,26 can be assumed to be 1 and 1.5 and their Raman spectra used as νO–O values for dissociated O22− and O2˙−, respectively. In reality, both oxides will have some slight covalent character, however, even without considering this, and also the contributions from anharmonicity in the O–O bond vibration (which are relatively small and decrease in magnitude from O2+ to O22−),9 we see good agreement between the BO and νO–Ox/νperoxideO–O ratios in Table 3. Fitting bond parameters in Fig. 5 with respect to known BO values allows simple fits (eqn (6) and Table S2, ESI†) for estimating O2x bond parameters to be derived. The trends are approximately linear, however, more accurate cubic fits where used. Therefore, provided the νO–O of a O2x is know, it is suggested that all other bond parameters can be estimated.
| y = Ax3 + Bx2 + Cx + D | (6) |
 | ||
| Fig. 5 Fitted plots of O2x bond parameters from Table 3 against the BO. Colour-coordinated axis labels are shown above the graph. Cubic lines of best fits are shown by dashed lines. Fit values shown in Table 4. | ||
To further qualify that the relationship between the νO–O of O2x and its bond parameters are approximately linear/cubic: it would be expected that a O2x species with secondary covalency (i.e. a O2x species with the outer valence electron partially shared with its coordinating environment) would have a BO between that of two fully dissociated O2x species. For example, a O2x species with a BO between that of O22− (BO = 1) and O2˙− (BO = 1.5) would be expected to have a BO of ∼1.25, and would have a π*(2p) orbital structure between that of a O22−, [↿⇂ ↿⇂], and O2˙−, [↿⇂ ↿], species. Thus, such a O2x species would have a detectable bond vibration and νO–O band somewhere between that of a strongly coordinated O22− species (e.g. H2O2: 875 cm−1) and a fully-dissociated O2˙− (e.g. a [TBA+⋯O2˙−]: ∼1108 cm−1) species.67 Therefore, νO–O values between those of these two species can be considered to have secondary covalent character, with valence bond electron density being shared by the O2x anion with its coordinating environment. Such a O2x species would be expected to have a partial dipole moment induced by the coordination interaction and the νO–O band would be both Raman and IR active.73 Searching the literature this was indeed found to be the case for the νO–O of organic peroxyls,74,75 transition metal superoxo-complexes,6,76,77 and metalloenzymes,78 which all had Raman and/or IR values reported in the range between 875–1108 cm−1. Also, this trend in νO–O would be expected to be the same for O2x species with superoxo-oxyl and oxo-dioxygenyl character which was also observed to be the case and is discussed in detail below. To clarify language, the O2x valence electron is assumed to be partially shared with the coordinating species and:
• Peroxo-superoxyl refers to a coordinated O2x species with a π*(2p) valence orbital structure between [↿⇂ ↿⇂]–[↿⇂ ↿], a BO between 1–1.5 and a νO–O value between 875–1108 cm−1.
• Superoxo-oxyl refers to a coordinated O2x species with a π*(2p) valence orbital structure between [↿⇂ ↿]–[↿ ↿], a BO between 1.5–2 and a νO–O value between 1179–1552 cm−1.
• Oxo-dioxygenyl refers to a coordinated O2x species with a π*(2p) valence orbital between [↿ ↿]–[↿], a BO between 2–2.5 and a νO–O value between 1552–1825 cm−1.
3.5. Secondary covalent bonding
All the above discussed νO–O spectral bands for various O2x species (>200) have had their estimated bond properties calculated (using eqn (6) and Table 4) and have been plotted against their calculated BO (Fig. 6). O2x species with BO values divisible by 0.5 can be considered ionic or neutral whilst those with BO values in-between can be considered to have some amount of electron donation occurring between O2x and its coordinating environment, i.e. secondary covalent bonding. Therefore, the BO is assumed to be on a spectrum and to vary depending on how strongly coordinated the O2x diatom is (and therefore, how much of its valence electron it shares).| x | y | A | B | C | D |
|---|---|---|---|---|---|
| B O | ν O–O | 592 | −550 | 884 | −184 |
| B O | l | −0.0933 | 0.52 | −1.157 | 2.22 |
| B O | k | −2.607 | 15 | −17.948 | 8.15 |
| B O | H | 108 | −632 | 1489 | −816 |
 | ||
| Fig. 6 Fitted plots of estimated bond parameters for various O2x species calculated from the νO–O values reported in the literature (see Table S2 for values, ESI†). Light green shaded regions signify O2x species that are ionic or neutral with valence bond electrons concentrated in the π2px,y* orbitals. Light orange regions signify O2x species with secondary covalent interactions with the coordinate environment and where the outermost valence electron is shared with the coordinator. Colour coordinated axis labels are shown above the graph. | ||
Experimental data on O–O bond parameters have been reported throughout the scientific literature for different O2x complexes. XRC or neutron diffraction techniques have been used to measure the BL of many species, therefore, the estimated BO and BL values calculated from the νO–O value can be cross-compared with experimental results to gauge their accuracy. Where the information was available for some of these cross-comparisons are listed in Table S2 (ESI†) with the difference between the measured and calculated BL values shown as a percentage (the literature is exhaustive and largely disorganised, i.e. individual bond parameters and νO–O values tend to be reported in different chemical, crystallographic, spectroscopic journals, and could warrant further compilation in future). Overall, the experimentally reported BL and the estimated BL values match well (generally <4% difference), supporting the correlation well. This relationship is useful for analysing O–O properties from experimental νO–O results.
 | (7) |
Considering the change in the estimated BO value of O2x species (calculated using the measured νO–O values) between strong and weak coordination, the secondary covalent character (i.e. amount of electron donation/abstraction between O2x and its coordinating environment) can be roughly estimated (eqn (7)). This is another useful, low-cost, method for estimating the interaction between a O2x species and its environment based solely on its experimental νO–O bond vibration (see examples below). Thus, a value for the amount of electron donation/abstraction for a O2x can be teased out of the νO–O literature. One side note, these values are not suggested to be precise; as contributions from anharmonicity are excluded etc., rather they are useful tools for quickly calculating approximate values for O2x bond parameters, which confirm and enhance the understanding of its vibrational spectra. This is particularly useful for helping to understand dynamic systems that are in flux such as at an electrode surface where countless thermodynamic, kinetic and charge transfer processes are occurring simultaneously, allowing for a general understanding of reaction processes to be rationalised with respect to O2x in terms of its νO–O. This also enables O2x species to be used as diagnostic molecules to probe the coordination strength of its environment by measuring the generated νO–O band.
Some examples calculations are given: NaO2 (1156 cm−1), TBAO2 (∼1108 cm−1), Cu:O2 complex A (1033 cm−1),6 have calculated BO values of 1.549, 1.5, and 1.409 and electron donation values of 19.5, 0 and −36.4%, respectively. Values greater than ±50% can be considered to have significant secondary covalent character. In NaO2, Na+ can be thought of as abstracting ∼20% of an electron from the outer electron bond density of O2˙−, which has slight oxygen character, relative to TBAO2. While in Cu:O2 complex A, the Cu-centred ligand can be thought of as donating ∼36% of an electron to O2˙− giving it slight peroxide character, relative to TBAO2.
Therefore:
It should be emphasised this method is not meant to be precise, rather to be used as a tool for approximating O–O bond properties, at a glance, using empirically derived νO–O values for O2x species’ with complex structures or coordinate environments. This approach of deriving bond properties from spectral bond vibration values in different coordination environments could deliver comparable results for other homonuclear bonds and provide similar quick approximations, though this would require further work.
3.6. The trouble with lithium superoxide
Meta-analysis of reported Raman bands of LiO2 shows that it sticks out like a sore-thumb in terms of both a wide range of reported values and that these values, are in the main, fall outside the trend of all other measured superoxide species (Fig. 2 and 3).28 Raman spectral bands in the O2˙− region (1100–1200 cm−1) have been reported as being either chemically stable LiO2 or from polyvinylidene fluoride (PVDF) binder degradation during cycling of non-aqueous Li–O2 cells (Fig. 7).27,38,79 Fundamental in situ SERS studies also report the presence of LiO2 as an intermediate produced during ORR at the roughened Au (rAu) electrode surface.10,11,26 LiO2 has long been believed to be both thermodynamically and kinetically unstable at temperatures above 25 K10,50,80–85 and it is still unclear whether this observed intermediary species is a pure LiO2 phase or a partially electrolyte/electrode stabilised [Li+⋯O2˙−] complex.86,87 This has led to some uncertainty over whether LiO2 can exist as a stable discharge product, reaction intermediate, or at all. In light of the trend in νO–O of O2˙− discussed previously, looking at the νO–O spectra of these reports can add to the debate.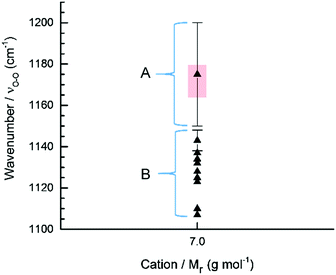 | ||
| Fig. 7 Plot of νO–O spectral bands attributed to LiO2 in the non-aqueous Li–O2 battery literature (see Table S1, ESI†). The expected νO–O for LiO2 based on the meta-analysis would be 1167 ± 10 cm−1, with this range highlighted by the red box. | ||
Variation in reported bands comes down to the following: (1) O2˙− is reacting with PVDF abstracting a proton and forming an alkene bond that causes a concomitant shift in the G-band with a serendipitously similar bond vibration to O2˙− observed in situ. (2) δ+ proton sites in the structure of PVDF ([–CH2–CF2–]n) binder are stabilising O2˙− and Li+ interactions allowing a stabilised [(Li+)x⋯O2˙−] complex to deposit and grow on the cathode/binder. This could explain the accompanying distorted carbon G-band (∼1505 cm−1). (3) Due to similarities in the wavenumber of their spectral bands, A Li2O2·2H2O species, similar to the Na2O2·2H2O species (∼1135 cm−1)48 observed in non-aqueous Na–O2 batteries, is being formed when H2O is present in the electrolyte. (4) A thermodynamically irregular or amorphous LiO2 phase or a weakly coordinated [Li+⋯O2˙−] complex is formed. (5) A partially intercalated O2˙− species in the carbon cathode that allows Li+ to bind but inhibits disproportionation to Li2O2 is formed. The interaction between O2˙− and the graphitic layers could produce the observed G-band (∼1505 cm−1) shift.
From the derived 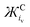 relationship, the expected νO–O for LiO2 was estimated to be 1167 ± 10 cm−1, with this range shown via a red box in Fig. 7. Region (A) νO–O values would fit with the expected value of a LiO2 species. Only one value matched this and it was reported by Xia et al. who observed a broad νO–O band (1150–1200 cm−1) after discharging a non-aqueous Li–O2 battery.36 Region (B) νO–O values would be expected to be partially stabilised [Li+⋯O2˙−] species’ or incorrectly assigned bands. Other reports of νO–O in a variety of different systems (Table S1, ESI†) are likely surface/solution stabilised [Li+⋯O2˙−] species or possibly PVDF degradation products.27,42,88
relationship, the expected νO–O for LiO2 was estimated to be 1167 ± 10 cm−1, with this range shown via a red box in Fig. 7. Region (A) νO–O values would fit with the expected value of a LiO2 species. Only one value matched this and it was reported by Xia et al. who observed a broad νO–O band (1150–1200 cm−1) after discharging a non-aqueous Li–O2 battery.36 Region (B) νO–O values would be expected to be partially stabilised [Li+⋯O2˙−] species’ or incorrectly assigned bands. Other reports of νO–O in a variety of different systems (Table S1, ESI†) are likely surface/solution stabilised [Li+⋯O2˙−] species or possibly PVDF degradation products.27,42,88
In summary, it is suggested that many of the νO–O values reported as LiO2 are too low and instead environmental influences (electrolyte and electrode) are helping to stabilise a [(Li+)x⋯O2˙−] complex (where x < 1). Current evidence suggests; that for species generated on cathodes with PVDF binder (1) is the most probable cause of these reported ‘νO–O’ spectral bands. However, (2) and (5) are other possibilities, but again are not a pure LiO2 product. In addition, during in situ spectroelectrochemical investigations of the interface partially electrolyte stabilised [Li+⋯O2˙−] complexes are being detected. Though, the report by Xia et al. suggests that it may still be feasible to produce a pure LiO2 phase during discharge if the conditions are right though the presence of toroid discharge product morphologies (associated with water containing electrolytes)89,90 may suggest HO2 was being detected rather than LiO2.
4. Conclusions
Superoxide (O2˙−) vibrational spectral bands reported in the literature were collated (>50 species) and trends in their coordinating environment were observed and described. The Ж parameter based on the mass-to-charge ratio and ionic volume of the coordinating ion was derived, which gave an excellent approximation of the collated results. The Ж parameter can be calculated with relative ease for most ions and is analogous to charge density and gives a simple low-cost method of quantifying an ions Coulombic attractive strength over oppositely charged species. It was determined that O2˙− can be used as a diagnostic molecule to probe the coordination strength of its immediate environment, by observing its vibrational spectrum. Furthermore, dioxygen vibrational spectral bands reported in the literature were collated (>200 species). The trends due to the changes in the coordinating environment were observed, where changes in the O–O vibrational spectral band were shown to be a result of electron abstraction/donation from/into the O–O bond via a ‘secondary covalent’ bonding interaction between the dioxygen species and its coordinating environment. A simple cubic approximation was drawn that enabled the bond order, bond dissociation enthalpy, bond length and bond force constants to be estimated solely using experimentally measured O–O spectral bond vibrations. For the bond length this approximation gave estimated values that matched extremely well with reported values (0.5–5%) measured experimentally using X-ray crystallography. It was shown by estimating the bond order allowed for the level of e− abstraction by the environment (i.e. the strength of the secondary covalent interaction) can also be estimated for any dioxygen species based solely on its vibrational spectra.Raman spectrum of LiO2 was analysed and most reported bands were found to be too low to be a pure LiO2 phase, suggesting that coordinate [Li+⋯O2˙−] complexes or degradation products are the most likely cause of these spectral reports in the non-aqueous Li–O2 battery literature.
Nomenclature
| O2+ | Dioxygen cation |
| O2 | Dioxygen |
| O2˙− | Superoxide anion |
| O22− | Peroxide anion |
| ROS | Reactive oxide species |
| O2x | Dioxide species, where x = −2, −1, 0, +1 |
| ν O–O | O-O symmetric stretching vibration |
| [M+⋯ O2˙−] | Alkali-metal superoxide complex |
| [C+⋯ O2˙−] | Cation coordinated superoxide complex |
| C+ | Coordinate cation |
| M r Q −1 | Molecular mass-to-charge ratio |
| M r | Relative molecular mass (mol g−1) |
| [(Li+)x⋯O2˙−] | Superoxide rich lithium coordinate complex |
| XRC | X-ray crystallography |
| i v | Ionic volume |
| i s.a. | Ionic surface area |
| B O | Bond order |
| B L | Bond length |
| B k | Bond force constant |
| B H | Bond dissociation enthalpy |
| C | Cation |
| A | Anion |
| Ж | ‘Ionic charge dispersion’ |
| q | No. of bonding electrons |
| q* | No. of anti-bonding electrons |
| Q | Charge on an ion (C) |
Conflicts of interest
There are no conflicts to declare.Acknowledgements
We recognise funding from the joint Engineering and Physical Sciences Research Council (EPSRC) and Innovate UK grant PLAB (Practical Lithium-Air Batteries) EP/L505274/1 that enabled this work. Dr Peter Goodrich and Professor Christopher Hardacre at Queens University Belfast for the supply of ionic liquids, as well scientific discussions with Dr Sarah Ball, at Johnson Matthey, are gratefully acknowledged.Notes and references
- D. T. Sawyer, Oxygen chemistry, Oxford University Press, 1991 Search PubMed.
- M. Hayyan, M. A. Hashim and I. M. AlNashef, Superoxide Ion: Generation and Chemical Implications, Chem. Rev., 2016, 116, 3029–3085 CrossRef CAS PubMed.
- O. Warburg, On the Origin of Cancer Cells, Science, 1956, 123, 309–314 CrossRef CAS PubMed.
- L. C. Greaves, A. K. Reeve, R. W. Taylor and D. M. Turnbull, Mitochondrial DNA and disease, J. Pathol., 2012, 226, 274–286 CrossRef CAS PubMed.
- C. R. Reczek and N. S. Chandel, The Two Faces of Reactive Oxygen Species in Cancer, Annu. Rev. Cancer Biol., 2017, 1, 79–98 CrossRef.
- C. E. Elwell, N. L. Gagnon, B. D. Neisen, D. Dhar, A. D. Spaeth, G. M. Yee and W. B. Tolman, Copper–Oxygen Complexes Revisited: Structures, Spectroscopy, and Reactivity, Chem. Rev., 2017, 117, 2059–2107 CrossRef CAS PubMed.
- G. Herzberg, Molecular spectra and molecular structure, vol. 1, 1950 Search PubMed.
- G. W. E. Nathan Kornblum, J. Shamir, J. Binenboym, H. H. Claassen, G. W. E. Nathan Kornblum, J. Shamir, J. Binenboym and H. H. Claassen, The vibrational frequency of the oxygen molecule (O2+) cation, J. Am. Chem. Soc., 1968, 90, 6223–6224 CrossRef.
- T. Livneh, A. Band and R. Tenne, Raman scattering from the peroxide ion in Cs2O2, J. Raman Spectrosc., 2002, 33, 675–676 CrossRef CAS.
- Z. Peng, S. A. Freunberger, L. J. Hardwick, Y. Chen, V. Giordani, F. Bardé, P. Novák, D. Graham, J.-M. Tarascon and P. G. Bruce, Oxygen reactions in a non-aqueous Li+ electrolyte, Angew. Chem., Int. Ed., 2011, 50, 6351–6355 CrossRef CAS PubMed.
- L. Johnson, C. Li, Z. Liu, Y. Chen, S. A. Freunberger, P. C. Ashok, B. B. Praveen, K. Dholakia, J.-M. Tarascon and P. G. Bruce, The role of LiO2 solubility in O2 reduction in aprotic solvents and its consequences for Li–O2 batteries, Nat. Chem., 2014, 6, 1091–1099 CrossRef CAS PubMed.
- K. M. Abraham and Z. Jiang, A polymer electrolyte-based rechargeable lithium/oxygen battery, J. Electrochem. Soc., 1996, 143, 1–5 CrossRef CAS.
- J. A. Creighton and E. R. Lippincott, Vibrational Frequency and Dissociation Energy of the Superoxide Ion, J. Chem. Phys., 1964, 40, 1779 CrossRef CAS.
- J. C. Evans, The Peroxide-ion Fundamental Frequency, J. Chem. Soc. D, 1969, 682–683 RSC.
- J. B. Bates, M. H. Brooker and G. E. Boyd, Raman spectra of O2− and O3− ions in alkali-metal superoxides and ozonides, Chem. Phys. Lett., 1972, 16, 391–395 CrossRef CAS.
- F. J. Blunt, P. J. Hendra and J. R. Mackenzie, The laser Raman spectra of salts containing the anions O2− and O22−, J. Chem. Soc. D, 1969, 278 RSC.
- M. B. W. Kanzig, Molekul- und Gitterschwingungen im Natriumhyperoxid, Phys. Kondens. Mater., 1973, 112, 107–112 Search PubMed.
- H. H. Eysel and S. Thym, Raman Spectra of Peroxides, Z. Anorg. Allg. Chem., 1975, 411, 97–102 CrossRef CAS.
- D. A. Hatzenbuhler, Raman and Infrared Spectra of LiO2 in Oxygen Matrices, J. Chem. Phys., 1972, 56, 3398 CrossRef CAS.
- R. R. Smardzewski and L. Andrews, Raman spectra of the products of rubidium and cesium atom argon matrix reactions with oxygen molecules, J. Phys. Chem., 1973, 77, 801–804 CrossRef CAS.
- L. Andrews and R. R. Smardzewski, Argon matrix Raman spectrum of LiO2. Bonding in the M+O2− molecules and the ionic model, J. Chem. Phys., 1973, 58, 2258–2261 CrossRef CAS.
- D. T. Sawyer, T. S. Calderwood, K. Yamaguchi and C. T. Angelis, Synthesis and characterization of tetramethylammonium superoxide, Inorg. Chem., 1983, 22, 2577–2583 CrossRef CAS.
- W. Holzer, W. F. Murphy, H. J. Bernstein and J. Rolfe, Raman spectrum of O2− ion in alkali halide crystals, J. Mol. Spectrosc., 1968, 26, 543–545 CrossRef CAS.
- V. S. Bryantsev, J. Uddin, V. Giordani, W. Walker, D. Addison and G. V. Chase, The Identification of Stable Solvents for Nonaqueous Rechargeable Li-Air Batteries, J. Electrochem. Soc., 2012, 160, A160–A171 CrossRef.
- I. M. Aldous and L. J. Hardwick, Influence of Tetraalkylammonium Cation Chain Length on Gold and Glassy Carbon Electrode Interfaces for Alkali Metal–Oxygen Batteries, J. Phys. Chem. Lett., 2014, 5, 3924–3930 CrossRef CAS PubMed.
- T. A. Galloway and L. J. Hardwick, Utilizing in Situ Electrochemical SHINERS for Oxygen Reduction Reaction Studies in Aprotic Electrolytes, J. Phys. Chem. Lett., 2016, 7, 2119–2124 CrossRef CAS PubMed.
- J. K. Papp, J. D. Forster, C. M. Burke, H. W. Kim, A. C. Luntz, R. M. Shelby, J. J. Urban and B. D. McCloskey, Poly(vinylidene fluoride) (PVDF) Binder Degradation in Li–O2 Batteries: A Consideration for the Characterization of Lithium Superoxide, J. Phys. Chem. Lett., 2017, 8, 1169–1174 CrossRef CAS PubMed.
- W.-J. Kwak, J.-B. Park, H.-G. Jung and Y.-K. Sun, Controversial Topics on Lithium Superoxide in Li–O2 Batteries, ACS Energy Lett., 2017, 2, 2756–2760 CrossRef CAS.
- X. Li and A. A. Gewirth, Oxygen electroreduction through a superoxide intermediate on Bi-modified Au surfaces, J. Am. Chem. Soc., 2005, 127, 5252–5260 CrossRef CAS PubMed.
- I. Janik and G. N. R. Tripathi, The nature of the superoxide radical anion in water, J. Chem. Phys., 2013, 139, 014302 CrossRef PubMed.
- J. Kim and A. A. Gewirth, Mechanism of Oxygen Electroreduction on Gold Surfaces in Basic Media, J. Phys. Chem. B, 2006, 110, 2565–2571 CrossRef CAS PubMed.
- I. Aldous, Non-aqueous Spectroelectrochemistry of Dioxygen for Alkali Metal-Oxygen Batteries, PhD thesis, University of Liverpool, 2016.
- C. Li, O. Fontaine, S. A. Freunberger, L. Johnson, S. Grugeon, S. Laruelle, P. G. Bruce and M. Armand, Aprotic Li–O2 Battery: Influence of Complexing Agents on Oxygen Reduction in an Aprotic Solvent, J. Phys. Chem. C, 2014, 118, 3393–3401 CrossRef CAS.
- F. S. Gittleson, W. Ryu and A. D. Taylor, Operando Observation of the Gold–Electrolyte Interface in Li–O2 Batteries, ACS Appl. Mater. Interfaces, 2014, 6, 19017–19025 CrossRef CAS PubMed.
- J. T. Frith, A. E. Russell, N. Garcia-Araez and J. R. Owen, An in-situ Raman study of the oxygen reduction reaction in ionic liquids, Electrochem. Commun., 2014, 46, 33–35 CrossRef CAS.
- C. Xia, M. Waletzko, L. Chen, K. Peppler, P. J. Klar and J. Janek, Evolution of Li2O2 Growth and Its Effect on Kinetics of Li–O2 Batteries, ACS Appl. Mater. Interfaces, 2014, 6, 12083–12092 CrossRef CAS PubMed.
- D. Zhai, H.-H. Wang, J. Yang, K. C. Lau, K. Li, K. Amine and L. A. Curtiss, Disproportionation in Li-O2 batteries based on a large surface area carbon cathode, J. Am. Chem. Soc., 2013, 135, 15364–15372 CrossRef CAS PubMed.
- D. Zhai, H. Wang, K. C. Lau, J. Gao, P. C. Redfern, F. Kang, B. Li, E. Indacochea, U. Das, H. Sun, K. Amine and L. A. Curtiss, Raman Evidence for Late Stage Disproportionation in a Li–O2 Battery, J. Phys. Chem. Lett., 2014, 5, 2705–2710 CrossRef CAS PubMed.
- D. Zhai, K. C. Lau, H. Wang, J. Wen, D. J. Miller, J. Lu, F. Kang, B. Li, W. Yang, J. Gao, E. Indacochea, L. A. Curtiss and K. Amine, Interfacial Effects on Lithium Superoxide Disproportionation in Li-O2 Batteries, Nano Lett., 2015, 15, 1041–1046 CrossRef CAS PubMed.
- J. Yang, D. Zhai, H.-H. Wang, K. C. Lau, J. A. Schlueter, P. Du, D. J. Myers, Y. Sun, L. A. Curtiss and K. Amine, Evidence for lithium superoxide-like species in the discharge product of a Li-O2 battery, Phys. Chem. Chem. Phys., 2013, 15, 3764–3771 RSC.
- J. Lu, Y. Jung Lee, X. Luo, K. Chun Lau, M. Asadi, H.-H. Wang, S. Brombosz, J. Wen, D. Zhai, Z. Chen, D. J. Miller, Y. Sub Jeong, J.-B. Park, Z. Zak Fang, B. Kumar, A. Salehi-Khojin, Y.-K. Sun, L. A. Curtiss and K. Amine, A lithium–oxygen battery based on lithium superoxide, Nature, 2016, 529, 377–382 CrossRef CAS PubMed.
- A. C. Luntz and B. D. McCloskey, Nonaqueous Li–Air Batteries: A Status Report, Chem. Rev., 2014, 114, 11721–11750 CrossRef CAS PubMed.
- W. H. Ryu, F. S. Gittleson, M. Schwab, T. Goh and A. D. Taylor, A mesoporous catalytic membrane architecture for lithium-oxygen battery systems, Nano Lett., 2015, 15, 434–441 CrossRef CAS PubMed.
- T. A. Galloway, L. Cabo-Fernandez, I. Aldous, F. Braga and L. Hardwick, Shell Isolated Nanoparticles for Enhanced Raman Spectroscopy Studies in Lithium-Oxygen Cells, Faraday Discuss., 2016, 205, 469–490 RSC.
- A. Bösch and M. Känzig, Optische Eigenschaften und Elektronische Struktur von Alkali-Hyperoxide-Kristallen, Helv. Phys. Acta, 1975, 48, 743–785 Search PubMed.
- I. M. Aldous and L. J. Hardwick, Solvent Mediated Control of the Electrochemical Discharge Products of Non-aqueous Sodium Oxygen Electrochemistry, Angew. Chem., Int. Ed., 2016, 55, 8254 CrossRef CAS PubMed.
- P. Hartmann, C. L. Bender, M. Vračar, A. K. Dürr, A. Garsuch, J. Janek and P. Adelhelm, A rechargeable room-temperature sodium superoxide (NaO2) battery, Nat. Mater., 2013, 12, 228–232 CrossRef CAS PubMed.
- I. Landa-Medrano, R. Pinedo, X. Bi, I. Ruiz de Larramendi, L. Lezama, J. Janek, K. Amine, J. Lu and T. Rojo, New Insights into the Instability of Discharge Products in Na–O2 Batteries, ACS Appl. Mater. Interfaces, 2016, 8, 20120–20127 CrossRef CAS PubMed.
- N. Zhao and X. Guo, Cell Chemistry of Sodium–Oxygen Batteries with Various Nonaqueous Electrolytes, J. Phys. Chem. C, 2015, 119, 25319–25326 CrossRef CAS.
- N. Ortiz-Vitoriano, T. P. Batcho, D. G. Kwabi, B. Han, N. Pour, K. P. C. Yao, C. V. Thompson and Y. Shao-Horn, Rate-Dependent Nucleation and Growth of NaO2 in Na–O2 Batteries, J. Phys. Chem. Lett., 2015, 6, 2636–2643 CrossRef CAS PubMed.
- I. I. Abate, L. E. Thompson, H.-C. Kim and N. B. Aetukuri, Robust NaO2 Electrochemistry in Aprotic Na–O2 Batteries Employing Ethereal Electrolytes with a Protic Additive, J. Phys. Chem. Lett., 2016, 7, 2164–2169 CrossRef CAS PubMed.
- J. Kim, H. Park, B. Lee, W. M. Seong, H.-D. Lim, Y. Bae, H. Kim, W. K. Kim, K. H. Ryu and K. Kang, Dissolution and ionization of sodium superoxide in sodium-oxygen batteries, Nat. Commun., 2016, 7, 10670 CrossRef CAS PubMed.
- S. A. Hunter-Saphir and J. A. Creighton, Resonance Raman Scattering from the Superoxide Ion, J. Raman Spectrosc., 1998, 29, 1997–1999 CrossRef.
- D. T. Sawyer, T. S. Calderwood, K. Yamaguchi and C. T. Angelis, Synthesis and Characterization of Tetramethylammonium Superoxide, Inorg. Chem., 1983, 22, 2577–2583 CrossRef CAS.
- X. Ren and Y. Wu, A Low-Overpotential Potassium–Oxygen Battery Based on Potassium Superoxide, J. Am. Chem. Soc., 2013, 135, 2923–2926 CrossRef CAS PubMed.
- P. D. C. Dietzel, R. K. Kremer and M. Jansen, Superoxide compounds of the large pseudo-alkali-metal ions tetramethylammonium, -phosphonium, and -arsonium, Chem. – Asian J., 2007, 2, 66–75 CrossRef CAS PubMed.
- J. Li and R. J. Davis, Raman spectroscopy and dioxygen adsorption on Cs-loaded zeolite catalysts for butene isomerization, J. Phys. Chem. B, 2005, 109, 7141–7148 CrossRef CAS PubMed.
- A. Band, A. Albu-Yaron, T. Livneh, H. Cohen, Y. Feldman, L. Shimon, R. Popovitz-Biro, V. Lyahovitskaya and R. Tenne, Characterization of oxides of cesium, J. Phys. Chem. B, 2004, 108, 12360–12367 CrossRef CAS.
- P. D. C. Dietzel, R. K. Kremer and M. Jansen, Tetraorganylammonium Superoxide Compounds: Close to Unperturbed Superoxide Ions in the Solid State, J. Am. Chem. Soc., 2004, 126, 4689–4696 CrossRef CAS PubMed.
- Q. Yu and S. Ye, In Situ Study of Oxygen Reduction in Dimethyl Sulfoxide (DMSO) Solution: A Fundamental Study for Development of the Lithium–Oxygen Battery, J. Phys. Chem. C, 2015, 119, 12236–12250 CrossRef CAS.
- P. Vandenabeele, Practical Raman Spectroscopy – An Introduction ALS Catalog, John Wiley & Sons, Ltd, Chichester, UK, 2013 Search PubMed.
- I. M. Aldous and L. J. Hardwick, Solvent-Mediated Control of the Electrochemical Discharge Products of Non-Aqueous Sodium-Oxygen Electrochemistry, Angew. Chem., Int. Ed., 2016, 55, 8254–8257 CrossRef CAS PubMed.
- M. Schmeisser, P. Illner, R. Puchta, A. Zahl and R. van Eldik, Gutmann donor and acceptor numbers for ionic liquids, Chemistry, 2012, 18, 10969–10982 CrossRef CAS PubMed.
- W. Xu, J. Wang, F. Ding, X. Chen, E. Nasybulin, Y. Zhang and J.-G. Zhang, Lithium metal anodes for rechargeable batteries, Energy Environ. Sci., 2014, 7, 513 RSC.
- L. Popović, D. De Waal and J. C. A. Boeyens, Correlation between Raman wavenumbers and P-O bond lengths in crystalline inorganic phosphates, J. Raman Spectrosc., 2005, 36, 2–11 CrossRef.
- E. A. Robinson and M. W. Lister, A linear relation between bond orders and stretching force constants, Can. J. Chem., 1963, 41, 2988–2995 CrossRef CAS.
- C. J. Cramer, W. B. Tolman, K. H. Theopold and A. L. Rheingold, Variable character of O–O and M–O bonding in side-on (2) 1
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 metal complexes of O2, Proc. Natl. Acad. Sci. U. S. A., 2003, 100, 3635–3640 CrossRef CAS PubMed.
1 metal complexes of O2, Proc. Natl. Acad. Sci. U. S. A., 2003, 100, 3635–3640 CrossRef CAS PubMed. - C. E. Housecroft and E. C. Constable, Chemistry: An introduction to organic, inorganic and physical chemistry, Prentice Hall/Pearson Education, 2010 Search PubMed.
- P. A. Giguére and T. K. K. Srinivasan, A Raman study of H2O2 and D2O2 vapor, J. Raman Spectrosc., 1974, 2, 125–132 CrossRef.
- A. Weber and E. A. McGinnis, The Raman spectrum of gaseous oxygen, J. Mol. Spectrosc., 1960, 4, 195–200 CrossRef CAS.
- A. J. Edwards, W. E. Falconer, J. E. Griffiths, W. A. Sunder and M. J. Vasile, Syntheses and some properties of dioxygenyl fluorometallate salts, J. Chem. Soc., Dalton Trans., 1974, 1129 RSC.
- V. V. Pushkarev, V. I. Kovalchuk and J. L. D’Itri, Probing Defect Sites on the CeO2 Surface with Dioxygen, J. Phys. Chem. B, 2004, 108, 5341–5348 CrossRef CAS.
- T. Shibahara and M. Mori, Raman and Infrared Spectra of μ-O2 Dicobalt(III) Complexes, Bull. Chem. Soc. Jpn., 1978, 51, 1374–1379 CrossRef CAS.
- J. Oxley, J. Smith, J. Brady, F. Dubnikova, R. Kosloff, L. Zeiri and Y. Zeiri, Raman and Infrared Fingerprint Spectroscopy of Peroxide-Based Explosives, Appl. Spectrosc., 2008, 62, 906–915 CrossRef CAS PubMed.
- D. Lin-Vien, N. B. Colthup, W. G. Fateley and J. G. Grasselli, The Handbook of Infrared and Raman Characteristic Frequencies of Organic Molecules, 1991, pp. 68–72 Search PubMed.
- K. Qin, C. D. Incarvito, A. L. Rheingold and K. H. Theopold, A structurally characterized chromium(III) superoxide complex features ‘side-on’ bonding, Angew. Chem., Int. Ed., 2002, 41, 2333–2335 CrossRef CAS PubMed.
- L. M. Mirica, X. Ottenwaelder and T. D. P. Stack, Structure and Spectroscopy of Copper–Dioxygen Complexes, Chem. Rev., 2004, 104, 1013–1046 CrossRef CAS PubMed.
- E. I. Solomon, D. E. Heppner, E. M. Johnston, J. W. Ginsbach, J. Cirera, M. Qayyum, M. T. Kieber-Emmons, C. H. Kjaergaard, R. G. Hadt and L. Tian, Copper Active Sites in Biology, Chem. Rev., 2014, 114, 3659–3853 CrossRef CAS PubMed.
- J. Lu, Y. Jung Lee, X. Luo, K. Chun Lau, M. Asadi, H.-H. Wang, S. Brombosz, J. Wen, D. Zhai, Z. Chen, D. J. Miller, Y. Sub Jeong, J.-B. Park, Z. Zak Fang, B. Kumar, A. Salehi-Khojin, Y.-K. Sun, L. A. Curtiss and K. Amine, A lithium–oxygen battery based on lithium superoxide (Supplementary information), Nature, 2016, 529, 1–7 CrossRef PubMed.
- H. Yadegari, Q. Sun and X. Sun, Sodium-Oxygen Batteries: A Comparative Review from Chemical and Electrochemical Fundamentals to Future Perspective, Adv. Mater., 2016, 28, 7065–7093 CrossRef CAS PubMed.
- C. L. Bender, P. Hartmann, M. Vračar, P. Adelhelm and J. Janek, On the thermodynamics, the role of the carbon cathode, and the cycle life of the sodium superoxide (NaO2) battery, Adv. Energy Mater., 2014, 4, 2–11 Search PubMed.
- R. H. Snow, Thermodynamic Evaluation of the Possibility of Lithium Superoxide Production, Contrails, 1965, 34 Search PubMed.
- V. S. Bryantsev, M. Blanco and F. Faglioni, Stability of lithium superoxide LiO2 in the gas phase: computational study of dimerization and disproportionation reactions, J. Phys. Chem. A, 2010, 114, 8165–8169 CrossRef CAS PubMed.
- N. Seriani, Ab initio thermodynamics of lithium oxides: from bulk phases to nanoparticles, Nanotechnology, 2009, 20, 1–7 CrossRef PubMed.
- A. I. Belova, D. G. Kwabi, L. V. Yashina, Y. Shao-Horn and D. M. Itkis, On the Mechanism of Oxygen Reduction in Aprotic Li-Air Batteries: The Role of Carbon Electrode Surface Structure, J. Phys. Chem. C, 2017, 121, 1569–1577 CrossRef CAS.
- D. G. Kwabi, V. S. Bryantsev, T. P. Batcho, D. M. Itkis, C. V. Thompson and Y. Shao-Horn, Experimental and Computational Analysis of the Solvent-Dependent O2/Li+-O2− Redox Couple: Standard Potentials, Coupling Strength, and Implications for Lithium-Oxygen Batteries, Angew. Chem., Int. Ed., 2016, 55, 3129–3134 CrossRef CAS PubMed.
- G. Yang, Y. Wang and Y. Ma, A Stable, Magnetic, and Metallic Li3O4 Compound as a Discharge Product in a Li–Air Battery, J. Phys. Chem. Lett., 2014, 5, 2516–2521 CrossRef CAS PubMed.
- R. Black, S. H. Oh, J.-H. Lee, T. Yim, B. Adams and L. F. Nazar, Screening for Superoxide Reactivity in Li-O2 Batteries: Effect on Li2O2/LiOH Crystallization, J. Am. Chem. Soc., 2012, 134, 2902–2905 CrossRef CAS PubMed.
- N. B. Aetukuri, B. D. McCloskey, J. M. García, L. E. Krupp, V. Viswanathan and A. C. Luntz, Solvating additives drive solution-mediated electrochemistry and enhance toroid growth in non-aqueous Li–O2 batteries, Nat. Chem., 2014, 7, 50–56 CrossRef PubMed.
- D. Aurbach, B. D. McCloskey, L. F. Nazar and P. G. Bruce, Advances in understanding mechanisms underpinning lithium–air batteries, Nat. Energy, 2016, 1, 16128 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Tabulated data from meta-analysis. See DOI: 10.1039/c8cp04652b |
| This journal is © the Owner Societies 2019 |