Intramolecular π–hole interactions with nitro aromatics

Abstract

A thorough evaluation of the CSD and DFT computations were conducted to assess if intramolecular π–hole interactions can stabilize a conformer of nitro aromatics. It was found that this can only be the case when the nitro N-atom and an interacting electron-rich atom are separated by at least four bonds. Data from the solid state correspond well to the gas phase calculations and stabilizing energies were estimated to be as large as about 2–3 kcal mol⁻¹, which is in the order of weak hydrogen bonding interactions.

---

Introduction

Intramolecular interactions such as hydrogen bonding can direct the formation of the three-dimensional structure of large molecules such as synthetic polymers,¹ artificial foldamers² and proteins.³ The structure and function of proteins can also be affected by other intramolecular forces such as n → π* interactions⁴ and halogen bonding.⁵ Conformation-directing effects of intramolecular hydrogen bonds are also prevalent in small molecules,⁶ which raises the question what other types of intramolecular non-covalent forces can stabilize conformers.

It is known that the N-atom in nitro (–NO₂) compounds bears a positive potential, which has been classified as a so-called π–hole (see Fig. 1a).⁷ Such π–holes can establish favorable intermolecular interactions with lone-pair electrons, for example in nitrate esters.⁸ This is even the case for the ubiquitous nitrate anion when its negative charge is sufficiently spread out by hydrogen bonding⁹ or coordination to a metal.¹⁰ The same holds for nitro aromatics,¹¹ which are synthetically very accessible and thermally robust. In fact, small nitro aromatic molecules are widely studied for their pharmacological properties‡ and many are approved by the U.S. Food and Drug Administration and regularly administered.¹² For example, nitro aromatic dihydropyridine derivatives such as nifedipine (Adalat)¹³ and nisoldipine (Sular)¹⁴ are calcium channel blockers used to treat hypertension and angina.¹⁵

Fig. 1 Molecular electrostatic potential map of nitrobenzene indicating the location of the π–hole (a, DFT/MP2/6-311+G**, from −22 (red) tot +24 kcal mol⁻¹ (blue)) and the general queries used to retrieve data from the CSD for nitro aromatics where a possibly interacting atom (X or ElR) is three, four, or ≥ five bonds removed from the nitro's N-atom (i.e. five bonds for n = 1, six bonds for n = 2 and so forth). X can be any atom except H; ElR = N, P, As, O, S, Se, Te, F, Cl, Br, I or At. α = the angle between the NO₂ plane and the plane of the aryl ring. The blue dashed lines indicate that all types of bonds were allowed and the red dashed lines indicate the intramolecular N^NO₂⋯ElR distance. The O-atoms of the nitro moiety were constrained to those bound only to N (thus excluding structures that were coordinated to a metal).

As it is known that conformation-directing effects can be relevant for medicinal chemistry,¹⁶ we wondered if there is any evidence for conformer stabilization of intramolecular π–hole interactions within nitro aromatics. To this end, we scrutinized the geometric data of small molecules that are present in the Cambridge Structure Database (CSD) and conducted computational studies on model systems.

Materials and methods

The CSD version 5.39 including two updates (until February 2018) was inspected using ConQuest version 1.21 (build 168 220) and all searches were limited to single crystal X-ray structures that contained 3D coordination and had an R-factor ≤ 0.1. As depicted in Fig. 1, several separate analyses were performed on datasets where the number of bonds between the nitro's N (N^NO₂) atom and the possibly interacting electron-rich atom (ElR, i.e., N, P, As, O, S, Se, Te, F, Cl, Br, I or At) was confined to three, four or ≥ five bonds (depending on n).

DFT calculations were performed either with the Turbomole 7.0 program (energy profiles at the PBE0¹⁷-D3¹⁸/def2-TZVP¹⁹ level of theory) or with the Amsterdam Density Functional (ADF)²⁰ modelling suite at the B3LYP²¹-D3¹⁸/TZ2P¹⁹ level of theory (no frozen cores, also used for ‘atoms in molecules’²² analyses). The def2-TZVP/TZ2P basis sets give an accurate energy at reasonable computational cost and a very low basis set superposition error (BSSE).¹⁹

Results and discussion

Three bonds of separation

The dataset involving entries with three bonds between N^NO₂ and ElR actually comprises substituents directly ortho to the nitro moiety. Because the distance between N^NO₂ and ElR is thus relatively fixed, the overlap of van der Waals shells cannot be taken as an indicator for stabilizing interactions. To evaluate these data, the angle between the aryl ring plane and the NO₂ plane was measured (α). The search was done for specific substituents X, namely, o-H, o-Me, o-OCR₃, o-SCR₃, o-F, o-Cl, o-Br, and o-I (R = any atom). The number of CIFs and hits within these CIFs are collected in Table 1, together with the angle range that characterized most of the hits within a certain dataset (see Fig. S1† for distributions). Also shown in the table are the angle α of the energetic minimum and the barrier of α rotation for model nitro aromatics (R = H) computed with 10 degree intervals at the DFT/PBE0-D3/def2-TZVP level of theory (see Fig. S2† for full energy profiles).

Table 1 Overview of CSD and DFT data involving nitro aromatics with various ortho substituents (i.e. X-atoms/groups that are three bonds removed from the nitro N-atom)

X	N CIFs	N Hits	α in CSD^a (DFT)^b	Barrier^c
a The CSD data were plotted at 10 degree intervals of α as shown in Fig. S1; listed in the table are the intervals with most data. b Conformational isomers were computed with 10 degree intervals of α at the DFT/PBE0-D3/def2-TZVP level of theory, as shown in Fig. S2. c Energies in kcal mol^−1. All the energetic maxima were characterized by α = 90°. d In the CSD analysis, R can be any atom and in the DFT calculations R = H. These datasets were also used to generate Fig. 2.
o-H	16 058	24 959	0–10 (0)	6.0
o-CH3	165	323	30–50 (30)	2.8
o-OCR3	239	328	30–40 (40)^d	1.5
o-SCR3	67	72	0–10 (0)^d	5.2
o-F	34	47	10–20 (20)	2.5
o-Cl	113	167	40–50 (40)	1.2
o-Br	29	136	80–90 (40)	1.0
o-I	20	31	30–40 (40)	1.2

---

For X = H, the CSD data are tightly grouped near α = 0° and DFT predicts the energetic minimum at α = 0° with a rotational barrier of 6.0 kcal mol⁻¹. These data are congruent with the absence of any steric constraints for a co-planar arrangement of the aryl ring and the nitro group, and perhaps some stabilization of NO₂⋯HC hydrogen bonding interactions. Indeed, for the more sterically demanding X = CH₃, most CSD data are found near α = 40° and the minimum is computed at α = 30° with a smaller barrier of rotation (3.8 kcal mol⁻¹). Interestingly, the distribution is similar for o-methoxy nitro arenes with the calculated minimum at α = 40°. The energetic penalty for adopting the α = 90° position is merely 1.5 kcal mol⁻¹, half that for the sterically similar o-CH₃. Unexpectedly, the data for o-SR₃ are skewed to a geometry with α = 0° and DFT indeed predicts a coplanar geometry with the second highest rotational barrier of 5.2 kcal mol⁻¹. In accordance with DFT, the o-F data are nearly co-planar (α = 10–20°) while the CSD data of the other halogens are not (α = 40–90°). The rotational barrier for all halogens is rather low (∼1 kcal mol⁻¹), which might explain the wide distribution of CSD data (spanning nearly the whole region α = 0–90°).

The rather large difference in (α) between o-SCR₃ (α = 0°) and both its O-analogue and the larger halides (α = 40°) prompted us to scrutinize the o-SCR data further. To this end, comparative heat plots were generated for α versus the C–C–O/S–CR₃ torsion angle (β) for o-OCR₃ and o-SCR₃. From these plots shown in Fig. 2, it is evident that the data for o-SCH₃ are much more tightly grouped near α = 0° and β = 180°. An energy minimization at the DFT/B3LYP-D3-TZ2P level of theory for both nitro arenes is shown at the top of Fig. 2 and corroborates the observed difference in α.

Fig. 2 β(α) heat plots of the CSD data involving derivatives of o-methoxynitrobenzene (left, N = 328) and o-methylsulphanylnitrobenzene (right, N = 72). The colour code from blue to red is in percentages as indicated in the inset figures. The molecules displayed at the top are the energy minima at the DFT/B3LYP-D3/def2-TZ2P level of theory with accompanying atoms in molecules analysis. Indicated bond critical points are in arbitrary units.

An ‘atoms in molecules’ (AIM) analysis reveals a bond critical point (bcp) between an NO₂–O atom and O or S with bond densities of 0.013 and 0.026, respectively, which is indicative of a σ–hole interaction (O/S–C). The larger rotational barrier and bcp density for o-SCH₃ suggest that this interaction is significant with sulphur and similar to weak hydrogen bonding interactions (similar barrier of α rotation as in nitrobenzene). This is in accordance with literature data that the larger and more polarizable S-atoms readily engage in σ–hole interactions.^7b,23 Based on the above results, it is concluded that there are no intramolecular π–hole interactions within nitroarenes and electron-rich atoms that are separated by three bonds. Surprisingly, it was found that weak O^NO₂ → S σ–hole interactions are likely with o-methylsulphanylnitrobenzene derivatives.

Four bonds of separation

In total, 5780 hits were found within 2582 CIFs where the nitro N-atom and an electron-rich atom were four bonds removed from each other (see middle query in Fig. 1). These data were analyzed using heat plots of the van der Waals corrected N^NO₂⋯ElR distance d′ (i.e.: d – the van der Waals radius of N and ElR) as a function of α. Structures where X = NH (730 hits) were omitted because NO₂⋯H–N hydrogen bonding interactions skewed the data to a feature at d′ ≈ 1.2 Å and α ≈ 5°(see Fig. S3†). The resulting dataset contained 5031 hits and the d′(α) heat plot is shown in Fig. 3.

Fig. 3 d′ (α) heat plot for data (N = 5301) obtained with query b in Fig. 1 where X ≠ NH (see also Fig. S3†). The color code represents percentages from low (blue) to high (red) as indicated in the inset figure. Contour lines were added as a guide to the eye.

The data are clearly not randomly distributed and there is a correlation between α and d′ in the region 0° ≥ α ≤ 70° and −0.6 ≥ d ≤ 0.6 with a significant amount of data involved in the van der Waals overlap, particularly near α ≈ 55°. A systematic evaluation of X and ElR is detailed in Fig. S4† and revealed mostly datasets that are too small for further analysis. Shown in Fig. 4 are the d′(α) heat plots for datasets that contained a sufficient amount of data: imides (a), diazenes (b) O/N methylenes (c), amides (d), acids and esters (e) and sulfonyls (f). For model compounds, geometry optimizations and subsequent AIM analysis were performed for a conformer where ElR is pointing towards (ElR → N^NO₂) or away from the nitro moiety (top in each figure in Fig. 4). Energy profiles as a function of the C–C–X–ElR torsion angle were also obtained (see Fig. S5†).

Fig. 4 d′ (α) heat plots for: a) C = NR (N = 121 within 121 CIFs), b) N = NR (N = 93 within 51 CIFs), c) CR₂OR and CR₂NR₂ (N = 302 within 239 CIFs), d) C(O)NR₂ (N = 122 within 91 CIFs), e) CO₂ (N = 847 within 538 CIFs) and f) SO₂ (N = 533 within 521 CIFs). For both CO₂ and SO₂, only the shortest N⋯O distance was used in the plot. The color code represents percentages from low (blue) to high (red) as indicated in the inset figures. The inset molecules are simple geometry optimized models (DFT/B3LYP-D3/def2-TZ2P) starting from a conformer where ElR is pointing towards (left) or away from (right) the nitro group. Energies are in kcal mol⁻¹ and the angles α are given in each case. The bond critical points (small red dots) are <0.018 a.u. in each case except the H-bonding interactions with the amide in (d) (0.027) and the carboxylic acid in (e) (0.042).

For imide-like structures (Fig. 4a), there is a tight grouping around [1.2;30] and virtually no N^NO₂⋯N van der Waals overlap is present. Computations of the model imides reveal that the N → N^NO₂ conformer is 3.6 kcal mol⁻¹ higher in energy than the conformer where ElR is pointing away from the nitro moiety. The observed energy minimum might well be due to weak H-bonding with the imide CH and/or a O^NO₂ → C = NH π–hole interaction. Similarly, most data in the dataset for diazenes (Fig. 4b) have ElR (N) pointing away from the nitro group (d′ ≈ 1 Å) and this conformer of a model diazene is indeed the most stable (1.3 kcal mol⁻¹). The feature around [−0.25;35] is indicative of compounds with an N → N^NO₂ interaction geometry. That such a feature is observed for diazenes and not for imides is ascribed to the much smaller energetic difference between the two conformers. It is also consistent with the energy profiles of a rotating C–C–X–ElR torsion angle, which revealed one clear minimum for the imide but another (smaller) minimum for the diazene (see Fig. S5†).

The dataset involving O/N methylenes (Fig. 4c) again has the majority of data in a conformer that cannot have a N → N^NO₂ interaction at [1.4;25]. Interestingly, a small feature is present at [−0.25;55], which – on manual inspection – turned out to be mostly amines. Indeed, model computations of methylamines show that the geometry congruent with a π–hole interaction is 1.3 kcal mol⁻¹ more stable. The reverse (also 1.3 kcal mol⁻¹) is the case for the methoxy analogue (not shown). This is in line with the energy profiles of C–C–C–ElR rotation (Fig. S5†) which shows one true minimum for ElR = O and two minima of the same magnitude for ElR = N.

The datasets involving amides (Fig. 4d) and –CO₂ moieties (Fig. 4e) are similar and display a clear d′(α) correlation with a large portion of van der Waals overlap (31% and 45%, respectively). In both cases, the most stable conformer has an O-atom pointing towards the nitro moiety. The energy difference between the conformers considered is negligible for the methylamide (0.21 kcal mol⁻¹) and significant for the carboxylic acid (2.1 kcal mol⁻¹). This is in line with the energy profiles of C–C–C–O rotation (Fig. S5†) revealing two minima of similar magnitude for the amide and one clear minimum for the carboxylic acid. It is noteworthy that in both cases the conformer with an intramolecular H-bonding interaction is the least stable. This is likely due to the stabilising effect of complementary N=O⋯C=O π–hole interactions.

Nearly all the data involving sulfonyls (Fig. 4f, 78%) are involved in the van der Waals overlap and grouped around [−0.25;55]. In agreement with this, calculations of a methylsulfonyl revealed only one clear minimum (see also Fig. S5†). Starting from a geometry where the methyl group is pointing toward the nitro moiety led to the same minimum. The small feature at [0.75;55] is caused by the N-atoms of sulfonamides, which are likely pointing away from NO₂ due to steric hindrance of the R-groups in –SO₂NR₂.

In summary, the AIM analysis never yielded a clear N^NO₂⋯N bcp. However, geometries congruent with intramolecular π–hole interactions involving the nitroarene are most stable when X-ElR is methylamine (−1.3 kcal mol⁻¹), methylamide (−0.2 kcal mol⁻¹), carboxylic acid (−2.1 kcal mol⁻¹) or a methylsulfonyl (only minimum). These stabilizations are rather small, yet are reflected in the CSD as represented by the d′(α) plots in Fig. 4.

Five bonds of separation

Shown in the left-hand side of Fig. 5 is the d′(α) plot obtained for query c in Fig. 1 (with n = 1) where structures containing metals were omitted; metals skewed the data by acting as a bridge (X) between ElR and a nitro aromatic compound (see Fig. S6† for details). The data are clearly distributed non-randomly and the feature at [2,10] was found to be due to structures with an o-NH substituent (detailed in Fig. S6†).

Fig. 5 Overview of data for nitro aromatics potentially interacting with an ElR atom five bonds away from the nitro functionality. Left: d′(α) heat plot generated using query c in Fig. 1 (with n = 1, excluding structures with X = a metal; N = 2736). Middle: Several nitro aromatics that were subjected to computational analysis by geometry optimization of a conformer where ElR is pointing as far away from N^NO₂ as possible and one in which ElR is pointing towards N^NO₂. Relative energies of ElR → N^NO₂ geometries are given in kcal mol⁻¹ (see also Fig. S6†). Right: AIM analysis of geometry optimized structures of 4 and 8. Calculations were done at the DFT/B3LYP-D3/def2-TZ2P level of theory.

The feature around [1.8,40] cannot involve structures with ElR → N^NO₂ interactions while the feature at [−0.25,35] clearly can. Manual inspection of all 321 CIFs with structures where −0.25 Å ≤ d′ ≥ −0.25 Å and 20° ≤ d′ ≥ 60° revealed a very broad range of structures, none of which was numerous enough for an individualized d′(α) plot. The structures around [−0.25,35] included most of the nitro aromatics 1–12 shown in the middle of Fig. 5. Structures 1–12 have similar groups to the structures that were evaluated for data with four bonds of separation (see Fig. 4). For each of these structures, two geometry optimizations were done: one for a conformer where ElR is pointing as far away from N^NO₂ as possible and one in which ElR is pointing towards N^NO₂ (such as schematically shown in the figure, see Fig. S7† for details). The relative energies of these ElR → N^NO₂ interaction geometries are shown in the figure (in kcal mol⁻¹).

Apparently, structures 1, 2, 7, 8 and 10–12 are most stable when the potentially interacting atom is pointing away from N^NO₂. This is most likely due to the minimization of steric hindrance (12 in particular) and/or the formation of intramolecular hydrogen bonding interactions (see also Fig. S7†). The large energy difference of 8.1 kcal mol⁻¹ for amide 8 can be rationalized by the formation of two intramolecular hydrogen bonding interactions that form six-membered rings. This is illustrated in the right-hand side of Fig. 5 (top) by means of an AIM analysis. This analysis shows two clear bcps; one between NO₂⋯HN (ρ = 0.040 a.u.) and one between C=O⋯HC (ρ = 0.020 a.u.).

For nitro aromatics 3–6 and 9, the geometry congruent with an O/N → N^NO₂ interaction is the most stable. That 4 is the most stable (−2.2 kcal mol⁻¹) can be rationalized by an intramolecular N⋯O π–hole interaction; indeed, an AIM analysis of 4, shown in the bottom right of Fig. 5, reveals a clear bcp between N^NO₂⋯O (ρ = 0.010 a.u.).

It is worth pointing out that the strain of bending the propyl chain in 12 from linearity towards the nitro moiety has an energy penalty of about 1.5 kcal mol⁻¹. Such a penalty is likely of similar magnitude in many of the other structures considered.²⁴ This in turn entails that, for example, the negligible stabilization computed for ether 3 (−0.12 kcal mol⁻¹) is actually about 1.5 kcal mol⁻¹; there is indeed a N^NO₂⋯O bcp found for 3 (ρ = 0.008 a.u.). Applying such a rationale to amine 5, which is already stabilized by −1.8 kcal mol⁻¹ and has a N⋯N bcp (ρ = 0.010 a.u.), suggests that the total amount of stabilization is about −3.3 kcal mol⁻¹. This is slightly smaller than that of the water dimer (−4.7 kcal mol⁻¹)²⁵ and the intermolecular adducts of nitrobenzene with dimethyl ether (−4.4 kcal mol⁻¹) and trimethylamine (−6.2 kcal mol⁻¹).^11a Such intermolecular adducts have to cope with an intrinsic translational entropic penalty that is often ignored in computations. Despite the entropy penalty, the N → NO₂ π–hole adduct between trimethylamine and nitro ethane (computed enthalpy of −5.7 kcal mol⁻¹) has been observed with rotational spectroscopy.²⁶ The counteracting effect of a positive translational entropy does not apply to the intramolecular π–hole interactions discussed here. Moreover, while the intramolecular π–hole interactions with nitro aromatics are weak, it is well known that weak interactions can be relevant, also in biological systems. For example: weak H–π interactions can be directional,²⁷ such as by directing the crystal packing of indolcarbazoles;²⁸ weak H-bonding interactions are present between water and the α-H of amino acid side chains;²⁹ weak S⋯π⁺ interactions can be relevant for bio-catalysis;³⁰ carbonyl–carbonyl π–hole interactions³¹ can direct protein folding;^4b weak C–H⋯π interactions with carbohydrates in protein pockets³² or artificial receptors.³³

In summary, there is ample evidence that π–hole interactions can stabilize conformers when the interacting atom is five bonds away for the N-atom of a nitro aromatic compound. The stabilization energy can be as large as −2.2 kcal mol⁻¹ calculated for 4. This might actually be higher when considering that bending towards the nitro moiety involves an energy penalty of about 1.5 kcal mol⁻¹ as calculated for 12.

Six bonds of separation

A search in the CSD for structure with six bonds between a nitro moiety and ElR (c in Fig. 1 with n = 2) resulted in merely 139 CIFs with structures too diverse to generate meaningful statistical plots. Manual inspection of these entries led to several structures with short N^NO₂⋯ElR distances. For two of these structures, QEPZAO and UVACAW, the experimental coordinates were truncated and a single point computation and subsequent AIM analysis were conducted as displayed in Fig. 6. In both instances, a N^NO₂⋯O bcp is present with the ester group. Interestingly, both optimized geometries are −1.1 kcal mol⁻¹ more stable than their conformational isomers where the nitro aromatic compound has been rotated by 180° (thus pointing ‘down’ in Fig. 6, not shown).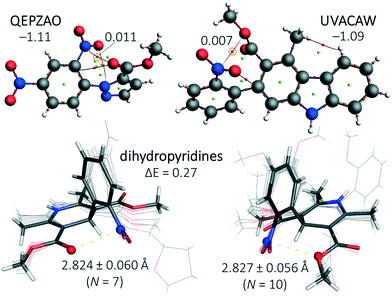

Fig. 6 Top: Truncated structures of QEPZAO (left) and UVACAW (right) and an accompanying AIM analysis. The energies shown indicate the stabilization of the structures shown versus a conformation where the nitro aromatic compound has been flipped along the xz plane (i.e., the nitro pointing ‘downwards’, not shown). Bottom: Structural overlays of nitro aromatic dihydropyridines found within the CSD that have a close contact between the nitro N-atom and the ester carbonyl O-atom (left, involving structures ASATOD, BELHIJ, BICCIZ, JENMOH, KIXQIU, QUPRUP and YARGON01) or the sp³ O-atom of an ester (right, involving structures BICCIZ01, BICCIZ02, BICCIZ03, FULPAD, JENMUN, JENMUN01, MALFEN, PAZCUP, SUZGEA and XITMAP). Both isomers differ by merely 0.3 kcal mol⁻¹ and an AIM analysis of their energy minima reveals a N^NO₂⋯O bcp with ρ = 0.01 a.u. (see Fig. S8† for details). All calculations were done at the DFT/B3LYP-D3/def2-TZ2P level of theory and relative energies are given in kcal mol⁻¹.

In addition, the CSD contained many dihydropyridine derivatives, including nifedipine (Adalat)¹³ and nisoldipine (Sular).¹⁴ Both are calcium channel blockers and approved by the U.S. Food and Drug Administration (FDA) to treat hypertension and angina.¹⁵ Shown in the bottom of Fig. 6 are structural overlays of two conformational isomers of nifedipine and very similar molecules where a nitro aromatic moiety is flanked by two esters.§ The nitro moiety is always in close proximity to one of the two O-atoms of an ester with short N^NO₂⋯O distances of (on average) 2.824 Å (with the carbonyl-O, bottom left in Fig. 6) or 2.827 Å (with an sp³ hybridized O, bottom right in Fig. 6). The energy difference between these two isomers is negligible (0.3 kcal mol⁻¹, see Fig. S8† for details). The conformations where both carbonyl O-atoms point towards or away from the nitro aromatic are, respectively, 3.0 kcal mol⁻¹ less and more stable than the structures shown in the bottom of Fig. 6 (see Fig. S8† for details). The most stable conformer is also found in the nifedipine ligand present within structure 6jp5,³⁴ an Oryctolagus cuniculus calcium channel membrane protein. The observed N^NO₂⋯O distance of 2.58 Å is 0.49 Å within the sum of the van der Waals radii of N (1.55) + O (1.52) = 3.07 Å.³⁵ Structures where an ElR atom and a nitro group were 7 bonds or more from one another were not scrutinized (using query c in Fig. 1 with n = 3, 4, 5 and so forth).

In summary, the CSD contains too few structures with short N^NO₂⋯ElR distances in structures with six or more bonds between N^NO₂ and ElR to perform a meaningful statistical evaluation. However, in several highlighted structures such as the drugs nifedipine and nisoldipine a stabilizing effect of an intramolecular π–hole interaction was encountered.

Summary and conclusion

No evidence was found for the stabilizing effect of N^NO₂⋯ElR interactions in nitro aromatic molecules when N^NO₂ and ElR are separated by three bonds. The d′(α) plots for such structures separated by four or five bonds clearly reflect a stabilizing effect, which was estimated by DFT to be as large as about 2–3 kcal mol⁻¹. Several structures were highlighted where N^NO₂⋯ElR interactions stabilize a conformer of structures where N^NO₂ and ElR are six bonds apart, including the drugs nifedipine and nisoldipine. It is thus concluded that intramolecular π–hole interactions can stabilize conformers by as much as 3 kcal mol⁻¹ when N^NO₂ and ElR are at least four bonds apart from one another. These conformer-directing interactions might find application in the fine-tuning of the energy minimum 3D structure of drugs or organo(metallic) catalysts.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

A. F. and A. F. thank the MINECO of Spain (project CTQ2017-85821-R, FEDER funds) for funding. We also thank the “Centre de Tecnologies de la Informació” (CTI) at the UIB for computational facilities. T. J. M. conducted the work with funds from the research program ‘VIDI’ with project number 723.015.006, which is financed by the Netherlands Organization for Scientific Research (NWO).

References

1. R. Nomura, J. Tabei and T. Masuda, J. Am. Chem. Soc., 2001, 123, 8430.
2. N. Chandramouli, Y. Ferrand, G. Lautrette, B. Kauffmann, C. D. Mackereth, M. Laguerre, D. Dubreuil and I. Huc, Nat. Chem., 2015, 7, 334.
3. (a) G. D. Rose and R. Wolfenden, Annu. Rev. Biophys. Biomol. Struct., 1993, 22, 381; (b) D. W. Bolen and G. D. Rose, Annu. Rev. Biochem., 2008, 77, 339.
4. (a) A. Choudhary, D. Gandla, G. R. Krow and R. T. Raines, J. Am. Chem. Soc., 2009, 131, 7244; (b) G. J. Bartlett, A. Choudhary, R. T. Raines and D. N. Woolfson, Nat. Chem. Biol., 2010, 6, 615; (c) R. W. Newberry, G. J. Bartlett, B. VanVeller, D. N. Woolfson and R. T. Raines, Protein Sci., 2014, 23, 284.
5. (a) A. R. Voth, F. A. Hays and P. S. Ho, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 6188; (b) E. Danelius, H. Andersson, P. Jarvoll, K. Lood, J. Grafenstein and M. Erdelyi, Biochemistry, 2017, 56, 3265; (c) M. R. Scholfield, M. C. Ford, A. C. C. Carlsson, H. Butta, R. A. Mehl and P. S. Ho, Biochemistry, 2017, 56, 2794.
6. (a) S. H. Gellman, G. P. Dado, G. B. Liang and B. R. Adams, J. Am. Chem. Soc., 1991, 113, 1164; (b) G. P. Dado and S. H. Gellman, J. Am. Chem. Soc., 1994, 116, 1054; (c) P. Gilli, V. Bertolasi, V. Ferretti and G. Gilli, J. Am. Chem. Soc., 2000, 122, 10405.
7. (a) J. S. Murray, P. Lane, T. Clark, K. E. Riley and P. Politzer, J. Mol. Model., 2012, 18, 541; (b) A. Bauza, T. J. Mooibroek and A. Frontera, ChemPhysChem, 2015, 16, 2496.
8. A. Bauza, A. Frontera and T. J. Mooibroek, Cryst. Growth Des., 2016, 16, 5520.
9. A. Bauza, A. Frontera and T. J. Mooibroek, Nat. Commun., 2017, 8, 14522.
10. T. J. Mooibroek, CrystEngComm, 2017, 19, 4485.
11. (a) A. Bauza, T. J. Mooibroek and A. Frontera, Chem. Commun., 2015, 51, 1491; (b) A. Bauza, A. V. Sharko, G. A. Senchyk, E. B. Rusanov, A. Frontera and K. V. Domasevitch, CrystEngComm, 2017, 19, 1933.
12. D. Olender, J. Zwawiak and L. Zaprutko, Pharmaceuticals, 2018, 11, 29.
13. P. A. Poole-Wilson, J. Lubsen, B. A. Kirwan, F. J. van Dalen, G. Wagener, N. Danchin, H. Just, K. A. A. Fox, S. J. Pocock, T. C. Clayton, M. Motro, J. D. Parker, M. G. Bourassa, A. M. Dart, P. Hildebrandt, A. Hjalmarson, J. A. Kragten, G. P. Molhoek, J. E. Otterstad, R. Seabra-Gomes, J. Soler-Soler, S. Weber and A. Investigators, Lancet, 2004, 364, 849.
14. (a) R. S. Kass, J. Pharmacol. Exp. Ther., 1982, 223, 446; (b) R. O. Estacio, B. W. Jeffers, W. R. Hiatt, S. L. Biggerstaff, N. Gifford and R. W. Schrier, N. Engl. J. Med., 1998, 338, 645.
15. W. J. Elliott and C. V. S. Ram, J. Clin. Hypertens., 2011, 13, 687.
16. B. Kuhn, P. Mohr and M. Stahl, J. Med. Chem., 2010, 53, 2601.
17. C. Adamo and V. Barone, J. Chem. Phys., 1999, 110, 6158.
18. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 19.
19. (a) F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297; (b) F. Weigend, Phys. Chem. Chem. Phys., 2006, 8, 1057.
20. G. te Velde, F. M. Bickelhaupt, E. J. Baerends, C. F. Guerra, S. J. A. van Gisbergen, J. G. Snijders and T. Ziegler, J. Comput. Chem., 2001, 22, 931.
21. (a) C. T. Lee, W. T. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785; (b) A. D. Becke, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 3098.
22. R. F. W. Bader, Acc. Chem. Res., 1985, 18, 9.
23. S. Benz, M. Macchione, Q. Verolet, J. Mareda, N. Sakai and S. Matile, J. Am. Chem. Soc., 2016, 138, 9093–9096.
24. (a) J. Skolnick and E. Helfand, J. Chem. Phys., 1980, 72, 5489; (b) A. Bauza, T. J. Mooibroek and A. Frontera, Phys. Chem. Chem. Phys., 2014, 16, 19192; (c) K. B. Wiberg and M. A. Murcko, J. Am. Chem. Soc., 1988, 110, 8029; (d) G. D. Smith and R. L. Jaffe, J. Phys. Chem., 1996, 100, 18718.
25. (a) P. Reinhardt and J. P. Piquemal, Int. J. Quantum Chem., 2009, 109, 3259–3267; (b) J. M. Andric, G. V. Janjic, D. B. Ninkovic and S. D. Zaric, Phys. Chem. Chem. Phys., 2012, 14, 10896–10898.
26. W. Li, L. Spada, N. Tasinato, S. Rampino, L. Evangelisti, A. Gualandi, P. G. Cozzi, S. Melandri, V. Barone and C. Puzzarini, Angew. Chem., Int. Ed., 2018, 57, 13853.
27. T. J. Mooibroek and P. Gamez, CrystEngComm, 2012, 14, 8462.
28. H. Jiang, P. Hu, J. Ye, A. Chaturvedi, K. K. Zhang, Y. X. Li, Y. Long, D. Fichou, C. Kloc and W. P. Hu, Angew. Chem., Int. Edit., 2018, 57, 8875–8880.
29. S. Scheiner, T. Kar and Y. L. Gu, J. Biol. Chem., 2001, 276, 9832.
30. K. E. Ranaghan, J. E. Hung, G. J. Bartlett, T. J. Mooibroek, J. N. Harvey, D. N. Woolfson, W. A. van der Donk and A. J. Mulholland, Chem. Sci., 2014, 5, 2191.
31. F. H. Allen, C. A. Baalham, J. P. M. Lommerse and P. R. Raithby, Acta Crystallogr., Sect. B: Struct. Sci., 1998, 54, 320–329.
32. (a) N. K. Vyas, M. N. Vyas and F. A. Quiocho, Science, 1988, 242, 1290; (b) K. L. Hudson, G. J. Bartlett, R. C. Diehl, J. Agirre, T. Gallagher, L. L. Kiessling and D. N. Woolfson, J. Am. Chem. Soc., 2015, 137, 15152.
33. (a) T. J. Mooibroek, M. P. Crump and A. P. Davis, Org. Biomol. Chem., 2016, 14, 1930; (b) P. Rios, T. J. Mooibroek, T. S. Carter, C. Williams, M. R. Wilson, M. P. Crump and A. P. Davis, Chem. Sci., 2017, 8, 4056; (c) T. S. Carter, T. J. Mooibroek, P. F. N. Stewart, M. P. Crump, M. C. Galan and A. P. Davis, Angew. Chem., Int. Ed., 2016, 55, 9311; (d) T. J. Mooibroek, J. M. Casas-Solvas, R. L. Harniman, C. Renney, T. S. Carter, M. P. Crump and A. P. Davis, Nat. Chem., 2016, 8, 69–74; (e) P. Rios, T. S. Carter, T. J. Mooibroek, M. P. Crump, M. Lisbjerg, M. Pittelkow, N. T. Supekar, G. J. Boons and A. P. Davis, Angew. Chem., Int. Ed., 2016, 55, 3387–3392.
34. H. M. Berman, J. Westbrook, Z. Feng, G. Gilliland, T. N. Bhat, H. Weissig, I. N. Shindyalov and P. E. Bourne, Nucleic Acids Res., 2000, 28, 235.
35. A. Bondi, J. Phys. Chem., 1964, 68, 441.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c9ce01015g

‡ The Reaxys® database lists 156,991 nitro aromatic structures with available pharmacological data (April 4th 2019).

§ Besides the structures stacked in Fig. 6, there were several simple and good quality structures of dihydropyridines where one of the esters was replaced by an H-atom (CIZQAE), an aldehyde (ECUYIL, COSCOF, XAWCAB), or a nitrile (FIJFAF), or where both esters were mutated to amides (SEMKUQ), a ketone and an amine (LOHPIH), a ketone (TELNUT) or a nitrile (DAKBAS and RIJVAH). In half of these structures, a contact distance was found. In addition to dihydropyridine derivatives, there were 12 analogues with a pyran ring (BEQYIF, IROZIY, LERZEP, MEZXOE, MIYJUA, NODXEK, QIMPEK, SAKXIO, UXUSOX, VAQHOL, VAQHUR and ZAKWIU), one with a cyclohexadiene ring (IZOMUF) and one structure where the dihydropyridine was coordinated to Cu (BEFVIS, and thus formally negatively charged). In half of these structures, a contact distance was found.

---